Neuromechanical simulation
- Neuroscience Institute, Georgia State University, Atlanta, GA, USA
The importance of the interaction between the body and the brain for the control of behavior has been recognized in recent years with the advent of neuromechanics, a field in which the coupling between neural and biomechanical processes is an explicit focus. A major tool used in neuromechanics is simulation, which connects computational models of neural circuits to models of an animal’s body situated in a virtual physical world. This connection closes the feedback loop that links the brain, the body, and the world through sensory stimuli, muscle contractions, and body movement. Neuromechanical simulations enable investigators to explore the dynamical relationships between the brain, the body, and the world in ways that are difficult or impossible through experiment alone. Studies in a variety of animals have permitted the analysis of extremely complex and dynamic neuromechanical systems, they have demonstrated that the nervous system functions synergistically with the mechanical properties of the body, they have examined hypotheses that are difficult to test experimentally, and they have explored the role of sensory feedback in controlling complex mechanical systems with many degrees of freedom. Each of these studies confronts a common set of questions: (i) how to abstract key features of the body, the world and the CNS in a useful model, (ii) how to ground model parameters in experimental reality, (iii) how to optimize the model and identify points of sensitivity and insensitivity, and (iv) how to share neuromechanical models for examination, testing, and extension by others.
Introduction
The nervous systems of animals evolved largely to guide and control their movements. This is apparent from observing animals that move and those, like barnacles and sea squirts, that settle, stop moving about and lose their brains (Wolpert, 2009). The guidance and control of oriented movement depends on multiple parallel streams of sensory input which the movement itself changes from moment to moment. The result is a closed feedback loop that links the sensory world to the nervous system, and the nervous system to the generation of movements that change the pattern of sensory input.
In recent years, the importance of the interaction of the body with the brain and the world has been recognized with the advent of neuromechanics, a field in which the coupling between neural and biomechanical processes is an explicit focus (Shadmehr and Wise, 2005; Chiel et al., 2009). For a variety of animals, the neural substrates of a behavior, the kinematics, and dynamics of the behavior itself, and the biomechanical mechanisms that mediate their connection have been studied in a coordinated fashion. The mechanisms of the control of flight by fruit flies (Dickson et al., 2006), of the feeding behavior of Aplysia (Novakovic et al., 2006; Proekt et al., 2008), and of locomotion by stick insects (Buschges et al., 2008), cockroaches (Ritzmann and Buschges, 2007), and lobsters (Ayers, 2004) are a few prominent examples from among invertebrate animals studied. Swimming in lampreys (Grillner et al., 2008), walking in cats (Pearson, 2008), postural control in cats and humans (Ting and McKay, 2007), and reaching and pointing in primates (Shadmehr and Wise, 2005), are correspondingly prominent examples from vertebrates.
In all of these studies, a major challenge has been the technical limitations of our ability to record central nervous activity in freely behaving animals. Experimental studies of movement and behavior in unrestrained animals necessarily can include only minimal arrangements for recording simultaneous neural responses; similarly, studies of neural circuitry are usually performed on anesthetized, restrained, and dissected preparations that cannot move. In these latter preparations, recordings of fictive motor output can give some indication of the expected pattern of muscle contraction, but this can be misleading. Depending on their work loop, muscles can act to move limbs or brake the movement of limbs; they can also transfer force along a limb or act as springs of varying stiffness (Dickinson et al., 2000). Moreover, these functions can vary dynamically during the course of a behavioral cycle – changes that are only apparent in the behaving animal. While these behavioral and neurophysiological experiments are critically important for understanding the how individual parts of the system work, they cannot tell us how the entire system – the nervous system, the sensory organs, and musculo-skeleton system, and the body’s interaction with the world – functions dynamically to produce the behavior of a freely moving animal.
This challenge has been addressed by several investigators through neuromechanical simulation, which links a computational model of the animal’s neural circuits to a model of its body to study how the nervous system and body interact to achieve dynamic control of behavior (Ekeberg, 1993; Loeb et al., 1999; Pearson et al., 2006). Neuromechanical simulation helps provide an integrated understanding of truly complex systems (Dickson et al., 2006). It allows investigators to ask whether the current understanding of a neural circuit is sufficient to account for the dynamic control of behavior (Ivashko et al., 2003; Ekeberg et al., 2004; Cofer et al., 2010b). It can help identify synergies between patterns of motor command and biomechanical mechanisms (Chiel et al., 2009), and it can highlight the importance of sensory feedback in guiding behavioral performance (Ekeberg and Grillner, 1999; Ivashko et al., 2003; Yakovenko et al., 2004; Ekeberg and Pearson, 2005).
Each of these studies also confronts a common set of procedural questions: How to create simplified descriptions of the physical world, the body, and the neural network that capture the key features of all three? How to ground model parameters in experimental reality? How to explore a vast and heterogeneous parameter space to optimize the model and identify points of sensitivity and insensitivity? How to share neuromechanical models to permit them to be examined, tested, modified, and extended by others?
The purpose of this review is to acquaint neuroethologists with the role that simulation plays in neuromechanics, and how it has helped address questions about functional connections between the nervous system, sensory and musculo-skeletal systems, and the body’s movement in the physical world. To do this, I will use three recently described sets of neuromechanical models on fly flight, locust jump, and cat walking to focus first on how neuromechanical simulations can help us to understand very complex systems, then on how they help us determine whether our understanding of the mechanisms is sufficient to account for the animal’s behavior, and finally on the importance of sensory feedback for adaptive motor performance. The issues of synergies between neural and biomechanical mechanisms mentioned above have recently been explored in an excellent review (Chiel et al., 2009), and so will not be addressed here. Individual answers to the common procedural questions will emerge from the account of each study. The final question, how to share neuromechanical models, is critical for the development of neuromechanics and will be addressed at the end.
Understanding Complex Systems
The biomechanics of multi-joint animal movement is often surprisingly complex (McMahon, 1984), and the mechanisms of neuronal control of that movement is even more so. Experimental analysis of such complex systems necessarily occurs piecemeal, as particular mechanisms or functions are isolated experimentally. These include the kinematics (i.e., the pattern of movement) and dynamics (the physical forces at play in the movement) of the movement, the patterns of motor command and sensory feedback that occur during the movement, and the circuit and synaptic organization of the part of the nervous system that controls the movement. Once the several mechanisms that compose the system have been described, the remaining challenge is to integrate abstract descriptions of each of them into a functioning model that adequately characterizes the system’s performance under closed-loop, hands-off conditions. This can only be done through simulation, where changes in all the system’s parameters can be observed as they unfold in simulated time, and the sensitivity of the overall system’s performance to each parameter can be assessed.
As anyone who has tried to catch a fly knows, the aerodynamic control of the body during flight is among the most impressive behaviors that animals perform; it is also among the most challenging for experimenters to investigate. The flight behavior of flies is driven by a flight motor in which the thorax behaves like a mechanically resonant box (e.g., a drum) that is activated by asynchronous excitation of the dorso-ventral and dorsal-longitudinal muscles that span the height and length of the box, respectively (Dickinson and Tu, 1997). The wings are attached laterally and so vibrate up and down with it. However, the control of flight depends on the pitch of the wings during each phase of their stroke, and on the movements of the head and thorax relative to each other and the wings. These respond to a variety of proprioceptive and exteroceptive sensory inputs that provide signals to initiate, maintain, modulate and stop flight as part of a dynamic, closed-loop control system.
Dickinson and his colleagues have studied flight in the fruit fly, Drosophila, and used a variety of techniques to describe the kinematics of take-off and flight (Card and Dickinson, 2008a,b; Fontaine et al., 2009), the role of vision and mechanosensation in guidance Sherman and Dickinson, 2004; Budick et al., 2007), the biomechanics of flight (Balint and Dickinson, 2004), muscle physiology and mechanics (Gordon and Dickinson, 2006), and aerodynamics (Fry et al., 2005; Lentink and Dickinson, 2009). This experimental work indicates that the fly’s nervous system combines a vast amount of sensory information from different modalities into a motor code that controls the activity of a relatively small number of steering motor neurons (MNs), which in turn generate rather subtle changes in the pattern of wing motion (Dickinson, 2006).
These results enabled Dickinson’s group to build an integrated model of flight control in the fly that contains five components: an articulated body, a model of aerodynamic forces and moments, a model of visual and mechanosensory inputs, a control structure, and a model of the environment that interacts with the fly (Figure 1) (Dickson et al., 2006). The body model includes a pair of wings connected to a rigid body by a pair of ball joints. The wings and body have dimensions and shapes which approximate those of the fly, with estimates of the mass, center of mass and inertia tensor for each. Wind forces and moments on the wings and body are calculated using a quasi-steady-state aerodynamics model based on force and moment coefficients measured in a scaled-up physical model of the flying fly. The environment model provides visual and mechanosensory inputs to the eyes and halteres, respectively, and both steady forces (i.e., wind streams) and perturbations (i.e., wind gusts) to the aerodynamic model. A computer model of 3-D terrain and visual objects provides input to the visual system; the graphical presentation is continuously updated to reflect the movement of the fly. The visual processing model begins with the time- and spatial filtering that occurs in the retinular cells of each ommatidium. Retinular cell outputs provide inputs to Hassenstein–Reichardt (H–R) elementary horizontal motion detectors. Wide-field horizontal motion detectors collect the summed inputs of 500 H–R motion detectors and respond to rotation of the visual world as the fly turns and give a null response during linear flight. Because little is known of the neural circuitry that underlies flight control in the fly, the control model is algorithmic. It consists of a set of rules that determine how the outputs of the sensory system alter wing kinematics through changes in a set of wing deformation modes. These changes then create forces to produce body attitude changes, including pitch, yaw, and roll, and the overall aerodynamic force on the model.
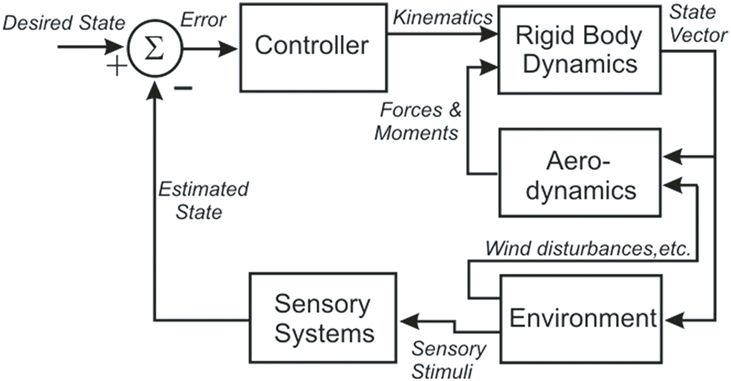
Figure 1. A block diagram illustrating the organization of the fly flight model, showing the five distinct models (Controller, Rigid Body Dynamics, Aerodynamics, Environment, and Sensory Systems) and the signals that pass between them (in italics).
The model has been tested in a closed-loop, visually based flight within a virtual tunnel, and found “to fly up the tunnel while successfully avoiding the walls.” The authors emphasize that this is more a proof of concept than a biologically accurate representation, but as such it provides a strong foundation for the development of a more accurate and useful model. The fly model demonstrates that the neuromechanics of fly flight are understandable despite the tremendous complexity of the system and its environmental interactions. Perhaps most important, the model provides a means of addressing hypotheses about the flight control system that would be practically impossible to test via direct experimentation. Finally, it specifies what the neural control structures must do to control flight, and so provides a functional template that can guide experimental analysis of the underlying neural circuits.
Sufficiency of Our Current Understanding
Our understanding of the neural control of animal behavior often depends on how we imagine the neural activity patterns recorded in a stationary, dissected preparation apply to the freely behaving animal. This issue was particularly salient in efforts to understand the neural control of the locust jump. Recordings from leg nerves and muscles made during preparation for a jump presented an ambiguous picture. To resolve the issue, attention was switched to a similar behavior, kicking, which could be evoked by locusts held upside down while intracellular recordings were made from elements of the thoracic ganglia. These recordings revealed that both the flexor and extensor motorneurons of the corresponding muscles that span the femoral-tibial joint of the back legs were co-active before the kick (Heitler, 1974). Aided by a large mechanical advantage, the flexor muscle produced sufficient tension to hold the leg in a flexed position even as the extensor muscle contracted to produce nearly 15 times greater force. The kick was triggered when the flexors were inhibited, removing opposition to a rapid extensor contraction (Heitler and Braunig, 1988) that produced the kick (Burrows and Morris, 2001).
Although the similarities between the kick and the jump made it likely that the same motor program was used for both (Heitler and Burrows, 1977a), differences between the two behaviors raised the possibility that their motor programs were different. The kick is unloaded, whereas the thrust of the legs has to overcome the inertia and gravity of the animal’s body to produce the jump. As a result, the kick takes only a few milliseconds to complete, whereas the locust takes about 25 ms to leave the ground during the jump.
To determine whether the kick motor program could also produce the jump, Cofer et al. (2010a,b) built a neuromechanical model of a locust using the simulator program AnimatLab1. The simulated locust body was created from an anatomically accurate 3-D graphical mesh obtained commercially. The body was divided into separate body and limb segments that were then re-connected with hinge joints. Hill-type muscle models represented the extensor and flexor muscles of the leg; model parameters were set to experimentally determined values (Cofer et al., 2010b).
A particular challenge was to capture the biomechanics of the femoral-tibial joint, where the femur is linked to the tibia through a piece of flexible cuticle called the semi-lunar process (SLP). When the leg is flexed and the flexor and extensor muscles co-contract before a jump, half the energy of the extensor muscle is used to bend the SLP like an archery bow. That stored energy is then released with the energy stored in the extensor tension to power the jump. As the SLP unbends, the hinge with the tibia is accelerated distally as the tibia rotates around it to extend the leg. In the simulation, the SLP was represented by a small mass attached to the femur by a spring; the SLP mass was then attached to the tibia by a hinge joint (Cofer et al., 2010a,b). During simulated co-contraction of flexor and extensor muscles in the flexed leg, the SLP mass and attached tibia were pulled proximally by the model extensor muscle and the spring was stretched. The amplitude and direction of the force produced by bending the SLP was represented by the tension and direction of the stretched spring. When a jump was triggered, the tension in the SLP spring accelerated both the SLP mass and the tibia distally, while the extensor muscle pulled the proximal end of the tibia forward. The combined torques produced by the SLP spring and the extensor muscle at what is effectively a doubly hinged joint accelerated tibial extension, much like the rotations of the arm and hand of a baseball pitcher accelerates a pitched baseball.
The model neural circuit was laid out according to the published descriptions from the in vitro studies, with integrate-and-fire model MNs attached to the muscles through conductance-mediated neuromuscular junctions (Figure 2A, Cofer et al., 2010b). As the neuronal sources that drive both the flexor and extensor MNs are still unidentified, the model MNs were driven by appropriate stimuli to reproduce the patterns of activity recorded during the kick experiments (Figure 2B, Burrows and Morris, 2001). Leg extension was triggered by activation of a pair of inhibitory neurons, the flexor inhibitor MN that inhibits the flexor muscle, and the M cell, which inhibits the flexor MNs (Heitler and Burrows, 1977b; Gynther and Pearson, 1989).
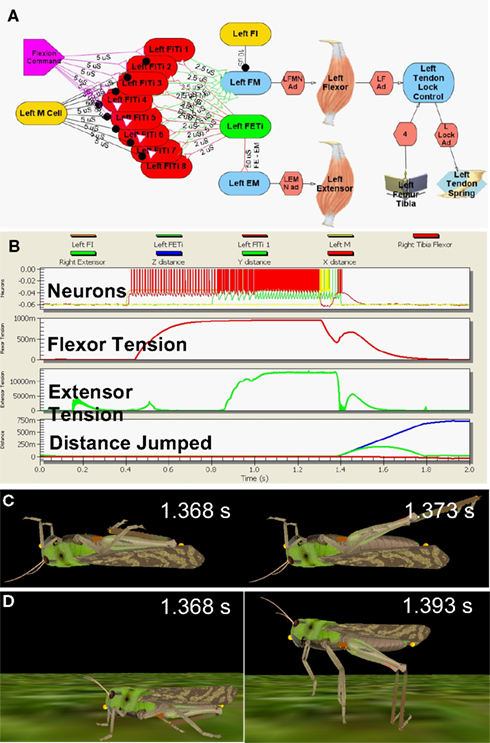
Figure 2. Simulated locust kick and jump. (A) Neural circuit, with flexor (red) and extensor (green) motor neurons, inhibitory (gold) neurons, flexor command (lavender) neuron, the flexor and extensor muscles, and the tendon lock mechanism that prevents premature extension. (B) Jump motor program. Top: flexor (red), extensor (green), and inhibitory motor neurons (gold); 2nd: Flexor muscle tension; 3rd: Extensor muscle tension; Bottom: longitudinal (blue) and vertical (green) distance moved. (C) The kick immediately before (left) and 5 ms later (right). (D) The jump immediately before (left) and 25 ms later (right) as the feet leave the ground. Adapted from Cofer et al., 2010b.
The motor program was activated first with the model locust upside down, where it could produce a kick (Figure 2C), and then right side up, where it could jump (Figure 2D; Cofer et al., 2010b). The motor program began with an early tonic command to the set of flexor MNs that was followed by activation of the extensor MN to produce co-contraction of the flexor and extensor muscles. An excitatory synapse between the extensor and flexor MNs (Figure 2A) increased the excitation of the flexor MNs, and tension rose to nearly 1 N in the flexor muscle and 14 N in the extensor muscle (Figure 2B). A burst of activity in the M cell and flexor inhibitor MN led to a drop in flexor muscle tension that freed the tibia to extend under the force of both the extensor muscle and the SLP. The kick was over in 5 ms, while the animal took 25 ms to leave the ground after the start of the jump. By various measures, including the height, distance, and duration of the jump, the duration of the jump impulse, and the peak jump velocity, acceleration and power, the simulated jump matched experimentally determined values (Bennet-Clark, 1975; Heitler and Burrows, 1977a; Burrows and Morris, 2001; Cofer et al., 2010b). Similarly, the simulated kick velocity and duration also matched the experimental measures of the kick. Cofer et al. (2010b) concluded that the simulation captured the main features of both the kick and the jump, and that the same motor program could readily produce both behaviors.
In addition, the simulation of the SLP mechanism showed that it has opposing effects before and during the jump. Before the jump it helps maintain leg flexion against the increasing extensor tension. As the jump begins, it contributes strongly to leg extension to power the jump. This switch occurs as the leg begins to extend, when rotation of the femoral-tibial joint causes the SLP force vector to pass through the joint and promote leg extension. The SLP then effectively doubles the power of the jump, enabling the locust to jump twice as far as it could without the SLP (Cofer et al., 2010b).
The Effect of Sensory Feedback in the Closed-Loop
Ever since the seminal work of Sherrington (1910) and Brown (1911), the relationship between centrally generated rhythmic activity and proprioceptive feedback in the generation of motor patterns has been the subject of lively research and debate (Rossignol et al., 2006; Windhorst, 2007; Jankowska, 2008; Kiehn et al., 2008; Pearson, 2008). Neuromechanical simulation has begun to play an important role in this debate (Frigon and Rossignol, 2006; Pearson et al., 2006). Here I will briefly discuss four studies that focused on the locomotor control of the cat hind limbs (Figure 3). The first asked whether known circuitry and common assumptions about the control of walking can account for the basic patterns of locomotion (Ivashko et al., 2003). The second addressed the issue raised by Brown and Sherrington to ask about the relative contributions of proprioceptive feedback and central pattern generation to stable walking (Yakovenko et al., 2004). The third eliminated the CPG to ask which of two different proprioceptive signals can promote stable stance-to-swing transitions (Ekeberg and Pearson, 2005), while the fourth showed how these proprioceptive signals can tune the CPG to rhythms that are appropriate for the environmental and kinematic context in which the animal is walking (Prochazka and Yakovenko, 2007).
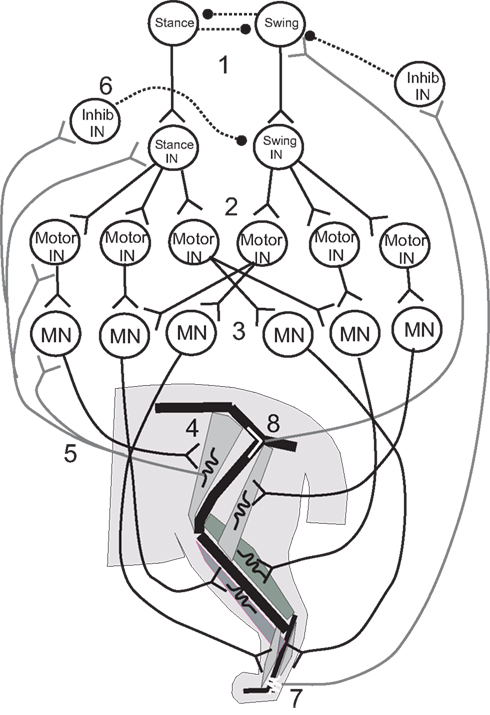
Figure 3. Illustrative diagram of the neuromechanical system of the cat hind leg; details differ from those presented in the four papers reviewed. 1. Swing/stance CPG. 2. Stance and Swing INs excite Motor INs. 3. Motor INs excite overlapping pools of Motor Neurons. 4. Motor Neurons excite leg muscles. 5, 6. Muscle spindle Ia and II afferents provide excitatory feedback to Motor Neurons, Motor INs, and Stance/Swing INs, and cross inhibition of antagonists. 7, 8. Ankle extensor afferents inhibit and hip extensor afferents excite Swing CPG elements to promote stance–swing transition.
Ivashko et al. (2003) wished to determine whether realistic models of spinal circuits, muscles, and limb biomechanics could interact to account for the major features of locomotion in the cat, including the kinematics, EMG patterns and ground reaction forces. The cat hind limbs were each modeled as a set of three rigid segments coupled by frictionless joints and linked to a common segment that represented the pelvis and trunk. The anterior end of the trunk segment was maintained at a constant level from the ground. Muscles were represented by a Hill-type biomechanical model, and a single compartment Hodgkin–Huxley-like model represented the neurons. The movement of each leg was produced by the contractions of nine muscles that spanned either one or two joints (Figure 3). Local control of each leg was governed by a circuit consisting of an alpha MN, a Renshaw inhibitory interneuron (IN), and INs that responded to Ia and Ib-type signals from the muscles. This circuit was in turn controlled by two layers of central pattern generator (CPG) INs: “principal” CPG INs that produced each phase of the movement and “switching” CPG INs that produced phase transitions during the movement. Together these CPGs excited alpha MNs and excited or inhibited the Ia and Ib INs to excite or inhibit agonist and antagonist MNs and inhibit unwanted reafference according to the phase of the rhythm. The organization of the CPG circuitry was based on the CPG circuitry that controls breathing in the medulla (Ivashko et al., 2003). The model was able to account for most features of the locomotor pattern, but differed from experimental recordings in the activation pattern of some muscles and in the ground reaction forces produced. Despite these differences, the Ivashko et al., model demonstrated that the interaction of a CPG network with proprioceptive feedback could produce stable walking rhythms that closely approximated those of the cat.
Proprioceptive feedback had been found to contribute up to 30% of the extensor muscle activation in the stance phase of the step cycle (Prochazka et al., 2002), which raised the question of how proprioceptive inputs contributed to stable walking. Yakovenko et al. (2004) used a similar model to address this question. Spindle and tendon organ models provided Ia and Ib responses related to the length and force developed by the muscles, respectively (Figure 3, #5,7); the responses were delayed by 35 ms before contributing to the activation of the alpha MNs to reflect the recorded delay of up to 40 ms. The Ia and Ib afferents each contributed 15% of the total activation of the alpha MN activity, with the CPG providing the remaining 70%. Simulations showed that without proprioceptive feedback, the CPGs could produce a stable gait over a broad range of muscle activation levels. When CPG activation was reduced to levels that could not support stable walking alone, proprioceptive feedback provided the needed stability. At higher levels of CPG activation, proprioceptive feedback improved stability somewhat and caused the walking gait to become more erect and vigorous.
In these last simulations, one role of sensory feedback was to excite resistance reflexes that opposed gravity (Figure 3, #5, 6). In addition, transitions between the stance and swing phases were known to depend on sensory feedback (Figure 3, #7, 8), and so the model was used to explore the effect of rule-based transitions on locomotor stability. Such rules use the phase (stance or swing) of the limb movement and proprioceptive sensory information that describes its position to determine whether the conditions are met for a transition between states. The rule for determining the stance-to-swing transition was “IF stance AND hip is extended AND leg is unloaded, THEN swing”; a similar rule determined the swing-to-stance transition. These rules cut short the motor activation pattern for a given state if the criteria for transition were met, effectively resetting the rhythm at each half cycle. Use of the rules extended the range of stable cadences and locomotor velocities obtained with a fixed CPG frequency and set of swing and stance muscle activation patterns by enabling the biomechanical feedback to determine when the phase transitions would occur.
The proprioceptive contributions to the IF-THEN rules that governed locomotor phase transitions were examined more closely by Ekeberg and Pearson (2005) in a three-dimensional model of the cat hind limbs. Hearkening back to Sherrington (1910), they studied which proprioceptive feedback signals could signal transitions between walking phases according to these rules and produce stable locomotion in the absence of a CPG. Experiments had identified hip extension (Figure 3, #8) and unloading ankle extensors (Figure 3, #7) as two factors that were important for timing the transition from the stance phase of stepping to the swing phase (Donelan and Pearson, 2004; McVea et al., 2005). Ekeberg and Pearson used their model to determine how either factor affected the stepping pattern when used alone or together to govern the transition. The stance-to-swing transition occurred when the force in the ankle extensor decreased sufficiently and/or the hip joint was sufficiently extended; muscles were then excited simultaneously to lift the foot off the ground and begin the swing phase. The simulations showed that transitions promoted by the two signals separately had different effects on stability. When liftoff depended on a sufficient drop in ankle extension force (the “unloading rule”), alternating stepping of the two legs was preserved in the face of a perturbation of either leg. A reduction in ankle extension force occurred as the load shifted to the opposite leg, so that perturbations of either leg may affect when the transition occurred, but not the relationship between the two legs. However, perturbations of one leg changed the timing away from alternate stepping when the hip extension rule was used alone, and this change decreased the locomotor stability. These simulations demonstrated the importance of mechanical linkages between legs for maintaining stability during locomotor state transitions, and how proprioceptive triggers for those transitions might affect that stability.
Although these last two studies showed that CPGs and proprioception-dependent phase switching could each produce stable locomotion, it was apparent that together they could produce stable walking over a larger range of gaits and contexts. However, it was unclear how they would interact to produce the locomotor pattern adopted by an animal walking in a particular context. That pattern is characterized by a pair of “phase/duration plots”, in which the duration of each phase, stance or swing, is plotted against step duration, and a bout of locomotion follows a pair of operating points along those curves. In intact animals, the stance phase/duration plot is higher and steeper (more “dominant”) than the swing phase plot. In “fictive walking” preparations, where the proprioceptive feedback is eliminated, either stance or swing are dominant in a given preparation. These experimental results suggested that proprioceptive reafference helps to bias the system towards the stance phase during normal walking. Prochazka and Yakovenko (2007) examined this with their neuromechanical cat model, and found that the stance phase was always dominant in walking simulations where proprioceptive feedback helped time transitions between phases. This result indicates that the kinematics of walking and the sensory feedback it generates normally help bias the system in favor of the stance phase. Moreover, the feedback may also help adjust the CPG rhythm to match the constraints imposed on the walking kinematics by the body and environment. For example, if the walking surface is slippery, the leg may move backward and finish stance before the stance portion of the CPG cycle is done. Sensory feedback from the extended leg would terminate the stance phase early on each cycle until the CPG had adjusted by moving the operating point along the phase/duration curve to shorter step durations. They suggested that walking could be made stable over a wide range of CPG frequencies if the central drive adjusted the operating points on the curves to match the constraints placed by the terrain and sensory feedback on state transitions.
These simulation studies of cat walking emphasize the importance of proprioceptive feedback for the neural control of movement, particularly in uncertain environments, where feedback during each step is needed for stable, coordinated movement. While CPGs provide the basic pattern of motor activation, proprioceptive feedback helps maintain posture, increases locomotor stability, and helps time state transitions in the face of immediate biomechanical demands.
While these are clear accomplishments, they are just the beginning. For example, cats can vary their posture during walking, to adopt a high, erect posture when facing an opponent, and a low posture when stalking a prey. The coordination between postural states and circuits and locomotor states is largely undescribed. The memory of the location of an object in the path of a hind leg can guide a stepping motion over it (McVea and Pearson, 2006); this suggests that locomotor programs result from motor plans that predict the consequences of movement and are continually updated based on recent experience, perceptions of the terrain, and the intentions of the animal.
The set of neuromechanical simulations reviewed here make clear that the neural control of movement cannot be understood outside of the neuromechanical context, and they show how this complexity can be addressed. Indeed, it is hard to contemplate approaches to the future questions asked above without neuromechanical simulation as an essential tool. Neuromechanical simulation enables descriptions of the body parts and their relationships to each other and the environment to be assembled into a model. The model can be challenged first to replicate the experiments that provided the data on which it is based, and then to simulate neural and behavioral interactions that cannot be studied experimentally. Simulations can help determine whether the current understanding of those interactions is sufficient to account for the animal’s behavior, identify parameters to which the system is sensitive and insensitive, and reveal the mechanisms behind emergent properties of the system. Although everyone works to build successful models, it is likely that neuromechanical models make their most valuable contribution when they fail, for it is then that gaps in our understanding are revealed that must be spanned by additional experiments or additional thought.
Sharing Neuromechanical Models
The strength of experimental science is that any finding can be tested, modified, or extended by any properly trained and equipped scientist because the subjects of study are available to all. This is not the case with most neuromechanical models, which are developed to run on custom software that is not readily used by other investigators. This difficulty in sharing is arguably the single most important impediment to the widespread use of neuromechanical simulation by the neuroscience community (Pearson et al., 2006). The challenge of learning to use a single-purpose simulator to test, modify, and extend another investigator’s model is likely to be too great even for those whose research is directly affected by the model’s results. In addition, the challenge of creating both a neuromechanical model and a simulator on which to run it makes contributions to the field difficult for all but those with a background in programming and numerical solving techniques.
The problem can be addressed through the development of a general-purpose neuromechanical simulator, much like NEURON (Hines and Carnevale, 2001) and GENESIS (Bower and Beeman, 2007) provide for neuronal simulations and OPENSIM (Delp et al., 2007) provides for biomechanical simulations. One solution is provided by AnimatLab1, a free, open-source neuromechanical simulator for any skeletal animal (Cofer et al., 2010a). AnimatLab has been used to simulate locust jumping (described above) (Cofer et al., 2010b), crayfish walking (Rinehart and Belanger, 2009), cat paw shaking (Klishko et al., 2008), and human arm flexion (Cofer et al., 2010a). To my knowledge, AnimatLab is presently unique in its ability to simulate a wide variety of neuromechanical systems, and so could become a common platform where models are built, tested, shared, and extended. Regardless of whether it or some other neuromechanical simulator becomes the common tool of choice, some such means for sharing, testing, modifying, and extending neuromechanical models must be adopted by the research community to achieve the rapid development that the field of neuromechanics deserves.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgment
I would like to thank M.H. Dickinson for very helpful comments on this paper. This work was supported by NSF research grant 0641326.
Footnote
References
Balint, C. N., and Dickinson, M. H. (2004). Neuromuscular control of aerodynamic forces and moments in the blowfly, Calliphora vicina. J. Exp. Biol. 207, 3813–3838.
Bennet-Clark, H. C. (1975). The energetics of the jump of the locust Schistocerca gregaria. J. Exp. Biol. 63, 53–83.
Bower, J. M., and Beeman, D. (2007). Constructing realistic neural simulations with GENESIS. Methods Mol. Biol. 401, 103–125.
Brown, T. G. (1911). The intrinsic factors in the act of progression in the mammal. Proc. R. Soc. Lond. B Biol. Sci. 84, 308–319.
Budick, S. A., Reiser, M. B., and Dickinson, M. H. (2007). The role of visual and mechanosensory cues in structuring forward flight in Drosophila melanogaster. J. Exp. Biol. 210, 4092–4103.
Burrows, M., and Morris, G. (2001). The kinematics and neural control of high-speed kicking movements in the locust. J. Exp. Biol. 204, 3471–3481.
Buschges, A., Akay, T., Gabriel, J. P., and Schmidt, J. (2008). Organizing network action for locomotion: insights from studying insect walking. Brain Res. Rev. 57, 162–171.
Card, G., and Dickinson, M. H. (2008a). Performance trade-offs in the flight initiation of Drosophila. J. Exp. Biol. 221, 341–353.
Card, G., and Dickinson, M. H. (2008b). Visually mediated motor planning in the escape response of Drosophila. Curr. Biol. 18, 1–8.
Chiel, H. J., Ting, L. H., Ekeberg, O., and Hartmann, M. J. (2009). The brain in its body: motor control and sensing in a biomechanical context. J. Neurosci. 29, 12807–12814.
Cofer, D., Cymbalyuk, G., Reid, J., Zhu, Y., Heitler, W. J., and Edwards, D. H. (2010a). AnimatLab: a 3D graphics environment for neuromechanical simulations. J. Neurosci. Methods 187, 280–288.
Cofer, D. W., Cymbalyuk, G., Heitler, W. J., and Edwards, D. H. (2010b). Neuromechanical simulation of the locust jump. J. Exp. Biol. 213, 1060–1068.
Delp, S. L., Anderson, F. C., Arnold, A. S., Loan, P., Habib, A., John, C. T., GuendeElman, E., and Thelen, D. G. (2007). OpenSim: open-source software to create and analyze dynamic simulations of movement. IEEE Trans. Biomed. Eng. 54, 1940–1950.
Dickinson, M. H., Farley, C. T., Full, R. J., Koehl, M. A., Kram, R., and Lehman, S. (2000). How animals move: an integrative view. Science 288,100–106.
Dickson, W. B., Straw, A. D., Poelma, C., and Dickinson, M. H. (2006). An integrative model of insect flight control. Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, No. AIaa-2006-0034, Reno, NV.
Dickinson, M. H., Tu, M. S. (1997). The function of dipteran flight muscle. Comp. Biochem. Physiol. A 116, 223–238.
Donelan, J. M., and Pearson, K. G. (2004). Contribution of force feedback to ankle extensor activity in decerebrate walking cats. J. Neurophysiol. 92, 2093–2104.
Ekeberg, O. (1993). A combined neuronal and mechanical model of fish swimming. Biol. Cybern. 69, 373–374.
Ekeberg, O., Blumel, M., and Buschges, A. (2004). Dynamic simulation of insect walking. Arthropod Struct. Dev. 33, 287–300.
Ekeberg, O., and Grillner, S. (1999). Simulations of neuromuscular control in lamprey swimming. Philos. Trans. R. Soc. Lond. B Biol. Sci. 354, 895–902.
Ekeberg, O., and Pearson, K. (2005). Computer simulation of stepping in the hind legs of the cat: an examination of mechanisms regulating the stance-to-swing transition. J. Neurophysiol. 94, 4256–4268.
Fontaine, E. I., Zabala, F., Dickinson, M. H., and Burdick, J. W. (2009). Wing and body motion during flight initiation in Drosophila revealed by automated visual tracking. J. Exp. Biol. 212, 1307–1323.
Frigon, A., and Rossignol, S. (2006). Experiments and models of sensorimotor interactions during locomotion. Biol. Cybern. 95, 607–627.
Fry, S. N., Sayaman, R., and Dickinson, M. H. (2005). The aerodynamics of hovering flight in Drosophila. J. Exp. Biol. 208, 2303–2318.
Gordon, S., and Dickinson, M. H. (2006). Role of calcium in the regulation of mechanical power in insect flight. Proc. Natl. Acad. Sci. U.S.A. 103, 4311–4315.
Grillner, S., Wallen, P., Saitoh, K., Kozlov, A., and Robertson, B. (2008). Neural bases of goal-directed locomotion in vertebrates: an overview. Brain Res. Rev. 57, 2–12.
Gynther, I. C., and Pearson, K. G. (1989). An evaluation of the role of identified interneurons in triggering kicks and jumps in the locust. J. Neurophysiol. 61, 45–57.
Heitler, W. J., and Braunig, P. (1988). The role of fast extensor motor activity in the locust kick reconsidered. J. Exp. Biol. 136, 289–309.
Heitler, W. J., and Burrows, M. (1977a). The locust jump. I. The motor programme. J. Exp. Biol. 66, 203–219.
Heitler, W. J., and Burrows, M. (1977b). The locust jump. II. Neural circuits of the motor programme. J. Exp. Biol. 66, 221–241.
Hines, M. L., and Carnevale, N. T. (2001). NEURON: a tool for neuroscientists. Neuroscientist 7, 123–135.
Ivashko, D. G., Prilutsky, B. I., Markin, S. N., Chapin, J. K., and Rybak, I. A. (2003). Modeling the spinal cord neural circuitry controlling cat hindlimb movement during locomotion. Neurocomputing 52–54, 621–629.
Jankowska, E. (2008). Spinal interneuronal networks in the cat: elementary components. Brain Res. Rev. 57, 46–55.
Kiehn, O., Quinlan, K. A., Restrepo, C. E., Lundfald, L., Borgius, L., Talpalar, A. E., and Endo, T. (2008). Excitatory components of the mammalian locomotor CPG. Brain Res. Rev. 57, 56–63.
Klishko, A., Prilutsky, B. I., Cofer, D. W., Cymbalyuk, G., and Edwards, D. H. (2008). “Interaction of CPG, spinal reflexes and hindlimb properties in cat paw shake: a computer simulation study.” in 2008 Neuroscience Meeting Planner Online, Program No. 375.12/OO11 (Washington, D.C.: Society for Neuroscience).
Lentink, D., and Dickinson, M. H. (2009). Rotational accelerations stabilize leading edge vortices on revolving fly wings. J. Exp. Biol. 212, 2705–2719.
Loeb, G. E., Brown, I. E., and Cheng, E. J. (1999). A hierarchical foundation for models of sensorimotor control. Exp. Brain Res. 126, 1–18.
McVea, D. A., Donelan, J. M., Tachibana, A., and Pearson, K. G. (2005). A role for hip position in initiating the swing-to-stance transition in walking cats. J. Neurophysiol. 94, 3497–3508.
McVea, D. A., and Pearson, K. G. (2006). Long-lasting memories of obstacles guide leg movements in the walking cat. J. Neurosci. 26, 1175–1178.
Novakovic, V. A., Sutton, G. P., Neustadter, D. M., Beer, R. D., and Chiel, H. J. (2006). Mechanical reconfiguration mediates swallowing and rejection in Aplysia californica. J. Comp. Physiol. A 192, 857–870.
Pearson, K., Ekeberg, O., and Buschges, A. (2006). Assessing sensory function in locomotor systems using neuro-mechanical simulations. Trends Neurosci. 29, 625–631.
Pearson, K. G. (2008). Role of sensory feedback in the control of stance duration in walking cats. Brain Res. Rev. 57, 222–227.
Prochazka, A., Gritsenko, V., and Yakovenko, S. (2002). Sensory control of locomotion: reflexes versus higher-level control. Adv. Exp. Med. Biol. 508, 357–367.
Prochazka, A., and Yakovenko, S. (2007). The neuromechanical tuning hypothesis. Prog. Brain Res. 165, 255–265.
Proekt, A., Wong, J., Zhurov, Y., Kozlova, N., Weiss, K. R., and Brezina, V. (2008). Predicting adaptive behavior in the environment from central nervous system dynamics. PLoS ONE 3, e3678. doi:10.1371/journal.pone.0003678.
Rinehart, M. D., and Belanger, J. H. (2009). “Biologically realistic limb coordination during multi-legged walking in the absence of central connections between the legs.” in 2009 Neuroscience Meeting Planner Online, Program No. 483.14 (Chicago, IL: Society for Neuroscience).
Ritzmann, R. E., and Buschges, A. (2007). Adaptive motor behavior in insects. Curr. Opin. Neurobiol. 17, 629–636.
Rossignol, S., Dubuc, R., and Gossard, J. P. (2006). Dynamic sensorimotor interactions in locomotion. Physiol. Rev. 86, 89–154.
Shadmehr, R., and Wise, S. P. (2005). The Computational Neurobiology of Reaching and Pointing. Cambridge, MA: MIT Press.
Sherman, A., and Dickinson, M. H. (2004). Summation of visual and mechanosensory feedback in Drosophila flight control. J. Exp. Biol. 207, 133–142.
Sherrington, C. S. (1910). Flexion-reflex of the limb, crossed extension-reflex, and reflex stepping and standing. J. Physiol. (Lond.) 40, 28–121.
Ting, L. H., and McKay, J. L. (2007). Neuromechanics of muscle synergies for posture and movement. Curr. Opin. Neurobiol. 17, 622–628.
Windhorst, U. (2007). Muscle proprioceptive feedback and spinal networks. Brain Res. Bull. 73, 155–202.
Wolpert, D. M. (2009). “Moving in an uncertain world: Computational principles of human motor control.” in 2009 Neuroscience Meeting Planner Online Program No. 111 (Chicago, IL: Society for Neuroscience).
Keywords: biomechanics, sensorimotor integration, behavior, motor control, sensory feedback, computational model, movement
Citation: Edwards DH (2010) Neuromechanical simulation. Front. Behav. Neurosci. 4:40. doi: 10.3389/fnbeh.2010.00040
Received: 14 April 2010;
Paper pending published: 15 May 2010;
Accepted: 20 June 2010;
Published online: 14 July 2010
Edited by:
William Kristan, University of California San Diego, USAReviewed by:
Ansgar Buschges, University of Cologne, GermanyÖrjan Ekeberg, Royal Institute of Technology, Sweden
Copyright: © 2010 Edwards. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Donald H. Edwards, Neuroscience Institute, Georgia State University, 100 Piedmont Avenue, Atlanta, GA 30303, USA. e-mail: dedwards@gsu.edu