Spike-timing dependent plasticity and feed-forward input oscillations produce precise and invariant spike phase-locking

1. Introduction

In the hippocampus and the neocortex, the coupling between local field potential (LFP) oscillations and spiking – termed spike phase – can be highly precise (Bragin et al., 1995; Lee et al., 2005; Siapas et al., 2005; Kayser et al., 2009). Specifically, in hippocampal place field recordings, both stable phase-locking and phase precession have been observed in various settings (O’Keefe and Recce, 1993; Pastalkova et al., 2008), with neurons firing one or two closely timed spikes per oscillation cycle (Pastalkova et al., 2008; Harvey et al., 2009; Schmidt et al., 2009). This LFP/spike phase coupling has been proposed to be a reliable method for information transfer (Sejnowski and Paulsen, 2006), and has been found to be robust across cell types and membrane parameters (Somogyi and Klausberger, 2005). The mechanism, however, by which such LFP/spike phase coupling is refined to such precision remains largely to be determined. In this note, we have investigated a simple mechanism for this process – the reliable, periodic modulation of presynaptic firing rates during oscillations, coupled with spike-timing dependent plasticity. We focus here on fixed point dynamics of the system, to understand the emergence of stable phase-locking behavior from tonic, oscillating inputs. With this formalism in place, the possibility of an extension to phasic inputs and dynamic LFP/spike phase relationships is straightforward.

We focused on a minimal model set up by considering a hypothetical hippocampal CA1 neuron receiving noisy, oscillating input from a large number of weak afferent inputs (see red inputs, Figure 1A). For purposes of introduction, we further assume that the neuron fires 1 spike per input oscillation cycle (see blue output, Figure 1A). We then note that when input oscillations are within the biological range (2–150 Hz), the firing rate of the inputs changes on a timescale highly relevant to spike-timing dependent plasticity (STDP). We also note that the defining feature of STDP is highly precise temporal asymmetry. When a presynaptic spike precedes a post-synaptic spike in time, the synapse between the two is potentiated. This is termed a PRE-POST pairing (see Figure 1B, right side of graph). Conversely, if a presynaptic spike follows a post-synaptic spike in time, the synapse between the two is de-potentiated, and this is termed a POST-PRE pairing (see Figure 1B, left side of graph).

FIGURE 1

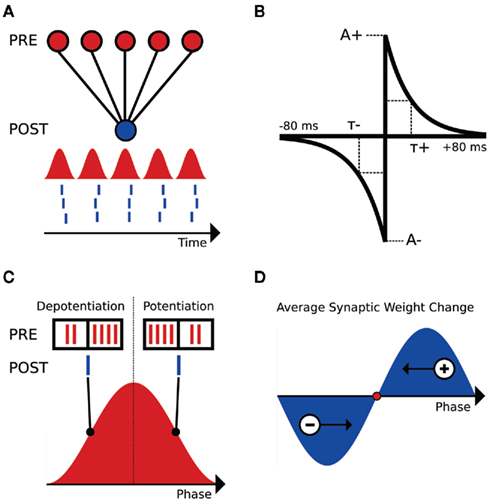
Figure 1. Schematic of the interplay between STDP and input oscillations. (A) Setup of the input/output feed-forward network. Input population rate is displayed as the red sinusoid. Output spikes are represented in blue below the input sinusoid. (B) STDP kernel used for analysis and computational simulations. The piecewise exponential is a function of the temporal difference between pre- and post-synaptic spikes (defined here as t_post − t_pre). A₊ and A₋ are the maximal changes for a synaptic weight, as a percentage of w_max. (C) Comparison of the inputs (red spikes) and output (blue spike) at two phases of the input oscillation cycle (90° and 270°, respectively). (D) Schematic weight change as a function of output spike phase. Late-phase spikes receive a net potentiation and fire earlier in subsequent cycles, while early phase spikes receive a net de-potentiation and fire later in subsequent cycles. The fixed point for this simple system is illustrated as a red dot.

Clearly, we expect this temporal asymmetry of STDP to create significant effects that depend on the phase of the output spike relative to the input oscillation. As an example, consider an output spike occurring on the rising phase of the inputs, where the input firing rate is increasing in time. Here, there will be more POST-PRE pairings than PRE-POST pairings, and hence we would expect a net de-potentiation (see Figure 1C, output spike at 90°). Conversely, an output spike on the falling phase of the input oscillation results in more PRE-POST pairings than POST-PRE pairings, and a net potentiation (see Figure 1C, output spike at 270°). Because the net excitation received by the cell determines spike phase within the 1:1 phase-locking regime (Brette and Guigon, 2003; McLelland and Paulsen, 2009), the late-phase cells, which receive a net potentiation, will fire at earlier phases in subsequent cycles (see Figure 1D). Conversely, the early phase spikes that receive a net de-potentiation will fire at later phases in subsequent cycles (see Figure 1D). These two effects cancel each other at a given point within the oscillation cycle, which is a zero crossing of the schematic weight change curve in Figure 1D. At this zero point, there is no net change in synaptic weights, and given that this point is dynamically stable, a reliable phase-locking behavior in the output neuron results.

Following these arguments, we expect STDP to structure the synaptic strengths of oscillating inputs to ensure a precise LFP-to-spike phase relationship. In fact, using analytic methods, we can calculate the location of stable phase-locking point for a neuron with STDP-modulated input synapses. We find that the location of this stable point depends on the oscillation frequency and depth of modulation of the inputs, the STDP time constants, and the ratio of de-potentiation to potentiation in the STDP rule. Because the effect of the STDP time constants and the STDP ratio – to change the relative area under each section of the piecewise exponential STDP curve – is roughly the same, in this work we consider only changing the STDP ratio. Additionally, we show that the location of this stable point is invariant to the properties of the post-synaptic neuron, such as membrane resistance or the net excitation initially applied.

2. Materials and Methods

2.1. Computational Simulations

For computational simplicity, the integrate-and-fire (IF) neuron model is used. The equation governing the IF neuron’s membrane potential is:

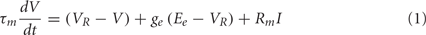
where τ_m (33 ms) is the membrane time constant, V_R (−70 mV) is the resting membrane potential, g_e is the synaptic input variable, E_e (0 mV) is the reversal potential for an excitatory synapse, R_m (200 MOhm) is the membrane resistance for the cell, and I is the applied DC current. Note that this equation for the IF neuron is a CUBA (current-based) model, following Vogels and Abbott (2005). When the membrane potential reaches the threshold value V_th (−54 mV), a spike is generated, and the membrane potential is reset to the resting membrane potential V_R.

Input connections to the IF neuron are mediated by exponential synapses, without delays. When a presynaptic spike occurs, the g_e parameter is incremented by an amount w (g_e → g_e + w). Otherwise, the g_e variable follows the equation:

where τ_e (5 ms) is the decay time constant for the exponential synapse. In these simulations, w is set to induce a subthreshold membrane potential oscillation, and a linearly spaced range of DC currents is then found to span the 1:1 phase-locking regime. It is important to note that the effect described in this work is extremely robust to the parameters of the output model neuron, and different parameter regimes have been tested to ensure this.

The 5000 presynaptic inputs to the IF neuron were modeled as inhomogeneous Poisson processes whose rate parameters oscillate in time, with a peak rate of 10 Hz. The input oscillation frequency is set to 20 Hz. To ensure that the lack of refractory period in the Poisson process inputs does not affect the results reported here, additional simulations have been performed with inputs that follow an inhomogeneous Gamma process.

The STDP rule is implemented in accordance with Song et al. (2000), with all-to-all spike pairings. Synaptic weights are restricted to range between 0 and w_max. For a given spike pairing with temporal difference s, the synapse between the pre- and post-synaptic neurons is modified according to (w → w + f(s) w_max). Thus, the value of the STDP kernel f(s) for a given temporal difference between a pre- and post-synaptic spike determines the percentage of w_max added to the synaptic weight (Song et al., 2000). Because we study a plastic system with intrinsic stability in the coupling between STDP and oscillations, it is not necessary to include a stabilizing mechanism in the STDP rule, provided that the learning rate A₊ is a reasonable value. Thus, we focus on an STDP rule with hard bounds (Song et al., 2000), so that we do not introduce extra stability arising from an STDP rule with soft bounds (van Rossum et al., 2000), though the combination of these two mechanisms could be interesting for future work.

These simulations were performed using the Brian simulator (Goodman and Brette, 2008, 2009), and a Python script to reproduce part of Figure 4 will be made available on ModelDB (https://senselab.med.yale.edu/modeldb/).

3. Results

3.1. Mathematical Analysis

We first assume an STDP rule with linear, all-to-all spike pairings. Following previous theoretical work on STDP (Song et al., 2000), we formulate the STDP rule as a piecewise exponential function:

where s is defined as the difference in pre- and post-synaptic spike times (t_post − t_pre), τ₊ and τ₋ are the STDP time constants for potentiation and de-potentiation, A₊ is the amount of potentiation for an optimally potentiating PRE-POST pairing, and A₋ is the same for a de-potentiating POST-PRE pairing. The ratio of de-potentiation to potentiation (A₋τ₋/A₊τ₊) will be termed the STDP ratio. For the case of identical time constants considered here, we simply write (A₋/A₊). The value of the function f(s) determines the percent change for a synaptic weight on a given pairing, relative to w_max.

The rates of the presynaptic spike trains are approximated by a continuous sinusoid (in simulations, below, we model inputs as inhomogeneous Poisson processes):

where v is the angular frequency, r is the peak firing rate, and c is a parameter controlling the depth of modulation (; Skaggs et al., 1996) of the oscillation:

The output spike train is formulated as a series of delta functions:

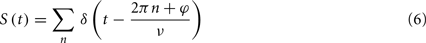
where φ is the phase offset of the output spikes. Here, the phase distribution of the output neuron is a delta function, reflecting the assumption of the 1:1 phase-locking regime; however, results will be similar for any moderately peaked, unimodal phase distribution.

To calculate the correlation function between the input oscillation and the output spike train S(t), one considers the integral:

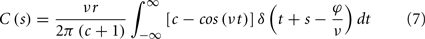
where s is the temporal difference between pre- and post-synaptic spikes (t_post − t_pre). This integral simplifies to:

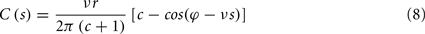
To calculate the expected weight change over time (dw/dt) as a function of output spike phase, we take the integral over the correlation function between pre- and post-synaptic spike trains multiplied by the STDP kernel:

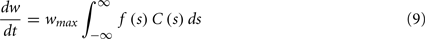
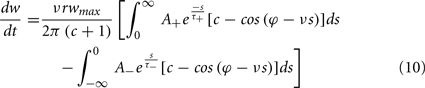
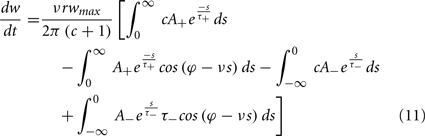
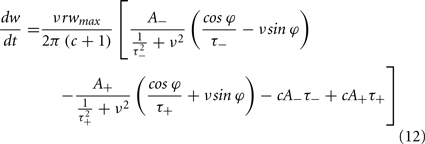
From Eq. 12, one can clearly see that the location of the zeros depends on the angular frequency (v), the STDP time constants (τ₊ and τ₋), the depth of modulation parameter c, and the strength of potentiation and de-potentiation in the STDP rule (A₊ and A₋). One can think of the A₊ terms as phase advancing and the A₋ terms as phase delaying, for the weight change versus spike phase curve. The location of the zero crossing of this solution depends on the STDP ratio (A₋/A₊), and not on the absolute magnitude of A₊ or A₋, because increasing the magnitude of these terms while keeping the ratio constant corresponds to scaling of the function, and thus will not change the location of the zero crossings. Similarly, the firing rate of the inputs (r) does not affect the location of the zeros.

The result of the calculation (dw/dt as a function of output phase) is plotted in Figure 2A, with the parameter c set equal to 1 for full depth of modulation in the input sinusoid. The oscillation frequency f is 20 Hz, the STDP time constants are equal and set to 20 ms, A₊ is 0.01, and the STDP ratio is 1.05 (Bi and Poo, 1998; Song et al., 2000). Note that the form of this solution matches the behavior expected from the heuristic argument depicted in Figures 1C,D – net potentiation for the late-phase spikes, net de-potentiation for early phase spikes. It is also important to note that the extrema of this analytic expression fall near 90° and 270°, which are the points at which the input firing rate is changing fastest in time.

FIGURE 2

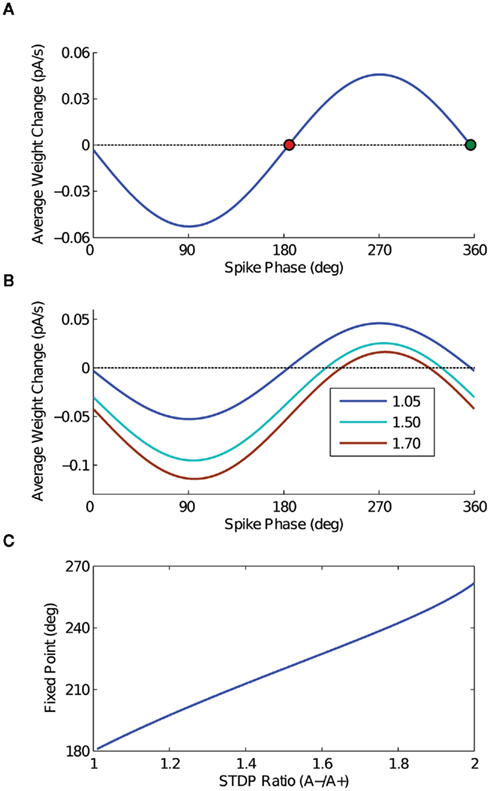
Figure 2. Analytic solution. (A) The analytic solution for weight change over time as a function of output spike phase. The STDP ratio (A₋/A₊) is 1.05 for this curve. The two fixed points of the weight change curve are plotted – the stable fixed point in red, and the unstable fixed point in green. (B) The analytic solution for weight change over time is plotted for several values of the STDP ratio, to demonstrate the effect of increasing the ratio of de-potentiation to potentiation on the output model neuron. Compare these curves to the results of the computational simulations in Figures 4B–D. (C) The point of stable phase-locking is plotted as a function of STDP ratio, demonstrating the shift of the stable phase point to later phases with increasing amounts of de-potentiation.

The analytic solution has two zero crossings – one stable, the other unstable. As spike phase is inversely related to input current in the 1:1 phase-locking regime for a model neuron with a positive phase response curve (PRC), it is straightforward to see that the early fixed point will be stable, with the later unstable. For an STDP ratio of 1.05, the location of this stable fixed point falls just after 180°. By changing the STDP ratio, however, stable phase-locking can be achieved throughout a wide range of the oscillation cycle. Thus, by increasing the STDP ratio (i.e., increasing the relative amount of de-potentiation), the point of stable phase-locking will occur later in the oscillation cycle; conversely, by decreasing the STDP ratio (i.e., increasing the relative amount of potentiation), the point of stable phase-locking will occur earlier in the oscillation cycle. The change in the shape of the analytic solution with different values of the STDP ratio is illustrated in Figure 2B, and the location of the fixed point as a function of the STDP ratio is plotted in Figure 2C.

The effect of the parameter c is detailed in Figure 3, in which the depth of modulation is varied from 100 (c = 1) to 40% (c = 4). In Figure 3A, the expected weight change is plotted as a function of output spike phase for an STDP ratio of 1.05, as in Figure 2A. In Figure 3B, the location of the stable fixed point is plotted as a function of the STDP ratio, for the three values of c. For input sinusoids with a smaller depth of modulation, a change in the STDP ratio has a greater effect on the location of the fixed point. The range, however, is similar for all cases.

FIGURE 3

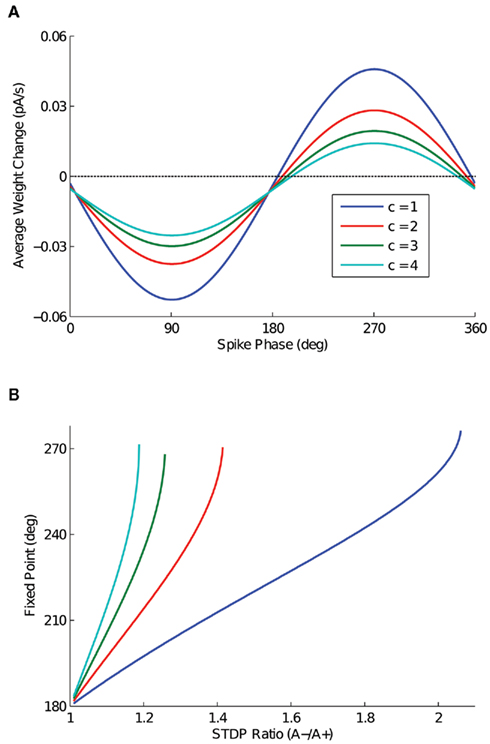
Figure 3. The effect of depth of modulation on analytic solution. (A) Expected weight change as a function of output spike phase, for a depth of modulation of the inputs ranging from 100 (c = 1) to 40% (c = 4) and an STDP ratio of 1.05. It is important to note that for this STDP ratio, the 40% depth of modulation (c = 4) does not have a zero crossing. (B) The location of the stable fixed point is plotted for the depth of modulation cases presented in (A), for all values of the STDP ratio that the function has a zero crossing.

3.2. Computational Simulations

To corroborate the analytic results, which approximate the input spike trains as a continuous sinusoid, with biophysically realistic input and output spiking processes, we performed computational simulations of an integrate-and-fire (IF) neuron and oscillating inhomogeneous Poisson process inputs. In these simulations, the IF neuron receives 5000 periodically modulated Poisson process spike inputs (see red inputs, Figure 1A). The number of inputs is chosen to be biologically realistic (Amaral et al., 1990), but also computationally feasible. Inputs are connected to the IF neuron by exponential, current-based synapses with a 5-ms decay time constant. Notably, as the analytic solution demonstrates, our STDP-based phase coupling mechanism is robust to the output neuron model. The only requirement is that the output model neuron has a positive PRC; thus, the IF neuron was chosen for computational simplicity.

In the control simulation without STDP (Figure 4A), a range of DC inputs are applied to the output neuron, so that the output will phase-lock to a range of phases of the input oscillation cycle. The mean phase of the output spike as a function of oscillation cycle over 50 trials for each DC input case is plotted in Figure 4A, with different colors for each DC input. It is important to note that after 1 s of simulation, stable phase-locking is achieved, and the initial transient has been integrated out, so that each neuron has reached an individual stable phase-locking point. This set of neurons with the various pre-STDP steady-state phase points can be interpreted as a population of cells, each with slightly different membrane parameters, such as membrane resistance or mean synaptic input.

FIGURE 4

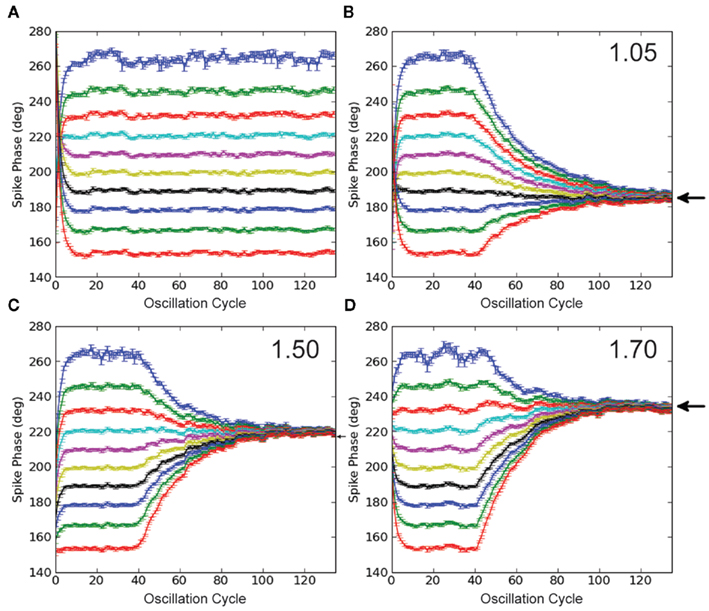
Figure 4. Simulations with STDP and input oscillations. (A) Control simulation. The phase of every spike in the simulation is plotted in each panel. The IF neuron receives a range of DC inputs, with STDP turned off, to demonstrate the phase-locking paradigm and its initial transient. (B–D) STDP simulations. Legend text indicates STDP ratio in each panel. STDP is turned off for the first 2 s of simulation, to integrate out the initial transient. With STDP turned on, the population of model output neurons quickly learns to phase-lock to a point within the input oscillation cycle. With increased de-potentiation relative to potentiation in the STDP rule, the population of model output neurons locks to later points within the input oscillation cycle. Black arrows mark predictions from the analytic solution. All data points represent an average over 50 trials, and error bars represent SEM.

The synapses connecting the oscillating inputs to the output model neuron express STDP with linear, all-to-all spike pairings. In these simulations, all synapses are initialized to the same weight. For the first 2 s of the simulation, STDP is turned off, during the initial 1 s transient. In this way, each neuron starts out at its individual stable phase. When STDP is turned on, our putative population of output neurons quickly converges to the unique stable spike phase predicted by the analytic solution in Figure 2B (prediction marked by black arrows, Figures 4B–D). The simulations in Figures 4B–D are done with STDP ratios increasingly weighted toward de-potentiation (1.05, 1.50, and 1.70), and correspond to the ratios for the analytic solution plotted in Figure 2B. For an STDP ratio of 1.05, the analytic solution predicts stable phase-locking at 185°; for STDP ratios of 1.50 and 1.70, stable phase-locking is predicted at 220° and 235°, respectively. Thus, by changing the STDP ratio, phase-locking can be achieved throughout the oscillation cycle.

To verify that a population of neurons will converge from outside the 1:1 phase-locking regime to our theoretically predicted stable fixed phase point, we made an additional test with an 800-neuron population receiving input from 10,000 excitatory cells. Each neuron is connected to an input with a 10% connection probability, giving an average of 1,000 input synapses per output neuron. The inputs oscillate, as above, but in this simulation, no extra DC input is added to the neurons. The simulation is run as follows. First, the simulation runs for 5 s, to integrate out any transients. Second, the simulation runs for an additional 5 s, to record the phase distribution before STDP (blue distribution, Figure 5). Third, STDP is applied during 30 s of simulation. Fourth, the simulation runs for a final 5 s, to record the converged phase distribution after STDP (green distribution, Figure 5). In comparing the recorded mean phase after STDP with the theoretically predicted value (cf. small vertical lines, Figure 5), we observe that the output phase distribution leaves the two spikes per cycle phase-locking regime and converges to within 1° of the theoretical value after 30 s of plasticity. The weight distribution of the inputs is depicted in the inset of Figure 5; as shown here, it is important that the learning rate (A₊) is relatively small, so that the weight distribution does not saturate to the hard bounds. The stability of the weight and phase distributions has been checked in longer simulations. Additionally, we have checked with simulations of neurons initially firing less than 1 spike per cycle that the mean of the phase distribution also converges to the theoretically predicted stable fixed point (data not shown).

FIGURE 5

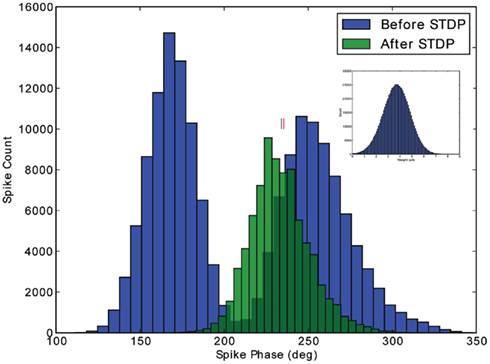
Figure 5. Verification of stability outside the 1:1 phase-locking regime. The phase distribution for a population of 800 excitatory cells is depicted, before and after application of STDP. Initially, the input strength induces two spikes per cycle in the excitatory population. After 30 s of plasticity, however, the phase distribution converges to the 1:1 phase-locking regime, with a mean phase (marked with blue line) within 1° of the theoretically predicted value (marked with red line). The Gaussian weight distribution produced by the STDP rule is depicted in the inset.

4. Discussion

In this note, we have demonstrated through both analysis and simulation that the combination of STDP, which is classically observed in the hippocampus and neocortex (Bliss and Lomo, 1973; Markram et al., 1997; Bi and Poo, 1998), and neuronal ensemble oscillations, which are also classically observed in the hippocampus and neocortex (Gray and Singer, 1989; Buzsaki, 2011), allows a population of neurons with heterogeneous membrane parameters to phase-lock to a specific point in an input oscillation cycle, invariant to differences in initial excitation. While precise phase-locking behavior is observed throughout the brain (Bragin et al., 1995; Lee et al., 2005; Siapas et al., 2005; Kayser et al., 2009), the mechanisms leading to this robust and invariant LFP-spike coupling are not well understood and in modeling this phenomenon, the precision of phase-locking observed often requires careful adjustment of parameters for the model neurons and applied currents. We have shown that these parameters can be learned by individual neurons under quite general conditions in the presence of STDP and neuronal oscillations. A similar mechanism has been observed experimentally in the olfactory system of the locust, where STDP synchronizes the response of downstream neurons to the peak of an upstream input oscillation (Cassenaer and Laurent, 2007), and it is likely that this mechanism affects hippocampal circuits as well. Additionally, it is important to note that the rate at which the population of model neurons converges to its fixed point depends on the magnitude of A₊ and A₋, but that the location of this point depends only on the parameters discussed above (input oscillation frequency, STDP time constants, and the STDP ratio). The point of stable phase-locking is quite insensitive to the magnitude of A₊ and A₋ – that is, learning in this system can happen either very quickly or very slowly, with the system converging to the same point. This is an interesting point in the context of hippocampal place field dynamics, during which NMDA receptor-dependent changes in neuronal firing patterns take place quite fast, within as few as five laps on a linear track (Mehta et al., 2002). The mechanism of STDP and oscillations explored here satisfies this fast yet stable learning observed during in vivo place field dynamics.

This note complements and extends the work of several previous studies in stability of single neurons with plastic synapses following an STDP rule (Song et al., 2000; van Rossum et al., 2000; Gütig et al., 2003; Babadi and Abbott, 2010; Gilson et al., 2010). Most notably, we extend here the concept of intrinsic stability within input/output bursts (Song et al., 2000) to the case of many weak tonic oscillatory inputs, and we relate the neuronal and synaptic parameters to the fixed phase at which the neuron will learn to spike. In this way, we provide an additional special case (i.e., oscillating inputs) under which stability is achieved with the standard STDP rule. This special case is orthogonal to studies of plasticity rules modified from the piecewise exponential form originally suggested for STDP in Bi and Poo (1998) [van Rossum et al. (2000), Gütig et al. (2003), Babadi and Abbott (2010)], and future work could complement this study by investigating these modified rules in the context of oscillating synaptic inputs, as studied here.

To produce the results outlined in this work, several general assumptions must hold. First, for modeling the feed-forward structures such as the hippocampal subfield CA1, we focus on the 1:1 phase-locking regime. This regime is a good approximation to the behavior of hippocampal pyramidal neurons in awake, behaving animals during spatial navigation, which fire single spikes or a closely timed 2–3 spike burst each oscillation cycle (e.g., Figure 4A of Harvey et al., 2009; Schmidt et al., 2009). The main simplification here is that we treat these complex spike events as single events for the sake of the STDP rule. Second, the input synapses are assumed to remain in the weak limit, so that many presynaptic cells contribute to driving the output cell to action potential threshold. This is also a good approximation for hippocampal pyramidal neurons, when considering the number of afferent inputs to these neurons and their mean firing rates (Amaral et al., 1990; Ahmed and Mehta, 2009). Third, we have assumed that individual spike pairings sum linearly in the STDP rule. This has been shown to be a valid approximation for hippocampal STDP (Wang et al., 2005), even though summation of STDP pairings may not be linear in some areas of the neocortex (Froemke and Dan, 2002; Froemke et al., 2006). Additionally, we have neglected any voltage dependence of the post-synaptic neuron on the summation of STDP pairings (Clopath et al., 2010), which could be an additional factor in the interaction of STDP and oscillations. Fourth, we have focused on fixed points occurring in the late half of the oscillation cycle, in light of the fact that most cell classes in the hippocampus have phase distributions peaked after 180° (Somogyi and Klausberger, 2005). In principle, computational simulations could also inspect phase-locking in the early half of the oscillation cycle. Lastly, it is important to note that Eq. 12 quantifies the average, or expected weight change of an input synapse as a function of output spike phase. With relatively small individual weight changes, however, this expected weight change approximates the actual weight change on any single trial quite well.

In summary, we have considered a very simple architecture – oscillating, feed-forward input synapsing onto a single output neuron – and developed a mechanistic view of spike phase in the presence of STDP. This view provides quantitative results on spike phase during hippocampal learning, and furthermore, this same mechanism can generalize to more complex network architectures and input/output phase relationships.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank O. Ahmed for a careful reading of the manuscript. Lyle Muller was supported by a doctoral grant from École des Neurosciences de Paris (ENP). Romain Brette was supported by the European Research Council (ERC StG 240132). Boris Gutkin was supported by ANR, NeRF, ENP, CNRS, and INSERM.

References

Ahmed, O. J., and Mehta, M. R. (2009). The hippocampal rate code: anatomy, physiology and theory. Trends Neurosci. 32, 329–338.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Amaral, D. G., Ishizuka, N., and Claiborne, B. (1990). Neurons, numbers and the hippocampal network. Prog. Brain Res. 83, 1–11.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Babadi, B., and Abbott, L. F. (2010). Intrinsic stability of temporally shifted spike-timing dependent plasticity. PLoS Comput. Biol. 11, e1000961. doi:10.1371/journal.pcbi.1000961

CrossRef Full Text

Bi, G. Q., and Poo, M. M. (1998). Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 18, 10464–10472.

Pubmed Abstract | Pubmed Full Text

Bliss, T. V. P., and Lomo, T. (1973). Long-lasting potentiation of synaptic transmission in the dentate area of the anaesthetized rabbit following stimulation of the perforant path. J. Physiol. 232, 331–356.

Pubmed Abstract | Pubmed Full Text

Bragin, A., Jando, G., Nadasdy, Z., Hetke, J., Wise, K., and Buzsaki, G. (1995). Gamma (40-100 Hz) oscillation in the hippocampus of the behaving rat. J. Neurosci. 15, 47–60.

Pubmed Abstract | Pubmed Full Text

Brette, R., and Guigon, E. (2003). Reliability of spike timing is a general property of spiking model neurons. Neural Comput. 15, 279–308.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Buzsaki, G. (2011). Hippocampus. Scholarpedia 6, 1468.

CrossRef Full Text

Cassenaer, S., and Laurent, G. (2007). Hebbian STDP in mushroom bodies facilitates the synchronous flow of olfactory information in locusts. Nature 448, 709–713.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Clopath, C., Büsing, L., Vasilaki, E., and Gerstner, W. (2010). Connectivity reflects coding: a model of voltage-based STDP with homeostasis. Nat. Neurosci. 13, 344–352.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Froemke, R. C., and Dan, Y. (2002). Spike-timing-dependent synaptic modification induced by natural spike trains. Nature 416, 433–438.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Froemke, R. C., Tsay, I. A., Raad, M., Long, J. D., and Dan, Y. (2006). Contribution of individual spikes in burst-induced long-term synaptic modification. J. Neurophysiol. 95, 1620–1629.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gilson, M., Burkitt, A. N., Grayden, D. B., Thomas, D. A., and van Hemmen, J. L. (2010). Representation of input structure in synaptic weights by spike-timing-dependent plasticity. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 82, 021912.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Goodman, D., and Brette, R. (2008). Brian: a simulator for spiking neural networks in Python. Front. Neuroinform. 2:5. doi:10.3389/neuro.11.005.2008

CrossRef Full Text

Goodman, D. F., and Brette, R. (2009). The Brian simulator. Front Neurosci. 3, 192–197.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gray, C. M., and Singer, W. (1989). Stimulus-specific neuronal oscillations in orientation columns of cat visual cortex. Proc. Natl. Acad. Sci. U.S.A. 86, 1698–1702.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gütig, R., Aharonov, R., Rotter, S., and Sompolinsky, H. (2003). Learning input correlations through nonlinear temporally asymmetric Hebbian plasticity. J. Neurosci. 23, 3697–3714.

Pubmed Abstract | Pubmed Full Text

Harvey, C. D., Collman, F., Dombeck, D. A., and Tank, D. W. (2009). Intracellular dynamics of hippocampal place cells during virtual navigation. Nature 461, 941–946.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kayser, C., Montemurro, M. A., Logothetis, N. K., and Panzeri, S. (2009). Spike-phase coding boosts and stabilizes information carried by spatial and temporal spike patterns. Neuron 61, 597–608.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lee, H., Simpson, G. V., Logothetis, N. K., and Rainer, G. (2005). Phase locking of single neuron activity to theta oscillations during working memory in monkey extrastriate visual cortex. Neuron 45, 147–156.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Markram, H., Lubke, J., Fortscher, M., and Sakmann, B. (1997). Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science 275, 213–215.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

McLelland, D., and Paulsen, O. (2009). Neuronal oscillations and the rate-to-phase transform: mechanism, model and mutual information. J. Physiol. 587, 769–785.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mehta, M. R., Lee, A. K., and Wilson, M. A. (2002). Role of experience and oscillations in transforming a rate code into a temporal code. Nature 417, 741–746.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

O’Keefe, J., and Recce, M. L. (1993). Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus 3, 317–330.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pastalkova, E., Itskov, V., Amarasingham, A., and Buzsáki, G. (2008). Internally generated cell assembly sequences in the rat hippocampus. Science 321, 1322–1327.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schmidt, R., Diba, K., Leibold, C., Schmitz, D., Buzsaki, G., and Kempter, R. (2009). Single-trial phase precession in the hippocampus. J. Neurosci. 29, 13232–13241.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sejnowski, T. J., and Paulsen, O. (2006). Network oscillations: emerging computational principles. J. Neurosci. 26, 1673–1676.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Siapas, A. G., Lubenov, E. V., and Wilson, M. A. (2005). Prefrontal phase locking to hippocampal theta oscillations. Neuron 46, 141–151.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Skaggs, W. E., McNaughton, B. L., Wilson, M. A., and Barnes, C. A. (1996). Theta phase precession in hippocampal neuronal populations and the compression of temporal sequences. Hippocampus 6, 149–172.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Somogyi, P., and Klausberger, T. (2005). Defined types of cortical interneurone structure space and spike timing in the hippocampus. J. Physiol. 562, 9–26.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Song, S., Miller, K. D., and Abbott, L. F. (2000). Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nat. Neurosci. 3, 919–926.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

van Rossum, M. C. W., Bi, G. Q., and Turrigiano, G. G. (2000). Stable Hebbian learning from spike timing-dependent plasticity. J. Neurosci. 20, 8812–8821.

Pubmed Abstract | Pubmed Full Text

Vogels, T. P., and Abbott, L. (2005). Signal propagation and logic gating in networks of integrate-and-fire neurons. J. Neurosci. 25, 10786–10795.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wang, H. X., Gerkin, R. C., Nauen, D. C., and Bi, G. Q. (2005). Coactivation and timing-dependent integration of synaptic potentiation and depression. Nat. Neurosci. 8, 187–193.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text