- 1 Departamento de Física, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires, Buenos Aires, Argentina
- 2 Department of Neurology and Brain Imaging Center, Goethe-University Frankfurt, Frankfurt am Main, Germany
- 3 Consejo Nacional de Investigaciones Científicas y Tecnológicas, Buenos Aires, Argentina
- 4 Departamento de Matemática y Ciencias, Universidad de San Andrés, Buenos Aires, Argentina
- 5 Facultad de Ciencias Médicas, Universidad Nacional de Rosario, Rosario, Argentina
- 6 David Geffen School of Medicine, University of California Los Angeles, Los Angeles, CA, USA
Functional magnetic resonance imaging (fMRI) techniques have contributed significantly to our understanding of brain function. Current methods are based on the analysis of gradual and continuous changes in the brain blood oxygenated level dependent (BOLD) signal. Departing from that approach, recent work has shown that equivalent results can be obtained by inspecting only the relatively large amplitude BOLD signal peaks, suggesting that relevant information can be condensed in discrete events. This idea is further explored here to demonstrate how brain dynamics at resting state can be captured just by the timing and location of such events, i.e., in terms of a spatiotemporal point process. The method allows, for the first time, to define a theoretical framework in terms of an order and control parameter derived from fMRI data, where the dynamical regime can be interpreted as one corresponding to a system close to the critical point of a second order phase transition. The analysis demonstrates that the resting brain spends most of the time near the critical point of such transition and exhibits avalanches of activity ruled by the same dynamical and statistical properties described previously for neuronal events at smaller scales. Given the demonstrated functional relevance of the resting state brain dynamics, its representation as a discrete process might facilitate large-scale analysis of brain function both in health and disease.
1. Introduction
Important efforts to understand brain function, both in health and disease, are concentrated in the analysis of large-scale spatiotemporal patterns of brain activity available from fMRI techniques (Greicius et al., 2003; Beckmann and Smith, 2004; Beckmann et al., 2005; Raichle, 2006; Fox and Raichle, 2007; Smith et al., 2009), allowing for instance the unraveling of the functional connectivity between all possible brain regions, as is done under the Connectome project (Sporns et al., 2005; Sporns, 2011)1. At the same time, similar efforts are dedicated to place brain phenomenology in the context of statistical physics theory (Chialvo, 2010; Rolls and Deco, 2010; Sporns, 2010; Steyn-Rose and Steyn-Rose, 2010). Novel techniques of analysis are needed because of the increasing difficulty in managing extremely large data sets, generated by advances in imaging technology continuously improving temporal and spatial resolution.
Recent work has shown that important features of brain functional connectivity at rest can be computed from the relatively large amplitude BOLD fluctuations (Tagliazucchi et al., 2010a,b) after the signal crosses some amplitude threshold. Here we pursue further the same general idea of data reduction. In particular we are interested in a method often used to study the structure and properties of attractors of dynamical systems, which consists in the introduction of a Poincaré section. By definition, this approach decreases the dimension of the phase space and consequently the size of the data sets, facilitating in this way further numerical investigations. In general, there exist two possibilities: the first one is to analyze the set of points which are the coordinates of the successive intersections of the secant Poincaré plane by the phase space trajectories. The second possibility is to study the series of time intervals between the consecutive intersections. The resulting time intervals constitute a so-called point process (Cox and Isham, 1980), a construction useful in many areas of science, including neuroscience. It has been shown that under certain conditions the most important statistical features of the dynamical regime can be condensed into a point process (Packard et al., 1980; Roux et al., 1980; Takens, 1980; Roux and Swinney, 1981; Grassberger and Procaccia, 1983; Castro and Sauer, 1997).
The motivation to attempt a similar approach in fMRI data is strengthened by the observation that, in response to neuronal activation, the BOLD signal often repeats a stereotypical pattern (Friston et al., 1995, 1998; Aguirre et al., 1998; Tagliazucchi et al., 2010a,b). This feature suggests that it should be possible to compress the data sets using the temporal marks of a Poincaré section of the BOLD signal. This is the hypothesis explored here, which implies that, in principle, the entire brain resting state functional connectivity can be reconstructed solely on the basis of the time and location of the BOLD signal threshold crossings. Besides its practical importance for fMRI signal processing, this approach may provide further clues on the dynamical organization of the resting state brain activity.
The paper is organized as follows: the results section starts with the definition of the point process, as well as its connection with deconvolution techniques. This is followed by the replication of the fMRI brain resting state networks (RSN) maps using the point process. As further validation, the method’s ability to evaluate functional connectivity changes is demonstrated for a motor task and for a pathological condition. The spatiotemporal statistics are then considered, revealing novel aspects of the brain dynamics which are scale-invariant, consistent with that shown for other systems at the critical state (Bak, 1996; Jensen, 1998; Chialvo, 2010; Expert et al., 2011). The paper closes with a discussion on the new questions raised by the current analysis. For readers’ convenience, the methods are described at the end of the paper.
2. Results
The fMRI dataset is reduced to a spatiotemporal point process by normalizing each BOLD signal by its own SD, and subsequently selecting the time points at which the signal crosses a given threshold (1 SD in this case) from below, as it is shown in the example of Figure 1. Notice that, despite the fact that in resting data there are not explicit inputs, the average BOLD signal around the extracted points (Figure 1B, termed rBeta function in Tagliazucchi et al., 2010b) still resembles the hemodynamic response function (HRF) evoked by an stimulus (Friston et al., 1995, 1998). The relation between the point process and the underlying HRF is exposed by the deconvolution of the BOLD signal with either the HRF (with default parameters) or the rBeta function (Tagliazucchi et al., 2010b) extracted from the time series in Figure 1. In both cases, as shown in Figure 1C, the peaks of the de-convolved BOLD signal coincide, on a great majority, with the timing of the point process in Figure 1A. At this point a remark is needed concerning the impulse-like signals in Figure 1C. They result from the deconvolution of the BOLD signal with a function similar to the HRF, and from a physiological viewpoint it can be conjectured that they constitute short-lived events triggering the relatively slow (up to 20 s) BOLD response. Notice, however, that the bulk of the present results is independent of the precise nature of these impulse-like signals. They serve to illustrate that a different and already established mathematical method (which is also amenable to a clear physiological interpretation) leads to similar inter-event timings than those derived from the Poincaré section. Therefore, these results show that important information is compressed in the timing and spatial location of the extracted points. For the parameter used here, from each voxel BOLD time series (240 samples) on the average only 15 ± 3 points are threshold crossings (about one point every 40 s) which corresponds to near 94% reduction of the data (additional details, including the robustness to changes in threshold, are discussed in the Materials and Methods Section).
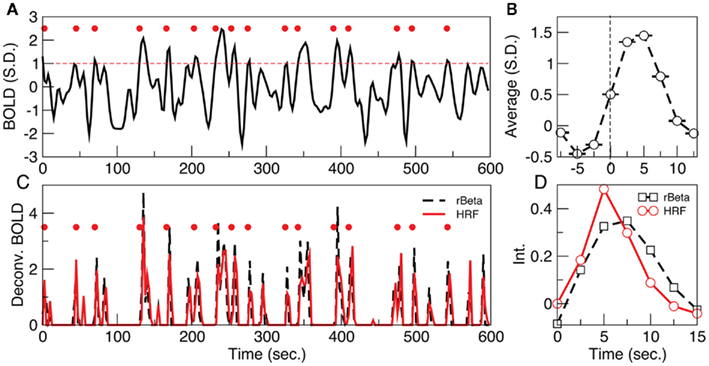
Figure 1. (A) Example of a point process (filled circles) extracted from the normalized BOLD signal. Each point corresponds to a threshold (dashed line at 1 SD) crossing from below. (B) Average BOLD signal (from all voxels of one subject) triggered at each threshold crossing. (C) The peaks of the de-convolved BOLD signal, using either the hemodynamic response function (HRF) or the rBeta function (Tagliazucchi et al., 2010b) depicted in (D), coincide on a great majority with the timing of the points shown in (A).
2.1. Resting State Networks and Activation Maps Can Be Derived from a Few Points
Despite the very large data reduction, we found that the information content of the few remaining points is very high. As a proof of principle, we first used the point process to calculate the spatial location of six well known RSN maps. These maps describe the major independent components of brain spontaneous activity, and as such they can be used as a relevant benchmark. We used the point process to obtain the RSN maps and compare them with maps computed from the full BOLD signal using a well established method (probabilistic independent component analysis – PICA; Beckmann et al., 2005). This is done by calculating in six RSNs the rate of points co-occurrence (up to 2 time units later in this case) between representative sites (“seeds”) and all other brain voxels and presented as maps in Figure 2A–C (see Materials and Methods for a detailed explanation of the computation). The seeds locations were selected according with previous work (see coordinates in Table 1 of Materials and Methods Section). The similarities between our conditional rate maps and the respective PICA maps (rightmost three columns and left column of Figure 2A respectively) is already obvious to the naked eye and confirmed by the correlation plotted in Figure 2C. The calculation shows that despite using less than 6% of the raw fMRI information, about 5 points (on average) are enough to obtain RSN maps that are highly correlated (95% confidence) with those obtained using PICA of the full BOLD signals. Similar good performance can be demonstrated in tracking physio-pathological changes of brain activation. This is presented in Figure 2D which shows the statistical differences in functional connectivity between a group of chronic back pain (CBP) patients and healthy controls already reported in Tagliazucchi et al., 2010a; comparison with seed correlation based in the DMN, increased correlation with bilateral insula in CBP). Finally, the data analysis from a finger tapping task (Tagliazucchi et al., 2010b) demonstrates also the merits of the current approach when compared with a seed correlation based in primary motor cortex contralateral to the tapping hand (Figure 2E).
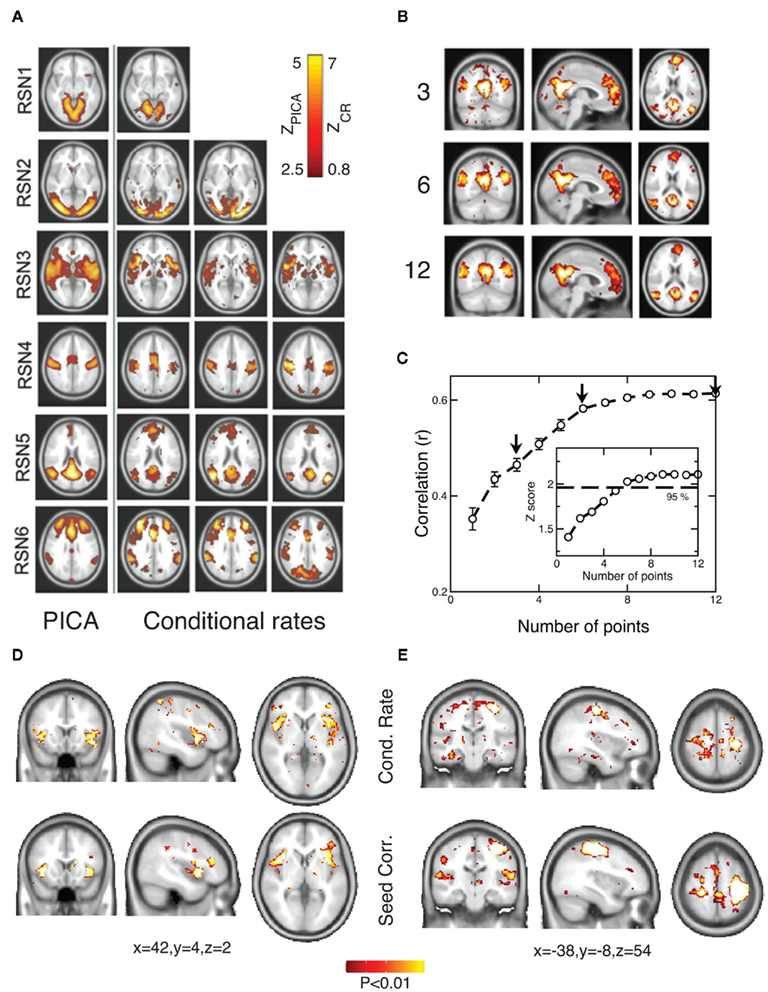
Figure 2. RSN maps constructed with the point process compare very well with standard PICA of the raw continuous data. (A) PICA spatial maps (left column) and rate of points conditional to activity at a given seed (rightmost three columns, each one corresponds to a different seed). (Slice z coordinates are −12, 0, 0, 36, 20, 26 for RSN 1–6; for seed coordinates see Table 1). Scales for PICA (ZPICA) and conditional rate (ZCR) calculations are depicted in the inset. (B) Conditional rate maps constructed using 3, 6, and 12 events of the point process at the ANGL seed (averaged for ten subjects. Slice coordinates are x = −4, y = −60, z = 18). (C) Correlation between RSN5 (the default-mode network, DMN) PICA-derived map and the point process-derived conditional rate maps, as a function of the number of points used. Arrows denote the examples of (B). Z scores (number of points as degrees of freedom) with the line of 95% confidence are plotted in the inset. (D) The point process is able to track the statistical differences between the functional connectivity maps of a group of chronic back pain patients and healthy controls already reported in (Tagliazucchi et al., 2010a). The conditional rate of points (top) reproduces well the standard seed correlation approach (bottom) derived from the same data. (E) The functional connectivity maps during a finger tapping task constructed from the conditional rate of points (top) compare well with the seed correlation maps derived from the same data (Tagliazucchi et al., 2010b).
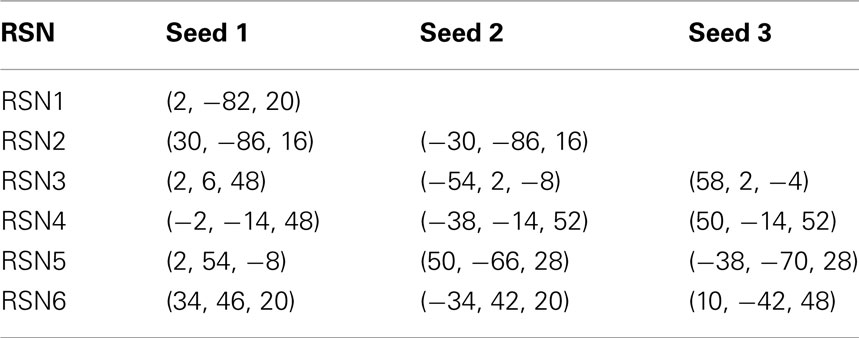
Table 1. MNI coordinates for the seeds used in Figure 2.
2.2. A Phase Transition in the Dynamics of the Active Clusters
The results in the previous section show that the point process can efficiently compress the information needed to reproduce the underlying brain activity in a way comparable with conventional methods such as seed correlation and independent component analysis. Importantly, while the former methods represent averages over the entire data sets, the point process, by construction, compresses, and preserves the temporal information. This potential advantage, unique of the current approach, may provide additional clues on brain dynamics. This is explored here by compiling the statistics and dynamics of clusters of points both in space and time. Clusters are groups of contiguous voxels with signal above the threshold at a given time, identified by a scanning algorithm in each fMRI volume (see Materials and Methods for details). Figure 3A shows examples of clusters (in this case non-consecutive in time) depicted with different colors. Typically (Figure 3B top) the number of clusters at any given time varies only an order of magnitude around the mean (~50). In contrast, the size of the largest active cluster fluctuates widely, spanning more than four orders of magnitude.
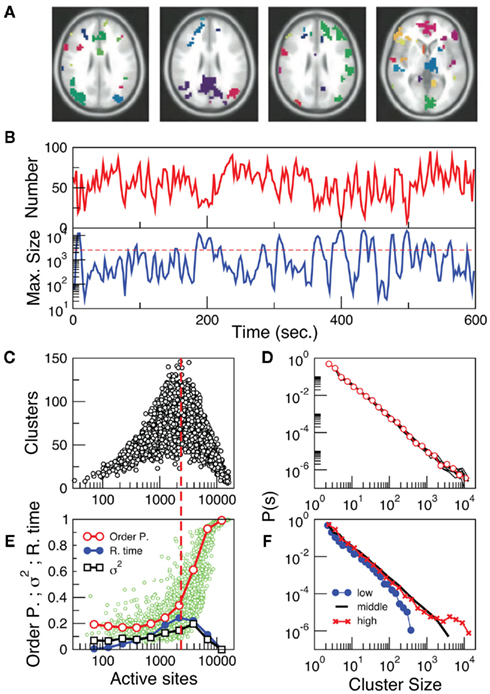
Figure 3. The level of brain activity continuously fluctuates above and below a phase transition. (A) Examples of co-activated clusters of neighbor voxels (clusters are 3D structures, thus seemingly disconnected clusters may have the same color in a 2D slice). (B) Example of the temporal evolution of the number of clusters and its maximum size (in units of voxels) in one individual. (C) Instantaneous relation between the number of clusters vs. the number of active sites (i.e., voxels above the threshold) showing a positive/negative correlation depending whether activity is below/above a critical value [~2500 voxels, indicated by the dashed line here and in (B)]. (D) The cluster size distribution follows a power law spanning four orders of magnitude. Individual statistics for each of the ten subjects are plotted with lines and the average with symbols. (E) The order parameter, defined here as the (normalized) size of the largest cluster is plotted as a function of the number of active sites (isolated data points denoted by dots, averages plotted with circles joined by lines). The calculation of the residence time density distribution (R. time, filled circles) indicates that the brain spends relatively more time near the transition point (which corresponds to about 0.4 of the largest giant cluster observed). Notice that the peak of the R. Time in this panel coincides with the peak of the number of clusters in (C). Note also that the variance of the order parameter (squares) increases as expected for a phase transition. (F) The computation of the cluster size distribution calculated for three ranges of activity (low: 0–800; middle: 800–5000; and high >5000) reveals the same scale invariance plotted in (D) for relatively small clusters, but shows changes in the cut-off for large clusters.
The analysis reveals four novel dynamical aspects of the cluster variability which hardly could have been uncovered with previous methods. (1) At any given time, the number of clusters and the total activity (i.e., the number of active voxels) follows a non-linear relation resembling that of percolation (Stauffer and Aharony, 1992). At a critical level of global activity (~2500 voxels, dashed horizontal line in Figure 3B, vertical in Figure 3C) the number of clusters reaches a maximum (~100–150), together with its variability. (2) The correlation between the number of active sites (an index of total activity) and the number of clusters reverses above a critical level of activity, a feature already described in other complex systems in which some increasing density competes with limited capacity (Stauffer and Aharony, 1992; Bak, 1996). (3) The rate at which the very large clusters (i.e., those above the dashed line in 3B) occurs (~ one every 30–50 s) corresponds to the low frequency range at which RSN are typically detected using PICA (Beckmann and Smith, 2004; Beckmann et al., 2005). (4) The distribution of cluster sizes (Figure 3D) reveals a scale-free distribution (whose cut-off depends on the activity level, see Figure 3F).
These four features remind of other complex systems undergoing an order-disorder phase transition (Bak, 1996; Jensen, 1998; Tsang and Tsang, 1999; Chialvo, 2010; Tagliazucchi and Chialvo, 2011) thus suggesting further exploration. Following standard techniques in statistical physics, two parameters were defined and computed from the same data plotted in Figure 3C. To represent the degree of order (i.e., the order parameter), the size of the largest cluster (normalized by the number of active sites) in the entire brain was computed and plotted as a function of the number of active points (i.e., the control parameter). This was done for all time steps and plotted in Figure 3E (small circles). We avoided the use of the branching ratio (Beggs and Plenz, 2003) as a control parameter because its estimation from the data is less than straightforward. It cannot be computed for each fMRI volume as required here and only converges to a stable quantity for relatively long time series. In addition, it requires the ad hoc definition of the number of bins and a suitable bin-width for its computation (Beggs and Plenz, 2003), therefore making its use cumbersome for the spatiotemporal resolution of the present study. On the other hand, the parameter used here (i.e., global level of activity) is computed in a straightforward manner, converges relatively fast, requires no fine tuning of parameters and has clear analogies to control parameters of well studied models of order-disorder transitions (the clearest example being percolation; Stauffer and Aharony, 1992).
Several key features are worth to mention, all highly suggestive of a phase transition: First, there is sharp increase in the average order parameter (empty circles), accompanied by an increase of its variability (empty squares). Second, the transition coincides with the peak in the function discussed in Figure 3C, which accounts for the number (not the size) of the clusters. Finally, a calculation of the relative frequency of the number of active sites was performed (i.e., residence times, filled circles) showing that the brain spends, on the average, more time near the transition than in the highly ordered or the highly disordered states. This is a remarkable support for earlier conjectures suggesting that the brain at large-scale works at criticality (Bak, 1996; Chialvo, 2010; Expert et al., 2011; Tagliazucchi and Chialvo, 2011).
2.3. Activity Spread is Scale-Free
The identification of a phase transition in the resting brain suggested additional work to characterize its properties, including a quantification of the dynamical properties of cluster spatial evolution. As shown in the example of Figure 4A an activated cluster can appear, grow to achieve a maximum size and then disappear (or translate or divide into sub-clusters). The present approach allows the study of two properties of the process. For each cluster we first measured a static space filling property, the average fractal dimension D. This is shown in Figure 4B which illustrates that D ~ 2.15 ± 0.02. While the fractal dimension D departs from this value for the highly ordered and disordered regimes (Figures 4D,E), the residence time distribution computed in Figure 3E indicates that most of the time the level of activity is around the critical value, thus on average D ~ 2. Second, we looked at the dynamics of the cluster propagation, which was found to happen in bursts. The statistics in Figure 4C shows that avalanches could last up to 30 s. with sizes up to 103 and have no preferred scale, a behavior very similar to that of neuronal avalanches described previously in smaller scales (Beggs and Plenz, 2003; Petermann et al., 2009; Chialvo, 2010).
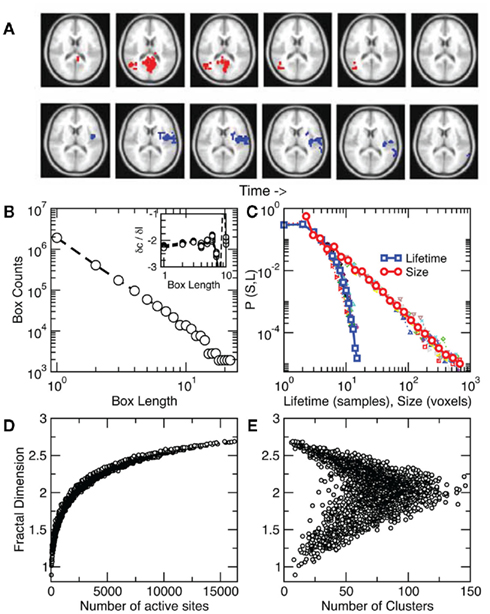
Figure 4. Clusters spread throughout the brain as scale-free avalanches. (A) Two examples of avalanches, one triggered from the visual cortex (top) and another from insular cortex (bottom). Note that only a partial 2D slice is depicted here since avalanches evolve in 3D. (B) Average cluster fractal dimension D ~ 2.15 ± 0.02 estimated by the slope of the counts vs. length plot. Inset: derivatives between points in the main plot for each subject. (C) Avalanche size and lifetime distribution function computed from about 8000 avalanches in each of 10 subjects (individual subjects with smaller symbols). While avalanche size follows a power law, their lifetimes density decreases faster as found previously for neuronal avalanches (Beggs and Plenz, 2003). The average cluster fractal dimension is plotted as a function of the number of active sites in (D) and of the number of clusters in (E).
3. Discussion
As far as we know, this is the first attempt to describe large-scale brain fMRI dynamics as a point process and the first to uncover a phase transition in the dynamics of the active clusters, with scale-free avalanching events in the whole human cortex. Regarding the point process analysis, the only previous report we are aware of (Vedel Jensen and Thorarinsdottir, 2007) dealt with the reverse situation: how to model the continuous fMRI signal starting from a spatiotemporal point process.
3.1. Why Few Points Suffice?
At first sight, the continuous nature of the fMRI BOLD signal, imposed by the nature of the neurovascular coupling itself (Friston et al., 1995, 1998), might have hindered the introduction of point process methods for its analysis. The situation is analogous to that of continuous rhythmic activity arising in scalp EEG due to predominant frequencies in the spiking activity and sub-threshold oscillations which underlie the generation of discrete action potentials (Traub et al., 1989; Steriade et al., 1993; Contreras and Steriade, 1995). We have shown that the application of HRF deconvolution gives a way to invert the process and find the train of impulse-like signals (of whatever origin) which closely resembles the point process. The fact that the majority of the points coincide with the peaks of the BOLD HRF-de-convoluted signal (i.e., Figure 1C) reinforces the view that upward going BOLD signals are non-linear events where the crossing times preserve the most relevant information. This is in line with recent findings of all-or-none “coherence potentials” macroscopically propagating in the monkey cortex, as observed in local field potential recordings (Thiagarajan et al., 2010). Therefore it seems reasonable the conjecture that, at this level of coarse graining, we are dealing with all-or-none intermittent avalanching events which involve short and long range cortical co-activations.
Another remark needs to be made concerning the HRF: while it is true that extensive work established the fundamental details of the brain’s BOLD HRF responding to a well defined (single or repetitive) stimulus, less is known about the BOLD response under the non-stationary conditions of resting state, in other words, the nature of the resting state HRF remains unknown. A theoretical formalism for the neuro-BOLD coupling at rest, as far as we know, has not been attempted but probably deserves to be considered in the future. Such studies should clarify up to what extent the HRF function obtained from stimuli spaced by relatively long intervals can predict the temporal evolution of the BOLD signal measured during resting state.
3.2. Scale-Invariant Brain Dynamics is Made up of Avalanches
The reduction of the fMRI BOLD signal to discrete events not only allows for the identification of well-described resting state networks as shown in Figure 2, but also reveals that large-scale brain activity organizes in avalanches of activity with power law size distributions. The point process approach allowed for the first time to identify explicitly the order and control parameters and to define the state of the resting brain as a fluctuation around a phase transition. The analysis shows not only that activity spreads as scale-free avalanches resembling those seen in smaller scales (Beggs and Plenz, 2003) but – and importantly – that the brain spends most of the time at a level of activity which corresponds to the critical point. These new findings add to the previous observations that the correlation function of fMRI BOLD signals exhibits fractal properties (Expert et al., 2011) and that the correlation length of the activity measured with fMRI diverges as predicted by the theory of phase transitions (Fraiman and Chialvo, 2010), supporting the hypothesis that brain dynamics operates at a critical point of a second order phase transition (Bak, 1996; Chialvo, 2010; Tagliazucchi and Chialvo, 2011).
In connection with previous experiments, one must emphasize that for a non-equilibrium system in a critical state avalanches are observed at a wide range of temporal and spatial scales. Observations at smaller scales (Beggs and Plenz, 2003) show a clear cut-off of the avalanche distribution at the size of the electrode array used for the recordings (signaling that the experimental technique is unable to sample larger events) as well as a distortion of the distribution caused by sub-sampling effects (Priesemann et al., 2009). Due to very good spatial resolution and whole brain coverage fMRI allows to overcome these issues in the macroscopic domain (≈1 mm). The observation of identically distributed avalanches at this level is direct evidence that the brain spatiotemporal dynamics is scale-free, as expected for a critical system. The present work also suggests the study of intermediate scales accessible by means of other experimental techniques to give further support for or against this hypothesis.
The observation that large-scale brain dynamics can be traced as discrete scale-free avalanches of activity raises the question of the physiologically relevance encoded in the timing of these large-scale events, already suggested by observations at smaller scales and computational models (Kinouchi and Copelli, 2006; Shew et al., 2009, 2011; de Arcangelis and Herrmann, 2010). For instance, although relatively rare, avalanches in the tail of the power law distribution emerge from a local origin and propagate as far as the length of the entire cortex, suggesting a role in the binding processes of far apart cortical regions. It would be interesting to investigate whether total or partial disruption of these large events, as well as alterations in the balance between activation and segregation into clusters are correlated with pathological conditions and with the level of awareness of the subject. Additionally, the non-linear relation between activated cortical tissue and number of clusters exhibits an optimal point, in which the level of brain activity is segregated into the maximum number of spatially isolated activations. We can hypothesize that this result is relevant to the solution of the integration/segregation dilemma long advocated by Tononi et al., 1994; Sporns, 2010) as the fundamental conundrum that the healthy cortex needs to be executing at any given time. If our hypothesis is true, we can predict, together with integration/segregation theories of consciousness (Tononi et al., 1994; Tononi, 2004), that a displacement of the optimal point should be observed for brain states of diminished conscious content such as deep sleep, anesthesia, or coma (Lee et al., 2009).
3.3. Synchrony Does not Always Implies Order
A special place in the discussion should be dedicated to analyze the similarities and differences between the definition of the order parameter and phase transition used here and the concept of synchrony widely used in previous studies. To place this point in context, it is appropriate to recall the earlier studies a decade ago, by Varela and colleagues (Rodriguez et al., 1999) investigating the brain electrical activity of subjects viewing ambiguous visual stimuli (perceived either as faces or as meaningless shapes). They were able to show for the first time that “only face perception induces a long-distance pattern of synchronization, corresponding to the moment of perception itself and to the ensuing motor response. A period of strong desynchronization marks the transition between the moment of perception and the motor response” (Rodriguez et al., 1999). These results lead to the authors to suggest that “this desynchronization reflects a process of active uncoupling of the underlying neural ensembles that is necessary to proceed from one cognitive state to another” (Rodriguez et al., 1999). A number of papers followed Varela et al. idea (Rodriguez et al., 1999) that synchrony is physiologically relevant. At the fMRI level the timing and length of these epochs of synchrony were used recently to infer the presence of criticality (Kitzbichler et al., 2009). The present results indicate that while order (as defined here) implies always synchrony, the reverse is not always true, since space is not manifest in the definition of synchrony and then one can have a very synchronic but (spatially) disordered pattern of brain activity. Since our results indicate that the brain at rest spends most of its time in a mix of order and disorder, it would be very interesting in future studies to relate Varela’s synchrony-asynchrony concept with the current ideas of proximity to a order-disorder transition.
3.4. Ad hoc Noise vs. Non-Equilibrium Dynamics
Attempts to construct biologically realistic equilibrium models of brain networks require as a main ingredient the introduction of (sometimes finely tuned) noise (Deco et al., 2009; Rolls and Deco, 2010). In this type of models, without the external noise the dynamics are stuck in a stable equilibrium state, thus noise must be introduced ad hoc to allow sufficient variability in the dynamical behavior of the system. One should be very careful, however, not to over-emphasize the biological relevance of a construct needed to overcome the shortcomings of a restricted class of models. Statistical physics results tell us that dynamical fluctuations around stationary states are small except near critical points (Prigogine, 1962).On the contrary, a non-equilibrium system undergoing criticality does not need the introduction of noise: variability is self-generated by the collective dynamics which spontaneously fluctuate near the critical point (for further discussion, see (Tagliazucchi and Chialvo, 2011)). Coincidently, the present results show that the spatiotemporal organization of the resting brain dynamics achieves maximum variability (i.e., Figures 3C,E) at a particular level of activation, and the analysis of the order and control parameters reveals that the origin of such variability can, in fact, be traced to a phase transition. Furthermore, the level of activity spends the largest amount of time around such transition. Then, these results point out that a different class of models is needed: one that emphasizes non-equilibrium self-generated variability over ad hoc introduced noise of uncertain origin.
3.5. Relation with Other Scales
The present results gathered in a large-scale domain can be also analyzed at the light of earlier observations of transient states at faster time scales, in which the scalp EEG is reduced to a certain number of stereotypical topographical maps (i.e., EEG microstates) (Koenig et al., 2002) and non-stationarities which define discrete segments of electrical activity are observed (Kaplan et al., 2005). Both descriptions of electrical scalp activity have also been shown to exhibit properties consistent with critical dynamics (Allegrini et al., 2010; Van De Ville et al., 2010). Further multimodal imaging studies could link these observations together in the context of discrete avalanches of neural activity propagating through the cortex and determine their functional relevance for health and disease (Greicius et al., 2004). Also, future work on the analysis of large-scale spontaneous fMRI signals as a train of activations should take advantage of the fact that the temporal information is not completely discarded (as in a straightforward correlation analysis) but kept in the timing of the events. The point process extracted from the BOLD signal can thus provide valuable information on the transient co-activations (or co-participation in an avalanche) of different brain regions. This measure can then be of value if correlated with the aforementioned EEG measures of instantaneous synchronization, as well with spontaneous index of perception or task performance.
3.6. Limitations of the Approach
The most obvious limitations of the point process approach stem from the spatiotemporal resolution of the fMRI recordings (i.e., TR and voxels dimensions) as well as the time constant of the BOLD HRF. Because of these limitations it is in principle impossible to distinguish two points in the process which are spaced by less than a characteristic time, as well as to detect very small clusters or avalanches whose size is smaller than the voxel dimensions. Therefore, it is impossible to guarantee that all points and clusters are included in the statistical analysis. However, since those which may be left out have (by definition) the smallest contributions, results are unlikely to be affected by this limitation. Another possible drawback of the method is that, while it yields more information than other methods such as linear correlation, there is a free parameter (threshold) to select. Nevertheless, in the Materials and Methods section we show that results are robust against different threshold choices.
3.7. Summing Up
Overall, the results show that the location and timing of the largest BOLD fluctuations define a spatial point process containing substantial information of the underlying brain dynamics. Despite the very large data reduction (>94%), the approach was validated by the favorable comparison of the conditional rate maps of avalanching activity with those constructed with the full fMRI BOLD signals using PICA as well by comparison with two distinct pathophysiological conditions (resting state in CBP patients and a finger tapping task). In addition to uncover new dynamical properties for the activated clusters, the method exposed scale-invariant features conjectured in the past (Chialvo, 2010) which are identical to those seen at smaller scales (Beggs and Plenz, 2003; Petermann et al., 2009; Chialvo, 2010). For the first time, the order and control parameters have been derived from human fMRI data allowing the identification of a phase transition and the demonstration that the resting brain spends most of the time near criticality. Beyond its potential value for fMRI signal processing, the ability of the present approach to capture relevant spatiotemporal brain dynamics underscoring non-linear aspects of the BOLD signal deserves further exploration.
4. Materials and Methods
4.1. fMRI Data Acquisition and Preprocessing
Data was obtained, after informed consent, from ten right-handed healthy volunteers (9 female, 1 male; mean age = 49, SD = 12), during 10 min, requested to keep their eyes closed and to avoid falling asleep. The study was approved by the Clinical Research Ethics Committee of the University of the Balearic Islands (Palma de Mallorca, Spain). fMRI data acquisition was performed with a GE Medical Systems Signa HDx 3 T scanner using echo-planar sequences, 240 volumes were acquired with a TR of 2500 ms, TE of 35 ms, and 90° flip angle. Thirty-six slices of 64 × 64 dimensions were obtained with a field of view of 200 mm and slice thickness of 3 mm. Structural images consisted of a T1-weighted scans of 176 × 512 × 512 voxels, with a TR of 7176 ms, TE of 3150 ms, flip angle of 12°, FOV 240 mm and slice thickness of 1 mm. Preprocessing of BOLD signal was performed using FMRIB Expert Analysis Tool (Jezzard et al., 2001)2, including motion correction using MCFLIRT, slice-timing correction using Fourier-space time series phase-shifting, non-brain removal using BET and spatial smoothing using a Gaussian kernel of full-width-half-maximum 5 mm. Brain images were normalized to standard space with FLIRT using the MNI 152 template and resampled to 4 mm × 4 mm × 4 mm resolution. Resting functional data was filtered with a zero lag finite impulse response band pass filter (0.01–0.1 Hz; Cordes et al., 2000, 2001). fMRI data used for the Figures 2D,E, as well as the preprocessing steps, were the same than in (Tagliazucchi et al., 2010a) and (Tagliazucchi et al., 2010b). Melodic was used for the PICA calculation of RSN (Beckmann and Smith, 2004) in Figure 2 as well as for denoising motion artifacts.
4.2. Definition of the Point Process
The point process is defined by the sequences of time points at which the BOLD signal crosses a given threshold from below. Formally, the problem is defined in an autonomous system as

where the dot denotes time derivative and 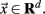 Let
Let 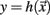 be a scalar observable function (such as the BOLD signal, for instance) and consider the plot of y versus t. The times at which y(t) upward (or downward) crosses some predetermined threshold y = yc determine a sequences of time points {tk}k=1,N which defines the so-called point process (see Figure 5).
be a scalar observable function (such as the BOLD signal, for instance) and consider the plot of y versus t. The times at which y(t) upward (or downward) crosses some predetermined threshold y = yc determine a sequences of time points {tk}k=1,N which defines the so-called point process (see Figure 5).
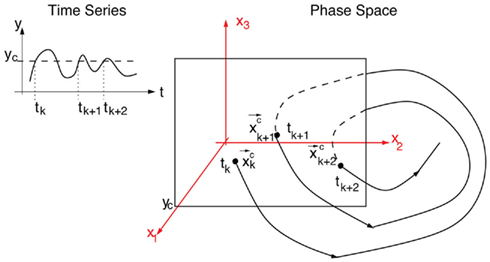
Figure 5. Example of a Poincaré section defined by successive intersections of the trajectories in phase space with the plane denoted as y = yc. The trajectory in phase space intersects the Poincaré section in space coordinates 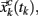 which then can be used as a map of the underlying dynamical process. Alternatively, a map can be defined by the sequence of crossing times {tk}k=1,N if the conditions mentioned in the text are fulfilled.
which then can be used as a map of the underlying dynamical process. Alternatively, a map can be defined by the sequence of crossing times {tk}k=1,N if the conditions mentioned in the text are fulfilled.
The Poincaré section of any given dynamical system reduces a d-dimensional continuous time description into an associated (d-1)-dimensional discrete map by finding the intersections of trajectories in phase space with a surface S transverse to the flow. If 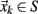 denotes the kth intersection of the trajectories with S, a Poincaré map is defined as
denotes the kth intersection of the trajectories with S, a Poincaré map is defined as

A sequence of crossing times may be taken as a Poincaré section as representative as the typical phase space coordinates, when certain conditions are satisfied: Let 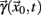 a solution of Eq.(1) in an open interval I = |t0, T| and let
a solution of Eq.(1) in an open interval I = |t0, T| and let 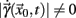 for all t ∈ I. In terms of the underlying dynamical system, this means that the dynamics is not in a fixed-point or equilibrium of the system (as one can assume for the BOLD signal and neural dynamics in general). Under this condition, the arc-length, defined as
for all t ∈ I. In terms of the underlying dynamical system, this means that the dynamics is not in a fixed-point or equilibrium of the system (as one can assume for the BOLD signal and neural dynamics in general). Under this condition, the arc-length, defined as 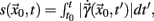 is a suitable observable in the sense of embedding theory (Hegger and Kantz, 1997) and it is possible to reconstruct the attractor of the system by measuring line segments
is a suitable observable in the sense of embedding theory (Hegger and Kantz, 1997) and it is possible to reconstruct the attractor of the system by measuring line segments 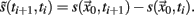
The derivative of s with respect to t, 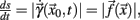 allows us to rewrite equation 1 as a set of differential equations in
allows us to rewrite equation 1 as a set of differential equations in 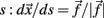 and this gives the possibility to use the time t as an usual variable, which is no longer the independent parameter but an usual coordinate as the variable
and this gives the possibility to use the time t as an usual variable, which is no longer the independent parameter but an usual coordinate as the variable 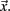 Thus, the embedding theorems also apply to time or properly defined time sequences and it is possible to reconstruct the attractor (i.e., the full properties of the underlying dynamical system) from this sequence of times (i.e., the point process), as discussed in Hegger and Kantz (1997).
Thus, the embedding theorems also apply to time or properly defined time sequences and it is possible to reconstruct the attractor (i.e., the full properties of the underlying dynamical system) from this sequence of times (i.e., the point process), as discussed in Hegger and Kantz (1997).
4.3. Deconvolution Process
The fMRI BOLD signal was de-convoluted using the deconvlucy.m function from Matlab3. For the Hemodynamic Response Function (HRF) standard parameters were those provided in the SPM8 package4. The deconvolution function follows the Lucy-Richardson algorithm (Richardson, 1972; Lucy, 1974) which converges to the maximum likelihood estimate of the de-convoluted process assuming a Poissonian source of noise. The results of the deconvolution, as in the example presented in Figure 1C, are impulse-like signals, whose underlying neural mechanisms are beyond the scope of the present work. Note that the deconvolution of all voxel’s time series is in principle possible, however its numerical implementation is several orders of magnitude less efficient than the simple thresholding used here.
4.4. Conditional Rate Maps
To construct the conditional rates reported in Figure 2 the point process is defined at a seed location and at the targets throughout the entire brain. Figure 6 illustrates the basic procedure. The BOLD signal is extracted from a seed region (top trace) and the points (arrows and vertical dashed lines) are defined by the crossings at 1 SD (horizontal dashed lines). Every time the signal at a target region crosses the threshold (asterisks) up to 2 time steps later than in the seed, the rate at the target is increased in one unit. This rate is normalized by the number of points in the seed. The top panel shows the location of the seed and of the two example targets, as well as the resulting average conditional rates maps (left) and DMN obtained from PICA (right). Medium panels show the BOLD signal at the seed and at the two example target regions. A similar procedure was used in (Tagliazucchi et al., 2010b) where the resting BOLD event triggered averages (rBeta) were calculated at similar seed and target regions. Table 1 contains the seed coordinates used to reproduce the RSNs.
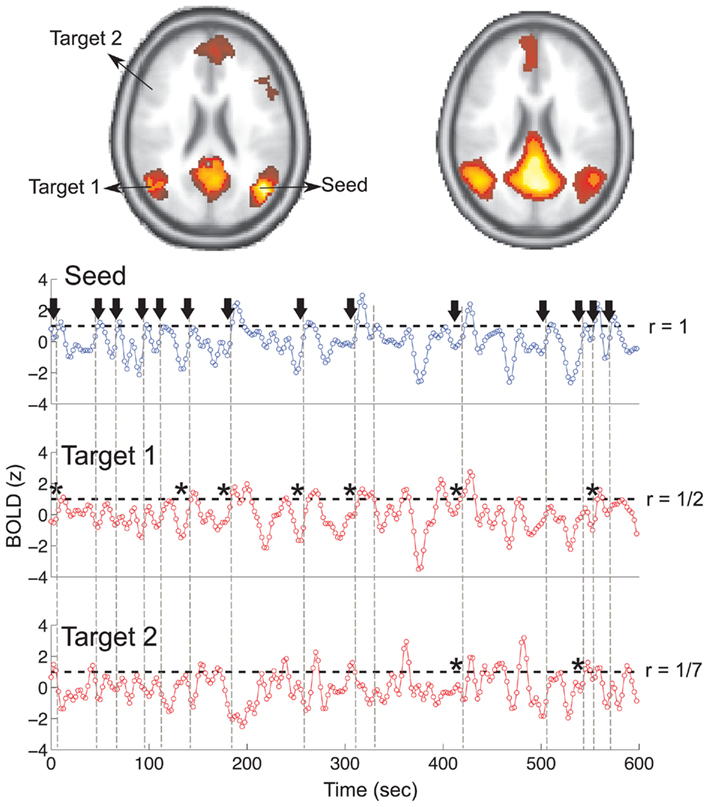
Figure 6. Illustration of the basic procedure to calculate the conditional rate maps presented in Figure 2. The r values on the right side of the traces correspond to the conditional rates between the 14 events at the seed and those at the two targets (1/2 and 1/7 in this example).
4.5. Clusters and Avalanches
Spatial clusters of activated voxels were identified using an algorithm implemented in MATLAB, based on the detection of connected components in a co-activated first neighbors graph. Clusters’ fractal dimension was calculated using a standard box-counting algorithm. Avalanches were defined (similar as in sandpile models, and others (Bak, 1996; Jensen, 1998)) as starting with the isolated activation (i.e., not by any of its neighbors) of a previously inactive voxel (or group of voxels), continuing while at least one contiguous voxel is active in the next time step and otherwise ends. The avalanche tracking algorithm implemented in this work uses as a criteria for avalanche membership the non-empty intersection with a previously identified cluster of the avalanche at a previous time. This is able to resolve shrinking and expanding of clusters, translation, and division, whenever there is spatial overlap at subsequent times.
4.6. Cluster Detection Algorithm
To detect contiguous clusters of activated voxels (defined as those crossing the threshold), for each time step, the problem was reduced to the detection of connected components in a suitably defined graph or network. More precisely, for each volume, a graph was constructed having each voxel as a node, and two nodes connected with a link if they were both activated (BOLD signal above 1 SD) and also first neighbors in the spatial sense. The connected components of this graph correspond to clusters of contiguous activated voxels isolated from other similarly defined clusters.
4.7. Avalanche Detection Algorithm
In simple terms an avalanche starts with the activation of a previously inactive voxel, follows while in the next time step at least one contiguous voxels is active and otherwise ends. The avalanche detection algorithm is based on the connected cluster decomposition. Clusters are followed during different volumes, belonging to the same avalanche if they have spatial intersection during consecutive times. Formally, the algorithm is as follows: Let 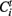 be the i-th cluster at time t. We consider a cluster i0 starting an avalanche at time t0 if for all j,
be the i-th cluster at time t. We consider a cluster i0 starting an avalanche at time t0 if for all j, 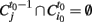 (i.e., no clusters were present in that region of the brain at the previous time step). An id is assigned to this avalanche and the same id is assigned to all clusters intersecting this cluster at the following time, this is all clusters i such that
(i.e., no clusters were present in that region of the brain at the previous time step). An id is assigned to this avalanche and the same id is assigned to all clusters intersecting this cluster at the following time, this is all clusters i such that 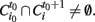 The same procedure is applied recursively to all clusters satisfying the former condition until no more intersections are found. When this happens, all clusters labeled with this id constitute the avalanche.
The same procedure is applied recursively to all clusters satisfying the former condition until no more intersections are found. When this happens, all clusters labeled with this id constitute the avalanche.
Robustness Against Threshold Changes
In this work, the only free parameter used in the definition of the point process is the threshold. In this sense, it is important to know how the main spatiotemporal statistical properties of the point process dynamics, namely cluster size distributions, avalanche size and duration distributions depend on threshold values. Figure 7 shows that these results are robust against changes in threshold over a wide range of choices.
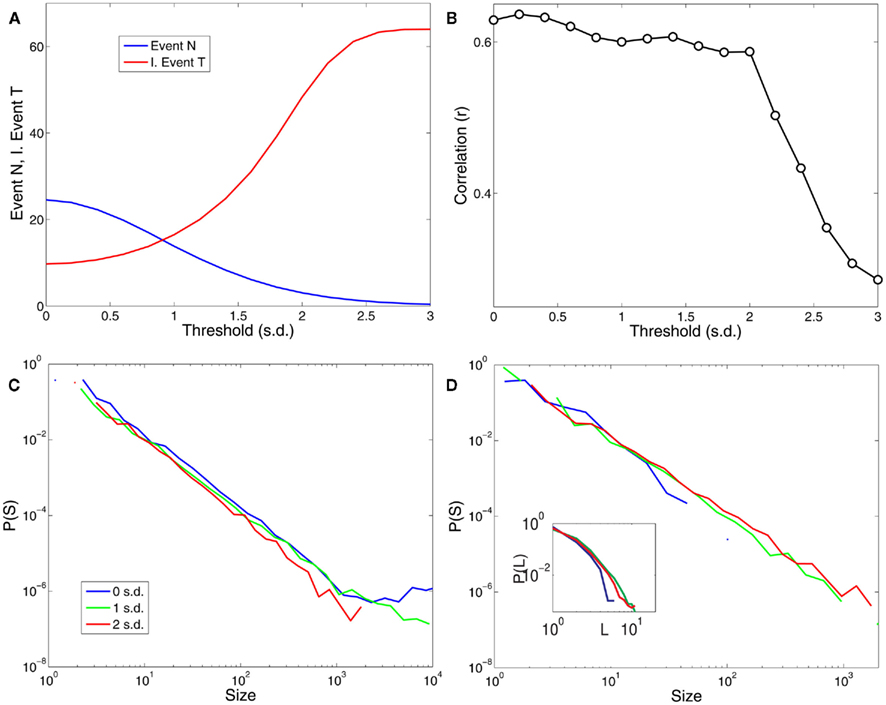
Figure 7. The results are robust to changes in the threshold over a reasonable range. (A) Shows the dependence of the number of points and the average inter-event time (expressed in units of samples or scanning volumes) for a range of threshold values (in units of SD). (B) Illustrates the dependence of the correlations plotted in Figure 2C (correlations with PICA DMN) with respect to the threshold values. (C) Shows the distribution of cluster sizes and (D) the avalanche sizes and avalanche durations (inset) for three different thresholds values (0, 1, and 2 SD).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Work supported by NIH (USA), CONICET (Argentina) PIP 0802/10 and the MCyT (Spain). Enzo Tagliazucchi was partially funded by an Estímulo Fellowship (Universidad de Buenos Aires, Argentina), by the Bundesministerium fur Bildung und Forschung (grant 01 EV 0703) and LOEWE Neuronale Koordination Forschungsschwerpunkt Frankfurt (NeFF). The authors thank Dr. P. Montoya (University of Isles Baleares, Mallorca, Spain) for discussions and help in data acquisition.
Footnotes
References
Aguirre, G. K., Zarahn, E., and D’Esposito, M. (1998). The variability of human BOLD hemodynamic responses. Neuroimage 8, 360–369.
Allegrini, P., Paradisi, P., Menicucci, D., and Gemignani, A. (2010). Fractal complexity in spontaneous EEG metastable-state transitions: new vistas on integrated neural dynamics. Front. Physiol. 1:128, 1–9.
Bak, P. (1996). How Nature Works: The Science of Self-Organized Criticality. New York: Copernicus Books.
Beckmann, C. F., DeLuca, M., Devlin, J. T., and Smith, S. M. (2005). Investigations into resting-state connectivity using independent component analysis. Philos. Trans. R. Soc. Lond. B Biol. Sci. 360, 1001–1013.
Beckmann, C. F., and Smith, S. M. (2004). Probabilistic independent component analysis for functional magnetic resonance imaging. IEEE Trans. Med. Imaging 23, 137–152.
Beggs, J. M., and Plenz, D. (2003). Neuronal avalanches in neocortical circuits. J. Neurosci. 23, 11167–11177.
Castro, R., and Sauer, T. (1997). Correlation dimension of attractors through interspike intervals. Phys. Rev. E 55, 287–290.
Contreras, D., and Steriade, M. (1995). Cellular basis of EEG slow rhythms: a study of dynamic corticothalamic relationships. J. Neurosci. 15, 604–622.
Cordes, D., Haughton, V. M., Arfanakis, K., Carew, J. D., Turski, P. A., Moritz, C. H., Quigley, M. A., and Meyerand, M. E. (2001). Frequencies contributing to functional connectivity in the cerebral cortex in “resting-state” data. Am. J. Neuroradiol. 22, 1326–1333.
Cordes, D., Haughton, V. M., Arfanakis, K., Wendt, G. J., Turski, P. A., Moritz, C. H., Quigley, M. A., and Meyerand, M. E. (2000). Mapping functional related regions of brain with functional connectivity MR imaging. Am. J. Neuroradiol. 21, 1636–1644.
de Arcangelis, L., and Herrmann, H. J. (2010). Learning as a phenomenon occurring in a critical state. Proc. Natl. Acad. Sci. U.S.A. 107, 3977–3981.
Deco, G., Jirsa, V., McIntosh, A. R., Sporns, O., and Kotter, R. (2009). Key role of coupling, delay, and noise in resting brain fluctuations. Proc. Natl. Acad. Sci. U.S.A. 106, 10302–10307.
Expert, P., Lambiotte, R., Chialvo, D. R., Christensen, K., Jensen, H. J., Sharp, D. J., and Turkheimer, F. (2011). Self-similar correlation function in brain resting state fMRI. J. R. Soc. Interface 8, 472–479.
Fox, M. D., and Raichle, M. E. (2007). Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nat. Rev. Neurosci. 8, 700–711.
Fraiman, D., and Chialvo, D. R. (2010). Optimal information-sharing in brain resting state networks. arXiv: 1011.1192.
Friston, K. J., Fletcher, P., Josephs, O., Holmes, A., Rugg, M. D., and Turnera, R. (1998). Event-related fMRI: characterizing differential responses. Neuroimage 7, 30–40.
Friston, K. J., Frith, C. D., Turner, R., and Frackowiak, R. S. J. (1995). Characterizing evoked hemodynamics with fMRI. Neuroimage 2, 157–165.
Grassberger, P., and Procaccia, I. (1983). Measuring the strangeness of strange attractors. Physica 9D, 189–208.
Greicius, M. D., Krasnow, B., Reiss, A. L., and Menon, V. (2003). Functional connectivity in the resting brain: a network analysis of the default mode hypothesis. Proc. Natl. Acad. Sci. U.S.A. 100, 253–258.
Greicius, M. D., Srivastava, G., Reiss, A. L., and Menon, V. (2004). Default-mode network activity distinguishes Alzheimer’s disease from healthy aging: Evidence from functional MRI. Proc. Natl. Acad. Sci. U.S.A. 101, 4637–4642.
Hegger, R., and Kantz, H. (1997). Embedding of sequences of time intervals. Europhys. Lett. 38, 267–272.
Jezzard, P., Mathews, P., and Smith, S. M. (2001). Functional MRI: An Introduction to Methods. New York: Oxford University Press.
Kaplan, A. Y., Fingelkurts, A. A., Fingelkurts, A. A., Borisov, S. V., and Darkhovsky, B. S. (2005). Nonstationary nature of the brain activity as revealed by EEG/MEG: methodological, practical and conceptual challenges. Signal Process. 85, 2190–2212.
Kinouchi, O., and Copelli, M. (2006). Optimal dynamical range of excitable networks at criticality. Nat. Phys. 2, 348–351.
Kitzbichler, M. G., Smith, M. L., Christensen, S. R., and Bullmore, E. (2009). Broadband criticality of human brain network synchronization. PLoS Comput. Biol. 5, e1000314. doi:10.1371/journal.pcbi.1000314
Koenig, T., Prichep, L., Lehmann, D., Valdes Sosa, P., Braeker, E., Kleinlogel, H., Isenhart, R., and John, E. R. (2002). Millisecond by millisecond, year by year: normative EEG microstates and developmental stages. Neuroimage 16, 41–48.
Lee, U., Mashour, G. A., Kim, S., Noh, G. J., and Choie, B. M. (2009). Propofol induction reduces the capacity for neural information integration: implications for the mechanism of consciousness and general anesthesia. Conscious. Cogn. 18, 56–64.
Lucy, L. B. (1974). An iterative technique for the rectification of observed distributions. Astron. J. 79, 745–754.
Packard, N., Crutchfield, J., Farmer, J. D., and Shaw, R. (1980). Geometry from a time series. Phys. Rev. Lett. 45, 712–716.
Petermann, T., Thiagarajan, T. C., Lebedev, M. A., Nicolelis, M. A. L., Chialvo, D. R., and Plenz, D. (2009). Spontaneous cortical activity in awake monkeys composed of neuronal avalanches. Proc. Natl. Acad. Sci. U.S.A. 106, 15921–15926.
Priesemann, V., Munk, M. H., and Wibral, M. (2009). Subsampling effects in neuronal avalanche distributions recorded in vivo. BMC Neurosci. 10, 40. doi:10.1186/1471-2202-10-40
Richardson, W. H. (1972). Bayesian-based iterative method of image restoration. J. Opt. Soc. Am. 62, 55–59.
Rodriguez, E., George, N., Lachaux, J. P., Martinerie, J., Renault, B., and Varela, F. J. (1999). Perception’s shadow: long-distance synchronization of human brain activity. Nature 397, 430–433.
Roux, J. C., Rossi, J., Bachelart, S., and Vidal, C. (1980). Representation of a strange attractor from an experimental study of turbulence. Phys. Lett. A 77, 391–393.
Roux, J. C., and Swinney, H. (1981). “Topology of chaos in a chemical reaction,” in Nonlinear Phenomena in Chemical Dynamics, eds C. Vidal and A. Pacault (Berlin: Springer-Verlag), 38–43.
Shew, W. L., Yang, H., Petermann, T., Roy, R., and Plenz, D. (2009). Neuronal avalanches imply maximum dynamic range in cortical networks at criticality. J. Neurosci. 24, 15595–15600.
Shew, W. L., Yang, H., Yu, S., Roy, R., and Plenz, D. (2011). Information capacity and transmission are maximized in balanced cortical networks with neuronal avalanches. J. Neurosci. 31, 55–63.
Smith, S. M., Fox, P. T., Miller, K. L., Glahn, D. C., Fox, P. M., Mackay, C. E., Filippini, N., Watkins, K. E., Toro, R., Laird, A. R., and Beckmann, C. F. (2009). Correspondence of the brain’s functional architecture during activation and rest. Proc. Natl. Acad. Sci. U.S.A. 106, 13040–13405.
Sporns, O., Tononi, G., and Kotter, R. (2005). The human connectome: a structural description of the human brain. PLoS Comput. Biol. 1, 245–251. doi:10.1371/journal.pcbi.0010042
Steriade, M., McCormick, D. A., and Sejnowski, T. J. (1993). Thalamocortical oscillations in the sleeping and aroused brain. Science 262, 679–685.
Steyn-Rose, S. A., and Steyn-Rose, M. (eds). (2010). Modeling Phase Transitions in the Brain. New York, NY: Springer.
Tagliazucchi, E., Balenzuela, P., Fraiman, D., and Chialvo, D. R. (2010a). Brain resting state is disrupted in chronic back pain patients. Neurosci. Lett. 485, 26–31.
Tagliazucchi, E., Balenzuela, P., Fraiman, D., Montoya, P., and Chialvo, D. R. (2010b). Spontaneous BOLD event triggered averages for estimating functional connectivity at resting state. Neurosci. Lett. 488, 158–163.
Takens, F. (1980). “Dynamical systems and turbulence, Warwick,” in Lecture Notes in Math Vol. 898, eds D. A. Rand and L.-S. Young (Berlin: Springer-Verlag), 366–381.
Thiagarajan, T. C., Lebedev, M. A., Nicolelis, M. A., and Plenz, D. (2010). Coherence potentials: loss-less, all-or-none network events in the cortex. PLoS Biol. 8, e1000278. doi:10.1371/journal.pbio.1000278
Tononi, G. (2004). An information integration theory of consciousness. BMC Neurosci. 5, 42. doi:10.1186/1471-2202-5-42
Tononi, G., Sporns, O., and Edelman, G. M. (1994). A measure for brain complexity: relating functional segregation and integration in the nervous system. Proc. Natl. Acad. Sci. U.S.A. 5033–5037.
Traub, R. D., Miles, R., and Wong, R. K. (1989). Model of the origin of rhythmic population oscillations in the hippocampal slice. Science 243, 1319–1325.
Tsang, I. R., and Tsang, I. J. (1999). Cluster size diversity, percolation and complex systems. Phys. Rev. E. 60, 2684–2698.
Van De Ville, D., Britz, J., and Michel, C. M. (2010). EEG microstate sequences in healthy humans at rest reveal scale-free dynamics. Proc. Natl. Acad. Sci. U.S.A. 107, 18179–18184.
Keywords: fMRI, criticality, brain dynamics, point processes
Citation: Tagliazucchi E, Balenzuela P, Fraiman D and Chialvo DR (2012) Criticality in large-scale brain fMRI dynamics unveiled by a novel point process analysis. Front. Physio. 3:15. doi: 10.3389/fphys.2012.00015
Received: 12 December 2011;
Paper pending published: 04 January 2012;
Accepted: 23 January 2012;
Published online: 08 February 2012.
Edited by:
Zbigniew R. Struzik, The University of Tokyo, JapanReviewed by:
Riccardo Barbieri, Massachusetts Institute of Technology, USAMasanori Shimono, Indiana University, USA
Copyright: © 2012 Tagliazucchi, Balenzuela, Fraiman and Chialvo. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Dante R. Chialvo, Department of Physiology, Northwestern University, 303 East Chicago Avenue, Chicago, IL 60611, USA. e-mail: dchialvo@ucla.edu
