- 1 Department of Physics, Indiana University, Bloomington, IN, USA
- 2 Biocomplexity Institute, Indiana University, Bloomington, IN, USA
Relatively recent work has reported that networks of neurons can produce avalanches of activity whose sizes follow a power law distribution. This suggests that these networks may be operating near a critical point, poised between a phase where activity rapidly dies out and a phase where activity is amplified over time. The hypothesis that the electrical activity of neural networks in the brain is critical is potentially important, as many simulations suggest that information processing functions would be optimized at the critical point. This hypothesis, however, is still controversial. Here we will explain the concept of criticality and review the substantial objections to the criticality hypothesis raised by skeptics. Points and counter points are presented in dialog form.
Introduction
The scene: Two scientists, Critio and Mnemo, are attending a neuroscience conference. They happen to sit at the same table for lunch and strike up a conversation. This paper contains a record of that conversation. In turn, the scientists discuss criticality, evidence for criticality in neural data, various objections to this evidence, and several responses to those objections.
Critio: Hello professor. I enjoyed your presentation this morning. Your group is doing some fascinating work on synaptic plasticity. I was particularly interested in your thoughts on how synaptic changes underlie memory.
Mnemo: Thank you! I can see from your badge that you are in a physics department. What brings you to a neuroscience conference?
Critio: Well, I have been using ideas from statistical mechanics to try to explain how groups of neurons collectively behave. One of my primary research interests is determining whether or not the brain is operating at a critical point.
Mnemo: I’ve seen several papers in that area and they seem to show some interesting results. There also appears to be a great deal of controversy about criticality in biology (Gisiger, 2001; Mitzenmacher, 2004) and in neural systems (Bedard et al., 2006; Touboul and Destexhe, 2010; Dehghani et al., 2012). However, I must admit that I haven’t had the time to follow that research topic very closely.
Critio: It is definitely true that there is significant disagreement in the research community about the role criticality plays in neural dynamics (Stumpf and Porter, 2012). I happen to believe that criticality plays an important role, but other researchers disagree.
Mnemo: Well, that’s to be expected. Many topics in science are hotly debated and that’s part of the fun of being a scientist!
Critio: Oh, I agree! I just want to say that, even given my view that criticality does play an important role in neural dynamics, I recognize that it is completely possible that criticality, in fact, does not play an important role in neural dynamics. Other methodologies, such as non-linear systems might better explain neural dynamics (May, 1976; Nicolis and Prigogine, 1989).
Mnemo: Well, this certainly sounds like an interesting topic. But since we have a few minutes here, why don’t you give me a quick description of your research? I probably won’t read a review, but I could learn a few things from you over lunch. Do you mind if I pick your brain, so to speak?
Critio: Not at all! I guess I could give you an overview of criticality and how it might apply to the brain. I am somewhat biased, but I’ll do my best to present arguments from researchers who disagree with my view of criticality in neural systems. You can help me by being as skeptical of my arguments as possible.
Topology and Criticality
Mnemo: That sounds great! But before we get started, I would like to clear one thing up that has been bugging me. Several of the other researchers at my institution study network topology. I always hear them talking about scale-free networks, power laws, and criticality. Are those all the same thing?
Critio: That is an excellent question and I think it gets at a point that isn’t widely made in the literature. If we’re interested in network topology, we’re interested in how the nodes of a network are connected to each other. A scale-free network has nodes that are connected in a certain way. If we’re interested in criticality, we’re interested in how the network behaves. The two topics are certainly related, but it is possible for non-scale-free networks to exhibit critical behavior and it is possible for scale-free networks to not exhibit critical behavior. The network connectivity affects the critical behavior of that network (Haldeman and Beggs, 2005; Beggs et al., 2007; Gray and Robinson, 2007; Hsu et al., 2007; Teramae and Fukai, 2007; Larremore et al., 2011; Rubinov et al., 2011), as we can discuss if you have the time, but network connectivity and criticality are conceptually quite different.
Explaining Criticality
Mnemo: That sounds complicated! But, since I hear most people discussing criticality, let’s discuss that first. So, what is criticality?
Critio: Criticality is a phenomenon that has been observed in physical systems like magnets, water, and piles of sand. Many systems that are composed of large numbers of interacting, similar units can reach the critical point. At that point, they behave in some very unusual ways. Some people, including myself, suspect that cortical networks within the brain may be operating near the critical point.
Mnemo: This all sounds intriguing, but I have no idea what you mean by the critical point. Can you give me a simple example?
Critio: Sure, let’s use a well explored model in this field: the Ising model (Brush, 1967; Cipra, 1987). [Critio grabs a napkin and sketches the left panel of Figure 1.]
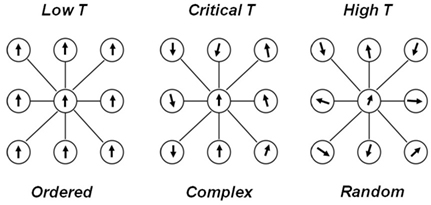
Figure 1. A simple diagram of spins in the Ising model. (Left) At low temperature, nearest neighbor interactions dominate over thermal fluctuations. As a result, almost all the spins align in the same direction, producing a very ordered state. (Right) At high temperature, thermal fluctuations dominate over nearest neighbor interactions. As a result, the spins point in different directions, producing a very disordered state. (Center) At some critical temperature, nearest neighbor interactions and thermal fluctuations balance to produce a complex state.
This model will illustrate the critical point pretty well. See these circles? They represent lattice sites in a piece of iron. At each site, there is an electron whose “spin” is either up or down. You can think of these arrows as little bar magnets, with the arrowhead being the North pole of the magnet. In a piece of iron, these bar magnets influence their nearest neighbors to align in the same direction. I will represent their influence on each other by drawing lines between the circles. So, when the temperature T is low, as in the left panel of Figure 1, these nearest neighbor interactions dominate and all the spins point in the same direction. This gives the piece of iron a net magnetization, and makes it behave like a magnet, sticking to your refrigerator. It is extremely ordered, almost boringly so. I have a movie here on my laptop from a talk I gave recently. [Critio opens up his laptop and plays Movie S1 in Supplementary Material.]
This movie shows a simulated piece of iron as the temperature is cooled. Each black square represents a spin pointed up, and each white square is a spin pointed down. See how, over time, all of the spins begin to point in the same direction? Pretty soon the whole sample will be either all black or all white. That behavior is caused by the nearest neighbor interactions.
Mnemo: So all iron is magnetic?
Critio: No, certainly not. Being ordered like that is just one phase that the piece of iron can be in. And that happens only at low T. If you heat it up, you can make it change into another phase.
Mnemo: Oh, I have heard some things about a “phase transition.” Is that where this is going?
Critio: Well, yes. If you heat up the iron quite a lot, then this increased thermal energy will begin to “jostle around” the spins. Even though they still have a tendency to align with each other, this will be overwhelmed by the added heat. [Critio sketches the right panel of Figure 1.] Now you have no order at all and things look like random static on a TV screen when it is disconnected from a cable. Here is the movie of the disordered phase. [Critio plays Movie S2 in Supplementary Material from his laptop.]
Mnemo: So is this why a magnet loses its ability to stick when it is heated up too much?
Critio: Exactly. All the spins are pointing in different directions and they cancel each other. There is no net magnetic field produced by the sample any more.
Mnemo: So now you have shown me the ordered and the disordered phases. What happens between them, at the so called “phase transition point?” Is this the same thing as the “critical point?”
Critio: Yes it is. If you add just the right amount of heat to get to the critical temperature, then the tendency for the spins to align is exactly counterbalanced by the jostling caused by the heat. Now you no longer have global order. Instead, there will be local domains where a group of spins are pointed up, and other domains where the spins are pointed down (Stanley, 1971; Yeomans, 1992). [Critio sketches the middle panel of Figure 1 above.] The sizes of these domains vary widely at this temperature; many are small but a few are quite large. So, this state is an interesting mix of order and disorder, and constantly changing over time. You can see that in this movie of a simulated piece of iron at the critical temperature. [Critio plays Movie S3 in Supplementary Material from his laptop.]
Mnemo: Wow, that is really interesting – some of the domains almost look like amoeba crawling across the screen, with boundaries that are extending and contracting. I can see that there are many different sized domains too. OK, you have been telling me a lot about this piece of iron, but how does this relate to the brain?
Criticality and Communication
Critio: Good question, but before we get to neural data, we need to understand a few more things about criticality. You certainly must agree that communication between neurons is very important for the brain. If we continue with the magnet analogy, we could ask how two spins at different lattice sites might communicate with each other.
Mnemo: Ok, go on…
Critio: A simple way to measure this would be to look at the dynamic correlation between two lattice sites. This is not the correlation that is usually used in statistics, but something that depends on coordinated fluctuations. Here is the equation for the dynamic correlation. Critio then writes down Eq. 1:
The angled brackets here indicate a time average, so 〈i〉 is the average value of the spin at site i. If the spin is pointed up, we could represent the state of the lattice site with a +1. Similarly, if the spin is pointed down, it would be represented with a −1. The average over a long time might be something like +0.2, say. So the term in the left parenthesis, (i − 〈i〉), represents the amount by which the spin at site i fluctuates from its average at a given time. Likewise, the term (j − 〈j〉) represents the amount by which site j fluctuates from its average at a given time. To make Cij large, both i and j must fluctuate, and they must do so in a coordinated manner, at the same time and in the same direction. So you need both fluctuations and coordination to have a large dynamic correlation.
Mnemo: Ok, that seems to make sense. Now I see why it is called the dynamic correlation – if both i and j are stuck pointing up, the dynamic correlation would be 0, but a static correlation would still give 1.
Critio: Great, you get it! Now let’s take a look at what happens to the dynamic correlation for the three different cases we talked about: low T, high T, and critical T. In the low T case, the piece of iron is extremely ordered and all the spins are pointed in the same direction. The dynamic correlation is low because there are no fluctuations and the terms in parentheses are both nearly 0 all the time. In contrast, for the high T case, there are plenty of fluctuations, as the spins are constantly deviating from their averages, but there is no coordination between sites i and j. One term in parenthesis might be positive, while the other might be negative. On another occasion, they might both be positive. So on average the dynamic correlation is again low. But at critical T, there is enough heat to allow fluctuations, but not so much heat that it destroys coordination between spin sites. The spins deviate from their averages, and they often do so together because the nearest neighbor influence is not completely overwhelmed by the added heat. Here, there is both fluctuation and coordination. When one of those “amoeba-like” domains that you saw in Movie S3 in Supplementary Material crawls across the screen, it might cause nearby spins to flip one after the other, setting up a dynamic correlation. I could sketch the positions of the spins, either up or down or in between, over time for the three different cases. [Critio now pulls out red and green markers, grabs another napkin and sketches Figure 2.]
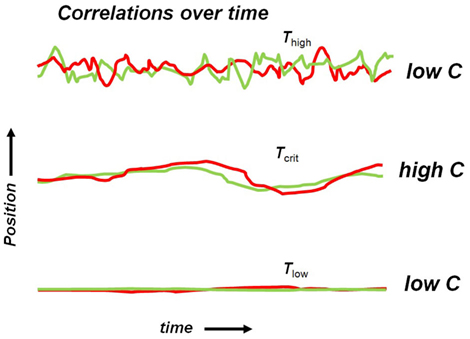
Figure 2. Hypothetical positions of two spins as a function of time. (Top) At high temperature, the spin orientations fluctuate greatly, but independently of one another, producing a low dynamic correlation value. (Middle) At the critical temperature, the spin orientations fluctuate somewhat and the fluctuations are coordinated, producing a high dynamic correlation value. (Bottom) At low temperature, the spin orientations do not fluctuate very much, yielding a low dynamic correlation value.
Mnemo: So there is dynamic correlation between spins only at the critical temperature?
Critio: Well, there might be some dynamic correlation in all three cases, but it is certainly strongest at the critical temperature. Another key difference is that the distance over which these correlations extend is greatest at the critical temperature.
Mnemo: Can you show me what you mean by that?
Critio: Sure. If we were to measure the dynamic correlation between two spin sites i and j as a function of distance, we would find out that it decreases with distance in all cases. Remember that in this model, we have only built in connections between nearest neighbor spins. So you wouldn’t expect the correlation to extend much beyond that, at least when the temperature is very high or very low. But at the critical temperature, we find that the dynamic correlation is above 0 well beyond the nearest neighbor distance. [Critio sketches Figure 3.]
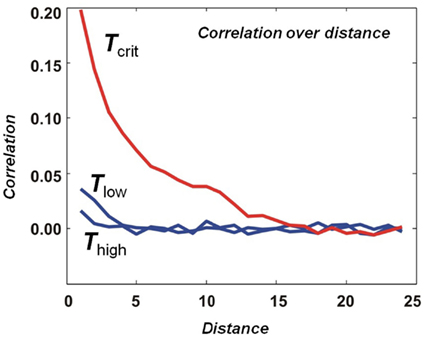
Figure 3. Average dynamic correlation as a function of distance. At high and low temperatures, the average dynamic correlation between two lattice sites decreases rapidly toward 0 as the distance between the lattice sites is increased. At the critical temperature, the average dynamic correlation also decreases toward 0 as the distance is increased, but much more gradually.
Critio: In this example from a simulation, the dynamic correlation at the critical temperature extends about 15 lattice sites before it drops down to near 0. We call the distance at which the dynamic correlation first reaches 0 the “correlation length” and it is often given by the Greek capital letter gamma, Γ; in this case the correlation length is 15 lattice sites long. We didn’t build this length into the model – it merely emerged at the critical temperature. At this temperature, when one spin flips from down to up, for example, it might influence one of its nearest neighbors to also flip, which might in turn influence one of its nearest neighbors and so on. In this way, the movement at one lattice site can propagate beyond the nearest neighbor length. You could draw the correlation length as a function of temperature, and it would show a sharp peak at the critical point. [Critio asks another person sitting at the table for a fresh napkin and draws Figure 4.]
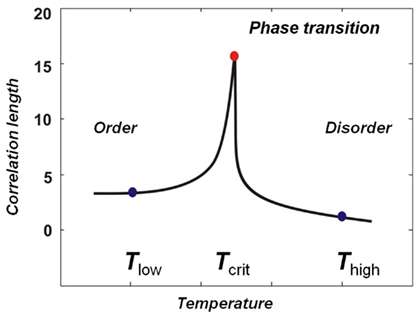
Figure 4. Correlation length as a function of temperature for a simulation of the Ising Model. Near the critical temperature the correlation length rapidly approaches a maximum value. This sharp peak separates the ordered phase from the disordered phase and occurs at the phase transition point.
Critio: Again, this shows the separation of phases nicely. On the left you have the ordered phase, with low temperature. This is sometimes called the subcritical regime. On the right you have the disordered phase, with high temperature, and this is sometimes called the supercritical regime. Between them you have the phase transition region, which is very narrow and occurs at the critical temperature.
Mnemo: I think I see what is going on. Only at the critical temperature can you have communication that spans large distances. So if I were to make an analogy with a neural network, it would be that at the critical point, the neurons can communicate most strongly and over the largest number of synapses, right?
Critio: Exactly!
Mnemo: But wait, what do you mean by “communication?” When the model is at low temperatures, the state of one lattice site strongly influences the state of lattice sites throughout the whole network. So, it would seem to me that communication is maximized when the temperature is low, not when the system is at the critical point.
Critio: Ah, that is a subtle point. Clearly, we haven’t been very rigorous with our definition of “communication,” but let me see if I can clarify my point. When the model is at low temperatures, the coupling between the lattice sites is strong, so coordination is high. However, the state of each lattice site doesn’t change very much through time, so fluctuations are low. Communication requires both coupling and variability, or in other words, both coordination and fluctuation. If communication is to take place, lattice sites must be able to influence each other and that influence must actually affect changes. Does that make more sense?
Mnemo: Yes, I see your point about the distinction between communication and coupling.
Critio: Great! So, at the critical point these two qualities of the system – coupling and variability – are balanced to produce long distance communication. And it turns out that it is not just communication that would be optimized at the critical point (Beggs and Plenz, 2003; Bertschinger and Natschlager, 2004; Maass et al., 2004; Ramo et al., 2007; Tanaka et al., 2009; Chialvo, 2010; Shew et al., 2011). Many other researchers have pointed out, with very general models, that information storage (Socolar and Kauffman, 2003; Kauffman et al., 2004; Haldeman and Beggs, 2005) and computational power (Bertschinger and Natschlager, 2004) are expected to be optimized there as well (Chialvo, 2004, 2010; Plenz and Thiagarajan, 2007; Beggs, 2008). In addition, the ability of the network to respond to inputs of many different sizes, called its dynamic range, is expected to be optimal at the critical point (Kinouchi and Copelli, 2006; Shew et al., 2009). Phase synchrony also appears to be optimized at the critical point (Yang et al., 2012).
Mnemo: So this sounds pretty reasonable to me so far. But it is only an analogy. You haven’t shown me any evidence to suggest that the brain might be doing this. What evidence, if any, do you have to make me think that this is connected to real neurons?
Criticality and Power Laws
Critio: Again, a very fair question. Before we can get to the neural data, I first need to show you how I got interested in this topic. Let me return for a moment to the plot of the average dynamic correlation length. If I were to change the axes by making them both logarithmic, then I would get something like this for the dynamic correlation, plotted now only for the critical case. [Critio draws Figure 5.]
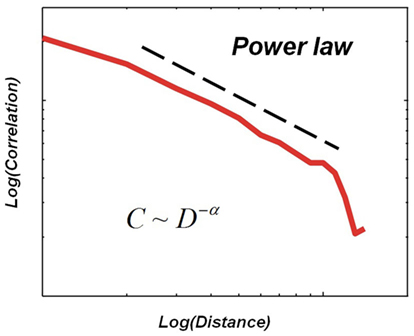
Figure 5. Hypothetical relationship between the average dynamic correlation between two lattice sites and the distance between those lattice sites at the critical temperature in a small simulation of the Ising model.
Critio: When plotted this way, the dynamic correlation approximates a straight line over part of its range. This suggests that it could be described by a so-called “power law,” where the dynamic correlation, C, is related to the distance, D, raised to some negative power, say −α. Note that the slope of the power law line when plotted logarithmically is given by −α. Well, the physics of critical phenomena tells us that near the critical point, a system will have many variables that can be described by power law functions (Stanley, 1971; Goldenfeld, 1992; Yeomans, 1992; Nishimori and Ortiz, 2011). In addition to the dynamic correlation as a function of distance, the distribution of domain sizes that we talked about earlier would also follow a power law at the critical point. The reason the straight line does not extend to larger distances is because the simulation had a limited size. The bigger the simulation, the further the power law line would extend.
Mnemo: Ok, for the moment I will assume you are right that this power law would extend to indefinitely large distances if the system were large enough. What is so special about a power law, besides the fact that it might suggest your system is critical?
Critio: An interesting feature of power laws is that they show no characteristic scale. When plotted in log-log coordinates, they produce a straight line that has the same slope everywhere. This implies that the data will have a fractal structure. For example, imagine what the distribution of correlation strength would look like if you were only able to sample separation distances from 101 to 102 units. It would be a straight line with a slope of −α when plotted logarithmically. Interestingly, this would look just like the distribution that you would observe if you were only able to sample separation distances from 102 to 103 units. Again, the exponent would be −α. This has caused some people to use the phrase “scale-free” when describing power law distributions (Stam and de Bruin, 2004). If you zoom in or zoom out, things look very similar (Teich et al., 1997). This self-similarity is a characteristic of fractals.
Mnemo: So is where the name “scale-free” network comes from?
Critio: Yes! In scale-free networks, the degree distribution – the distribution of the number of connections each node possesses – follows a power law. But notice, in the Ising model, the nodes are connected in a lattice and the Ising model exhibits critical behavior. So, here we can see the distinction between criticality and scale-free networks in action. The nodes are not connected as in a scale-free network, yet the activity is scale-free.
Mnemo: That is certainly interesting, but I am still searching for a strong argument, not nice pictures. So power laws are an indicator of criticality? And you are going to tell me that you see some power laws in your neural data? This is the argument? It must be more substantial than that! After all, this is science, not just loose associations!
Critio: A critical system will produce power laws, yes, but power laws do not prove criticality! There are many ways to get power laws, and I can tell you more about that in a minute. The key thing to remember here is that exhibiting power laws is strongly suggestive of criticality. However, power laws alone are not sufficient to establish criticality.
Mnemo: Ok, I want to ask about these other ways to get power laws in a minute. But to return to the issue I raised earlier, you are going to tell me about some neural data that display power laws?
Critio: Yes, I can tell you about that first and then we can get to all the potential objections.
Mnemo: That sounds fine. Proceed with the data.
Power Laws and Neural Data
Critio: Well, there were several early reports that the nervous system could produce power law distributions (Chen et al., 1997; Teich et al., 1997; Linkenkaer-Hansen et al., 2001; Worrell et al., 2002). These data all came from “one-dimensional” measurements, were a single variable, like spike count, temporal correlation, or total energy, was found to follow a power law distribution. While these important findings were very suggestive, they did not immediately provide insight as to what the underlying network was doing to produce these distributions. The earliest data to explore power law distributions at the network level came from recordings from microelectrode arrays that had 60 electrodes. There, the experimenters were able to observe bursts of spontaneous activity. They found that if they counted the number of electrodes activated in each distinct burst, that the burst sizes were distributed according to a power law (Beggs and Plenz, 2003). Because the statistics of these bursts followed the same equations used to describe avalanche sizes in critical systems, they called these events “neuronal avalanches.” I have on my laptop here a figure from one of their papers that shows the power law distribution of avalanche sizes, measured either as the total number of electrodes activated per avalanche, or as the total amplitude of local field potential (LFP) signal measured at all the electrodes involved in the avalanche. [Critio shows Figure 6 to Mnemo.]
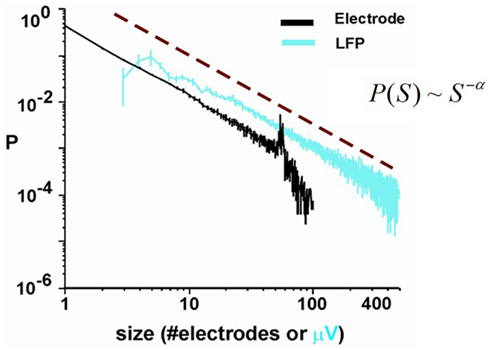
Figure 6. Probability distribution of neuronal avalanche size. (Black) Size measured using the total number of activated electrodes. (Teal) Size measured using total LFP amplitude measured at all electrodes participating in the avalanche (Beggs and Plenz, 2003).
Since these initial results, power law distributions of avalanche sizes have been reported in awake monkeys (Petermann et al., 2006, 2009), anesthetized rats (Gireesh and Plenz, 2008), isolated leech ganglion (Mazzoni et al., 2007), and dissociated cultures (Mazzoni et al., 2007; Pasquale et al., 2008), suggesting that this is a very general and robust phenomenon. It is interesting to mention that some of these reports have relied on spike data, and not just LFP data (e.g., Beggs, 2007, 2008; Mazzoni et al., 2007; Pasquale et al., 2008; Hahn et al., 2010; Friedman et al., 2011, 2012). Avalanche dynamics also have been reported in human brain oscillations (Poil et al., 2008) and there are several reports of power law scaling (Miller et al., 2009) even though these are not necessarily attributed to avalanches. In addition, the size of phase locking intervals in human fMRI has been reported to follow a power law, and the authors have related this to criticality in the awake, healthy human brain (Kitzbichler et al., 2009). This is intriguing, despite the fact that the temporal resolution of fMRI is much lower than that of electrophysiological signals from extra-cellular electrodes, so it is not yet clear if these power laws are directly related to neuronal avalanches at the local network scale.
Mnemo’s First Objection: Do the Neural Data Really Show Power Laws?
Mnemo: That is an impressive list of neural systems in which power laws have been observed. However, I seem to recall hearing that other researchers have found that these power laws were actually better fit by exponentials. Is that true?
Critio: That is true. Using sophisticated statistical tests, several researchers have shown that some data sets, none of which were from neuroscience, that were previously thought to be power law distributed are actually better fit by an exponential distribution (Clauset et al., 2009). Using analysis methods from that work, some researchers in neuroscience have argued that the supposed power laws associated with neural activity are not actually power laws, or that the power laws that have been found are artifacts (Bedard et al., 2006; Bedard and Destexhe, 2009; Touboul and Destexhe, 2010; Dehghani et al., 2012).
Mnemo: How do you escape that objection? It seems like so much of your argument is based on power laws. If those really aren’t there or if they are artifacts, then your system certainly isn’t operating at the critical point, is it?
Critio: You are right; this is a very important part of my argument. Let’s talk about each paper separately since they present distinct arguments and evidence. First, let’s discuss the papers that argue the observed power laws are artifacts. Some researchers have produced strong theoretical models that indicate that the extra-cellular medium may behave as a 1/f filter (Bedard and Destexhe, 2009). If the extra-cellular medium does, in fact, behave this way, that only explains the observed power law distribution in the LFP spectrum. But it does not necessarily explain the power law distribution in other neural phenomena, like the size distribution of neuronal avalanches. Another paper has made a notable argument that the power laws observed in avalanche size distributions are actually artifacts (Touboul and Destexhe, 2010). In that work, the authors analyzed avalanches using both positive and negative LFP peaks and found that both were fit by power laws. However, positive LFP peaks are significantly less correlated with neuron spiking activity than negative LFP peaks. So, those authors concluded that the power law avalanche size distribution is not associated with neuron spiking activity. In response, I think it is important to point out that the form of this argument is fallacious. The power law observed in the positive LFP peaks avalanche size distribution may be due to some other phenomenon and it could still be the case that the power law observed in the negative LFP peaks avalanche size distribution is related to spiking activity.
Mnemo: I see your point, what about the other papers?
Critio: Those papers argue that the power laws associated with neural phenomena that have been observed are not actually present. Several of the investigators who claimed to show that neural event size distributions were better fit by exponentials did not use many electrodes in their recordings. In some of their papers, they only had about eight electrodes (Bedard et al., 2006; Touboul and Destexhe, 2010). To really assess whether or not something follows a power law, you should have many closely-spaced electrodes. A recent paper showed that if you under-sample a critical process, you can get distributions that deviate substantially from power laws (Priesemann et al., 2009). The basic idea is that if your electrodes are too far apart, it will be extremely rare for an avalanche to occur that will span the distance between them. This will make it look like all the events are occurring independently, and this leads to a distribution with a short tail that is not a power law, even if the underlying process is indeed critical (Ribeiro et al., 2010). When people who do have data sets from large numbers of electrodes tested their data, they found contradictory results. A paper from 2011 showed that the data were better fit by power laws than by exponential distributions using the advanced statistical method I mentioned before (Clauset et al., 2009; Klaus et al., 2011). They performed this analysis using recordings taken from acute slices, in vivo recordings from rats, and in vivo recordings from primates. A more recent work used the same analysis method and found the opposite result using in vivo data from cats, monkeys, and humans (Dehghani et al., 2012). That study used a closely spaced 96 electrode array. So, at least for that study, it is very unlikely that under-sampling prevented the appearance of a power law. Therefore, it seems that this point about power laws is still somewhat controversial, and may take a few years to resolve. But remember, power laws are suggestive of criticality. They are not proof, and there may be better ways to establish criticality than by looking only at power laws. Hopefully we can talk later about these other ways of testing whether a system is critical or not.
Mnemo’s Second Objection: The Ising Model is an Equilibrium Model, but Neural Networks are Dynamic
Mnemo: Ok, but first let me understand this a bit more. You just told me about a magnetic model – the Ising model – and how that would settle into different equilibrium states at different temperatures. Now you are jumping to a network of neurons, where things do not settle at all. In fact, the Ising model seems like it would be pretty poor at describing how one neuron excites another, leading to cascades of activity spreading through the network.
Critio: As a neuroscientist, you have a very keen intuition for the physics! You are absolutely right to point out the potential problem. The Ising model is an equilibrium model, appropriate for describing how the system will settle at different temperatures, but this model does not explicitly account for time. To try to extend the Ising model into the range of dynamics, some people have applied a perturbation to the model – a slowly changing magnetic field for example – and watched how the system responds. Typically, when the model is at the critical temperature, applying a local magnetic field will cause several nearby spins to flip, so as to align with the applied field. These spins will in turn cause a change in the orientation preference for other nearby spins, and so will cause them to flip, leading to avalanches of spin flips. This is called the Barkhausen effect. In both theoretical work (Sethna et al., 2001) and in experiments (Papanikolaou et al., 2011), the sizes of these avalanches are distributed according to a power law when the system is at the critical temperature (Perkovic et al., 1995). Also, the exponents found in neuronal avalanches, typically near −1.5, are solidly in the range of exponents reported for the Barkhausen effect, which range from −1 to −2.8. These Barkhausen exponents vary because they apply to many different metals under various geometries and different models. It seems that there is a reasonable connection, then, between the equilibrium Ising model and dynamic avalanches (Liu and Dahmen, 2009).
Mnemo: So to follow your analogy, the neurons in the brain could be thought of as spins in a magnet at the critical point. When something comes along and delivers an input, this propagates through the system with maximum distance, because the correlation length is greatest at the critical point. The avalanches of activity have sizes distributed as a power law, and you mentioned that some experimenters have observed power law distributions of avalanche sizes in neural tissue as well.
Critio: That is a good summary of what I have said so far. Even though impressive progress has been made recently in applying the Ising model to neuronal activity patterns found in actual data (Schneidman et al., 2006; Shlens et al., 2006, 2009; Tang et al., 2008; Yu et al., 2008, 2011; Tkacik et al., 2009; Yeh et al., 2010) you are entirely right to say that the Ising model is far too simple to completely capture all neural phenomena. One problem with the Ising model is that, without applying an external magnetic field, all states of an individual lattice site are equally likely. Real neurons are far more likely to be in one state (quiescent) over another state (spiking). Researchers have developed many models to attempt to more fully incorporate neural behavior, and specifically to deal with temporal dynamics (Maass et al., 2002). Also, models have been created to better simulate damaged or malfunctioning neural behavior, such as models to simulate Alzheimer’s disease (Horn et al., 1993) and epilepsy (Netoff et al., 2004; Hsu et al., 2008)1. However, I believe the Ising model serves as an excellent introductory system for the topic of criticality.
Mnemo: I understand that no model is perfect and that it is easier to start with a simplified system, but I’m still dissatisfied.
Critio: What’s bothering you?
Mnemo’s Third Objection: Power Laws do not Prove Criticality
Mnemo: You’ve given me a nice story, but this is hardly proof. As you said, the existence of power laws is a necessary, but not sufficient condition for criticality. So, just because we’ve found some power laws in neural data, the existence of those power laws not prove that the neural systems are operating at the critical point. I don’t know about you, but I don’t like to affirm the consequent.
Critio: You are right to be skeptical. As I said, the power laws are consistent with the idea that the neural networks that have been studied are operating near the critical point, but the existence of these power laws is not proof.
Mnemo: Sure, it seems like now would be a good time for you to tell me about the many other ways in which power laws can be generated.
Critio: There are so many ways to generate power laws that it is hard to know where to begin. People have written entire articles devoted largely to this topic (Mitzenmacher, 2004; Newman, 2005; Stumpf and Porter, 2012). Perhaps the simplest mechanism to start with would be successive fractionation. Consider a stick of some length. Now break it into two parts at a randomly chosen location. Then break each of these parts in two, again at randomly chosen locations. If you keep successively doing this, you will eventually produce a power law distribution of fragment lengths. Related to this, multiplicative noise can also produce power laws (Sornette, 1998). In one of the papers that challenged the existence of power laws in neural data that we discussed earlier, the authors used a random process that, when thresholded, also produced power law distributions (Touboul and Destexhe, 2010). Another way to get power laws is through a combination of exponentials (Reed and Hughes, 2002). As you know, exponential processes are ubiquitous. If you have a process that grows exponentially over time, but is terminated at random times drawn from a negative exponential distribution, then you will also get a power law distribution of sizes. Reed and Hughes explored this in a paper whose title included “…Why power laws are incredibly common in nature” (Reed and Hughes, 2002). As just one more example, consider an array of processes that all decay exponentially, but with different time constants. Under the right conditions you can add these decay processes together and they will produce a power law as well (Fusi et al., 2005). There are several other mechanisms proposed to generate power laws (Mitzenmacher, 2004). So you are completely right to be skeptical. Just showing a power law by itself doesn’t tell you all that much.
Mnemo: It now seems that you have dug yourself into a hole from which you cannot escape. If power laws are so unexceptional, then why should I be so excited about seeing them in neural data?
Critio’s Response to Mnemo’s Third Objection: Evidence for Criticality Beyond Power Laws
Critio: The fact that other non-critical systems also produce power laws is very important. Fortunately, recent experiments by several groups have addressed this issue directly. There are three main ways to demonstrate that the power laws observed in neural tissue are the result of a critical mechanism: the ability to tune the network from a subcritical regime through criticality to a supercritical regime, the existence of mathematical relationships between the exponents of the power laws for a system, and the existence of a data collapse within neural data.
Tuning the network through criticality
Critio: First, recall that in a system that displays criticality, the power law will only occur when the system is between phases, in other words, at the phase transition point. So, for systems that really are critical, we should be able to observe different phases on either side of the critical point and get distributions there that do not follow power laws.
Mnemo: And you have evidence of this?
Critio: Actually, yes. By blocking excitatory synaptic transmission, you can dampen network excitability, leading to smaller avalanches (Mazzoni et al., 2007). Here is a figure I saw from a poster at the conference. [Critio pulls out a small copy of the poster and points to Figure 7.]
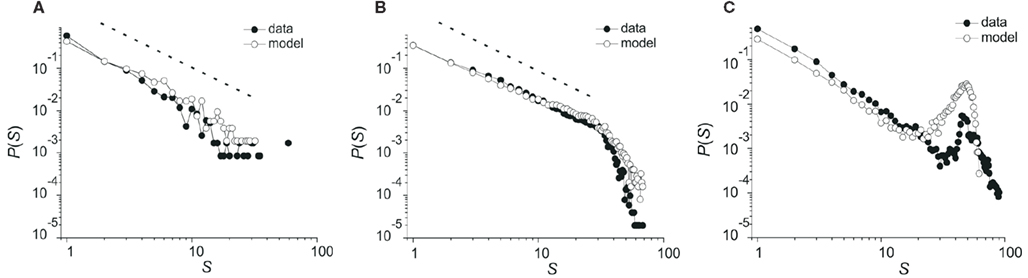
Figure 7. Avalanche size distributions in local field potential data collected with a 60-channel microelectrode array from rat cortical slice networks. (A) Subcritical regime; excitatory antagonist (3 mM CNQX) applied. (B) Critical regime; normal network. (C) Supercritical regime; inhibitory antagonist (2 mM PTX) applied (Haldeman and Beggs, 2005).
In Figure 7A, the resulting distribution of avalanche sizes is curved downward and has a smaller mean than in the control case shown in Figure 7B. In Figure 7A, the distribution is beginning to deviate from a power law. This looks like the subcritical or damped phase of the system, where activity dies out quickly. Conversely, by blocking inhibitory synaptic transmission, in Figure 7C, it is possible to make the tissue hyperexcited, leading to larger avalanches (Beggs and Plenz, 2003). The resulting distribution here is not a power law either, but has a big bump out in the tail, indicating that many extremely large avalanches occur. This looks like the supercritical phase, where activity is often amplified until it spans the entire system. The existence of these two phases, on either side of the critical point, which is shown in Figure 7B, strongly suggests that the power law arises from a mechanism that is related to a phase transition.
Critio: Related to this, there have been some very elegant experiments that have shown how information processing functions in the tissue approach optimal behavior near the critical point (Shew et al., 2009, 2011). This also suggests that different phases can be produced in the network.
Mnemo: What do you mean by that? And how is it related to the idea of phases?
Critio: Shew and colleagues looked at information transmission through cortical slice networks under three different conditions: where excitatory transmission is reduced; where there is no manipulation; and where inhibitory transmission is reduced. They showed that there was a peak in information transmission in the unperturbed condition, and that information transmission fell to either side of this point as perturbations increased. In many ways, they observed behavior just like that seen in the correlation function in the Ising model that we talked about earlier from Figure 4. Remember the plot that showed a sharp peak in the middle? – Their results are similar. In other experiments from the same group, they demonstrated that dynamic range in the network – similar to susceptibility in the Ising model – peaks in the unperturbed condition and declines as perturbations are increased. All of this suggests that these networks can be tuned from one phase to another, or left between phases at the critical point. And it underscores why it would be advantageous for brains to operate near the critical point, because that is where information processing is optimal. The presence of different phases indicates that the power law is related to a phase transition, because the power law is only seen between the phases. These peaks in information processing functions also occur between the phases, under the same conditions where the power law occurs.
Mnemo: So it seems that you need to be able to move the system from one phase to another if it is going to show a critical point. What you have been telling me is that these neural systems can be moved in this way.
Critio: That’s right. If a system displays criticality, then it must be tunable in some sense. Typically, a “control parameter” can be adjusted to determine the phase of the system. In the Ising model that we discussed earlier, the temperature is the control parameter. Sweeping the temperature from 0 to some high value would bring the system from the subcritical, ordered, phase, up to the critical point, and then into the supercritical, disordered, phase. The “order parameter” is what tells you the phase. In the case of the Ising model, the order parameter would be the net magnetic field produced by all the spins, called the magnetization. In the subcritical phase, all the spins are aligned and the magnetization has a large magnitude. In the supercritical phase, all the spins are pointing in random directions and the magnetization is 0. Near the critical point, we see the transition of the magnetization from some large magnitude toward 0. If a system is indeed critical, then all of the variables that could indicate its phase will depend on the control parameter.
Mnemo: To continue with the analogy, what would be the control parameter in neural systems?
Critio: That is a very good question. At the moment, it seems that the balance between excitation and inhibition can serve as a control parameter (Mazzoni et al., 2007; Shew et al., 2009; Benayoun et al., 2010; Hobbs et al., 2010). Too much inhibition will cause the system to be subcritical. Too much excitation will cause the system to be supercritical. A balance between them would lead to the critical point. But I must say that there is still a lot of work to be done in this area. Other things, like connection strengths (Haldeman and Beggs, 2005; Beggs et al., 2007; Chen et al., 2010), or the density or pattern of connections in the network (Gray and Robinson, 2007; Larremore et al., 2011; Rubinov et al., 2011), might also serve as control parameters. The key point is that experiments have shown the system can indeed display different phases, so it is tunable.
Mnemo: So you cannot tune the other, non-critical stochastic systems, like successive fractionation, or a combination of exponentials?
Critio: Well, you could tune them in some sense, but such tuning would only change the exponent of the resulting power law distribution. For example, let’s return to the combination of exponentials model proposed by Reed and Hughes (2002). Recall that there is a process that grows exponentially, let’s say with exponent α, and it is terminated at random times that are drawn from a distribution that has exponential decay, let’s say with exponent β. If you increase α or decrease β, you will decrease the exponent of the size distribution (thereby making the slope of the size distribution less steep when plotted logarithmically), but it will still be a power law. As long as such a process is adequately sampled, it will never curve downward or curve upward to produce a hump at the end of the distribution. So this type of non-critical process fails to show different phases. Therefore it cannot serve as a good model for what has been observed in the neural data, where clear phases exist. All of the non-critical models that have been proposed to generate power laws are like this – they fail to show phases.
Mnemo: I think I get it: if they don’t have different phases, then they are not operating at a phase transition point, even though they may produce power laws. That all sounds reasonable. But you told me that there were additional arguments to support your point, right?
Mathematical relationships between power law exponents
Critio: Yes, the second main argument comes from a slightly different aspect of critical phenomena. It will take me a minute or two to explain, but I think it will be helpful. As I said previously, if a system is truly critical, it will display power law distributions in more than one variable of interest (Stanley, 1971, 1999; Goldenfeld, 1992; Nishimori and Ortiz, 2011). For example, recall that in the Ising model the correlation as a function of distance followed a power law at the critical point. The domain size distribution also follows a power law at the critical point. Also, the susceptibility, the specific heat, and other variables will exhibit power laws as well. All of these power laws may have different exponents, and so will have different “characteristic” exponents. Far away from the critical point, these power laws break down. Right near criticality, though, there are multiple power laws.
Mnemo: Why are there multiple power laws?
Crito: Remember how I said that the phase of a critical system can be determined by a control parameter? Let me describe how important that parameter is. If we go back to that curve of the correlation length, recall that it had a sharp peak near Tc, the critical temperature. This type of curve is observed experimentally in diverse critical systems (Stanley, 1971; Yeomans, 1992) and would be expected to go to infinity right at Tc if you had an infinitely large system. A simple way to describe such a curve would be with an equation like this:
As T approaches Tc, the denominator goes to 0, and the correlation length, Γ, shoots up to infinity. The exponent ξ is another value that would be obtained from experimental data, and in general it would not always be 1. For convenience, physicists often use something called the “reduced temperature” given here by t, in describing critical phenomena:
In general, we don’t know precisely how the correlation length will depend on the reduced temperature, but I am able to write the correlation length as a power series in t, like this:
Near the critical point, the reduced temperature t approaches 0, so all the higher-order terms of this series become very small. We can then approximate the whole power series by something like this:
And you should recognize that this as a power law relationship. Using similar methods, other power laws can be found that relate other variables associated with the system, such as the relationship between the dynamic correlation value and distance between lattice sites in the Ising model (Figure 6). Furthermore, in the process of deriving these power laws, mathematic relationships between the exponents of the power law distributions can also be derived. It would take me a while to explain the details of how these exponent relationships come to be (Griffiths, 1965; Stanley, 1971; Yeomans, 1992), but for now it should be enough to say that near the critical point, many power laws exist, and they are mathematically related to one another.
Mnemo: Why wouldn’t successive fractionation produce a relationship between exponents?
Critio: In that simple, one-dimensional system, there is only one power law, and that is related to the lengths of the sticks. There is only one exponent, so it can’t be related to other exponents.
Mnemo: But what about something like a combination of exponentials?
Critio: Recall that in that model the exponents α and β are the rates at which exponential processes increase and decrease, not exponents of power laws observed in variables associated with the system. The event size distribution is a power law whose exponent is related to the ratio of α/β. So, again there is only one exponent, so it can’t be related to other exponents. In addition, α and β are independent input parameters in the model, so there can be no relationship between them.
Mnemo: Let us assume for the moment that I agree that you should have exponent relationships if your system is truly critical. Is there any evidence for this type of relationship in neural data collected so far?
Critio: In fact there is. There is a recent article (Friedman et al., 2012) where the investigators were recording neuronal avalanches of spikes from individual neurons. They showed that the exponent for the avalanche size distribution, α, and the exponent for the avalanche lifetime distribution, β, could be used to predict the exponent of the power law that related avalanche size to avalanche lifetime, γ, using Eq. 6.
They found that the exponent γ, predicted in this way, fit reasonably well to the actual data. So, this is another piece of evidence suggesting that the system can display critical behavior (Friedman et al., 2011, 2012).
Mnemo: Alright, this makes sense. It seems to be another way to assess whether or not the system is critical. But I would still like to hear more. What is your third argument that the neural data are collected from a critical process?
Data collapse
Critio: Remember when I said that power law distributions were scale-free? Recall that this was related to fractals that showed self-similarity?
Mnemo: Yes, I do. I have read some popular articles about fractals, so I am not completely new to this (Mandelbrot, 1982; Stewart, 2001).
Critio: Good, then I can build on your existing knowledge to explain my last argument about why the neural data suggest criticality. It goes like this: The critical point is characterized by power laws in many variables, all of which express fractal relationships. We know that neural activity propagates dynamically through networks of neurons in cascades of activity. If these cascades, or avalanches, are truly critical then there should be some way to capture a relationship between the avalanches in a fractal way. What if we could take something like avalanche shapes and show that they were fractal? If we could do this, it would allow us to go beyond power laws, and show a scaling relationship that captured the dynamics of these non-equilibrium systems.
Mnemo: This sounds pretty abstract! Could you give me a more concrete example of what you are talking about?
Critio: Yes, of course. Let me describe what I mean by the avalanche shape. Consider how an avalanche of neural activity might evolve. It could start with one or a few spiking neurons. These could activate others, so the number of active neurons would increase over time. Eventually this would decline to 0, marking the end of the avalanche. If we plotted the average number of active neurons over time, we might get something that looked like an inverted parabola. This is what I mean by the average avalanche shape. Now if the network is at the critical point, then I should be able to take average avalanche shapes from different durations and show that they are all fractal copies of each other. In other words, I should be able to rescale them with the appropriate critical exponents and get them all to lie on top of each other, in what is called a data collapse. [Critio sketches Figure 8.]
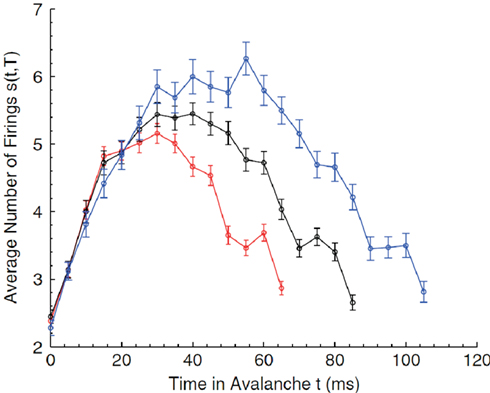
Figure 8. Average avalanche shapes for avalanches of three distinct durations (Friedman et al., 2012).
Critio: These are average avalanche shapes taken from avalanches of different durations. See how they look like they might have roughly the same shape?
Mnemo: Yes, sort of. They could be copies of one another at different scales, but how are you going to show this?
Critio: Well, if we divide each curve by its duration, then they will be rescaled to all have the same length. Then if we rescale their heights by their duration raised to an exponent, γ from Eq. 2, that is related to the critical exponents α and β that we discussed earlier, then we get a picture that looks like this. [Critio draws Figure 9.]
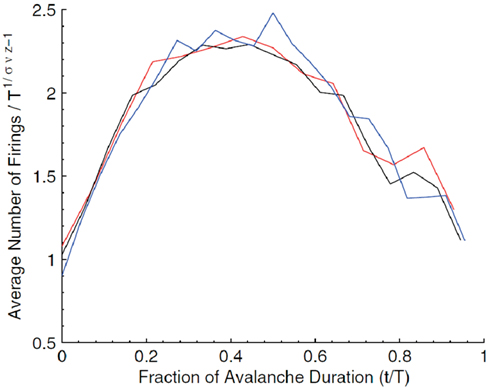
Figure 9. Rescaled avalanche shapes from Figure 8 (Friedman et al., 2012).
Mnemo: The curves do seem to lie on top of one another pretty closely. Each curve is an average of how many avalanches?
Critio: Yes, each average avalanche shape is produced by hundreds of avalanches. So this data collapse is highly unlikely to have occurred by chance. In fact, when the spike train times from the original data are randomly jittered by 50 ms, the curves no longer look like copies of each other, suggesting that this scaling relationship has relatively tight temporal precision (Friedman et al., 2012). This type of data collapse, based on average avalanche shape, has been explored for several years in a variety of different systems (Perkovic et al., 1999; Kuntz and Sethna, 2000; Mehta et al., 2006), and has recently been applied to Barkhausen noise experiments with good success (Papanikolaou et al., 2011). The fact that it also can be applied to some neural networks strongly suggests that these networks are operating near the critical point.
Mnemo: Although I can’t claim to understand all the math behind this, it certainly seems like your argument does not now rest on power laws alone. You have shown me a fractal relationship that ties together both space and time in the dynamic evolution of the avalanches. From all that you have told me, this should only occur near the critical point.
Critio: Yes, but it again sounds like you are not fully convinced!
Mnemo’s Fourth Objection: Influence of Lower Level Processes that Exhibit Power Laws
Mnemo: You are correct – I still have another question about all this. In particular, I seem to recall reading somewhere that fractals are everywhere in neuroscience.
Critio: That’s right. Some have shown that a plot of the number of spikes produced by a neuron looks roughly the same at all intervals (Teich et al., 1997). When you zoom out to very large time scales, this pattern of on and off firing appears to be just a copy of the pattern you see at short intervals. In addition, researchers have found that neurotransmitter secretion is fractal (Lowen et al., 1997), and that intervals between sodium channel openings follow a power law (Toib et al., 1998).
Mnemo: If all this is true, then I guess I shouldn’t be so surprised when you tell me that some networks of neurons also display fractal behavior. The activity in the network could just be reflecting power law statistics that appear at other scales below it.
Critio: You are right to bring this up – with so many fractals out there, why should I get excited about a power law distribution of activity in small, local networks of neurons? Well, I have two answers to this. First, I could say that all the evidence I just mentioned about fractals in phenomena related to individual neurons is actually in favor of my general argument. We might expect the brain and its underlying systems to operate near a critical point to optimize information processing. However, the existence of the expectation is certainly not an argument against that which is expected. It seems that many biological systems would approach optimality by operating in a regime where they produce power laws (Mora and Bialek, 2011). That could be why so many biological systems exhibit power laws. To give my second answer to your point, I first want to clarify what I think you are saying. It sounds like you are saying that these power laws at other scales might not be produced by criticality, and that the power laws that have been observed in neuronal avalanches are just a reflection of these non-critical processes at other scales. Is that what you are saying?
Mnemo: Yes, I think that is a fair description of my objection.
Critio: Ok, let us assume for the sake of argument that power laws in spike counts, transmitter secretion and channel dynamics are all produced by processes that are not critical. Is it really clear that if we combined such processes that the resulting cascades of activity on a network also would have to follow a power law? Would the resulting network therefore not be critical? We know from computer simulations that the pattern of network connectivity can have a profound effect on whether the network produces power laws or not (Teramae and Fukai, 2007; Tanaka et al., 2009; Rubinov et al., 2011). Not every pattern of connections leads to a power law. In addition, from experiments we know that the relative strength of inhibition to excitation can influence whether or not a network produces power law distributions (Beggs and Plenz, 2003; Stewart and Plenz, 2006; Shew et al., 2009). These manipulations are done globally at the network level, not at the lower levels, and yet they seem to have the effect of tuning the network. If it were true that power law behavior at the network level was simply a result of power law behavior on the cellular level, then we shouldn’t observe such effects by altering network level parameters. Furthermore, if the power law behavior observed at the network level is found to be critical using the methods discussed previously, then the network level behavior is critical regardless of whether or not the power law behavior of the underlying systems is also critical. Still, we don’t know why the network level behavior is critical, or at the very least why it exhibits power laws. Nor do we know how this behavior is related to network structure and the underlying systems.
Mnemo: Oh, is this where all that “self-organized criticality” literature comes in (Bak et al., 1987; Bak, 1996; Jensen, 1998)? I have heard that some physicists are extremely skeptical of that work. So I suppose I should approach your work with similar caution.
Critio: It is still an open question as to how the network operates at the critical point, if it is indeed operating a critical point, and there have been several interesting proposals and experiments related to this topic (Bienenstock, 1995; Chialvo and Bak, 1999; de Carvalho and Prado, 2000; Bak and Chialvo, 2001; Eurich et al., 2002; Freeman, 2005; Kozma et al., 2005; de Arcangelis et al., 2006; Hsu and Beggs, 2006; Abbott and Rohrkemper, 2007; Buice and Cowan, 2007, 2009; Juanico et al., 2007; Levina et al., 2007, 2009; Pellegrini et al., 2007; Hsu et al., 2008; Stewart and Plenz, 2008; Allegrini et al., 2009; Magnasco et al., 2009; Tanaka et al., 2009; Buice et al., 2010; de Arcangelis and Herrmann, 2010; Kello and Mayberry, 2010; Millman et al., 2010; Tetzlaff et al., 2010; Rubinov et al., 2011; Droste et al., 2012). Whether the network gets to criticality through self-organization or not, it does seem that at least some networks of neurons can operate at the critical point. But I would be surprised if this does not involve some form of self-organization, as synaptic strengths are constantly in flux.
Mnemo: I suppose we will have to settle this over another lunch, as I have to go to another talk!
Critio: Wow, it is late! Hey, do you mind if I write this up and submit it to a journal? I think you have raised some very interesting objections, and you have forced me to think through my positions more thoroughly.
Mnemo: Sure, go ahead. But I am still skeptical, so don’t plan to include me as a co-author.
Critio: Not a problem. Thanks for sharing lunch.
Mnemo: My pleasure. Good bye.
Supplementary material
The Movies S1–S3 for this article can be found online at http://www.frontiersin.org/Fractal_Physiology/10.3389/fphys.2012.00163/abstract
Movie S1. Simulation of an Ising model at low temperature.
Movie S2. Simulation of an Ising model at high temperature.
Movie S3. Simulation of an Ising model at the critical temperature.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnote
- ^Critio: As a brief aside, I’m very interested in models of Epilepsy. In epileptic tissue, seizures exist that take the form of widespread coordinated activity. So, when modeling epileptic neural activity, we must be careful to incorporate seizures into our understanding of when the model is critical. For instance, during seizures, the activities of many neurons are highly correlated, so the dynamic correlation between model neurons is very high, but, by examining other parameters of the network, the network is not at a critical point.
References
Abbott, L. F., and Rohrkemper, R. (2007). A simple growth model constructs critical avalanche networks. Prog. Brain Res. 165, 13–19.
Allegrini, P., Menicucci, D., Bedini, R., Fronzoni, L., Gemignani, A., Grigolini, P., West, B. J., and Paradisi, P. (2009). Spontaneous brain activity as a source of ideal 1/f noise. Phys. Rev. E 80, 061914. doi:10.1103/PhysRevE.80.061914
Bak, P. (1996). How Nature Works: The Science of Self-Organized Criticality. New York, NY: Copernicus.
Bak, P., and Chialvo, D. R. (2001). Adaptive learning by extremal dynamics and negative feedback. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 63, 031912.
Bak, P., Tang, C., and Wiesenfeld, K. (1987). Self-organized criticality: an explanation of the 1/f noise. Phys. Rev. Lett. 59, 381–384.
Bedard, C., and Destexhe, A. (2009). Macroscopic models of local field potentials and the apparent 1/f noise in brain activity. Biophys. J. 96, 2589–2603.
Bedard, C., Kroger, H., and Destexhe, A. (2006). Does the 1/f frequency scaling of brain signals reflect self-organized critical states? Phys. Rev. Lett. 97, 118102.
Beggs, J. M. (2007). Neuronal Avalanche. Available at: http:www.scholarpedia.org/article/Neuronal_avalanche [accessed on May 1, 2012].
Beggs, J. M. (2008). The criticality hypothesis: how local cortical networks might optimize information processing. Philos. Trans. A Math. Phys. Eng. Sci. 366, 329–343.
Beggs, J. M., Klukas, J., and Chen, W. (2007). “Connectivity and dynamics in local cortical networks,” in Handbook of Brain Connectivity, ed. R. M. V. Jirsa (Berlin: Springer), 91–116.
Beggs, J. M., and Plenz, D. (2003). Neuronal avalanches in neocortical circuits. J. Neurosci. 23, 11167–11177.
Benayoun, M., Cowan, J. D., Van Drongelen, W., and Wallace, E. (2010). Avalanches in a stochastic model of spiking neurons. PLoS Comput. Biol. 6, e1000846. doi:10.1371/journal.pcbi.1000846
Bertschinger, N., and Natschlager, T. (2004). Real-time computation at the edge of chaos in recurrent neural networks. Neural. Comput. 16, 1413–1436.
Buice, M. A., and Cowan, J. D. (2007). Field-theoretic approach to fluctuation effects in neural networks. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 75, 051919.
Buice, M. A., and Cowan, J. D. (2009). Statistical mechanics of the neocortex. Prog. Biophys. Mol. Biol. 99, 53–86.
Buice, M. A., Cowan, J. D., and Chow, C. C. (2010). Systematic fluctuation expansion for neural network activity equations. Neural. Comput. 22, 377–426.
Chen, W., Hobbs, J. P., Tang, A. N., and Beggs, J. M. (2010). A few strong connections: optimizing information retention in neuronal avalanches. BMC Neurosci. 11, 14. doi:10.1186/1471-2202-11-3
Chen, Y. Q., Ding, M. Z., and Kelso, J. A. S. (1997). Long memory processes (1/f(alpha) type) in human coordination. Phys. Rev. Lett. 79, 4501–4504.
Clauset, A., Shalizi, C. R., and Newman, M. E. J. (2009). Power law distributions in empirical data. arXiv:0706.1062v2.
de Arcangelis, L., and Herrmann, H. J. (2010). Learning as a phenomenon occurring in a critical state. Proc. Natl. Acad. Sci. U.S.A. 107, 3977–3981.
de Arcangelis, L., Perrone-Capano, C., and Herrmann, H. J. (2006). Self-organized criticality model for brain plasticity. Phys. Rev. Lett. 96, 028107.
de Carvalho, J. X., and Prado, C. P. C. (2000). Self-organized criticality in the Olami-Feder-Christensen model. Phys. Rev. Lett. 84, 4006–4009.
Dehghani, N., Hatsopoulos, N. G., Haga, Z. D., Parker, R. A., Greger, B., Halgren, E., Cash, S. S., and Destexhe, A. (2012). Avalanche analysis from multi-electrode ensemble recordings in cat, monkey and human cerebral cortex during wakefulness and sleep. arXiv:1203.0738v2.
Droste, F., Do, A. L., and Gross, T. (2012). Analytical investigation of self-organized criticality in neural networks. arXiv:1203.4942v1.
Eurich, C. W., Herrmann, J. M., and Ernst, U. A. (2002). Finite-size effects of avalanche dynamics. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 66, 066137.
Freeman, W. J. (2005). A field-theoretic approach to understanding scale-free neocortical dynamics. Biol. Cybern. 92, 350–359.
Friedman, N., Butler, T., Deville, R. E. L., Beggs, J. M., and Dahmen, K. (2011). Beyond critical exponents in neuronal avalanches. APS March Meeting, Dallas.
Friedman, N., Ito, S., Brinkman, B. A. W., Shimono, M., Deville, R. E. L., Dahmen, K. A., Beggs, J. M., and Butler, T. C. (2012). Universal critical dynamics in high resolution neuronal avalanche data. Phys. Rev. Lett. 108, 208102.
Fusi, S., Drew, P. J., and Abbott, L. F. (2005). Cascade models of synaptically stored memories. Neuron 45, 599–611.
Gireesh, E. D., and Plenz, D. (2008). Neuronal avalanches organize as nested theta- and beta/gamma-oscillations during development of cortical layer 2/3. Proc. Natl. Acad. Sci. U.S.A. 105, 7576–7581.
Gisiger, T. (2001). Scale invariance in biology: coincidence or footprint of a universal mechanism? Biol. Rev. 76, 161–209.
Goldenfeld, N. (1992). Lectures on Phase Transitions and the Renormalization Group. Reading, MA: Addison-Wesley, Advanced Book Program.
Gray, R. T., and Robinson, P. A. (2007). Stability and spectra of randomly connected excitatory cortical networks. Neurocomputing 70, 1000–1012.
Griffiths, R. (1965). Ferromagnets and simple fluids near critical point - some thermodynamic inequalities. J. Chem. Phys. 43, 1958–1968.
Hahn, G., Petermann, T., Havenith, M. N., Yu, S., Singer, W., Plenz, D., and Nikolic, D. (2010). Neuronal avalanches in spontaneous activity in vivo. J. Neurophysiol. 104, 3312–3322.
Haldeman, C., and Beggs, J. M. (2005). Critical branching captures activity in living neural networks and maximizes the number of metastable States. Phys. Rev. Lett. 94, 058101.
Hobbs, J. P., Smith, J. L., and Beggs, J. M. (2010). Aberrant neuronal avalanches in cortical tissue removed from juvenile epilepsy patients. J. Clin. Neurophysiol. 27, 380–386.
Horn, D., Ruppin, E., Usher, M., and Herrmann, M. (1993). Neural-network modeling of memory deterioration in Alzheimers-disease. Neural. Comput. 5, 736–749.
Hsu, D., and Beggs, J. M. (2006). Neuronal avalanches and criticality: a dynamical model for homeostasis. Neurocomputing 69, 1134–1136.
Hsu, D., Chen, W., Hsu, M., and Beggs, J. M. (2008). An open hypothesis: is epilepsy learned, and can it be unlearned? Epilepsy Behav. 13, 511–522.
Hsu, D., Tang, A., Hsu, M., and Beggs, J. M. (2007). Simple spontaneously active Hebbian learning model: homeostasis of activity and connectivity, and consequences for learning and epileptogenesis. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 76, 041909.
Jensen, H. J. (1998). Self-Organized Criticality: Emergent Complex Behavior in Physical and Biological Systems. Cambridge, NY: Cambridge University Press.
Juanico, D. E., Monterola, C., and Saloma, C. (2007). Dissipative self-organized branching in a dynamic population. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 75, 045105.
Kauffman, S., Peterson, C., Samuelsson, B., and Troein, C. (2004). Genetic networks with canalyzing Boolean rules are always stable. Proc. Natl. Acad. Sci. U.S.A. 101, 17102–17107.
Kello, C. T., and Mayberry, M. R. (2010). “Critical branching neural computation,” in The 2010 International Joint Conference on Neural Networks, Barcalona.
Kinouchi, O., and Copelli, M. (2006). Optimal dynamical range of excitable networks at criticality. Nat. Phys. 2, 348–352.
Kitzbichler, M. G., Smith, M. L., Christensen, S. R., and Bullmore, E. (2009). Broadband criticality of human brain network synchronization. PLoS Comput. Biol. 5, 13. doi:10.1371/journal.pcbi.1000314
Klaus, A., Yu, S., and Plenz, D. (2011). Statistical analyses support power law distributions found in neuronal avalanches. PLoS ONE 6, e19779. doi:10.1371/journal.pone.0019779
Kozma, R., Puljic, M., Balister, P., Bollobas, B., and Freeman, W. J. (2005). Phase transitions in the neuropercolation model of neural populations with mixed local and non-local interactions. Biol. Cybern. 92, 367–379.
Kuntz, M. C., and Sethna, J. P. (2000). Noise in disordered systems: the power spectrum and dynamic exponents in avalanche models. Phys. Rev. B 62, 11699–11708.
Larremore, D. B., Shew, W. L., Ott, E., and Restrepo, J. G. (2011). Effects of network topology, transmission delays, and refractoriness on the response of coupled excitable systems to a stochastic stimulus. Chaos 21, 025117. doi: 10.1063/1.3600760
Levina, A., Herrmann, J. M., and Geisel, T. (2007). Dynamical synapses causing self-organized criticality in neural networks. Nat. Phys. 3, 857–860.
Levina, A., Herrmann, J. M., and Geisel, T. (2009). Phase transitions towards criticality in a neural system with adaptive interactions. Phys. Rev. Lett. 102, 118110. doi: 10.1103/Phys-RevLett.102.118110
Linkenkaer-Hansen, K., Nikouline, V. V., Palva, J. M., and Ilmoniemi, R. J. (2001). Long-range temporal correlations and scaling behavior in human brain oscillations. J. Neurosci. 21, 1370–1377.
Liu, Y., and Dahmen, K. A. (2009). Unexpected universality in static and dynamic avalanches. Phys. Rev. E 79, 061124. doi: 10.1103/Phys-RevE.79.061124
Lowen, S. B., Cash, S. S., Poo, M., and Teich, M. C. (1997). Quantal neurotransmitter secretion rate exhibits fractal behavior. J. Neurosci. 17, 5666–5677.
Maass, W., Natschlager, T., and Markram, H. (2002). Real-time computing without stable states: a new framework for neural computation based on perturbations. Neural. Comput. 14, 2531–2560.
Maass, W., Natschlager, T., and Markram, H. (2004). Fading memory and kernel properties of generic cortical microcircuit models. J. Physiol. Paris 98, 315–330.
Magnasco, M. O., Piro, O., and Cecchi, G. A. (2009). Self-tuned critical anti-hebbian networks. Phys. Rev. Lett. 102, 258102. doi: 10.1103/Phys-RevLett.102.258102
Mazzoni, A., Broccard, F. D., Garcia-Perez, E., Bonifazi, P., Ruaro, M. E., and Torre, V. (2007). On the dynamics of the spontaneous activity in neuronal networks. PLoS ONE 2, e439. doi:10.1371/journal.pone.0000439
Mehta, A. P., Dahmen, K. A., and Ben-Zion, Y. (2006). Universal mean moment rate profiles of earthquake ruptures. Phys. Rev. E 73.
Miller, K. J., Sorensen, L. B., Ojemann, J. G., and Den Nijs, M. (2009). Power-law scaling in the brain surface electric potential. PLoS Comput. Biol. 5, e1000609. doi:10.1371/journal.pcbi.1000609
Millman, D., Mihalas, S., Kirkwood, A., and Niebur, E. (2010). Self-organized criticality occurs in non-conservative neuronal networks during ‘up’ states. Nat. Phys. 6, 801–805.
Mitzenmacher, M. (2004). A brief history of generative models for power law and lognormal distributions. Internet Math. 1, 226–251.
Mora, T., and Bialek, W. (2011). Are biological systems poised at criticality? J. Stat. Phys. 144, 268–302.
Netoff, T. I., Clewley, R., Arno, S., Keck, T., and White, J. A. (2004). Epilepsy in small-world networks. J. Neurosci. 24, 8075–8083.
Newman, M. E. J. (2005). Power laws, Pareto distributions and Zipf’s law. Contemp. Phys. 46, 323–351.
Nicolis, G., and Prigogine, I. (1989). Exploring Complexity: An Introduction. New York: W.H. Freeman.
Nishimori, H., and Ortiz, G. (2011). Elements of Phase Transitions and Critical Phenomena. New York: Oxford University Press.
Papanikolaou, S., Bohn, F., Sommer, R. L., Durin, G., Zapperi, S., and Sethna, J. P. (2011). Universality beyond power laws and the average avalanche shape. Nat. Phys. 7, 316–320.
Pasquale, V., Massobrio, P., Bologna, L. L., Chiappalonea, M., and Martinoia, S. (2008). Self-organization and neuronal avalanches in networks of dissociated cortical neurons. Neuroscience 153, 1354–1369.
Pellegrini, G. L., de Arcangelis, L., Herrmann, H. J., and Perrone-Capano, C. (2007). Activity-dependent neural network model on scale-free networks. Phys. Rev. E 76.
Perkovic, O., Dahmen, K., and Sethna, J. P. (1995). Avalanches, Barkhausen noise, and plain old criticality. Phys. Rev. Lett. 75, 4528–4531.
Perkovic, O., Dahmen, K. A., and Sethna, J. P. (1999). Disorder-induced critical phenomena in hysteresis: numerical scaling in three and higher dimensions. Phys. Rev. B 59, 6106–6119.
Petermann, T., Lebedev, M., Nicolelis, M., and Plenz, D. (2006). Neuronal avalanches in vivo. Soc. Neurosci. Abstr. 531.
Petermann, T., Thiagarajan, T. C., Lebedev, M. A., Nicolelis, M. A. L., Chialvo, D. R., and Plenz, D. (2009). Spontaneous cortical activity in awake monkeys composed of neuronal avalanches. Proc. Natl. Acad. Sci. U.S.A. 106, 15921–15926.
Plenz, D., and Thiagarajan, T. C. (2007). The organizing principles of neuronal avalanches: cell assemblies in the cortex? Trends Neurosci. 30, 101–110.
Poil, S. S., Van Ooyen, A., and Linkenkaer-Hansen, K. (2008). Avalanche dynamics of human brain oscillations: relation to critical branching processes and temporal correlations. Hum. Brain Mapp. 29, 770–777.
Priesemann, V., Munk, M. H., and Wibral, M. (2009). Subsampling effects in neuronal avalanche distributions recorded in vivo. BMC Neurosci. 10, 40. doi:10.1186/1471-2202-10-40
Ramo, P., Kauffman, S., Kesseli, J., and Yli-Harja, O. (2007). Measures for information propagation in Boolean networks. Phys. D Nonlin. Phenomena 227, 100–104.
Reed, W. J., and Hughes, B. D. (2002). From gene families and genera to incomes and internet file sizes: why power laws are so common in nature. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 66, 067103.
Ribeiro, T. L., Copelli, M., Caixeta, F., Belchior, H., Chialvo, D. R., Nicolelis, M. A. L., and Ribeiro, S. (2010). Spike avalanches exhibit universal dynamics across the sleep-wake cycle. PLoS ONE 5, e14129. doi:10.1371/journal.pone.0014129
Rubinov, M., Sporns, O., Thivierge, J. P., and Breakspear, M. (2011). Neurobiologically realistic determinants of self-organized criticality in networks of spiking neurons. PLoS Comput. Biol. 7, e1002038. doi:10.1371/journal.pcbi.1002038
Schneidman, E., Berry, M. J. 2nd, Segev, R., and Bialek, W. (2006). Weak pairwise correlations imply strongly correlated network states in a neural population. Nature 440, 1007–1012.
Shew, W. L., Yang, H., Petermann, T., Roy, R., and Plenz, D. (2009). Neuronal avalanches imply maximum dynamic range in cortical networks at criticality. J. Neurosci. 29, 15595–15600.
Shew, W. L., Yang, H., Yu, S., Roy, R., and Plenz, D. (2011). Information capacity and transmission are maximized in balanced cortical networks with neuronal avalanches. J. Neurosci. 31, 55–63.
Shlens, J., Field, G. D., Gauthier, J. L., Greschner, M., Sher, A., Litke, A. M., and Chichilnisky, E. J. (2009). The structure of large-scale synchronized firing in primate retina. J. Neurosci. 29, 5022–5031.
Shlens, J., Field, G. D., Gauthier, J. L., Grivich, M. I., Petrusca, D., Sher, A., Litke, A. M., and Chichilnisky, E. J. (2006). The structure of multi-neuron firing patterns in primate retina. J. Neurosci. 26, 8254–8266.
Socolar, J. E. S., and Kauffman, S. A. (2003). Scaling in ordered and critical random Boolean networks. Phys. Rev. Lett. 90, 4.
Stam, C. J., and de Bruin, E. A. (2004). Scale-free dynamics of global functional connectivity in the human brain. Hum. Brain Mapp. 22, 97–109.
Stanley, H. E. (1971). Introduction to Phase Transitions and Critical Phenomena. New York: Oxford University Press.
Stanley, H. E. (1999). Scaling, universality, and renormalization: three pillars of modern critical phenomena. Rev. Mod. Phys. 71, S358–S366.
Stewart, C. V., and Plenz, D. (2006). Inverted-U profile of dopamine-NMDA-mediated spontaneous avalanche recurrence in superficial layers of rat prefrontal cortex. J. Neurosci. 26, 8148–8159.
Stewart, C. V., and Plenz, D. (2008). Homeostasis of neuronal avalanches during postnatal cortex development in vitro. J. Neurosci. Methods 169, 405–416.
Tanaka, T., Kaneko, T., and Aoyagi, T. (2009). Recurrent infomax generates cell assemblies, neuronal avalanches, and simple cell-like selectivity. Neural. Comput. 21, 1038–1067.
Tang, A., Jackson, D., Hobbs, J., Chen, W., Smith, J. L., Patel, H., Prieto, A., Petrusca, D., Grivich, M. I., Sher, A., Hottowy, P., Dabrowski, W., Litke, A. M., and Beggs, J. M. (2008). A maximum entropy model applied to spatial and temporal correlations from cortical networks in vitro. J. Neurosci. 28, 505–518.
Teich, M. C., Heneghan, C., Lowen, S. B., Ozaki, T., and Kaplan, E. (1997). Fractal character of the neural spike train in the visual system of the cat. J. Opt. Soc. Am. A. Opt. Image Sci. Vis. 14, 529–546.
Teramae, J. N., and Fukai, T. (2007). Local cortical circuit model inferred from power-law distributed neuronal avalanches. J. Comput. Neurosci. 22, 301–312.
Tetzlaff, C., Okujeni, S., Egert, U., Worgotter, F., and Butz, M. (2010). Self-organized criticality in developing neuronal networks. PLoS Comput. Biol. 6, e1001013. doi:10.1371/journal.pcbi.1001013
Tkacik, G., Schneidman, E., Berry, J., and Bialek, W. (2009). Spin glass models for a network of real neurons. arXiv:0912.5409v1.
Toib, A., Lyakhov, V., and Marom, S. (1998). Interaction between duration of activity and time course of recovery from slow inactivation in mammalian brain Na+ channels. J. Neurosci. 18, 1893–1903.
Touboul, J., and Destexhe, A. (2010). Can power-law scaling and neuronal avalanches arise from stochastic dynamics? PLoS One 5, 14. doi:10.1371/journal.pone.0008982
Worrell, G. A., Cranstoun, S. D., Echauz, J., and Litt, B. (2002). Evidence for self-organized criticality in human epileptic hippocampus. Neuroreport 13, 2017–2021.
Yang, H. D., Shew, W. L., Roy, R., and Plenz, D. (2012). Maximal variability of phase synchrony in cortical networks with neuronal avalanches. J. Neurosci. 32, 1061–1072.
Yeh, F. C., Tang, A. N., Hobbs, J. P., Hottowy, P., Dabrowski, W., Sher, A., Litke, A., and Beggs, J. M. (2010). Maximum entropy approaches to living neural networks. Entropy 12, 89–106.
Yu, S., Huang, D., Singer, W., and Nikolic, D. (2008). A small world of neuronal synchrony. Cereb. Cortex doi:10.1093/cercor/bhn047
Keywords: criticality, scale-free, avalanche, network, multi-electrode array, statistical physics, Ising model
Citation: Beggs JM and Timme N (2012) Being critical of criticality in the brain. Front. Physio. 3:163. doi: 10.3389/fphys.2012.00163
Received: 21 February 2012; Accepted: 07 May 2012;
Published online: 07 June 2012.
Edited by:
Tjeerd W. Boonstra, University of New South Wales, AustraliaReviewed by:
Alain Destexhe, Information and Complexité Centre National de la Recherche Scientifique, FranceWoodrow Shew, University of Arkansas, USA
Copyright: © 2012 Beggs and Timme. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: John M. Beggs, Department of Physics, Indiana University, 727 East, 3rd Street, Bloomington, IN 47405-7105, USA. e-mail: jmbeggs@indiana.edu
