- 1 Department of Psychology and Neuroscience, University of Colorado at Boulder, Boulder, CO, USA
- 2 Department of Psychiatry and Behavioral Sciences, Stanford University, Stanford, CA, USA
- 3 Department of Neurology and Neurological Sciences, Stanford University, Stanford, CA, USA
- 4 Symbolic Systems Program, Stanford University, Stanford, CA, USA
- 5 Program in Neuroscience, Stanford University, Stanford University, Stanford, CA, USA
- 6 Department of Psychology, San Diego State University, San Diego, CA, USA
Although the detrimental effects of math anxiety in adults are well understood, few studies have examined how it affects younger children who are beginning to learn math in a formal academic setting. Here, we examine the relationship between math anxiety and math achievement in second and third graders. In response to the need for a grade-appropriate measure of assessing math anxiety in this group we first describe the development of Scale for Early Mathematics Anxiety (SEMA), a new measure for assessing math anxiety in second and third graders that is based on the Math Anxiety Rating Scale. We demonstrate the construct validity and reliability of the SEMA and use it to characterize the effect of math anxiety on standardized measures of math abilities, as assessed using the Mathematical Reasoning and Numerical Operations subtests of the Wechsler Individual Achievement Test (WIAT-II). Math achievement, as measured by the WIAT-II Math Composite score, was significantly and negatively correlated with SEMA but not with trait anxiety scores. Additional analyses showed that SEMA scores were strongly correlated with Mathematical Reasoning scores, which involves more complex verbal problem solving. SEMA scores were weakly correlated with Numerical Operations which assesses basic computation skills, suggesting that math anxiety has a pronounced effect on more demanding calculations. We also found that math anxiety has an equally detrimental impact on math achievement regardless of whether children have an anxiety related to numbers or to the situational and social experience of doing math. Critically, these effects were unrelated to trait anxiety, providing the first evidence that the specific effects of math anxiety can be detected in the earliest stages of formal math learning in school. Our findings provide new insights into the developmental origins of math anxiety, and further underscore the need to remediate math anxiety and its deleterious effects on math achievement in young children.
Introduction
Researchers and educators alike have long recognized the role of mathematics in academic and professional success. One factor that influences the learning and mastery of mathematics is anxiety. Math anxiety, in particular, can negatively impact an individual’s initial learning of mathematics, leading over time to poor math skills which, in turn, can have an adverse effect on longer-term career choices and professional success (Hembree, 1990; Meece et al., 1990; Ma, 1999; Krinzinger et al., 2009). Research has also shown that, in adults, math anxiety can negatively impact performance of basic numerical operations, such as counting and simple addition, which serve as the building blocks for more complex mathematical concepts (Ashcraft and Faust, 1994; Ashcraft, 2002; Maloney et al., 2010).
Previous studies have shown that individuals with math anxiety inevitably experience more difficulty with greater performance pressure and more complicated calculations (Ashcraft and Moore, 2009). The end result is a feedback loop in which adults with math anxiety often perform poorly on standardized math tests (Hembree, 1990; Ashcraft and Krause, 2007), avoid arithmetic classes (Hembree, 1990; Ashcraft and Moore, 2009), and foster negative beliefs regarding their own math abilities (Lent et al., 1991; Ashcraft and Kirk, 2001), and in turn experience greater math anxiety and avoidance. Indeed, math anxiety has also long been cited as one of the main causes of low female enrollment in math and science courses (Ernest, 1976; Tobias and Weissbrod, 1980; Meece et al., 1982; Hembree, 1990).
Given the long-term and detrimental effects of math anxiety, it is important to understand how math anxiety affects the learning of mathematics. The majority of the research on math anxiety has been conducted in young adults, with far less emphasis on the effect of math anxiety in younger participants. In his review of math anxiety studies, Hembree (1990) found that math anxiety was consistently correlated with poor performance on math achievement tests. However, of the 122 studies he examined, only seven of them included participants who were of pre-college age. Furthermore, none of the studies included children below the fifth grade, a time period that is crucial for the initial learning of mathematics. Consequently, more research is necessary to understand whether math anxiety exists in younger students, such as in early elementary school, and if it does indeed exist, how it affects math learning and achievement.
The studies that have been conducted on pre-college-aged populations have focused primarily on adolescents and students in upper elementary school. In adolescents, math anxiety scores were found to significantly and negatively correlate with term grades, final exam grades, and tests of mathematic aptitude (Richardson and Suinn, 1972; Resnick et al., 1982; Wigfield and Meece, 1988). Math anxiety was also significantly and negatively correlated with all of the mathematics subtests, as well as the total mathematics score, of the Stanford Achievement Test (SAT). The subtests measured understanding of math concepts, applications, and computation and correlations with math anxiety ranged from −0.26 to −0.31.
Subsequent research also supported the detrimental effects of math anxiety on academic achievement in the upper elementary grades (Chiu and Henry, 1990; Hembree, 1990; Ma, 1999). For example, Chiu and Henry found that in fifth, sixth, and eight graders, levels of math anxiety were significantly and negatively correlated with semester math grades. These studies also found that a high prevalence of anxiety for math exists in older elementary school-aged children (Chiu and Henry, 1990) and that levels of math anxiety tend to increase in severity in children over time (Ma, 1999), further underscoring the importance of early identification of math anxiety.
We are currently aware of only three studies that have examined the nature of math anxiety in the early stages of math learning. The first study, published as a conference paper by Thomas and Dowker (2000), used a measure (i.e., Math Anxiety Questionnaire, MAQ) created by the authors to examine the relationship between math ability, performance, and math-related attitudes, anxiety, and self-perceived performance in children between the ages of six and nine. Although Thomas and Dowker found that math anxiety does indeed exist in this age group, they found no significant relationship between math anxiety and calculation ability. Although this study was the first to examine the nature of math anxiety in this age group, it has several limitations. First, it is unclear whether Thomas and Dowker’s “calculation ability” refers to an individual’s grade-based math achievement (such as those measured by standardized tests of math achievement) or overall aptitude (as measured by general measures such as the Weschler Intelligence Scales for Children). Second, the lack of psychometric data on the MAQ leaves the validity and reliability of this anxiety measure unclear.
The second study of math anxiety in this age group was conducted by Krinzinger et al. (2009). This study used a German translation of the MAQ to examine the longitudinal effects of math anxiety on “calculation ability” in children in first through third grade. Children in this study were asked to orally solve a set of single-digit addition and subtraction problems as quickly as possible. Calculation ability was defined as the number of correctly answered problems per minute. This study, like the one by Thomas and Dowker (2000), did not find math ability to be correlated with math anxiety.
Taken together, the results of these two studies suggest that children do experience math anxiety in the earliest stages of schooling. More importantly, however, these results contradict findings in the adult literature, which have consistently found that individuals with math anxiety perform worse on tests of math achievement. Although Thomas and Dowker explain that the lack of a significant relationship may be due to developmental changes in the relationship between math performance and math anxiety, they also emphasize that further studies are necessary to understand or clarify why these results differ between adults and children. More recently, Ramirez et al. (in press) examined math anxiety on first and second grade children using a short-form questionnaire based on the Math Anxiety Rating Scale (MARS)-E. In contrast to the prior two studies, they found that math anxiety did indeed have a negative impact on math achievement, but only in children who had higher levels of working memory capacity. These results are intriguing, in part because such a dichotomy has not been found in adults and because they suggest that math anxiety may have a selective impact on math learning in children.
The main goals of the current study were to develop and validate standardized measures of math anxiety in young children and to examine the relationship between math anxiety and math achievement in 7- to 9-year-old children at one of the earliest stages of formal math learning. We improved upon previous studies (Thomas and Dowker, 2000; Krinzinger et al., 2009) in several ways. First, we used standardized measures (Wechsler Individual Achievement Test, second edition, WIAT-II and Wechsler Abbreviated Scale of Intelligence, WASI) to measure assess math achievement and aptitude. Second, we focused on a narrow age range which included only second and third grades, and incorporated test items that are relevant to problems that children in this age group are routinely exposed to in the classroom. Third, we also assessed and controlled for trait anxiety in order to remove the effect of general anxiety, an important issue that previous studies in children have overlooked. Finally, we created an age-appropriate math anxiety measure (Scale for Assessing Early Mathematics Anxiety; SEMA) based on the MARS (Richardson and Suinn, 1972) and the MARS – Elementary (Suinn et al., 1988). The MARS and MARS-E are two of the most widely used measures in the adult and adolescent math anxiety literature and provide the best validated means of assessing math anxiety.
Measures of Math Anxiety
The MARS (Richardson and Suinn, 1972) was the first published measure of math anxiety. The MARS was created to assess context-specific anxiety “associated with the single area of the manipulation of numbers and the use of mathematical concepts” in adults (Richardson and Suinn, 1972, p. 551). In order to study math anxiety in older children and adolescents, new math anxiety measures were subsequently developed that were tailored to this age group. First, the MARS was adapted by Suinn and Edwards (1982) for middle and high school students. Suinn et al. (1988), an alternate version of the MARS was created to include items that were more appropriate for elementary school children in the forth through sixth grades (MARS-E). Later, Chiu and Henry (1990) developed a new math measure, the Mathematics Anxiety Scale for Children (MASC; Chiu and Henry, 1990), for use in children in both upper elementary (i.e., fifth grade) to middle school. Subsequent research with these measures supported the detrimental effects of math anxiety on academic achievement in upper elementary of grades 4 through 6 (Hembree, 1990; Ma, 1999; Chiu and Henry, 1990) and suggests that a high prevalence of anxiety for math exists in older elementary school-aged children (Chiu and Henry, 1990). Research also found that math anxiety tends to increase in severity in 5th through 12th graders over time (Ma, 1999), further underscoring the importance of early identification of math anxiety.
Math Anxiety Measures for Children in Early Elementary School
Measures such as MARS-E and the MASC have been useful for measuring math anxiety for middle school and upper elementary school-aged children. However, neither of these measures is appropriate for use in children in the second and third grades, the level at which children begin learning multiple math concepts and operations. An adequate measure of math anxiety for these children would need to assess anxiety specifically related to addition, subtraction, number patterns, and spatial reasoning in a problem solving context appropriate for second and third graders, based on the curriculum recommended by the National Council of Teachers of Mathematics (2012).
To date, we know of only two measures of math anxiety that are appropriate for use with children in second and third grade. As previously mentioned, the MAQ, was constructed by Thomas and Dowker (2000) to assess math anxiety in 6- to 9-year-old children. The other measure appropriate for use with third graders is the Mathematics Anxiety Survey (MAXS), which was developed by Gierl and Bisanz (1995). The MAXS was written to assess the two constructs of math anxiety that were first identified by Suinn et al. (MARS-E; 1988) in older elementary school students: test and problem solving anxiety (Suinn et al., 1988). Unfortunately, the MAXS only extends the age range of the MARS-E by 1 year; the MARS-E was designed for use in children grades 4 through 6, whereas the MAXS is intended for children in grades 3 through 6. Given that children begin learning more complex math in the second grade, more appropriate measures are needed to assess math anxiety in relation to math proficiency in both the second grade and third grades.
We developed the SEMA with several objectives in mind. Our first objective was to create a math anxiety measure that was appropriate and valid for use in second and third graders. Our second objective was to base our measure on the MARS and the MARS-E, because both measures have robust psychometric properties and have been widely used. In order to ensure that the SEMA’s assessment of anxiety was not being confounded by differences in exposure between the two grades, the content of the questions was equally representative of second and third grade math curriculum. We followed the format and content of the MARS and MARS-E by including questions that assessed (1) anxiety related to completing math-related work and problems, and (2) anxiety stemming from social and testing situations that require the use of math. The third objective was to explore and clarify the effect of math anxiety on math achievement as measured by a well-validated standardized measure, the WIAT-II (Wechsler, 2005). Given the contradictory nature of past findings with regards to math anxiety both within the developmental literature and between adult and child studies, we examined its impact on two different types of math skills. Specifically, we characterize the relationship between math anxiety and math abilities as assessed using two standardized measures of the WIAT-II measures – Mathematical Reasoning and Numerical Operations (see Materials and Methods below). In contrast to Numerical Operations, which assesses the ability to solve symbolically presented problems, Mathematical Reasoning examines a child’s ability to reason about complex word problems. We therefore predicted that math anxiety would not only impact overall math abilities but would also differentially impact Mathematical Reasoning since it places greater load on working memory processes that are known to be impacted by anxiety (Beilock, 2008). Critically, we examine the effects of trait anxiety on both math anxiety and math ability. We hypothesized that math anxiety would significantly predict math achievement above and beyond trait anxiety. Our final objective is to disseminate SEMA to the wider research community to further research on math anxiety in young children (Wu and Menon, 2012).
Materials and Methods
Participants
Participants were 162 children from the greater San Francisco Bay Area. Children were recruited via flyers sent to public and private elementary schools, as well as advertisements in magazines, websites, and learning disability groups. The average age of the children was 8.08 years (SD = 0.64), and the group consisted of 86 second graders (M = 7.61 years, SD = 0.41) and 76 third graders (M = 8.61 years, SD = 0.39). Ninety participants were boys, and 72 were girls. A Pearson’s Chi-Square indicated that there was no difference in the distribution of boys and girls between the two grades, χ2(1) = 1.79, p = ns. Of all of the participants, only one met criteria for a mathematical disability (MD; math achievement score at 10th percentile or below).
Procedure
SEMA questionnaire
As previously discussed, the MARS-E and MARS, which were created by Suinn et al. (1972, 1988), served as the primary model for the SEMA. The content of the items was based on a content analysis of the second and third grade curricula obtained from the Offices of Education of the following school districts within the Northern California Bay Area: San Francisco, San Jose, Santa Clara, and San Mateo. We also conducted an analysis of the standardized curriculum of the California Department of Education. Across the various school districts and the Department of Education, the five most commonly cited concepts for second and third graders were number sense, basic mathematical functions, measurement, geometry, and mathematical reasoning.
The SEMA’s first 10 items were based on second and third grade mathematics curriculum and were worded to assess the anxiety related to solving problems that involved these five concepts. The last 10 questions were designed to assess the anxiety related to social and testing situations that second and third graders often encounter while learning the aforementioned five concepts. These situations were modeled after those included in the MARS and MARS-E. Scale for Early Math Anxiety in Appendix shows the 20 questions that comprise the SEMA.
Although the format of the MARS-E and MARS was easily adopted for use with second and third graders, the task of creating grade-appropriate questions involved several choices. First, we wanted a measure that would mirror a two-factor structure similar to those of the MARS and MARS-E, but one that would also be appropriate for children who were in the early stages of math learning. In addition, the measure had to account for a wide range of math experiences and aptitudes such that the questions did not elicit high levels of anxiety by virtue of being too difficult for second graders. For example, an item related to solving 23 + 97 would inevitably cause more anxiety than 2 + 3. Thus, we based the content of the SEMA questions on math concepts that were consistently used in second and third grade math curricula across a variety of school districts. We were careful to note content of the math curriculums and included only basic single-digit two-addend addition problems, for example, instead of more complex three-addend or double-digit addition problems.
Administration of the SEMA
Children were administered the measure individually in a one-on-one setting with an assessor. In addition to the actual test items, practice problems (see Appendix) were included in order to ensure that the children understood the instructions. Each of the 20 questions on the SEMA was presented on a piece of paper and also simultaneously read aloud by the examiner. After each question, the children were asked to rate how anxious they felt. As in the MARS-E, ratings were made on a five-point response. Ratings were shown with graded anxious and non-anxious faces in order to assist the children in identifying their anxiety levels. Children responded by selecting one of the faces or by verbally replying how anxious or non-anxious they felt. The tester recorded the child’s response, making sure to ask for clarification if there was any ambiguity. An individual’s SEMA score was computed by summing the 20 items’ ratings.
Assessment of trait anxiety
We used the Child Behavior Checklist (CBCL/6-18; Achenbach, 1991; Achenbach et al., 2003), a widely used and well-validated standardized measure that rates social and behavioral problems in children between the ages of 6 and 18. Parents, close relatives, or guardians were asked to rate 113 items describing whether the child was currently exhibiting or had exhibited within the last 6 months specific behavioral and emotional problems or traits. Items were rated on a scale of 0 (not true), 1 (somewhat true), or 2 (very true). The CBCL yields several subscales: aggressive Behavior, Anxious/Depressed, Attention Problems, Rule-Breaking Behavior, Social Problems, Somatic Complaints, Thought Problems, Withdrawn/Depressed, Affective Problems, Anxiety Problems, Somatic Problems, Attention Deficit/Hyperactivity Problems, Oppositional Defiant Problems, and Conduct Problems. In the present study, we used the Anxiety Problems subscale in order to control for trait anxiety in the children.
Assessment of math, reading, and cognitive abilities
Several measures were used in order to assess the children’s math, reading, and cognitive abilities. The WASI is a nationally standardized IQ test that produces three scores: verbal, performance, and full scale IQ (FSIQ; Wechsler, 1999). Verbal IQ is a measure of the ability to use language to explain vocabulary and concepts. Performance IQ is a measure of an individual’s ability to complete non-verbal tasks such as puzzles and patterns. The FSIQ is a composite measure derived from both Verbal IQ and Performance IQ.
Wechsler Individual Achievement Test, Second Edition (Wechsler, 2005) is a standardized test designed to determine grade-specific academic skills in math and reading. The Numerical Operations and Mathematical Reasoning subtests of the WIAT-II, as well as the composite scores derived from these subtests, were used to measure math abilities. As described in the WIAT-II manual, Numerical Operations “assesses the ability to identify and write numbers, count using 1:1 correspondence, and solve written calculation problems and simple equations involving the basic operations of addition, subtraction, multiplication and division.” In contrast, Mathematical Reasoning “presents a series of problems with both verbal and visual prompts that assess the ability to reason mathematically.” For example, some of the questions require the participants to solve “single- and multi-step work problems.” The Word Reading and Reading Comprehension subtests of the WIAT-II, as well as the composite scores derived from these subtests, were used to measure reading abilities. As described in the WIAT-II manual, Word Reading “assesses early reading (phonological awareness) and word recognition and decoding skills.” In contrast, Reading Comprehension “assesses the type of reading comprehension skills taught in the classroom or used in everyday life.”
Although the WIAT-II allows for a standardized Math Composite score based on the Numerical Operations and Mathematical Reasoning subtests, there is no analogous Reading Composite that can be created from the two afore mentioned reading subtests. In order to maintain consistency in how the reading and math composites were calculated, we averaged the standardized scores of the two math and reading subtests. This method yielded indistinguishable results when compared against analyses that used the normed WIAT-II Math Composite. For the purposes of the current manuscript, the terms “Math Composite” and “Reading Composite” will refer to the numerical average of the standardized subscale scores, and not the WIAT-II normed composite scores.
Results
Normative Data
The demographics of the sample are provided in Table 1. The SEMA score was calculated by adding the scores across the 20 items. The mean SEMA score for all the participants was 34.35 (possible range of 20–100), with a standard deviation of 11.60. For the second graders, the mean SEMA score was 34.65 (SD = 12.74) and 33.79 (SD = 10.22) for the third graders. Mean scores and percentiles are presented in Table 2. No significant difference was found between the SEMA scores for the second and third graders, t(160) = 0.585, p = ns.
Reliability
Internal consistency of the SEMA, as measured by Cronbach’s α, was 0.870. We also examined the Cronbach’s α of the scale that would be obtained if each item were deleted. When individual questions were deleted, α values ranged from 0.861 to 0.872. This suggests that each of items contribute to the scale in a stable and consistent manner. Item-total correlations ranged from 0.170 to 0.560 with 10 of the items having item-total correlations of greater than 0.50. Split-half reliability, as measured by Spearman–Brown Coefficient, was 0.774.
Structural Validity
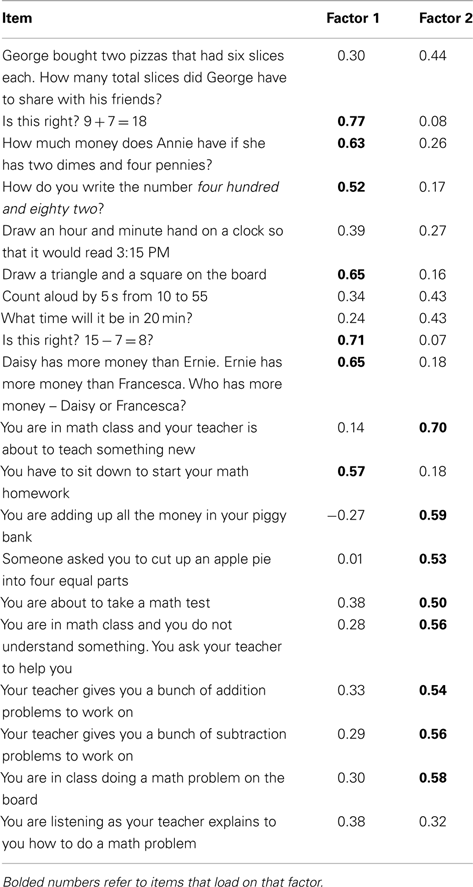
We examined the structural validity of SEMA by conducting an exploratory factor analysis using Principal Components Analysis with varimax rotation. The results confirmed the two-factor structure found in the MARS and the MARS-E with 29.73 and 8.56% of the variance being accounted for by the first and second factors, respectively. Using the rotated component matrix, items were extracted for a particular factor if they had a loading of at least 0.50 on that factor and no greater than 0.40 on the other factor. Given this criteria, none of the items loaded on both of the factors. The analyses indicated that seven items loaded on Factor 1, termed Numerical Processing Anxiety, with loadings ranging from 0.52 to 0.77 (Factor Loadings for Factors 1 and 2 in Appendix). Eight items loaded on Factor 2, termed Situational and Performance Anxiety, with loadings ranging from 0.50 to 0.70. Items that loaded on the first factor included the following: “Is this right?: 9 + 7 = 18” or “Is this right?: 15 − 7 = 8?” whereas questions that loaded on the second factor included: “You are in math class and your teacher is about to teach something new” or “You are in class doing a math problem on the board.” A parallel analysis further confirmed that a two-factor structure best represented the data when eigenvalues from the current data set were compared against eigenvalues from a randomly generated data set: (a) Factor 1, 5.95 versus 1.76, and (b) Factor 2, 1.71 versus 1.55. There was a correlation of 0.529 (p < 0.001) between the two factors. Additionally, Cronbach’s α was 0.802 for the Numerical Processing Anxiety factor and 0.770 for the Situational and Performance Anxiety factor. All items were included in the total SEMA score, regardless of whether or not they loaded on one of the two factors.
Math Anxiety and Its Relation to Trait Anxiety
We first examined whether math anxiety was related to trait anxiety. SEMA scores were not significantly correlated with trait anxiety, as measured by the Anxiety Problems subscale of the CBCL (r = 0.08, p = 0.37, R2 = 0.01).
Math Anxiety and Its Relation to Math Achievement
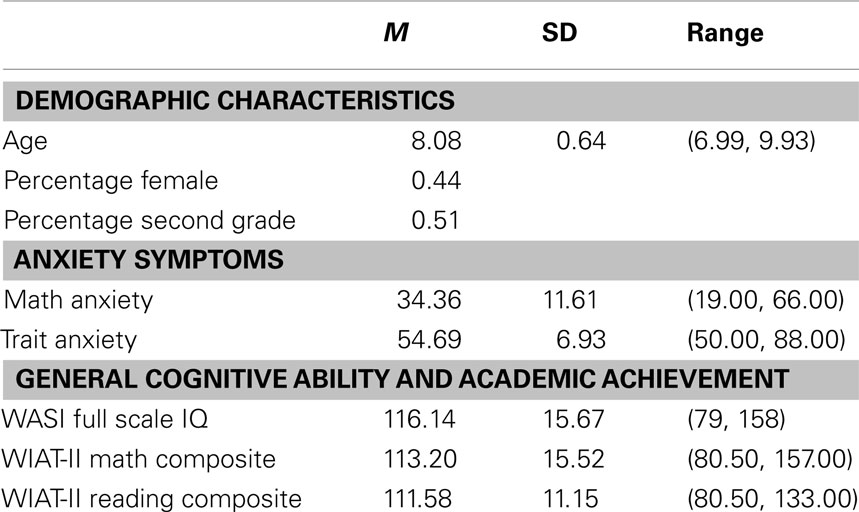
We then examined the relationship between math anxiety and math achievement by controlling for trait anxiety (CBCL) and FSIQ (WASI FSIQ). We controlled for FSIQ in order to remove the effects of differences in underlying aptitude. When controlling for these two variables, math anxiety was still significantly and negatively correlated with math achievement [Math Composite score; β = −0.26, t(126) = −2.62, p = 0.01, R2 = 0.43; Figure 1]. Additionally, a hierarchical regression indicated that trait anxiety did not explain a significant amount of variance in math achievement over SEMA and FSIQ (ΔR2 = 0.002, p = 0.49).
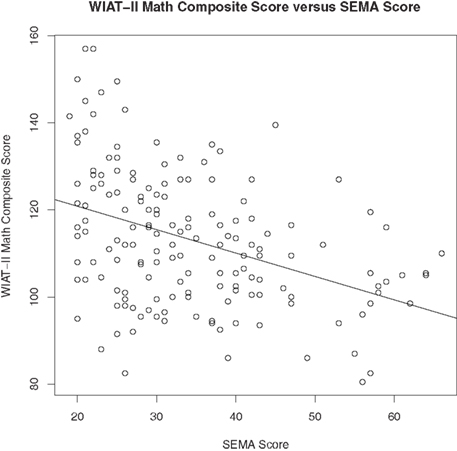
Figure 1. Math anxiety was significantly and negatively correlated with Math Achievement, as measured by WIAT-II Math Composite scores (R2 = 0.43).
Math Anxiety and Its Relation to Numerical Operations and Mathematical Reasoning Subtests
We further examined the relationship between math anxiety and the two WIAT-II Math subtests (Figure 2). When we controlled for trait anxiety and FSIQ using hierarchical regression analysis, we found the same results – math anxiety was significantly and negatively correlated with Mathematical Reasoning [β = −0.34, t(127) = −3.66, p < 0.001, R2 = 0.57] but not with Numerical Operations [β = −0.18, t(127) = −1.37, p = 0.17, R2 = 0.23]. Comparison of slopes indicated that this interaction was not significant (z = −1.10, p = 0.13). In order to account for the fact that fewer of the children tended rated themselves as “Very Very Nervous,” we conducted additional analyses by collapsing the “Very Nervous” and “Very Very Nervous” rating categories and recalculated the SEMA scores. This analyses indicated that SEMA was significantly correlated with both Mathematical Reasoning (ρ = −0.48, p < 0.001) and Numerical Operations ρ = −0.26, p < 0.01), even after controlling for FSIQ and trait anxiety. A difference of slopes test, however suggested that math anxiety has a significantly stronger effect on Mathematical Reasoning (z = −3.65, p < 0.0001).
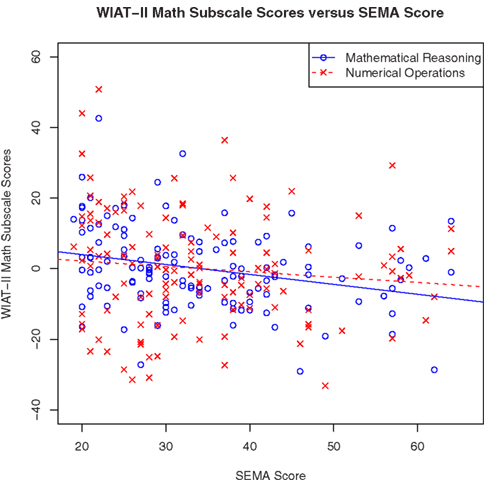
Figure 2. Math anxiety was significantly and negatively correlated with WIAT-II Mathematical Reasoning subtest (R2 = 0.57), but not the Numerical Operations subtest (R2 = 0.23). The figure above shows corrected means after controlling for FSIQ and trait anxiety.
Math Anxiety Subscales and Their Relation to Math Achievement
Finally, we examined whether the two SEMA subscales were differentially related to the WIAT-II Math Composite score (Figure 3). After controlling for FSIQ, the Numerical Processing Anxiety subscale of SEMA was significantly and negatively correlated with WIAT-II Math Composite scores (ρ = −0.21, p < 0.05) as was the Situational and Performance Anxiety subscale (ρ = −0.19, p < 0.05). Additional analyses revealed that Numerical Processing Anxiety and Situational and Performance Anxiety were correlated with Mathematical Reasoning (ρ = −0.27, p < 0.01; ρ = −0.28, p < 0.01, respectively) but not Numerical Operations (ρ = −0.13, p = 0.15; ρ = −0.09, p = 0.32, respectively).
Figure 3. Math achievement (WIAT-II Math Composite) was significantly correlated with both SEMA subscales.
Math Anxiety and Its Relation to Reading Achievement
We then examined whether math anxiety was significantly correlated with reading achievement, as measured by the Reading Composite score of the WIAT-II. After controlling for trait anxiety and FSIQ, math anxiety was not significantly correlated with the Reading Composite score [β = −0.09, t(126) = −1.45, p = 0.16, R2 = 0.14]. Additional analyses were conducted using the Reading Comprehension and Word Reading subtests of the WIAT-II. After controlling for trait anxiety and FSIQ, math anxiety was not significantly correlated with either Reading Comprehension [β = −0.08, t(127) = −1.21, p = 0.23, R2 = 0.13] or Word Reading [β = −0.11, t(127) = −1.22, p = 0.22, R2 = 0.10]. After controlling for FSIQ, neither of the SEMA subscales was significantly correlated with the Reading Composite, Word Reading, or Reading Comprehension subtests of the WIAT-II.
Discussion
The goal of our study was to examine the relationship between math anxiety and math achievement in the early stages of math learning. As previously discussed, prior studies have been inconclusive with respect to how math anxiety impacts children in early elementary school, with some studies suggested that it exists but does not have an impact and others suggesting that it differentially affects children. In order to achieve this goal, we created a measure of math anxiety that is appropriate for children in the early stages of formal math learning. We first discuss the structure, validity, and reliability of the SEMA and then discuss how this measure provides insights into the relation between math anxiety and math performance in young children.
Reliability of SEMA
The reliability estimates of SEMA were robust and showed both internal consistency and split-half reliability. Specifically, the internal consistency of SEMA was 0.870 (Cronbach’s α), similar to the reliability estimates found using MARS-E in older children (0.88). The high Cronbach’s α value ensures that SEMA items are a reliable measure of construct validity of math anxiety as a whole (Cronbach, 1951; Streiner, 2003). It also suggests that SEMA is able to achieve an internal consistency similar to those achieved with older children in MARS-E. The SEMA showed moderately high split-half reliability (0.774), but it cannot be compared against the split-half reliability of the MARS or the MARS-E, as neither study reported such measures (Richardson and Suinn, 1972; Suinn et al., 1988). Despite the fact that the SEMA has relatively fewer items as compared with the 98 items on the MARS, a split-half reliability of 0.774 is still robust, and suggests that the items are still strongly correlated with each other, even when randomly divided into halves.
Factor Structure of the SEMA
We established the structural validity of the SEMA using a factor analysis. Principal components factor analyses revealed that the SEMA has a two-factor structure, which replicated the structure found in both the MARS and the MARS-E. One factor was related to numerical concepts (Numerical Processing Anxiety), and the other was related to situations involving the execution of math (Situational and Performance Anxiety). Additionally, the two factors were shown to have internal consistency, and also were independently negatively and significantly correlated with math achievement. Future studies should explore the possibility of including additional items related to test, as opposed to performance, anxiety in third and possibly second graders as well. Nonetheless, taken together, these data suggest that the SEMA achieves a reliability and validity similar to that of the MARS and MARS-E and is an appropriate measure to use to assess math anxiety in second and third graders.
Math Anxiety and Math Achievement in 7- to 9-Year-Old Children
The main objective of our study was to evaluate if math anxiety impacted early math learning performance. Critically, in contrast with the prior studies involving some children in this age group (Thomas and Dowker, 2000; Krinzinger et al., 2009) we found that math anxiety was significantly and negatively correlated with math proficiency, even in children who were at or above grade level in math. Specifically, children with higher levels of math anxiety on the SEMA had lower performance on standardized measures of math achievement. Our findings are, however, consistent with several previous reports in adults and older children.
For example, Suinn et al. (1988) found that math anxiety scores from the MARS-E were negatively and inversely correlated with performance on the mathematics portion of the SAT in their study of elementary school children in grades 4 through 6. In a college sample, Richardson and Suinn (1972) found that MARS scores were significantly and inversely related to performance on the mathematics portion of the Differential Aptitude Test. In adults, Ashcraft and Krause (2007) also found that math anxiety was significantly and negatively correlated with performance on the Wide Range Achievement Test, a standardized test of math proficiency. Interestingly, they found that the effects of math anxiety became more pronounced as problems became more difficult. That is, individuals with high levels of anxiety performed significantly worse than the lower-anxiety groups on the more difficult problems, and performed similarly to the other groups on the easier problems. Furthermore, research has also suggested that math anxiety is related to more than just performance on standardized achievement tests. Ashcraft and Faust (1994) reported that individuals with high math anxiety were significantly slower and less accurate on performing complex 2-added addition problems than individuals without math anxiety. However, the same effects were not found when individuals were completing simpler addition and multiplication problems in an untimed and paper-and-pencil format (Faust et al., 1996).
In a sample of 6- to 9-year-old German children, Krinzinger et al. (2009) found that math anxiety as assessed by MAQ was significantly correlated only with attitude toward mathematics, but not math achievement. Whether the lack of behavioral effects is due to the factors that are specific to the cultures and education systems of the United States and Germany warrants further investigation. Another possible explanation is that the SEMA is simply a more sensitive measure of math anxiety than the measures previous researchers used. Furthermore, our use of the WIAT-II, a standardized measure of math performance provides greater generalizability than findings from most previous studies. It is therefore noteworthy that second and third grade children with higher levels of math anxiety tend to perform worse in math. While this finding is consistent with extant literature in adults and adolescents, it is still surprising that differences in achievement can be found so early in an individual’s math education.
The second major finding of this study is that SEMA scores were significantly correlated with lower levels of Mathematical Reasoning scores on the WIAT-II. Given that the Mathematical Reasoning section consists of complex word problems that often involve the manipulation of several numbers and numerical operations (e.g., both addition and subtraction), this relationship was in the predicted direction. In contrast, although SEMA scores were also negatively correlated with Numerical Operations scores of the WIAT-II, this effect was not statistically significant. Similar to Mathematical Reasoning, the Numerical Operations subtest assesses math aptitude but with a greater focus on simple calculation involving addition and subtraction. This finding may explain why Thomas and Dowker (2000) and Krinzinger et al. (2009) did not find a relationship between math anxiety and basic calculation ability. Our findings are interesting in light of studies which have suggested that new and novel computations tend to be the ones most hindered by performance anxiety, whereas more automatized skills that are well learned tend to be less affected (Beilock and Carr, 2001). Because simple computational skills are still nascent and not fully mastered in second and third graders (Geary, 2000; Jordan and Hanich, 2000; Jordan et al., 2003), one would have expected that the Numerical Operations scores would also be negatively impacted by math anxiety.
One potential explanation for these findings is suggested by findings in the adult cognitive psychology literature. Previous studies in adults have consistently shown that math anxiety can hinder performance by limiting working memory resources (Hopko et al., 1998; Ashcraft and Kirk, 2001; Beilock and Carr, 2001, 2005; Ashcraft and Krause, 2007). More recently, Ramirez et al. (in press) examined the effect of math anxiety on math achievement first and second grade children using a short-form questionnaire based on the MARS-E. They found that children who were high in working memory were particularly prone to being negatively impacted by math anxiety Further studies are needed to investigate exactly whether these children rely more on working memory during computations and are therefore impacted to a greater extent by math anxiety.
Because the Numerical Operations subtest of the WIAT-II assesses simpler math concepts that can be completed using paper-and-pencil, they may not have taxed the children’s working memory capacity as much. Furthermore, children were given unlimited time to complete the Numerical Operations problems and were therefore not under any time pressure. In contrast, problems in the Mathematical Reasoning subtest required children to listen to a problem that was being read out loud, retain the numbers, manipulate the numbers, and decide on the operation to be performed in order to produce an answer. Problems were read only twice and not provided in written form, requiring that participants attend carefully and retain relevant information. This format of problems places a greater load on working memory resources and may explain why math anxiety had a more pronounced effect on performance on both the Mathematical Reasoning but not the Numerical Operations subtests. Because our sample did not endorse the highest levels of math anxiety, we conducted additional analysis in which we collapsed across the “Very Very Nervous” and “Very Nervous” categories. This analysis revealed that math anxiety had a significant effect on performance on both the Mathematical Reasoning as well as the Numerical Operations subtests. However, the effects of math anxiety was stronger on Mathematical Reasoning (which involves more complex verbal problem solving), compared to Numerical Operations (which assesses basic computation skills), suggesting that math anxiety has a pronounced effect on more demanding calculations.
Further studies with math fluency measures such as those recently introduced in WIAT-II are also needed to assess whether math anxiety also impacts performance on basic symbolic computations under time pressure. Indeed, intriguing new evidence suggests that math anxiety may interfere at a more basic level of mathematical information processing; Maloney et al. (2010) found that math anxiety had a negative impact on numerical processing (as measured by a number comparison task) in adults. Adults who were high in math anxiety were slower on the number comparison task relative to participants who were low in math anxiety. These findings are surprising because they suggest that math anxiety may compromise even basic math skills that do not require working memory. Because complex math skills are predicated on the mastery of the more basic ones, an individual who struggles initially with math may be more prone to developing math anxiety, which in turn may negatively impact computational processes that dependent more on working memory.
Finally, we examined whether Numerical Processing Anxiety and Situational and Performance Anxiety, the two SEMA subscales, are differentially correlated with math achievement. Our findings mirrored those that were conducted with the SEMA total; after controlling for FSIQ, Numerical Processing Anxiety, and Situational and Performance Anxiety were both significantly correlated with the WIAT-II Math Composite score and the Mathematical Reasoning subscale, but not with Numerical Operations. These findings suggest that math anxiety has an equally detrimental impact on math achievement regardless of whether children have an anxiety related to numbers or to the social experience of doing mathematics. This suggests that remediation of math anxiety may require attention to both its domain-specific (numerical information processing) and domain-general (situational and social) aspects.
Math and Trait Anxiety in 7- to 9-Year-Old Children
Our results extend previous studies by separating the influence of math anxiety from trait anxiety. This is important because some previous studies have suggested that the relationship between performance and math anxiety is influenced by a more dispositional form of anxiety (Dew et al., 1983; Hembree, 1990; Baloglu and Koçak, 2005); that is, high math anxiety is potentially related to elevated anxiety levels. We found that the correlation between SEMA and WIAT-II math scores was still robust after we controlled for trait anxiety. Trait anxiety scores did not account for a significant amount of additional variance in the SEMA scores (only a non-significant 0.2%) and these scores did not predict WIAT-II math performance. Further, trait anxiety scores were not significantly correlated with SEMA scores. In addition, math anxiety scores were not significantly correlated with WIAT-II reading scores, suggesting that SEMA is indeed measuring a math specific anxiety, and not a more general academic or testing-related anxiety.
Our analysis eliminates trait anxiety as a primary cause of math anxiety, raising questions about other possible causes of math anxiety. Meece et al. (1990) found that students’ own perceptions of their math abilities, expectations about their performance, and their perceptions about the value of math significantly predicted levels of math anxiety. Other researchers (Kelly and Tomhave, 1985; Jackson and Leffingwell, 1999) have found that teacher’s attitudes toward and their methods of teaching mathematics are related to math anxiety levels in their students. Beilock et al. (2010) extended these studies and found that female elementary school teachers’ levels of math anxiety were significantly related to both the math achievement levels of the girls in their classes, and the beliefs the girls endorsed about their own mathematical abilities. Interestingly, teachers’ math anxiety levels did not predict math achievement or beliefs about abilities in boys. These results suggest that stereotype threat effects can contribute to math anxiety, with detrimental consequences for math achievement in middle and high school (Spencer et al., 1998; Else-Quest et al., 2010).
Conclusion
We have developed SEMA, a reliable and valid measure for assessing math anxiety in second and third graders. SEMA’s content is based on math curriculum and problem solving situations that are common to second and third graders, as previously available measures of math anxiety such as the MARS, MARS-E, or MAS are not appropriate for use with children in this age group. Using SEMA we show that the effects of math anxiety on math achievement can be detected in the earliest stages of formal math learning in school, even in children who are at or above grade level in math. Our findings may have implications for children who are at the lower extremes of math achievement. That is, children who underperform at math may be more prone to having even higher levels of math anxiety than those reported here. In addition, our study shows that math anxiety has a more pronounced effect on math problems that require complex verbal reasoning and problem solving, as opposed to numerical operations that require basic symbolic processing and fact retrieval. Additional research is necessary to clarify the behavioral and neural mechanisms by which math anxiety influences math learning in second and third grades. Developing and validating math anxiety measures in younger children using age-appropriate items remains an important question for future research. Critically, our findings underscore the need to remediate early math anxiety and its deleterious effects on math achievement in young children. Continued development and evaluation with larger samples is needed to further validate and standardize SEMA, and to facilitate its more general use in identifying math anxiety during the earliest stages of math skill development. Toward this goal, we are making SEMA freely available to researchers (Wu and Menon, 2012).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was supported by grants from the National Institutes of Health (HD047520, HD059205) and the National Science Foundation (DRL-0750340). It is a pleasure to thank Dr. Richard Suinn for his assistance with the development of the SEMA, and for his constructive feedback and encouragement.
References
Achenbach, T. M. (1991). Manual for the Child Behavior Checklist/4-18 and 1991 Profile. Burlington, VT: University of Vermont.
Achenbach, T. M., Dumenci, L., and Rescorla, L. A. (2003). DSM-oriented and empirically based approaches to constructing scales from the same item pools. J. Clin. Child Adolesc. Psychol. 32, 328–340.
Ashcraft, M. H. (2002). Math anxiety: personal, educational, and cognitive consequences. Curr. Dir. Psychol. Sci. 11, 181–185.
Ashcraft, M. H., and Faust, M. W. (1994). Mathematics anxiety and mental arithmetic performance: an exploratory investigation. Cogn. Emot. 8, 97–125.
Ashcraft, M. H., and Kirk, E. P. (2001). The relationships among working memory, math anxiety, and performance. J. Exp. Psychol. Gen. 130, 224–237.
Ashcraft, M. H., and Krause, J. A. (2007). Working memory, math performance, and math anxiety. Psychon. Bull. Rev. 14, 243–248.
Ashcraft, M. H., and Moore, A. M. (2009). Mathematics anxiety and affective drop in performance. J. Psychoeduc. Assess. 27, 197–205.
Baloglu, M., and Koçak, R. (2005). A multivariate investigation of the differences in mathematics anxiety. Pers. Individ. Dif. 40, 1325–1335.
Beilock, S. L. (2008). Math performance in stressful situations. Curr. Dir. Psychol. Sci. 17, 339–343.
Beilock, S. L., and Carr, T. H. (2001). On the fragility of skilled performance: what governs choking under pressure? J. Exp. Soc. Psychol. 130, 701–725.
Beilock, S. L., and Carr, T. H. (2005). When high-powered people fail: working memory and “choking under pressure” in math. Psychol. Sci. 16, 101–105.
Beilock, S. L., Gunderson, G. A., Ramirez, G., and Levine, S. C. (2010). Female teachers’ math anxiety affects girls’ math achievement. Proc. Natl. Acad. Sci. U.S.A. 107, 1860–1863.
Chiu, L. H., and Henry, L. L. (1990). Development and validation of the mathematics anxiety scale for children. Meas. Eval. Couns. Dev. 23, 121–127.
Cronbach, L. J. (1951). Coefficient alpha and the internal structure of tests. Psychometrika 16, 297–334.
Dew, K. M., Galassi, J. P., and Galassi, M. D. (1983). Mathematics anxiety: basic issues. J. Couns. Psychol. 30, 443–446.
Else-Quest, N. M., Hyde, J. S., and Linn, M. C. (2010). Cross-national patterns of gender differences in mathematics: a meta-analysis. Psychol. Bull. 136, 103–127.
Faust, M. W., Ashcraft, M. H., and Fleck, D. E. (1996). Mathematics anxiety effects in simple and complex addition. Math. Cogn. 2, 25–62.
Geary, D. C. (2000). From infancy to adulthood: the development of numerical abilities. Eur. Child. Adolesc. Psychiatry 9, 11–16.
Gierl, M. J., and Bisanz, J. (1995). Anxieties and attitudes related to mathematics in grades 3 and 6. J. Exp. Educ. 63, 139–158.
Hembree, R. (1990). The nature, effects, and relief of mathematics anxiety. J. Res. Math. Educ. 21, 33–46.
Hopko, D. R., Ashcraft, M. A., Gute, J., Ruggeriero, K. J., and Lewis, C. (1998). Mathematics anxiety and working memory: support for existence of a deficient inhibition mechanism. J. Anxiety Disord. 12, 343–355.
Jackson, C. D., and Leffingwell, J. R. (1999). The role of instructors in creating math anxiety in students from kindergarten through college. Math. Teach. 92, 583–586.
Jordan, N. C., and Hanich, L. B. (2000). Mathematical thinking in second-grade children with different forms of LD. J. Learn Disabil. 33, 567–578.
Jordan, N. C., Hanich, L. B., and Kaplan, D. (2003). Arithmetic fact mastery in young children: a longitudinal investigation. J. Exp. Child. Psychol. 85, 103–119.
Kelly, W. P., and Tomhave, W. K. (1985). A study of math anxiety/math avoidance in preservice elementary school teachers. Arithmetic Teach. 32, 51–53.
Krinzinger, H., Kaufmann, L., and Willmes, L. (2009). Math anxiety and math ability in early primary school years. J. Psychoeduc. Assess. 27, 206–224.
Lent, R. W., Lopez, F. G., and Bieschke, K. J. (1991). Mathematics self-efficacy: sources and relation to science-based career choice. J. Couns. Psychol. 38, 424–430.
Ma, X. (1999). A meta-analysis of the relationship between anxiety towards mathematics and achievement in mathematics. J. Res. Math. Educ. 30, 520–540.
Maloney, E. A., Risko, E. F., Ansari, D., and Fugelsang, J. (2010). Mathematics anxiety affects counting but not subitizing during visual enumeration. Cognition 114, 293–297.
Meece, J., Parsons, J., Kaczala, C., Goff, S., and Futterman, R. (1982). Sex differences in math achievement: toward a model of academic choice. Psychol. Bull. 91, 324–348.
Meece, J. L., Wigfield, A., and Eccles, J. S. (1990). Predictors of math anxiety and its influence on young adolescents’ course enrollment intentions and performance in mathematics. J. Educ. Psychol. 82, 60–70.
National Council of Teachers of Mathematics. (2012). Principles and Standards of Pre-K Through Grade 2. Available at: http://www.nctm.org/standards/content.aspx?id=26976
Ramirez, G., Gunderson, E. A., Levine, S. C., and Beilock, S. L. (in press). Math anxiety, working memory and math achievement in early elementary school. J. Cogn. Dev.
Resnick, H., Viehe, J., and Segal, S. (1982). Is math anxiety a local phenomenon? A study of prevalence and dimensionality. J. Couns. Psychol. 29, 39–47.
Richardson, F. C., and Suinn, R. M. (1972). The mathematics anxiety rating scale. J. Couns. Psychol. 19, 551–554.
Spencer, S. S., Steele, C. M., and Quinn, D. M. (1998). Stereotype threat and women’s math performance. J. Exp. Soc. Psychol. 35, 4–28.
Streiner, D. L. (2003). Starting at the beginning: an introduction to coefficient alpha and internal consistency. J. Pers. Assess. 80, 99–103.
Suinn, R. M., Edie, C. A., Nicoletti, J., and Spinelli, P. R. (1972). The MARS, a measure of mathematics anxiety: psychometric data. J. Clin. Psychol. 28, 373–375.
Suinn, R. M., and Edwards, R. (1982). The measurement of mathematics anxiety: the mathematics anxiety scale for adolescents: MARS-A. J. Clin. Psychol. 38, 576–580.
Suinn, R. M., Taylor, S., and Edwards, R. W. (1988). Suinn mathematics anxiety rating scale for elementary school students (MARS-E): psychometric and normative data. Educ. Psychol. Meas. 48, 979–986.
Thomas, G., and Dowker, A. (2000). Mathematics anxiety and related factors in young children. Paper Presented at British Psychological Society Developmental Section Conference, Bristol.
Tobias, S., and Weissbrod, C. (1980). Anxiety and mathematics: an update. Harv. Educ. Rev. 50, 63–70.
Wechsler, D. (1999). Wechsler Abbreviated Scale of Intelligence. San Antonio, TX: Harcourt Assessment, Inc.
Wechsler, D. (2005). Wechsler Individual Achievement Test, 2nd Edn. San Antonio, TX: The Psychological Corporation.
Wigfield, A., and Meece, J. L. (1988). Math anxiety in elementary and secondary school students. J. Educ. Psychol. 80, 210–216.
Wu, S., and Menon, V. (2012). Scale for Early Mathematics Anxiety (SEMA) in Young Children. Available at: http://www.scsnl.stanford.edu
Appendix
Scale for Early Math Anxiety
Instructions: “Now I’m going to show you some math questions. I want you to read each question and pretend that you are going to answer it. Then I want you to tell me how nervous answering that question makes you feel. So remember, you do not actually have to answer the questions, but I just want you to pretend you are going to answer them and see how it makes you feel. It could make you feel not nervous AT ALL, a little nervous, somewhat nervous, very nervous, or VERY, VERY nervous. Do you understand? Let’s do one together:” Practice Item: Who’s the President of the United States?
1. George bought two pizzas that had six slices each. How many total slices did George have to share with his friends?
2. Is this right? 9 + 7 = 18.
3. How much money does Annie have if she has two dimes and four pennies?
4. How do you write the number four hundred and eighty two?
5. Draw an hour and minute hand on a clock so that it would read 3:15 PM.
6. Draw a triangle and a square on the board.
7. Count aloud by 5 s from 10 to 55.
8. What time will it be in 20 min?
9. Is this right? 15 − 7 = 8?
10. Daisy has more money than Ernie. Ernie has more money than Francesca. Who has more money – Daisy or Francesca?
Instructions: “Now I’m going to read you some sentences about situations that have to do with math. Try to pretend each situation is happening and think about how nervous it makes you feel. It could make you feel not nervous AT ALL, a little nervous, somewhat nervous, very nervous, or VERY, VERY nervous. Do you understand? Let’s try one. Pretend…” Practice Item: You’re about to ride a roller coaster.
11. You are in math class and your teacher is about to teach something new.
12. You have to sit down to start your math homework.
13. You are adding up all the money in your piggy bank.
14. Someone asked you to cut up an apple pie into four equal parts.
15. You are about to take a math test.
16. You are in math class and you do not understand something. You ask your teacher to help you.
17. Your teacher gives you a bunch of addition problems to work on.
18. Your teacher gives you a bunch of subtraction problems to work on.
19. You are in class doing a math problem on the board.
20. You are listening as your teacher explains to you how to do a math problem.
Factor Loadings for Factors 1 and 2
Keywords: math anxiety, mathematics achievement, early math learning, math anxiety assessment
Citation: Wu SS, Barth M, Amin H, Malcarne V and Menon V (2012) Math anxiety in second and third graders and its relation to mathematics achievement. Front. Psychology 3:162. doi: 10.3389/fpsyg.2012.00162
Received: 16 February 2012; Accepted: 06 May 2012
Published online: 07 June 2012.
Edited by:
Steven E. Mock, University of Waterloo, CanadaReviewed by:
Erin Anne Maloney, University of Chicago, USAJonathan Fugelsang, University of Waterloo, Canada
Copyright: © 2012 Wu, Barth, Amin, Malcarne and Menon. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Sarah S. Wu and Vinod Menon, Symbolic Systems Program, Program in Neuroscience, and Department of Psychiatry and Behavioral Sciences, 401 Quarry Road, Stanford, CA 94305-5719, USA. e-mail: sarah.wu@colorado.edu; menon@stanford.edu
†Maria Barth and Hitha Amin have contributed equally to this work.