- 1 Division of Sleep Medicine, Department of Psychiatry and Behavioral Sciences, Stanford University School of Medicine, Stanford, CA, USA
- 2 Division of Pharmacotherapies and Medical Consequences of Drug Abuse, National Institute on Drug Abuse, National Institutes of Health, Bethesda, MD, USA
The HIV risk-taking behavior scale (HRBS) is an 11-item instrument designed to assess the risks of HIV infection due to self-reported injection-drug use and sexual behavior. A retrospective analysis was performed on HRBS data collected from approximately 1,000 participants pooled across seven clinical trials of pharmacotherapies for either the treatment of cocaine dependence or methamphetamine dependence. Analysis faced three important challenges. The sample contained a high proportion of missing assessments after randomization. Also, the HRBS scale consists of two distinct behavioral components which may or may not coincide in response patterns. In addition, distributions of responses on the subscales were highly concentrated at just a few values (e.g., 0, 6). To address these challenges, a single probit regression model was fit to three outcomes variables simultaneously – the two subscale totals plus an indicator variable for assessments not obtained (non-response). This joint-outcome regression model was able to identify that those who left assessment early had higher self-reported risk of injection-drug use and lower self-reported risky sexual behavior because the model was able to draw on information on associations among the three outcomes collectively. These findings were not identified in analyses performed on each outcome separately. No evidence for an effect of pharmacotherapies was observed, except to reduce missing assessments. Univariate-outcome modeling is not recommended for the HRBS.
Introduction
Injection-drug users are not only susceptible to HIV infection through injection, especially given HIV’s extended viability within syringes (Abdala et al., 1999), but also through unprotected sexual contact with those infected with HIV, including other injection-drug users (Strathdee and Stockman, 2010). A recent estimate of the quantity of HIV infected injection-drug users worldwide is 0.8–6.6 million (Mathers et al., 2008).
The HIV risk-taking behavior scale (HRBS) is an 11-item instrument designed to assess “the behavior of intravenous drug users in relation to both injecting and sexual behavior” (Darke et al., 1991). Six items assess injection-drug use and five items assess sexual behavior. Darke et al. (1991) reported an estimated internal reliability of α ≈ 0.70, test–retest reliability of r ≈ 0.86, and item-level percentage agreement with surrogates exceeding 81%. Petry (2001) reported similar estimates of reliability in a separate study.
The Division of Pharmacotherapies and Medical Consequences of Drug Abuse at the National Institute on Drug Abuse has employed the HRBS in various clinical trials for the treatment of cocaine or methamphetamine dependence (e.g., Anderson et al., 2009; Kahn et al., 2009). In conducting the current study, generalized estimating equations (GEE) were considered and applied in early analyses, as this had been done with other outcomes in prior work by the Division; however, these initial analyses made evident that HRBS data collected from these studies pose three significant challenges that marginal-modeling such as GEE appeared ill-equipped to address. (1) Roughly one-quarter to one-half of those providing baseline assessments did not provide assessments post-randomization; and the possibility existed that assessments were missing in an informative way. (2) The HRBS consists of two distinct domains (injection-drug use and sexual behavior), which may not coincide in their response to interventions designed to reduce substance dependence. (3) These subscale totals tend to be highly concentrated at one or two particular values creating sharply peaked and/or bimodal distributions, even though each subscale spans a range of possible totals (30 for injection-drug-use subscale and 25 for sexual-behavior subscale).
The purpose of this paper is to address the analytic challenges of the HRBS simultaneously in a single, comprehensive regression modeling framework and thereby provide investigators with a toolkit for evaluating longitudinal HRBS assessments. The method is described and justified in some detail and results are interpreted carefully in terms of quality of model fit. The paper concludes with discussion of implications for research in HIV risk behaviors.
Methods
The first of the three analytic issues to address was missing assessments after randomization. Whether or not a participant provides an assessment (i.e., non-response) may be just as much an outcome to an intervention as is the clinical outcome of interest itself (e.g., injection-drug-use subscale total). Statistical methods have been developed to model non-response and clinical outcomes together. Rather than fit one regression model for non-response and a separate regression model for clinical outcome, a single regression model is fit using both types of outcome variables simultaneously – i.e., “joint modeling.” Properly specified, joint modeling may reduce bias when one of the response variables is non-response and responsiveness is “informative” in the sense that participants are failing to provide assessments for reasons related to their clinical outcomes (see references in Guo and Carlin, 2004). Joint modeling also permits both subscale totals to be modeled simultaneously, providing insights into the multivariate nature of HIV behaviors. As a bonus, joint modeling can also improve statistical power through increasing the stability (efficiency) of regression coefficient estimates, because each outcome can leverage information from the other. This property has been recognized for some time and, for example, is the motivation behind the method of seemingly unrelated regressions (Pindyck and Rubinfeld, 1981).
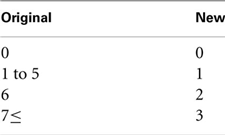
The third analytic issue concerns the strongly peaked and/or bimodal distributions of the subscale totals. This was addressed in the present study by re-coding each scale and use of probit regression. Due to the very high proportions of zeroes for the injection-drug-use subscale total (see Results), this outcome was transformed to a binary scale of 0, for a total of 0, and 1, for any total greater than zero. Because totals of 0 and 6 accounted for ∼30% and ∼22%, respectively, of all responses on the sexual-behavior subscale, transformation was to an ordinal scale as follows.
Non-response was coded as 1 for each visit on which an HRBS assessment was not obtained (both subscale totals missing) and 0 otherwise. Trivariate probit regression permitted joint modeling of non-response and both of the two HRBS outcomes (subscale totals) using these binary and ordinal scales. Initially, separate bivariate probit models were fit to these data, one for each subscale outcome and the missing assessment outcome; but it was recognized that potentially valuable information about the relationship between subscales was being ignored. The trivariate probit model assumed that each true outcome was an unobserved (latent) continuous variable; and that the outcome observed was an ordered partitioning of the unobserved scale. One can think of the three latent outcomes in this study as continuous measures of the tendency to (1) engage in risky injection-drug use, (2) engage in risky sexual behavior, and (3) not provide HRBS assessments (non-response). Analogously to Kim (1995), we allowed underlying latent variables to be correlated.
We modeled this correlation using a shared random effect (Hedeker and Gibbons, 2006). After controlling for other factors, a shared random-effect represents the combined effects of one to many latent factors that are associated with deviations of individuals’ HIV risk behaviors and non-response from the group mean. Here “group” is all individuals with the same set of baseline traits (including randomization assignment). To facilitate estimation (i.e., “identification”), the shared random-effect regression coefficient was set to 1 for non-response, to serve as the reference outcome; the shared random-effect’s mean was set to zero and its variance was set to 1.
Data were pooled from seven randomized, placebo-controlled, double-blind clinical trials (modafinil–cocaine, tiagabine–cocaine, reserpine–cocaine, ondansetron–cocaine, baclofen–cocaine, bupropion–methamphetamine, and ondansetron– methamphetamine). The regression model contained the following baseline regressors that were captured under each of these protocols: self-reported use of target substance of dependence during the 30-days prior to baseline, age (years), race, and gender. An additional regressor was included for the type of therapy (individual or group) provided to both study arms throughout the active-intervention period per the trial’s protocol. In early analyses, selection models were fit separately by trial. We realized that pooling trials would be more efficient. The regressors of use 30 days prior to baseline, age, race, and gender were included to adjust for possible population differences across trials. Categorical regressors were coded as 0/1 binary indicator variables. Race variables were created for African-American and white via two binary variables so that each represents comparison to other racial groups (i.e., neither White nor African-American). No distinction was made between multiple active doses within a trial (e.g., 200 and 400 mg of modafinil) in coding the regressor for placebo vs. active. Intercept terms were excluded from these trivariate probit models to facilitate identification on latent scales (Mahabadi and Ganjali, 2010).
Trials varied in the quantity of scheduled assessments at which the HRBS was to be captured (one baseline plus one or two post-randomization assessments) and in length of the active-intervention period (8 or 12 weeks). All trials had one post-randomization assessment scheduled at the end of the active-intervention period and some had a subsequent post-randomization assessment at end of ensuing follow-up. The trivariate probit model employed a set of regressors for time. Time was coded as days elapsed since randomization so that baseline assessments had negative time values and all post-randomization assessments had positive time values. Use of a continuous piecewise linear spline allowed the slope to be zero prior to randomization, to possibly become non-zero after randomization, and then possibly change in value again from the end of the active-intervention period through follow-up. First-order interactions between time and study arm (placebo or active) allowed slopes to differ between these two groups during the active-intervention period and during follow-up. No main effect for study arm was included because this would estimate the difference between study arms at randomization, which randomization should have forced to zero. Time effects were not included for the non-response outcome for two reasons. The first was that a follow-up period assessment was only provided by protocol for two of the seven trials; so, for the majority of trials, a non-response outcome was only possible at one assessment after randomization. The second reason is that the timing of an assessment was not recorded if no assessment was made, creating a missing value for time where non-response occurred. Non-response was coded as missing (and thereby treated as non-informative) for the third assessment of those five trials where the protocol only required assessments at baseline and end of active-intervention period.
To facilitate fitting-algorithm convergence, the regressors were mean-centered and scaled to unit SD. For time and its spline term, centering and scaling followed Gram–Schmidt orthogonalization to eliminate any collinearity that could inflate SE and reduce statistical power. Attained significance levels of p < 0.05 were declared statistically significant. All analyses were performed in SAS® v. 9.2 (SAS Institute, Cary, NC, USA).
All trials in the pooled sample were reviewed and approved by Institutional Review Boards, at the participating sites, and by a central Data and Safety Monitoring Board. Informed consent was obtained from all participants. This manuscript was internally approved by the Division of Pharmacotherapies and Medical Consequences of Drug Abuse (NIDA).
Results
Three observations were dropped as part of data quality control because they occurred either more than 1 year prior or 1 year after the date of randomization and almost certainly represented gross date coding errors. An additional observation was dropped due to a missing value on a baseline regressor. This left a total sample size of 999 participants.
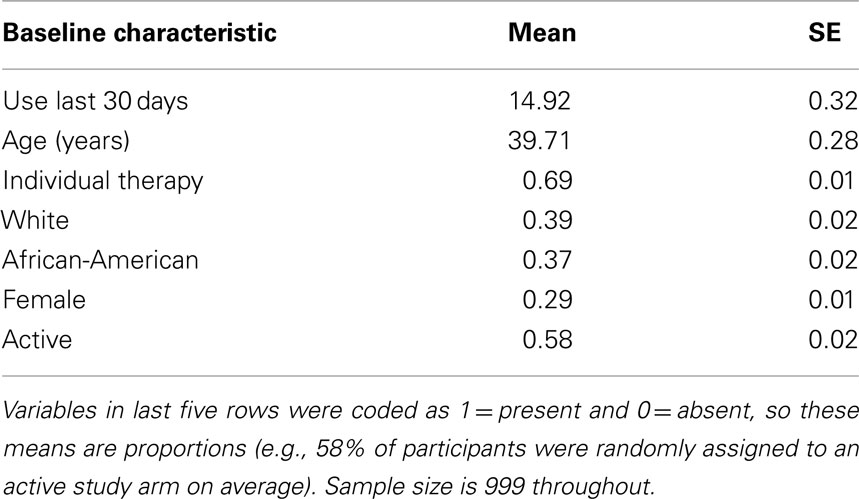
Table 1 provides the baseline characteristics of the participants in the pooled sample. Participants self-reported using the drug of dependence for about 15 out of the 30-days prior to baseline. Average age was ∼40 years. African-Americans and Whites together constituted roughly 75% of the sample. 58% of participants were randomly assigned to an active study arm.
Table 2 demonstrates that the observed sample means declined across the three successive assessments. Sample size also declined post-randomization. By the end of the active-intervention period, only 71% of baseline respondents provided assessments (n = 705). Sample size dropped substantially by the third assessment because only two of the seven trials (modafinil–cocaine and tiagabine–cocaine) required a third assessment by protocol.
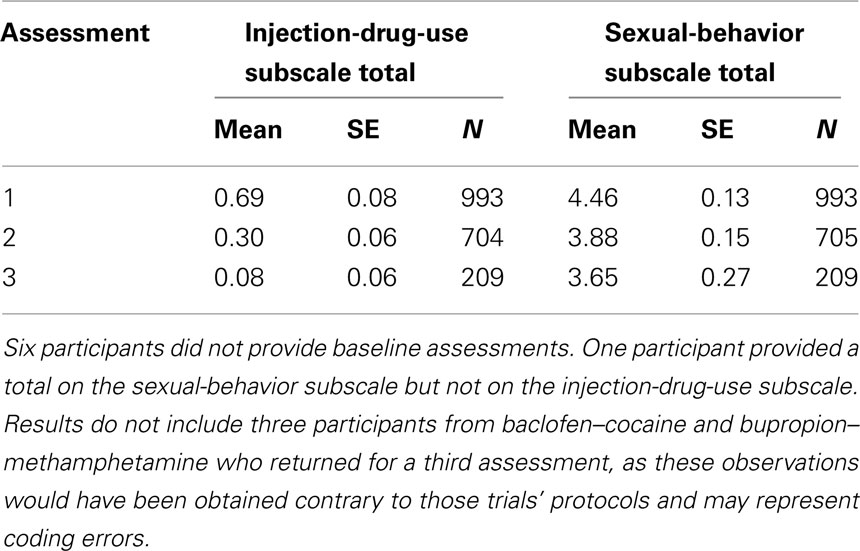
Table 2. Summary of outcomes by assessment: 1 = baseline, 2 = end of active-intervention period, and 3 = end of follow-up.
Table 3 summarizes regression findings for joint modeling of non-response, drug-use subscale total, and sexual-behavior subscale total. Risky sexual behavior and non-response may both decline with increasing age (p ≤ 0.0004). Risky sexual behavior (p = 0.0039) and non-response (p < 0.0001) may also both be associated with individual therapy, although association appears to be in opposite directions per their regression coefficient estimates. How to interpret this finding is not clear since only cocaine trials employed individual therapy and only methamphetamine trials employed group therapy. Table 3 also indicates that whites may demonstrate significantly more risky injection-drug use than other racial groups (p = 0.0283); and non-response was lower in active arms (p = 0.0200).
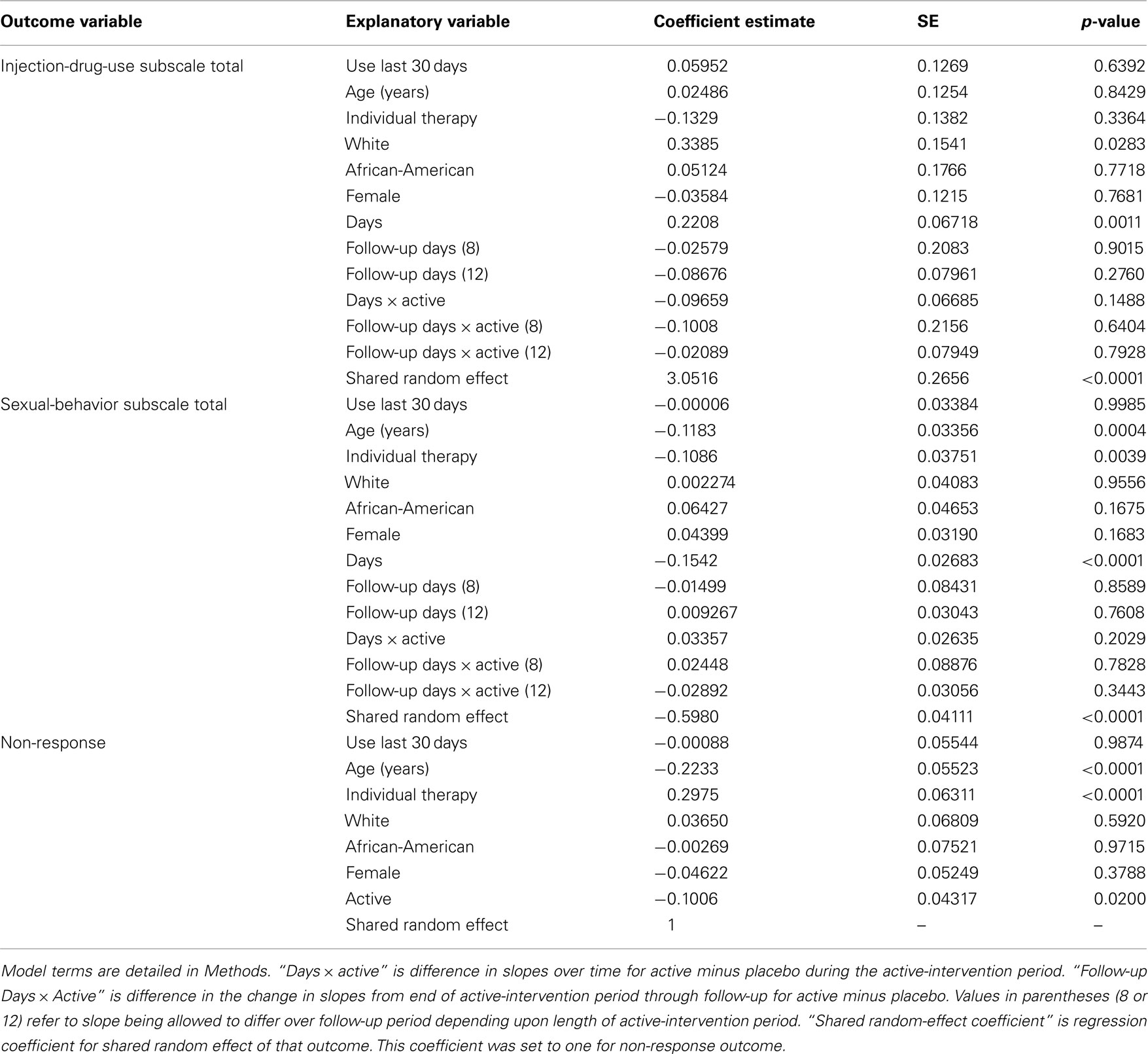
Table 3. Fit of trivariate probit regression model simultaneously to the three outcome variables of (1) dichotomized injection-drug-use subscale total, (2) four-category ordinal scale for sexual-behavior subscale total, and (3) non-response. Coefficient estimates are on scale of latent (unobserved) variables.
The coefficient estimate of the shared random effect for the injection-drug-use subscale total was positive and statistically significant (3.05, p < 0.0001), which contrasts with the negative coefficient for the sexual-behavior subscale total (−0.598, p < 0.0001). Together, the signs of the three shared random-effect coefficients indicate that one or more latent factors couple an increased tendency for non-response (+ coefficient) with an increased tendency for risky injection-drug use (+ coefficient) and a reduced tendency for risky sexual behavior (− coefficient). Assessments appear to be missing in an informative way. In practical terms, after accounting for the other factors in the model, those who choose not to provide assessments may also be doing worse in terms of injection-drug-use risk-taking and better in terms of sexual-behavior risk-taking.
These findings are consistent with detected trends in means over time. After adjusting for non-response, self-reported risky injection-drug-use appears to increase over time between baseline and end of the active-intervention period (p = 0.0011). Those who are leaving assessment have elevated risky injection-drug use and that is causing injection-drug risk-taking to increase on average within the population over time. Due to the formulation of the regression model, this time trend is, strictly speaking, only for those on placebo. However, no differences in slopes were detected between active and placebo during active intervention or follow-up for the injection-drug-use subscale total (p ≥ 0.1488). In contrast, because non-response was associated with lower sexual-behavior subscale totals, outcome on this subscale is estimated to decline on average over the active-intervention period (p < 0.0001). That is, the population self reports less risky sexual-behavior over time. For this subscale total, no evidence is observed for a difference in slopes between active and placebo during active intervention or follow-up (p ≥ 0.2029).
The potential advantages here of joint modeling are bias reduction through correction for informatively missing assessments, increased statistical power, and additional insights into the relationship between the two HRBS subscales. For comparison, univariate probit regression models were fit, with a model for injection-drug-use subscale total as an outcome and a separate model for sexual-behavior subscale total as an outcome. Like the trivariate-outcome model, univariate-outcome analyses found that whites demonstrate more risky injection-drug use than other racial groups (regression coefficient = 0.367, p = 0.0139); and risky sexual-behavior declines with age (regression coefficient = −0.174, p = 0.0006) and is negatively associated with individual therapy (regression coefficient = −0.152, p = 0.0066). Further, as with the trivariate-outcome model, univariate-outcome modeling found a decline in risky sexual-behavior over the active-intervention period (regression coefficient = −0.142, p < 0.0001). No other effects were detected for the univariate-outcome models (data not shown), which contrasts to the trivariate-outcome model’s finding that risky injection-drug-use increases during active intervention (Table 3). Presumably this difference arose because trivariate-outcome modeling allowed the fit for each outcome to leverage information from the others via the shared random effect. Univariate-outcome modeling is not recommended for the HRBS.
Does evidence of positive association exist between non-response and risky injection-drug use in the observed data? Obviously, observed data cannot provide a complete answer because the unobserved responses were unobserved and probit modeling is on the outcomes’ underlying latent scales. Even so, a rough approximation is available from the observed data. Table 4 provides the sample mean for each HRBS subscale total at baseline as stratified by non-response status at the end of the active-intervention period. Compared to respondents, non-respondents’ baseline mean was approximately 13% higher on the injection-drug-use subscale total, which is in the same direction as detected by the trivariate-outcome model. In contrast, on the sexual-behavior subscale total, non-respondents’ baseline mean was 5% higher than respondents’, which is opposite in direction from that detected by the trivariate-outcome model but also nearly threefold smaller than the difference between respondents’ and non-respondents’ means for the injection-drug-use subscale total.
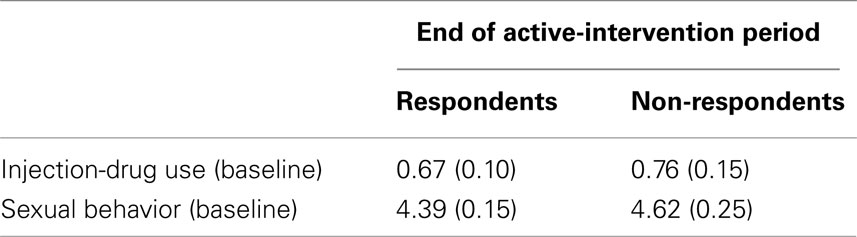
Table 4. Estimated sample mean (SE) of HRBS subscale totals at baseline stratified by non-response status at the end of the active-intervention period.
Also, the signs of the subscales’ coefficients for the shared random effect were opposite, indicating negative association (Table 3). The observed data also contains evidence for a negative association between these two HRBS components. Table 5 reveals that the only detectable association between these two subscale totals was negative in sign (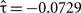 , p = 0.0255).
, p = 0.0255).
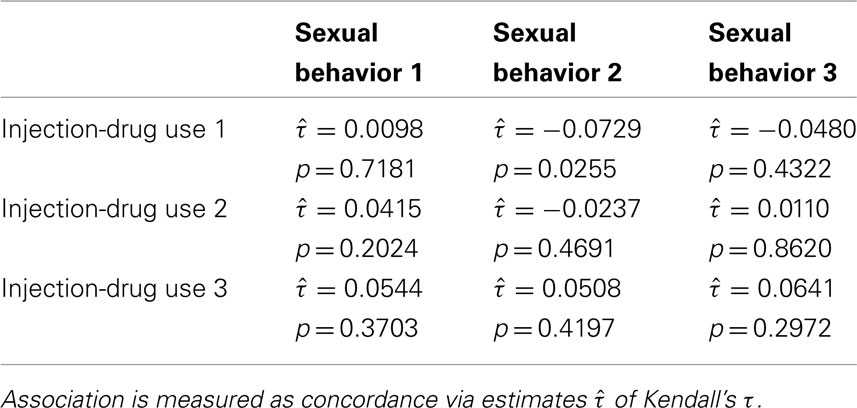
Table 5. Association between HRBS subscale totals for assessments 1 = baseline, 2 = end of active-intervention period, and 3 = end of follow-up.
A look at the distribution of the estimated shared random effect does provide some additional insights into its latent structure (Figure 1). Per standard approach, the regression model assumed that the shared random effect has a normal distribution of mean zero. Clearly, neither of those assumptions are met. The histogram and a non-parametric density estimator reveal a distribution that is bimodal with the larger of the two modes below zero. Interestingly, the smaller mode is approximately located at zero. The reason for this departure may be that, while random effects are typically used to estimate the collective impact of many small latent factors, in this population perhaps included among those smaller effects is a dominant larger latent effect. In particular, this appears to be a grouping variable, which would explain the presence of two distinct modes with one at zero. The implication is that the regression model could be more correctly specified if the identity of this large, latent grouping factor were known. A clue to its identity is suggested by the fact that the shared random effect has a particularly strong association with the non-response outcome (r = 0.59, p < 0.0001) but more modest associations with the HIV risk-taking subscale totals at baseline (|r| ≤ 0.42, p < 0.0001).
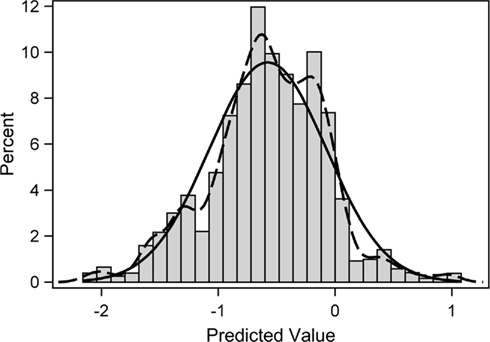
Figure 1. Frequency histogram of predicted shared random effect from the fitted trivariate probit regression model. Overlain on the histogram are a fitted normal distribution (solid line) and a non-parametric kernel density estimate (dashed line) of the distribution.
Discussion
Because the regression model incorporated associations among all three outcomes, analysis was able to identify that those who leave assessment may have more risky injection-drug use and less risky sexual-behavior subscale scores. Exactly why a negative association between these two HRBS components may exist is an open question and worthy of further investigation for the design of interventions to help reduce HIV risk-taking behaviors. Withdrawal-induced relapse and binging (Gawin and Ellinwood, 1988) may partly explain why those who leave substance-dependence treatment early have increased risk-taking with regard to injection-drug use. Self-reported risky sexual behaviors may have been more amenable to counseling and thereby declined because these behaviors were adjunct to the primary disorder (substance dependence) within the recruitment population. That risky sexual behaviors may have declined could be an important finding especially since reducing this risk has proven difficult among stimulant abusers (Metzger et al., 2010).
Analysis did not detect any evidence that HRBS response differs between active and placebo conditions despite the large size of this retrospective sample and adjustment for non-response. Univariate analyses reached the same conclusion (data not shown). This finding may not be surprising given that the active treatment conditions were targeted to reduce degree of dependence on cocaine or methamphetamine and not specifically to reduce HIV risk-taking behaviors. Even though none of the published analyses of the clinical trials within the pooled data set demonstrated improvement on their respective primary outcomes of drug dependence, perhaps the finding reported here that active condition reduced non-response (Table 3; p = 0.0200) suggests that some active medications can improve patient participation, which could be one component of an effective intervention for substance dependence and risky injection-drug behaviors. From a statistical perspective, though correlated, non-response, and outcome on HRBS subscales appear to be distinguishable processes, with non-response separably governed by at least one distinct factor, the active condition. This “exclusion restriction” may have been responsible for this study’s detection of selection bias in the HRBS subscales (Puhani, 2000).
Early analyses employed GEE; but GEE was abandoned due to its limitations. For example, GEE assumes that data are missing completely at random (Little and Rubin, 2002), which the above analyses suggest is incorrect for this population. The missing completely at random assumption can be relaxed slightly using a multiple-imputation version of GEE (MI-GEE; Beunckens et al., 2008); however, even MI-GEE does not allow for the possibility that assessments can be missing informatively (Beunckens et al., 2008). The MI-GEE approach also adds the complication of requiring development of an imputation model (Schafer, 1997). For the current study, initially a different univariate mixed modeling approach was tried that assumed a mixture distribution of the sexual-behavior subscale total, allowing for its observed bimodal structure. That complicated estimation substantially through reliance on an expectation–maximization algorithm (Little and Rubin, 2002); and that added computational complexity came without the benefits of the multivariate-outcome analysis, as detailed above. Shared-parameter models were also fit that employed a bivariate outcome: (1) the last value observed on each subscale outcome for each person and (2) the timing of that last outcome. These models suffered from fitting-algorithm convergence problems, probably because they only utilized one observation per person.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Tyson H. Holmes, Ph.D., was supported for this study by the National Institute on Drug Abuse through the Department of Veterans Affairs Cooperative Studies Program (Interagency Agreement No. Y1-DA4006). The authors are grateful for the editorial contributions of Dr. Roberta Kahn and the database assistance of An-ting Romano.
References
Abdala, N., Stephens, P. C., Griffith, B. P., and Heimer, R. (1999). Survival of HIV-1 in syringes. J. Acquir. Immune Defic. Syndr. Hum. Retrovirol. 20, 73–80.
Anderson, A., Reid, M., Li, S., Holmes, T., Shemanski, L., Slee, A., Smith, E., Kahn, R., Chiang, N., Vocci, F., Ciraulo, D., Dackis, C., Roache, J., Salloum, I., Somoza, E., Urschel, H. III, and Elkashef, A. (2009). Modafinil for the treatment of cocaine dependence. Drug Alcohol Depend. 104, 133–139.
Beunckens, C., Sotto, C., and Molenberghs, G. (2008). A simulation study comparing weighted estimating equations with multiple imputation based estimating equations for longitudinal binary data. Comput. Stat. Data Anal. 52, 1533–1548.
Darke, S., Hall, W., Heather, N., Ward, J., and Wodak, A. (1991). The reliability and validity of a scale to measure HIV risk-taking behaviour among intravenous drug users. AIDS 5, 181–185.
Gawin, F., and Ellinwood, E. (1988). Cocaine and other stimulants: actions, abuse, and treatment. N. Engl. J. Med. 318, 1173–1182.
Guo, X., and Carlin, B. (2004). Separate and joint modeling of longitudinal and event time data using standard computer packages. Am. Stat. 58, 16–24.
Kahn, R., Biswas, K., Childress, A., Shoptaw, S., Fudala, P., Gorgon, L., Montoya, I., Collins, J., McSherry, F., Li, S., Chiang, N., Alathari, H., Watson, D., Liberto, J., Beresford, T., Stock, C., Wallace, C., Gruber, V., and Elkashef, A. (2009). Multi-center trial of baclofen for abstinence initiation in severe cocaine-dependent individuals. Drug Alcohol Depend. 103, 59–64.
Kim, K. (1995). A bivariate cumulative probit regression model for ordered categorical data. Stat. Med. 14, 1341–1352.
Little, R. J. A., and Rubin, D. B. (2002). Statistical Analysis with Missing Data, 2nd Edn, Hoboken: John Wiley and Sons, Inc.
Mahabadi, S. E., and Ganjali, M. (2010). An index of local sensitivity to non-ignorability for multivariate longitudinal mixed data with potential non-random dropout. Stat. Med. 29, 1779–1792.
Mathers, B. M., Degenhardt, L., Phillips, B., Wiessing, L., Hickman, M., Strathdee, S. A., Wodak, A., Panda, S., Tyndall, M., Toufik, A., and Mattick, R. P. (2008). Global epidemiology of injecting drug use and HIV among people who inject drugs: a systematic review. Lancet 372, 1733–1745.
Metzger, D. S., Woody, G. E., and O’Brien, C. P. (2010). Drug treatment as HIV prevention: a research update. J. Acquir. Immune Defic. Syndr. 55, S32–S36.
Petry, N. (2001). Reliability of drug users’ self-reported HIV risk behaviors using a brief, 11-item scale. Subst. Use. Misuse 36, 1731–1747.
Pindyck, R. S., and Rubinfeld, D. L. (1981). Econometric Models and Economic Forecasts, 2nd Edn, New York: McGraw-Hill.
Puhani, P. A. (2000). The Heckman correction for sample selection and its critique. J. Econ. Surv. 14, 53–68.
Keywords: cocaine dependence, latent variables, methamphetamine dependence, missing assessment, multivariate outcome, probit regression
Citation: Holmes TH, Anderson AL, Li S-H and Elkashef AM (2011) Advantages of joint modeling of component HIV risk behaviors and non-response: application to randomized trials in cocaine-dependent and methamphetamine-dependent populations. Front. Psychiatry 2:41. doi: 10.3389/fpsyt.2011.00041
Received: 17 February 2011;
Paper pending published: 03 April 2011;
Accepted: 22 June 2011;
Published online: 07 July 2011.
Edited by:
Karl Goodkin, AIDS Healthcare Foundation, USAReviewed by:
Mark Bradley, Columbia University, USADavid Baron, University of Southern California, USA
Copyright: © 2011 Holmes, Anderson, Li and Elkashef. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Tyson H. Holmes, Department of Psychiatry and Behavioral Sciences, Stanford University School of Medicine, 401 Quarry Road, MC 5718, Stanford, CA 94305-5718, USA. e-mail: tholmes@stanford.edu