Stress Controls of Monogenetic Volcanism: A Review

Introduction

Monogenetic volcanism is the most extended type of volcanic activity on Earth (Walker, 2000). It is commonly represented by volcanic fields containing tens to thousands of small volcanoes, each being the product of a single eruptive episode, in which different phases or pulses may occur (Walker, 2000; Valentine and Gregg, 2008; Németh, 2010; Németh and Kereszturi, 2015). Monogenetic fields may be active for several millions of years with eruption recurrences ranging from several tens to tens of thousands of years. They are usually mafic in composition and generate relatively small volume eruptions that produce cinder cones and lava flows, as well as occasional phreatomagmatic deposits when interaction between magma and surface water occurs (Lorenz, 1986; Valentine and Gregg, 2008). The distribution of volcanic cones in basaltic monogenetic fields is clearly controlled by regional and local tectonics (Wood, 1980; Pasquarè et al., 1988; Connor, 1990; Connor et al., 1992; Tibaldi, 1995; Walker, 2000; Valentine and Perry, 2007; Le Corvec et al., 2013b). The great variety of eruptive styles, edifice morphologies and deposits in monogenetic volcanoes is the result of a complex combination of internal (magma composition, gas content, rheology, volume) and external (regional and local stress fields, stratigraphic and rheological contrasts in substrate rock, hydrogeology) parameters that characterize each volcanic system (Tibaldi and Lagmay, 2006; Valentine and Gregg, 2008; Németh, 2010; Martí et al., 2011). Monogenetic volcanoes may also occur as flank eruptions in association with polygenetic volcanoes (e.g., El Teide, Martí et al., 2008; Etna, Cappello et al., 2012).

Central or composite volcanoes are characterized by the presence of a magma chamber located a few kilometers below the surface, which exerts a stress field on its surroundings that is superimposed on the regional stress field, thereby controlling potential pathways for magma to the surface (Pinel and Jaupart, 2004; Gudmundsson and Brenner, 2005; Martí and Geyer, 2009, Figure 1). On the contrary, in a monogenetic volcanic systems magma does not accumulate in such shallow reservoirs or chambers and tends to rise to the surface from greater depths, usually from intermediate reservoirs located deep in the crust, or even from the source region or shallower levels in the mantle. Thus, the stress field controlling the magma ascent will depend on the stress distribution inside the lithosphere and in particular, on the regional stress field and local stress barriers corresponding to rheological and/or structural discontinuities (Menand, 2008, 2011; Maccaferri et al., 2010, 2011; Gudmundsson, 2011a,b; Bolós et al., 2015). Knowing how these structural controls work and how they may change from one eruption to the next one is crucial to understand why in monogenetic eruptive vents produced under the same regional stress field (i.e., same age period) will tend to cluster in the same area. These volcanic clusters may have lifetimes of hundreds of thousands of years, so there is always a chance that a new volcano will come up in the same place than an old one, just out of random chance, not necessarily implying the initiation of a polygenetic behavior.

FIGURE 1

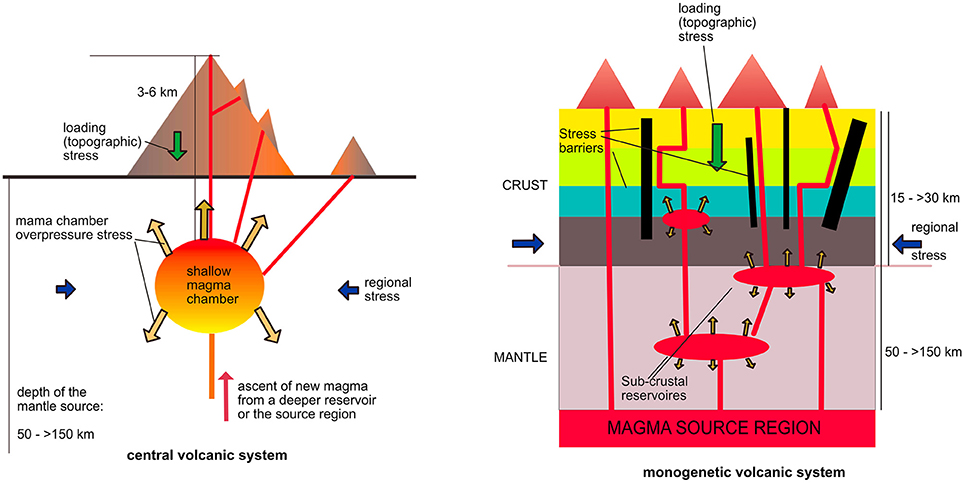
Figure 1. Differences between central and monogenetic volcanic systems (not to scale; see text for more explanation).

An important consequence of these different stress controls between central and monogenetic volcanoes is the accuracy in forecasting new eruptions. While in central volcanoes it is generally assumed that future eruptions will occur through the same vents that have been active in the past, in monogenetic systems forecasting the position of new vents is much more challenging due to this lack of a permanent shallow stress configuration. Spatial analysis addressed to infer the location of future vents (volcanic susceptibility, see Martí and Felpeto, 2010) in monogenetic volcanism generally assumes that the next eruption will occur close to the location of the previous ones (Connor, 1990; Connor et al., 1992, 2000; Ho, 1992, 1995; Martin et al., 1994; Ho and Smith, 1998; Connor and Conway, 2000; Alberico et al., 2002; Martí and Felpeto, 2010; Bebbington and Cronin, 2011; Cappello et al., 2012; Selva et al., 2012; Bartolini et al., 2013; Becerril et al., 2013a; Le Corvec et al., 2013a; Bevilacqua et al., 2015). The reason to make this assumption is based on the fact that in last eruptive episodes volcanoes had formed near previous ones (forming a cluster), so we assume that this behavior will continue. However, this does not necessarily mean they will not occur outside a cluster, just that the probability is weighted by the existence of the cluster.

The transport of magma occurs mostly through sheet intrusions and the conditions of flow in such magma-filled cracks will be governed by rock and fluid mechanics (Pollard, 1969, 1973; Pollard and Muller, 1976; Delaney and Pollard, 1981, 1982; Delaney et al., 1986; Pollard and Segall, 1987; Rubin, 1993a,b, 1995; Dahm, 2000; Gudmundsson, 2011a). Studies on monogenetic volcanism reveal how sensitive magma migration is to the existence of changes in the stress field produced by regional and/or local tectonics or rheological contrasts (stratigraphic discontinuities, sheet intrusions, tectonic fractures, Delaney et al., 1986; Dahm, 2000; Gudmundsson and Philipp, 2006; Gaffney et al., 2007; Menand, 2008, 2011; Taisne and Jaupart, 2009; Maccaferri et al., 2010, 2011; Taisne et al., 2011; Gudmundsson, 2011b; Le Corvec et al., 2013b,c; Rivalta et al., 2015). The presence of such stress barriers may induce stress rotation and, consequently, changes in the direction of emplacement of magma. Therefore, knowledge of rock stress is crucial to understand how magma will move from its source regions up to the Earth's surface, and to forecast future eruptions.

In this review we will concentrate on the main concepts related to stress controls on magma transport in monogenetic fields, in order to offer a comprehensive picture on the paths that magma may follow inside the volcanic system and on why an eruption will occur from a particular point.

We do not pretend to discuss the different stress constraints that characterize monogenetic versus polygenetic volcanic systems, which would require a different approach. We basically concentrate on some important aspects of magma migration into the brittle lithosphere that certainly apply to monogenetic volcanism, and for which we include simple models specifically designed to understand magma migration in such volcanic systems. However, this does not exclude (for what concern the basic physics) that some of the considerations included here can also be aplicable to central volcanoes. Therefore, we will first review some basic concepts on rock stress, then we will focus our attention on the main physical controls on magma transport in monogenetic fields and, finally, we will discuss on the implications of the stress field on volcanic susceptibility and the forecast of monogenetic eruptions.

Stress in the Lithosphere

In the literature there are excellent experimental and theoretical approaches on magma transport and on the mechanics and fluid-dynamics of magma-filled cracks (e.g., Pollard, 1969, 1973; Pollard and Muller, 1976; Delaney and Pollard, 1981, 1982; Delaney et al., 1986; Pollard and Segall, 1987; Takada, 1989; Gudmundsson, 1990, 2011a,b; Lister and Kerr, 1991; Rubin, 1993a,b; Rubin, 1995; Dahm, 2000; Muller et al., 2001; Roman and Heron, 2007; Menand, 2008, 2011; Taisne and Jaupart, 2009; Maccaferri et al., 2010, 2011; Menand et al., 2010; Taisne et al., 2011; Gudmundsson, 2012; Le Corvec et al., 2013c; Rivalta et al., 2015), as well as on rock stress (e.g., Zang and Stephansson, 2010), and we address the reader to these contributions. In this section we only provide a basic background necessary to follow the rest of this review.

Knowledge of the state of stresses in the Earth's lithosphere is fundamental to understand how magma will migrate and accumulate inside it and, eventually, erupt at the Earth's surface. Stress in the lithosphere may have different origins: tectonic, gravitational, thermal, residual or fluid overpressure (Park, 1988; Zoback, 1992; Zoback and Zoback, 2002; Zang and Stephansson, 2010; Fossen, 2016). Tectonic stresses derive from the relative motion between mantle flow and plate motion, and may be subdivided into first order (plate scale), second order (regional scale), or third order (local scale), depending on the volume in which a stress component is supposed to be uniform in magnitude and orientation (Zoback, 1992; Heidbach et al., 2007; Zang and Stephansson, 2010). Gravitational (loading) stresses correspond to the overlaying rock mass; they increase with depth in the Earth's crust and consider also the stress resulting from Earth's topography near the surface (Zang and Stephansson, 2010). Thermal stresses result from temperature changes in crustal rocks when they are buried, uplifted or exposed to local heat sources (e.g., magma, Turcotte and Schubert, 1982; Fossen, 2016). Residual stresses are those preserved in crustal rocks after the external force or stress field has been changed or removed (e.g., metamorphic transformations, cooling of magmatic intrusions, Fossen, 2016). Finally, we must also consider those stresses that can be imposed on crustal rocks by fluid overpressure, like when fluid is present in porous rocks trapped between non-permeable layers or due to magmatic intrusions (Gudmundsson, 2011a)

All these types of stresses will become components of the stress field that will characterize any point in the Earth's crust, the magnitude and orientation of which will depend on the spatial and temporal scales of observation and the corresponding relative value of each stress component. In a broad sense, it is important to know that first order tectonic stresses (plate scale stresses) are assumed to be constant in the whole thickness of the tectonic plate. Second order tectonic stresses (regional or intraplate scale) may vary over short distances depending on the relative position of the reference point inside a plate and the location of main geological structures, such as regional fault systems, mountain belts, or upwelling mantle plumes, or even the presence of collapse calderas, volcanic edifices or rift systems. Local tectonic stresses are also known as structural stresses (Jaeger and Cook, 1979) and correspond to stress field variations caused by active faults, local inclusions, magmatic intrusions, detachment horizons, and density and rheological contrasts. These forces act as major controls on the stress field orientations when the magnitudes of the horizontal stresses are close to isotropic (Heidbach et al., 2007).

Gravitational or loading stresses may also show significant variations depending on the spatial scale we are considering. At a regional scale it is considered that gravitational stresses increase progressively with depth, and that at a certain depth there are distributed more or less isotropically, thus giving rise to a stress state called lithostatic. However, at more local scales and much shallower depths gravitational stresses may differ significantly from one point to another depending on lateral stratigraphic changes and abrupt variations in topography (Muller et al., 2001; Gudmundsson, 2012). Thermal stresses at regional scales derive from the rheological changes that are produced on crustal rocks due to temperature variations caused by burial or uplift processes in sedimentary basins and orogens, as well as those caused by mantle upwelling in intraplate environments (Turcotte and Schubert, 1982; Schrank et al, 2012). At more local scale, these stresses may be significant around magma intrusions. Residual stresses appear in a rock if elastic strain remains after the external stress field is removed, as it may happen in cementation caused by overburden, metamorphic transformations, or tectonic deformation (Fossen, 2016). Finally, crustal stresses derived from fluid overpressure will appear in relation to fluid filled porous rocks, geothermal fields or magma intrusions (Gudmundsson, 2011a; Shapiro, 2015).

When evaluating the importance of each component on the stress field we should also consider the time scale at which they act or at which they may have a significant role. Stresses and the strain they may produce on the crustal rocks are time dependent, so when estimating the state of stress of a certain point we need to consider also the duration of the stresses acting on that point. For example, while first and second order tectonic stresses and gravitational stresses are more or less constant with regard to time, residual and thermal stresses will only be effective at long-term time scales (thousands to millions of years). In a similar way, fluid overpressure stresses may be effective in very short time scales (e.g., magma intrusions, pore-fluids in surface rock) or at longer time-scales when corresponding to buried fluid-saturated rock (e.g., oil reservoirs). Therefore, to understand how crustal stresses act on a specific point we will need to consider the spatial and temporal scales at which each stress component may operate.

Special attention is required for the local tectonic or structural stresses. These will depend on the mechanical characteristics of the rock mass we are considering. This may be classified as: (1) homogeneous, when the rock mass does not show rheological variations or structural discontinuities; (2) anisotropic, when rock properties vary with direction (i.e., there are rheological variations in the rock mass considered), and (3) heterogeneous, when inclusions of different rocks and/or structural discontinuities are present in the rock mass (Zang and Stephansson, 2010). The consequence of considering different rock mass characteristics is that the configuration of stresses in each of them may differ considerably from one to the other (Figure 2). Compared to homogenous rock masses in which the trajectories of the principal stresses will define a regular orthogonal pattern, anisotropic rocks formed by alternating stiff and soft materials will show a pattern oriented toward preferred anisotropy, as soft materials will accumulate higher strain while the stiff ones will attract higher stresses (Zang and Stephansson, 2010). In addition to anisotropies, crustal rock masses may show different scale heterogeneities caused by the presence of structural discontinuities.

FIGURE 2

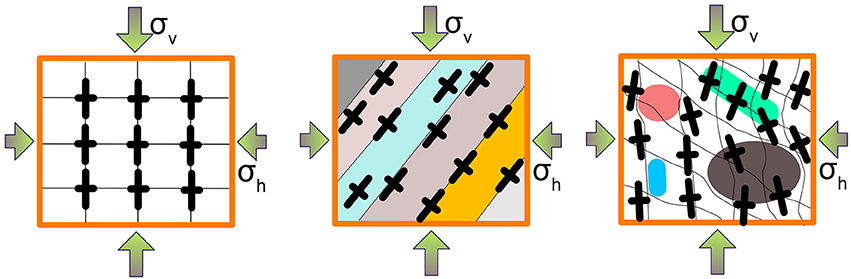
Figure 2. Sketch of the stress field and stress trajectories (solid bars) in homogeneous (left), anisotropic (center), and heterogeneous (right) rocks (adapted from Zang and Stephansson, 2010).

Magma Motion

Magma motion in the lithosphere will be basically controlled by the overpressure of magma over that of rock. How this magma overpressure is achieved will be discussed latter. Now it is sufficient to assume that magma is over-pressurized, so it will migrate through the lithosphere controlled by the regional and local stresses that act on it (Takada, 1994; Traversa et al., 2010).

In the source region, magma transport will be dominated by porous flow through a deformable and partially molten matrix, from which it will segregate by compaction of the mantle unmelted residuum (Spera, 1980; McKenzie, 1984, 1985; Rubin, 1993c, 1998). At such depths and when a sufficient volume of magma has been accumulated, thus becoming gravitationally unstable, it will tend to continue ascending in order to equilibrate its excess pressure. It has been assumed that basaltic magma in the mantle may ascent as buoyant diapirs when rocks surrounding magma may deform plastically due to their relative low viscosity (Spera, 1980; Rubin, 1998). This ascending movement of magma will continue until the rocks above behaves as a brittle solid, in moment magma will ascent through fractures in the host rock. The transition from porous flow to flow through magma driven cracks is not only a function of the temperature of the host rock, but also of the rate of strain and the stresses involved (Rubin, 1993c, 1998). The brittle-ductile transition in the crust may be located higher than initiation of dyke propagation, which may occur much deeper, even into the upper mantle. This is not because of the temperature differences in the host rock, but because the timescale of deformation around a dyke is small compared to the viscous relaxation time scale of the medium, so brittle behavior occurs (Rubin, 1993c, 1998). Magma ascent will be halted if the host rock does not fracture in response to the pushing action of magma (Turcotte and Schubert, 1982; Maaloe, 1985; Middleton and Wilcock, 1994). However, if magma overpressure exceeds the cohesive and confining stresses of host rock, this will be broken apart forming a fracture through which magma may intrude and continue its emplacement to shallower levels (Jaeger and Cook, 1979; Spera, 1980; Maaloe, 1985; Rubin, 1993c, 1998; Menand, 2011). This is the most effective mechanism of magma transport in the lithosphere, particularly in the crust, in comparison with the diapiric ascent. In fact, seismic evidence indicates that magma-filled cracks may start to form at depth of 40–50 km or even greater, as it is suggested by the existence of earthquakes generated at these depths and by the presence of ophiolite peridotite bodies and other mantle inclusions erupted onto surface (Maaloe, 1985).

Magma-filled fractures or cracks are known as sheets intrusions, being named dykes when they cut across bedding or foliation/fabric in the host material, and sills when they are concordant with that. However, for the purposes of this paper, we will refer vertical or subvertical cases as dykes, and horizontal as sills, with the understanding that in detail it depends on the cross cutting relationships (Figure 3). The formation of sheet intrusions is regarded in the framework of hydraulic fracturing. In this context, a hydrofracture is a tension fracture in which the driving tensile stress is the fluid overpressure, so, in our case, the magma overpressure (see Gudmundsson, 2011a). Therefore, to start a sheet intrusion it will require to achieve the conditions for rupture of the rock and hydrofracture initiation (Jaeger and Cook, 1979; Gudmundsson et al., 1999; Gudmundsson, 2011a):

$\begin{array}{ll}{p}_m\ge {\sigma }_3+T& (1)\end{array}$

where p_m is the total magma pressure, σ₃ is the minor principal compressive stress, and T is the local in situ tensile strength of the rock.

FIGURE 3

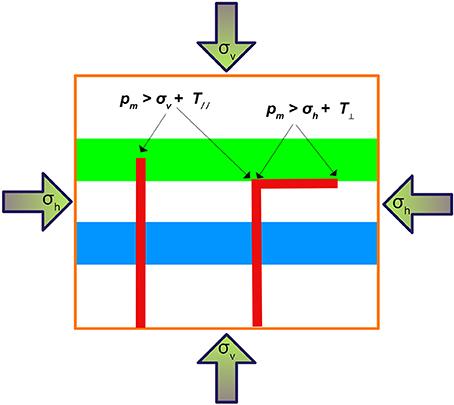
Figure 3. Stress conditions compatible with dyke and sill intrusions. Dykes: Total magma pressure (pm) must be greater than the principal horizontal stress (σ_h) plus the tensile strength of the rock tested in extension parallel to the bedding (T_//). Sill: pm is greater than the principal vertical stress (σ_v) plus the tensile strength of the rock tested in extension perpendicular to the bedding plane (T_⊥) (adapted from Price et al., 1990).

Magma migration will be controlled by the regional tectonics and the gravitational stresses but also by local stress barriers defined by crustal heterogeneities such as local tectonic structures and rheological changes in crustal rocks. This means that it will tend to follow a path normal to the minimum compressive stress. If in its ascent to the surface magma finds a rheological or structural contrast between rocks, magma may become arrested or intrude laterally forming a sill (Pasquarè and Tibaldi, 2007; Tibaldi and Pasquarè, 2008; Tibaldi et al., 2008; Maccaferri et al., 2010; Menand, 2011; Gudmundsson, 2011b).

As we see in Figure 3, the propagation of a sheet intrusion as a dyke or a sill in an anisotropic medium will depend on the stress configuration at the front of the intrusion. If the total magma pressure (p_m) is greater than the principal horizontal stress (σ_h), which may coincide with σ₃, plus the tensile strength of the rock tested in extension parallel to the bedding (T_//), the intrusion will propagate as a dyke. However, if p_m is greater than the principal vertical stress (σ_v) plus the tensile strength of the rock tested in extension perpendicular to the bedding plane (T_⊥) the intrusion will propagate as a sill (Price et al., 1990). If the sill is fed by a dyke, as it is illustrated in Figure 3, both conditions must be satisfied simultaneously at the junction of the feeder dyke and the sill. Therefore, it follows that (Price et al., 1990):

$\begin{array}{ll}({\sigma }_v-{\sigma }_h)<(T_{//}-T_{\perp })& (2)\end{array}$

The tensile strength of a pile of stratified rocks will be determined by the strength of the individual bedding planes, so T_⊥ will be approximately zero (Price et al., 1990; Gudmundsson, 2011a,b). On the other hand, the tensile strength of most unjoined or unfractured rocks is of the order of 10 MPa or considerably smaller if the rock contains joints or fractures (Touloukian et al., 1989; Price et al., 1990; Gudmundsson, 2011a,b). So, we can deduce that a sill will only occur when the differences in magnitude between the horizontal and vertical stresses are very small (Pollard, 1973; Price et al., 1990). In many situations, if a sill is fed from a perfectly vertical dyke it will favor propagation laterally at both sides of the plane of weakness, while if the feeder dykes is inclined (i.e., oblique to the strata) the sill will tend to propagate only toward the side opposite to the dyke dip (see Figure 4). This generalized behavior, however, may change under particular stress configurations and rock rheology contrasts (e.g., Tibaldi and Pasquarè, 2008).

FIGURE 4

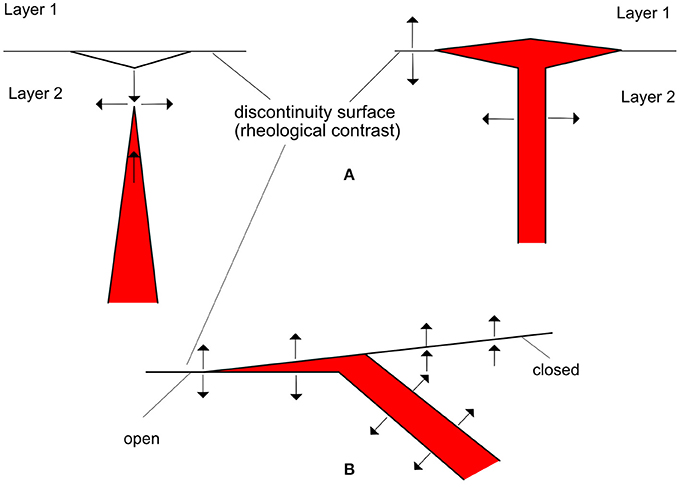
Figure 4. Schematic representation of a discontinuity plane, corresponding to a rheological contrast between two rock beds, in advance of a developing vertical (A) and inclined (B) dyke enabling it to form a symmetric (A) and an asymmetric (B) sill, respectively (adapted from Pollard, 1969, in Price et al., 1990).

The orientation of the stress field may change (i.e., may rotate with respect to a reference position) depending on the exact contribution of each stress component at each point (Pollard and Muller, 1976; Pollard and Segall, 1987). At the time scale of magma propagation through a fracture (days to months) the near-tip stress field will be essentially controlled by the first and second order stresses, structural and gravitational stresses, the stresses associated with the magma overpressure, which will depend on the fracture geometry and total volume of magma, and occasionally by thermal stresses generated by thermal variations in the magma during emplacement (Turcotte and Schubert, 1982). To predict the direction of propagation of a magma-driven fracture and the possible location of the next monogenetic eruption it is important to understand how these stresses, or the resulting stress field, change with depth.

Sheet Intrusions and Magma Overpressure

The plumbing system of a monogenetic volcanic field (Figure 1) may include a source zone, where magma generates and migrates upwards by gravitationally-induced porous flow, and a series of intermediate reservoirs where magma may stop and differentiate for a while before continuing its ascent to the surface. This is clearly indicated by the petrology and geochemistry of magmas from monogenetic eruptions, which evidence certain degree of differentiation in most cases and occasional assimilation of crustal rocks that occurred at different depths (Thirlwall et al., 2000; Klügel et al., 2005; Stroncik et al., 2009; Valentine and Hirano, 2010; Brenna et al., 2011; Rowe et al., 2011; Hernando et al., 2014; Albert et al., 2015, 2016; Klugel et al., 2015). These intermediate reservoir zones, which will normally be located at rheological or structural discontinuities inside the lithosphere, do not need to be stable or permanent along the whole history of the volcanic field. Also, there is evidence that in some cases magma erupts directly from the source region, without suffering any differentiation in its journey to the surface (Bacon et al., 1995; Garcia et al., 1995). The reasons magma will either stop at different depths before reaching the surface or will ascend straight from the source region or a deep reservoir, depend on the magma overpressure and the state of stresses inside the lithosphere. This balance between magma pressure and lithospheric stresses will decide whether magma will be able to follow a straight path to the surface or will stop at certain depth, arresting its ascent or continuing it until internal pressure conditions are favorable again. Also, it will control the exact path that magma will follow and, finally, the location of the new vent in case magma has been able to reach the surface. In fact, the proportion of magmatic intrusions that become feeder dykes is minimum compared to the total number of dykes that may be generated during the whole life of a volcanic system (Gudmundsson et al., 1999). So, in order to know if a magma intrusion will reach the surface and cause an eruption we need to ask: (1) will magma have sufficient driving force (magma overpressure) to reach the surface)?, and (2) what is the path it will follow?

To answer the first question we need to understand which is the driving force of magma intrusions. It is obvious that for the same magma driving force, a different stress distribution may either reduce or enhance the possibilities for this magma to reach the surface. Figure 5 illustrates the concepts of total magma pressure (p_m), magma excess pressure (p_e) and magma overpressure or driving pressure (p_o), which are fundamental to understand magma migration (see Dahm, 2000; Gudmundsson, 2012). We consider a lithostatic reference state, which is the simplest stress model for the interior of the lithosphere, so there is no differential stress at depth (σ₁ = σ₃). In such situation and in equilibrium the total pressure of a deep magma reservoir will be equal to the lithostatic pressure (ρ_rgh). If a new injection of magma from the source region (or from a deeper reservoir) enters into the magma reservoir, it will increase the total magma pressure (p_m = p_l + p_e) (see Blake, 1981). We assume that the resident and the new magmas are under-saturated in volatiles, so no free gas phase is present, which is a good assumption for basaltic magmas at depths of several tens of kilometers. The increase of magma pressure (excess pressure, p_e) inside the reservoir will force the volume of the reservoir to increase. Depending on the rigidity of the surrounding rocks they will be able to deform elastically to a certain limit, so the reservoir will expand a little bit. If the volume increase permitted by elastic expansion of the host rock is sufficient to accommodate the pressure increase, the situation will return to equilibrium until a new intrusion of magma arrives. However, if the elasticity the host rock is exceeded it will fracture due to the tensile stresses, which are generated around the reservoir walls, and magma will be injected into the host rock. Previous calculations have indicated that volume fractions of new injected magma of approximately 0.1% of the volume of the reservoir in the absence of any gas phase are sufficient to produce the excess pressure necessary to trigger a magma injection (Blake, 1981). This volume fraction may increase to approximately 1% of the volume of the reservoir when a gas phase is present in the resident magma (i.e., at much shallower depths) due to the higher compressibility of the resident magma (Bower and Woods, 1997; Folch and Martí, 1998).

FIGURE 5

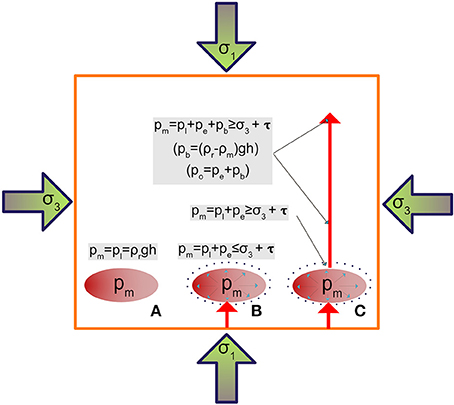
Figure 5. Sketch illustrating the concepts of total magma pressure (p_m), magma excess pressure (p_e) and magma overpressure or driving pressure (p_o), as defined in the text. We consider a lithostatic reference state, which is the simplest stress model for the interior of the lithosphere, so there is no differential stress at depth (σ_{1 =} σ₃) (see text for more explanation).

The progression of a magma-driven fracture will depend on the total magma pressure, as indicated by Equation (1), which at the moment of the reservoir rupture can be rewritten as (Gudmundsson et al., 1999; Gudmundsson, 2012):

$\begin{array}{ll}{p}_m=p_l+p_e\ge {\sigma }_3+T& (3)\end{array}$

where p_l is the lithostatic pressure and p_e is the excess pressure above the lithostatic necessary to initiate the rupture of the reservoir walls. At the moment in which magma starts to abandon the reservoir intruding the rock, and because at these depths magma tends to be less dense than the host rock, a buoyancy force (p_b) resulting from the difference between the average densities of the host rock and magma, will be added to the initial magma excess pressure to help driving the sheet intrusion, so the resulting overpressure will be (Gudmundsson et al., 1999; Gudmundsson, 2012):

$\begin{array}{ll}{p}_o=p_e+p_b=p_e+({\rho }_r-{\rho }_m)gh+{\sigma }_d& (4)\end{array}$

where ρ_r is the average host-rock density, ρ_m is the average magma density, g is acceleration due to gravity, h is the depth of the source, and σ_d is the differential stress (σ_d = σ₁ − σ₃), which in the case of an isotropic (lithostatic) situation will be 0. To continue the intrusion, magma overpressure must be large enough to fracture the rock and to overcome the viscous forces of resistance opposing to flow (Middleton and Wilcock, 1994). And this will be achieved if a sufficient volume of magma is available at the reservoir from which the intrusion is being pumped up. However, for simplification we have not considered in our calculations the viscous pressure dissipation along the length of the dyke due to magma flow. The exact volume of magma needed to ensure that an intrusion will reach the surface will depend on each case on the physical characteristic of magma and host rock (see Traversa et al., 2010, Equations 15 and 38). Also, magma intrusion must occur at sufficient high rate in order to avoid much cooling of magma that could increase its viscosity in excess, halting motion. If magma intrusion progresses enough to reach shallower levels, it may start degassing due to the decrease of lithostatic pressure. If this gas is retained at the tip of the sheet intrusion it will represent an additional increase of pressure at the interior of the intrusion, but if it escapes through the rock porosity, pressure will decrease as magma density will increase.

As indicated before, to know the exact path a magma intrusion will follow and where it will intersect the surface, we have to consider how the orientation of the stress field may change all along the magma pathway. This requires to know the internal structure of the system, including the location and size of stratigraphic, lithological, rheological and structural discontinuities, lateral and vertical extent of major tectonic features, horizontal distribution of deviatoric stresses, and distribution of loading stresses due to complex topographies. Obviously, this is not an easy task. In fact, in comparison with classical sedimentary basins, the internal geometry of volcanic systems is much more complex due to the irregular stratigraphic relationships shown by volcanic materials, their contrasting lithologies, their affectation by active tectonics, and the numerous magmatic intrusions that may be present. Imaging the interior of volcanic systems at lithospheric or crustal scales with geophysical methods does not provide models sufficiently detailed to detect dykes or sills. In recent years, the application of high resolution shallow geophysical methods has opened a new window to visualize in great detail the internal geology of volcanic systems (e.g., Mrlina et al., 2009; Cassidy and Locke, 2010; Bolós et al., 2012; Barde-Cabusson et al., 2013; Blaikie et al., 2014), but their resolution does not penetrate deeper than a few hundreds of meters. Therefore, obtaining a precise picture of the interior of a volcanic system and how a new injection of magma may cross it to reach the surface is, by now, still difficult. However, having a minimum knowledge at a lithospheric and crustal scale of the main stratigraphic units, the distribution of the main tectonic structures, the orientation of the current regional stress field, and the topography of the area, we can infer the main stress constraints that sheet intrusions may have.

Dynamics and Mechanics of Sheets Intrusions in the Lithosphere

We will start examining the conditions to drive a sheet intrusion (dyke) to the surface from four different reservoirs located at different depths, in an isotropic and homogeneous lithosphere. Each reservoir is recharged from below in order to cause the excess pressure necessary to initiate the sheet intrusion (Figure 6). The conditions for p_m, p_e, and p_o are as explained above and in Figure 5. For each case, we will study the critical influence of the magma reservoir size on eruption likelihood, quantifying the volume required for the creation and growth of a dyke from the reservoir to the Earth's surface, and the magma overpressure achieved in each case inside the dyke. In all cases, we will assume that the geometry of the reservoir allows tensile stresses to concentrate at the center of its upper part, so the sheet intrusion will propagate vertically toward the surface.

FIGURE 6

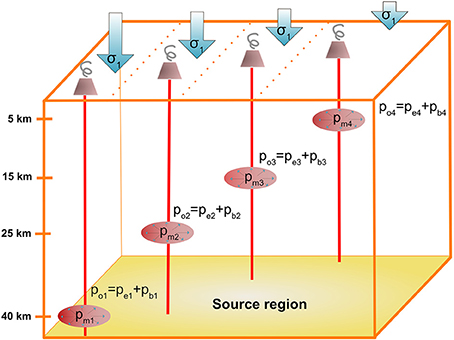
Figure 6. Sketch illustrating a sheet intrusion in a homogeneous and isotropic lithosphere, as described in text.

To compute the critical volume required for the creation and growth of a dyke we use the mathematical approximation performed by Traversa et al. (2010), which relates the magma reservoir volume, Vr, and the reservoir excess pressure variations due to dyke propagation:

$\begin{array}{ll}{V}_r=\frac{\Delta V_r}{\text{exp}\left(\Delta P_{rvar}(\frac{4G+3K}{4GK})\right)-1}& (5)\end{array}$

where ΔVr is the variation (decrease) in reservoir volume produced by the magma injected in the dyke, ΔP_rvar is the corresponding decrease of the reservoir excess pressure, and G and K are the shear and bulk moduli of the host rock.

Combining Equation (5) with Equation (4), which gives us the magma overpressure in the dyke, p_o, and assuming that the decrease of reservoir overpressure is (mainly) caused by the dyke propagation up to the surface, we may establish the approximation:

$\begin{array}{ll}\Delta P_{rvar}\approx p_o& (6)\end{array}$

With this relation we can calculate the minimum reservoir volume, Vr, required for a dyke injection, ΔVr, for different reservoir depths and density contrast (ρ_r − ρ_m) scenarios. Figure 7 shows the results of model calculations for each scenario. We show different plots with the evolution of the magma overpressure at the dyke tip (in blue) propagating up from the reservoir roof (at 5, 15, 25, and 40 km depth) through the crust. Using Equations (4) and (5) we have calculated the corresponding minimum size of the reservoir at different heights of the dyke (in red) for a common priori magma injection ΔVr = 1.0 × 10⁸ m³, which represents the maximum value of intrusions associated with the historical eruptions in the Canary Islands (Becerril et al., 2013b). As excess pressure, p_e, at the time of hydrofracturing formation is normally equal to the tensile strength of the rock (Gudmundsson, 2012), we used a constant = 3 MPa, that represents the most common value of the crustal rocks tensile strength (Gudmundsson, 2012). To estimate the magma overpressure at the dyke tip, p_o, we have also considered the contribution of magma buoyancy, p_b, as indicated in Equation (3). The results obtained applying this simple model (i.e., isotropic and homogeneous lithosphere) show that, depending on where it starts inside the lithosphere, any sheet intrusion will require a specific available volume of magma and a critical overpressure to ensure that it will arrive at the Earth's surface (Figure 7). A more realistic approach, even assuming an isotropic and homogeneous lithosphere, would have required considering the exact rheological behavior of the host rock (elastic or rigid) in front of the pressure changes in the reservoir, the rheological changes of magma due to pressure and temperature changes during dyke emplacement, and also the pressure drop due to viscous flow of the magma (see Turcotte and Schubert, 1982; Gudmundsson, 2011a). However, our model offers a first order approach that we consider valid for the purpose of this review. The implications derived from this model will not change in the case of a more realistic heterogeneous and anisotropic lithosphere. However, it will be necessary to know the exact distribution of potential stress barriers inside the lithosphere to be able to predict a magma path. In such cases, any stress barrier caused by a density or rheological contrast, presence of a tectonic structure, or existence of a differential stresses may induce stress rotation and make the sheet intrusion divert from the direction it was propagating, or even to arrest it in case the overpressure required to surpass that obstacle is not achieved. This may explain how dykes may divert into sills forming new magma reservoirs (Menand et al., 2010; Gudmundsson, 2011a), or how dykes or sills may propagate for tens of kilometers inside the crust before becoming vertical again and erupting at surface (e.g., Martí et al., 2013) or stopping before it reaches it (e.g., Wright et al., 2006; Ayele et al, 2007).

FIGURE 7

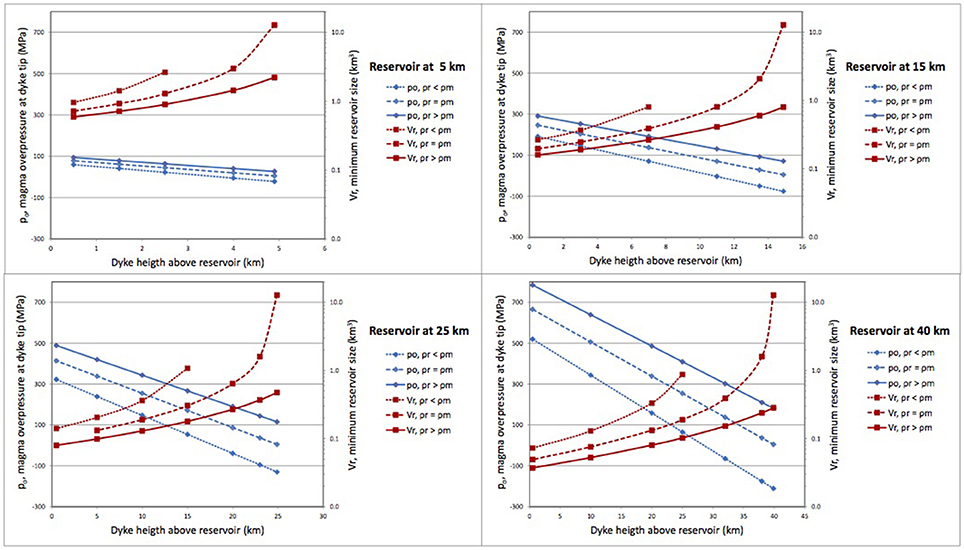
Figure 7. Graph plots showing results concerning magma overpressures and magma volumes required in each scenario of Figure 5. We show different plots with the evolution of the magma overpressure at the dyke tip (in blue) propagating up from the reservoir roof (at 5, 15, 25 and 40 km depth) thought the crust, and the minimum size of the reservoir at different heights of the dyke (in red) for a common priori magma injection ΔVr = 1.0 × 10⁸ m³. We have considered three possible cases of positive, null and negative density contrast between the magma and the host rock, with 2.55 × 10³ kg/m³ for a mean value of the magma density range (Murase and Mcbirney, 1973) and 3.0 × 10³, 2.55 × 10³ and 2.0 × 10³ kg/m³ for host rock, assuming that most crustal rock densities are in that range (Gudmundsson, 2012). We used K = 1.0 × 10⁹ Pa for the bulk modulus and G = 1.13 × 10⁹ Pa for the shear modulus.

Assuming similar conditions to the previous case for the magma reservoir, we consider now an heterogeneous and anisotropic lithosphere with rheological differences (layers with different color, Figure 8) or presence of faults or cracks (black bars, Figure 8), each one representing a different stress component in the total stress field. We also include an intermediate stop with the formation of a new intermediate reservoir for calculating what is needed in that case, first to stop magma migration for a while, and second to initiate and sustain a new sheet intrusion from that shallower position, assuming a continuous connection with the deeper reservoir. We assume that rock rheological contrasts hinder magma migration and that the presence of faults and fractures facilitate it (see Delaney et al., 1986; Gaffney et al., 2007; Le Corvec et al., 2013c).

FIGURE 8

Figure 8. Sketch illustrating the progression of a sheet intrusion in a heterogeneous and anisotropic lithosphere. We include an intermediate stop with the formation of a new intermediate reservoir for calculating what is needed in that case, first to stop magma migration for a while, and second to initiate and sustain a new sheet intrusion from that shallower position, assuming a continuous connection with the deeper reservoir. We assume that rock rheological contrasts hinder magma migration and that the presence of faults and fractures facilitate it. We also indicate the mechanical constraints at each contact between layers of different rheologies, the stress conditions at the tip of the sheet intrusion at different steps of its propagation to the surface, and the magma overpressure in the sheet intrusion at any moment of its emplacement (see text for more explanation).

With regard to structural discontinuities we have to differentiate between faults (discontinuity in an homogeneous rock mass that has undergone some relative shear displacement and that is assumed to have material toughness in fracture mode I (extension) equal or close to 0), and fissures, joints or cracks that would represent tensional pre-existing or newly formed rock rupture zones that present a considerable toughness. In other words, it is assumed that faults are already open while joints or cracks will offer a variable resistance to open and propagate under tensile stress depending on the material they form in.

Therefore, for a dyke to open a pre-existing fault magma pressure has to overcome the compressive normal stress on the fault (that keeps the fault closed). Once magma opens the fault, it will starts flowing inside and magma intrusion will continue through the fault plane while the mechanical conditions along it do not change. However, if the fault plane is intersected by other fractures, particularly in the hanging wall, these may capture magma if the pressure required to propagate any of the hanging fractures is less than the pressure required to open and flow along the fault plane (Gaffney et al., 2007). Gaffney et al. (2007), proposed an analytical solution to approximate the conditions under which magma will flow either along the fault or upwards into the hanging wall.

In a heterogeneous rock that contain faults and joints, magma will open a pre-existent fault if magma overpressure is:

$\begin{array}{ll}{p}_o\ge {\sigma }_{n,fault}& (7)\end{array}$

and will open a tensile fracture if magma overpressure is greater than the sum of the normal stress in the fracture, plus the material toughness Γ_I in fracture mode I (an extension fracture). For a fracture length, a, in an infinite or semi-infinite medium with a stress-intensity factor at the fracture tip due to magma pressure inside the fracture, K_I, the condition can be written as follows:

$\begin{array}{ll}{P}_m\ge \frac{K_I}{\beta \sqrt{\pi a}}+{\sigma }_{n,fracture}& (8)\end{array}$

where the coefficient β accounts for the geometry of the fracture, being in the simplest form (uniform pressurized elliptical flat crack of radius, a, at the edge of a semi-infinite plane), β = 1.12 (Dundurs, 1969; Rice, 1980; Gaffney et al., 2007).

If the fault has a dip angle, α, the stress normal to the fault will be:

$\begin{array}{ll}{\sigma }_n={\sigma }_{v}co{s}^2\alpha +{\sigma }_{h}si{n}^2\alpha & (9)\end{array}$

Assuming that the vertical stress is gravitational, σ_v = ρgd (ρ the density of the rock, g the gravity acceleration and d the depth) and that the horizontal stress, σ_h, (positive compressive, negative tensile) is proportional to the vertical stress (σ_h = k.σ_v), the minimum fracture length required for a dyke to propagate vertically in a medium where the normal stress on the fracture plane is approximated by the far-field stress, σ = σ_h, is:

$\begin{array}{ll}{a}_c=\frac{{{\Gamma }_I}^2}{\pi {(\beta \rho gd)}^2{\left[k\left(si{n}^2\alpha -1\right)+{\text{cos}}^2\alpha \right]}^2}& (10)\end{array}$

and the critical depth, d_c, for a given fracture length, a, greater the total depth, d, the dyke will propagate vertically:

$\begin{array}{ll}{d}_c=\frac{{\Gamma }_I}{\beta \rho g\sqrt{\pi a}{\left[k\left(si{n}^2\alpha -1\right)+{\text{cos}}^2\alpha \right]}^{}}& (11)\end{array}$

Figure 9 shows the results of these second calculations. These results are in good agreement with those obtained by Gaffney et al. (2007). Both show that the minimum length of a vertically-oriented hanging-wall fracture needed to divert magma from a fault plane diminishes considerably with depth. Therefore, for a dyke to be captured by a pre-existing fault that it intersects, the fault will need to be either relatively high-angle, and/or the intersection will be at shallow depths (<3 km). In other words, it is not straightforward for magma to enter a fault in the first place. Once that has happened, then the analysis shown in Figure 9 applies to the magma subsequently being diverted upward from the fault plane. Therefore, for magma to propagate horizontally at great depth, it will require specific structural and/or mechanical conditions that will force such type of movement instead of migrating vertically toward shallower levels. Another implication of the results shown in Figure 9 is that, as earthquake magnitude is proportional to the fracture length, the smaller magnitude earthquakes (that would correspond to small fractures opening at the hanging wall) would be observed from very deep to close to the surface, while the greater magnitude earthquakes will only occur closer to the surface (Figure 9D).

FIGURE 9

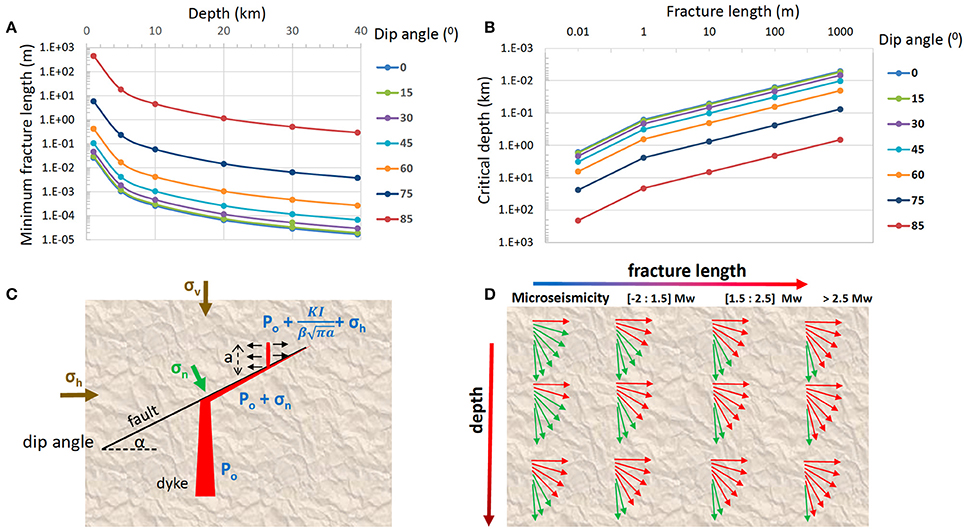
Figure 9. Graph plots showing the results from the scenario illustrated in Figure 8. (A) the minimum length of a vertically-oriented hanging-wall fracture needed to divert magma from a fault plane with normal stress σ_n (B) the critical depth for different fault dip angles, α = [0°, 15°, 30°, 45°, 60°, 75°, and 85°], according to the model shown in (C). We have used a fracture toughness typical of basalts, Γ_I = 4 MPa m^1/2, β = 1.12 and k = 1/3. In (D) we summarize (A,B) results: the critical fracture length decreases with depth and for the same depth it is shorter for lower fault dip angles. This means that in the presence of a fractured media, except close to the surface, it will be improbable that a dyke propagates along low angle fault planes (red arrows). However, propagation along long angle fault planes will be facilitated (green arrows) at much lower depths (or much lower σ_v values).

In the case of a dyke intersecting a stratigraphic discontinuity that represents a rheological contrast between two rock layers, the dyke may become arrested, penetrate the contact, or be deflected along it (He and Hutchison, 1989; He et al., 1994; Gudmundsson, 2011a,b). The general stress conditions for the dyke to continue its propagation or to become a sill have been analyzed before (see Figures 3, 4, and Equation 2). We will examine here the influence of different mechanical properties at both sides of the rheological contact. Following the formulation presented by He and Hutchison (1989) and He et al. (1994) for the case of a dyke crossing a mechanical discontinuity, the condition for penetrating it depends on the rate of the strain energy release associated with dyke penetration:

$\begin{array}{ll}{G}_p=\left({}^{(1-{\upsilon }_1)}{/}_{2{\mu }_1}\right).K_l^2& (12)\end{array}$

and the strain energy rate associated with deflection (sill formation):

$\begin{array}{l}{G}_d=\left(\left({}^{(1-{\upsilon }_1)}{/}_{{\mu }_1}\right)+\left({}^{(1-{\upsilon }_2)}{/}_{{\mu }_2}\right)\right).\\ \left(K_I^2+K_{II}^2\right)/\left(4.cos{h}^2\pi \epsilon \right)& (13)\end{array}$

where, K_I, is the mode I (tensile) stress-intensity factor, K_II, the model II (shear) stress-intensity factor, which depends on the magma pressure inside the dyke and on the geometrical properties of the contact, and υ and μ area the Poisson's ratio and shear modulus, respectively, corresponding to layer 1 (upper) and layer 2 (lower), when the dyke in layer 2 tries to penetrate into layer 1.

The dyke is likely to continue its vertical path penetrating into layer 1 if:

$\begin{array}{ll}\frac{G_d}{G_p}<\frac{{\Gamma }_D}{{\Gamma }_1}& (14)\end{array}$

where Γ₁ is the layer 1 mode I toughness and Γ_D is the toughness on layer 2 for the combined models I and II.

For a given dyke-segment length a, reaching the contact, the rate G_d/G_p depends only on the relation of the mechanical properties of both layers and not on the magma pressure, so an increase in magma pressure will imply a longer distance reached by the sheet intrusion but will not influence the direction of emplacement. He and Hutchison (1989) showed that a dyke becomes deflected between two layers of contrasted mechanical properties only if the material toughness of layer 2 is less that 26% of the material toughness of layer 1. So, a dyke will deflect into a sill when Γ_D < 0.26 Γ₁ and will continue as a dyke crossing the rheological contact when Γ_D > 0.26 Γ₁. Moreover, when the stiffness (Young modulus, E) of the layer 1 (upper) is less that the stiffness of layer 2, there is generally much less tendency for deflection of a dyke into a sill (Gudmundsson, 2011b), and conversely, being improbable the dyke to penetrate in layer 1 when E₁ >> E₂.

Therefore, despite magma overpressure being the driving force for magma to move upwards, it will not control whether a dyke will be deflected into a sill at a rheological contrast or will continue straight. This will be determined by the mechanical contrast between the two rocks. This is an important concept, as higher magma overpressures will only represent longer emplacement distances but not necessarily higher capacities to cross heterogeneous lithologies and to reach the surface. This is particularly applicable to unfractured media. If an ascending dyke intersects a much stronger layer, it is still more likely to continue vertically if there are any vertical/subvertical fractures in that stronger layer, particularly if this occurs at depth as previously indicated by Gaffney et al. (2007), and now in this study (Figure 9). Faults and fractures may facilitate paths for magma ascent, as they represent zones of more favorable stress conditions for magma to penetrate into the host rock with lesser energy consumption, as it seems to be confirmed by the structural control in the location of vents observed in most of the monogenetic volcanic fields (e.g., Le Corvec et al., 2013b). However, the effectiveness of structural features to direct magma migration depends on the depth and dip angle of each structure, the pre-existing normal or transtensional faults being very effective in transporting magma at very shallow depths.

Discussion

In this review we have considered the main aspects that govern magma migration in monogenetic volcanic systems. We have tried to offer a comprehensive review of what happens in the plumbing systems of such type of volcanoes and how they prepare for new eruptions. We have not intended to provide a complete review of monogenetic volcanism, for which there are already excellent studies (e.g., Wood, 1980; Tibaldi, 1995; Connor and Conway, 2000; Walker, 2000; Valentine and Gregg, 2008; Németh, 2010; Le Corvec et al., 2013b; Németh and Kereszturi, 2015), but we have tried to clarify the most relevant concepts that need to be understood when conducting hazard assessment in such volcanic fields and, in particular, during the probabilistic analysis of analysis of vent opening (volcanic susceptibility). In this sense, we have concentrated our attention on dyke ascent processes in response to the surrounding environment (stress fields, structures, etc.), but have not considered specifically the potential effect of magma flux and magmatism-induced stresses on the ambient ones. This effect was studied by Valentine and Perry (2007) and Le Corvec et al. (2013c), among others. We have considered it as a long term effect that will determine whether the magmatism responsible for the formation of the volcanic field will respond passively to or will actively overwhelm ambient tectonism, so its potential contribution should be added to the stress field. However, it will not significantly modify the stress configuration that governs sheet intrusion.

The reason why magma will erupt at one specific point and not at any other on the volcanic field depends on how the magma driving force will act against the stresses configuration inside the lithosphere, and not only at surface. This 3D stress configuration results from a combination of regional and local stress components that define for each point a resultant stress field that will determine whether magma will continue or halt its migration, and the path it will follow in the first case. Through the definition of a series of basic concepts and the application of two very simple models, we have tried to explain the first order physical requirements for magma to migrate inside the host rock and why that migration will follow a certain path or direction and not any other.

Monogenetic volcanic fields are well distributed all around the world and in most geodynamic environments. This implies that the geodynamic constraints (i.e., the regional tectonic stresses) do not determine whether or not such type of volcanism will be present in a specific tectonic setting, but contribute to the distribution and extent of monogenetic volcanic fields. A quantitative comparison of a large number of volcanic fields in different settings was provided by Le Corvec et al. (2013b). Monogenetic fields present different characteristics, including eruption frequency, total erupted volumes, or long term magma fluxes, and may correspond to different tectonic settings. However, magma migration processes are basically the same in all cases and differences in location of volcanic vents, extension of the volcanic fields, eruptive recurrence, or temporal and spatial evolution of vent clustering, may be easily interpreted as due to the different regional stresses (tectonics) governing each of them, as a consequence of the different geodynamic settings where they are located.

We have analyzed how magma acquires the necessary overpressure to cause a hydraulic fracture and migrate through it to shallower levels. We have assumed in all cases a scenario defined by the presence of a reservoir over-pressurized by intrusion of new magma from below, and it being this excess pressure that is the driving force to initiate and drive magma intrusion. Fracture propagation is then controlled by the magma overpressure that results from the excess pressure at the source reservoir and the buoyancy component derived from the density differences between magma and host rock. In this scenario there is always a connection between the source reservoir and the propagating sheet intrusion, so the overpressure required to ensure magma propagation is always depending on the source reservoir minimum volume. We have calculated this minimum volume and the resulting magma overpressures for different host rock configurations, and the results obtained show how shallower reservoirs require larger minimum volumes than deeper reservoirs to acquire the necessary magma overpressures to sustain sheet intrusion up to the surface. This is due to the fact that the buoyancy component of the magma overpressure is less effective at shallow depths, so the magma excess pressure (i.e., volume) in the reservoir needs to be higher. From these results it is also important to note the role of the density contrast between magma and host rock, as this also determines the magma excess pressure that will be necessary to ensure effective magma migration and, consequently, will determine the minimum volume the source reservoir will need to have. Magma migration through sheet intrusions in an anisotropic and heterogeneous host rock will be governed by the same principles but requiring higher overpressures to surpass stress barriers that may inhibit magma movement. This will normally imply changes in the direction of the intrusion, so making its paths toward shallower levels unpredictable, except the exact position of such stress barriers at the interior of the volcanic systems is well known. In a similar way, magma migration can change direction when finding structural discontinuities such as normal faults or tensional fractures that may trap magma facilitating its ascent toward shallower levels.

The scenario for magma intrusion that we have considered contrasts with other accepted models of magma propagation through fissures in which the sheet intrusion disconnects from its source as it migrates. In this case (see Rubin, 1995; Valentine and Gregg, 2008) it is assumed that the exsolved gas concentrates at the dyke tip and exerts the maximum overpressure, thus reducing the pressure at the base of the magma column causing the wall rocks to squeeze inward and push the magma upward. However, geophysical monitoring data recorded during recent eruptions (e.g., El Hierro, Martí et al., 2013; Bardarbunga, Gudmundsson et al., 2014; Sigmundsson et al, 2015) confirm that, at least in these cases, there was a continuous connection between the advancing sheet intrusion and an overpressure source during the whole event.

In this conceptualization of how magma migrates inside the host rock, we should not confuse the capacity for magma to create hydraulic fractures (i.e., magma overpressure) with the orientation that these fractures will have (determined by the external stress field components). From the models presented here we can deduce that only at very shallow depth (<3 km) magma overpressure will be the main component of the local stress field. This is an essential concept when dealing with volcano monitoring and eruption forecasting. Most volcanic models or methods that have been developed (Connor, 1990; Connor et al., 1992, 2000; Ho, 1992, 1995; Martin et al., 1994; Ho and Smith, 1998; Connor and Conway, 2000; Alberico et al., 2002; Martí and Felpeto, 2010; Cappello et al., 2012; Selva et al., 2012; Bartolini et al., 2013; Becerril et al., 2013a; Bevilacqua et al., 2015) consider the observable tectonic structures (eruptive fissures, joints, faults, dykes, sills, lineations, vent location) as indicators of paleostresses, so when they are combined with the age at which they formed we can obtain a picture of the stress evolution with time at surface. In this sense, the youngest structures will indicate the most recent stress configuration, and will define the areas with higher probabilities of hosting new vents. According to this assumption and regardless of the interpolation method used to estimate the spatial probabilities, the areas including the most recent structures will receive higher susceptibility values. And this would be a good approach and a reliable result if magma would ascent vertically from the source. However, none of these models consider the regional stress field or the variations of stress with depth. This implies that the result obtained may not be sufficiently precise according to the level of uncertainty that is acceptable in a hazard assessment. In fact, well monitored recent eruptions (e.g., Bardarbunga, El Hierro), even if they do not perfectly represent pure monogenetic eruptions, showed how magma may migrate horizontally for long distances inside the volcanic system, thus making the short term estimate of volcanic susceptibility (i.e., considering monitoring information, see Sobradelo and Martí, 2015) very challenging. Also, previous studies (e.g., Maccaferri et al., 2011; Menand, 2011; Taisne et al., 2011; Gudmundsson, 2011b) and the models presented here indicate how an ascending magma path may be diverted or arrested in a heterogeneous and anisotropic lithosphere, depending on how regional and local stress components will be distributed. Moreover, it is worth mentioning that each new intrusion episode (ending or not with an eruption) may induce changes in the local stress distribution creating new stress barriers that did not exist before and that may affect magma movement in further intrusions.

Therefore, one of the aims of this review has been to add some basic physics to the geological record based hazard models that are being used in monogenetic volcanism, in order to help understanding how they work and the uncertainly that their results may have associated with them. In fact, if volcanoes are clustered or aligned, it is reasonable to use that information to weight spatial probabilities for future events, but it is also important to know that the conditions for such particular distribution of vents depend on how stresses distribute inside the volcanic system and not only at surface. Unfortunately, the uncertainty in the deep subsurface processes and material properties is quite large and largely irreducible. The very basic dyke models we have provided in this review may not help to reduce the uncertainty in forecasting monogenetic eruptions, but we hope they will help to better understand which is the source of that uncertainty.

Of course, if no changes occur in the distribution of regional and gravitation stresses in the area between two successive eruptions, we may consider that magma migration will follow a similar path in both if it starts from a source located in a similar position. So, consequently, the next eruption may occur close to the previous one. The difference in the final position of the new vent may be caused by the influence of very shallow stress barriers created by the intrusion(s) remaining from the last eruptive event. However, the occurrence of clusters of vents of different location and age suggests the existence of significant stress changes at a timescale longer than the eruptive recurrence of the system. Therefore, eruptions occurring under the same regional stress configuration will tend to vent one close to the other, but when tectonic changes have occurred the location of vents will probably change, clustering in another sector of the volcanic field, as it is observed in many monogenetic fields. So, if the time scale for a hazard forecast is short compared to the time scale for changes in the ambient stresses and material properties and magma generation at depth, then a hazard forecast based on a sufficient portion of the history of the volcanic field is reasonable. Anyway, it will be also necessary to assess whether the behavior of the volcanic field has changed over long time scales, and whether there is evidence for sufficient change in a very recent time scale that is not yet reflected in the pattern of volcanism (e.g., Connor et al., 2000, 2009, and references herein).

As we have explained before, when we conduct long term hazard assessment one of the first actions we have to undertake is the evaluation of spatial probability of vent opening. This task will essentially be undertaken based on structural indicators such as position of vents, eruptive fissures, fractures, faults, and dykes, which will be computationally weighted according to their relative age. It will be also important to consider the current configuration of regional horizontal stresses and gravitational stresses in case of abrupt topographies. However, in a volcanic crisis we will need to systematically update this information in real time as soon as monitoring information arrives (see Sobradelo and Martí, 2015; Bartolini et al., 2016), as the evolution in the position of magma at depth and its potential arrival at surface may change with respect to what was predicted in the long-term susceptibility analysis. Anticipating possible changes of the unrest activity and, consequently, of the potential location of a future vent, will depend on the characteristics of our monitoring network, but also on the knowledge we may have of the internal structure of the volcanic system. The better this is, the more accurate (i.e., less uncertainty) will result our forecasting of the possible eruption.

Final Remarks

Monogenetic volcanic fields are not easy to forecast due to the apparent random character of magma migration inside them. Even during unrest episodes, in which we have real time monitoring data, it is not an easy task to forecast well in advance where the new vent will form, as drastic changes in the direction of magma propagation may occur due the presence of unforeseen stress barriers at the interior of the volcanic system. This review has intended to clarify some basic aspects of magma transport in monogenetic fields, in order to help understanding the sources of uncertainty associated with eruption forecasting in such systems. It is obvious that the more information we will be able to provide on the internal structure of monogenetic fields, the better will be the interpretation of unrest episodes and the anticipation to future eruptions. Unfortunately, it is not easy to know how crustal stresses change with depth and where significant stress barriers may be located in such volcanic systems. Therefore, it is worth insisting on the need to combine geological studies, aimed at characterizing the nature and age of the main structural features observable at surface, together with geophysical studies (e.g., seismic, magnetotelluric, and electric tomographies, high resolution gravimetry, etc) imaging the interior of the volcanic systems, as well as with geodynamic models on regional stresses, to better characterize vents distribution in monogenetic fields. Moreover, the information provided by such multidisciplinary studies should be incorporated and computed into the long and short term susceptibility analysis of such volcanic systems in order to get more precise hazard assessments and, thus, to be able to forecast more accurately what may happen in case of new eruptions.

Author Contributions

All authors have participated in the elaboration of this study. JM and CL have written the final version of the manuscript and have participated, together with SB in the elaboration of the models. SB, LB, and AG have elaborated the analysis of different natural examples and have contributed to the preparation of all preliminary drafts.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This research was funded by the European Commission (FP7 Theme: ENV.2011.1.3.3-1; Grant 282759: VUELCO and EC ECHO Grant SI2.695524: VeTOOLS). AG thanks the support provided by the Ramón y Cajal research program (RYC-2012-11024). We thank Gregg Valentine and Alessandro Tibaldi for their useful and constructive reviews.

References

Alberico, I., Lirer, L., Petrosino, P., and Scandone, R. (2002). A methodology for the evaluation of long-term volcanic risk from pyroclastic flows in Campi Flegrei (Italy). J. Volcanol. Geotherm. Res. 116, 63–78. doi: 10.1016/s0377-0273(02)00211-1

CrossRef Full Text | Google Scholar

Albert, H., Costa, F., and Martí, J. (2015). Timing of magmatic processes and unrest associated with mafic historical monogenetic eruptions in Tenerife Island. J. Petrol. 56, 1945–1966. doi: 10.1093/petrology/egv058

CrossRef Full Text

Albert, H., Costa, F., and Martí, J. (2016). Years to weeks of seismic unrest and magmatic intrusions precede monogenetic eruptions. Geology 44, 211–214. doi: 10.1130/g37239.1

CrossRef Full Text | Google Scholar

Ayele, A., Jacques, E., Kassim, M., Kidane, T., Omar, A., Tait, S., et al (2007), The volcano-seismic crisis in Afar, Ethiopia, starting September 2005. Earth Planet. Sci. Lett. 255, 177–187.

Google Scholar

Bacon, C. R., Bruggman, P. E., Christiansen, R. L., Clynne, M. A., Donnelly-Nolan, J. M., and Hildreth, W. (1995). Primitive magmas at fives Cascade volcanic fields: melts from hot, heterogeneous sub-arc mantle. Can. Mineral. 35, 397–423.

Barde-Cabusson, S., Bolós, X., Pedrazzi, D., Lovera, R., Serra, G., Martí, J., et al. (2013). Electrical resistivity tomography revealing the internal structure of monogenetic volcanoes. Geophys. Res. Lett. 40, 2544–2549. doi: 10.1002/grl.50538

CrossRef Full Text | Google Scholar

Bartolini, S., Cappello, A., Martí, J., and Del Negro, C. (2013). QVAST: a new Quantum GIS plugin for estimating volcanic susceptibility. Nat. Hazards Earth Syst. Sci. 13, 3031–3042.

Google Scholar

Bartolini, S., Sobradelo, R., and Martí, J. (2016). ST-HASSET for volcanic hazard assessment: a Python tool for evaluating the evolution of unrest indicators. Comput. Geosci. 93, 77–87. doi: 10.1016/j.cageo.2016.05.002

CrossRef Full Text | Google Scholar

Bebbington, M. S., and Cronin, S. (2011). Spatio-temporal hazard estimation in the Auckland Volcanic Field, New Zealand, with a new event-order model. Bull. Volcanol. 73, 55–72. doi: 10.1007/s00445-010-0403-6

CrossRef Full Text | Google Scholar

Becerril, L., Cappello, A., Galindo, I., Neri, M., and Del Negro, C. (2013a). Spatial probability distribution of future volcanic eruptions at El Hierro Island (Canary Islands, Spain). J. Volcanol. Geotherm. Res. 257, 21–30.

Google Scholar

Becerril, L., Galindo, I., Gudmundsson, A., and Morales, J. M. (2013b). Depth of origin of magma in eruptions. Sci. Rep. 3:2762.

PubMed Abstract | CrossRef Full Text | Google Scholar

Bevilacqua, A., Isaia, R., Neri, A., Vitale, S., Aspinall, W. P., Bisson, M., et al. (2015). Quantifying volcanic hazard at Campi Flegrei caldera (Italy) with uncertainty assessment: 1. Vent opening maps. J. Geophys. Res. Solid Earth 120, 2309–2329. doi: 10.1002/2014JB011775

CrossRef Full Text | Google Scholar

Blaikie, T. N., Ailleres, L., Betts, P. G., and Cas, R. A. F. (2014). A geophysical comparison of the diatremes of simple and complex maar volcanoes, Newer Volcanics Province, south-eastern Australia. J. Volcanol. Geoth. Res. 276, 64–81. doi: 10.1016/j.jvolgeores.2014.03.001

CrossRef Full Text | Google Scholar

Blake, S. (1981). Volcanism and dynamics of open magma chambers. Nature 289, 783–785. doi: 10.1038/289783a0

CrossRef Full Text | Google Scholar

Bolós, X., Martí, J., Becerril, L., Planagomà, L., Grosse, P., and Barde-Cabusson, S. (2015). Volcano-structural analysis of La Garrotxa Volcanic Field (NE Iberia): implications for the plumbing system. Tectonophysics 642, 58–70. doi: 10.1016/j.tecto.2014.12.013

CrossRef Full Text | Google Scholar

Bolós, X., Barde-Cabusson, S., Pedrazzi, D., Martí, J., Casas, A., Himi, M., et al. (2012). Investigation of the inner structure of La Crosa de Sant Dalmai maar (Catalan Volcanic Zone, Spain). J. Volcanol. Geotherm. Res. 247–248, 37–48. doi: 10.1016/j.jvolgeores.2012.08.003

CrossRef Full Text | Google Scholar

Bower, S., and Woods, A. (1997). Control of magma volatile content and chamber depth on the mass erupted during explosive volcanic eruptions. J. Geophys. Res. 102, 10273–10290. doi: 10.1029/96jb03176

CrossRef Full Text | Google Scholar

Brenna, M., Cronin, S. J., Németh, K., Smith, I. E. M., and Sohn, Y. K. (2011). The influence of magma plumbing complexity on monogenetic eruptions, Jeju Island, Korea. Terra Nova 23, 70–75. doi: 10.1111/j.1365-3121.2010.00985.x

CrossRef Full Text | Google Scholar

Cappello, A., Neri, M., Acocella, V., Gallo, G., Vicari, A., and Del Negro, C. (2012). Spatial vent opening probability map of Etna volcano (Sicily, Italy). Bull. Volcanol. 74, 2083–2094. doi: 10.1007/s00445-012-0647-4

CrossRef Full Text | Google Scholar

Cassidy, J., and Locke, C. A. (2010). The Auckland volcanic field, New Zealand: geophysical evidence for structural and spatio-temporal relationships. J. Volcanol. Geotherm. Res. 195, 127–137. doi: 10.1016/j.jvolgeores.2010.06.016

CrossRef Full Text | Google Scholar

Connor, C. B. (1990). Cinder cone clustering in the transMexican Volcanic Belt: implications for structural and petrologic models. J. Geophys. Res. 95, 19395–19405. doi: 10.1029/jb095ib12p19395

CrossRef Full Text | Google Scholar

Connor, C. B., Chapman, N. A., and Connor, L. J. (2009). Volcanic and Tectonic Hazard Assessment for Nuclear Facilities. Cambridge, UK: Cambridge University Press. doi: 10.1017/cbo9780511635380

CrossRef Full Text | Google Scholar

Connor, C. B., Condit, C. D., Crumpler, L. S., and Aubele, J. C. (1992). Evidence of regional structural controls on vent distribution: springerville Volcanic Field, Arizona. J. Geophys. Res. 97, 12349–12359. doi: 10.1029/92jb00929

CrossRef Full Text | Google Scholar

Connor, C. B., and Conway, F. M. (2000). “Basaltic volcanic fields,” in Encyclopedia of Volcanoes, ed H. Sigurdsson (New York, NY: Academic Press), 331–343.

Connor, C., Stamatakos, J. A., Ferrill, D. A., Hill, B. E., Ofoegbu, G. I., Conway, F. M., et al. (2000). Geologic factors controlling patterns of small-volume basaltic volcanism: application to a volcanic hazards assessment at Yucca Mountain, Nevada. J. Geophys. Res. 105, 417–432. doi: 10.1029/1999jb900353

CrossRef Full Text | Google Scholar

Dahm, T. (2000). Numerical simulations of the propagation path and the arrest of fluid-filled fractures in the Earth. Geophys. J. Int. 141, 623–638. doi: 10.1046/j.1365-246x.2000.00102.x

CrossRef Full Text | Google Scholar

Delaney, P. T., and Pollard, D. D. (1981). Deformation of host rocks and flow of magma during growth of minette dykes and breccia-bearing intrusions near Ship Rock, New Mexico, U.S. Geol. Surv. Prof. Pap. 1202, 1981.

Delaney, P. T., and Pollard, D. D. (1982). Solidification of basaltic magma during flow in a dyke. Am. J. Sci. 282, 856–885.

Google Scholar

Delaney, P. T., Pollard, P. P., Ziony, J. I., and McKee, E. H. (1986). Field relations between dykes and joints: emplacement processes and paleostress analysis. J. Geophys. Res. 91, 4920–4938.

Google Scholar

Dundurs, J. (1969). Edge-bonded dissimilar orthogonal wedges. J. Appl. Mech. 36, 650–652.

Folch, A., and Martí, J. (1998). The generation of overpressure in felsic magma chambers by replenishment. Earth Planet. Sci. Lett. 163, 301–314. doi: 10.1016/S0012-821X(98)00196-4

CrossRef Full Text | Google Scholar

Fossen, H. (2016). Structural Geology. Cambridge: Cambridge University Press.

Google Scholar

Gaffney, E. S., Damjanac, B., and Valantine, G. A. (2007). Localization of volcanic activity: 2. Effects of pre-existing structure. Earth Planet. Sci. Lett. 263, 323–338.

Google Scholar

Garcia, M. O., Hulsebosch, T. P., and Rhodes, J. M. (1995). Olivine-rich submarine basalts from the southwest rift zone of Mauna Loa volcano: implications for magmatic processes and geo-chemical evolution. Geophys. Monogr. 92, 219–239. doi: 10.1029/gm092p0219

CrossRef Full Text | Google Scholar

Gudmundsson, A. (1990). Emplacement of dykes, sills and crustal magma chambers at divergent plate boundaries. Tectonophysics 176, 257–275. doi: 10.1016/0040-1951(90)90073-H

CrossRef Full Text | Google Scholar

Gudmundsson, A. (2011a). Rock Fractures in Geological Processes. Cambridge: Cambridge University Press. doi: 10.1017/CBO9780511975684

CrossRef Full Text | Google Scholar

Gudmundsson, A. (2011b). Deflection of dykes into sills at discontinuities and magma-chamber formation Tectonophysics 500, 50–64.

Google Scholar

Gudmundsson, A. (2012). Magma chambers: formation, local stresses, excess pressures, and compartments. J. Volcanol. Geotherm. Res. 237–238, 19–41. doi: 10.1016/j.jvolgeores.2012.05.015

CrossRef Full Text | Google Scholar

Gudmundsson, A., and Brenner, S. L. (2005). On the conditions of sheet injections and eruptions in stratovolcanoes. Bull. Volcanol. 67, 768–782. doi: 10.1007/s00445-005-0433-7

CrossRef Full Text | Google Scholar

Gudmundsson, A., Lecour, N., Mohajeri, N., and Thordarson, T. (2014). Dyke emplacement at Bardarbunga, Iceland, induces unusual stress changes, caldera deformation, and earthquakes. Bull. Volcanol. 76:869.

Google Scholar

Gudmundsson, A., Marinoni, L. B., and Martí, J. (1999). Injection and arrest of dykes: implications for volcanic hazards. J. Volcanol. Geotherm. Res. 88, 1–13. doi: 10.1016/s0377-0273(98)00107-3

CrossRef Full Text | Google Scholar

Gudmundsson, A., and Philipp, S. L. (2006). How local stress fields prevent volcanic eruptions. J. Volcanol. Geotherm. Res. 158, 257–268. doi: 10.1016/j.jvolgeores.2006.06.005

CrossRef Full Text | Google Scholar

He, M. Y., Evans, A. G., and Hutchinson, J. W. (1994). Crack deflection at an interface between dissimilar elastic materials: role of residual stresses. Int. J. Solids Struct. 31, 3443–3455. doi: 10.1016/0020-7683(94)90025-6

CrossRef Full Text | Google Scholar

He, M. Y., and Hutchison, J. W. (1989). Crack deflection at an interface between dissimilar elastic materials. Int. J. Solids Struct. 25, 1053–1067.

Google Scholar

Heidbach, O., Reinecker, J., Tingay, M., Müller, B., Sperner, B., Fuchs, K., et al. (2007). Plate boundary forces are not enough: second- and third-order stress patterns highlighted in the World Stress Map database. Tectonics 26:TC6014. doi: 10.1029/2007TC002133

CrossRef Full Text | Google Scholar

Hernando, I. R., Aragon, E., Frei, R., Gonzalez, P. D., and Spakman, W. (2014). Constraints on the origin and evolution of magmas in the Payún Matrú Volcanic Field, Quaternary Andean back-arc of Western Argentina. J. Petrol. 55, 209–239. doi: 10.1093/petrology/egt066

CrossRef Full Text | Google Scholar

Ho, C. H. (1992). Risk assessment for the Yucca Mountain high-level nuclear waste repository site: estimation of volcanic disruption. Math. Geol. 24, 347–364. doi: 10.2172/196582

CrossRef Full Text | Google Scholar

Ho, C. H. (1995). Sensitivity in volcanic hazard assessment for the Yucca Mountain high-level nuclear waste repository site: the model and the data. Math. Geol. 27, 239–258. doi: 10.1007/bf02083213

CrossRef Full Text | Google Scholar

Ho, C. H., and Smith, E. I. (1998). A spatial-temporal/3-D model for volcanic hazard assessment: application to the Yucca Mountain region, Nevada. Math. Geol. 30, 497–510.

Google Scholar

Jaeger, J. C., and Cook, N. G. W. (1979). Fundamentals of Rock Mechanics, 3rd Edn. London: Chapman ang Hall.

Google Scholar

Klügel, A., Hansteen, T. H., and Galipp, K. (2005). Magma storage and underplating beneath Cumbre Vieja Volcano, La Palma (Canary Islands). Earth Planet. Sci. Lett. 236, 211–226. doi: 10.1016/j.epsl.2005.04.006

CrossRef Full Text | Google Scholar

Klugel, A., Longpré, M. A., García-Cañada, L., and Stix, J. (2015). Deep intrusions, lateral magma transport and related uplift at ocean island volcanoes. Earth Planet. Sci. Lett. 431, 140–149. doi: 10.1016/j.epsl.2015.09.031

CrossRef Full Text | Google Scholar

Le Corvec, N., Bebbington, M. S., Linsay, J. M., and McGee, L. E. (2013a). Age, distance, and geochemical evolution within a monogenetic volcanic field: analyzing patterns in the Auckland Volcanic Field eruption sequence. Geochem. Geophys. Geosyst. 14, 3648–3665.

Google Scholar

Le Corvec, N., Spörli, K. B., Rowland, J., and Lindsay, J. (2013b). Spatial distribution and alignments of volcanic centers: clues to the formation of monogenetic volcanic fields. Earth Sci. Rev. 124, 96–114.

Le Corvec, N., Menand, T., and Lindsay, J. (2013c). Interaction of ascending magma with pre-existing crustal fractures in monogenetic basaltic volcanism: an experimental approach. J. Geophys. Res. Solid Earth 118, 968–984.

Google Scholar

Lister, J., and Kerr, R. (1991). Fluid-mechanical models of crack propagation and their application to magma transport in dykes. J. Geophys. Res. 94, 10049–10077. doi: 10.1029/91jb00600

CrossRef Full Text | Google Scholar

Lorenz, V. (1986). On the growth of maars and diatremes and its relevance to the formation of tuff rings. Bull. Volcanol. 48, 265–274. doi: 10.1007/bf01081755

CrossRef Full Text | Google Scholar

Maaloe, S. (1985). Principles of Igneous Petrology. Berlin: Springer-Verlag. doi: 10.1007/978-3-642-49354-6

Maccaferri, F., Bonafede, M., and Rivalta, E. (2010). A numerical model of dyke propagation in layered elastic media. Geophys. J. Int. 180, 1107–1123. doi: 10.1111/j.1365-246X.2009.04495.x

CrossRef Full Text | Google Scholar

Maccaferri, F., Bonafede, M., and Rivalta, E. (2011). A quantitative study of the mechanisms governing dyke propagation, dyke arrest and sill formation. J. Volcanol. Geotherm. Res. 208, 39–50.

Google Scholar

Martí, J., and Felpeto, A. (2010). Methodology for the computation of volcanic susceptibility. An example for mafic and felsic eruptions on Tenerife (Canary Islands). J. Volcanol. Geotherm. Res. 195, 69–77.

Google Scholar

Martí, J., and Geyer, A. (2009). Central vs flank eruptions at Teide–Pico Viejo twin stratovolcanoes (Tenerife, Canary Islands). J. Volcanol. Geotherm. Res. 181, 47–60.

Google Scholar

Martí, J., Geyer, A., Andujar, J., Teixidó, F., and Costa, F. (2008). Assessing the potential for future explosive activity from Teide–Pico Viejo stratovolcanoes (Tenerife, Canary Islands). J. Volcanol. Geotherm. Res. 178, 529–542.

Google Scholar

Martí, J., Pinel, V., López, C., Geyer, A., Abella, R., Tárraga, M., et al. (2013). Causes and mechanisms of the 2011–2012 El Hierro (Canary Islands) submarine eruption. J. Geophys. Res. Solid Earth 118, 823–839.

Google Scholar

Martí, J., Planagumà, L., Geyer, A., Canal, E., and Pedrazzi, D. (2011). Complex interaction between Strombolian and phreatomagmatic eruptions in the Quaternary monogenetic volcanism of the Catalan Volcanic Zone (NE of Spain). J. Volcanol. Geotherm. Res. 201, 178–193.

Google Scholar

Martin, A. J., Umeda, K., Connor, C. B., Weller, J. N., Zhao, D., and Takahashi, M. (1994). Modeling long-term volcanic hazards through Bayesian inference: an example from the Tohuku volcanic arc Japan. J. Geophys. Res. 109, B10208.

McKenzie, D. (1984). The generation and compaction of partially molten rock. J. Petrol. 25, 713–765. doi: 10.1093/petrology/25.3.713

CrossRef Full Text | Google Scholar

McKenzie, D. (1985). The extraction of magma from the crust and mantle. Earth Planet. Sci. Lett. 74, 81–91.

Google Scholar

Menand, T. (2008). The mechanics and dynamics of sills in layered elastic rocks and their implications for the growth of laccoliths and other igneous complexes. Earth Planet. Sci. Lett. 267, 93–99. doi: 10.1016/j.epsl.2007.11.043

CrossRef Full Text | Google Scholar

Menand, T. (2011). Physical controls and depth of emplacement of igneous bodies: a review. Tectonophysics 500, 11–19. doi: 10.1016/j.tecto.2009.10.016

CrossRef Full Text | Google Scholar

Menand, T., Daniels, K. A., and Benghiat, P. (2010). Dyke propagation and sill formation in a compressive tectonic environment. J. Geophys. Res. 115, B08201. doi: 10.1029/2009jb006791

CrossRef Full Text | Google Scholar

Middleton, G. V., and Wilcock, P. R. (1994). Mechanics in the Earth and Environmental Sciences. Cambridge: Cambridge University Press.

Google Scholar

Mrlina, J. H., Kämpf, C., Kroner, J., Mingram, M., Stebich, A., Seidl, M., et al. (2009). Discovery of the first Quaternary maar in the Bohemian Massif, Central Europe, based on combined geophysical and geological surveys. J. Volcanol. Geoth. Res. 182, 97–112. doi: 10.1016/j.jvolgeores.2009.01.027

CrossRef Full Text | Google Scholar

Muller, J. R., Ito, G., and Martel, S. J. (2001). Effects of volcano loading on dyke propagation in an elastic half-space. J. Geophys. Res. 106, 11101–11113.

Google Scholar

Murase, T., and Mcbirney, A. R. (1973). Properties of some common igneous rocks and their melts at high temperatures. Geol. Soc. Amer. Bull. 84, 3563–3592. doi: 10.1130/0016-7606(1973)84<3563:poscir>2.0.co;2

CrossRef Full Text | Google Scholar

Németh, K. (2010). “Monogenetic volcanic fields: Origin, sedimentary record, and relationship with polygenetic volcanism,” in What Is a Volcano? eds E. Cañón-Tapia and A. Szakács (Boulder, CO: Geological Society of America), 43–66. doi: 10.1130/2010.2470(04)

CrossRef Full Text

Németh, K., and Kereszturi, G. (2015). Monogenetic volcanism: personal views and discussion. Int. J. Earth Sci. 104, 2131–2146. doi: 10.1007/s00531-015-1243-6

CrossRef Full Text | Google Scholar

Park, R. G. (1988). Geological Structures and Moving Plates. Glasgow: Blackie & Sons Ltd; Bishopbriggs. doi: 10.1007/978-94-017-1685-7

CrossRef Full Text | Google Scholar

Pasquarè, G., Tibaldi, A., Attolini, C., and Cecconi, G. (1988). Morphometry, spatial distribution and tectonic control of Quaternary volcanoes in norhern Michoacan, Mexico. Rend. Soc. It. Min. Petr. 43, 1215–1225.

Pasquarè, F. A., and Tibaldi, A. (2007). Structure of a sheet-laccolith system revealing the interplay between tectonic and magma stresses at Stardalur Volcano, Iceland. J. Volcanol. Geotherm. Res. 161, 131–150.

Google Scholar

Pinel, V., and Jaupart, C. (2004). Magma storage and horizontal dyke injection beneath a volcanic edifice. Earth Planet. Sci. Lett. 221, 245–262. doi: 10.1016/S0012-821X(04)00076-7

CrossRef Full Text | Google Scholar

Pollard, D. D. (1969). Aspects of the Mechanics of Sheets Intrusions. Unpublished M. Sc. dissertation, University of London, UK

Pollard, D. D. (1973). Derivation and evaluation of a mechanical model for sheet intrusions. Tectonophysics 1, 233–269. doi: 10.1016/0040-1951(73)90021-8

CrossRef Full Text | Google Scholar

Pollard, D. D., and Muller, O. H. (1976). The effects of gradients in regional stress and magma pressure on the form of sheet intrusions in cross section. J. Geophys. Res. 81, 975–984. doi: 10.1029/jb081i005p00975

CrossRef Full Text | Google Scholar

Pollard, D. D., and Segall, P. (1987). “Theoretical displacements and stresses near fractures in rocks: With applications to faults, joints, veins, dykes, and solutions surfaces,” in Fracture Mechanics of Rock, ed B. B. Atkinson (San Diego, CA; Academic), 277–349. doi: 10.1016/b978-0-12-066266-1.50013-2

CrossRef Full Text

Price, N. J., and Cosgrove, J. W. (1990). Analysis of Geological Structures. Cambridge: Cambridge University Press.

Google Scholar

Rice, J. R. (1980). “Mathematical analysis in the mechanics of fracture,” in Fracture, An Advanced Treatise, Vol II, ed H. Liebowitz (New York, NY: Academic Press), 191–311.

Rivalta, E., Taisne, B., Bunger, A. P., and Katz, R. F. (2015). A review of mechanical models of dyke propagation: schools of thought, results and future directions. Tectonophysics 638, 1–42. doi: 10.1016/j.tecto.2014.10.003

CrossRef Full Text | Google Scholar

Roman, D. C., and Heron, P. (2007). Effect of regional tectonic setting on local fault response to episodes of volcanic activity. Geophys. Res. Lett. 34, L13310. doi: 10.1029/2007gl030222

CrossRef Full Text | Google Scholar

Rowe, M. C., Peate, D. W., and Ukstins-Peate, I. (2011). An investigation into the nature of the magmatic plumbing system at Paricutin volcano, Mexico. J. Petrol. 52, 2187–2220. doi: 10.1093/petrology/egr044

CrossRef Full Text | Google Scholar

Rubin, A. M. (1993a). Tensile fracture of rock at high confining pressure: implications for dyke propagation. J. Geophys. Res. 98, 919–935.

Google Scholar

Rubin, A. M. (1993b). On the thermal viability of dykes leaving magma chambers. Geophys. Res. Lett. 20, 257–260.

Google Scholar

Rubin, A. M. (1993c). Dykes vs. diapirs in viscoelastic rock, Earth Planet. Sci. Lett. 119, 641–659.

Google Scholar

Rubin, A. M. (1995). Propagation of magma-filled cracks. Annu. Rev. Earth Planet. Sci. 8, 287–336. doi: 10.1146/annurev.ea.23.050195.001443

CrossRef Full Text

Rubin, A. M. (1998). Dyke ascent in partially molten rock. J. Geophys. Res. 103, 20, 901–920.

Schrank, C. E., Fusseis, F., Karrech, A., and Regenauer-Lieb, K. (2012), Thermal-elastic stresses the criticality of the continental crust. Geochem. Geophys. Geosyst. 13, Q09005.

Google Scholar

Selva, J., Orsi, G., Di Vito, M., Marzocchi, W., and Sandri, L. (2012). Probability hazard map for future vent opening at the Campi Flegrei caldera, Italy. Bull. Volcanol. 74, 497–510. doi: 10.1007/s00445-011-0528-2

CrossRef Full Text | Google Scholar

Shapiro, S. A. (2015). Fluid Induced Seismicity. Cambridge: Cambridge University Press. doi: 10.1017/cbo9781139051132

CrossRef Full Text | Google Scholar

Sigmundsson, F. et al. (2015). Segmented lateral dyke growth in a rifting event at Bardarbunga volcanic system, Iceland. Nature 517, 191–195.

PubMed Abstract | Google Scholar

Sobradelo, R., and Martí, J. (2015). Short-term volcanic hazard assessment through Bayesian inference: retrospective application to the Pinatubo 1991 volcanic crisis. J. Volcanol. Geotherm. Res. 290:111. doi: 10.1016/j.jvolgeores.2014.11.011

CrossRef Full Text | Google Scholar

Spera, F. J. (1980). “Aspects of magma transport.” in Physics of Magmatic Processes, ed R. B Hargraves (Princeton, NJ: Princeton University Press), 265–323.

Stroncik, N. A., Klügel, A., and Hansteen, T. H. (2009). The magmatic plumbing system beneath El Hierro (Canary Islands): constraints from phenocrysts and naturally quenched basaltic glasses in submarine rocks. Contrib. Mineral. Petrol. 157, 593–607. doi: 10.1007/s00410-008-0354-5

CrossRef Full Text | Google Scholar

Taisne, B., and Jaupart, C. (2009). Dyke propagation through layered rocks. J. Geophys. Res. 114, B09203.

Google Scholar

Taisne, B., Tait, S., and Jaupart, C. (2011). Conditions for the arrest of a vertical propagating dyke. Bull. Volcanol. 73, 191–204. doi: 10.1007/s00445-010-0440-1

CrossRef Full Text | Google Scholar

Takada, A. (1989). Magma transport and reservoir formation by a systems of propagating cracks. Bull. Volcanol. 52, 118–126. doi: 10.1007/BF00301551

CrossRef Full Text | Google Scholar

Takada, A. (1994). The influence of regional stress and magmatic input on styles of monogenetic and polygenetic volcanism. J. Geophys. Res. 99, 563–513. doi: 10.1029/94jb00494

CrossRef Full Text | Google Scholar

Thirlwall, M. F., Singer, B. S., and Marriner, G. F. (2000). 39Ar±40Ar ages and geochemistry of the basaltic shield stage of Tenerife, Canary Islands, Spain. J. Volcanol. Geother. Res. 103, 247–297.

Google Scholar

Tibaldi, A. (1995). Morphology of pyroclastic cones and tectonics. J. Geophys. Res. 100, 24521–24535. doi: 10.1029/95jb02250

CrossRef Full Text | Google Scholar

Tibaldi, A., and Lagmay, A. M. F. (2006). Interaction between volcanoes and their basement. J. Volcanolo. Geother. Res. 158, 1–5. doi: 10.1016/j.jvolgeores.2006.04.011

CrossRef Full Text

Tibaldi, A., and Pasquarè, F. (2008). A new mode of inner volcano growth: the “flower intrusive structure”. Earth Planet. Sci. Lett. 271, 202–208. doi: 10.1016/j.epsl.2008.04.009

CrossRef Full Text | Google Scholar

Tibaldi, A., Vezzoli, L., Pasquarè, F. A., and Rust, D. (2008). Strike-slip fault tectonics and the emplacement of sheet-laccolith systems: the thverfell case study (SW Iceland). J. Struct. Geol. 30, 274–290. doi: 10.1016/j.jsg.2007.11.008

CrossRef Full Text | Google Scholar

Touloukian, Y. S., Judd, W. R., and Roy, R. F. (1989). “Physical properties of rocks and minerals,” in CINDAS Data Series on Material Properties, Group II Properties of special materials, Vol 1–2. New York, NY: McGraw-Hill.

Traversa, P., Pinel, V., and Grasso, J. (2010). A constant influx model for dyke propagation: implications for magma reservoir dynamics. J. Geophys. Res. 115, B01201.

Google Scholar

Turcotte, D. L., and Schubert, G. (1982). Geodynamics: Applications of Continuum Physics to Geological Problems. New York, NY: John Wiley.

Valentine, G. A., and Gregg, T. K. P. (2008). Continental basaltic volcanoes—Processes and problems. J. Volcanol. Geother. Res. 177, 857–873. doi: 10.1016/j.jvolgeores.2008.01.050

CrossRef Full Text | Google Scholar

Valentine, G. A., and Hirano, N. (2010). Mechanisms of low-flux intraplate volcanic fields – basin and range (North America) and northwest Pacific Ocean. Geology 38, 55–58. doi: 10.1130/g30427.1

CrossRef Full Text | Google Scholar

Valentine, G. A., and Perry, F. V. (2007). Tectonically controlled, time-predictable basaltic volcanism from a lithospheric mantle source (central Basin and Range Province, USA). Earth Planet. Sci. Lett. 261, 201–216. doi: 10.1016/j.epsl.2007.06.029

CrossRef Full Text | Google Scholar

Walker, G. P. L. (2000). “Basaltic volcanoes and volcanic systems,” in Encyclopedia of Volcanoes, ed H. Sigurdsson (San Francisco, CA: Academic Press), 283–289.

Wood, C. A. (1980). Morphometric evolution of cinder cones. J. Volcanol. Geother. Res. 7, 387–413. doi: 10.1016/0377-0273(80)90040-2

CrossRef Full Text | Google Scholar

Wright, T. J., Ebinger, C., Biggs, J., Ayele, A., Yirgu, G., Keir, D., et al. (2006). Magma-maintained rift segmentation at continental rupture in the 2005 Afar dyking episode. Nature 442, 291294. doi: 10.1038/nature04978

PubMed Abstract | CrossRef Full Text | Google Scholar

Zang, A., and Stephansson, O. (2010). Stress Field of the Earth's Crust. Heidelberg: Springer. doi: 10.1007/978-1-4020-8444-7

CrossRef Full Text | Google Scholar

Zoback, M. D., and Zoback, M. L. (2002). “Stress in the Earth's lithosphere,” in Encyclopedia of Physical Science and Technology, 3rd Edn., ed R. A. Meyers (San Diego, CA: Academic Press), 143–154.

Zoback, M. L. (1992). First- and second-order patterns of stress in the lithosphere: the world stress map project. J. Geophys. Res. 97, 11703–11728. doi: 10.1029/92jb00132

CrossRef Full Text | Google Scholar