Mathematics at Your Fingertips: Testing a Finger Training Intervention to Improve Quantitative Skills
- 1Sheffield Hallam University, Sheffield, United Kingdom
- 2University of Bristol, Bristol, United Kingdom
Previous research indicates that the use of fingers as representations of ordinal and cardinal number is an important part of young children’s mathematics learning. Further to this, some studies have shown that a finger training intervention can improve young children’s quantitative skills. In this article, we argue that fingers represent a means for children to connect different external representations of number (including verbal, symbolic, and non-symbolic representations). Therefore, we predicted that an intervention that combined finger training with experience playing games involving multiple representations would lead to greater increases in quantitative skills than either aspect of the intervention alone. One hundred and thirty-seven children aged between 6 and 7 years old took part in an intervention study over the course of 4 weeks. The study tested the impact of five different conditions on participants’ quantitative skills, their finger gnosis, and their ability to compare magnitudes of two non-symbolic representations of number. Relative to a control group, those children receiving a finger training intervention saw gains in finger gnosis skills (the ability to differentiate fingers when touched, without visual cues). Those children who played number games saw an increase in their non-symbolic magnitude comparison skills. However, only those children who experienced both aspects of the intervention saw increases in quantitative skills, which were assessed using an instrument informed by Gelman and Gallistel’s (1978) five principles of counting. The findings show that a finger training intervention, when combined with intensive exposure to multiple representations of number can support young children’s development of quantitative skills. This adds to evidence in the literature regarding the role of fingers in children’s mathematics learning and may have implications for pedagogical approaches.
Introduction
Finger gnosis (sometimes referred to alternatively as “finger sense,” or “finger localization”) is the ability to mentally represent and differentiate the fingers (Gerstmann, 1940). It is generally indexed by children’s ability to tell without looking which fingers have been touched. Studies have shown that there is a relationship between finger gnosis and quantitative skills in young children. However, the mechanism through which fingers and arithmetic connect to one another is not yet fully understood, and there have been only a small number of studies that have demonstrated a causal relationship. In this article, we make the case that fingers are used by children as a means to connect other representations of number to one another, thus playing a part in children’s developing quantitative skills. This article reports a study designed to test a two-part intervention, bringing together work to improve children’s coordination and sensing of their fingers with work to improve children’s ability to translate between different representations of number through games. We predict that the combined intervention will be more effective in promoting arithmetic fluency than either aspect carried out in isolation, as the benefit of finger training is to give children a more efficient means to bridge among multiple representations of number.
This section first sets out the evidence for a relationship between finger gnosis and quantitative skills, together with some discussion of a possible theoretical framework connecting these phenomena. We then describe the intervention tested in this study, designed to support children’s developing understanding of number.
Evidence for an Association between Finger Gnosis and Arithmetic Fluency
The majority of evidence for an association between finger gnosis and arithmetic fluency is correlational, but this evidence comes from a number of studies. Fayol et al. (1998) and Marinthe et al. (2001) report that measures of finger gnosis taken at the age of 5 years are excellent predictors of numerical ability 3 years later. Noël (2005) reports that measures of finger gnosis taken when children were 6 years old predicted scores on numeracy ability, but not reading ability tests, 15 months later. The predictive power of finger gnosis for later numerical ability is generally explained with reference to the localization hypothesis or to the functional hypothesis.
Localization Hypothesis
The relationship between finger gnosis and numerical ability may simply be a result of the fact that the part of the brain that responds to number lies in close proximity to the area that is activated whenever subjects perform pointing and grasping activities. fMRI studies have provided compelling evidence of such a link between finger movements and response to number. Of the three parietal circuits described by Dehaene et al. (2003) that relate to number sense, two are in close proximity to the area responsible for finger activity. Simon et al. (2002) note that the horizontal segment of the intraparietal sulcus area was activated both when subjects were performing mathematical tasks, and when carrying out pointing and grasping tasks. A later study by Andres et al. (2012) analyzed fMRI scans of adult brains and also found evidence to suggest that the circuits in the brain which involve finger representation were an intrinsic component of arithmetic operations in adults.
Functional Hypothesis
Butterworth (1999) argues for a functional relationship between finger gnosis and numerical ability. Evidence for this comes from a number of sources. Butterworth (1999) refers to evolutionary evidence to suggest that our use of the base 10 system is due to the fact that we have 10 fingers. Fingers are typically used by children to support the learning and recitation of the count sequence—the fingers on the right hand used to represent the numbers one to five, and the left to represent six to ten (Sato and Lalain, 2008). Fingers are used as indicators of cardinal numbers (Brissiaud, 2003) and to point at objects when counting a set (Gallistel and Gelman, 1992). Alibali and DiRusso (1999) investigated the role of the fingers in counting a set of objects in more detail. They found that when children were prevented from using their fingers when counting a set of objects, they were more likely to make errors involving a loss of coordination between number words and items counted. Thus, it appears that fingers may function as a bridge between different mental representations of number.
Further evidence for the functional hypothesis comes from the study by Gracia-Bafalluy and Noël (2008), who carried out an intervention study to test the effect of finger training on young children’s numeracy abilities. In their study, children were trained to differentiate between their fingers in four activities: following a colored pathway with a particular finger with a similarly colored sticker on it; pointing at particular colored circles with particular fingers; following a sequence of colors on a keyboard with the same color-coded fingers; and the final task included performing strong grips between the thumb and each other finger on the hand. Gracia-Bafalluy and Noël showed that children who had received the finger training intervention scored more highly on measures of finger gnosis. Their results also demonstrated improvements in ordinality judgments, counting fingers, and subitizing skills that were greater than their peers who did not receive finger training.
Moeller et al. (2011) discussed two accounts of the role of finger counting; from a neurocognitive perspective, and from a mathematics education perspective. Both perspectives adhere to the functional hypothesis of finger gnosis and quantitative skills described here. However, from the neurocognitive perspective, finger-based numerical representations are integral to numerical development, while from the mathematics education perspective finger counting is often a starting point in representing number but should be replaced with mental representations over time. The development of an intervention that encourages finger gnosis to increase quantitative skills makes sense from either perspective. However, from the neurocognitive perspective, such an intervention would work by developing lasting connections between finger representations and other symbolic and/or non-symbolic representations of number, while from a mathematics education perspective, the intervention would use finger representations to temporarily bridge between other representations so that a direct connection could be made more easily.
Development of an Intervention to Improve Quantitative Skills
The literature reviewed above provides support for a functional relationship between finger movements and quantitative skills. More specifically, it appears that children’s fingers may function as a bridge, or mediator, between other verbal and symbolic representations of number. This leads us to posit the idea that an intervention to improve quantitative skills may be more effective if it combines finger training with other activities that involve other (verbal, symbolic, and non-symbolic) representations of number.
There is some evidence that games involving symbolic and non-symbolic representations of number can support the development of quantitative skills in young children. Siegler and Ramani (2008), for example, found that when children played a simple numerical board game for four 15-min sessions, their numerical estimation abilities improved. Skwarchuk et al. (2014) found that parental reports of children’s exposure to games at home that involve number predicted children’s performance in a non-symbolic arithmetic test. Studies such as these have not explicitly promoted finger training, although fingers are certainly used in many games. However, given that games like these generally involve children making connections between multiple representations of number (matching the number of dots on a die with a number of moves on a board, for example), they represent a promising source of activity to combine with a finger training intervention.
The motivation to research novel interventions to support young children’s numerical understanding derives from research findings showing that a secure foundation of quantitative skills is essential for children to succeed in their later mathematics learning (Jordan et al., 2003). In turn, achievement in mathematics is associated with broader academic and economic success in later life (Butterworth et al., 2011). Successful interventions to support young children’s quantitative skills must account for the complexity of the thinking and learning required. Dowker (2008) has shown that individual difference in arithmetic ability is best explained with a componential model of expertise and that an intervention that addresses the particular components that a child is experiencing difficulty which has the best chance of success. However, there has, to date, been little research of potential interventions that account for possible interactions between such components. This is a potentially rich seam, as previous research has shown that such interactions are an important aspect of children’s mathematics learning (Mundy and Gilmore, 2009; LeFevre et al., 2010).
The Present Study
An intervention study was designed in order to test the hypothesis that a combined finger training and number games intervention would be effective in improving children’s quantitative skills, and more effective than either intervention alone.
The intervention designed for this study was based on those used in studies described above (particularly, Gracia-Bafalluy and Noël, 2008; Siegler and Ramani, 2008; Skwarchuk et al., 2014) and comprised the following activities.
Finger Gnosis Activities
Each session began with the teacher demonstrating, and the pupils joining in with, various finger movement activities. The content varied across sessions but included a combination of the following activities designed to improve children’s recognition of the cardinal and ordinal properties of number and strengthening links between these and the visual and physical representations given by the fingers:
• Counting 1, 2, 3…, 10 and 10, 9, 8……., 1 verbally together with representations using fingers.
• Counting in 2s, 5s, and 10s with fingers.
• “Show me” activity. The teacher says “show me 7” (for example), and children show 7 fingers (using numbers 1–10).
• Matching fingers from the left hand with fingers on the right hand. “Match 3 to 7” for example, would require children to touch the middle finger of the right hand (3) to the first finger of the left hand (7).
• Pressing on fingers 1, 2, 3…., 10 for the same number of seconds.
• A group of counters is put in front of each pupil and they must guess how many. Then, they count using the matching finger (third finger for a set of three, for example).
• Hold up fingers to represent a calculation—show 6 + 2 = 8, or 7 – 3 = 4, for example, by raising or lowering fingers to add or subtract from an initial set.
• Matching finger representations to a number pointed to on a number line—e.g., 34 would be 10, 10, 10, and 4 fingers.
• Draw numbers 1, 2, 3, 4, 5 large, or draw maze lines from top left to bottom right of page. Children follow numbers and mazes with different fingers.
Number Games Activities
Each session began with the teacher or researcher explaining and demonstrating a different game and the pupils playing in pairs wherever possible. The teacher and other adults in the class moved around the groups to encourage the pupils to verbalize the numbers they were seeing and to ensure that the rules of the games were understood and being followed. Different games were used during each session:
• Dominoes: Used for matching equal sets of dots; or for finding combinations that add to a given number.
• Playing cards: Used for “snap” game—matching same number of symbols; or for a memory game finding pairs when the cards are face-down.
• Snakes and ladders board game.
• “Smiley face” game: A counter is placed on a template of a face when the total from two dice being thrown is closer to 10, and taken away if closer to 0.
• “Shut the box”: 2 dice are thrown and pupils have to turn over any of their 1–9 cards to make the same total.
Materials and Methods
Design
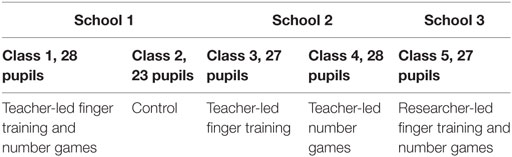
A between-groups quasi-experimental design was employed in order to compare five different conditions:
• Teacher-led finger training intervention.
• Teacher-led symbolic number games intervention.
• Teacher-led finger training and symbolic number games combined intervention.
• Researcher-led (Julie Betenson) finger training and symbolic number games combined intervention.
• Control condition; teacher-led business-as-usual.
All conditions, except for the control condition, involved eight 30-min sessions; two sessions per week for 4 weeks. Two days of training was given to teachers in participating schools prior to the study to explain the rationale for the experiment and to give teachers some experience of the intervention activities described above. During the intervention, the researcher led the first session of the week for all the groups except the control group. The teacher led the second session of the week, apart from the researcher-led group where both sessions were delivered by the researcher. This additional input from the researcher was designed to remind the teachers of the activities and suitable mathematical language to use during the sessions, as had been practised during the training days.
In line with previous research, we expected the finger training intervention to lead to improvement in finger gnosis scores (Gracia-Bafalluy and Noël, 2008), and the number games intervention to give rise to improvements in non-symbolic arithmetic scores (Skwarchuk et al., 2014). We expected all groups bar the control group to show improvements in quantitative skills, with the highest level of improvement expected for those in the combined finger training and number games groups.
Participants
One hundred and thirty-seven children aged 6–7 years old took part in the study. They were drawn from three primary schools in a city in the South of England. Other than the age of the children, no specific criteria were used during recruitment other than an enthusiasm to take part in the research. The three schools are all larger than average sized primary schools, with pupils of similar, diverse, ethnic backgrounds. The use of three schools allowed for five different classes to be randomly allocated different elements of the intervention program in order to reduce selection bias (see Table 1).
Instruments and Measures
A set of measures were taken from all participants both before and after the intervention sessions took place, in order to assess different aspects of finger gnosis, symbolic number sense, and arithmetic fluency.
Finger Gnosis Testing
The finger gnosis test was administered on a one-to-one basis using a task adapted from the study by Gracia-Bafalluy and Noël (2008). Each participant was asked to put their hand flat on the table inside a box so that the participant could not see their fingers. The researcher then lightly pressed the pupil’s fingers in a predetermined non-sequential order so that the pupil could say the number corresponding to the finger which had been touched. Thirty trials were completed in the same manner. The same set of trials was used for each pupil in order to ensure consistency and to ensure no advantage was gained from a particular finger being pressed more often than others. Participants’ responses were voice recorded so that they could be checked and collated after the testing had taken place. A correct answer was scored as 1 and therefore a maximum total of 30 could be achieved on this test.
A further set of measures were combined so that they could be administered to children in groups, as a series of pencil-and-paper tests, as follows:
Quantitative Skills Tests
Number system knowledge was tested using an instrument based on the study by Gelman and Gallistel’s (1978) five implicit principles of counting. The first page (count) required the pupil to count numbers of objects which involved the one-to-one correspondence principle where “one” and “two” are assigned to each counted object, the abstraction principle which allows objects of any kind to be collected together and counted and the cardinality principle where the final word tag defines the number of items counted. The second page (dice) involved the recognition and the adding together of regular dot arrays displayed as dice. This activity also involved the one-to one correspondence, abstraction, and cardinality principles. The third page (number) included the identification of the larger number of two, the ordering numbers up to 102 and the placing of different numbers in the correct order on a number line. This was based on the stable order principle where the order of the word tags does not vary between sets of numbers. The fourth page (sequencing) involved the completion of number sequences going forwards and backwards in ones, twos, fives, and tens. This also used the stable order principle. The final page (manipulation) involved splitting numbers into their composite parts and creating a larger number from a combination of two or three smaller numbers. This incorporated the order irrelevance principle where numbers can be put together in any sequence to make a given tagged number. The test pages used both symbolic and non-symbolic representations of number and were arranged on five different sheets of paper. One minute was allowed for completion of each page. A maximum score of 126 was possible on these five pages. Although the pages tested different aspects of counting, it was expected that there would be a strong correlation between the scores for each of the five pages, as each incorporated the five principles of counting. The tasks were all piloted and refined with children of the same age as the sample of this study, and in collaboration with experienced teachers.
Magnitude Comparison Test
A 1 -min paper-and-pencil test of magnitude comparison was used following a format from the study by Nosworthy et al. (2013). Pupils were given 1 min to compare 20 pairs of dot arrays and to tick the larger set of dots each pair. The differences between the numbers of dots in each pair varied between one and six dots. The test was designed as a simple accuracy measure giving a maximum total of 20 marks.
Procedure
All pupils completed the group-administered mathematics achievement tests, which consisted of numeration and calculation tests, and the magnitude comparison tests, prior to intervention in January 2014. These were delivered in their usual classroom space with their teacher present to reduce any possible effects on performance for children who found change in personnel or surroundings distracting. The finger gnosis testing was administered individually in a quiet space outside the children’s classroom used for group work. This would reduce distraction from noises within the classroom and yet to be in a space which was familiar to the students and therefore aid confidence. All tests were repeated after the intervention sessions had been completed in March 2014.
Results
Analysis of Pretest Data
The set of five tests used to measure quantitative skills showed a high level of reliability (five items; Cronbach’s α = 0.814). Therefore, subsequent analysis used a composite “quantitative skills” score generated by adding scores from the five components.
There was a significant positive correlation between finger gnosis and quantitative skills at pretest (r = 0.33, n = 133, p < 0.0005), in line with previous research. There were also significant positive correlations between quantitative skills and magnitude comparison (r = 0.37, n = 133, p < 0.0005), and between finger gnosis and magnitude comparison (r = 0.171, n = 133, p = 0.05). However, the correlation between finger gnosis and magnitude comparison disappeared when quantitative skills were partialed out (r = 0.058, n = 133, p = 0.511).
Analysis of Posttest Data
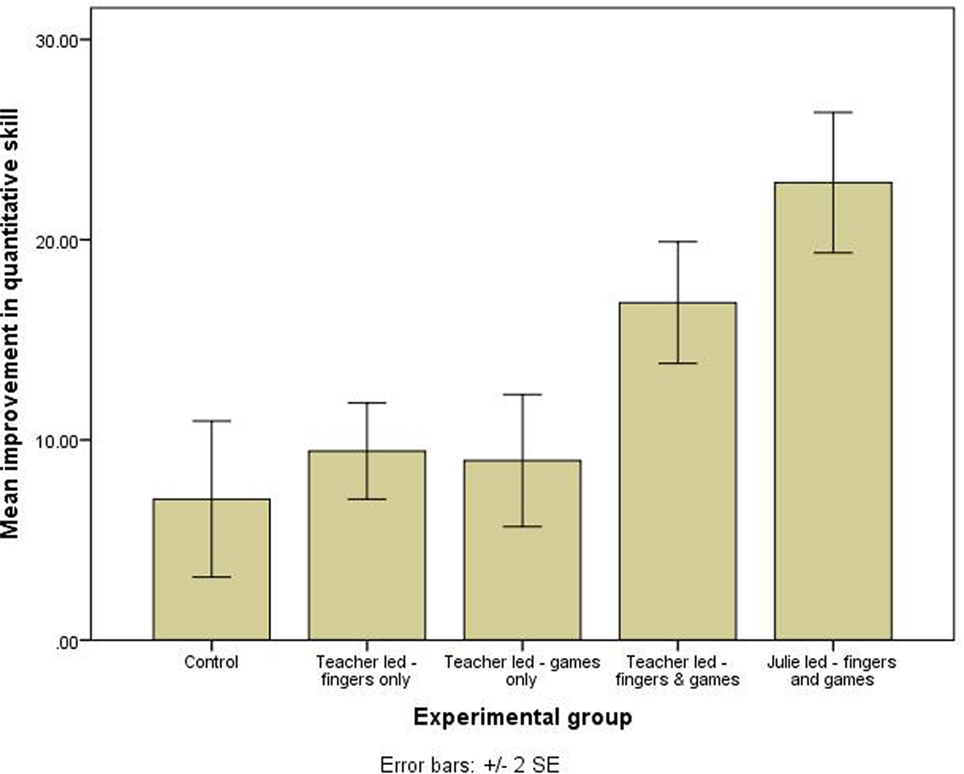
A one-way ANOVA was used to compare improvement in quantitative skills between the five experimental conditions. This revealed a significant effect of condition (F4, 128 = 16.71, p < 0.0005). Post hoc tests showed that both versions of the combined intervention (teacher-led and researcher-led) led to greater improvements in quantitative skills than the other three conditions, which did not differ from one another (see Figure 1). The two versions of the combined intervention did not differ significantly from one another in terms of improvement in quantitative skills.
In order to calculate an effect size for improvement in quantitative skills, the two combined intervention groups were combined, and compared with the three other groups combined; Hedges’ g = 1.32, a very large effect. See Table 2 for descriptive statistics for the combined groups.
In order to determine whether the finger training aspect of the intervention had been effective in improving finger gnosis scores, groups that received finger training were combined and compared with those that did not. Descriptive statistics can be seen in Table 3, and an independent t-test revealed a significant difference in improvement in finger gnosis scores (t = 2.53, df = 131, p = 0.013).
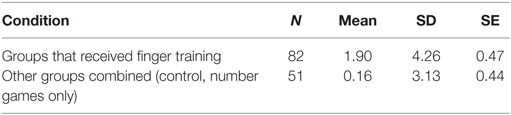
Table 3. Improvement in finger gnosis score—those that received finger training compared with other groups.
In order to determine whether the number games aspect of the intervention had an effect on non-symbolic magnitude comparison, groups that received the number games intervention were combined and compared with those that did not. Descriptive statistics can be seen in Table 4, and an independent t-test revealed a significant difference in improvement in magnitude comparison scores (t = 2.38, df = 131, p = 0.019).

Table 4. Improvement in magnitude comparison score—those that received the number games intervention compared with other groups.
Summary
The results show that the finger training aspect of the intervention was effective in improving participants’ finger gnosis scores, but on its own was not effective in improving scores on the quantitative skills test. Similarly, the number games aspect of the intervention was effective in improving non-symbolic magnitude comparison scores, but on its own was not sufficient to improve quantitative skills. The two versions of the intervention that combined both the finger training and number games aspects were successful in improving participants’ quantitative skills relative to controls, and with a large effect size.
Discussion and Conclusion
The findings show that the combined intervention, incorporating both finger training and symbolic number games, gave rise to significant improvements in participants’ numeration scores. Neither intervention alone had an effect on numeration scores. This is an important and original contribution to knowledge in this field, as this combination of interventions has not been tested before, to our knowledge. This finding suggests that children’s developing number sense is best supported by experience of a combination of representations of number—in this case including fingers plus verbal, symbolic and non-symbolic representations—rather than by a particular set in isolation. Confidence in the finding is added by the fact that the intervention led by a class’s usual teacher showed a similar increase in number sense as did the group led by the researcher.
Prior to the intervention taking place, the pretest data showed a correlation between finger gnosis and number sense. This supports previous findings from the study by Fayol et al. (1998) and Andres et al. (2012). The findings do not fully corroborate the findings of Gracia-Bafalluy and Noël (2008), who found that an 8-week finger training intervention alone improved quantification skills in a sample of 6–7-year-old children (approximately the same duration and age-range as in the current study). A possible explanation for this difference is that Gracia-Bafalluy and Noël selected participants who had poor finger gnosis at the outset of their study, while the present study included participants with a full range of initial levels of finger gnosis. However, the findings presented here do agree with the main findings of Gracia-Bafalluy and Noël, in that a finger training intervention—when combined with the number gains intervention—did lead to gain in finger gnosis, and that these gains were accompanied by gains in quantitative skills.
The findings of the present study do not fully align with those of the study by Siegler and Ramani (2008), Skwarchuk et al. (2014), and others who have found that playing games involving symbolic representations of numbers can improve children’s numerical knowledge. However, Siegler and Ramani (2008) worked with a sample of low-income children with low levels of numerical knowledge at the outset of their experiment, which again differed from the range of participants included in the present study. Again, though, in combination with the finger training, the number games intervention did lead to gains in quantitative skills.
The findings presented here suggest that for an intervention to be successful in increasing children’s quantitative skills—when the children are starting within the normal range of ability—then the intervention should involve a combination of number representations, rather than one particular set of representations.
Confidence in the above interpretation is added by the fact that the finger training intervention (but not the number games intervention) was shown to improve participants’ finger gnosis scores, and the number games intervention (but not the finger training intervention) was shown to improve non-symbolic magnitude comparison scores. This supports the argument that while both aspects of the intervention have a potential role to play in supporting children’s learning, it is only in combination that they can be shown to improve children’s quantitative skills. We argue that this provides evidence for the functional hypothesis, regarding the relationship between finger gnosis and quantitative skills (Butterworth, 1999), whereby fingers act as a bridge, or mediator, between other representations of number.
Multiple Components of Numerical Understanding
Further consideration is needed here, of possible mechanisms to explain the fact that the finger training and number games interventions led to significant increases in quantitative skills when combined, but not in isolation. It will be useful to draw on previous research relating to the complexity of numerical understanding, and its componential nature.
One possibility is that the effects were additive, and only reached significance in combination. This is somewhat unlikely as each intervention in isolation led to levels of quantitative skills that were very close to those of the control group (Figure 1). However, although differences were not significant, the mean scores of the finger training-only group and the number games-only group were higher than that of the control group, and so it is not possible to discount this possibility without replication of the current study.
A second possibility is that the combined intervention led to better results as it was more likely to match children’s particular needs. Dowker (2005, 2008) has shown that there are several components involved in children’s developing understanding of number and arithmetic and that intervention is most effective when it addresses the particular component that child is experiencing difficulty with. In the case of the current study, it is possible that some children may have needed more intervention in finger gnosis and others in symbolic number manipulation or magnitude comparison.
A third possibility is that the combined intervention helped children to make connections between representations of number. This possibility follows from the functional hypothesis regarding the relationship between finger gnosis and quantitative skills. Children generally need explicit exposure to relationships between numerical phenomena or relationships in order to internalize them (Fuson, 1986). It may be that the combination of activities in the intervention helped make relationships between different representations of number for participating children. This hypothesis would place the current study within a growing body of work showing that children often find it difficult to make connections between different aspects of number. Goffin and Ansari (2016), for example, show that children’s judgments of cardinality and ordinality of number independently predict individual differences in arithmetic fluency, and that there is a lack of relationship between them. Similarly, De Smedt et al. (2013) noted a lack of relationship between skills in processing symbolic and non-symbolic representations of number. Further work is needed in order to determine which relationships are necessary for the development of expertise with number, and how children experience barriers and enablers for these in their learning.
Limitations
Each of the five experimental groups comprised children who normally worked together as a class. This means that there may have been unobserved intra-cluster factors that affected learning and performance. For example, children in one class could conceivably respond more positively or more flexibly to an intervention than those in another class, with another teacher. A future fully randomized study could address this issue and provide more convincing evidence for the effectiveness of the intervention.
A second limitation relates to the fact that posttests were carried out soon after the last session of the intervention. It is therefore not possible to know whether the gains in quantitative skills demonstrated by the two groups participating in the combined intervention would have persisted long enough to show an effect on a delayed test. If an intervention such as this is to be useful in a school context then it will be important to show both that gains persist and that they contribute to a more flexible foundation for further learning.
Despite the limitations of the study, we argue that it has provided promising evidence that a combined finger training and number games intervention can contribute to young children’s quantitative skills and their developing mathematical understanding. We understand that further research will be needed in order to fully determine the underlying mechanisms by which the interventions leads to gains in skill, and to add confidence in the effectiveness of the intervention, but argue that sufficient evidence has been gained from this study to warrant such further work.
Conclusion
This study has shown that an intervention that combines finger training with number games can improve quantitative skills among 6–7-year-old children. It supports the findings of previous research arguing for a functional relationship between finger gnosis and numeracy. We argue that this study provides evidence that fingers represent a means for children to bridge between other (verbal, symbolic, and non-symbolic) representations of number and that this contributes to children’s developing understanding. The large effect size suggests that with further refinement and replication, the combined finger training and number games intervention could be a useful tool for teachers to use to support children’s developing understanding of number.
Ethics Statement
The study was approved by the ethics committee of the Graduate School of Education, University of Bristol. Opt-out consent was gained from all parents of children who participated. Informed consent was gained from head teachers and classroom teachers of all children who participated.
Author Contributions
The study reported in this article was carried out as part of Dr. Betenson’s doctoral studies at the University of Bristol, supervised by Dr. Jay. Dr. Jay adapted the article from Dr. Betenson’s thesis, carrying out a reanalysis of data and additional literature review.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Funding
The research reported in this article was carried out as part of the second author’s doctoral study, funded by the UK Economic and Social Research Council at the University of Bristol.
References
Alibali, M., and DiRusso, A. (1999). The function of gesture in learning to count: more than keeping track. Cogn. Dev. 14, 37–56. doi: 10.1016/S0885-2014(99)80017-3
Andres, M., Michaux, N., and Pesenti, M. (2012). Common substrate for mental arithmetic and finger representation in the parietal cortex. Neuroimage 62, 1520–1528. doi:10.1016/j.neuroimage.2012.05.047
Butterworth, B., Varma, S., and Laurillard, D. (2011). Dyscalculia: from brain to education. Science 332, 1049–1053. doi:10.1126/science.1201536
De Smedt, B., Noël, M. P., Gilmore, C., and Ansari, D. (2013). The relationship between symbolic and non-symbolic numerical magnitude processing and the typical and atypical development of mathematics: a review of evidence from brain and behavior. Trends Neurosci. Educ. 2, 48–55. doi:10.1016/j.tine.2013.06.001
Dehaene, S., Piazza, M., Pinel, P., and Cohen, L. (2003). Three parietal circuits for number processing. Cogn. Neuropsychol. 20, 487–586. doi:10.1080/02643290244000239
Dowker, A. (2005). Individual Differences in Arithmetic: Implications for Psychology, Neuroscience and Education. Hove: Psychology Press.
Dowker, A. (2008). Individual differences in numerical abilities in preschoolers. Dev. Sci. 11, 650–654. doi:10.1111/j.1467-7687.2008.00713.x
Fayol, M., Barrouillet, P., and Marinthe, C. (1998). Predicting arithmetical achievement from neuropsychological performance: a longitudinal study. Cognition 68, 63–70. doi:10.1016/S0010-0277(98)00046-8
Fuson, K. (1986). Roles of representation and verbalization in the teaching of multi-digit addition and subtraction. Eur. J. Psychol. Educ. 1, 35–56. doi:10.1007/BF03172568
Gallistel, C., and Gelman, R. (1992). Preverbal and verbal counting and computation. Cognition 44, 43–74. doi:10.1016/0010-0277(92)90050-R
Gelman, R., and Gallistel, C. (1978). Young Children’s Understanding of Numbers. Cambridge, MA: Harvard University Press.
Gerstmann, J. (1940). Syndrome of finger agnosia, disorientation for right and left, agraphia and acalculia: local diagnostic value. Arch. Neurol. Psychiatry 44, 398–408. doi:10.1001/archneurpsyc.1940.02280080158009
Goffin, C., and Ansari, D. (2016). Beyond magnitude: judging ordinality of symbolic number is unrelated to magnitude comparison and independently relates to individual differences in arithmetic. Cognition 150, 68–76. doi:10.1016/j.cognition.2016.01.018
Gracia-Bafalluy, M., and Noël, M. P. (2008). Does finger training increase young children’s numerical performance? Cortex 44, 368–375. doi:10.1016/j.cortex.2007.08.020
Jordan, N., Hanich, L., and Kaplan, D. (2003). A longitudinal study of mathematical competencies in children with specific mathematics difficulties versus children with comorbid mathematics and reading difficulties. Child Dev. 74, 834–850. doi:10.1111/1467-8624.00571
LeFevre, J. A., Fast, L., Skwarchuk, S. L., Smith-Chant, B. L., Bisanz, J., Kamawar, D., et al. (2010). Pathways to mathematics: longitudinal predictors of performance. Child Dev. 81, 1753–1767. doi:10.1111/j.1467-8624.2010.01508.x
Marinthe, C., Fayol, M., and Barrouillet, P. (2001). “Gnosies digitales et développement des performances arithmétiques,” in Troubles du Calcul et Dyscalculies chez l’Enfant, eds A. Van Hout, C. Meljac, and J. Fischer (Paris: Masson), 239–254.
Moeller, K., Martignon, L., Wessolowski, S., Engel, J., and Nuerk, H. C. (2011). Effects of finger counting on numerical development – the opposing views of neurocognition and mathematics education. Front. Psychol. 2:328. doi:10.3389/fpsyg.2011.00328
Mundy, E., and Gilmore, C. K. (2009). Children’s mapping between symbolic and nonsymbolic representations of number. J. Exp. Child Psychol. 103, 490–502. doi:10.1016/j.jecp.2009.02.003
Noël, M. (2005). Finger gnosia: a predictor of numerical abilities in children? Child Neuropsychol. 11, 413–430. doi:10.1080/09297040590951550
Nosworthy, N., Bugden, S., Archibald, L., Evans, B., and Ansari, D. (2013). A two-minute paper-and-pencil test of symbolic and nonsymbolic numerical magnitude processing explains variability in primary school children’s arithmetic competence. PLoS ONE 8:e67918. doi:10.1371/journal.pone.0067918
Sato, M., and Lalain, M. (2008). On the relationship between handedness and hand-digit mapping in finger counting. Cortex 44, 393–399. doi:10.1016/j.cortex.2007.08.005
Siegler, R. S., and Ramani, G. B. (2008). Playing linear numerical board games promotes low-income children’s numerical development. Dev. Sci. 11, 655–661. doi:10.1111/j.1467-7687.2008.00714.x
Simon, O., Mangin, J.-F., Cohen, L., Le Bihan, D., and Dehaene, S. (2002). Topographical layout of hand, eye, calculation and language related areas in the human parietal lobe. Neuron 33, 475–487. doi:10.1016/S0896-6273(02)00575-5
Keywords: numeracy, quantitative skills, finger gnosis, intervention studies, counting
Citation: Jay T and Betenson J (2017) Mathematics at Your Fingertips: Testing a Finger Training Intervention to Improve Quantitative Skills. Front. Educ. 2:22. doi: 10.3389/feduc.2017.00022
Received: 13 February 2017; Accepted: 04 May 2017;
Published: 07 June 2017
Edited by:
Ana Lucia Pereira, Ponta Grossa State University, BrazilReviewed by:
Ann Dowker, University of Oxford, United KingdomCraig Speelman, Edith Cowan University, Australia
Copyright: © 2017 Jay and Betenson. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tim Jay, t.jay@shu.ac.uk
 Tim Jay
Tim Jay Julie Betenson
Julie Betenson