The demand side in economic models of energy markets: the challenge of representing consumer behavior
- Department of Business and Economics, University of Basel, Basel, Switzerland
Energy models play an increasing role in the ongoing energy transition processes either as tools for forecasting potential developments or for assessments of policy and market design options. In recent years, these models have increased in scope and scale and provide a reasonable representation of the energy supply side, technological aspects and general macroeconomic interactions. However, the representation of the demand side and consumer behavior has remained rather simplistic. The objective of this paper is twofold. First, we review existing large-scale energy model approaches, namely bottom-up and top-down models, with respect to their demand-side representation. Second, we identify gaps in existing approaches and draft potential pathways to account for a more detailed demand-side and behavior representation in energy modeling.
Introduction
Reducing energy demand, or at least its growth, is one of the central objectives in the transition processes in many national and international energy markets. For example, the European vision of a low-carbon economy identifies energy efficiency as a key driver of the transition (European Commission, 2014), the Swiss Energy Strategy 2050 aims for a significant reduction of per capita energy consumption of 54% by 2050 (SFOE, 2012), and the IEA’s World Energy Outlook considers a reduction in energy consumption as one of the main measures to achieve a significant reduction in CO2 emissions (IEA, 2014a).
Despite this importance of the energy demand side, there still exist significant knowledge gaps as to what factors determine energy demand and how it can be influenced. Besides descriptive statistics on specific energy consumption patterns and profiles and the technological linkage between service demand and energy needs (for example, different options to satisfy transport or heating demand), little is known about the underlying decision and behavioral processes. The fact that consumers seldom demand energy in itself but services and products which require energy for their provision links this challenge to a general understanding of consumption decision processes.
The energy demand aspects extend into the modeling dimension. In the last decades, energy system and market modeling has gained an increasingly important role within the policy process; i.e., forecasts based on models like the IEA World Energy Outlook using the World Energy Model (IEA, 2014b) or the Energy Trends of the European Commission based on the PRIMES model (European Commission, 2013) are important resources for economic and political decision makers. Model-based scenarios also form the basis of energy market processes like the network development planning in Germany and Switzerland (SFOE, 2013; NEP, 2014). Finally, models are used for ex post policy evaluation and are, apart from field experiments, the only way to gain knowledge about the necessary intensity of policy interventions. The existing energy system and market models were designed with a focus on the different technology options on the supply and transport side whereas demand was often assumed to be derived from external drivers like GDP or following classic price and substitution elasticities. Thus, they are limited in their capability to capture important psychological or social elements and aspects beyond the technology or price dimension.
The objective of this paper is to assess the role of the demand side and consumer behavior within economic energy market modeling, identify gaps in existing approaches, and design potential pathways to account for a more detailed demand side and behavior representation in energy modeling. In Section “Review on the Demand-Side Representation in Energy Market Models”, we review existing model approaches for energy markets used for policy design and evaluation with special focus on their demand-side representation. Section “Energy Demand: Toward Richer Models” provides concepts to extend the existing models to facilitate a more detailed description of energy demand. In Section “Transferring New Approaches into Numerical Modeling”, we discuss how these concepts can be used in numerical modeling and Section “Conclusion” concludes.
Review on the Demand-Side Representation in Energy Market Models
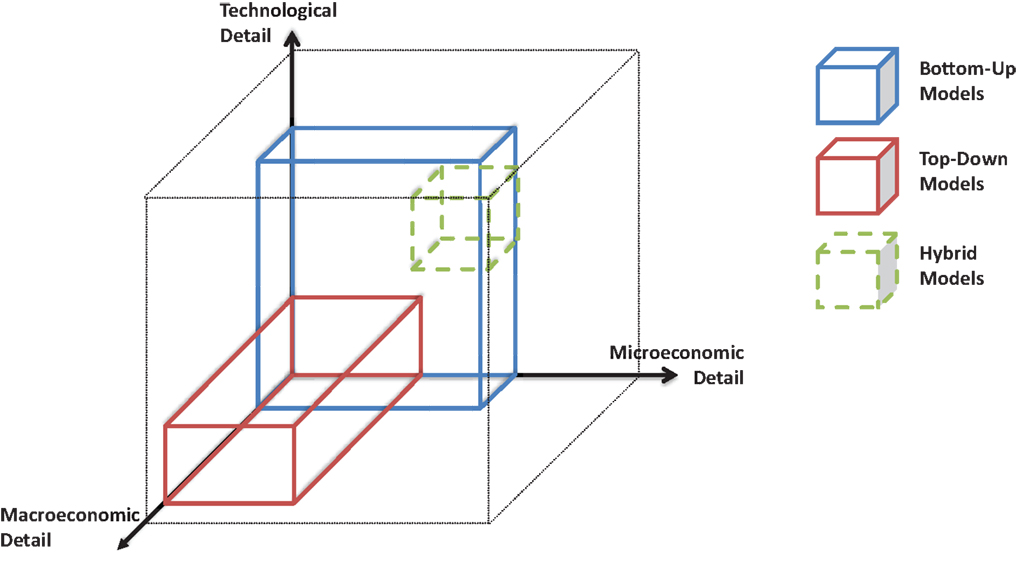
There exists a multitude of modeling approaches for energy-related questions. Within this section, we focus on large-scale models covering markets, sectors, or the whole energy system and economy.1 Generally, those types of models can roughly be clustered in two streams: bottom-up (BU) and top-down (TD) models that are both able to address a specific range of relevant drivers (Figure 1). The former cover techno-economic models that provide a detailed representation of technical aspects of a market or energy sectors, like conversion or transport specifications, as well as microeconomic market representations that address the interaction of different market participants, like producers, traders, and consumers within wholesale markets. The latter cover macroeconomic models that are able to capture the interaction among several sectors and overall welfare effects. A related differentiation between the two clusters would be the terms “disaggregated” for BU models and “aggregated” for TD models (Böhringer and Rutherford, 2009).
Usually, the strengths of one model cluster are the weaknesses of the other. BU models allow a detailed representation of specific market characteristics, the impact of policies on a sector, and the costs and challenges of technological change. However, their focus on a single sector or a set of (energy) sectors limits the possibility to capture further cross-sectoral effects, the price driven influences are often limited to cost optimization, and they omit overall economy impacts like employment, trade, and income effects. Consequently for TD models the reverse is true (Herbst et al., 2012).
Following Hourcade et al. (2006) energy models can be structured along three dimensions: the technological, microeconomic, and macroeconomic detail. Generally, applied energy models are tailored to capture a specific dimension and have to omit other aspects. The first dimension represents the technological explicitness of a model including their ability to capture technological restrictions and how policies affect technological developments. The second refers to behavioral realism of the model including the representation of consumer choice and the impact of market structures on policy effectiveness. The third refers to macroeconomic feedbacks linking energy supply and demand to the general economic structure and development.
Bottom-up models typically rank high with respect to technological details and allow the modeling of different technology developments. Similarly, they allow the inclusion of microeconomic aspects like strategic company behavior or game theoretic approaches. However, typically BU model approaches that rank high on the microeconomic dimension need to rely on mixed complementarity formulations. This in turn limits the representation of technological details that require mixed-integer formulations like unit commitment of power plants. The opposite also holds. In contrast, TD models capture the macroeconomic interactions of economies and are based on the basic microeconomic rational of utility maximizing agents but lack technological detail and typically also fall short in addressing more detailed microeconomic behavior beyond perfect competitive market interaction.
Theoretically, a hybrid model capturing all three dimensions would provide the most structure for evaluating energy markets (Hourcade et al., 2006), but potentially at the expense of model focus and transparency of results. In recent years, research on models breaching the gaps between TD and BU has increased with several approaches of hybrid modeling emerging. In the following sections, we briefly present selected BU and TD models and methods as well as hybrid and other model approaches focusing on their representation of the energy demand side.
Bottom-Up Techno-Economic Models
Bottom-up models are characterized by their high degree of detail on the technology side and their representation of market structure and market architecture aspects. They are basically disaggregated representations of specific sectors or markets and therefore have to omit the more general economic interactions. They can be used both for short-term evaluations, like electricity market dispatch analysis, and long-term simulations, like investment scenarios. However, BU models rely on a set of externally defined parameters, which capture those economic aspects that are not covered by the model-like economic growth and demand or fuel prices of energy sectors. Defining these parameters is challenging, in particular for long-term evaluations, but BU models are one of the few options to simulate the impact of future conditions that deviate considerably from historic or current market conditions.
Bottom-up models are typically formulated as optimization problem or complementarity problem.2 Especially techno-economic models that focus on supply and transport restrictions or operational details often rely on linear optimization techniques.
The large-scale energy system models are the IEA World Energy Model (IEA, 2014b), the PRIMES model (E3MLab/ICCS, 2014), the POLES model (Enerdata, 2014), and the MARKAL/TIMES family of models (ETSAP, 2014), which are covering several regions and sectors in a partial equilibrium setup. Typically, such large-scale energy system models consist of several modules or sub-models covering specific regions, sectors, or value-chain elements, which are linked via iterative simulations. Due to their long-term perspective, they capture investment decisions but neglect short-term dynamics. In recent years, those model families already started to breach the gaps between BU and TD modeling by integrating more macroeconomic aspects into their models.
Sectoral models focus on one specific fuel and the underlying markets. Consequently, there exist a large number of different models for the specific energy markets; for example, for electricity markets, the ELMOD model (Leuthold et al., 2012) or the DIMENSION model (Richter, 2011) for Europe and RFF’s Haiku model for the US (Paul et al., 2009), the World Gas Model (Egging et al., 2010) or the COLUMBUS model (Hecking and Panke, 2012) for the global gas markets, the TREMOVE model for the transport sector (Capros and Siskos, 2012), or residential stock models for the building sector [see Kavgic et al. (2010) for a review], to name a few. The focus on a specific market or sector enables those models to capture much more details, such as network restrictions (e.g., pipeline or transmission line capacities), specific technology restrictions (e.g., power plant start-up times), and detailed regional and temporal resolutions (e.g., daily or seasonal demand patterns), than the large-scale energy system models mentioned above. Their specific model setup varies strongly and is often tailored to the specific research question at hand; that is, short-term technical questions, long-term investment aspects, or market design and strategic interaction, and consequently includes linear, non-linear, and equilibrium approaches.
In general, BU models are well suited to evaluate changes and impacts on the supply and transport side of energy markets. They can capture a wide range of different production restrictions and facilitate a corresponding detailed evaluation of policies. But their mathematical structure limits the representation of demand-side behavior. There are roughly speaking two main types of BU models with respect to price and demand-side representation, both being widely applied:
First, techno-economic BU models designed as linear or linear mixed-integer optimization problems. They are required to take the demand side as a fixed input and thus cannot capture price or budget feedbacks. Changes in the demand side can only be incorporated as shifts of the load level, for example, via a new hourly demand profile, due to demand-side management technologies; an increasing demand level, due to economic growth; or different demand scenarios based on energy efficiency assumptions. Furthermore, the linear structure leads to a classical cost optimal result that corresponds to a perfect competitive market framework, whereas imperfect competition cannot easily be captured within this model framework.
Second, BU models designed as complementarity problems or non-linear optimization problems incorporate demand-side functionalities, typically a relation between demand and price. Non-linear optimization problems can include welfare maximization instead of a pure cost minimization as the objective. This captures the price interaction but still keeps the models limited to perfect competitive benchmark outcomes. In addition, BU models using the equilibrium framework allow the representation of multiple agents with individual optimization rationales and thereby facilitate the simulation of strategic firm behavior, imperfect competition, or the impact of structural changes. Similar to the linear type BU models, the demand functionalities need to be externally defined, especially regarding the price elasticities. Consequently, general economic interrelations, such as budget effects or substitution-effects across markets, cannot be captured directly. However, the endogenous price formation makes it possible to cover direct price-quantity effects within the respective sector.
Top-Down CGE Models
Top-down models aim at representing the whole economy instead of only energy sectors and thereby capture the feedback effects across the economy. This modeling approach requires a high degree of aggregation and cannot represent the same technological detail as BU models. The most prominent macroeconomic model approach in energy economics are computable general equilibrium (CGE) models. Those models have a highly aggregated representation of the energy system and the other sectors of an economy. The equilibrium concept ensures that all modeled markets clear (supply equals demand on each market), given supply and demand characteristics. This equilibrium is obtained by endogenous price adjustments following the microeconomic rational of utility maximizing agents and profit maximizing firms. However, the agents in CGE models are highly aggregated; most often, a representative household is used. Due to their aggregation level and equilibrium concept, CGE models are well suited for long-term evaluations of changes in the policy or market frame and not for short-term operational simulations.
Due to the high abstraction level of CGE models, the production technology process is transferred into production functions with constant elasticities of substitution (ESUB). The different inputs and outputs are linked via nesting structures; that is, the energy input into a production function is itself an aggregate of different energy types, like electricity and fossil fuels that can be substituted for each other. As these elasticities determine the degree of substitution between inputs, they are thereby an important driver of the effects of policy changes. To capture the effect of technological change in the energy sector – basically a shift of the production functions – exogenous shift parameters are often used, like the autonomous energy efficiency index (AEEI). The AEEI represents a price-independent energy efficiency increase, which is sometimes used to carry out sensitivity analyses.
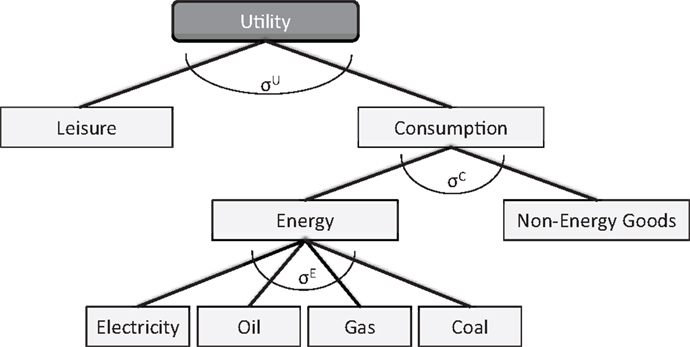
The same logic is applied to the demand side of CGE models. Figure 2 shows an exemplary demand-side structure for a CGE model with detailed energy specifications. Demand is derived from maximizing the utility function of a representative household, given a budget restriction. Consumption and other “goods,” such as leisure time, form the aggregated utility good. Consumption itself is split into direct energy use and consumption of other goods. The energy use in turn can be satisfied by different fuels which can be substituted for each other given the elasticity σE; that is, switching from oil to electricity for heating. The energy needed for the other goods, the embedded energy, is obtained by a similar structure on the production side. This allows CGE models to capture indirect energy effects due to changes in consumption.
There exist a large number of CGE models that address different economic aspects. Bergman (2005) provides a general introduction to CGE models and a review on different environmental- and resource-related CGE models. Those models can be (broadly) clustered into global, multi-regional, and single-country CGEs. Within the first group, examples are given by the MIT-EPPA model (Paltsev et al., 2005) and the DICE and RICE model family (Nordhaus, 2012). The GEM-E3 model of the European Commission (Capros et al., 2013), the related GEMINI-E3 model (Bernard and Vielle, 2008), and the PACE modeling framework (Böhringer et al., 2009) are examples for energy-related multi-regional models. Finally, the GENESwIS for Switzerland (Vöhringer, 2012) and the MIT U.S. Regional Energy Policy Model (Lanz and Rausch, 2011) are examples for single-country CGEs.
Top-down computable general equilibrium models are well suited to capture price-based demand side effects across different sectors via budget effects. This is particularly important for the estimation of rebound effects that result from such indirect effects. They also are well suited for public finance evaluations of taxes and other instruments. However, the underlying parameters for the different ESUBs and the AEEI are typically based on estimates and expert judgments (Bataille et al., 2006). This poses two challenges: first, data and estimations on both ESUBs, and particular AEEI, are incomplete, and second, estimates based on past and present data do not necessarily have to be an accurate description of future behavior making TD models less suited for the analysis of extensive system shifts in comparison to BU models.
Hybrid Models and Other Model Approaches
Due to the limitations of both BU and TD approaches, researchers are developing methods to merge both lines of models for policy analyses. The resulting hybrid models can be clustered into three categories (Böhringer and Rutherford, 2008): First, soft-linked models, in which independent BU and TD models are linked by passing data between the models or via direct convergence mechanisms, as, for example, in Schäefer and Jacoby (2006), who link the MIT-EPPA CGE model with the MARKAL model. This approach faces the challenge of consistency of the disaggregated and aggregated results; that is, the electricity generation of different power plant types of a BU electricity model run need to match the aggregated fuel consumption of the electricity sector in the TD model. Second, a reduced form version of one model is incorporated into another model, as, for example, in Bosetti et al. (2006) or Leimbach et al. (2009). Third, integrating technological details directly via the mixed complementarity problem formulation of a CGE model, see, for example, Böhringer and Rutherford (2008, 2009).
From a demand perspective, hybrid approaches facilitate the combination of detailed sectoral effects, like shifts in demand profiles, with general macroeconomic feedbacks, such as indirect rebound effects. This is of particular relevance for energy efficiency evaluations. Furthermore, the potential to model higher temporal resolutions in BU approaches makes it possible to combine short- and long-term economic feedbacks. Nevertheless, the demand representation is still limited to the above presented characteristics and focused on quantity-price relations and/or externally defined levels and trends.
In addition to CGE models and optimization and partial equilibrium BU models, there are a number of additional model approaches in energy economics [see Catenazzi (2009) and Herbst et al. (2012)]. These include input–output models, system dynamics approaches, and econometric models. The latter often include multiple consumer groups [i.e., the E3ME model has 13 types of household, Camecon (2014)]. But due to their reliance on historic data, they are not well suited to analyze significant system shifts. On the BU side, there are furthermore simulation models and agent-based models. The former are often more technology driven and can represent whole energy systems with great detail; see, for example, the LEAP model (Heaps, 2012). The latter results from a relatively new model approach in energy economics [e.g., see Weidlich and Veit (2008) for a review of electricity market related agent-based models]. Instead of a closed mathematical market formulation, individual market participants are modeled as agents with autonomous behavior that interact with each other. This makes it possible to model different behavior of the market participants and thereby capture choice related aspects.
Summarizing the different existing energy model approaches, we see that they are typically designed to capture supply side related market aspects while demand-side aspects are much less detailed. This is partly a result of the underlying computational structure but also a result of the historic market development; for a long time, electricity and natural gas systems were regulated markets in which cost optimal energy supply was the main focus. Furthermore, most of the recent energy-related developments took place on the supply side, such as, the emergence of renewable energy technologies.
It is thus not surprising that existing models typically lack endogenous demand-side influences beside price-quantity relations. Furthermore, most models treat the demand side as an aggregate with little detail on specific consumer aspects and differentiated consumers.3
Despite these problems, existing models are well suited to analyze small, price-induced changes on the demand side as well as the effects of pre-defined (scenario-based) changes to energy consumption on markets and energy supply. However, with an increasing focus on energy efficiency and the liberalization of former monopolistic markets, the demand side will become increasingly important: policies directly aimed at end users will increase, companies will need to compete for consumers with better products or services, and finally consumer will also become active market participants providing their own energy supply and storage potential as ‘prosumers’. In particular, it will be necessary to develop models that capture consumer choices with respect to energy provision and that can describe the relation between changes in individual behavior and demand-side policies.
Energy Demand: Toward Richer Models
As discussed above, most applied economic models describe energy demand as being a function of prices and income only. From a theoretical perspective, this is warranted by the basic microeconomic model of consumer choice, where an individual maximizes her utility U(e, x) over a bundle of energy goods e and other goods x subject to the condition that total expenditure does not exceed income y for a given vector of energy prices z and other prices p:
This results in a demand function for energy e = f (z, p, y). Under conventional assumptions, demand for each energy good is a decreasing function of this good’s price and an increasing or a decreasing function of the prices of other goods, depending on substitution possibilities. Typically, the above consumer is used in the sense of a (descriptive) representative consumer, that is, the consumer is used as an “average” of all consumers, so that the characteristics of aggregate demand (over all consumers) are identical to the characteristics of this consumer’s energy demand. This approach forms the basis of most CGE models, whereas BU models rely on further simplifications.
The above basic setup is useful to describe the response of energy demand to price changes, in particular, the effects of changes in energy markets or of some policy instruments, such as energy taxation. In fact, numerous studies have assessed the price responsiveness of demand for different energy goods, see, for example, Filippini (2011) or Krishnamurthy and Kriström (2015). Furthermore, it can be used to examine simple indirect phenomena, like the above discussed rebound effects.
However, to assess other types of demand-side policies or more general effects, the model lacks structure. A simple but powerful extension is to consider heterogeneous consumers, for example, groups of consumers that differ regarding their income or preferences. Such an extension makes it possible to assess the distributive impacts of energy policies. Furthermore, such a model can be used to assess potential benefits of group-specific interventions.
But even with this extension, the model does not capture many effects that have been found to be relevant in field studies.4 Most importantly, the above model assumes that consumers are perfectly aware of all actions to reduce their energy consumption, so that information-based policies are ineffective by definition, and that there are no interactions among consumers, apart from market interactions. Furthermore, preferences are considered as being given and constant, so that there is no leeway for changes to individual lifestyles that are not “forced” by changing conditions (such as, prices or income).
In the next subsections, we will discuss how the above model can be adjusted in simple ways to capture the potential relevance of information, social interactions, and changing preferences.
Modeling the Influence of Information on Energy Demand
To make room for potential effects of information-based approaches to steer energy demand, a necessary assumption is that consumers are not perfectly aware of all options for changing their energy demand. For example, they might not know which energy-efficient appliances exist, what quality and prices they have, and where they can be bought. Thus, if they want to change their behavior, they need to search for new solutions. There is a long tradition of search models in economics, with applications mostly to labor markets, explaining price dispersion, and innovation. Chandra and Tappata (2011) use such a model to explain differences in gasoline prices among stations; Kortum (1997) as well as Makri and Lane (2007) use a search model to explain how firms find new technological solutions.
To transfer the main insights of these models to individual energy demand, it is useful to assume that consumers need to invest in appliances (some goods x, in our above notation) to alter their ability of adjusting energy use e. However, they are not aware of the properties of the relevant goods x and thus need to spent time or money searching for an appliance that meets their requirements. From a modeling perspective, we could assume that consumers know a distribution of possible characteristics of appliances, that is, they know which qualities, costs, usage characteristics, and energy reductions are technically feasible. However, without gathering information, they do not know which appliance has which properties.
Thus consumers can either buy an appliance without this information or invest time (modeled via fixed opportunity costs S) to ascertain the characteristics of one appliance (they randomly draw an appliance from the overall distribution and learn its properties). If they invest in this search, they can afterward decide to buy this good or to research another one. This decision will be made based on the overall distribution of possible characteristics, that is, on their knowledge what is feasible; whenever the good comes sufficiently close to having the preferred characteristics among all feasible goods, a consumer will not invest in a new search (the probability of finding a better solution is too small) and rather buy this good.
Such a model is able to describe some interesting effects. First, changing energy consumption induces one-time costs (search costs). Thus potential gains in energy efficiency will only be reaped, if these gains compensate for the search costs, in other words, small changes to energy prices will have little, but somewhat larger changes might have substantial effects. Furthermore, the model explains why different consumers will resort to different solutions in the short run (and thus explain technological variety, e.g., different alternatives to conventional light bulbs) but might converge to similar solutions later on, when they observe the choices of others. Finally, and most importantly, the model can describe an impact of information-based policies. Such policies would lead to a reduction of search costs, implying an earlier start of the search process and thus making it easier to reap small gains in energy efficiency.
However, as preferences remain unchanged, the model also highlights an important constraint of information-based policies: Such policies only reduce frictions, and they do not alter a consumer’s overall assessment of whether it is beneficial to reduce his energy consumption. Thus in the context of this framework, information-based policies will be ineffective; if consumers do not reduce their energy consumption, because the individual gains (savings from using less energy) do not cover the individual costs (in terms of expenses or reduced quality of life).
Social Interactions and Social Norms
A different way of influencing individual behavior is to provide information about the behavior of others or (implicit) information about social norms regarding energy consumption. This approach has been found to be effective in a number of studies. For example, Allcott (2011) shows in a large-scale field study with 600,000 households that using such non-price instruments can have similar short-run effects on total energy consumption as an 11–20% increase in energy prices.
Again, there is some tradition in other fields of economics of modeling social norms. A convenient approach is to include a “disutility” of not meeting a social norm in the description of individual behavior, see, for example, Lindbeck et al. (1999), where such an approach is used in the context of social security. Other contexts where this modeling approach is used are the explanation of tipping behavior, see, for example, Azar (2004), and green consumption, as in Nyborg et al. (2006).
In a general framework, this can be modeled by a slight extension of the above basic model. To this end, assume that the utility of individual i (out of n individuals) depends not only on her consumption (ei, xi) but also on a social norm N:
The social norm is in turn a result of the behavior of all individuals in the society (which might, however, have different influence on norm formation):
In such a model, changes in individual behavior can result in adjustments of social norms, which in turn will lead to further changes in individual behavior.5 This approach thus introduces a feedback effect in the basic model. Furthermore, it is possible that there are several equilibria, for example, an equilibrium with low and one with high energy consumption, which are each stabilized via the endogenously formed social norm (Lindbeck et al., 1999).
An information-based policy could be described either as manipulating the social norm or as making people more aware of an existing norm. In the first case, it might be possible to suggest that the norm is low energy consumption, which could move the system to an equilibrium with lower energy consumption (if multiple equilibria exist). In the second case, the policy could increase the disutility from not being close to the norm, which would induce both a direct change in behavior and an according adjustment of the norm. Such increases in disutility could be achieved by providing information about the behavior of other consumers. An example is given in Traxler (2010), who shows how changing the beliefs of tax payers regarding the incidence of tax evasion (and thus their disutility from not meeting a social norm) can change overall outcomes rather drastically.
A slightly more elaborate version of the above model would not use a single social norm but rather a set of group-specific norms, whose formation may be interrelated. This would facilitate the modeling of social interactions or peer pressure within groups.
However, a major problem is the quantification of the effects that social norms have on individual decisions. Some authors argue [see, e.g., Camerer and Fehr (2004) or Krupka and Weber (2013)] that laboratory experiments can be used to gain at least an approximate quantification. Others, such as Levitt and List (2007), are more critical and point out that questions regarding a limited transferability of experimental situations to every-day-behavior have particular relevance for the case of adherence to social norms. Field experiments provide another option, see, for example, Shang and Croson (2009), who study the influence of social information on public good provision. However, as field experiments are rather costly, this option usually implies a transfer across contexts and countries, as it is not possible to implement a field experiment in every situation where the influence of social norms on energy use needs to be assessed.
Modeling Changing Preferences and Sufficiency
Another, much discussed, approach toward reducing energy consumption is sufficiency. This term is used in the literature in different ways [see, Oikonomou et al. (2009) or Alcott (2008) for an overview]. Most importantly, sufficiency needs to be disentangled from efficiency, which is not trivial, as the economic concept of efficiency covers both changes in technology and changes in behavior.
Often, sufficiency is considered to be an enforced or voluntary frugal way of living (Oikonomou et al., 2009). In case of enforced frugality, this might imply reduced individual well-being. In contrast, if sufficiency is to be chosen voluntarily, an individual has to get a sufficient recompense for the reduced consumption, which might take the form of an increased self-esteem, utility from contributing to a socially desirable outcome, or an increase in leisure time (due to be able to cope with less income).
However, a salient question is if sufficiency gains exist, why have they not yet been fully reaped? Building on the concept of social norms discussed in the preceding subsection, one argument might be that different societal equilibria exist and individuals are “trapped” in a situation where the benefits of sufficiency cannot be reaped, because they depend on similar behavior by others. This would reduce the problem of modeling sufficiency to the cases discussed in the preceding subsection and interventions toward sufficiency would need to address social norms.
A different approach to sufficiency would be to remain on the individual level and to assume that individuals can only assess the quality of life in situations that they have already experienced. Thus they know how to live in the way they are currently living and how to react to small shocks. However, there might be different ways of living that reduce energy consumption without sacrificing well-being that the individual has not yet experienced and thus does not know.
In terms of modeling, we could assume that preferences consist of a set of local preferences (each defined in a neighborhood of a given consumption bundle) out of which an individual knows only one (her current) local preferences. The other preferences (i.e., ways of living) are not known to exist but their properties (how much utility can be gained, how goods can be substituted) are uncertain until this way of living has been tried. In such a setting, a risk-averse consumer would not alter his way of living until “forced” to do so (either by changing energy prices or by other interventions). Once a new way of living has been tried, the respective local preferences become known. If the driving force of the change vanishes (energy prices come down again), the consumer might either maintain this way of living or switch back to her original consumption pattern.
The benefit of this approach is that it captures much of the essence of the sufficiency concept and introduces an effect into the energy economic modeling that is not present so far: a one-time intervention can have lasting effects for some but not all parts of the population. For example, an oil price shock might initially increase the number of people not using cars. However, once oil price go down again, some consumers might switch back to their original way of living, whereas others have experienced a new and preferred lifestyle, which they voluntarily maintain.
However, it should be noted that if sufficiency gains are to be depicted in a model, this model cannot use per capita consumption, GDP, or total costs to assess demand-side policies. Rather, a measure of welfare has to be used that is based on individual utility and that captures either utility derived from adhering to social norms or the above mentioned uncertainty. Whereas this is common in theory, it is hard to implement in numerical models, as the necessary data is lacking.
Transferring New Approaches into Numerical Modeling
Obviously, existing numerical energy models will need adjustments and extensions to address the challenges in relation to increased energy efficiency and demand-side policies. For all changes, a necessary first step is the inclusion of heterogeneous consumers into the existing model structures. For CGE models, this basically refers to a more disaggregated structure on the demand side of the market transferring the oftentimes single representative household into several household types; for example, households representing different income classes that differ in their demand elasticities for specific goods.6 This is less a modeling challenge, as the basic computational model structure remains unaltered, but more a question of data availability. Detailed data on different household types, their income, the split of income across sources, and consumption choices would be needed. For BU models, such a disaggregation is possible but will only result in a differently shaped aggregate demand function without much impact on overall computational model structure. Again, the main bottleneck for such a development is data availability like sufficient spatial or temporal resolution.
Building on this, it might be feasible to include richer models, such as those presented in Sections “Modeling the Influence of Information on Energy Demand,” “Social Interactions and Social Norms,” and “Modeling Changing Preferences and Sufficiency.” Some extensions might be fairly easy to achieve, for example, the basic structure of norm-based interactions does not differ much conceptually from the inclusion of public knowledge on the production side in endogenous growth [see, for example, Bretschger and Suphaphiphat (2014)] and should thus be transferable to numerical CGE modeling. Including sufficiency or search processes would be much more difficult, as this requires the inclusion of uncertainty, which is hard to achieve in large-scale numerical models.
For BU models, a stepwise or time-dependent model structure as used in dynamic investment models, unit commitment models, or rolling planning models can be used as starting point. Within a period t the consumption decision is derived from externally defined parameters including, for example, norm driven aspects. The resulting consumption will then have an influence on the impact of norms in the following period t + 1. Whether this influence is handled outside the model, that is, by adjusting the demand function accordingly, or within the model depends on the scope and structure of the model. The former should easily be accommodated by most BU model approaches, including linear optimization problem following a myopic logic. The latter introduces dynamic elements similar to path dependent investment aspects which increases the model complexity.
However, the proposed concepts require a quantification of their effects before they can be included into numerical models. Given our current knowledge on energy demand and particular on non-price driven influences this represents a significant non-modeling challenge. Consequently, to properly address those aspects in economic models we will first need a better understanding of the fundamental drivers of consumers energy demand.
Conclusion
Overall, this paper has two main messages. First, most of the currently available applied energy models do not use sophisticated approaches to describe the demand side. In fact, most models cannot describe or assess demand-side interventions apart from price changes. However, the second part shows that this is not a restriction imposed by the general economic approach to modeling consumer behavior. Much richer models are feasible and are used in other fields of economics. In particular, it is feasible to model many effects, such as social norm or social interactions that have been found to be relevant in field studies.
In our view, there are two reasons why these approaches are currently not used in energy modeling. First, there is a lack of demand. For decades, energy policy has focused on the supply side; whereas billions have been spent to enact changes in energy supply, demand-side policies have typically a small budget.7 Accordingly, demand for policy assessments is biased toward supply side policies and thus most applied energy models have a highly detailed supply and a fairly simple demand structure.
Second, applied modeling requires not only concepts but also data. Whereas data on energy supply is abundant, there is a lack of data regarding the structure of energy consumption and its main determinants apart from prices and technologies. Few countries have a micro census that includes more than some elementary energy-related items, so that projects aiming for a better description of the demand side have to collect their own data. Given the different foci of such projects, there is little chance of combining their data to a sufficiently broad database.
As energy strategies in many countries are based on a strong reduction in per capita energy consumption, the first reason will vanish rather rapidly; the need for more qualified assessments of demand-side policies will strongly increase within the next years. However, the second bottleneck (missing data) will not dissolve in a likewise manner. Thus if better models of energy consumption are desirable, generating the necessary data should be the main priority.
The need for detailed data also extends to a more general lack of understanding the fundamental drivers and mechanisms of energy demand beyond the technological layer. Overcoming this knowledge gap will require fundamental research in social and political science as well as psychological and consumer behavior research and the transfer of those insights into the economic model community. How such an integrated interdisciplinary framework could be achieved is addressed in Burger et al. (2015) in the same issue of Frontiers in Energy Research.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgment
We would like to thank Jan Abrell and Sebastian Rausch for helpful input. This research is part of the activities of SCCER CREST (Swiss Competence Center for Energy Research), which is financially supported by the Swiss Commission for Technology and Innovation (CTI).
Footnotes
- ^Small-scale analyses focusing on single processes or regional aspects, e.g., like micro-grids or single building optimizations, can address detailed demand aspects but naturally cannot capture general policy or market interactions.
- ^Note that also TD models are formulated as complementarity problems. The differentiation between the BU and TD complementarity problems is in their coverage: while TD models are formulated as general equilibrium covering the whole economy with capital and labor effects, BU models only capture a subset of sectors or only a single sector and therefore are also termed partial equilibrium models.
- ^Note that especially energy system models often rely on different demand modules (e.g., one for transport demand, one for heating demand etc.) and combine/aggregate detailed consumer information to derive those modules. Many demand aspects are therefore part of the parameterization and not endogenous model aspects.
- ^For a review of energy-related intervention studies, see, e.g., Abrahamse et al. (2005).
- ^To ensure that this process converges, it can be useful to assume that the second (norm-induced) effect on individual behavior is always smaller than the original change in behavior.
- ^There are numerous examples of this approach in the context of social security evaluation and climate policy. For example, Nijkamp et al. (2005) use this approach to study inequality across countries under different international climate policy regimes and Yang (2010) uses different local households in a CGE model.
- ^A notable exception is policies targeting energy efficiency in residential buildings.
References
Abrahamse, W., Steg, L., Vlek, C., and Rothengatter, T. (2005). A review of intervention studies aimed at household energy conservation. J. Environ. Psychol. 25, 273–291. doi: 10.1016/j.jenvp.2005.08.002
Alcott, B. (2008). The sufficiency strategy: would rich-world frugality lower environmental impact? Ecol. Econ. 64, 770–786. doi:10.1016/j.ecolecon.2007.04.015
Allcott, H. (2011). Social norms and energy conservation. J. Public Econ. 95, 1082–1095. doi:10.1016/j.jpubeco.2011.03.003
Azar, O. (2004). What sustains social norms and how they evolve? The case of tipping. J. Econ. Behav. Organ. 54, 49–64. doi:10.1016/j.jebo.2003.06.001
Bataille, C., Jaccard, M., Nyboer, J., and Rivers, N. (2006). Towards general equilibrium in a technology-rich model with empirically estimated behavioral parameters. Energy J. 27, 93–112.
Bergman, L. (2005). CGE modeling of environmental policy and resource management. Handbook Environ. Econ. 3, 1273–1306. doi:10.1016/S1574-0099(05)03024-X
Bernard, A., and Vielle, M. (2008). GEMINI-E3, a general equilibrium model of international–national interactions between economy, energy and the environment. Comput. Manag. Sci. 5, 173–206. doi:10.1007/s10287-007-0047-y
Böhringer, C., Löschel, A., and Rutherford, T. (2009). “Policy analysis based on computable equilibrium (pace),” in Modelling Sustainable Development: Transitions to a Sustainable Future, eds V. Bosetti, R. Gerlagh, and S. P. Schleicher (Cheltenham: Edward Elgar), 1648–1661.
Böhringer, C., and Rutherford, T. F. (2008). Combining bottom-up and top-down. Energy Econ. 30, 574–596. doi:10.1016/j.eneco.2007.03.004
Böhringer, C., and Rutherford, T. F. (2009). Integrated assessment of energy policies: decomposing top-down and bottom-up. J. Econ. Dyn. Control 33, 1648–1661. doi:10.1016/j.jedc.2008.12.007
Bosetti, V., Carraro, C., Galeotti, M., Massetti, E., and Tavoni, M. (2006). WITCH: a world induced technical change hybrid model. Energy J. 27, 13–37.
Bretschger, L., and Suphaphiphat, N. (2014). Effective climate policies in a dynamic North-South model. Eur. Econ. Rev. 69, 59–77. doi:10.1016/j.euroecorev.2013.08.002
Burger, P., Bezençon, V., Bornemann, B., Brosch, T., Carabias-Hütter, V., Farsi, M., et al. (2015). Advances in understanding energy consumption behavior and the governance of its change – outline of an integrated framework. Front. Energy Res.
Camecon. (2014). Available at http://www.camecon.com/EnergyEnvironment/EnergyEnvironmentEurope/ModellingCapability/E3ME.aspx
Camerer, C., and Fehr, E. (2004). “Measuring social norms and preferences using experimental games,” in A Guide for Social Sciences in Foundations of Human Society: Economic Experimants and Ethnographic Evidence from Fifteen Small-Scale Societies, ed. J. Henrich (Oxford: Oxford University Press), 55–95.
Capros, P., and Siskos, P. (2012). PRIMES-TREMOVE Transport Model v3 Model Description. Athens: Energy-Economy-Environment Modeling Laboratory.
Capros, P., Van Regemorter, D., Paroussos, L., Karkatsoulis, P., Fragkiadakis, C., Tsani, S., et al. (2013). GEM-E3 Model Documentation (No. JRC83177). Seville: Institute for Prospective and Technological Studies, Joint Research Centre.
Catenazzi, G. (2009). Advances in Techno-Economic Energy Modeling (Doctoral Dissertation, ETH Zurich). Zurich: Swiss Federal Institute of Technology (ETH)
Chandra, A., and Tappata, M. (2011). Consumer search and dynamic price dispersion: an application to gasoline markets. Rand J. Econ. 42, 681–704. doi:10.1111/j.1756-2171.2011.00150.x
E3MLab/ICCS. (2014). PRIMES MODEL 2013-2014 Detailed Model Description. Athens: E3MLab/ICCS at National Technical University of Athens.
Egging, R., Holz, F., and Gabriel, S. A. (2010). The world gas model: a multi-period mixed complementarity model for the global natural gas market. Energy 35, 4016–4029. doi:10.1016/j.energy.2010.03.053
Enerdata. (2014). Available at: http://www.enerdata.net/enerdatauk/solutions/energy-models/poles-model.php
ETSAP. (2014). Available at: http://www.iea-etsap.org/web/Times.asp
European Commission. (2013). Trends to 2050: EU Energy, Transport and GHG Emissions Reference Scenario 2013. Luxemburg: International Energy Agency.
European Commission. (2014). Energy Efficiency and its Contribution to Energy Security and the 2030 Framework for Climate and Energy Policy. Brussels: International Energy Agency.
Filippini, M. (2011). Short- and long-run time-of-use price elasticities in Swiss residential electricity demand. Energy Policy 39, 5811–5817. doi:10.1016/j.enpol.2011.06.002
Heaps, C. G. (2012). Long-range Energy Alternatives Planning (LEAP) System. [Software version 2014.0.1.20]. Somerville, MA: Stockholm Environment Institute. Available at: www.energycommunity.org
Hecking, H., and Panke, T. (2012). COLUMBUS-A Global Gas Market Model (No. 12/06). Cologne: EWI Working Paper.
Herbst, A., Toro, F., Reitze, F., and Jochem, E. (2012). Introduction to energy systems modelling. Swiss J. Econ. Stat. 148, 111–135.
Hourcade, J. C., Jaccard, M., Bataille, C., and Ghersi, F. (2006). Hybrid modeling: new answers to old challenges introduction to the special issue of the energy journal. Energy J. 27, 1–11.
IEA. (2014b). World Energy Model Documentation 2014 Version. Paris: International Energy Agency (IEA).
Kavgic, M., Mavrogianni, A., Mumovic, D., Summerfield, A., Stevanovic, Z., and Djurovic-Petrovic, M. (2010). A review of bottom-up building stock models for energy consumption in the residential sector. Build. Environ. 45, 1683–1697. doi:10.1016/j.buildenv.2010.01.021
Kortum, S. (1997). Research, patenting and technological change. Econometrica 65, 1389–1419. doi:10.2307/2171741
Krishnamurthy, B., and Kriström, B. (2015). A cross-country analysis of residential electricity demand in 11 OECD-countries. Resource Energy Econ. 39, 68–88. doi:10.1016/j.reseneeco.2014.12.002
Krupka, E., and Weber, R. (2013). Identifying social norms using coordination games: why does dictator game sharing vary? J. Eur. Econ. Assoc. 11, 495–524. doi:10.1111/jeea.12006
Lanz, B., and Rausch, S. (2011). General equilibrium, electricity generation technologies and the cost of carbon abatement: a structural sensitivity analysis. Energy Econ. 33, 1035–1047. doi:10.1016/j.eneco.2011.06.003
Leimbach, M., Bauer, N., Baumstark, L., and Edenhofer, O. (2009). Mitigation costs in a globalized world: climate policy analysis with REMIND-R. Environ. Model. Assess. 15, 155–173.
Leuthold, F. U., Weigt, H., and von Hirschhausen, C. (2012). A large-scale spatial optimization model of the European electricity market. Network Spatial Econ. 12, 75–107. doi:10.1007/s11067-010-9148-1
Levitt, S., and List, J. (2007). What do laboratory experiments measuring social preferences reveal about the real world? J. Econ. Perspect. 21, 153–174. doi:10.1257/jep.21.2.153
Lindbeck, A., Nyberg, S., and Weibull, J. W. (1999). Social norms and economic incentives in the welfare state. Q. J. Econ. 114, 1–35. doi:10.1162/003355399555936
Makri, M., and Lane, P. J. (2007). A search theoretic model of productivity, science and innovation. RD Manag. 37, 303–317. doi:10.1111/j.1467-9310.2007.00477.x
NEP. (2014). Available at: http://www.netzentwicklungsplan.de/
Nijkamp, P., Wang, S., and Kremers, H. (2005). Modeling the impacts of international climate change policies in a CGE context: the use of the GTAP-E model. Econ. Model. 22, 955–974. doi:10.1016/j.econmod.2005.06.001
Nordhaus, W. (2012). Available at: http://www.econ.yale.edu/~nordhaus/homepage/RICEmodels.htm
Nyborg, K., Howarth, R., and Brekke, K. (2006). Green consumers and public policy: on socially contingent moral motivation. Resource Energy Econ. 28, 351–366. doi:10.1016/j.reseneeco.2006.03.001
Oikonomou, V., Becchis, F., Stegc, L., and Russolillo, D. (2009). Energy saving and energy efficiency concepts for policy making. Energy Policy 37, 4787–4796. doi:10.1016/j.enpol.2009.06.035
Paltsev, S., Reilly, J. M., Jacoby, H. D., Eckaus, R. S., McFarland, J. R., Sarofim, M. C., et al. (2005). The MIT Emissions Prediction and Policy Analysis (EPPA) Model: Version 4. Cambridge: MIT Joint Program on the Science and Policy of Global Change.
Paul, A., Burtraw, D., and Palmer, K. (2009). Haiku documentation: RFF’s electricity market model. Resources Future 52, 222.
Richter, J. (2011). Dimension-A Dispatch and Investment Model for European Electricity Markets (No. 11/03). Cologne: EWI Working Paper.
Schäefer, A., and Jacoby, H. D. (2006). Vehicle technology under CO 2 constraint: a general equilibrium analysis. Energy Policy 34, 975–985. doi:10.1016/j.enpol.2004.08.051
SFOE. (2013). Strategie Stromnetze; Detailkonzept im Rahmen der Energiestrategie 2050. Berne: Swiss Federal Office of Energy.
Shang, J., and Croson, R. (2009). A field experiment in charitable contribution: the impact of social information on the voluntary provision of public goods. Econ. J. 119, 1422–1439. doi:10.1111/j.1468-0297.2009.02267.x
Traxler, C. (2010). Social norms and conditional cooperative taxpayers. Eur. J. Polit. Econ. 26, 89–103. doi:10.1016/j.ejpoleco.2009.11.001
Vöhringer, F. (2012). Linking the Swiss emissions trading system with the EU ETS: economic effects of regulatory design alternatives. Swiss J. Econ. Stat. 148, 167–196.
Weidlich, A., and Veit, D. (2008). A critical survey of agent-based wholesale electricity market models. Energy Econ. 30, 1728–1759. doi:10.1016/j.eneco.2008.01.003
Keywords: energy modeling, bottom-up, top-down, demand side, consumer behavior
Citation: Krysiak FC and Weigt H (2015) The demand side in economic models of energy markets: the challenge of representing consumer behavior. Front. Energy Res. 3:24. doi: 10.3389/fenrg.2015.00024
Received: 15 February 2015; Accepted: 27 April 2015;
Published: 19 May 2015
Edited by:
Tobias Brosch, University of Geneva, SwitzerlandReviewed by:
Jay Zarnikau, The University of Texas, USASonia Yeh, University of California Davis, USA
Copyright: © 2015 Krysiak and Weigt. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Frank C. Krysiak, Department of Business and Economics, University of Basel, Peter Merian-Weg 6, Basel CH-4002, Switzerland, frank.krysiak@unibas.ch
 Frank C. Krysiak
Frank C. Krysiak Hannes Weigt
Hannes Weigt