Solar panels reduce both global warming and urban heat island
- 1Météo-France/CNRS, Centre National de Recherches Météorologiques/Groupe d'étude de l'atmosphère Météorologique, Toulouse, France
- 2Laboratoire de Recherche en Architecture, Toulouse, France
- 3Centre Scientifique et Technique du Bâtiment, Marne-La-Vallée, France
- 4French Center for Aerospatial Research, Toulouse, France
The production of solar energy in cities is clearly a way to diminish our dependency to fossil fuels, and is a good way to mitigate global warming by lowering the emission of greenhouse gases. However, what are the impacts of solar panels locally? To evaluate their influence on urban weather, it is necessary to parameterize their effects within the surface schemes that are coupled to atmospheric models. The present paper presents a way to implement solar panels in the Town Energy Balance scheme, taking account of the energy production (for thermal and photovoltaic panels), the impact on the building below and feedback toward the urban micro-climate through radiative and convective fluxes. A scenario of large but realistic deployment of solar panels on the Paris metropolitan area is then simulated. It is shown that solar panels, by shading the roofs, slightly increases the need for domestic heating (3%). In summer, however, the solar panels reduce the energy needed for air-conditioning (by 12%) and also the Urban Heat Island (UHI): 0.2 K by day and up to 0.3 K at night. These impacts are larger than those found in previous works, because of the use of thermal panels (that are more efficient than photovoltaic panels) and the geographical position of Paris, which is relatively far from the sea. This means that it is not influenced by sea breezes, and hence that its UHI is stronger than for a coastal city of the same size. But this also means that local adaptation strategies aiming to decrease the UHI will have more potent effects. In summary, the deployment of solar panels is good both globally, to produce renewable energy (and hence to limit the warming of the climate) and locally, to decrease the UHI, especially in summer, when it can constitute a health threat.
1. Introduction
Renewable energy is seen as a necessary step toward sustainable energy development, diminution of the use of fossil fuels and mitigation of climate change, as stated for example by Elliott (2000): “With concerns about Climate Change growing, the rapid development of renewable energy technologies looks increasingly important.” However, the recent analysis of Nugent and Sovacool (2014) showed that, when their complete life-cycle is considered, renewable energies are not CO2 sinks yet. Nevertheless their greenhouses gas emission rate per unit of energy produced is much less than for energy sources based on fossil fuels and slightly less than for nuclear power. They also “uncover best practices in wind and solar design and deployment that can better inform climate change mitigation efforts in the electricity sector.” Elliott (2000) underlines that renewable energy deployment requires a new paradigm, of decentralized energy production and small production systems. The implementation of renewable energy will need social and institutional changes, even if technology for these systems already exists (Gross et al., 2003, while still needing improvements and further research Jader-Waldau, 2007). Funding, incentive policies and statutory obligations on electricity suppliers may be needed to develop renewable energy faster. Lund (2007) demonstrates that, in Denmark, a transition toward 100% of renewable energy production is possible. Sovacool and Ratan (2012) conclude that nine factors linked to policy, social and market aspects favor or limit the development of wind turbines and solar energy, and explain why renewable energy is growing fast in Denmark and Germany compared to India and the USA.
Sims et al. (2003) show that most renewable energies can, in certain circumstances, reduce cost as well as CO2 emissions, except for solar power, which remains expensive. However, Hernandez et al. (2014) review the environmental impacts of utility-scale solar energy installations (solar farms), which are typically implemented in rural areas, and show that they have low environmental impacts relative to other energy systems, including other renewables. Furthermore, solar power is also one of the few renewable energy sources that can be implemented on a large scale within cities themselves. Arnette (2013) shows that, compared to solar farms, individual rooftop solar panels are a very cost-effective means of increasing renewable energy generation and decreasing greenhouse gas emissions. So they conclude that solar panel implementation on roofs should be part of a balanced approach to energy production. Here, we aim to evaluate the environmental impacts on the local climate, of implementing such a strategy at city scale.
The main impact of cities on the local weather is the Urban Heat Island (UHI). Cities are warmer than the surrounding countryside, and this can lead to a health crisis during heat waves, as was the case in Paris in 2003 with 15,000 premature deaths (Fouillet et al., 2006) or in Moscow with 11,000 premature deaths in 2010 (Porfiriev, 2014). It also has to be considered that, due to climate warming, the UHI impacts will become even larger than they are now (Lemonsu et al., 2013). Therefore, several strategies are being studied to reduce the UHI in summer. Gago et al. (2013) have reviewed several research works analyzing strategies to mitigate the UHI, including changes in green spaces, trees, albedo, pavement surfaces, vegetation, and building types and materials. Santamouris et al. (2011) have reviewed of several advanced cool materials systems usable to reduce the UHI. Such materials could be implemented on roofs in order to reflect more energy to the sky (high albedo, high emissivity) or to delay the heat transfer toward the inside the building (phase change materials). Masson et al. (2013) showed that changes in agricultural practices in the vicinity of Paris and the use of cool materials for roofs and pavement would decrease the UHI by 2 K and 1 K, respectively. However, the question of the ability of solar panels to contribute to the same goal is not addressed in these papers, and extremely few studies focus on, or even take into account, the effect of solar panels on the UHI.
It is thus necessary to analyze whether the two objectives of mitigating the global climate warming by increasing renewable energy production in cities, especially through solar panels, and of attenuating the UHI are compatible. Solar panels modify the nature of the rooftop and may thus influence the energy transfers to the atmosphere and the resulting UHI. The aim of this paper is then to evaluate the impact of solar panels, known to be good for global warming mitigation, on the local climate, especially the UHI.
2. Solar Panels into the Urban Canopy Model TEB
The objective of this section is to present how solar panels can be included in the Town Energy Balance (TEB, Masson, 2000) scheme, in terms of both energy production and interactions with the roofs below (shading, modification of the roof energy balance, etc.). The solar panels themselves can be either photovoltaic panels or thermal panels that heat water.
2.1. Modeling Strategy
The solar panel exchanges energy with the other components of the system. Very few parameterizations taking these exchanges into account exist in the literature. The level of detail depends strongly on the objectives of the authors. On the one hand, when looking at the building scale, it is possible to consider some implementation characteristics of the panels, as in Scherba et al. (2011), who modified the Energy+ software (software dedicated to building energetics) to improve its previous solar panel model (which only computed the energy production). Their solar panel model considers the tilting of the panels and associated sky-view factors. They then perform an analysis of the impact of several types of roofs on sensible heat fluxes toward the atmosphere, but are unable to link these fluxes to the UHI, which needs to take all the buildings of the entire city into account. On the other hand, Taha (2013) studies the impact of solar panels on the whole urban area of Los Angeles. To do this, he uses the very simplified approach of effective albedo, which accounts for both the albedo and the solar conversion efficiency (linked to the energy produced). This approach estimates the impact on the UHI, but does not take account of the interactions with the urban canopy below (solar panel shadowing may lead to less cooling energy being used in buildings for example, leading to less waste heat outside).
In order to study the impact of solar panels implementations on the urban atmosphere and on the population and buildings, we need an approach that looks at both spatial scales: buildings and city. The TEB scheme is able to simulate the energy, water and momentum exchanges between cities and the atmosphere at a resolution as high as the urban block (say down to 100 m by 100 m). The energetics of buildings have also been included in TEB by Bueno et al. (2012) and Pigeon et al. (2014), to simulate the energy behavior of a typical building representative of the block. The focus is to keep the maximum of key processes, while making some approximations in the geometry that are pertinent at block scale (building shapes are averaged into road canyons, only one thermal zone is kept in the buildings, individual windows are averaged into a glazing fraction, etc.). Gardens and greenroofs modules have also been implemented (Lemonsu et al., 2012; DeMunck et al., 2013a). The modeling strategy chosen here for the implementation of solar panels is similar: key processes are kept while some geometrical assumptions are made to avoid unnecessary details of individual buildings.
In TEB, it is necessary to take account not only of the production of energy by the panels but also the influence of the panels on the underlying roofs. We must therefore calculate the complete energy balance of the panel to determine what is exchanged with the roof or the atmosphere. The TEB model will then be able to estimate the impact of solar panel implementation on the UHI at city scale, as well as the production of energy.
2.2. Energy Balance of the Solar Panel
Geometrically, the solar panels are assumed to be horizontal when calculating the radiative heat exchange with the other elements: exchanges between the roof, the solar panels and the sky above are considered to be purely vertical (Figure 1). Note that we take the inclination of the panel into account to calculate the irradiance for power production.
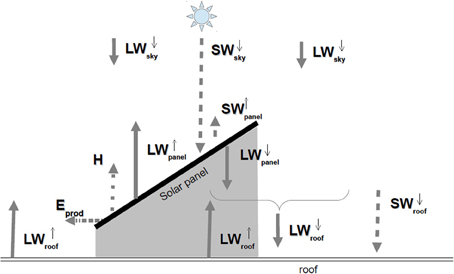
Figure 1. Schematic diagram of the energy balance of the solar panel and its impact on radiation received by the roof (dashed arrows: solar fluxes; plain arrows: long-waves fluxes; dotted arrow: sensible heat flux; dotted-dashed arrow: energy produced).
The energy balance equation of the solar panel is written:
The terms on the left hand side are incoming energy to the solar panel:
SW↓sky is the incoming Short-Wave radiation from the sun. It can be diffuse or direct, and is considered as forcing data for TEB.
LW↓sky is the incoming Long-Wave radiation from the atmosphere. It is diffuse and is also used as forcing data for TEB.
LW↑roof is the Long-Wave radiation coming up from the roof and being intercepted by the solar panel. It is computed by TEB from the roof emissivity and surface temperature and the long-wave radiation received by the roof:
The terms on the right hand side of Equation (1) are outgoing energy from the panel:
SW↑panel is the solar radiation reflected by the solar panel. It is classically parameterized using the albedo of the solar panel (αpanel): SW↑panel = αpanelSW↓panel. It is also assumed to go back to the sky (we neglect the effect of the inclination of the solar panel on the direction of the reflected light). According to Taha (2013), the value of the albedo of the solar panel ranges from 0.06 to 0.1. We performed measurements of the albedo for a sample of solar panel (under several inclinations) by integrating the hemispheric directional reflectance measured with a goniometer (see section 2.4 for details). From our measurements, the value of 0.11 is used for αpanel in the present paper.
LW↑panel is the long-wave radiation emitted (and reflected) by the solar panel to the sky. It depends on the surface temperature of the solar panel, which is estimated following the ISPRA center method:
where Tair is the air temperature, Irr is the irradiance received by the solar panel (cf section 2.5) and kT is a constant coefficient equal to 0.05 K/(Wm−2). In this formulation, the nocturnal dependency of the panel surface temperature on the sky temperature proposed by Scherba et al. (2011) is not used. It would be an improvement to be considered in the future. Also using the emissivity of the solar panel ϵpanel, equal to 0.93 in our measurements (cf section 2.4), the upward long-wave radiation from the solar panel can be written:
LW↓panel is the long-wave radiation emitted by the solar panel to the roof (downwards). It is computed under the hypothesis that the temperature of the downward face of the solar panel is always approximately equal to the air temperature. This is probably a limitation of our model during daytime. However, even if the temperature of the downwards face of the solar panel is underestimated (due to the warming of the solar panel and the heat diffusion inside it), this temperature will still be higher than the sky temperature. So, from the point of view of the roof below the solar panel, the incoming radiation will be higher. This captures at least the first order of an effect of the solar panel on the roof. Given the uncertainties, we also neglect the dependency in emissivity for this face of the panel. This gives:
Eprod is the energy produced by the panel. It depends of the nature (thermal or photovoltaic) and characteristics of the panel, the irradiance on the panel, the inclination of the panel (not taken into account in the other terms), and the air temperature. Details are given in sections 2.5, 2.6 for PV and thermal panels, respectively.
H is the sensible heat flux from the solar panel to the atmosphere. We assume that the solar panel is thin, has no significant thermal mass and hence is in quasi-equilibrium. This means that the sensible heat flux, the only term that is not parameterized, is taken to be equal to the residue of the solar panel energy budget. Besides the fact that it is difficult to have a parameterization of this term, this ensures conservation of energy balance.
2.3. Modification of the Energy Balance of the Roof
For the energy balance of the roof, the most important key parameter will, of course, be the proportion of roof area occupied by the solar panels. As mentioned above, we only consider the projection of the panels onto the horizontal surface (it would be absurd to make accurate calculations taking the inclination of the panels into account—except as noted above for production—when it is already assumed in TEB that all roofs are flat). The fraction of the roof covered by solar panels is noted fpanel.
The following simplifying assumptions are made:
• An average temperature is still calculated for the roof, without distinguishing between the parts of the roof under or beside the panel. This is reasonable, in particular for flat roofs with inclined panels, because the shadows cast by the panels can modify the radiative contribution to the roof beside as well as below the panels.
• The coefficient for heat transfer from the roof to the sensible heat flux is not changed (it is already in a heterogeneous environment with a roughness length of 5 cm).
• The effect of humidity on panels is neglected: the water interception reservoir treating rainwater and evaporation concerns the whole surface of the roof.
• The effect of solar panels on snow is neglected. The snow mantel, if any, accumulates uniformly on the roof. Note that snow might change the energy produced by the solar panel (but this is not taken into account yet).
These assumptions allow us to change only the radiative contributions to the energy balance of the roof. Assuming that the surface area of the shadows is equal to the surface area of the solar panels, the incoming solar radiation on the roof is:
The long-wave incoming radiation on the roof is modified by the long-wave radiation emitted downwards by the solar panels:
This way of implementing the interactions between solar panels and the roof below allows the considerations of the way the roof is built to be separated from the question of whether there are solar panels on it or not. For example, although it is not the case in this paper, it is possible to have greenroofs with or without solar panels. If there are solar panels, the vegetation of the greenroof will simply be more in the shade and receive slightly more infrared radiation.
2.4. Radiative Characteristics of Solar Panels
To establish the energy balance of the equivalent urban canyon, the TEB model needs the albedo (integrated between 0.4 and 2.5 μm) and the emissivity in the thermal infrared (integrated between 5 and 12 μm) for the following main areas: road, roofs, facades, glazing. The French Center for Aerospace Research (ONERA) laboratory maintains a current database of optical properties of urban materials. Specific measurements were made for emerging materials: rough white paints, photovoltaic solar panels, metal cladding, and glass (including low emissivity). The measurements for large samples of materials, e.g., for solar panels, were made using a goniometer (Figure 2, left).

Figure 2. Left: Goniometer used for albedo measurements. Right: Instrument used for emissivity measurements.
The measurement process is fully automated in the 0.4–2.5 μm spectral domain. The position measurements acquired by the detector are regular in azimuth (0–180° range) and zenith (0–60° range) with an angular accuracy of 1°, except for the region of specular reflection, which is meshed more precisely.
The reflectance is measured with reference to a reflectance reference (Spectralon). Thereafter, the reflectance of the solar panel placed in the center of the goniometer is acquired for all recorded positions of the detector and the light source. The reference measurement is repeated at the end of the process.
The albedo of the solar panels is then computed by integrating the radiance in all directions over the entire spectral range. It typically varies from 11 to 16% depending on the position of the sun and the sensor inclination. When the panel is favorably oriented relative to the sun (and hence when the incoming radiation per square meter of panel is the largest), as is usually implemented, the albedo is in the low range, and equal to about 11%.
The emissivity was measured using a SOC 400T apparatus (Figure 2, right). It measures the directional hemispheric reflectance for wavelengths between 2.5 and 20 μm. The resulting emissivity was 0.93 for solar panels.
2.5. Energy Produced by Photovoltaic Panels
In TEB, two different types of solar panels: thermal and photovoltaic (PV) are considered. The aim of thermal solar panels is to warm the water necessary for the occupants of the building. They are much more efficient (in terms of energy produced) than photovolatic panels, but only produce heat, not electricity.
For PV panels, the energy produced is usually parameterized as:
where EffPV is the conversion efficiency of the PV panel and R(Tpanel) a coefficient to reproduce the fact that solar panels are most efficient at 25°C and present a decrease in efficiency for warmer panel temperatures. The efficiency coefficient varies from 5% to 19% (Taha, 2013), with values as high as 30% possible in the far future (Nemet, 2009). In France, most PV panels use the usual crystalline silicon (xSi) technology (Leloux et al., 2012), for which the efficiency is approximately EffPV = 14%. To relate the irradiance received by the panel (possibly tilted) to the incident radiation on a horizontal surface (SW↓sky), it is possible either to perform geometric calculations on the relative position of the sun and panels or to apply a priori correction factors. This second, simpler approach is chosen here, and the coefficient of the French thermal Regulations of 2005 is used:
The correction factor FT is typically 1.11 on annual average for a South facing panel in Paris. Assuming that solar panels are placed fairly optimally, i.e., with an approximately 30° tilt and oriented between South-East and South-West (as is usually the case in France, Leloux et al., 2012), we can estimate that the coefficient FT is equal to FT = 1.10 in France. The temperature dependent coefficient can be written as:
Finally, the production of the PV panels is parameterized, also using the relationship between panel temperature and irradiance, as:
2.6. Energy Produced by Thermal Solar Panels
The amount of energy produced by solar thermal panels is usually defined on an annual basis (Philibert, 2006). This can partly be justified by the fact that the limitation of energy production is not linked solely to the available sunlight but also to the objective in terms of quantity of water heated (there is no point in heating water beyond the set-point, typically 60°C for hot water, nor for more people than those actually occupying the building, 32l per person). From French regulations, for one person, the annual production with thermal solar panels is:
where ΔT is the temperature difference between cold and hot water (typically 45 K in France). The factor comes from an adjustment to account for the fact that only a part of the need for warm water can be covered by solar energy. This factor can vary depending on location, climate (frequency of presence of clouds), seasonality (less sun radiation in winter) and technical features of the installation (ADEME, 2002). A typical value of is taken here. Furthermore, it is considered that this per capita energy requirement can be satisfied by 1 m2 of thermal panel. So, the power averaged over the year would be:
Here, in order to better take the variability in production due to solar irradiation into account, instead of an annual mean computation, instantaneous production is considered in connection with the daily need for warm water. This mimics the fact that the water is heated during the day and stored until it is used during the next 24 h. So, using the regulation information above, the target energy production for 1 day can be defined as:
The factor has disappeared here because we consider ideal heating (i.e., sunny) conditions for the definition of the target. The production of the thermal panel is then computed in three steps:
1. The instantaneous production is defined as Ether prod = Effther × Irr (W/m2 of solar panel) where Effther is the efficiency coefficient of the thermal panel and Irr the irradiance received by the panel. The efficiency of new thermal solar panels typically ranges between 0.70 and 0.80. However, in real conditions of use, especially in cities, dirt and dust on the panel reduce its energy production. Elminir et al. (2006) found a decrease of between 6% and 20% in the output power due to dust (17.4% for a 45° tilt angle of the solar panel). A similar effect of dirt had already been found by Garg (1974), with attenuation of 10–20% for tilt angles between 45° and 30°. Therefore, in the present study Effther was set to 0.60.
2. The total amount of energy produced is summed from midnight the previous night to the current time t: ∫tmidnight Ether prod dt (J/m2 of panel).
3. If the quantity of energy produced since midnight reaches the target Ether target, then any additional production during the same day is wasted and further energy production is set to zero.
To summarize, for solar thermal panels, the production is parameterized as:
2.7. Hypotheses on Types of Solar Panels
As the model is able to consider both thermal and PV solar panels, it is now necessary to define some hypotheses on the use of each type of panel. This is, of course, a scenario-dependent element, in the sense that it can be modified for each study. For example, Taha (2013) only studied the implementation of PV panels in the Los Angeles metropolitan area. The interest of also considering the deployment of thermal solar panels in this paper is that this energy production technology is less greenhouse gas emissive per unit of energy produced (considering its whole life-cycle) than PV (Nugent and Sovacool, 2014). Here, it will thus be supposed that both types of panels are possible. The main hypotheses are:
• On residential buildings and houses, the priority is given to thermal solar panels, which are more efficient. The thermal production is of course limited by the area of panels on the roof but it is also limited by the population in the building: it is not necessary to heat more water than required by the number of people who are going to use it. Therefore, once the necessary area of thermal solar panels is reached, the remaining space allocated for solar panels on the roof will be devoted to PV panels.
• On other types of buildings (offices, commercial, industrial, etc…) only PV panels will be installed.
The total fraction of the building's roof where solar panels (any type) can be installed is noted fpanel (this quantity is also scenario dependent). It is then necessary to define what proportion of the roof area is required for thermal panels, and how much area remains available for PV panels. In France, in residential buildings, the density is typically 1 occupant per 30 m2 of floor area1. Furthermore, as mentioned above, 1 m2 of thermal panel is needed per capita. This means 1 m2 of panel per 30 m2 of floor area. For single story accommodation, 1/30 of the roof is then equipped with thermal panels, and (fpanel − 1/30) by PV panels. If the building has two stories, thermal panels will occupy 2/30 of the roof area, and so on.
So if Nfloor is the number of floors of the building (variable calculated in TEB), the proportions of thermal panels (fther panel) and PV panels (fphot panel) are calculated as:
The total production of the solar panels on the roofs can then be written:
This is this quantity that is involved in the energy balance of the panel (section 2.2).
3. Impact of Solar Panels on Paris Urban Heat Island
3.1. Simulation Configuration and Scenarios
We are now able to simulate the impact of the implantation of solar panels in a city on the UHI. The simulations are performed on the Paris metropolitan area, with TEB, coupled with the vegetation scheme ISBA (Noilhan and Planton, 1989) for rural areas, within the SURFEX modeling software (Masson et al., 2013b). The simulation domain is 100 km by 100 km, with a resolution of 1 km. At such a resolution, only the main characteristics of the buildings within the blocks in the grid mesh are kept. Geometric parameters are averaged in order to conserve the surface areas (for walls, roofs, gardens, roads, water, rural areas), while a majority rule applies for the architectural characteristics of buildings (age, materials, equipment) and the use to which they are put (residential, offices, commercial or industrial). These urban data are provided by a database at 250 m resolution (Figure 3 of Masson et al., 2014), which contains block types as well as 60 urban indicators. Some parameters needed by TEB, such as albedos, thermal characteristics or equipment within buildings, are deduced for each 1-km-by-1-km grid mesh from urban block types and from the use and age of the majority of buildings. Countryside parameters, such as land use and vegetation characteristics are deduced from the ecoclimap database at 1 km resolution (Masson et al., 2003). The methodology presented in Masson et al. (2014), based on a simplified Urban Boundary Layer generator (Bueno et al., 2013; Le Bras, 2014) is chosen, in order to be able to perform a simulation over an entire year. The chosen year of study is 2003, because it demonstrates the impact the solar panels would have during a heat wave.
Some hypotheses have to be made on the proportions of roofs equipped with solar panels. Hypotheses similar to those presented as “reasonably high deployment” in Taha (2013) are taken. On sloping roofs, typically on domestic houses but also old Hausmannian buildings in the historical core of Paris, of the part of the roof oriented between South-East and South-West (after Leloux et al., 2012) is assumed to be covered by solar panels (thermal or PV, or a mix of the two). This corresponds to approximately 19% of the roof being covered. On flat roofs, however, more space is available, and solar panels are taken to be installed on 50% of each roof.
Current albedos of roofing prior to the implementation of solar panels are estimated for each type of building from an architectural analysis. Historical Hausmannian buildings in the very center of Paris are roofed with zinc on top of wood, so their albedo is very high, set to 0.6. In this regard, the solar panels, even maybe thermal ones, would decrease the albedo of the city there, and might tend to increase the UHI. However, only a small proportion of this type of buildings is eligible for solar panels (19% of roofs in our hypothesis), and the spatial coverage of this type of old city blocks is limited (see Figure 3 of Masson et al., 2014). Except for the most recent industrial buildings (built after 1975), for which roof albedo is 0.5 and which, again do not cover a significant part of the metropolitan area, roof albedo for most buildings is estimated as 0.2 (e.g., tiles for houses and old industrial buildings or gray concrete roofs for collective buildings). Therefore, the impact of solar panels on historical or industrial buildings is probably counterbalanced by the other parts of the urban area, where solar panels will probably reduce the amount of solar radiation absorbed by the buildings (due to the reflection and conversion into energy by the solar panels).
Two simulations are run: one is the reference simulation corresponding to Paris in its actual state (without many solar panels) and the second is the one with the reasonably high deployment of solar panels. A comparison of the two simulations will assess the effect of the solar panels on the urban area.
3.2. Results for Energy Production and Consumption
The impacts of solar panels are discussed in terms of energy production, of course, but also impact on energy consumption and, in the next section, on the UHI and thermal comfort. At the city scale, the production by thermal solar panels is larger than by PV. This comes both from the fact that their deployment is favored for domestic buildings and from their much higher efficiency (the former being linked to the latter). It should nevertheless be noted that, from April to August, production by thermal solar panels saturates (enough hot water is produced), so their real efficiency decreases. Over the entire year, on average for the whole city, the thermal solar panels would produce approximately 265 MJ/year/m2 of building and the PV panels 113 MJ/year/m2 of building. This would cover an equivalent of 28% of the energy consumption for domestic heating and air-conditioning.
The solar panels also slightly modify the energy consumption of the buildings. During winter, the solar panels could induce a decrease of the energy consumption due to more infra-red energy reaching the roof, or increase it by reducing the amount of solar radiation received or by their effect on the UHI. Overall, the domestic heating demand increases by 3% per year in our scenario. During summer the need for air-conditioning will probably decrease, thanks to the shading of the roofs and the cooling induced in the urban climate (see below). The comparison between the two simulations indicates that the air-conditioning energy demand decreases by 12%. Because the energy consumption for air-conditioning is low compared to that for domestic heating, the balance between the loss in energy in winter and the gain in summer induces an increase of total energy consumption by buildings of 1%. However, in the future, when climate warming induces milder winters and hotter summers, insulation will (hopefully) be better and air-conditioning equipment, currently not widely installed in France, will (probably) take on greater importance so this balance may change. Then, massive installation of solar panels may even be beneficial for energy consumption.
3.3. Results on Urban Heat Island
The deployment of solar panels in the Paris metropolitan area would not be neutral in terms of urban climate. Figure 3 presents the difference in the daily minimum and maximum air temperature between the two simulations (for two contrasting months: January and August). In wintertime, when the sun is low, the impact of the solar panels on the air temperature is relatively small. Their implementation reduces the maximum air temperature by approximately 0.05 K in the city center and the UHI by more than 0.1 K in Paris and its dense suburbs, and by 0.05 K on the whole metropolitan area. However, we have seen that this is large enough to have a noticeable (if limited) influence on energy consumption for domestic heating.
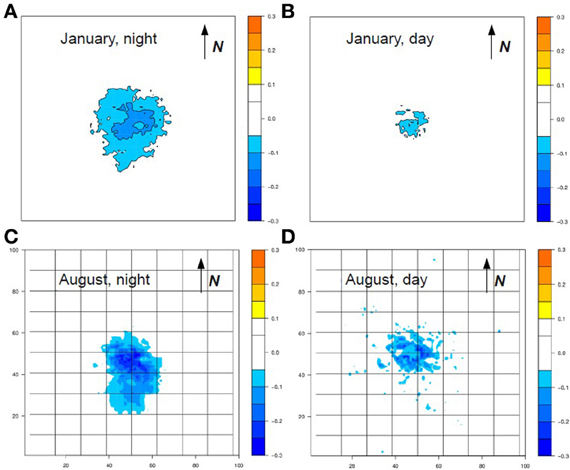
Figure 3. Difference of minimum or maximum air temperature between simulations with and without solar panels. Each panel (A–D) is a monthly average. Horizontal and vertical axes are in km.
During the month of August, in the first half of which the famous 2003 heat wave occurred, the impacts of solar panels on air temperature would be larger. In daytime, the presence of solar panels would decrease the air temperature by more than 0.2 K, especially in the dense suburbs, where the density of solar panels is the highest, due to both the high density of building and the fact that unlike the Haussmanian buildings of the city center, the suburban apartment and commercial buildings are flat roofed. This cooling value is consistent with, even though larger than, the value of 0.05 K found for the July 2005 heat wave episode in the Los Angeles area reported by Taha (2013) for present PV panels. When the efficiency of PV panels is improved (up to 30%), Taha (2013) predicts that the cooling will reach 0.15 K. There are two possible explanations for the fact that more intense cooling is simulated for Paris. First, the presence of the sea breeze in Los Angeles could limit local cooling due to solar panels in the city while extending the area of cooling by advection of the (slightly) cooler air. This can explain why a large portion of the metropolitan area of Los Angeles is impacted by the solar panels in these simulations. Second, only PV panels were simulated by Taha (2013). The efficiency of these panels was assumed to be relatively high (20%), larger than the value used in the present study, but much smaller than the efficiency of thermal solar panels (60%). As we investigate a scenario with deployment of both types of solar panels here, the absorption of energy is larger than for PV alone.
At night, the impact of the solar panels is quite strong, even larger than during daytime, with cooling reaching 0.3 K. To the authors' knowledge, this effect is not investigated in the literature. This increased cooling at night is due to a combination of several urban micro-climate processes. First, the heat storage within the buildings is reduced in presence of solar panels, especially thermal ones, because they intercept the solar radiation. The implementation of solar panels as a separate element of the urban surface energy balance system, as done here, allows a fine description of their impact on the underlying building energetics. Second, at night, the urban boundary layer is much thinner than during the day (typically 200 m high instead of 1500 m high in summer). So any modification of the surface energy balance will have up to 10 times more influence on the air temperature at night. Such a counter-intuitive phenomenon was found by DeMunck et al. (2013b) for air-conditioning, which was shown to have more impact at night than in the day (although the heat release itself was, of course, larger in daytime). Here too, while the solar panels primarily modify the daytime processes (by absorption and transformation of the solar radiation into thermal or electrical energy), the influence on air temperature is larger at night, due to the urban fabric and the boundary layer structure.
This cooling effect, though relatively small, can improve the thermal comfort of the inhabitants. For example, it reduces the number of people exposed to any given intensity (e.g., 2 K) of the UHI by 4% (±0.5%) of the total population of the metropolitan area. The thermal comfort can also be evaluated by considering more environmental parameters, such as the wind, radiation and humidity, that all have an influence on human physiology. The Universal Thermal Climate Index, UTCI (www.utci.org/), is such an indicator. Figure 4 shows the proportion of the population of the urban area that is under moderate heat stress when outside (in shade). It displays the number of hours per day that a person spends in this or any stronger level of stress. Solar panels, probably by their effect of temperature, decrease the level on thermal stress of the population. For example, while 17% of the total population is affected by heat stress for more than half a day (12 h) in the present city, the implementation of solar panels would reduce this number to 13%. While this difference seems small, it still represents a large number of people. On average, approximately 15 min of comfort is gained for outdoor conditions. This slight improvement in exposure to heat stress, although unplanned (solar panels are primarily implemented for energy production), can add to larger ones, specifically aimed at urban climate cooling, such as greening of the city.
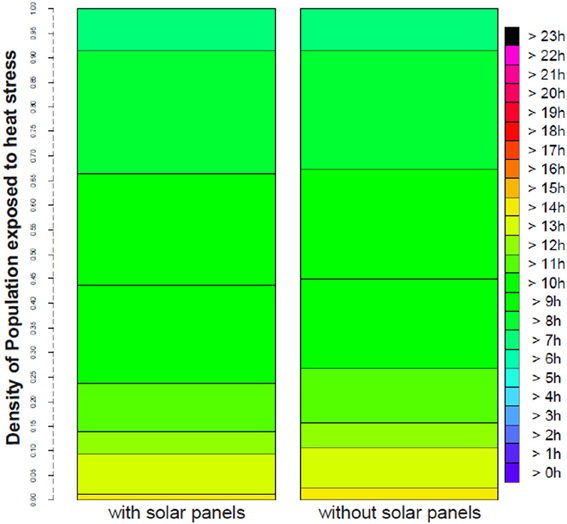
Figure 4. Population exposed to moderate heat stress in August 2003 (monthly average). Left: with solar panels. Right: without solar panels. The figure reads this way: 100% of the population is affected by at least 7 h of heat stress per day, but only a few percents (in yellow) by more than 14 h of heat stress per day.
4. Discussion
Solar panels absorb solar energy to produce energy usable in buildings, either directly in the form of heat (typically to warm water) or as electricity. However, in doing so, they modify the energy balance of the urban surface in contact with the atmosphere, and so possibly influence the urban micro-climate. They also change the radiation received by the roof, and hence the building energy balance. The present paper presents a way to include solar panels in the TEB scheme. This parameterization simulates their production in a relatively precise way, as it depends on the evolving meteorological conditions, rather than simply using a rule of thumb annual production as is often done in building design. The panels also influence the building energetics and the heat fluxes (radiative and convective) to the atmosphere. Thus, it is possible to evaluate the influence of solar panels implementation strategies on the UHI.
A scenario of large but realistic deployment of solar panels in the Paris metropolitan area has been simulated. A comparison with the reference, present-day city without (many) solar panels, enables the impact of this scenario to be estimated. Unlike work previously reported in the literature, the present study implemented both thermal and PV solar panels in the model. This allowed realistic scenarios to be simulated, where thermal panels are introduced first. It is shown that solar panels, by shading of the roof, slightly increase the need for domestic heating (3%). With future improvements in insulation, this impact will probably be less significant. In summer, however, the solar panels reduce the energy needed for air-conditioning (by 12%), thanks to the shading of the roof. They also lead to a reduction of the UHI.
During summer, when sunlight is strong, the deployment of solar panels can reduce the temperature by 0.2 K. At night, a simplistic analysis would suggest that the solar panels have no effect (as there is no sunlight). However, the physical simulation performed here shows that the presence of solar panels leads to a mitigation of up to 0.3 K of the UHI at night (so more than during the day). This counter-intuitive result is due to the interaction between the urban surface energy balance (the evolution of which has been modified by solar panels) and the night-time structure of the atmospheric layer above the city. These impacts are larger than those found in previous works, because of the use of thermal panels (that are more efficient than PV panels) and due to the geographical position of Paris, which is relatively far from the sea. This means that it is not influenced by sea breezes, and hence that its UHI is stronger than for a coastal city of the same size. But it also means that local adaptation strategies aiming at decreasing the UHI will have more potent effects.
In addition to these theoretical results, some practical issues have to be taken into consideration in order to better inform decision makers. Installing PV panels or thermal solar collectors on roofs of existing buildings will change the visual appearance of the urban areas concerned. This change may be a difficult issue in towns like Paris, where the tourist industry is important, and installation will probably not be accepted on all potential surfaces. Moreover, the outdoor urban environment is highly polluted and dirt deposits on panel and collector surfaces will inevitably decrease the effectiveness of solar equipment. Regular cleaning could be a way to limit this impact but the consequences of this maintenance activity need to be evaluated (e.g., access paths, security equipment, manpower). Fire risk may also be an issue for PV panels: a series of cases were recorded for newly equipped buildings in Europe in 2013. The products implicated were withdrawn from the market but this situation calls for a rigorous selection of products and contractors as well as for a maintenance plan of the installations. The above mentioned issues require further investigation in the perspective of an economic evaluation taking both positive and negative externalities into account.
To sum up, the deployment of solar panels is good both for producing energy (and hence contributing to a decrease of greenhouse gas emissions) and for decreasing the UHI, especially in summer, when it can be a threat to health. In future climate conditions, solar panels would also help to decrease the demand of air-conditioning. Future work will focus on studying urban adaptation strategies in the long term (as far as the end of the twenty-first century) taking a large panel of possible planning options into consideration, such as city greening, improved insulation, changes in occupants' behavior, different forms of urban expansion and the deployment of renewable energy systems.
Funding
This work has received support from the French National Research Agency for the MUSCADE project (reference ANR-09-VILL-0003) and from the thematic advanced research network on Aeronautics and Space for the ACCLIMAT project (RTRA STAE—ACCLIMAT).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors thank Colette Marchadier for her work in the MUSCADE and ACCLIMAT projects' management.
Footnotes
References
ADEME. (2002). “Eau chaude solaire - manuel pour la conception, le dimensionnement et la réalisation des installations collectives,” in Technical Report, Agence de l'Environnement et de la Maîtrise de l'Energie in French, 110.
Arnette, A. N. (2013). Integrating rooftop solar into a multi-source energy planning optimization model. Appl. Energ. 111, 456–467. doi: 10.1016/j.apenergy.2013.05.003
Bueno, B., Hidalgo, J., Pigeon, G., Norford, L., and Masson, V. (2013). Calculation of air temperatures above the urban canopy layer from measurements at a rural operational weather station. J. Appl. Meteorol. Climatol. 52, 472–483. doi: 10.1175/JAMC-D-12-083.1
Bueno, B., Pigeon, G., Norford, L. K., Zibouche, K., and Marchadier, C. (2012). Development and evaluation of a building energy model integrated in the TEB scheme. Geosci. Model Dev. 5, 433–448. doi: 10.5194/gmd-5-433-2012
DeMunck, C. S., Lemonsu, A., Bouzouidja, R., Masson, V., and Claverie, R. (2013a). The greenroof module (v7.3) for modelling green roof hydrological and energetic performances within TEB. Geosci. Model Dev. 6, 1941–1960. doi: 10.5194/gmd-6-1941-2013
DeMunck, C. S., Pigeon, G., Masson, V., Meunier, F., Bousquet, P., Tréméac, B., et al. (2013b). How much air conditioning can increase air temperatures for a city like Paris (France)? Int. J. Climatol. 33, 210–227. doi: 10.1002/joc.3415
Elliott, D. (2000). Renewable energy and sustainable futures. Futures 32, 261–2747. doi: 10.1016/S0016-3287(99)00096-8
Elminir, H. K., Ghitas, A. E., Hamid, R. H., El-Hussainy, F., Beheary, M. M., and Abdel-Moneim, K. M. (2006). Effect of dust on the transparent cover of solar collectors. Energ. Conver. Manag. 47, 3192–3203. doi: 10.1016/j.enconman.2006.02.014
Fouillet, A., Rey, G., Laurent, F., Pavillon, G., Bellec, S., Guillenneuc-Jouyaux, C., et al. (2006). Excess mortality related to the August 2003 heat wave in France. Int. Arch. Occup. Environ. Health 80, 16–24. doi: 10.1007/s00420-006-0089-4
Gago, E. J., Roldan, J., Pacheco-Torres, R., and Ordonez, J. (2013). The city and urban heat islands: a review of strategies to mitigate adverse effects. Renew. Sust. Energ. Rev. 25, 749–758. doi: 10.1016/j.rser.2013.05.057
Garg, H. P. (1974). Effect of dirt on transparent covers in flat-plate solar energy collectors. Solar Energ. 15, 299–302. doi: 10.1016/0038-092X(74)90019-X
Gross, R., Leach, M., and Bauen, A. (2003). Progress in renewable energy. Environ. Int. 29, 105–122. doi: 10.1016/S0160-4120(02)00130-7
Hernandez, R. R., Easter, S. B., Murphy-Mariscal, M. L., Maestre, F. T., Tavassoli, M., Allen, E. B., et al. (2014). Environmental impacts of utility-scale solar energy. Renew. Sust. Energ. Rev. 29, 766–779. doi: 10.1016/j.rser.2013.08.041
Jader-Waldau, A. (2007). Photovoltaics and renewable energies in Europe. Renew. Sust. Energ. Rev. 11, 1414–1437. doi: 10.1016/j.rser.2005.11.001
Le Bras, J. (2014). “Fast urban heat island model for thermal comfort studies,” in 11th Symposium on the Urban Environment (Atlanta, CA: American Meteorological Society).
Leloux, J., Narvarte, L., and Trebosc, D. (2012). Review of the performance of residential PV systems in France. Renew. Sust. Energy. Rev. 16, 1369–1376. doi: 10.1016/j.rser.2011.07.145
Lemonsu, A., Kounkou-Arnaud, R., Desplat, J., Salagnac, J.-L., and Masson, V. (2013). Evolution of the Parisian urban climate under a global changing climate. Clim. Change 116, 679–692. doi: 10.1007/s10584-012-0521-6
Lemonsu, A., Masson, V., Shashua-Bar, L., Erell, E., and Pearlmutter, D. (2012). Inclusion of vegetation in the town energy balance model for modeling urban green areas. Geosci. Model Dev. 5, 1377–1393. doi: 10.5194/gmdd-5-1295-2012
Lund, H. (2007). Renewable energy strategies for sustainable development. Energy 32, 912–919. doi: 10.1016/j.energy.2006.10.017
Masson, V. (2000). A physically-based scheme for the urban energy budget in atmospheric models. Bound. Layer Meteorol. 94, 357–397. doi: 10.1023/A:1002463829265
Masson, V., Champeaux, J.-L., Chauvin, F., Meriguet, C., and Lacaze, R. (2003). A global database of land surface parameters at 1-km resolution in meteorological and climate models. J. Clim. 16, 1261–1282. doi: 10.1175/1520-0442-16.9.1261
Masson, V., LeMoigne, P., Martin, E., Faroux, S., Alias, A., Alkama, R., et al. (2013b). The SURFEXv7.2 land and ocean surface platform for coupled or offline simulation of earth surface variables and fluxes. Geosci. Model Dev. 6, 929–960. doi: 10.5194/gmd-6-929-2013
Masson, V., Lion, Y., Peter, A., Pigeon, G., Buyck, J., and Brun, E. (2013). Grand Paris: regional landscape change to adapt city to climate warming. Clim. Change 117, 769–782. doi: 10.1007/s10584-012-0579-1
Masson, V., Marchadier, C., Adolphe, L., Aguejdad, R., Avner, P., Bonhomme, M., et al. (2014). Adapting cities to climate change: a systemic modelling approach. Urban Climate. doi: 10.1016/j.uclim.2014.03.004
Nemet, G. F. (2009). Net radiative forcing from widespread deployment of photovoltaics. Environ. Sci. Technol. 43, 2173–2178. doi: 10.1021/es801747c
Noilhan, J., and Planton, S. (1989). A simple parameterization of land surface processes for meteorological models. Mon. Wea. Rev. 117, 536–549. doi: 10.1175/1520-0493(1989)117<0536:ASPOLS>2.0.CO;2
Nugent, D., and Sovacool, B. K. (2014). Assessing the lifecycle greenhouse gas emissions from solar PV and wind energy: a critical meta- survey. Energ. Pol. 65, 229–244. doi: 10.1016/j.enpol.2013.10.048
Philibert, C. (2006). “Barriers to technology diffusion: the case of solar thermal technologies,” in Technical report, International Energy Agency, Organisation for Economic Cooperation and Development. Available online at: http://www.iea.org/publications/freepublications/publication/Solar_Thermal.pdf
Pigeon, G., Zibouche, K., Bueno, B., Le Bras, J., and Masson, V. (2014). Evaluation of building energy simulations with the TEB model against energyplus for a set of representative buildings in Paris. Build. Environ. 76, 1–14. doi: 10.1016/j.enbuild.2013.10.038
Porfiriev, B. (2014). Evaluation of human losses from disasters: the case of the 2010 heat waves and forest fires in Russia. Int. J. Disast. Risk Reduct. 7, 91–99. doi: 10.1016/j.ijdrr.2013.12.007
Santamouris, M., Synnefa, A., and Karlessi, T. (2011). Using advanced cool materials in the urban built environment to mitigate heat islands and improve thermal comfort conditions. Solar Energ. 85, 3085–3102. doi: 10.1016/j.solener.2010.12.023
Scherba, A., Sailor, D. J., Rosenstiel, T. N., and Wamser, C. C. (2011). Modeling impacts of roof reflectivity, integrated photovoltaic panels and green roof systems on sensible heat flux into the urban environment. Build. Environ. 46, 2542–2551. doi: 10.1016/j.buildenv.2011.06.012
Sims, R. E. H., Rogner, H.-H., and Gregory, K. (2003). Carbon emission and mitigation cost comparisons between fossil fuel, nuclear and renewable energy resources for electricity generation. Energ. Pol. 31, 1315–1326. doi: 10.1016/S0301-4215(02)00192-1
Sovacool, B. K., and Ratan, P. L. (2012). Conceptualizing the acceptance of wind and solar electricity. Renew. Sust. Energ. Rev. 16, 5268–5279. doi: 10.1016/j.rser.2012.04.048
Keywords: urban heat island, solar energy, solar panels, cities, adaptation to climate change
Citation: Masson V, Bonhomme M, Salagnac J-L, Briottet X and Lemonsu A (2014) Solar panels reduce both global warming and urban heat island. Front. Environ. Sci. 2:14. doi: 10.3389/fenvs.2014.00014
Received: 04 March 2014; Paper pending published: 31 March 2014;
Accepted: 29 April 2014; Published online: 04 June 2014.
Edited by:
Rémy Roca, Laboratoire d'Etudes en Géophysique et Océanographie Spatiales, FranceReviewed by:
Bijoy Vengasseril Thampi, Science Systems and Applications, Inc., USADavid J. Sailor, Portland State University, USA
Copyright © 2014 Masson, Bonhomme, Salagnac, Briottet and Lemonsu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Valéry Masson, Météo-France/CNRS, Centre National de Recherches Météorologiques/Groupe d'étude de l'atmosphère Météorologique, 42 av Coriolis, 31057 Toulouse, France e-mail: valery.masson@meteo.fr
 Valéry Masson
Valéry Masson Marion Bonhomme2
Marion Bonhomme2  Xavier Briottet
Xavier Briottet