Improved Measurements of RNA Structure Conservation with Generalized Centroid Estimators

Identification of non-protein-coding RNAs (ncRNAs) in genomes is a crucial task for not only molecular cell biology but also bioinformatics. Secondary structures of ncRNAs are employed as a key feature of ncRNA analysis since biological functions of ncRNAs are deeply related to their secondary structures. Although the minimum free energy (MFE) structure of an RNA sequence is regarded as the most stable structure, MFE alone could not be an appropriate measure for identifying ncRNAs since the free energy is heavily biased by the nucleotide composition. Therefore, instead of MFE itself, several alternative measures for identifying ncRNAs have been proposed such as the structure conservation index (SCI) and the base pair distance (BPD), both of which employ MFE structures. However, these measurements are unfortunately not suitable for identifying ncRNAs in some cases including the genome-wide search and incur high false discovery rate. In this study, we propose improved measurements based on SCI and BPD, applying generalized centroid estimators to incorporate the robustness against low quality multiple alignments. Our experiments show that our proposed methods achieve higher accuracy than the original SCI and BPD for not only human-curated structural alignments but also low quality alignments produced by CLUSTAL W. Furthermore, the centroid-based SCI on CLUSTAL W alignments is more accurate than or comparable with that of the original SCI on structural alignments generated with RAF, a high quality structural aligner, for which twofold expensive computational time is required on average. We conclude that our methods are more suitable for genome-wide alignments which are of low quality from the point of view on secondary structures than the original SCI and BPD.

1 Introduction

Many studies have recently discovered essential roles of non-protein-coding RNAs (ncRNAs) in cells such as translation, post-transcriptional gene regulation and maturation of rRNAs, tRNAs, and mRNAs (Eddy, 2001; Mattick and Makunin, 2006). Therefore, to identify ncRNAs in genomes and analyze their functions is a crucial task for not only molecular cell biology but also bioinformatics.

It is well-known that such biological functions of ncRNAs are deeply related to their secondary structures since most of ncRNA families share consensus secondary structures but contain highly diversed sequences in terms of sequence identity. This means that standard methods for sequence analysis based on the primary sequence may not help ncRNA analysis, and secondary structures should be employed as a key feature of ncRNA analysis.

An RNA secondary structure consists of hydrogen-bonded base pairs including the Watson–Crick base pairs (A-U and G-C), the wobble base pairs (G-U), and other non-canonical base pairs. These base pairs stabilize the structure of RNAs in terms of the free energy. Thus, the secondary structure with the minimum free energy (MFE) has been regarded as the most reliable prediction of RNA secondary structures.

However, Rivas and Eddy (2000) have indicated that MFE alone could not be an appropriate measure for identifying ncRNAs since the free energy is heavily biased by the nucleotide composition. Therefore, several comparative approaches for identifying ncRNAs have been proposed (Rivas and Eddy, 2001; di Bernardo et al., 2003; Coventry et al., 2004; Washietl et al., 2005b; Pedersen et al., 2006). In general, most of these methods employ the following strategy: (1) construct a pairwise or multiple alignment of two or more RNA sequences; (2) predict whether each mutation in the alignment occurs under a structurally conservative model or an independent model. Rivas and Eddy (2001) have developed QRNA which classifies a given pairwise alignment as one of three models: the coding model (COD) in which substitutions between synonymous codons occur frequently to conserve amino acid sequences, the non-coding model (RNA) in which covariances of base pairs occur frequently to conserve secondary structures, and the others (OTH). Pedersen et al. (2006) have developed EvoFold based on phylo-SCFGs which assume that any mutations on each column of a given multiple alignment would occur under a given phylogenetic tree of sequences, and the mutation on single bases would occur more frequently than that on base pairs in conserved secondary structures. These assumptions improve the accuracy of predicting secondary structures (Knudsen and Hein, 1999). Washietl et al. (2005b) have developed RNAz which detects a structurally conserved region from a multiple alignment by support vector machines. RNAz employs the averaged z-score of MFE for each sequence and the structure conservation index (SCI). The key idea is that MFE for the common secondary structure is close to that for each sequence if a given multiple alignment is structurally conserved. Thus, SCI is defined as the rate of MFE for the common secondary structure to the averaged MFE for each sequence. MFE values for each sequence and the common secondary structure are calculated by RNAfold and RNAalifold in Vienna RNA package (Hofacker, 2003). Gruber et al. (2008) have employed the base pair distance (BPD) as a measurement of structure conservation. BPD has been originally defined as the normalized Hamming distance between two RNA secondary structures (Flamm et al., 2001). In (Gruber et al., 2008), BPD has been shown to be as accurate as SCI.

RNAz with SCI has been used for ncRNA screens in several organisms including humans (Washietl et al., 2005a), nematodes (Missal et al., 2006), plasmodium (Mourier et al., 2008), and arabidopsis (Song et al., 2009), showing that RNAz is one of the most accurate tools for identifying ncRNAs. However, for practical use of RNAz on the genome-wide search, a relatively high false discovery rate has unfortunately been estimated (Washietl et al., 2007). It is conceivable that multiple alignments produced by a standard aligner that does not consider any secondary structures are not suitable for identifying ncRNAs in some cases and incur high false discovery rate. Wang et al. (2007) have also suggested that the genome-wide alignments in the UCSC Genome Browser (Kent et al., 2002) produced by MULTIZ (Blanchette et al., 2004) should be improved in some regions for identifying ncRNAs. To improve the accuracy, two strategies can be considered: the one is to employ a structural aligner such as RAF (Do et al., 2008) to produce high quality alignments, and the other is to develop a more robust method against low quality alignments. Since the former strategy will consume impractical execution time for structural alignments, this study takes the latter strategy.

Recently, several researchers have studied high-dimensional space estimation based on maximizing expected accuracy (MEA) including sequence alignment and RNA secondary structure prediction (Ding et al., 2005; Do et al., 2005, 2006; Carvalho and Lawrence, 2008; Hamada et al., 2009, 2011), showing that MEA-based estimation is more reliable than the maximum likelihood estimation. CENTROIDFOLD and CENTROIDFOLD employ one of MEA-based estimators called γ-centroid estimators for predicting RNA (common) secondary structures, and have been shown to be more accurate than other existing tools such as MFE-based methods (Hamada et al., 2009, 2011). Especially, CENTROIDFOLD can predict much more accurate common secondary structures for low quality multiple alignments produced by CLUSTAL W (Thompson et al., 1994) than RNAalifold.

In this study, we propose improved measurements for structure conservation based on γ-centroid estimators for RNA (common) secondary structure prediction, instead of MFE-based predictions by RNAfold and RNAalifold, to incorporate the robustness against low quality multiple alignments. We call them C-SCI and C-BPD, which use centroid structures instead of MFE structures to calculate SCI and BPD. Our experiments show that the proposed methods achieve higher accuracy than the original SCI and BPD for not only human-curated structural alignments but also low quality alignments produced by CLUSTAL W. Furthermore, the accuracy of C-SCI on CLUSTAL W alignments is comparable with that of the original SCI on RAF alignments for which twofold expensive computational time is required on average.

2 Materials and Methods

2.1 RNA Secondary Structure Prediction with γ-Centroid Estimator

CENTROIDFOLD implements a γ-centroid estimator which predicts secondary structures with the maximum expected accuracy by a kind of posterior decoding methods on the base-pairing probability matrix (Hamada et al., 2009).

Let Σ = {A,C,G,U} and Σ^* denote the set of all finite RNA sequences consisting of bases in Σ. For a sequence x = x₁ x₂…x_n ∈ Σ^*, let |x| denote the number of symbols appearing in x, which is called the length of x. Let 𝒮(x) be a set of secondary structures of an RNA sequence x. An element y ∈ 𝒮 (x) is represented as a |x| × |x| binary-valued triangular matrix y = (y_ij)_i < j, where y_ij = 1 means that bases x_i and x_j form a base pair.

CENTROIDFOLD employs a gain function between a true secondary structure θ ∈ 𝒮(x) and a predicted secondary structure y ∈ 𝒮(x) defined as

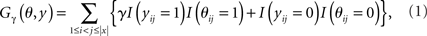
where γ is a weight for base pairs, and I(condition) is the indicator function, which takes 1 or 0 depending on whether condition is true or false. The gain function (1) is equal to the weighted sum of the number of true positives and the number of true negatives of base pairs.

CENTROIDFOLD predicts a secondary structure y ∈ 𝒮(x) which maximizes the expectation of G_γ(θ, y) with respect to an ensemble of all possible secondary structures 𝒮(x) which is distributed under a posterior distribution p(θ|x),

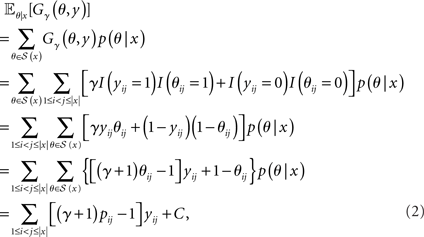
where C is a constant independent of y, and p_ij = 𝔼_θ|x[θ_ij] is the base-pairing probability that the i-th and j-th bases form a base pair. The optimal secondary structure can be calculated efficiently by using the following Nussinov-style DP algorithm:

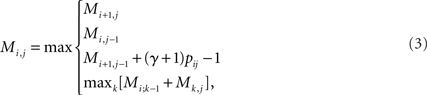
and tracing back from M_1,|x| to recover ŷ. The model of the posterior distribution p(θ|x) can be chosen from various implementations including the McCaskill (1990) model based on the Boltzmann free energy and the CONTRAfold model (Do et al., 2006) based on a machine learning technique. In our experiments, we used the McCaskill model with Boltzmann likelihood parameters (Andronescu et al., 2010).

The weight γ in the definition (1) controls the number of predicted base pairs, that is, the trade-off between specificity and sensitivity of predicted base pairs. If γ = 1, this estimator is equivalent to the centroid estimator (Ding et al., 2005; Carvalho and Lawrence, 2008).

CENTROIDFOLD can predict a common secondary structure of a multiple alignment of RNA sequences by using the γ-centroid estimator under the mixture of the RNAalifold model and the McCaskill model (Hamada et al., 2011). Let A be an alignment of RNA sequences that contains #A sequences. CENTROIDFOLD employs a gain function defined as the sum of the gain function (1) for all x ∈ A:

CENTROIDFOLD predicts a common secondary structure y ∈ 𝒮(A) which maximizes the expectation of 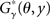under the mixed distribution of the McCaskill model and the RNAalifold model:

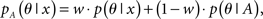
where p(θ|x) and p(θ|A) are the McCaskill model and the RNAalifold model, respectively. Here, w ∈ [0,1] is a weight between two distributions (w = 0.5 in our experiments). The optimal common secondary structure can similarly be calculated by using the recursion (3) with the averaged base-pairing probability defined as

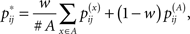
instead of p_ij, where and

CENTROIDFOLD and CENTROIDFOLD have been shown to be more accurate than other existing tools (Hamada et al., 2009, 2011). Especially, CENTROIDFOLD can predict much more accurate common secondary structures than RNAalifold for low quality multiple alignments produced by CLUSTAL W.

2.2 MFE-Based Measurements of Structure Conservation

In this section, we introduce two existing measurements of structure conservation based on prediction of RNA secondary structures that minimizes free energy.

2.2.1 Structure conservation index

The SCI evaluates secondary structure conservation of a given multiple alignment of RNA sequences in terms of the MFE. SCI is defined as

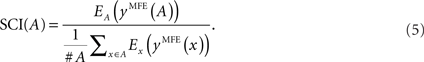
For a single sequence x, E_x(y) denotes the free energy of a secondary structure y ∈ 𝒮(x), and y^MFE(x) = arg min_y∈𝒮(x) E_x(y) is defined to be the MFE structure of x calculated by RNAfold (Hofacker, 2003). Similarly, for an alignment A, E_A(y) is the free energy of a consensus structure y ∈ 𝒮(A), and y^MFE(A) = arg min_y∈𝒮(A) E_A(y) is the consensus MFE structure of A calculated by RNAalifold (Hofacker et al., 2002; Bernhart et al., 2008). The free energy of a consensus structure is defined as the average of the energy contributions of the single sequences plus covariance scores for bonuses of compensatory and consistent co-mutation in the alignment.

The consensus MFE alone could be used to identify functional RNAs in terms of thermodynamic stability of consensus structures. However, it is difficult to make straightforward use of it, since the folding energy is heavily biased by the nucleotide composition and the length of the alignment. SCI solved this problem by normalizing E_A[y^MFE(A)] with the average of E_x[y^MFE(x)] for all x ∈ A. From a different view, SCI reflects the idea that for a well-conserved alignment the structure of each sequence resembles each other and the consensus structure resembles all of them, so E_A[y^MFE(A)] would have as low value as E_x[y^MFE(x)], otherwise E_A[y^MFE(A)] would not. SCI is near 0 for an alignment that is not structurally conserved, whereas SCI is near 1 or above for an alignment that is structurally conserved. Especially, if the alignment is structurally well-conserved and compensatory and consistent mutations often occur, SCI may be above 1.

As shown in the definition (5), SCI obviously depends on the accuracy of common secondary structure prediction, which is also deeply influenced by the quality of multiple alignments of RNAs. This fact is supported by a previous study (Gruber et al., 2008) and our results shown in Section 3. For the genome-wide search, high quality alignments that consider RNA secondary structures cannot be obtained easily due to the computational cost for calculating structural alignments. Therefore, a robust method that does not require high quality alignments is desired.

2.2.2 Base pair distance

The BPD evaluates secondary structure conservation of a given multiple alignment of RNA sequences by comparing predicted secondary structures directly rather than MFE (Flamm et al., 2001; Gruber et al., 2008). BPD is based on the normalized Hamming distance between two RNA secondary structures defined as:

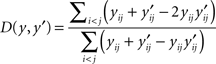
for y ∈ 𝒮(x) and y′ ∈ 𝒮(x′) for two RNA sequences x and x′ with the same length |x| = |x′|. Two variations of BPD can be defined: the first is the mean over all the combination of pairwise distances in the alignment A, that is,

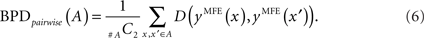
The second is the mean distance from the consensus structure to each individual structure in the alignment A, that is,

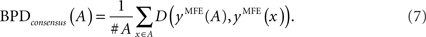
Note that x,x′ ∈ A in Eqs (6) and (7) may contain the gaps (“−”) resulting from the alignment A so that the Hamming distance can be defined.

Both variants of BPD have the same drawback as SCI since MFE-based structures are used, that is, unreliable prediction of (common) secondary structures will result in inaccurate identification of ncRNAs.

2.3 Centroid-Based Measurements of Structure Conservation

Now, we improve the above-mentioned measurements of secondary structure conservation by employing CENTROIDFOLD and CENTROIDFOLD instead of RNAfold and RNAalifold, respectively, for (common) secondary structure prediction to incorporate the robustness against low quality multiple alignments.

2.3.1 C-SCI

We propose C-SCI based on SCI which employs centroid structures instead of MFE structures. First, we predict the consensus centroid structure for an alignment A, denoted by y^c(A), and centroid structures for each sequence x ∈ A, denoted by y^c(x). We map a predicted structure onto each sequence x and calculate its free energy E_x[y^c(x)] for all of the sequences. For an alignment, we map a predicted consensus structure onto each sequence x and get rid of gaps and corresponding parts of the structure. To calculate the energy, we use RNAeval (Hofacker, 2003) with the predicted structure on the sequence. The free energy of a consensus secondary structure is calculated from the averaged free energy for all sequences and the covariance score which is implemented according to RNAalifold (Hofacker et al., 2002).

Then, C-SCI is calculated as follows:

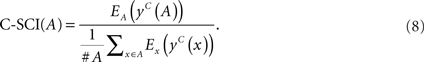
C-SCI has two parameters which affect the discrimination capability. We denote γ_A as the parameter γ for predicting consensus secondary structures on multiple alignments, and γ_S as γ for predicting secondary structures on individual sequences. The two parameters for centroid-based measurements were determined empirically; γ_a = 1.0 and γ_s = 6.0, which on average gave us accurate results in various conditions.

2.3.2 C-BPD

Since BPD directly compares RNA secondary structures, a more accurate and robust method for predicting RNA secondary structures is desired. We can employ centroid structures instead of MFE structures to calculate BPD. We call this C-BPD. As well as BPD, we can consider two variations of C-BPD:

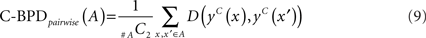
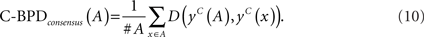
3 Results

3.1 Dataset and Evaluation

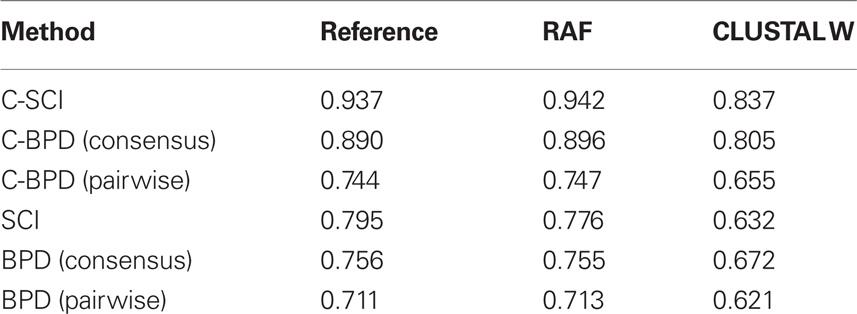
To confirm the discrimination capability of C-SCI and C-BPD, we performed the experiments in accordance with the previous study (Gruber et al., 2008) on BRAliBase 2.1 data set (Wilm et al., 2006), which includes 18,990 reference alignments of 36 RNA families. Reference alignments in BRAliBase 2.1 are human-curated alignments which are made from Rfam database (Griffiths-Jones et al., 2005) aiming for evaluating structural alignments. We produced multiple alignments using CLUSTAL W (Thompson et al., 1994) version 1.83 with default settings to investigate the discrimination capability on low quality alignments. We also produced structural alignments using RAF (Do et al., 2008) version 1.00 with default settings. RAF is one of the most efficient structural aligners based on the Sankoff (1985) algorithm which simultaneously aligns and folds given RNA sequences. However, RAF is much slower than CLUSTAL W since secondary structures are taken into account. For each alignment, we generated 10 negative controls by utilizing SISSIz (Gesell and Washietl, 2008), which randomizes columns of a given alignment to destroy its common secondary structure, while maintaining gap patterns, dinucleotide compositions, and sequence length. These alignments were binned according to their normalized Shannon entropy by the size of 0.05. The normalized Shannon entropy is defined as the average of the Shannon entropy of the individual column over all columns in the alignment whose length is |A|:

where j is in the alphabet Σ = {A,U,G,C, −} consisting of the four nucleotides and the gap character “−,” and 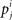is the relative frequency observing the character j in the column i. We clustered the alignments into the bins from 0.05 to 1.15 stepping with 0.05 of normalized Shannon entropy. Figure 1 shows the distribution of the reference alignments on the bins of the normalized Shannon entropy.

FIGURE 1

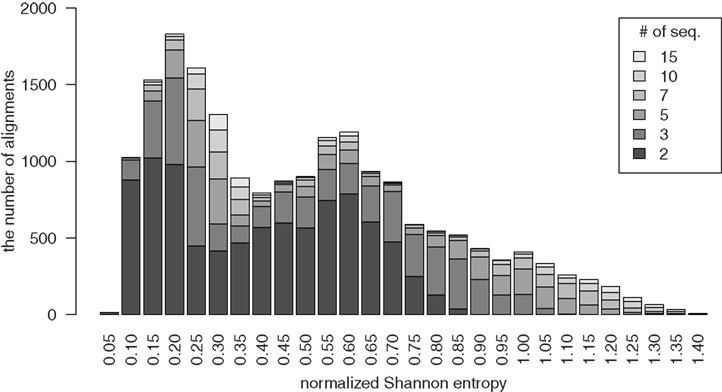
Figure 1. The distribution of the reference alignments over the bins of the normalized Shannon entropy. The density of each bar indicates the number of sequences in the alignments.

To evaluate the performance of the various strategies, we performed the receiver operating characteristic (ROC) curve analysis. An ROC curve is a plot of true positive rate versus false positive rate in varying the discrimination threshold of a classifier. The area under the ROC curve (AUC) is used for evaluation of the discrimination; the AUC value closer to 1 means better discrimination capability.

In our study, we compared C-SCI and C-BPD (pairwise, consensus) with the original SCI and BPD. To compute SCI, we used the program scif available at http://www.biophys.uni-duesseldorf.de/bralibase/. The two variants of BPD were calculated by a modified scif which uses a utility function for the BPD in Vienna RNA package. We implemented C-SCI and C-BPD based on CENTROIDFOLD package version 0.0.9 for predicting (common) secondary structures, and Vienna RNA Package version 1.8.5 for calculating the free energy of predicted structures.

3.2 Discrimination Capability

Figure 2 shows the results of ROC curve analysis of C-SCI and C-BPD comparing with SCI and BPD on the BRAliBase reference alignments and the CLUSTAL W alignments for each bin of normalized Shannon entropy, indicating that C-SCI achieved the highest AUC, especially on low entropy region.

FIGURE 2

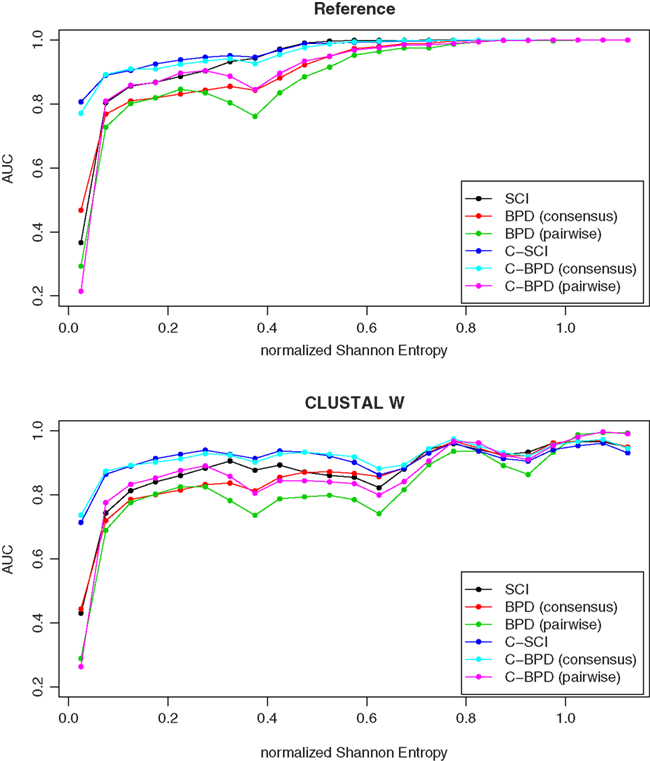
Figure 2. The discrimination capacity of C-SCI, C-BPD, SCI, and BPD in AUC on the reference alignments and the CLUSTAL W alignments for each bin of normalized Shannon entropy.

Table 1 shows the discrimination accuracies for all the alignments of all the methods. This indicates that the centroid-based measurements achieve higher AUC scores on the alignments by all the aligners than their MFE-based counterparts.

TABLE 1

Table 1. Area under the ROC curve of all the methods.

3.3 Computational Complexity

To address the genome-wide search, the computational cost is a serious problem. As shown in Table 1, it is obvious that the use of reference alignments which are structurally corrected by human curation is desirable. However, it is impractical to always obtain such reference alignments since high quality alignments cannot be obtained due to limited human resources and knowledge. Two alternative approaches are to use structural aligners which can align RNA sequences conserving their secondary structures, and to use the standard aligners like CLUSTAL W.

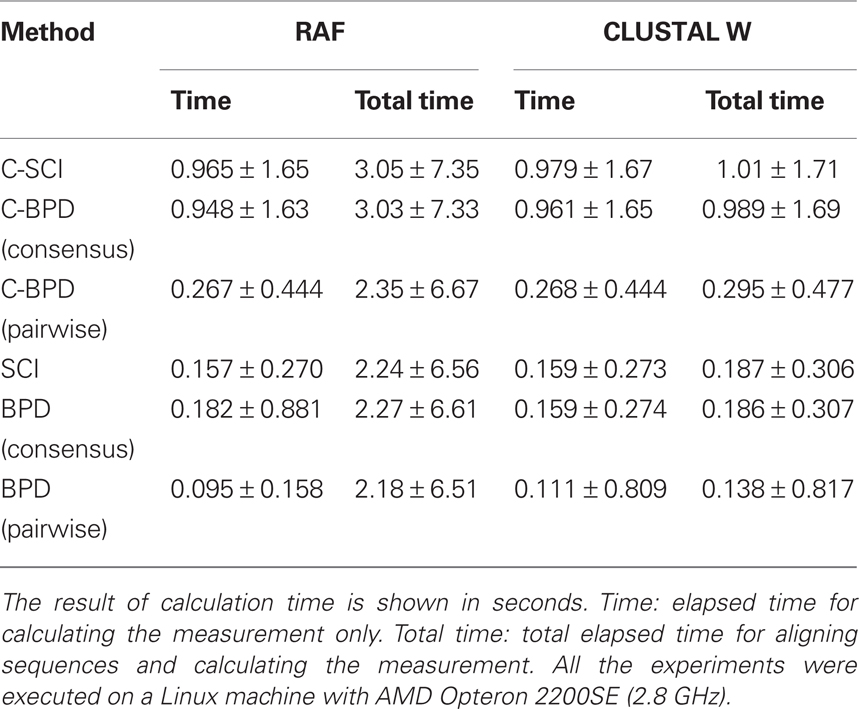
As shown in Table 1, all the measurements on RAF alignments achieve as high accuracy as those on reference alignments, and much higher accuracy than those on CLUSTAL W alignments. However, huge computational time is required for producing structural alignments even by RAF (2.84 s on average), which is known as one of the most efficient structural aligner, comparing with CLUSTAL W (0.0277 s on average). On the other hand, the centroid-based measurements have an advanced property of robustness against low quality alignments. In fact, Table 1 indicates that C-SCI on CLUSTAL W alignments is more accurate than or comparable to SCI on RAF alignments. Furthermore, as shown in Table 2, the elapsed time for calculating SCI through RAF alignments is twice as long as that for C-SCI through CLUSTAL W alignments on average. Figure 3 shows the detailed analysis of elapsed time with respect to the sequence length of the alignments of five sequences, indicating that the non-negligible number of alignments took more than 5 s to compute SCI through RAF alignments even for short sequences less than 200 nt. Therefore, in case that structural alignments might be unavailable such as the genome-wide search, C-SCI is practical to use and is expected to have as high discriminant power as SCI on structural alignments.

TABLE 2

Table 2. Calculation time of each measurement.

FIGURE 3

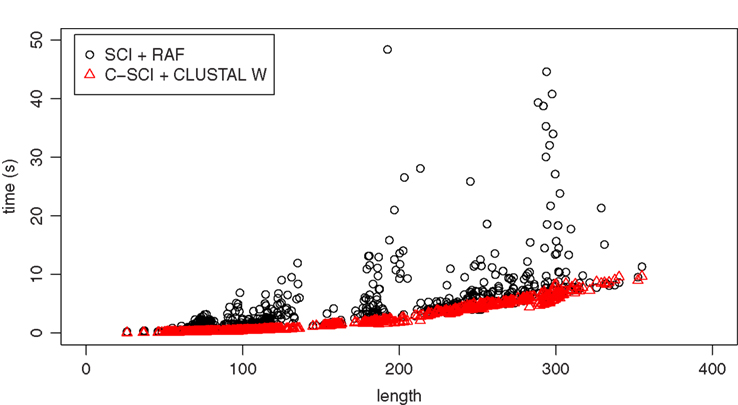
Figure 3. Elapsed time of calculating SCI following RAF alignments and C-SCI following CLUSTAL W alignments for the alignments of five sequences with respect to the length of sequences. All the experiments were executed on a Linux machine with AMD Opteron 2200SE (2.8 GHz).

4 Discussion

We proposed centroid-based measurements of secondary structure conservation, and examined their performance. The results clearly show that C-SCI and C-BPD are more accurate than the original SCI and BPD. The discrimination capability of C-SCI for CLUSTAL W alignments is more accurate than or comparative to SCI for RAF structural alignments. This means that our methods are more suitable for genome-wide alignments which are low quality from the point of view on secondary structures.

As shown in Figure 2, the original SCI and BPD are inaccurate, especially for low entropy regions, that is, highly conserved alignments. For a highly conserved alignment, the common secondary structure predicted by RNAalifold will be very similar with the individual secondary structure predicted by RNAfold for each sequence in the alignment. This means that the original SCI and BPD cannot distinguish structurally conserved alignments from structurally non-conserved alignments for low entropy regions because of the definition of the original SCI and BPD. Therefore, important genes which are highly conserved would be undetectable as ncRNAs even if such genes could fortunately be aligned between related species by a sequence-based aligner. This is a serious drawback of SCI and BPD.

Figure 2 also indicates that our methods are robust on low entropy regions compared with SCI and BPD. For the centroid-based measurements, we used γ_a = 1.0 and γ_s = 6.0, which are the weight for base pairs of predicting secondary structures for alignments and individual sequences, respectively. The previous study has shown that almost the best accuracy of predicting secondary structures for individual sequences can be achieved at γ_s = 6.0 (Hamada et al., 2009), whereas only highly reliable base pairs for alignments might be predicted at γ_a = 1.0. Therefore, our methods can detect only the alignments with reliable base pairs as structurally conserved. This results in reducing false detections of ncRNAs for low entropy regions as shown in Figure 4.

FIGURE 4

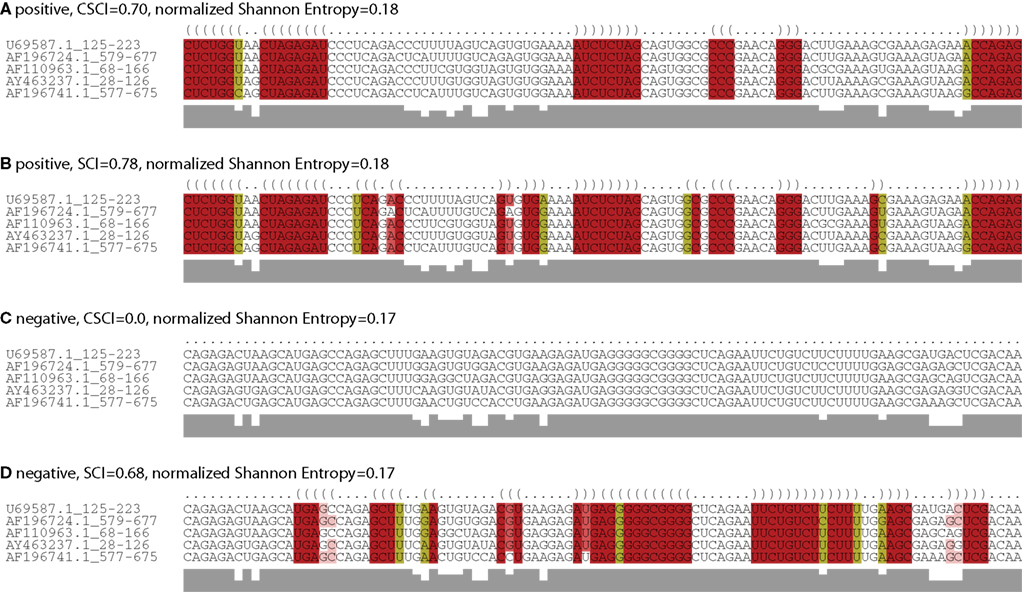
Figure 4. An example of the results on CLUSTL W alignments with low entropy. Predicted common secondary structures of five sequences in HIV_PBS family are shown. (A) The common secondary structure predicted by CentroidAlifold with γ_a = 1.0. (B) The common secondary structure predicted by RNAalifold. (C) The common secondary structure predicted by CentroidAlifold with γ_a = 1.0 for one of the negative control alignments generated by SISSIz. (D) The common secondary structure predicted by RNAalifold for one of the negative control alignments.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was supported in part by a grant from “Functional RNA Project” funded by the New Energy and Industrial Technology Development Organization (NEDO) of Japan, and was also supported in part by Grant-in-Aid for Scientific Research on Priority Area “Comparative Genomics” from the Ministry of Education, Culture, Sports, Science, and Technology of Japan. We thank Michiaki Hamada for fruitful discussions.

References

Andronescu, M., Condon, A., Hoos, H. H., Mathews, D. H., and Murphy, K. P. (2010). Computational approaches for RNA energy parameter estimation. RNA 16, 2304–2318.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bernhart, S., Hofacker, I., Will, S., Gruber, A., and Stadler, P. (2008). RNAalifold: improved consensus structure prediction for RNA alignments. BMC Bioinformatics 9, 474. doi: 10.1186/1471-2105-9-474

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Blanchette, M., Kent, W. J., Riemer, C., Elnitski, L., Smit, A. F. A., Roskin, K. M., Baertsch, R., Rosenbloom, K., Clawson, H., Green, E. D., Haussler, D., and Miller, W. (2004). Aligning multiple genomic sequences with the threaded blockset aligner. Genome Res. 14, 708–715.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Carvalho, L. E., and Lawrence, C. E. (2008). Centroid estimation in discrete high-dimensional spaces with applications in biology. Proc. Natl. Acad. Sci. U.S.A. 105, 3209–3214.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Coventry, A., Kleitman, D. J., and Berger, B. (2004). MSARI: multiple sequence alignments for statistical detection of RNA secondary structure. Proc. Natl. Acad. Sci. U.S.A. 101, 12102–12107.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

di Bernardo, D., Down, T., and Hubbard, T. (2003). ddbRNA: detection of conserved secondary structures in multiple alignments. Bioinformatics 19, 1606–1611.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ding, Y., Chan, C. Y., and Lawrence, C. E. (2005). RNA secondary structure prediction by centroids in a Boltzmann weighted ensemble. RNA 11, 1157–1166.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Do, C. B., Foo, C.-S., and Batzoglou, S. (2008). A max-margin model for efficient simultaneous alignment and folding of RNA sequences. Bioinformatics 24, i68–i76.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Do, C. B., Mahabhashyam, M. S. P., Brudno, M., and Batzoglou, S. (2005). ProbCons: probabilistic consistency-based multiple sequence alignment. Genome Res. 15, 330–340.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Do, C. B., Woods, D. A., and Batzoglou, S. (2006). CONTRAfold: RNA secondary structure prediction without physics-based models. Bioinformatics 22, e90–e98.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Eddy, S. R. (2001). Non-coding RNA genes and the modern RNA world. Nat. Rev. Genet. 2, 919–929.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Flamm, C., Hofacker, I. L., Maurer-Stroh, S., Stadler, P. F., and Zehl, M. (2001). Design of multistable RNA molecules. RNA 7, 254–265.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gesell, T., and Washietl, S. (2008). Dinucleotide controlled null models for comparative RNA gene prediction. BMC Bioinformatics 9, 248. doi: 10.1186/1471-2105-9-248

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Griffiths-Jones, S., Moxon, S., Marshall, M., Khanna, A., Eddy, S. R., and Bateman, A. (2005). Rfam: annotating non-coding RNAs in complete genomes. Nucleic Acids Res. 33, D121–D124.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gruber, A. R., Bernhart, S. H., Hofacker, I. L., and Washietl, S. (2008). Strategies for measuring evolutionary conservation of RNA secondary structures. BMC Bioinformatics 9, 122. doi: 10.1186/1471-2105-9-122

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hamada, M., Kiryu, H., Sato, K., Mituyama, T., and Asai, K. (2009). Prediction of RNA secondary structure using generalized centroid estimators. Bioinformatics 25, 465–473.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hamada, M., Sato, K., and Asai, K. (2011). Improving the accuracy of predicting secondary structure for aligned RNA sequences. Nucleic Acids Res. 39, 393–402.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hofacker, I. L. (2003). Vienna RNA secondary structure server. Nucleic Acids Res. 31, 3429–3431.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hofacker, I. L., Fekete, M., and Stadler, P. F. (2002). Secondary structure prediction for aligned RNA sequences. J. Mol. Biol. 319, 1059–1066.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kent, W. J., Sugnet, C. W., Furey, T. S., Roskin, K. M., Pringle, T. H., Zahler, A. M., and Haussler, D. (2002). The human genome browser at UCSC. Genome Res. 12, 996–1006.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Knudsen, B., and Hein, J. (1999). RNA secondary structure prediction using stochastic context-free grammars and evolutionary history. Bioinformatics 15, 446–454.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mattick, J. S., and Makunin, I. V. (2006). Non-coding RNA. Hum. Mol. Genet. 15, R17–R29.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

McCaskill, J. S. (1990). The equilibrium partition function and base pair binding probabilities for RNA secondary structure. Biopolymers 29, 1105–1119.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Missal, K., Zhu, X., Rose, D., Deng, W., Skogerbø, G., Chen, R., and Stadler, P. F. (2006). Prediction of structured non-coding RNAs in the genomes of the nematodes Caenorhabditis elegans and Caenorhabditis briggsae. J. Exp. Zool. B Mol. Dev. Evol. 306, 379–392.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mourier, T., Carret, C., Kyes, S., Christodoulou, Z., Gardner, P. P., Jeffares, D. C., Pinches, R., Barrell, B., Berriman, M., Griffiths-Jones, S., Ivens, A., Newbold, C., and Pain, A. (2008). Genome-wide discovery and verification of novel structured RNAs in Plasmodium falciparum. Genome Res. 18, 281–292.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pedersen, J. S., Bejerano, G., Siepel, A., Rosenbloom, K., Lindblad-Toh, K., Lander, E. S., Kent, J., Miller, W., and Haussler, D. (2006). Identification and classification of conserved RNA secondary structures in the human genome. PLoS Comput. Biol. 2, e33. doi: 10.1371/journal.pcbi.0020033

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rivas, E., and Eddy, S. R. (2000). Secondary structure alone is generally not statistically significant for the detection of noncoding RNAs. Bioinformatics 16, 583–605.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rivas, E., and Eddy, S. R. (2001). Noncoding RNA gene detection using comparative sequence analysis. BMC Bioinformatics 2, 8. doi: 10.1186/1471-2105-2-8

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sankoff, D. (1985). Simultaneous solution of the RNA folding, alignment and protosequence problems. SIAM J. Appl. Math. 45, 810–825.

CrossRef Full Text

Song, D., Yang, Y., Yu, B., Zheng, B., Deng, Z., Lu, B. L., Chen, X., and Jiang, T. (2009). Computational prediction of novel non-coding RNAs in Arabidopsis thaliana. BMC Bioinformatics 10(Suppl. 1), S36. doi: 10.1186/1471-2105-10-S1-S36

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Thompson, J. D., Higgins, D. G., and Gibson, T. J. (1994). CLUSTAL W: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res. 22, 4673–4680.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wang, A. X., Ruzzo, W. L., and Tompa, M. (2007). How accurately is ncRNA aligned within whole-genome multiple alignments? BMC Bioinformatics 8, 417. doi: 10.1186/1471-2105-8-417

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Washietl, S., Hofacker, I. L., Lukasser, M., Hüttenhofer, A., and Stadler, P. F. (2005a). Mapping of conserved RNA secondary structures predicts thousands of functional noncoding RNAs in the human genome. Nat. Biotechnol. 23, 1383–1390.

CrossRef Full Text

Washietl, S., Hofacker, I. L., and Stadler, P. F. (2005b). Fast and reliable prediction of noncoding RNAs. Proc. Natl. Acad. Sci. U.S.A. 102, 2454–2459.

CrossRef Full Text

Washietl, S., Pedersen, J. S., Korbel, J. O., Stocsits, C., Gruber, A. R., Hackermüller, J., Hertel, J., Lindemeyer, M., Reiche, K., Tanzer, A., Ucla, C., Wyss, C., Antonarakis, S. E., Denoeud, F., Lagarde, J., Drenkow, J., Kapranov, P., Gingeras, T. R., Guigò, R., Snyder, M., Gerstein, M. B., Reymond, A., Hofacker, I. L., and Stadler, P. F. (2007). Structured RNAs in the ENCODE selected regions of the human genome. Genome Res. 17, 852–864.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wilm, A., Mainz, I., and Steger, G. (2006). An enhanced RNA alignment benchmark for sequence alignment programs. Algorithms Mol. Biol. 1, 19.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text