Can excited electronic states of macromolecules with extended pi-systems be reliably predicted? A case study on P3HT
- Institute for Solid State Theory and Center for Multiscale Theory & Computation, University of Münster, Münster, Germany
1. Introduction
Predicting molecular properties in excited electronic states has always posed a particular challenge compared to the electronic ground state. Since the breakthrough of time-dependent density functional response theory (TDDFT) in the late 1990s (Casida, 1995; Marques et al., 2006), electronic excitation energies can often be calculated to a fraction of an electron volt at roughly the same computational cost as the ground state. Due to the wide availability of efficient implementations of TDDFT and its quasi “black box” nature, the method became extremely popular, not only among theoreticians but also among experimentalists. Typically, the calculation of an absorption spectrum merely involves a geometry optimization in the ground state followed by a TDDFT calculation. Even the few well-known failures of standard TDDFT, such as charge-transfer and Rydberg excitations, can be easily cured by introducing a long-range correction into the exchange-correlation functional (Iikura et al., 2001; Dreuw et al., 2003, 2010; Dreuw and Head-Gordon, 2004; Yanai et al., 2004; Baer and Neuhauser, 2005; Zhang et al., 2012). However, for very large molecules, it is very difficult to assess the accuracy of TDDFT, because potentially more accurate ab initio methods are no longer applicable due to their prohibitive computational cost. The situation becomes more complicated when vibrational effects or even conformational dynamics play an important role, e.g., in spectral broadening. If only a single potential well is involved, one may sample molecular structures from a Wigner distribution (Beutier et al., 2014). If, however, multiple potential minima contribute to the overall spectrum, molecular configurations need to be sampled by molecular dynamics or Monte Carlo simulation.
Moreover, the nature of the molecular environment can crucially impact on the conformational distribution. Hence single molecule calculations are generally insufficient to reproduce experimental spectra. In this article, we will focus on the example of Poly(3-hexylthiophene) (P3HT) – a polymer that is frequently used in organic solar cells and semiconductors and has been studied extensively both experimentally and theoretically (Pope and Swenberg, 1999; Perepichka and Perepichka, 2009; Bhatt et al., 2014; Poelking et al., 2014) (see Figure 1A).
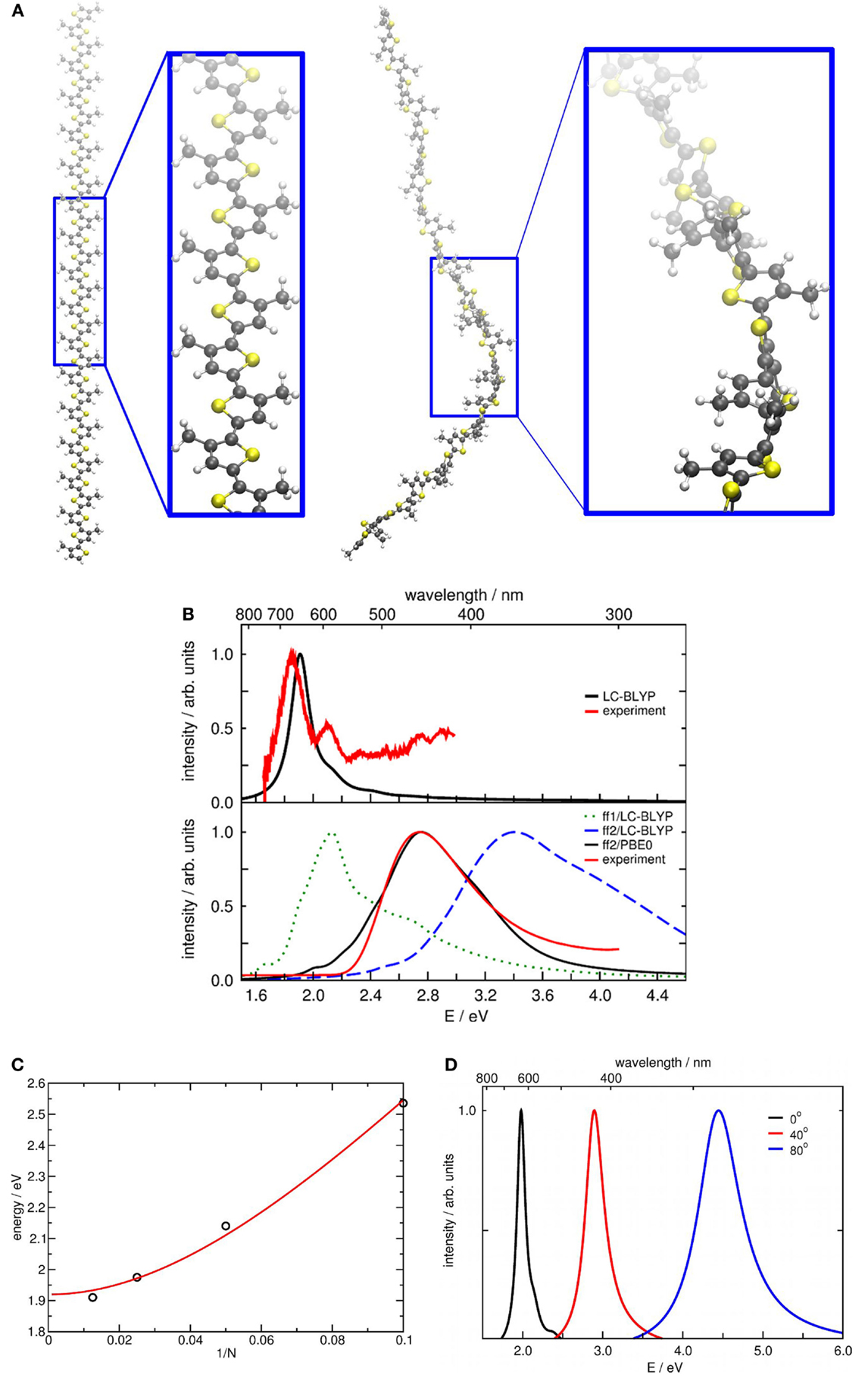
Figure 1. (A) Molecular structure of P3HT in the crystal (left) and a snapshot from the MD simulation in CHCl3 solution with force field II (right). For clarity, the hexyl groups have been replaced by methyl groups. (B) Top panel: theoretical LC-BLYP (red) and experimental (black) absorption spectra of P3HT in a perfect crystal. Bottom panel: theoretical absorption spectra of P3HT in CHCl3 solution obtained with force field I and LC-BLYP (green dotted line), force field II and LC-BLYP (blue dashed line), and force field II and PBE0 (black solid line) compared to the experimental spectrum (black solid line) (Rahimi et al., 2014). (C) Dependence of the position of the main absorption peak of planar P3HT oligomers on the repetition length n. The black circles have been obtained from TDDFT/LC-BLYP/6-31+G* calculations, while the red line is a Kuhn fit according to equation (1). (D) Dependence of theoretical absorption spectra of a P3HT 32mer in CHCl3 solution on the S–C–C–S torsional angle θ. Each spectrum is for a single geometry with fixed θ: θ = 0°(black), θ = 40°(red), θ = 80°(blue). Lorentz broadening with a FWHM of 50 nm has been applied.
2. Discussion
Figure 1B shows the absorption spectra of P3HT in an ordered crystal and in solution (Rahimi et al., 2012, 2014). Experimentally, the main absorption maximum in solution is at 450 nm, while the crystal spectrum exhibits a large red-shift to about 700 nm. The spectrum of an amorphous film is situated in between the two extremes (Rahimi et al., 2012, 2014). To understand the origin of the spectral shifts, it is necessary to disentangle the many-body effect on the electronic structure from the differences in the conformational distributions. From a computational point of view, calculating the absorption spectrum of a condensed phase system becomes a rather hopeless task if the intermolecular interactions are too strong to approximate the overall spectrum as the sum of the individual molecular spectra. But even if the molecules can be treated as isolated entities as far as their electronic structure is concerned, precise knowledge of their conformations is still a prerequisite for the accurate prediction of absorption spectra in condensed phases. This is where it becomes a multiscale problem. The structure of the – disordered – condensed phase system has to be generated by a molecular dynamics (MD) or Monte Carlo (MC) simulation. In the case of polymeric materials, ab initio sampling techniques are out of the question because their computational cost is too high for the large time and length scales involved in these systems. Somewhat paradoxically, however, some ab initio calculations are generally still necessary to reparametrize the atomistic force field for the specific system under study, since most “out-of-the-box” force fields have been developed for biological molecules. Poor force field parameters can lead to dramatic failures as the calculated absorption spectrum of P3HT in CHCl3 solution shown in the bottom panel of Figure 1B illustrates. The main peak of the theoretical spectrum calculated with TDDFT/LC-BLYP/6-31G* for geometries sampled from an MD simulation with force field I (see Computational Details) is situated at about 2.1 eV, a staggering 0.7 eV away from the experimental maximum at ca. 2.8 eV. This can mainly be attributed to the fact that the torsional potential between neighboring five-membered rings is too stiff in the standard GROMOS 45a3 force field. We can exclude the possibility that the deviation is due to the TDDFT calculation, since the absorption spectrum of the ordered crystal with planar molecules can be reproduced rather accurately using the LC-BLYP functional and the 6-31+G* basis set. For the comparison of theoretical and experimental spectra, we need to bear in mind that the typical repetition length n in commercial P3HT materials is of the order of 100, which is too large for TDDFT calculations (n = 32 was used here). A practical solution that has been applied in the literature is to carry out a series of calculations on small oligomers and extrapolate to long chains (Gierschner et al., 2007). In particular, the Kuhn extrapolation formula for excitation energies (Kuhn, 1948),
has been used successfully for a number of different polymer species. In equation (1), N is the number of double bonds along the backbone connecting the terminal carbon atoms (N = 2n in the case of P3HT), E0 is their individual vibrational energy, k0 their force constant, and k′ their coupling constant. A Kuhn fit to the vertical excitation energies of P3HT oligomers calculated with TDDFT/LC-BLYP/6-31+G* is shown in Figure 1C. It demonstrates that the excitation energy of the 32mer used for calculating the spectra in Figure 1B is close to the asymptotic limit. It is worth mentioning that typically only a modest basis set can be used for large molecules, introducing a further source of error. In the present case, increase the basis to cc-pVTZ leads to a decrease in excitation energy of the 5mer by 0.02 eV.
Now that we have established that TDDFT in combination with a range-separated functional is able to reproduce accurately the spectrum of a planar conformation, let us take a closer look at disordered phases with non-planar polymers. The role of the torsion becomes clear when the MD simulation is repeated with a more accurate – much softer – torsional potential derived from ab initio calculations (see Computational Details). As can be seen from the bottom panel of Figure 1B, the main absorption maximum obtained with the LC-BLYP functional shifts to a value of about 3.4 eV (blue dashed line) as the torsional angles increase on average. The reason for the shift is thus not the interaction between the solute and the solvent, but rather the temperature dependent conformational change of the P3HT solute. By twisting the monomeric thiophene units of the polymeric chain against each other, the extended π electron system is interrupted and broken down into smaller units as illustrated by the snapshot shown on the rhs of Figure 1A. Figure 1D illustrates how the absorption spectrum shifts as a function of the torsional angle θ when all thiophene units are twisted by the same angle.
To some extent, the absorption spectrum of P3HT in solution can thus be approximated as that of a distribution of shorter chains. According to equation (1), an excitation energy of 3.4 eV corresponds to a repetition length of n = 3 (see also Figure 1C). This in turn raises the question as to whether a long-range corrected exchange-correlation functional such as LC-BLYP is still appropriate for a distorted chain. It has been shown that range-separated functionals significantly overestimate excitation energies of local transitions (Nguyen et al., 2011). The present observation that the LC-BLYP spectrum is blue-shifted by roughly 0.6 eV with respect to experiment seems to confirm that. A hybrid functional would appear to be a better choice here. Indeed, the PBE0 spectrum seen in Figure 1B is in excellent agreement with experiment (B3LYP red-shifts the spectrum by 0.1 eV). This is plausible as the majority of conformations accessed during the dynamics are highly twisted and the minority of near-planar conformations does not significantly influence the average absorption spectrum. For those minority conformations, the PBE0 functional, nevertheless, dramatically underestimates the excitations energies.
The most difficult scenario is the intermediate case between the planar conformation of the crystal and the twisted geometries of the solution. This is true, for example, for a thin, amorphous film of P3HT, whose main absorption peak was measured to lie at about 2.4 eV (Rahimi et al., 2014). Which functional should one choose to describe this situation in which extended π systems are of equal importance as twisted geometries, or many conformations are twisted to a lesser degree than in solution? One might be able to define geometric criteria to assign individual conformations to one or the other extreme, but this would certainly require extensive prior investigation. Furthermore, such a procedure would still not provide a solution for how to deal with intermediate geometries.
3. Conclusion
In conclusion, we have shown using the illustrative example of P3HT that the calculation of excited electronic states of polymeric materials is inherently a multiscale problem. Since the electronic properties of each molecule sensitively depend on its conformation, it is imperative to first obtain reliable information about the atomistic structure of the material. For disordered, non-crystalline materials this implies large-scale molecular dynamics or Monte Carlo simulations, often requiring a coarse-grained representation. As an aside, we pointed out that the construction of atomistic and coarse-grained force fields is itself a multiscale task, as the parametrization of each level relies on a suitable set of reference data on the level below.
Once the molecular structure has been established with sufficient accuracy, the electronic structure problem can be addressed. The method with the best accuracy to cost ratio to calculate excited states is certainly TDDFT. However, which functional is the most appropriate crucially depends on the molecular conformation. Range-separated functionals need to be used when the π delocalization is uninterrupted, while hybrid functionals might be the best choice for highly twisted geometries. What is needed is a functional that is able to yield accurate results over a wide range of distances.
4. Computational Details
All absorption spectra were calculated with the Gaussian 09 Rev. D.01 quantum chemistry package (Frisch et al., 2009) using the TDDFT method with the LC-BLYP (Becke, 1988; Lee et al., 1988; Iikura et al., 2001) or PBE0 (Adamo and Barone, 1999) exchange-correlation functional. The default basis set was 6-31G*. The crystal spectrum was modeled by single, planar, and regioregular oligomers cut out from the crystal x-ray structure Dudenko et al. (2012). The lowest energy absorption peak was recalculated with the 6-31+G* basis set for the 5mer, 10mer, and 20mer; a 6-31+G* estimate for the 40mer lowest excited state was obtained by subtracting the shift determined for the smaller oligomers (0.04 eV) from the corresponding 6-31G* value.
For the liquid phase simulation, a P3HT 32mer was embedded in 32653 CHCl3 molecules in a cubic periodic unit cell of length 15.952 nm. A molecular dynamics run was performed with the Gromacs 4.5.3 program (Van der Spoel et al., 2005; Gromacs, 2015) at 400 K using the Gromos 45a3 force field, a timestep of 1 fs, and a Berendsen thermostat. The point charges were modified according to a ChelpG electrostatic potential fit (Breneman and Wiberg, 1990) for the optimized 4mer with the B3LYP functional (Becke, 1993) and the 6-31G* basis set. We refer to this force field as force field I. As it turned out, the torsional potential between adjacent thiophene rings is too stiff in force field I. Therefore, a second force field was designed (force field II) whose S–C–C–S dihedral term was reparametrized according to B3LYP/6-31G* reference calculations [more details will be published separately (Böckmann et al., forthcoming)]. The solution phase absorption spectrum was calculated by averaging over ten P3HT geometries sampled at random from the 2 ns MD trajectory. In each TDDFT calculation, the lowest 30 excited states were computed. Only the P3HT solute was treated explicitly, while the solvent was taken into account through a PCM model with UFF atomic radii. In the present case, the solvatochromic shift was found to be small; the peak is red-shifted by just 0.03 eV using the PCM compared to calculations in vacuum. Inclusion of explicit solvent molecules might introduce another shift. It should also be noted that sampling a larger number of configurations from the MD run might again slightly change the position and shape of the spectrum, but the high computational effort generally prevents one from doing so for macromolecules.
Author Contributions
MB carried out the calculations and contributed to the manuscript. ND conceived the work and wrote the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We are grateful to Günter Reiter for providing the experimental absorption spectra. Funding: This work has been funded by DFG within TRR 61.
References
Adamo, C., and Barone, V. (1999). Toward reliable density functional methods without adjustable parameters: the PBE0 model. J. Chem. Phys. 110, 6158. doi: 10.1063/1.478522
Baer, R., and Neuhauser, D. (2005). Density functional theory with correct long-range asymptotic behavior. Phys. Rev. Lett. 94, 043002. doi:10.1103/PhysRevLett.94.043002
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Becke, A. D. (1988). Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 38, 3098. doi:10.1103/PhysRevA.38.3098
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Becke, A. D. (1993). Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 98, 5648.
Beutier, J., Borgis, D., Vuilleumier, R., and Bonella, S. (2014). Computing thermal Wigner densities with the phase integration method. J. Chem. Phys. 141, 084102.
Bhatt, M., Magurudeniya, H., Rainbolt, E., Huang, P., Dissanayake, D., Biewer, M., et al. (2014). Poly(3-hexylthiophene) nanostructured materials for organic electronics applications. J. Nanosci. Nanotechnol. 14, 1033–1050. doi:10.1166/jnn.2014.8892
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Breneman, C. M., and Wiberg, K. B. (1990). Determining atom-centered monopoles from molecular electrostatic potentials. The need for high sampling density in formamide conformational analysis. J. Comput. Chem. 11, 361. doi:10.1002/jcc.540110311
Casida, M. E. (1995). “Time-dependent density-functional response theory for molecules,” in Recent Advances in Density-Functional Methods, ed. D. P. Chong (Singapore: World Scientific), 155.
Dreuw, A., and Head-Gordon, M. (2004). Failure of time-dependent density functional theory for long-range charge-transfer excited states: the zincbacteriochlorin-bacteriochlorin and bacteriochlorophyll-spheroidene complexes. J. Am. Chem. Soc. 126, 4007–4016. doi:10.1021/ja039556n
Dreuw, A., Plötner, J., Wormit, M., Head-Gordon, M., and Dean Dutoi, A. (2010). An additive long-range potential to correct for the charge-transfer failure of time-dependent density functional theory. Z. Phys. Chem. 224, 311–324. doi:10.1524/zpch.2010.6107
Dreuw, A., Weisman, J., and Head-Gordon, M. (2003). Long-range charge-transfer excited states in time-dependent density functional theory require non-local exchange. J. Chem. Phys. 119, 2943–2946. doi:10.1063/1.1590951
Dudenko, D., Kiersnowski, A., Shu, J., Pisula, W., Sebastiani, D., Spiess, H. W., et al. (2012). A strategy for revealing the packing in semicrystalline π-conjugated polymers: crystal structure of bulk poly-3-hexyl-thiophene (P3HT). Angew. Chem. Int. Ed. Engl. 51, 11068–11072. doi:10.1002/anie.201205075
Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2009). Gaussian 09, Revision D.01. Wallingford, CT: Gaussian, Inc.
Gierschner, J., Cornil, J., and Egelhaaf, H.-J. (2007). Optical bandgaps of π-conjugated organic materials at the polymer limit: Experiment and theory. Adv. Mater. 19, 173. doi:10.1002/adma.200600277
Gromacs. (2015). Available from: http://www.gromacs.org/
Iikura, H., Tsuneda, T., and Hirao, K. (2001). A long-range correction scheme for generalized-gradient-approximation exchange functionals. J. Chem. Phys. 115, 3540. doi:10.1063/1.1383587
Kuhn, W. (1948). Über das Absorptionsspektrum der Polyene. Helv. Chim. Acta 31, 1780. doi:10.1002/hlca.19480310644
Lee, C., Yang, W., and Parr, R. C. (1988). Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 37, 785. doi:10.1103/PhysRevB.37.785
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Marques, M. A. L., Ullrich, C., Nogueira, F., Rubio, A., and Gross, E. K. U. (eds) (2006). Lecture Notes in Physics, Vol. 706. Berlin: Springer.
Nguyen, K. A., Day, P. N., and Pachter, R. (2011). The performance and relationship among range-separated schemes for density functional theory. J. Chem. Phys. 135, 074109. doi:10.1063/1.3624889
Perepichka, I. F., and Perepichka, D. F. (eds) (2009). Handbook of Thiophene-Based Materials: Applications in Organic Electronics and Photonics. Chichester: Wiley, 1.
Poelking, C., Daoulas, K., Troisi, A., and Andrienko, D. (2014). Morphology and charge transport in p3ht: a theorists perspective. Adv. Polymer Sci. 265, 139–180. doi:10.1007/12_2014_277
Pope, M., and Swenberg, C. E. (1999). Electronic Processes in Organic Crystals and Polymers. New York, NY: Oxford University Press.
Rahimi, K., Botiz, I., Agumba, J. O., Motamen, S., Stingelin, N., and Reiter, G. (2014). Light absorption of poly(3-hexylthiophene) single crystals. RSC Adv. 4, 11121. doi:10.1039/C3RA47064D
Rahimi, K., Botiz, I., Stingelin, N., Kayunkid, N., Sommer, M., Koch, F. P. V., et al. (2012). Controllable processes for generating large single crystals of poly(3-hexylthiophene). Angew. Chem. Int. Ed. 51, 11131–11135. doi:10.1002/anie.201205653
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Van der Spoel, D., Lindahl, E., Hess, B., Groenhof, G., Mark, A. E., and Berendsen, H. J. C. (2005). GROMACS: fast, flexible, and free. J. Comput. Chem. 26, 1701–1718. doi:10.1002/jcc.20291
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Yanai, T., Tew, D., and Handy, N. (2004). A new hybrid exchange-correlation functional using the coulomb-attenuating method (cam-b3lyp). Chem. Phys. Lett. 393, 51–57. doi:10.1016/j.cplett.2004.06.011
Zhang, X., Li, Z., and Lu, G. (2012). A non-self-consistent range-separated time-dependent density functional approach for large-scale simulations. J. Phys. Condens. Matter 24, 205801. doi:10.1088/0953-8984/24/20/205801
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Keywords: polymers, excited states, TDDFT, multiscale modeling, exchange-correlation functionals
Citation: Böckmann M and Doltsinis NL (2015) Can excited electronic states of macromolecules with extended pi-systems be reliably predicted? A case study on P3HT. Front. Mater. 2:25. doi: 10.3389/fmats.2015.00025
Received: 02 February 2015; Paper pending published: 20 February 2015;
Accepted: 13 March 2015; Published online: 07 April 2015.
Edited by:
Simone Taioli, Bruno Kessler Foundation, ItalyReviewed by:
Elise Dumont, Ecole Normale Supérieure de Lyon, FranceCopyright: © 2015 Böckmann and Doltsinis. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: nikos.doltsinis@uni-muenster.de
 Marcus Böckmann
Marcus Böckmann Nikos L. Doltsinis
Nikos L. Doltsinis