A Simple Experimental Model to Investigate Force Range for Membrane Nanotube Formation
- 1Biological Engineering and Small-scale Technologies Graduate Program, School of Engineering, University of California Merced, Merced, CA, USA
- 2Physics Department, School of Natural Science, University of California Merced, Merced, CA, USA
- 3Developmental and Cell Biology, School of Biological Sciences, University of California Irvine, Irvine, CA, USA
The presence of membrane tubules in living cells is essential to many biological processes. In cells, one mechanism to form nanosized lipid tubules is via molecular motor induced bilayer extraction. In this paper, we describe a simple experimental model to investigate the forces required for lipid tube formation using kinesin motors anchored to 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) vesicles. Previous related studies have used molecular motors actively pulling on the membrane to extract a nanotube. Here, we invert the system geometry; molecular motors are used as static anchors linking DOPC vesicles to a two-dimensional microtubule network and an external flow is introduced to generate nanotubes facilitated by the drag force. We found that a drag force of ≈7 pN was sufficient for tubule extraction for vesicles ranging from 1 to 2 μm in radius. By our method, we found that the force generated by a single molecular motor was sufficient for membrane tubule extraction from a spherical lipid vesicle.
Introduction
The lipid membrane is a self-assembled system, which can take on various shapes simply by changing its composition, changing the concentration of specific lipids, or applying a force. Lipids are amphipathic and thus self-assemble into a bilayer in the cell known as the plasma membrane. The membrane forms a barrier that compartmentalizes different cellular processes. Inside the cell, lipid nanotubes are one of various shapes that help facilitate the organization of cellular processes. It has been shown that networks of lipid nanotubes play a role in cellular communication and transport, for example in the immunological synapses (Carlin et al., 2001; McCann et al., 2007), connections between the Golgi and endoplasmic reticulum (Hirschberg et al., 1998; Martinez-Menarguez et al., 1999), and in chemical signaling (Watkins and Salter, 2005). The smooth endoplasmic reticulum is an example of a lipid nanotube system that branches out from the rough endoplasmic reticulum and nuclear envelope. These membrane nanotubes are found to colocalize with fundamental biopolymers in cells known as microtubules; when the microtubules depolymerize, the lipid tubules retract (Terasaki et al., 1986). Recent studies also demonstrated that a minimal system of microtubules and molecular motors were sufficient for tubule extraction (Roux et al., 2002).
Molecular motors are nature’s nanomachines, and they drive mechanical translocation of cellular materials along their biopolymer tracks (microtubules) in cells. Kinesin (conventional kinesin or kinesin-1) is a major microtubule-based molecular motor that utilizes the chemical energy stored in ATP to actively step along the microtubule (Schnitzer and Block, 1997). In the absence of ATP, individual kinesin motors associate with and remain strongly bound to the microtubule, with an unbinding energy of ~5 pN per kinesin motor (Uemura et al., 2002). When multiple kinesins are present to bind the same cargo to the microtubule, the unbinding energy (or the force necessary to detach their common cargo) scales linearly with motor number (Mallik et al., 2005; Vershinin et al., 2007, 2008; Shubeita et al., 2008; Jamison et al., 2010; Xu et al., 2012a,b).
In biological membranes, the lipid bilayer behaves like a flexible thin molecular sheet with fluid-like in-plane properties. The lipid molecules forming the bilayer diffuse freely in the plane of the bilayer with a mobility often characterized by the molecular diffusion constant, D. The biological membrane has a complicated composition, including many different saturated, unsaturated, and cholesterol lipids plus a large number of protein structures and other membrane associated molecules. Each component in the membrane has an effect on the fluidity and packing structure. For example, the addition of cholesterol into 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) membrane decreases membrane fluidity while it increases in DOPC membranes (Mills et al., 2009; Gracia et al., 2010). In addition, membranes composed of mixtures of different lipid components may create in-plane phase separation and domains (or “rafts”) with differing elastic properties, for example, in DOPC/DPPC mixtures (Mills et al., 2009; Schmidt et al., 2009). However, in the experiment presented here, we used only one membrane composition with well-known elasticity to simplify our analysis of the multi-component system.
It is widely known that lipid tubules can be extracted from flat bilayers (or vesicles) given enough applied force. Membrane tubules can be extracted from membranes on application of a force with methods, such as micropipette aspiration (Mannerville et al., 2001; Cuvelier et al., 2005), optical tweezers (Cuvelier et al., 2005; Inaba et al., 2005; Koster et al., 2005), molecular motor pulling (Koster et al., 2003; Leduc et al., 2004; Shaklee et al., 2008), and assisted shear flow (Brazhnik et al., 2005; Sekine et al., 2012). Each of these techniques investigates the mechanical forces necessary to deform the lipid membrane into tubules from giant unilamellar vesicles (GUVs) or lamellar structures. Techniques such as force spectroscopy in atomic force microscopy (Scheffer et al., 2001; Picas et al., 2012) and the Langmuir–Blodgett trough (Nichols-Smith et al., 2004) had also been used to quantify the elastic parameters of various membranes without tubulation.
In this study, we coated the glass surface with microtubules for specific binding of kinesin motor proteins, which act as static anchor sites for GUV linkages. By applying a flow to the system, free GUVs were carried by the flow but anchored GUVs experienced a resisting force due to the microtubule-bound motors. Anchored GUVs either pull out lipid nanotubes or remain immobilized or release from the anchor site. This new experimental system is motivated by previous studies where lipid tubulation was induced through a cluster of arriving and departing kinesins walking along the microtubule (Koster et al., 2003). In our case, we anchored the kinesin motors to microtubules and controlled the detachment of kinesin by the force generated on the motor by GUV deformation and displacement.
Materials and Methods
Materials
All of the lipids 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC), 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), 1,2-dioleoyl-sn-glybero-3-[(N-(5-amino-1-carboxypentyl)iminodiacetic acid) succinyl] (ammonium salt) (DGS-NTA), and 1,2-dioleoyl-sn-3-phosphoethanolamine-N-(7-nitro-2-1,3-benzoxadiazol-4-yl) (ammonium salt) (DOPE-NBD) were purchased from Avanti Polar Lipids in chloroform and used without further purification. Lyophilized tubulins were purchased from Cytoskeleton (Cat. T240). Recombinant kinesin protein (K560) was purified as previously described (Xu et al., 2012b). Silicon beads of 2.47 μm (SS04N) and 4.56 μm (SS06N) in water were purchased from Bangs Laboratories, Inc.
Giant Unilamellar Vesicles
To prepare GUVs, we used the method of electroformation to produce GUVs between 1 and 10 μm (Pott et al., 2008). The 94.95 mol% DPPC or DOPC was mixed with 5 mol% DGS-NTA and 0.05 mol% DOPE-NBD to a final concentration of 5 mM in chloroform. DGS-NTA was chosen because it can bind directly by ionic interaction to the HIS-tag of the kinesin protein (Herold et al., 2012). DOPE-NBD is a labeled lipid with absorbance at 460 nm and emission at 535 nm for fluorescence imaging. Droplets of the lipid mixtures were then deposited onto clean indium tin oxide (ITO) slides and allowed to dry in a vacuum chamber overnight to remove excess chloroform. The slides were then assembled into an electroformation chamber to produce GUVs. Two ITO slides were placed between a greased Teflon O-ring with the dried lipid sides facing each other. The chamber was filled with 200 mM sucrose. Once the chamber is assembled, a 2-V sinusoidal voltage with 7.5 Hz was applied across the chamber and incubated at 45°C for 3 h. GUVs are formed by budding from the stack of bilayers that were hydrated at the ITO glass surface. GUV solution were harvested and stored in centrifuge tubes for further use. GUVs produced from this parameter range from 1 to 10 μm.
Lipid Nanotube Formation
To assemble microtubules, 5 μg/μl tubulin in PEM80 buffer (80 mM PIPES pH 6.9, 2 mM MgCl2, and 0.5 mM EGTA) supplemented with 1 mM GTP and 5% of glycerol was incubated in ice for 3 min and then in water bath at 37°C for 20 min. The assembled microtubules were stabilized by mixing in equal volume in PEM80 buffer supplemented with 50 μM Taxol and 2 mM of GTP and then incubated for another 20 min at 37°C. Flow cells were prepared by sandwiching a poly-l-lysine coated cover glass (22 mm × 40 mm) on top of a microscope glass slide (3 in × 3 in × 1 mm) using two double-sided tape strips. The strips were placed 3 mm apart from each other at the middle of the glass slide creating a flow channel (Figure S1 in Supplementary Material). The resulting flow cell volume was ≈12 μl. To pattern the flow cell with microtubules, 12 μl of microtubule solution (15 μg/ml in PEM80, supplemented with 1 mM GTP and 25 μM Taxol) was introduced to the flow cell. After 5 min of incubation, unbound microtubules were washed away with 12 μl of wash solution (PEM25 supplemented with 1 mM GTP and 25 μM Taxol). The flow cell was then blocked with 5.55 mg/ml casein supplemented with 1 mM GTP and 25 μM Taxol to prevent non-specific attachment of kinesin onto bare glass. Then, 10 μl of kinesins (4 μM) was introduced into the flow cell to allow for binding to microtubules. After 5 min, excess kinesin was washed away with 12 μl wash solution (PEM80 ed with 1 mM GTP and 25 μM Taxol) and GUVs were introduced into the flow cell and allowed to settle for 10 min. The GUV solution was diluted by 10× with microtubule solution, thus making the GUV interior composed of the sucrose solution. The sucrose makes the GUVs heavy so that they will sink to the surface. To generate lipid tubules, 20 μl wash buffer was drawn through the flow cell using filter paper.
Lipid Diffusion Measurement Using FRAP
The diffusion constant, D, for GUVs containing 5 mol% DGS-NTA was assessed using fluorescence recovery after photo bleaching (FRAP) on supported lipid bilayers. Lipid mixtures of 94.95 mol% DOPC, 5 mol% DGS-NTA, and 0.05 mol% DPPE-NBD (dye) were mixed in chloroform and vacuum dried to remove excess chloroform. Dried lipids were then rehydrated with Milli-pore water to final concentration. Small unilamellar vesicles were formed via tip sonication and drop casted onto a clean glass slide coated with bovine serum albumin. Then the sample was incubated at 50°C for 1 h to allow for fusion on the surface forming a single bilayer. The bilayer was observed using fluorescence microscopy and a small circular region overexposed by high power to bleach the region. The recovery of the bleached region was recorded for analysis of the diffusion constant for the lipid mixture. Snapshots of bleached region recovery were captured by Qimaging camera at 120-s interval for 20 min. Diffusion constant, D, was determined by first-fitting Soumpasis formula to the data (Figure S2 in Supplementary Material) (Soumpasis, 1983).
where f(t) is the normalized fluorescence, τD is the characteristic time for diffusion, I0 is the fluorescence intensity, and t is the time. τD is determined from the fit, which we can now calculate the D value for a bleached region of radius ω using
Results and Discussion
Using our experimental system, we observed many examples of successful flow-induced nanotube extraction from lipid GUVs. Kinesin dimers (heads of the kinesin protein) bind to the tubulin of the microtubule. The tail of the kinesin was tagged with histidine polymer, which can bind to the amine group at the head of the DGS-NTA lipid as shown in Figure 1.
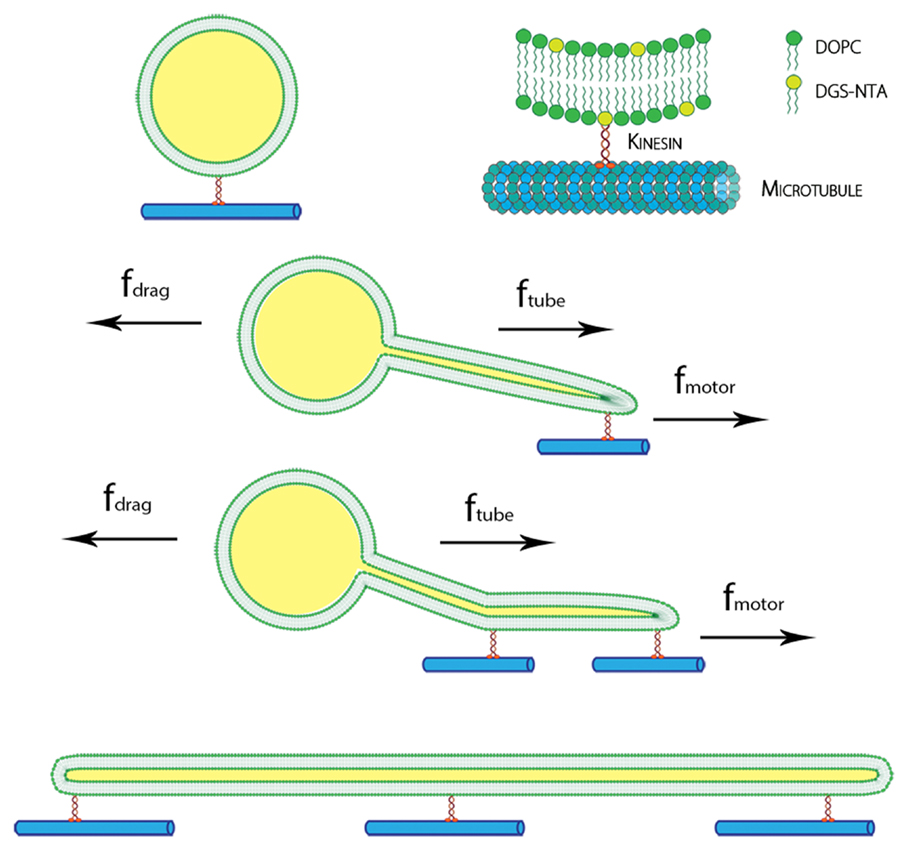
Figure 1. Schematic of the kinesin-lipid anchor system and formation of lipid nanotube. DGS-NTA lipids were attached to kinesin motors, which bind to immobilized microtubule on glass. With an applied force by inducing flow, GUVs moved along the direction of flow and lipid nanotubes were pulled out by the kinesins. Multiple anchors of DGS-NTA stabilized the lipid nanotubes seen in tethered GUVs and cylinders.
By using filter paper to induce a flow, the anchored kinesins pulled out nanotubes from the moving GUVs. After a flow was introduced and subsequently stopped, examples of spherical GUVs, tethered GUVs (vesicle with tube pulled out), and fully elongated vesicles which become cylinders were observed as shown in Figure 2. Lipid bilayer cylinders as long as 100 μm were generated using this method. A control experiment was done without kinesin, and as expected, all GUVs were washed away from the flow cell without binding to the microtubules.
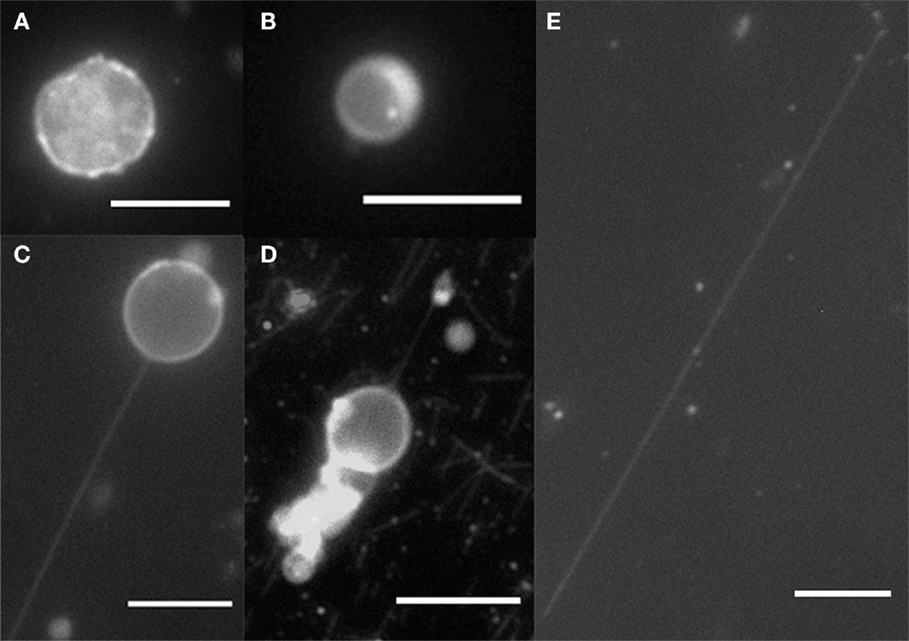
Figure 2. Fluorescence microscopy of GUVs and nanotubes. (A) DPPC/DGS-NTA (5 mol%) crumple vesicle, (B) DOPC/DGS-NTA (5 mol%) vesicle, (C) DOPC/DGS-NTA (5 mol%) tethered GUV, (D) DOPC/DGS-NTA (5 mol%) tethered GUV with labeled microtubules, and (E) DOPC/DGS-NTA (5 mol%) lipid nanotube. Scale bar: 10 μm.
Under high flow rates, we observed that most GUVs >4.5 μm in diameter were washed away from the flow cell leaving smaller ones that were anchored. However, with a lower flow rate, anchored GUVs with diameters up to 10 μm remain in the flow cell. To quantify the flow rate, we calculated the speed of flowing 2.47 μm glass beads using bright field optical microscopy. For a low flow rate, 20 μl of the wash buffer was deposited at one end of the channel. This created a low flow as the solution spread in every direction due to surface tension. We generated a high flow rate using a strip of 1 cm × 4 cm filter paper to absorb 20 μl of wash solution to the opposite end of the flow cell. We measured an average low flow rate of 61.3 ± 3.7 μm/s and high flow rate of 177.6 ± 18.2 μm/s. We were aware that the flow rate in either case was not constant, and therefore, we calculated an average flow rate for the first 2-s of flow, during which time we expected to generate the fastest flow as the water was wicked into the filter paper. We noted that bigger GUVs were not washed from the flow cell channel under a low flow rate, while the high flow rate was sufficient to detach the big vesicles from the anchor points.
To compare the effects of membrane composition on tabulation, we also prepared GUVs with a different membrane bending rigidity, kb. The bending rigidity is the membrane’s resistance to bending deformation. At room temperature, DOPC is in fluid phase (Lα) with kb = 85 pNnm (Rawicz et al., 2000), but DPPC exhibits the gel phase (Lβ) at the same temperature with kb = 1100 pNnm (Lee et al., 2000). To compare these radically different membrane rigidities in our experiment, we formed GUVs with the DPPC membrane by electroformation and followed up with the above-described procedure to produce lipid nanotubes (Pott et al., 2008). At room temperature, DPPC GUVs are not perfectly spherical but crumpled due to their tilted packing in the bilayer (Figure 2A) (Hirst et al., 2013). Therefore, because of their very high bending rigidity, no lipid nanotubes were formed. With DOPC, the bending rigidity is much lower; therefore, it was easier to extract lipid tubules.
Figure 3 shows a 3-μm diameter GUV being stretched under high flow rate. It was being stretched into an ellipsoid and retracted back to its initial position. There was no lipid nanotube formed. When the flow stopped, the stretched GUV retracted back to a spherical vesicle. A lipid nanotube cannot be formed possibly due to having multiple anchors of DGS-NTA lipids to kinesins. Also, the generated drag force from the size of the GUV may not be high enough to extract a lipid nanotube. A discussion of this phenomenon will be discussed later in the paper.
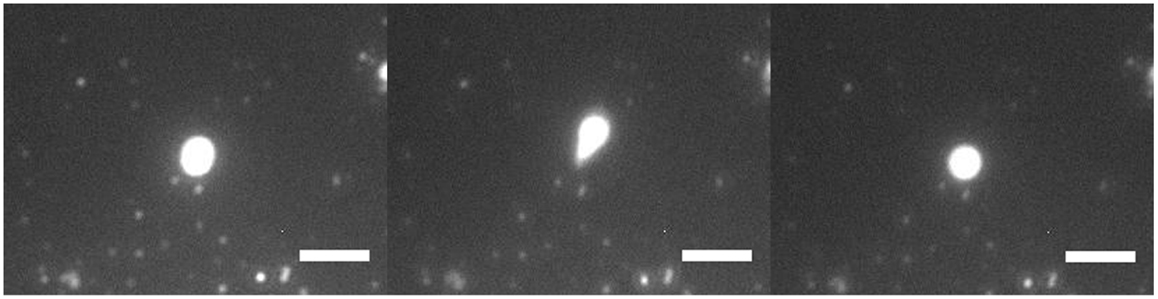
Figure 3. Fluorescence microscopy of GUV retraction under high flow. A DOPC/DGS-NTA (5 mol%) GUV of 3 μm in diameter was being stretched by the flow with an anchor. The GUV stretched into an ellipsoid and retracted back into GUV. Scale bar: 5 μm.
In Figure 4, we see a 2-μm diameter GUV forming a lipid nanotube under high flow rate. This lipid nanotube was formed under a flow of 177.6 ± 18.2 μm/s and stretched to 57 μm in length. Since we imaged the lipid nanotubes using fluorescence microscopy, an optical technique, we cannot accurately measure the radii. However, various methods have been used by other research groups and found that nanotubes extracted from GUVs were between 20 and 110 nm (Roux et al., 2002; Tokarz et al., 2007; Adams et al., 2010; Stepanyants et al., 2012).

Figure 4. Fluorescence microscopy of lipid tubulation under high flow. A lipid nanotube was extracted from a DOPC/DGS-NTA (5 mol%) GUV of 2 μm in diameter by the applied flow. The nanotube was about 57 μm in total. Scale bar: 10 μm.
Discussion
The lipid membrane forms a bilayer in aqueous solution and can be represented as a soft flexible elastic sheet that can bend out of plane or stretch laterally by increasing the distance between each lipid molecule. Applying a point force perpendicular to the bilayer will deform the membrane from its equilibrium curvature potentially causing a tube to be extracted. For our system, a GUV binds to a kinesin that anchors to a microtubule. When a flow is applied, a nanotube is extracted from the moving GUV due to the force applied by the anchored kinesin. In a flow, GUVs experience a drag force given by Stoke’s equation:
where r is the GUV radius under a fluid flow of velocity, v, in a medium of viscosity, η. The viscosity of a dilute aqueous solution near the glass surface in the flow cell can be estimated as η = g (1e−3 N s/m2), where g is a correction factor for flow close to a surface according to Faxen’s law1.
where h is the distance from the glass surface and r is the GUV radius. For example, in our flow cell, we approximate g = 2.36 for a 1-μm radius GUV, 100 nm above the surface (Hirokawa and Noda, 2008). The g value is typically between 1 and 3 and only valid for when h − r ≥ 0.02r. We calculated the drag force shown in Figure 5 for DOPC GUVs under high and low flow rates.
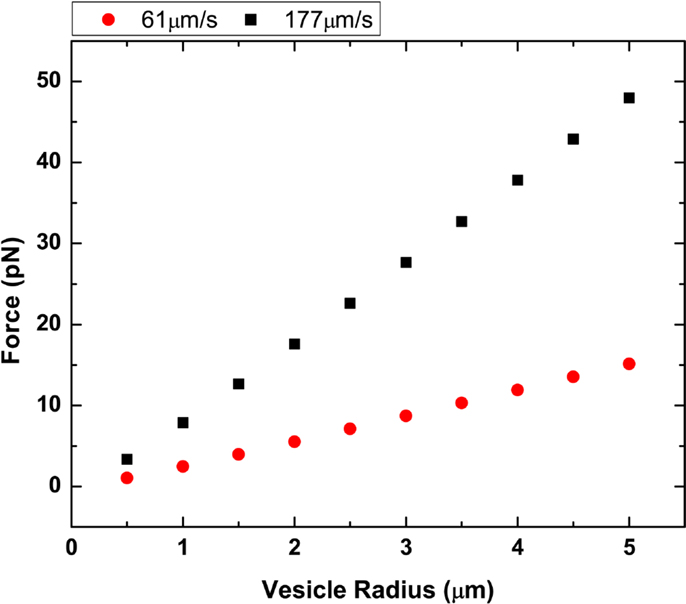
Figure 5. Plot of vesicle radius vs. drag force. Two different flow rates at 61.3 and 177.6 μm/s were plotted using both Stoke’s law and Faxen’s law.
We can first considered a simple non-deformable system of either glass beads or GUVs with a high bending rigidity, such as DPPC in the gel phase, anchored to a microtubule by kinesin. In such a case, we do not expect a nanotube to form, and we can write that fdrag ≤ fmotor. If fdrag (drag force on the GUV) exceeds the maximum attachment force of the cumulative motors, fmotor, then the anchored kinesin/GUV should detach from the microtubule. If fdrag is less or equal to the fmotor, then the GUV is immobilized. We see clear evidence of this effect with DPPC GUVs, they either detach and are washed away by the flow or remained attached without tube formation.
In the case of softer elastic membranes, such as DOPC in the fluid phase at room temperature, lipid nanotubes can be pulled from the GUV as the membrane deforms at the kinesin anchor point. We can describe the free energy cost of extracting a tubule of radius r and length L from the GUV using the Helfrich formula assuming no increase in membrane surface area A and volume V (Deuling and Helfrich, 1976; Derenyi et al., 2002).
where kb is the membrane bending rigidity, H is the mean curvature, (1/R1 + 1/R2)/2, σ is the surface tension, and ρ is pressure. In tethered GUVs, the energy of surface tension (minimizing the surface area) acts against the energetic costs of bending, pressure induced volume increase, and tube elongation to minimize the total free energy. Without the action of deformation forces, the bilayer takes the shape of a spherical vesicle. In the formation of the nanotube, the pressure difference inside the GUV and tether is 0, otherwise it would rupture. In order to find the force required to extract a tube of radius r, we calculated ∂F/∂R = 0 and ∂F/∂L = 0 for an extracted tube in equilibrium, thus arriving at
which leads to a single equation, f = 2πk/r. From here, we can calculate the force, ftube, it takes to pull a tube of radius r out of a GUV with bending rigidity, kb. In our system, the kb values for DOPC and DPPC are 85 pNnm (Rawicz et al., 2000; Pan et al., 2008) and 1100 pNnm (Lee et al., 2000), respectively. We use fluorescence microscopy to observe the lipid nanotubes; however, measuring the tube radius is quite complicated due to the limits of optical resolution. Several prior studies have determined the radius of these tubes to be in the range of 20–110 nm (Roux et al., 2002; Tokarz et al., 2007; Adams et al., 2010; Stepanyants et al., 2012). If a tube has a radius of 50 or 100 nm, then we get tube forces (ftube) of 10.7 and 5.35 pN, respectively, using our analysis. The difference between the fdrag and the sum of ftube for all attached motors results in the net force exerted by the motors on the vesicle, fdrag − nftube = fvnet, where n is the number of tubes generated. Although this equation takes into consideration the possibility of multiple tubes, such a state is less likely and coalescence tether experiments have shown that nanotubes generated close to each other will fuse into a single nanotube (Cuvelier et al., 2005). We observed no more than one lipid nanotube per GUV in our experiments.
In our experiments, we observe three different cases:
(1) fvnet > nfmotor: large GUVs are washed from the flow cell after the onset of flow. Large GUVs generate a fvnet higher than the nfmotor from anchored kinesin(s). Kinesin motors’ resisting force is not sufficient to overcome the strong drag force, and thus, the large GUV is swept away from the surface.
(2) fvnet ≤ nfmotor: under our high flow rate of ≈177 μm/s, smaller GUVs <5 μm anchored to the microtubule via kinesin are not washed from the flow cell. fvnet is not strong enough to detach the motors from their bound state. Depending on the number of motors being attached to the microtubule and their distribution, a tube may be pulled out from the vesicle, given a sufficiently deformable membrane.
(3) fvnet « nfmotor: the net force from the drag force and tube force is too low compared to the max force from the total number of bound kinesins. In this group of GUVs, no nanotube is generated because it would cost too much energy to make tubes per anchored motor. In this case, having too many bound anchor sites and a stiff membrane prohibits the GUV from either washing away or pulling out nanotubes.
In Figure 6, we plotted two phase diagrams indicating the theoretical result (nanotube formation, GUV detachment, or immobilization) as a function of number of attached motors and vesicle radius for the two different flow regimes. We calculated the theoretical minimal number of motors needed to successfully anchor a GUV and generate a nanotube given the calculated drag force (Figure 5). As described in case 1, large GUVs were washed from the flow cell under high flow – they generated a high drag force that overcame the resistance force from the combined anchored motors. This calculation of motor number assumed that each motor has a maximum binding force of 5 pN to the microtubule. Here, we assumed that lipid nanotubes extracted from the GUVs are 67.6 nm in radius. This value was an estimation based on f = 2πk/r for the smallest GUV in which nanotubes were observed. These calculations demonstrated that nanotubulation requires a minimum of just one or two motors under both flow conditions. According to the graph, if there are more motor/lipid linkages than the estimated value, then the GUV does not form a nanotube and remains immobilized. However, if there are fewer kinesin/DGS-NTA linkages, then the GUV flows away.
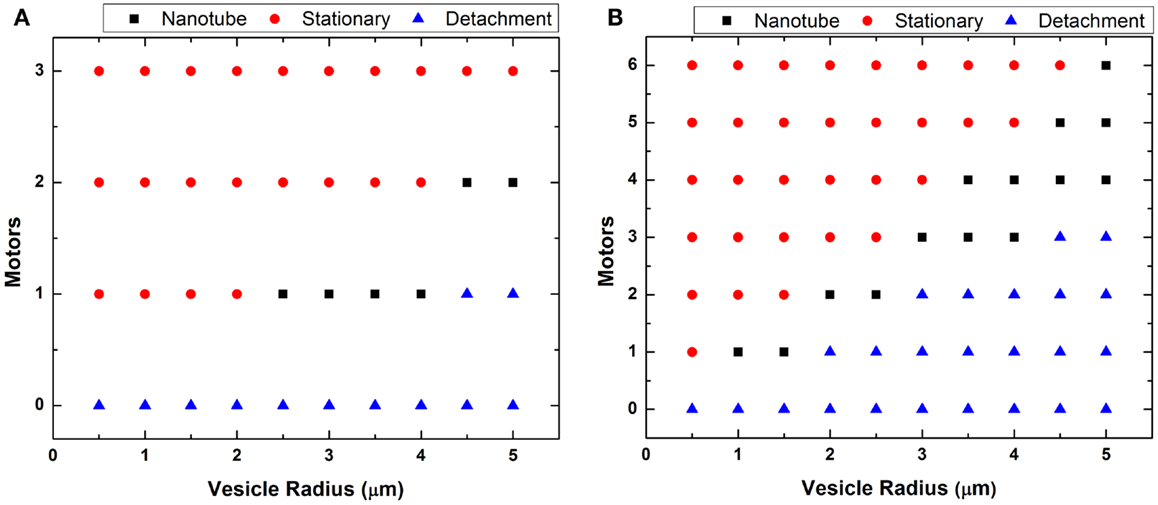
Figure 6. Plot of vesicle radius vs. motors. The minimum number of motors necessary to generate lipid nanotubes was estimated for each GUV radius at (A) low and (B) high flow. The calculation assumed generated nanotubes to be 67.6 nm in radius.
A theoretical estimation of the number of motors required for nanotube formation is shown in Figure 6, and our experiments showed a general qualitative agreement with these results. However, we did not observe nanotubes over the full range indicated in the phase diagrams. In Figure 6B, we plotted for GUVs up to 5 μm in radius but only observed nanotubes for GUVs between 1 and 2 μm. We believed it is possible to form nanotubes in GUVs >2 μm by increasing the concentration of kinesin motors and microtubules on the substrate. However, these linkages have to be distanced enough from each other, which can be quite difficult. If too many motors anchored are close together, which is likely the case especially on the same microtubule, only the motor at the tip experiences the force from the vesicle. Having too many anchor sites may not cause a point deformation but rather an area deformation, stretching the GUVs into an ellipsoid. An example of this was seen in Figure 3. We observed GUVs stretched into ellipsoids in the presence of the flow and retracted back to a sphere when the flow was stopped.
Tethered GUVs and fully stretched GUVs forming cylinders are evidence of multiple linkages. During the flow process, tubulation can be observed from displaced anchored GUVs. When the flow slowed down or stopped, GUVs retracted back to their initial location. However, during the process of tubulation, if a GUV is able to make another lipid/kinesin linkage, then a “tethered” GUV is stabilized because the tube only retracts back to its most recent anchor. For fully stretched vesicles (cylindrical tubes), both ends of the cylinder must have anchor sites. The probability of making additional tube-microtubule motor linkages is high with our lipid mixture of DOPC with 5 mol% of DGS-NTA. The lateral diffusion of DOPC/DGS-NTA lipid molecules at room temperature is high, 9.01 ± 0.58 μm2/s, compared to pure DOPC at 8.2 μm2/s (Figure S2 in Supplementary Material) (Lindblom and Oradd, 2009). The hydrophobic tails of both lipid molecules are the same, but DGS-NTA have a bigger hydrophilic head, which may contribute to increased lateral diffusion. This suggests that for a moving GUV traveling along microtubule coated with kinesin motors, there is a high probability that a DGS-NTA lipid will be present at the bottom of the GUV to bind with incoming kinesin. Increasing the concentration of kinesin motors potentially increases the number of fully stretched GUVs as extra-binding sites can act to hold the tubule in place; however, there will be a trade-off because too many motors present in the system will affect its ability to even form a nanotube and elongate in the case of multiple initial bindings. The fully stretched tethered tubules we observed (Figure 2E) were very stable and straight and they all stretched in the direction of the flow. We also observed that once stabilized, further stretching due to additional flow did not occur. This was likely because with a cross-section of only ≈140 nm, the nanotubes did not generate enough drag force to detach the multiple-bound kinesin motors from the microtubules and allow further extension.
Conclusion
We have developed a simple experimental system to generate flow-induced lipid nanotubes using kinesin molecular motors anchored to microtubules. By this method, we demonstrated that one can estimate the number of motors necessary for anchoring and tubulation. Our calculations, confirmed by experiments, demonstrated that it takes as little as one to two motors to pull out a tube from a GUV provided we are in a suitable GUV size range. The fabrication of the flow cell and experimental procedure is simple, quick, and should provide fast readout of the motor count if tubes are observed. A flow cell with better flow rate control will be fabricated in the future for quantitative analysis. The presence of nanotube stability requires multiple anchors for GUVs that do not fully retract back to its initial position and fully stretched nanotubes. This may provide possible insight to stability of nanotube networks in cells.
Author Contributions
CL and JL carried out the experiments and analyzed the data; MM-H purified proteins; LH, JX, and CL designed the experiments and wrote the paper.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Funding
This work was supported by the National Science Foundation (DMR BMAT 0852791 to LH), the UC Merced Health Sciences Research Institute Biomedical Seed Grant (to LH and JX), and the UC Merced Academic Senate Committee on Research Award (to JX and LH).
Supplementary Material
The Supplementary Material for this article can be found online at https://www.frontiersin.org/article/10.3389/fmats.2016.00006
Footnote
References
Adams, K. L., Engelbrektsson, J., Voinova, M., Zhang, B., Eves, D. J., Karlsson, R., et al. (2010). Steady-state electrochemical determination of lipidic nanotube diameter utilizing an artificial cell model. Anal. Chem. 2010, 1020. doi: 10.1021/ac902282d
Brazhnik, K., Vreeland, W. N., Hutchison, J. B., Kishore, R., Wells, J., Helmerson, K., et al. (2005). Directed growth of pure phosphatidylcholine nanotubes in microfluidic channels. Langmuir 21, 10814–10817. doi:10.1021/la047151q
Carlin, L. M., Eleme, K., McCann, F. E., and Davis, D. M. (2001). Intercellular transfer and supramolecular organization of human leukocyte antigen C at inhibitory natural killer cell immune synapses. J. Exp. Med. 194, 1507–1517. doi:10.1084/jem.194.10.1507
Cuvelier, D., Derenyi, I., Bassereau, P., and Nassoy, P. (2005). Coalescence of membrane tethers: experiments, theory, and applications. Biophys. J. 88, 2714–2726. doi:10.1529/biophysj.104.056473
Derenyi, I., Julicher, F., and Prost, J. (2002). Formation and interaction of membrane tubes. Phys. Rev. Lett. 88, 238101. doi:10.1103/PhysRevLett.88.238101
Deuling, H. J., and Helfrich, W. (1976). Red blood cell shapes as explained on the basis of curvature elasticity. Biophys. J. 16, 861–868. doi:10.1016/S0006-3495(76)85736-0
Gracia, R. S., Bezlyepkina, N., Knorr, R. L., Lipowsky, R., and Dimova, R. (2010). Effect of cholesterol on the rigidity of saturated and unsaturated membranes: fluctuation and electrodeformation analysis of giant vesicles. Soft Matter 6, 1472–1482. doi:10.1039/b920629a
Herold, C., Leduc, C., Stock, R., Diez, S., and Schwille, P. (2012). Long-range transport of giant vesicles along microtubule networks. Chemphyschem 13, 1001–1006.
Hirokawa, N., and Noda, Y. (2008). Intracellular transport and kinesin superfamily proteins, KIFs: structure, function, and dynamics. Physiol. Rev. 88, 1089–1118. doi:10.1152/physrev.00023.2007
Hirschberg, K., Miller, C. M., Ellenberg, J., Presley, J. F., Siggia, E. D., Phair, R. D., et al. (1998). Kinetic analysis of secretory protein traffic and characterization of Golgi to plasma membrane transport intermediates in living cells. J. Cell Biol. 143, 1485–1503. doi:10.1083/jcb.143.6.1485
Hirst, L. S., Ossowski, A., Fraser, M., Geng, J., Selinger, J. V., and Selinger, R. L. B. (2013). Morphology transition in lipid vesicles due to in-plane order and topological defects. Proc. Natl. Acad. Sci. U.S.A. 110, 3242–3247. doi:10.1073/pnas.1213994110
Inaba, T., Ishijima, A., Honda, M., Nomura, F., Takiguchi, K., and Hotani, H. (2005). Formation and maintenance of tubular membrane projections require mechanical force, but their elongation and shortening do not require additional force. J. Mol. Biol. 348, 325–333. doi:10.1016/j.jmb.2005.02.060
Jamison, D. K., Driver, J. W., Rogers, A. R., Constantinou, P. E., and Diehl, M. R. (2010). Two kinesins transport cargo primarily via the action of one motor: implications for intracellular transport. Biophys. J. 99, 2967–2977. doi:10.1016/j.bpj.2010.08.025
Koster, G., Cacciuto, A., Derenyi, I., Frenkel, D., and Dogterom, M. (2005). Force barriers for membrane tube formation. Phys. Rev. Lett. 94, 068101. doi:10.1103/PhysRevLett.94.068101
Koster, G., VanDujin, M., Hofs, B., and Dogterom, M. (2003). Membrane tube formation from giant vesicles by dynamic association of motor proteins. Proc. Natl. Acad. Sci. U.S.A. 100, 15583–15588. doi:10.1073/pnas.2531786100
Leduc, C., Campas, O., Zeldovich, K. B., Roux, A., Jolimaitre, P., Bourel-Bonnet, L., et al. (2004). Cooperative extraction of membrane nanotubes by molecular motors. Proc. Natl. Acad. Sci. U.S.A. 101, 17096–17101. doi:10.1073/pnas.0406598101
Lee, C., Lin, W., and Wang, J. (2000). Measuring the bending rigidity of giant unilamellar liposomes with differential confocal microscopy. CLEO, 592–593.
Lindblom, G., and Oradd, G. (2009). Lipid lateral diffusion and membrane heterogeneity. Biochim. Biophys. Acta 1788, 234–244. doi:10.1016/j.bbamem.2008.08.016
Mallik, R., Petrov, D., Lex, S. A., King, S. J., and Gross, S. P. (2005). Building complexity: an in vitro study of cytoplasmic dynein with in vivo implications. Curr. Biol. 15, 2075–2085. doi:10.1016/j.cub.2005.10.039
Mannerville, J. B., Bassereau, P., Ramaswamy, S., and Prost, J. (2001). Active membrane fluctuations studied by micropipette aspiration. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 64, 021908. doi:10.1103/PhysRevE.64.021908
Martinez-Menarguez, J. A., Geuze, H. J., Slot, J. W., and Klumperman, J. (1999). Vesicular tubular clusters between the ER and Golgi mediate concentration of soluble secretory proteins by exclusion from COPI-coated vesicles. Cell 98, 81–90. doi:10.1016/S0092-8674(00)80608-X
McCann, F. E., Eissmann, P., Önfelt, B., Leung, R., and Davis, D. M. (2007). The activating NKG2D ligand MHC class I-related chain a transfers from target cells to NK cells in a manner that allows functional consequences. J. Immunol. 178, 3418–3426. doi:10.4049/jimmunol.178.6.3418
Mills, T. T., Huang, J., Feigenson, G. W., and Nagle, J. F. (2009). Effects of cholesterol and unsaturated DOPC lipid on chain packing of saturated gel-phase DPPC bilayers. Gen. Physiol. Biophys. 28, 126–139. doi:10.4149/gpb_2009_02_126
Nichols-Smith, S., Teh, S., and Kuhl, T. L. (2004). Thermodynamic and mechanical properties of model mictochondrial membranes. Biochim. Biophys. Acta 1663, 82–88. doi:10.1016/j.bbamem.2004.02.002
Pan, J., Tristram-Nagle, S., Kucerka, N., and Nagle, J. F. (2008). Temperature dependence of structure, bending rigidity, and bilayer interactions of dioleoylphosphatidylcholine bilayers. Biophys. J. 94, 117–124. doi:10.1529/biophysj.107.115691
Picas, L., Rico, F., and Scheuring, S. (2012). Direct measurement of the mechanical properties of lipid phases in supported bilayers. Biophys. J. 102, L01–L03. doi:10.1016/j.bpj.2011.11.4001
Pott, T., Bouvrais, H., and Meleard, P. (2008). Giant unilamellar vesicles formation under physiologically relevant conditions. Chem. Phys. Lipids 154, 115–119. doi:10.1016/j.chemphyslip.2008.03.008
Rawicz, W., Olbrich, K. C., McIntosh, T., Needham, D., and Evans, E. (2000). Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys. J. 79, 328–339. doi:10.1016/S0006-3495(00)76295-3
Roux, A., Cappello, G., Cartaud, J., Prost, J., Goud, B., and Bassereau, P. (2002). A minimal system allowing tubulation with molecular motors pulling on giant liposomes. Proc. Natl. Acad. Sci. U.S.A. 99, 5394–5399. doi:10.1073/pnas.082107299
Scheffer, L., Bitler, A., Ben-Jacob, E., and Korenstein, R. (2001). Atomic force pulling: probing the local elasticity of the cell membrane. Eur. Biophys. J. 30, 83–90. doi:10.1007/s002490000122
Schmidt, M. L., Ziani, L., Boudreau, M., and Davis, J. H. (2009). Phase equilibria in DOPC/DPPC: conversion from gel to subgel in two component mixtures. J. Chem. Phys. 131, 175103. doi:10.1063/1.3258077
Schnitzer, M. J., and Block, S. M. (1997). Kinesin hydrolyses one ATP per 8-nm step. Nature 388, 386–390. doi:10.1038/41111
Sekine, Y., Abe, K., Shimizu, A., Sasaki, Y., Sawada, S., and Akiyoshi, K. (2012). Shear flow-induced nanotubulation of surface-immobilized liposomes. RSC Adv. 2, 2682–2684. doi:10.1039/c2ra00629d
Shaklee, P. M., Idema, T., Koster, G., Storm, C., Schmidt, T., and Dogterom, M. (2008). Bidirectional membrane tube dynamics driven by nonprocessive motors. Proc. Natl. Acad. Sci. U.S.A. 105, 7993–7997. doi:10.1073/pnas.0709677105
Shubeita, G. T., Tran, S. L., Xu, J., Vershinin, M., Cermelli, S., Cotton, S. L., et al. (2008). Consequences of motor copy number on the intracellular transport of kinesin-1-driven lipid droplets. Cell 135, 1098–1107. doi:10.1016/j.cell.2008.10.021
Soumpasis, D. (1983). Theoretical analysis of fluorescence photo bleaching recovery experiments. Biophys. J. 41, 95–97. doi:10.1016/S0006-3495(83)84410-5
Stepanyants, N., Jeffries, G. D. M., Orwar, O., and Jesorka, A. (2012). Radial sizing of lipid nanotubes using membrane displacement analysis. Nano Lett. 12, 1372–1378. doi:10.1021/nl203983e
Terasaki, M., Chen, L. B., and Fujiwara, K. (1986). Microtubules and the endoplasmic reticulum are highly interdependent structures. J. Cell Biol. 103, 1557–1568. doi:10.1083/jcb.103.4.1557
Tokarz, M., Hakonen, B., Dommersnes, P., Orwar, O., and Akerman, B. (2007). Electrophoretic transport of latex particles in lipid nanotubes. Langmuir 23, 7652. doi:10.1021/la700336u
Uemura, S., Kawaguchi, K., Yajima, J., Edamatsu, M., Toyoshima, Y. Y., and Ishiwata, S. (2002). Kinesin-microtubule binding depends on both nucleotide state and loading direction. Proc. Natl. Acad. Sci. U.S.A. 99, 5977–5981. doi:10.1073/pnas.092546199
Vershinin, M., Carter, B. C., Razafsky, D. S., King, S. J., and Gross, S. P. (2007). Multiple motor based transport and its regulation by Tau. Proc. Natl. Acad. Sci. U.S.A. 104, 87–92. doi:10.1073/pnas.0607919104
Vershinin, M., Xu, J., Razafsky, D. S., King, S. J., and Gross, S. P. (2008). Tuning microtubule-based transport through filamentous MAPs: the problem of dynein. Traffic 9, 882–892. doi:10.1111/j.1600-0854.2008.00741.x
Watkins, S. C., and Salter, R. D. (2005). Functional connectivity between immune cells mediated by tunneling nanotubules. Immunity 23, 309–318. doi:10.1016/j.immuni.2005.08.009
Xu, J., Reddy, B. J., Anand, P., Shu, Z., Cermelli, S., Mattson, M. K., et al. (2012a). Casein kinase 2 reverses tail-independent inactivation of kinesin-1. Nat. Commun. 3, 754. doi:10.1038/ncomms1760
Keywords: biological membrane, nanotubes, lipid bilayer, kinesin, molecular motors, microtubules
Citation: Lor C, Lopes JD, Mattson-Hoss MK, Xu J and Hirst LS (2016) A Simple Experimental Model to Investigate Force Range for Membrane Nanotube Formation. Front. Mater. 3:6. doi: 10.3389/fmats.2016.00006
Received: 01 November 2015; Accepted: 25 January 2016;
Published: 15 February 2016
Edited by:
Malcolm Xing, University of Manitoba, CanadaReviewed by:
Gwendolen Clair Reilly, University of Sheffield, UKMichael Ming-Yuan Wei, University of Texas at Arlington, USA
Copyright: © 2016 Lor, Lopes, Mattson-Hoss, Xu and Hirst. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jing Xu, jxu8@ucmerced.edu;
Linda S. Hirst, lhirst@ucmerced.edu
 Chai Lor
Chai Lor Joseph D. Lopes
Joseph D. Lopes Michelle K. Mattson-Hoss
Michelle K. Mattson-Hoss Jing Xu
Jing Xu Linda S. Hirst
Linda S. Hirst