Parametrization in Models of Subcritical Glass Fracture: Activation Offset and Concerted Activation

Introduction

The chemistry of glass fracture has been under scientific debate for a long time (Fairbarn and Tate, 1859; Griffith, 1921). However, a quantitative description of the underlying mechanisms of crack propagation, critical to the further development of crack-resistant glasses, is presently unavailable (Wondraczek et al., 2011; Freiman, 2012). This is largely due to the fundamental nature of cracking as it occurs in the broad group of brittle oxides, and especially in glassy silicates: crack propagation reflects a complex and, as of yet, not fully understood interplay of chemical and physical interactions (Ciccotti, 2009). In particular, below a critical value of applied stresses (the subcritical regime), chemical reactions and the effects of mechanical loading are so intertwined that the separation of the governing parameters becomes an extremely challenging task. The subcritical crack growth and its dependence on environmental conditions have profound consequences for the glass industry and the suitability of glass as a structural material. Here, parametric knowledge is needed not only for the focused development of new material compositions and toughening procedures but also for enabling better time-to-failure estimations (Freiman et al., 2009). Beyond materials development, this need encompasses other related areas such as the understanding of geophysical fracture processes (Atkinson, 1982; Brantut et al., 2013; Zhang and Zhao, 2014).

Generally speaking, the kinetics of crack propagation below Mode I critical stress concentration K_Ic can be divided into three regimes: in region I, even though the applied stresses are much smaller than the critical value, the crack propagates through a directional corrosion reaction on stressed bonds. For the case of molecular water as the reaction partner, a theoretical framework has been developed (Michalske and Freiman, 1982; Michalske and Bunker, 1984, 1987) (Figure 1). In this region, the crack propagation velocity depends strongly on the applied stresses, temperature, and environment. In region II, the crack growth velocity becomes increasingly limited by the transport of the reactive molecules to the crack tip, resulting in a constant crack velocity with increasing stress intensity. Finally, in region III, the applied stresses are high enough to break the stressed atomic bonds without environmental help, so the crack velocity is again strongly dependent on the applied stresses and temperature, but not on the environment.

FIGURE 1

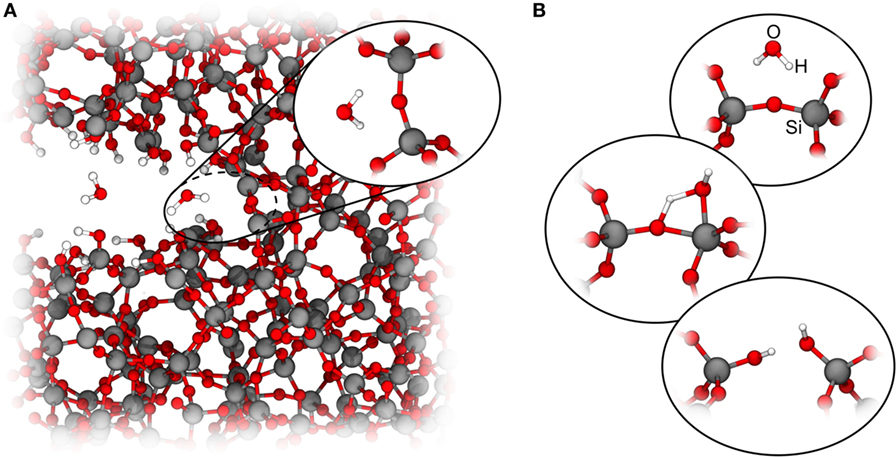
Figure 1. Reactive crack propagation in silica. (A) Atomistic view of a crack tip in silica glass; (B) subcritical crack growth mechanism (Michalske and Freiman, 1982). In the vicinity of the crack tip, one or more water molecules adsorb at a stressed Si–O–Si linkage (I), the Si–O bond is cleaved via a transition structure (II) and finally converted to surface silanol groups (III).

Activation Offset

Generally, the rate of crack growth v is modeled as ν = λ⋅k (Michalske and Bunker, 1984; Schoeck, 1990), where λ is a geometrical parameter depending on the matrix through which the crack is growing, and k is the rate of success for the crack to advance by λ units. The reaction rate is then framed within the transition state theory, and written in the form of an Arrhenian expression, k = k₀ exp(−ΔF/RT), where k₀ is the attempt frequency based on the oscillations of the system around an equilibrium position and ΔF is the molar energy difference between the initial and final states, in this case representing the energy barrier to break the bond. While working on the delayed fracture of glasses, Wiederhorn and coworkers (Wiederhorn, 1967; Wiederhorn et al., 1974a,b) pioneered a semiempirical equation to describe the phenomenon of subcritical crack growth in the presence of water:

$v=v_{0}a{\left({\text{H}}_2\text{O}\right)}^n\text{exp}\left(-\frac{E^{\ast }-b{K}_I}{\mathit{RT}}\right).$ (1)

Here, v₀ is the pre-exponential term, a(H₂O) is the water activity, n is the number of water molecules which interact with the Si–O–Si bond during its cleavage, E* is the activation energy, K_I is the stress concentration factor at the crack tip, and b is a function of the activation volume and the crack tip radius (Wiederhorn et al., 1974a,b). The mathematical formulation for the activation energy in Eq. 1 is analogous to the enthalpy of gasses under constant pressure, only the pressure term is substituted by the applied stresses (Wiederhorn, 1967; Wiederhorn and Bolz, 1970). This expression has found widespread use in the literature, influencing a great part of the developments on the understanding of subcritical crack growth since its inception.

For the moment, we note that the primary feature of Eq. 1 is the reduction of E* by the strain energy U_strain = bK_I. This can be understood as an offset contribution in the potential well of the considered bond, increasing the probability for breakage (case I in Figure 2).

FIGURE 2

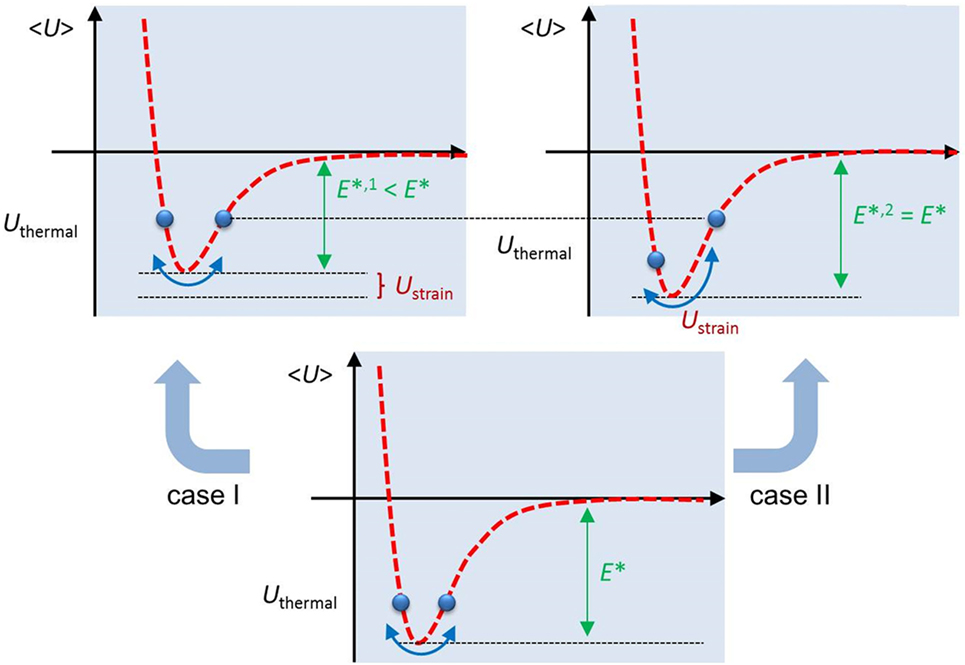
Figure 2. Schematic representation of how temperature and applied stresses interact with the potential energy well of the chemical bond at the crack tip. <U > is the average potential energy of the bond as a function of distance, U_thermal is the thermal energy, U_strain is the strain energy, and E*, E*^,1, and E*^,2 are the activation energies for bond cleavage for non-strained bonds and strained bonds, case I and II, respectively.

Concerted Activation

The derivation of Eq. 1 assumes that the applied mechanical field offsets the potential energy at the considered bond, thus reducing the activation energy of the breakage event and increasing breakage probability. However, this appears as only one of two extremes: the second is an increase in the overall excitation of the system (case II in Figure 2) without directly affecting the activation barrier. This interpretation is a natural result of the democratic fiber bundle model (DFBM), in which the material is represented as a series of springs connecting two parallel bars and oriented perpendicular to the direction of crack propagation. These springs are considered to be ideally elastic, ideally brittle with random failure threshold (modeling inherent structural disorder), and the load on each spring is also subjected to thermal noise (Kun et al., 2000; Roux, 2000; Ciliberto et al., 2001; Scorretti et al., 2001).

Here, we consider first the energetic equilibrium for cracks growing at rates below the limit of dynamic stability (Fineberg and Marder, 1999),

$G=\frac{1-{\mathrm{\mu }}^2}{E}{A}_I\left(v\right)K_I^2=\mathrm{2\gamma },$ (2)

where G is the strain release rate, μ is Poisson’s ratio, E is the elastic modulus, A_I is a material and crack speed dependent variable, and γ is the surface energy. Equation 2 can be reasonably approximated by Freund (1990),

$G=\frac{\left(1-v∕c_R\right)K_I^2}{E∕\left(1-{\mathrm{\mu }}^2\right)}=\mathrm{2\gamma },$ (3)

$\therefore v=c_R\left(1-\frac{2E\mathrm{\gamma }}{\left(1-{\mathrm{\mu }}^2\right)K_I^2}\right),$ (4)

with c_R being the Rayleigh wave speed. However, Eq. 4 is only valid for K_I > K_Ic, so to extend the range for which the equation is applicable, it has to be rewritten. Here, we consider the term $\left[1-\left(2E\mathrm{\gamma }∕\left(1-{\mathrm{\mu }}^2\right)K_I^2\right)\right]$ as equivalent to the first two terms of a Taylor series expansion, leading to this original equation:

$v=c_R\text{exp}\left(-\frac{2E\mathrm{\gamma }}{\left(1-{\mathrm{\mu }}^2\right)K_I^2}\right).$ (5)

Equation 5 fulfills the requirement of convergence to Eq. 4 for K_I > K_Ic, and additionally it produces a non-zero crack growth velocity at K_I = K_Ic and v = 0 for K_I = 0. From the transition state theory, we can write that

$v=k_0\text{exp}\left(-\frac{\mathrm{\Delta }F}{\mathit{RT}}\right)=v_0\text{exp}\left(-\frac{\mathrm{2\gamma }\left(N_A∕{\mathrm{\rho }}_A\right)}{\mathit{RT}}\right),$ (6)

where the energy difference between the initial and final states ΔF is approximated by the ratio between the energy needed to create two surfaces and the number of chemical bonds that make up this surface, so N_A is Avogadro’s constant and surface bond density (ρ_A). This approach is consistent with the approximation of ideally brittle fracture and the lattice trapping understanding of fracture (Hsieh and Thomson, 1973; Lawn et al., 1980; Michalske and Bunker, 1984; Schultz et al., 1994; Zhu et al., 2004). Putting Eqs 5 and 6 together yields:

$v={v\prime }_0\text{exp}\left[-\frac{\mathrm{2\gamma }}{\left(\mathit{RT}{\mathrm{\rho }}_A∕N_A\right)+\left(\left(1-{\mathrm{\mu }}^2\right)K_I^2∕E\right)}\right]$ (7)

or alternatively,

$v={v\prime }_0\text{exp}\left(-\frac{E^{\ast }}{\mathit{RT}+C{K}_I^2}\right),$ (8)

where ${v\prime }_0$ is the pre-exponential term, E* = 2γN_A/ρ_A and C = (1 − μ²)N_A/Eρ_A. As noted above, Eq. 8 shares the Arrhenian scaling with the approach of activation offset, and by including both thermal as well as structural noise into its variance, there is a clear parallel with the average time-to-failure predictions derived through DFBM (Kun et al., 2000; Roux, 2000; Ciliberto et al., 2001; Scorretti et al., 2001). The main difference to Eq. 1 is that instead of decreasing the magnitude of the energy barrier to bond failure, the strain energy U_strain = CK_I² acts concertedly with the thermal energy RT, increasing the excitation level of the bond in question. This collaborative action can be intuitively thought as stemming from the fact that elastic deformation and thermal expansion have its origin on how the acting stress and temperature interact with the interatomic bond potential, leading to the same outcome: a shift on the interatomic equilibrium distance.

Application to Experimental Data

While the empirical usefulness of Eq. 1 is widely accepted in glass science, here, we focus on testing the parallel validity of Eq. 8. This is challenging because literature provides a relatively broad scatter in the values of activation energy for Si–O bond rupture, ranging from approximately 50–150 kJ mol⁻¹ (Lindsay et al., 1994; Walsh et al., 2000; Del Bene et al., 2003; Zhu et al., 2005). Such a variation may result in prediction errors of crack velocity of several orders of magnitude. Therefore, we used a highly accurate multilevel CCSD(T):MP2//DFT approach for generating data on the homogeneous dissociation of the Si–O bond. Specifically, we evaluated the energy of 624 kJ mol⁻¹ for the central Si–O bond of a dimeric hydridosilsesquioxane molecule. This model is used to reflect the energetics of straining and breakage of a single silica bond at the crack tip because it is small enough to be computationally accessible, but provides a level of accuracy of <2 kJ mol⁻¹, unmatched by alternative methods on larger systems (Feller et al., 2011). Since the energy was used to create two “surfaces,” we will be using the value of 312 kJ mol⁻¹ for comparison to experimental data on region III cracking. Calculations were also performed for Si–O bond cleavage in the presence of one, two, and three H₂O molecules (mimicking region I cracking), yielding values of 164.2, 166.6, and 158.3 kJ mol⁻¹, respectively. No simulation was performed for more than three water molecules interacting with the DHS molecule; experimental data suggest that the hydration number of the Si–O–Si bond in amorphous silica lies between 2.4 and 1.8 (Fournier and Marshall, 1983). These values will be used in the following for reference.

Applying Eq. 8 to published experimental data on subcritical crack growth of silica (Suratwala and Steele, 2003) and a soda–lime silicate glass (Wiederhorn, 1967; Wiederhorn and Bolz, 1970), we first calculate the constant C. Theoretical calculations yield values of 1.13 × 10⁻⁶ and 1.05 × 10⁻⁶ m⁴ (N mol)⁻¹, respectively, for the two different glasses. In parallel, rearranging Eq. 8 allows for the experimental determination of C, i.e., using the slope of a plot of T versus K_I²,

$T\left(K_I\right)=-\frac{C}{R}{K}_I^2+\frac{E^{\ast }}{R\text{ln}\left(v_0∕v\right)}.$ (9)

In Figure 3, the relation above is applied to subcritical crack growth data of soda–lime silicate glass measured between 2 and 90°C (Wiederhorn and Bolz, 1970). The value of C does not remain constant through the complete range of temperature–stress intensity data, and even as it stabilizes there is a disparity of 4 orders of magnitude between the experimental fit and the theoretical calculation. This effectively means that the actual “conversion factor” of strain to thermal energy is much smaller than the theoretical one, which might be due to many different effects which are not covered by our approach: first, for lower crack growth velocities, the applied stress intensity factor is much closer to the threshold value K_th [the static fatigue limit, below which the crack ceases to grow (Fett et al., 2005)]. This means that the stresses around the crack tip become increasingly shielded from the applied stresses due to diffusive exchange between mobile ions in the glass and the hydronium ions in the environment, leading to an increased slope of the T × K_I² graph. Second, in parallel with the DFBM approach (Scorretti et al., 2001), the parameter C can be interpreted as a measure of structural disorder, related to how the applied stresses are preferentially concentrated on the bonds located closer to the crack tip. However, the stress concentration is assumed to follow a Gaussian distribution, and that might not reflect the actual distribution, leading to the disagreement between the experimental and theoretical values. It is also worth noting that Eq. 8 is derived under the assumption of static crack growth with constant K_I, while the experimental tests were conducted under constant load. Therefore, following the observed disparity, we used the experimentally fitted values to construct the Arrhenius plots shown in Figure 4.

FIGURE 3

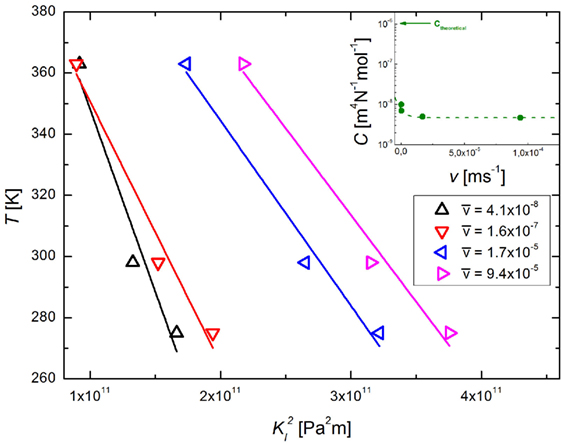
Figure 3. Determination of molar strain energy in subcritical crack growth. The temperature is plotted as a function of the square of the stress intensity factor at the crack tip for constant crack velocity. A linear fit (straight lines) yields the C-parameter. The inset shows the apparent dependence of C on crack velocity. Here, the dotted line is just a guide to the eye.

FIGURE 4

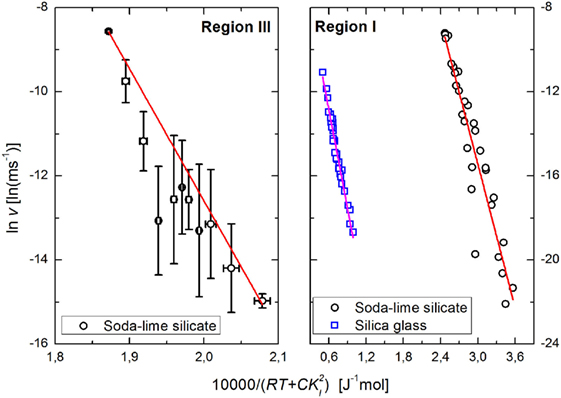
Figure 4. Rate of subcritical crack growth as a function of total stored energy based on experimental data for soda–lime silicate glass on region I (right) (Wiederhorn and Bolz, 1970) and on region III (left) (Wiederhorn, 1967) and for silica glass on region I (Suratwala and Steele, 2003) (see text for details). Lines represent linear fits.

The authors are unaware of published crack growth rates of silica glass under vacuum; therefore, the comparison has to be made using crack growth in water vapor. Silica glass exhibits accelerated water diffusion under stress (Tomozawa et al., 1991), which causes the crack surfaces to expand, creating compressive stresses and shielding the crack tip from the applied stresses (Fett et al., 2005; Wiederhorn et al., 2011). This explains the apparently anomalous results reported for silica (Suratwala and Steele, 2003), and silica aerogels (Despetis et al., 2004), where the measured crack propagation speed decreases with increasing temperature. Wiederhorn et al. (2013b) have developed a formalism that enables the direct calculation of the shielding stresses as a function of both applied stresses and temperature. The estimated activation energies for region I are 114 ± 8 kJ mol⁻¹ for the soda–lime silicate glass and 156 ± 5 kJ mol⁻¹ for silica glass; for region III the activation energy for the soda–lime silicate is 314 ± 9 kJ mol⁻¹.

As commented before, on a first approximation of ideal brittleness (Célarié et al., 2003a,b; Guin and Wiederhorn, 2004, 2006; Wiederhorn et al., 2013a,b), the only contribution to the strain release rate G during fracture is the creation of the fracture surface. Therefore, with proper knowledge of the Si–O–Si surface bond density, the energy required to break each Si–O bond can be estimated by the surface energy. As its value depends only on the type of bond that is being broken, the calculated values for glassy and crystalline silica should be similar. The surface energy of silica glass under N₂ atmosphere and at 300 K is reported (Wiederhorn, 1969) to be approximately 4.4 J m⁻²; while MD simulations (Leed and Pantano, 2003) yield an area density of Si–O–Si bonds of 7.2 bonds nm⁻², resulting on an activation energy of 360 kJ mol⁻¹. This is remarkably consistent with monocrystalline α-quartz, with values of 310 and 340 kJ mol⁻¹ [for cracks propagating on the $a<11\overline{2}0>$ plane, on directions normal to the planes $z<01\overline{1}1>$ and $r<10\overline{1}1>$, respectively] calculated using fracture (Atkinson, 1979; Timms et al., 2010) and bond density data (Bloss and Gibbs, 1963) under inert atmosphere.

The activation energy values calculated from cleavage in monocrystals and the simulation data obtained by CCSD(T):MP2//DFT agree to a remarkable extent with the results from Eq. 8, which leads us to believe that our proposed equation provides accurate predictions of crack propagation rates.

As noted initially, the principal difference between the two approaches rests on how the applied mechanical strain affects the chemical bonds directly at the crack tip. The offset approach [as seen in Eq. 1, but also revised elsewhere (Henderson et al., 1970; Bartenev, 1973)] considers that the applied stresses decrease the energy barrier for bond breakage. Some simulation studies (Gagnon et al., 2001) support this interpretation, but they also give a very different mechanistic description of crack propagation, following the coalescence of voids forming ahead of the crack tip; a model that seems to be at odds with the most recent experimental investigation (Wiederhorn et al., 2013a). A possible route for resolving this apparent discrepancy would be to combine these considerations with the aspect of concerted activation, in which the applied stresses play a role analogous to temperature, increasing the overall excitation level of the system without altering the energy profile of the chemical bonds (Stillinger, 1995; Sciortino, 2005). Thereby, it is important to acknowledge the empirical nature of both Eqs 1 and 8, if applied individually. We hypothesize that in reality, the physical reactions taking place may be best understood on the basis of simultaneous reactions of activation offset and concerted activation.

Conclusion

We considered parametrization of models for crack propagation in brittle glasses. The action of strain energy can be modeled in two empirical ways, i.e., acting either as an offset to the activation barrier for bond rupture, or concertedly with the thermal energy of the system. Both approaches provide accurate reproductions of experimental data. However, non-empirical treatment is expected to require simultaneous implementation.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Funding

The authors gratefully acknowledge financial support by the German Science Foundation through its priority program 1594, grant no. WO1220/10.

References

Atkinson, B. K. (1979). A fracture mechanics study of subcritical tensile cracking of quartz in wet environments. Pure Appl. Geophys. 117, 1011–1024. doi: 10.1007/BF00876082

CrossRef Full Text | Google Scholar

Atkinson, B. K. (1982). Subcritical crack propagation in rocks: theory, experimental results and applications. J. Struct. Geol. 4, 41–56. doi:10.1016/0191-8141(82)90005-0

CrossRef Full Text | Google Scholar

Bartenev, G. M. (1973). Theory of fracture of defect-free inorganic glasses. Mater. Sci. 6, 347–351.

Google Scholar

Bloss, F. D., and Gibbs, G. V. (1963). Cleavage in quartz. Am. Mineral. 48, 821–838.

Google Scholar

Brantut, N., Heap, M. J., Meredith, P. G., and Baud, P. (2013). Time-dependent cracking and brittle creep in crustal rocks: a review. J. Struct. Geol. 52, 17–43. doi:10.1016/j.jsg.2013.03.007

CrossRef Full Text | Google Scholar

Célarié, F., Prades, S., Bonamy, D., Ferrero, L., Bouchaud, E., Guillot, C., et al. (2003a). Glass breaks like metal, but at the nanometer scale. Phys. Rev. Lett. 90, 075504. doi:10.1103/PhysRevLett.90.075504

PubMed Abstract | CrossRef Full Text | Google Scholar

Célarié, F., Prades, S., Bonamy, D., Dickelé, A., Bouchaud, E., Guillot, C., et al. (2003b). Surface fracture of glassy materials as detected by real-time atomic force microscopy (AFM) experiments. Appl. Surf. Sci. 212–213, 92–96. doi:10.1016/S0169-4332(03)00029-1

CrossRef Full Text | Google Scholar

Ciccotti, M. (2009). Stress-corrosion mechanisms in silicate glasses. J. Phys. D Appl. Phys. 42, 214006. doi:10.1088/0022-3727/42/21/214006

CrossRef Full Text | Google Scholar

Ciliberto, S., Guarino, A., and Scorretti, R. (2001). The effect of disorder on the fracture nucleation process. Physica D 158, 83–104. doi:10.1016/S0167-2789(01)00306-2

CrossRef Full Text | Google Scholar

Del Bene, J. E., Runge, K., and Bartlett, R. J. (2003). A quantum chemical mechanism for the water-initiated decomposition of silica. Comput. Mater. Sci. 27, 102–108. doi:10.1016/S0927-0256(02)00432-9

CrossRef Full Text | Google Scholar

Despetis, F., Etienne, P., and Etienne-Calas, S. (2004). Subcritical crack growth in silica aerogel. J. Non Cryst. Solids 344, 22–25. doi:10.1016/j.jnoncrysol.2004.07.017

CrossRef Full Text | Google Scholar

Fairbarn, W., and Tate, T. (1859). On the resistance of glass globes and cylinders to collapse from external pressure; and on the tensile and compressive strength of various kind of glass. Philos. Trans. Royal Soc. London 149, 213–247. doi:10.1098/rstl.1859.0012

CrossRef Full Text | Google Scholar

Feller, D., Peterson, K. A., and Hill, J. G. (2011). On the effectiveness of CCSD(T) complete basis set extrapolations for atomization energies. J. Chem. Phys. 135, 044102. doi:10.1063/1.3613639

PubMed Abstract | CrossRef Full Text | Google Scholar

Fett, T., Guin, J.-P., and Wiederhorn, S. M. (2005). Interpretation of effects at the static fatigue limit of soda-lime-silicate glass. Eng. Fract. Mech. 72, 2774–2791. doi:10.1016/j.engfracmech.2005.07.002

CrossRef Full Text | Google Scholar

Fineberg, J., and Marder, M. (1999). Instability in dynamic fracture. Phys. Rep. 313, 1–108. doi:10.1016/S0370-1573(98)00085-4

CrossRef Full Text | Google Scholar

Fournier, R. O., and Marshall, W. L. (1983). Calculation of amorphous silica solubilities at 25° to 300°C and apparent cation hydration numbers in aqueous salt solutions using the concept of effective density of water. Geochim. Cosmochim. Acta 47, 587–596. doi:10.1016/0016-7037(83)90280-6

CrossRef Full Text | Google Scholar

Freiman, S. (2012). The fracture of glass: past, present, and future. Int. J. Appl. Glass Sci. 3, 89–106. doi:10.1111/j.2041-1294.2012.00091.x

CrossRef Full Text | Google Scholar

Freiman, S. W., Wiederhorn, S. M., and Mecholsky, J. J. (2009). Environmentally enhanced fracture of glass: a historical perspective. J. Am. Ceram. Soc. 92, 1371–1382. doi:10.1111/j.1551-2916.2009.03097.x

CrossRef Full Text | Google Scholar

Freund, L. B. (1990). Dynamic Fracture Mechanics. Cambridge: Cambridge University Press.

Google Scholar

Gagnon, G., Patton, J., and Lacks, D. J. (2001). Energy landscape view of fracture and avalanches in disordered materials. Phys. Rev. E 64, 051508. doi:10.1103/PhysRevE.64.051508

PubMed Abstract | CrossRef Full Text | Google Scholar

Griffith, A. A. (1921). The phnenomena of rupture and flow in solids. Philos. Trans. Royal Soc. London A 221, 163–198. doi:10.1098/rsta.1921.0006

CrossRef Full Text | Google Scholar

Guin, J.-P., and Wiederhorn, S. M. (2004). Fracture of silicate glasses: ductile or brittle? Phys. Rev. Lett. 92, 215502. doi:10.1103/PhysRevLett.92.215502

PubMed Abstract | CrossRef Full Text | Google Scholar

Guin, J.-P., and Wiederhorn, S. M. (2006). Surfaces formed by subcritical crack growth in silicate glasses. Int. J. Fract. 140, 15–26. doi:10.1007/s10704-006-6729-6

CrossRef Full Text | Google Scholar

Henderson, C. M. B., Graham, P. H., and Robinson, C. N. (1970). A comparison of reaction rate models for the fracture of solids. Int. J. Fract. Mech. 6, 33–40. doi:10.1007/BF00183657

CrossRef Full Text | Google Scholar

Hsieh, C., and Thomson, R. (1973). Lattice theory of fracture and crack creep. J. Appl. Phys. 44, 2051–2063. doi:10.1063/1.1662512

CrossRef Full Text | Google Scholar

Kun, F., Zapperi, S., and Herrmann, H. J. (2000). Damage in fiber bundle models. Eur. Phys. J. B 17, 269–279. doi:10.1007/PL00011084

CrossRef Full Text | Google Scholar

Lawn, B. R., Hockey, B. J., and Wiederhorn, S. M. (1980). Atomically sharp cracks in brittle solids: an electron microscopy study. J. Sci. Mater. 15, 1207–1223. doi:10.1007/BF00551810

CrossRef Full Text | Google Scholar

Leed, E. A., and Pantano, C. G. (2003). Computer modeling of water adsorption on silica and silicate glass fracture surfaces. J. Non Cryst. Solids 325, 48–60. doi:10.1016/S0022-3093(03)00361-2

CrossRef Full Text | Google Scholar

Lindsay, C. G., White, G. S., Freiman, S. W., and Wong-Ng, W. (1994). Molecular orbital study of an environmentally enhanced crack growth process in silica. J. Am. Ceram. Soc. 77, 2179–2187. doi:10.1111/j.1151-2916.1994.tb07115.x

CrossRef Full Text | Google Scholar

Michalske, T. A., and Bunker, B. C. (1984). Slow fracture model based on strained silicate structures. J. Appl. Phys. 56, 2686–2693. doi:10.1063/1.333789

CrossRef Full Text | Google Scholar

Michalske, T. A., and Bunker, B. C. (1987). Steric effects in stress corrosion fracture of glass. J. Am. Ceram. Soc. 70, 780–784. doi:10.1111/j.1151-2916.1987.tb04879.x

CrossRef Full Text | Google Scholar

Michalske, T. A., and Freiman, S. W. (1982). A molecular interpretation of stress corrosion in silica. Nature 295, 511–512. doi:10.1038/295511a0

CrossRef Full Text | Google Scholar

Roux, S. (2000). Thermally activated breakdown in the fiber-bundle model. Phys. Rev. E 62, 6164–6169. doi:10.1103/PhysRevE.62.6164

PubMed Abstract | CrossRef Full Text | Google Scholar

Schoeck, G. (1990). Thermally activated crack-propagation in brittle materials. Int. J. Fract. 44, 1–14. doi:10.1007/BF00012548

CrossRef Full Text | Google Scholar

Schultz, R. A., Jensen, M. C., and Bradt, R. C. (1994). Single crystal cleavage of brittle materials. Int. J. Fract. 65, 291–312. doi:10.1007/BF00012370

CrossRef Full Text | Google Scholar

Sciortino, F. (2005). Potential energy landscape description of supercooled liquids and glasses. J. Stat. Mech. P05015, 1–34. doi:10.1088/1742-5468/2005/05/P05015

CrossRef Full Text | Google Scholar

Scorretti, R., Ciliberto, S., and Guarino, A. (2001). Disorder enhances the effects of thermal noise in the fiber bundle model. Europhys. Lett. 55, 626–632. doi:10.1209/epl/i2001-00462-x

CrossRef Full Text | Google Scholar

Stillinger, F. H. (1995). A topographic view of supercooled liquids and glass formation. Science 267, 1935–1939. doi:10.1126/science.267.5206.1935

PubMed Abstract | CrossRef Full Text | Google Scholar

Suratwala, T. I., and Steele, R. A. (2003). Anomalous temperature dependence of sub-critical crack growth in silica glass. J. Non Cryst. Solids 316, 174–182. doi:10.1016/S0022-3093(02)01799-4

CrossRef Full Text | Google Scholar

Timms, N. E., Healy, D., Reyes-Montes, J. M., Collins, D. S., Prior, D. J., and Paul Young, R. (2010). Effects of crystallographic anisotropy on fracture development and acoustic emission in quartz. J. Geophys. Res. 115, 1–19. doi:10.1029/2009JB006765

CrossRef Full Text | Google Scholar

Tomozawa, M., Han, W.-T., and Lanford, W. A. (1991). Water entry into silica glass during slow crack growth. J. Am. Ceram. Soc. 74, 2573–2576. doi:10.1111/j.1151-2916.1991.tb06801.x

CrossRef Full Text | Google Scholar

Walsh, T. R., Wilson, M., and Sutton, A. P. (2000). Hydrolysis of the amorphous silica surface. II. Calculation of activation barriers and mechanisms. J. Chem. Phys. 113, 9191–9201. doi:10.1063/1.1320057

CrossRef Full Text | Google Scholar

Wiederhorn, S. M. (1967). Influence of water vapor on crack propagation in soda-lime glass. J. Am. Ceram. Soc. 50, 407–414. doi:10.1111/j.1151-2916.1967.tb15145.x

CrossRef Full Text | Google Scholar

Wiederhorn, S. M. (1969). Fracture surface energy of glass. J. Am. Ceram. Soc. 52, 99–105. doi:10.1111/j.1151-2916.1969.tb13350.x

CrossRef Full Text | Google Scholar

Wiederhorn, S. M., and Bolz, L. H. (1970). Stress corrosion and static fatigue of glass. J. Am. Ceram. Soc. 53, 543–548. doi:10.1111/j.1151-2916.1970.tb15962.x

CrossRef Full Text | Google Scholar

Wiederhorn, S. M., Fett, T., Rizzi, G., Fünfschilling, S., Hoffmann, M. J., and Guin, J.-P. (2011). Effect of water penetration on the strength and toughness of silica glass. J. Am. Ceram. Soc. 94, 196–203. doi:10.1111/j.1551-2916.2011.04530.x

CrossRef Full Text | Google Scholar

Wiederhorn, S. M., Evans, A. G., Fuller, E. R., and Johnson, H. (1974a). Application of fracture mechanics to space-shuttle windows. J. Am. Ceram. Soc. 57, 319–323. doi:10.1111/j.1151-2916.1974.tb10910.x

CrossRef Full Text | Google Scholar

Wiederhorn, S. M., Johnson, H., Diness, A. M., and Heuer, A. H. (1974b). Fracture of glass in vacuum. J. Am. Ceram. Soc. 57, 336–341. doi:10.1111/j.1151-2916.1974.tb10917.x

CrossRef Full Text | Google Scholar

Wiederhorn, S. M., Fett, T., Guin, J.-P., and Ciccotti, M. (2013a). Griffith cracks at the nanoscale. Int. J. Appl. Glass Sci. 4, 76–86. doi:10.1111/ijag.12025

CrossRef Full Text | Google Scholar

Wiederhorn, S. M., Fett, T., Rizzi, G., Hoffmann, M. J., and Guin, J.-P. (2013b). The effect of water penetration on crack growth in silica glass. Eng. Fract. Mech. 100, 3–16. doi:10.1016/j.engfracmech.2012.04.026

CrossRef Full Text | Google Scholar

Wondraczek, L., Mauro, J. C., Eckert, J., Kühn, U., Horbach, J., Deubener, J., et al. (2011). Towards ultrastrong glasses. Adv. Mater. Weinheim 23, 4578–4586. doi:10.1002/adma.201102795

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Q. B., and Zhao, J. (2014). A review of dynamic experimental techniques and mechanical behaviour of rock materials. Rock Mech. Rock Eng. 47, 1411–1478. doi:10.1007/s00603-013-0463-y

CrossRef Full Text | Google Scholar

Zhu, T., Li, J., Lin, X., and Yip, S. (2005). Stress-dependent molecular pathways of silica-water reaction. J. Mech. Phys. Solids 53, 1597–1623. doi:10.1016/j.jmps.2005.02.002

CrossRef Full Text | Google Scholar

Zhu, T., Li, J., and Yip, S. (2004). Atomistic configurations and energetics of crack extension in silicon. Phys. Rev. Lett. 93, 205504. doi:10.1103/PhysRevLett.93.205504

PubMed Abstract | CrossRef Full Text | Google Scholar