- FB2: Marine Biogeochemistry, Helmholtz-Zentrum für Ozeanforschung Kiel, Kiel, Germany
It is now well established that Iron (Fe) is a limiting element in many regions of the open ocean. Our current understanding of the key processes which control iron distribution in the open ocean have been largely based on thermodynamic measurements performed under the assumption of equilibrium conditions. Using this equilibrium approach, researchers have been able to detect and quantify organic complexing ligands in seawater and examine their role in increasing the overall solubility of iron. Our current knowledge about iron bioavailability to phytoplankton and bacteria is also based heavily on carefully controlled laboratory studies where it is assumed the chemical species are in equilibrium in line with the free ion association model and/or its successor the biotic ligand model. Similarly most field work on iron biogeochemistry generally consists of a single profile which is in essence a “snap-shot” in time of the system under investigation. However it is well known that the surface ocean is an extremely dynamic environment and it is unlikely if thermodynamic equilibrium between all the iron species present is ever truly achieved. In sunlit waters this is mostly due to the daily passage of the sun across the sky leading to photoredox processes which alter Fe speciation by cycling between redox states and between inorganic and organic species. Episodic deposition events, dry and wet, are also important perturbations to iron cycling as they bring in new iron to the system and alter the equilibrium between iron species and phases. Here we utilize new field data collected in the open ocean on the complexation kinetics of iron in the surface ocean to identify the important role of weak iron binding ligands (i.e., those that cannot maintain iron in solution indefinitely at seawater pH: αFeL < αFe′) in allowing transient increases in iron solubility in response to iron deposition events. Experiments with the thermal source SOTS-1 also indicate the short term impact of this species on iron solubility also with relevance to the euphotic zone. This data highlights the roles of kinetics, redox, and weaker iron binding ligands in the biogeochemical cycling of iron in the ocean.
Introduction
That Iron (Fe) is an important limiting nutrient for primary productivity over large areas of the ocean has been clearly demonstrated in iron enrichment experiments in the open ocean over the last 20 years (Martin et al., 1994; Boyd et al., 2000; de Baar et al., 2005). Since the first proposals that linked low productivity in the open ocean with distance from the coast and iron sources (Gran, 1931; Harvey, 1937), and since the first evidence showing the link between low iron and slow growth in the open ocean (Martin and Fitzwater, 1988), studies on the (geo)chemical aspects of iron biogeochemistry were mainly focused on conditions of thermodynamic equilibrium. The thermodynamically favored redox form of Fe in seawater, Fe(III), is only weakly soluble in seawater (Millero, 1998). The reduced form, Fe(II), is found in oxic waters as a transient species, primarily generated by photochemical processes (Johnson et al., 1994; Croot et al., 2008), and existing at extremely low concentrations (picomolar or less) because of rapid oxidation by O2 and H2O2 in warm surface waters. The oxidation of Fe(II) to the less soluble Fe(III) species, leads to the formation of colloidal oxyhydroxide (Kuma et al., 1996) species which coagulate and form particulate iron (Johnson et al., 1997). Dissolved iron (<0.4 μm) has been shown to be strongly organically complexed throughout the water column (Rue and Bruland, 1995; Boye et al., 2001) and is comprised of colloidal material or truly soluble (<100 kDa) complexes (Boye et al., 2010). In the absence of organic ligands iron solubility is extremely low (<80 pM) Fe (Kuma et al., 1996; Liu and Millero, 2002). Iron solubility however varies in the ocean with higher concentrations in coastal waters (Kuma et al., 1998b, 2000; Schlosser and Croot, 2009), than in the Open Ocean (Kuma et al., 1998a; Nakabayashi et al., 2001).
The main supply routes for iron to the open oceans is via upwelling or atmospheric dust deposition (Jickells et al., 2005). Dust deposition is episodic in nature and alters the equilibrium between soluble, colloidal, and particulate iron phases. The daily cycle of the sun also strongly imprints a photo-induced redox iron cycle in the euphotic zone (Johnson et al., 1994) and involves transient Fe(II) species existing (Croot et al., 2001, 2008; Roy et al., 2008) at concentrations far above that predicted by thermodynamic equilibrium calculations. Indeed it also has been known for some time that iron uptake by phytoplankton is under kinetic rather than thermodynamic control (Hudson and Morel, 1990, 1993). Thus information about the kinetics of exchange between these phases is critically important to our understanding of the biogeochemical cycling of iron in seawater as the system is normally far from any thermodynamic equilibrium state.
A key controlling factor in the kinetics is the rate of water exchange (or loss) for the inner coordination sphere of Fe, as this sets the upper rate at which ligand exchange reactions can occur. The inorganic speciation of Fe(III) in seawater is dominated by hydroxide complexes and measurements of the water exchange rate under seawater conditions for Fe′ (the sum of all the inorganic Fe(III) species) has been measured kex = 8 × 106 M−1 s−1 (Hudson et al., 1992). This is consistent with measurements in simple solutions for the individual iron hydroxy species: Fe(III) 1.6 × 102 M−1 s−1 and Fe(OH)2+ 1.2 × 105 M−1 s−1 (Grant and Jordan, 1981), (Schneider, 1988). The rate of water exchange for the aquo Fe(II), kex ∼ 1 × 107 M−1 s−1 (Helm and Merbach, 1999), is considerably faster than that of Fe(III). Once formed an iron organic complex may dissociate via either an adjunctive pathway, involving the direct attack of the incoming species on the initial complex and the formation of a ternary intermediate species, or a disjunctive pathway involving complete dissociation of the initial complex (Hering and Morel, 1990a,b). For a complete description of the mechanisms involved in the different dissociation pathways the reader is referred to Morel and Hering (1993). It has been found for many Fe(III) siderophore complexes that adjunctive pathways are important with the loss of the iron initiated by the formation of a ternary complex with another ligand (inorganic or organic) resulting in either the simple exchange of the iron or a subsequent reduction to Fe(II) via an external reductant or photochemical process followed by release of the iron from the complex (Dhungana and Crumbliss, 2005; Mies et al., 2006).
A small number of studies performed over the last 20 years have indicated that thermodynamically weak iron binding ligands, i.e., those that cannot maintain iron in solution indefinitely at seawater pH (i.e., αFeL < αFe′), may be important as transient species either as short term soluble species (Gerringa et al., 2007) or for their involvement in photochemically induced redox cycling (Kuma et al., 1995). The mesoscale iron enrichment experiments performed over the last 20 years, for a summary see de Baar et al. (2005), are now classic examples of the functioning of the iron biogeochemical cycle to a transient episodic event and how the system responds. Based on these and other recent findings we use Figure 1 to illustrate the key processes and exchange mechanisms affecting dissolved iron concentrations identified to date. Figure 1 also highlights the main natural inputs that perturb the system and prevent it from achieving “geochemical” thermodynamic equilibrium. Note that in this context iron in upwelled waters may be considered closer to equilibrium due to the water mass age and so is neglected here. In the present work we focus on the kinetics of processes involving weak ligands with regard to important iron transformation pathways in the surface ocean. In particular in the here we focus on the role that weak ligands can play in maintaining soluble iron in the surface ocean over short time scales through a series of kinetic experiments employing different analytical approaches (voltammetry and radiotracers). This work highlights the importance of kinetic processes in the temporal evolution of iron speciation and biogeochemistry in dynamic marine systems.
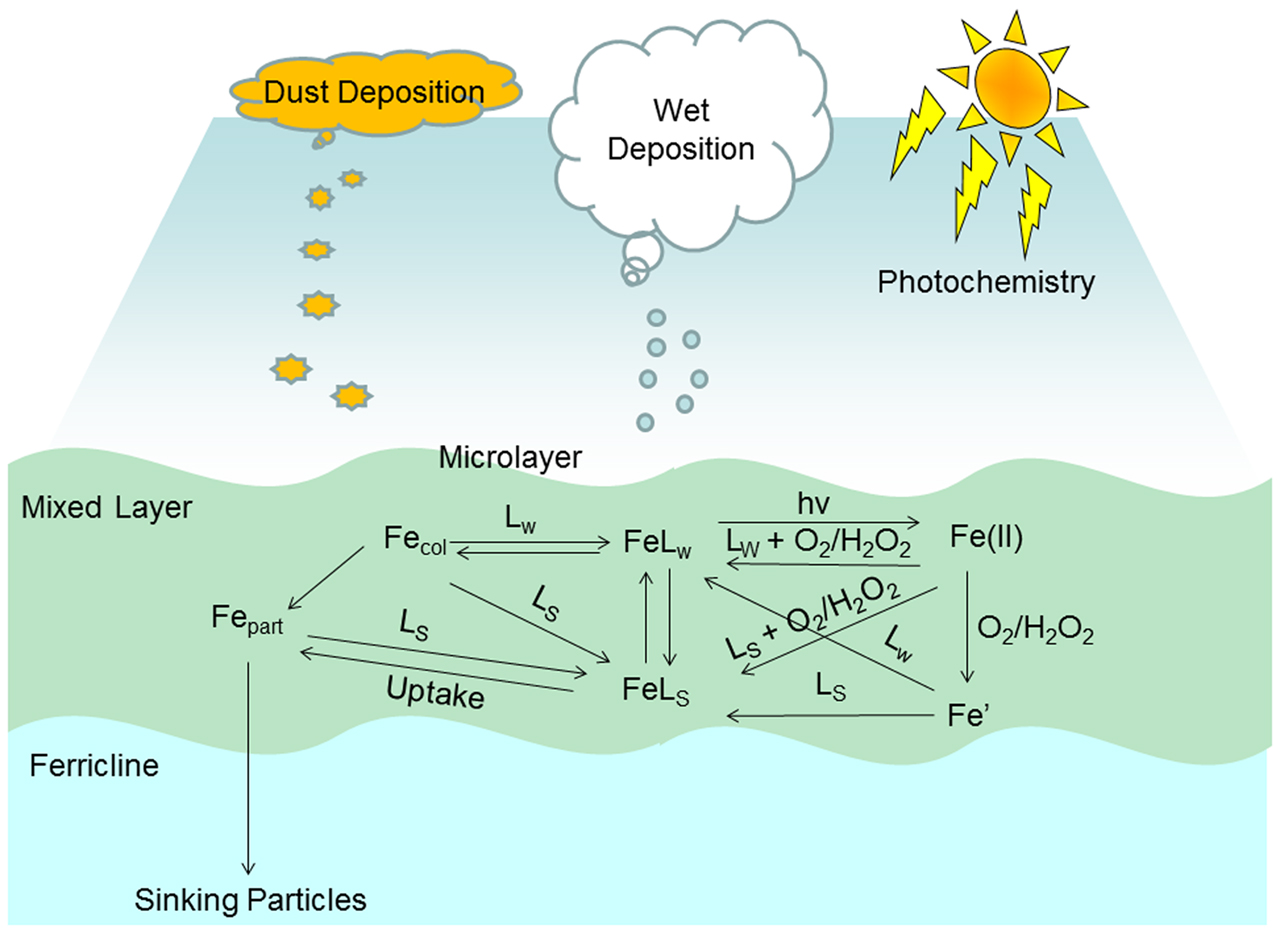
Figure 1. Schematic of key processes in the biogeochemical cycling of dissolved iron in the surface ocean. Abbreviations used in figure (see main text for details): LS, strong iron binding ligand; LW, weak iron binding ligand; FeLS, iron complexed by strong iron binding ligand; FeLw, iron complexed by weak iron binding ligand; Fe(II), all sum of all Fe(II) species; Fe′, the sum of all inorganic Fe(III) species; Fecol, colloidal iron species; Fepart, iron in the particulate phase; hv, photon flux; O2, dissolved oxygen; and H2O2, dissolved hydrogen peroxide.
Materials and Methods
Iron Speciation
Competitive ligand exchange-cathodic stripping voltammetry
In the present work we determined conditional stability constants for natural iron binding ligands using an established cathodic stripping voltammetry (CSV) technique (Croot and Johansson, 2000) utilizing the ligand 2-(2-thiazolylazo)-4-methylphenol (TAC). A brief description of the procedure for TAC is listed here: Sub-samples (20 mL) of seawater were pipetted into a series of pre-cleaned Teflon bottles (125 mL) and 100 μL of 1 M EPPS buffer [N-(2-hydroxyethyl)piperazine-N′-2-propanesulfonic acid; pKa 8.00; SigmaUltra] added. Iron was added to all but two of the bottles, yielding concentrations from 0 to 12 nM. The added Fe was left to equilibrate with the natural ligands for 1 h at laboratory temperature (21.0 ± 0.1°C). At the end of this equilibration period, 20 μL of 10 mM TAC was added and the sample left to equilibrate for a further 12 h before analysis by voltammetry (Metrohm VA757). The samples were then transferred to a Teflon cell cup, the sample deaerated for 4 min with dry nitrogen gas, subsequently the Fe(TAC)2 complexes in the sample were adsorbed onto a fresh Hg drop at an applied potential of −0.40 V for 10 min, while the sample was stirred. At the completion of the adsorption period, the stirrer was stopped and the potential was scanned using the fast linear sweep mode from −0.40 to −0.90 V at 10.1 V s−1 and the stripping current from the adsorbed Fe(TAC)2 recorded. The Teflon cups were rinsed only with MQ between analyses and the samples were run in the order of increasing Fe additions. Two +0 samples were run, as a check for possible contamination of the cell. Each Teflon bottle was consistently used for a constant Fe addition. Full details of the theory behind the CSV approach can be found in Croot and Johansson (2000). Values for the total iron binding ligand concentration (LT) and conditional stability constant (Log k) were determined by non-linear methods (Gerringa et al., 1995).
Kinetic method for Fe speciation (CSV-KIN)
Rate constants for FeL formation (kf), and FeL dissociation (kd), were determined at seawater pH using the same kinetic approach as earlier (Wu and Luther, 1995; Witter and Luther, 1998; Witter et al., 2000) with the exception that the CSV ligand used in those works, 1-Nitroso-2-Naphthol (1N2N), was replaced by TAC (Croot and Johansson, 2000). A similar approach using TAC has been made earlier by Gerringa et al. (2007), as the TAC method (Croot and Johansson, 2000) is more sensitive and better suited for Fe determination at seawater pH than 1N2N. As noted by Witter and Luther (1998), for consistency we note that Fe′ indicates all inorganic forms of Fe(III), Fe3+ is only the hexaaquo species [Fe(H2O)6]3+, and FeL is the ligand complex. Note that in the following we also use the commonly used term Fe′L, to represent the iron ligand complex formed from Fe′ and L however we are not suggesting the existence of a mixed inorganic and organic ligand complex as there is no information currently available for this with respect to the natural iron binding ligands.
Determination of kf for FeL formation
The formation rate constant, kf, of the Fe3+-organic ligand complex (represented as FeL) was estimated from the initial rate of complexation of an aliquot of Fe′ added to seawater containing natural organic ligands at ambient pH.
The rate law for formation of FeL used to calculate the formation rate constant, kf is shown below:
Experimentally this involved the addition of Fe to a seawater sample and at different time intervals, the competing ligand TAC was added and the TAC labile iron measured. Mass balance considerations resulted in the calculation of FeL. For the purposes of Eq. 2, the initial concentration of Fe′ was set to the iron concentration added (in this case typically ∼7 nM) and [L] was estimated from the amount of free ligand present at equilibrium (L = LT − FeL) as determined in the Competitive Ligand Exchange-Cathodic Stripping Voltammetry (CSV-CLE) titration.
Calculation of kd (rate of dissociation for recovery of Fe from FeL)
The dissociation rate constant, kd, for recovery of added Fe from FeL could be determined after addition of TAC to seawater which had been pre-equilibrated with an aliquot of 7 nM Fe at ambient pH. Reaction between TAC and Fe (from FeL) results in electroactive complexes which are detected at the hanging mercury drop electrode. In the present work we modified the approach of Witter and Luther (1998) to determine the dissociation rate of both weak and strong ligands. Full details can be found in the appendix to this manuscript.
Measurement of iron solubility kinetics (FESOL-KIN)
The experimental design was principally the same as described previously for iron solubility experiments (Kuma et al., 1996; Nakabayashi et al., 2002; Schlosser and Croot, 2009; Schlosser et al., 2011). An adaptation of these studies was required for the filtration of the samples, as the 0.02 μm Anotop syringe filter (Whatman) previously used (Schlosser and Croot, 2009) were not obtainable and the alternative filter material (Millipore MF) was not available in a syringe filter. The change in filter material required a new filtration system to be constructed. All the equipment used was constructed from Teflon components available commercially (Savillex). The collection vessel was a 500 mL standard jar with transfer closure and two tube ports. A 47 mm filter holder, incorporating the 47 mm diameter 0.025 μm filter (Millipore MF), was connected in between the first of the tube ports and a 200 mL reservoir tube. The sample solution was poured into the reservoir tube immediately prior to filtration. To the second tube port of the jar, vacuum tubing was attached and connected to a trace metal clean Teflon lined vacuum pump (ILMVAC MPR060E) to allow vacuum filtration of the samples.
In this work we used the radioisotope 55Fe (Perkin Elmer) for all experiments: specific activity 1985.42 MBq/mg Fe, concentration 1466.79 MBq/mL. The 55Fe solution was dissolved in 0.1 M HCl and dilution standards were produced with MQ water and acidified with Q-HCl to a pH <2. Seawater (200 mL) collected from different depths throughout the water column using trace metal clean GO-FLO sampling bottles was transferred into Teflon FEP bottles (1 L) and an aliquot of 55Fe was added to the bottles to give an addition of 21 nM. Sub-samples (20 mL) for filtration were taken after 3, 6, 24, and 48 h and were filtered through 47 mm 0.025 μm Millipore MF filters using the above described Teflon filtration unit (Savillex), the filtrate was collected in a Teflon vial. Duplicate samples of both filtered (0.025 μm) and unfiltered seawater (400 μL) were acidified and transferred into 6 mL vials in which 4.5 mL of scintillation fluid (Lumagel Plus®) were added. Sample storage, treatment, and measurement were performed at room temperature (23°C) in the isotopic container located on the RV Polarstern. The activity of the 55Fe solutions were determined by scintillation counting (Packard, Tri-Carb 2900TR) and then converted to soluble Fe concentrations, taking into account the activity of the added isotope solution and the in situ dissolved Fe concentration of each sample. Quench curves for 55Fe were produced by adding an identical amount of radiotracer and scintillation fluid to a series of samples containing a range of seawater additions.
Kinetic analysis of iron solubility
This approach has recently been described (Croot et al., 2011) however a brief account is given here. Starting from the mass balance for soluble iron in seawater:
Where [Fe′] represents here the sum of all the inorganic species [predominantly ] and [FeLi] is the organically bound iron and Li classes of natural organic ligands. The speciation of Fe(II) is not considered in this case, as due to the long equilibration times used in these experiments almost all Fe(II) should have been oxidized. Reactions between one class of the natural ligands and Fe′ can be expressed as:
L′ is the Fe binding ligand not already bound to Fe(III). The equilibrium expression is then:
is the conditional stability constant under the specific conditions in seawater (in this case pH 8.0) with respect to Fe′. To convert to the conditional stability constant for FeL with respect to free Fe3+, the relationship between Fe′ and Fe3+, αFe′ = [Fe′]/[Fe3+], can be used (e.g., = αFe′ ).
The approach applied here uses the assumption that the detected decrease in soluble iron with time is due to the exchange of Fe between the weak organic ligands and the colloidal phase which does not pass through the filter. This assumption is supported by the finding that inorganic iron colloids will rapidly form due to oversaturation in the solution (Nowostawska et al., 2008) and be considerably larger (Hove et al., 2007, 2008) than the cutoff of the filter (Millipore MF 0.025 μm). Earlier work by Okumura confirms that in the absence of a strong chelator over 95% of the Fe is found in the >0.025 μm fraction (Okumura et al., 2004).
The formation and dissociation of Fe complexes are thus described by Eqs 4a and 4b from above. We now further assume that the ligands can be divided into two classes, a strong ligand (LS) that is practically inert to dissociation and a weaker ligand (LW) that at equilibrium is not able to keep iron in solution. The time dependence of the soluble Fe fraction can then be described by the following equation, assuming that the formation of both weak and strong complexes is equally fast.
Fesol is the detected soluble iron, FeLS is the concentration of the strong ligand and FeLW is the concentration of the weaker ligands, which at thermodynamic equilibrium do not prevent the precipitation of iron from solution, and k is the observed dissociation rate of the weaker iron organic complexes. The measured values of Fesol are fitted then to Eq. 6 using a non-linear least squares fitting procedure implemented in Labview™ (National Instruments).
Examination of the influence of on iron solubility kinetics
For a limited number of iron solubility experiments we also examined the influence of on the solubility of iron by additions of SOTS-1 [Di(4-carboxybenzyl)hyponitrite; Molecular weight 330.3 gmol−1; Heller and Croot, 2010a] as a thermal source. SOTS-1 is an azo-compound which can be stored stably at −80°C but at higher temperatures decomposes thermally to yield either directly or indirectly electron rich carbon-centered radicals that react with O2 to yield carbocations and (Ingold et al., 1997). Five hundred micrograms aliquots of SOTS-1 were used as received (Cayman Chemicals) and stored at −80°C until required. Immediately prior to the start of any experiment the 500 μg SOTS-1 aliquots were dissolved in DMSO (Fluka, puriss p.a. ≥99.9%) before further dilution in seawater. The final concentration calculated for produced from SOTS-1 in this study was 1.51 μM (500 μg SOTS-1 in 200 μL DMSO, 40 μL in 200 mL). Experiments in which only DMSO was added showed no discernable difference when compared to the controls (no DMSO, no SOTS-1). For the experiments presented in this work, we used paired samples following the same protocol as for the iron solubility kinetics experiments described above. After the addition of the radiotracer (see above) to both samples, SOTS-1 was added immediately to one of the paired samples (experimental) and the other was left unamended (control). The iron solubility was assessed at different time points as described above. In the current work we use the ratio between the experimental (E) and the control (C), ratio = [Fesol]E/[Fesol]C, to assess the impact of on iron solubility.
Results and Discussion
Iron Kinetics as Determined by CSV
Kinetic experiments (Table 1) were performed on samples from the chlorophyll maximum along a west to east transect in the Tropical North Atlantic in Oct/Nov 2002 during the Meteor 55 research expedition. Data on the dissolved iron concentrations found along this transect have been published previously (Croot et al., 2004). The results of the five kinetic experiments performed can be found in Table 1. Figure 2 illustrates the time course in TAC labile Fe as a function of the reaction time (here denotes as the TAC exchange time) for two different initial time points; immediately and 14 h after the addition of Fe to the sample. In Figure 2 it can be clearly seen that the amount of TAC labile iron decreases with the time since iron addition and that much of this iron was recoverable after the addition of TAC. The gradual increase in the TAC labile Fe is interpreted as the exchange of all the weakly complexed Fe with TAC, though it will ultimately include a contribution from strong iron complexes related to the thermodynamic equilibrium finally established between TAC and the natural ligands. Figure 3 illustrates the decrease in the labile Fe(TAC) concentration with incubation time resulting from the increase in FeL as the natural ligands complex the iron in solution.
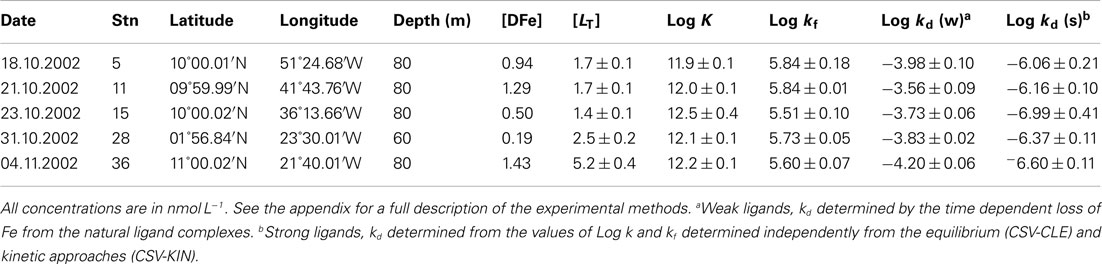
Table 1. CSV-KIN: results from the Meteor Expedition (M55) in the Tropical North Atlantic: Formation and Dissociation rates of natural iron ligands as determined by CSV.
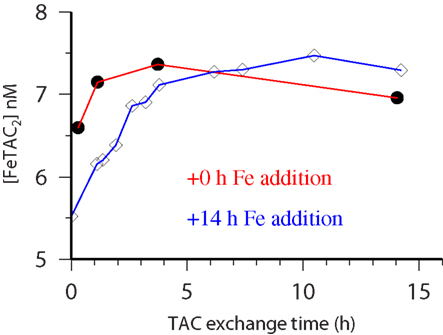
Figure 2. CSV-KIN: time course of recovery of Fe by TAC from natural iron binding ligands. Water sample is from 60 m at Station 28 (see Table 1 for more details) during the Meteor 55 cruise. Black circles TAC added immediately after Fe addition, open diamonds, TAC added 14 h after iron addition.
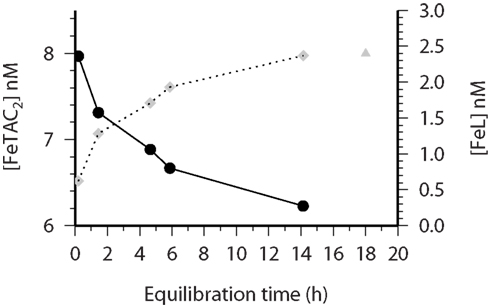
Figure 3. CSV-KIN: time course of initial Fe(TAC)2 (closed circles) concentrations, black circles (solid line) measured over the course of a 14 h incubation experiment (at t = 0 Fe was added to the sample, at subsequent time points a subsample was removed, TAC added and the labile Fe measured by CSV). The corresponding FeL concentration, as determined by mass balance, is plotted as gray diamonds (dotted line). The gray triangle represents the [L] determined by the conventional thermodynamic CSV titration after 18 h equilibration between the added Fe and TAC. Water sample is from 80 m at Station 36 (see Table 1 for more details) during the Meteor 55 cruise.
Upon addition of TAC the exchange of iron between the natural ligands and TAC begins. Figure 4 illustrates that this exchange is effectively come to equilibrium within 6 h and the resulting Fe(TAC) concentration is identical to that found in the 12 h equilibration used in the determination of the thermodynamic data (Croot and Johansson, 2000). It is clear though from the data in Figure 4 that equilibration times less than 6 h would be insufficient to reach equilibrium. Data like this for the other ligands used in the CSV determination of iron organic complexation (Rue and Bruland, 1995; van den Berg, 2006) is urgently needed to address this issue as some studies have incorporated equilibration times as short as 15 min.
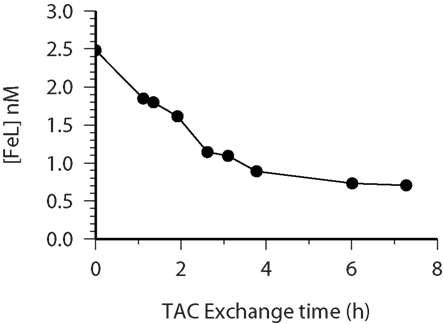
Figure 4. CSV-KIN: time course of FeL (closed circles) concentrations as determined by mass balance from repeated CSV measurements over 8 h. This data is used for the determination of kd. The samples had been equilibrated with Fe for 14 h prior to the addition of TAC. Water sample is from 60 m at Station 28 (see Table 1 for more details) during the Meteor 55 cruise.
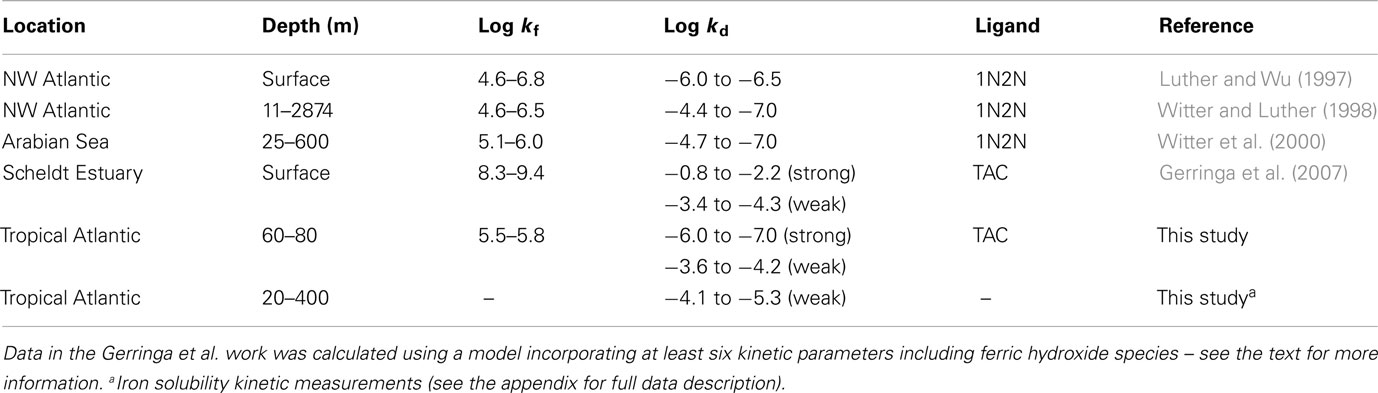
Estimates of the formation rate constant for the natural iron complexes were relatively constant throughout the samples measured (Table 1) and similar to other open ocean studies (Table 2). In our study kf values were slightly lower than that found for the siderophore desferrioxamine B (DFO-B), 2 × 106 M−1 s−1 (Hudson et al., 1992) but is similar to measurements of other model Fe ligands (Witter et al., 2000). Dissociation rates found in our work were also similar to other published data from the open ocean (Tables 1 and 2).
Comparison with the estuarine data of Gerringa et al. (2007) revealed problems with their model based results, as they indicate that the thermodynamically stronger ligands have both faster dissociation and formation kinetics than the weak ligands. It is highly unlikely that the formation rates for the strong ligands are faster than the water exchange for Fe′ in seawater 8 × 106 M−1 s−1 (Hudson et al., 1992). While this is mathematically feasible it does not make chemical sense and indicates that their model was optimizing for the stability constant (K) of the process and that there were insufficient constraints on the kinetic rates. This can easily arise when there are six or more independent variables but only one or two measured components and no other constraints in place.
Recently there have been a number of general speciation models (thermodynamic) that have treated iron complexation in the ocean as a continuum of ligand binding strengths based on humic complexation (Hiemstra and van Riemsdijk, 2006; Stockdale et al., 2011). In these models there is a relationship between the ligand concentration and the binding strength, with weak ligands present in high concentrations and only trace amounts of strong ligands. Criticisms of this approach with regard to iron usually involve the production of siderophores by organisms as they are specific strong binding ligands capable of being produced in high concentrations in response to iron limitation (Vraspir and Butler, 2009; Butler and Theisen, 2010). However in terms of weak ligands this approach may have some validity but is yet to be applied in a kinetic approach and may be important for resolving the underlying processes occurring in the colloidal phase with regard to humic complexation (Batchelli et al., 2010).
Iron Solubility Kinetics
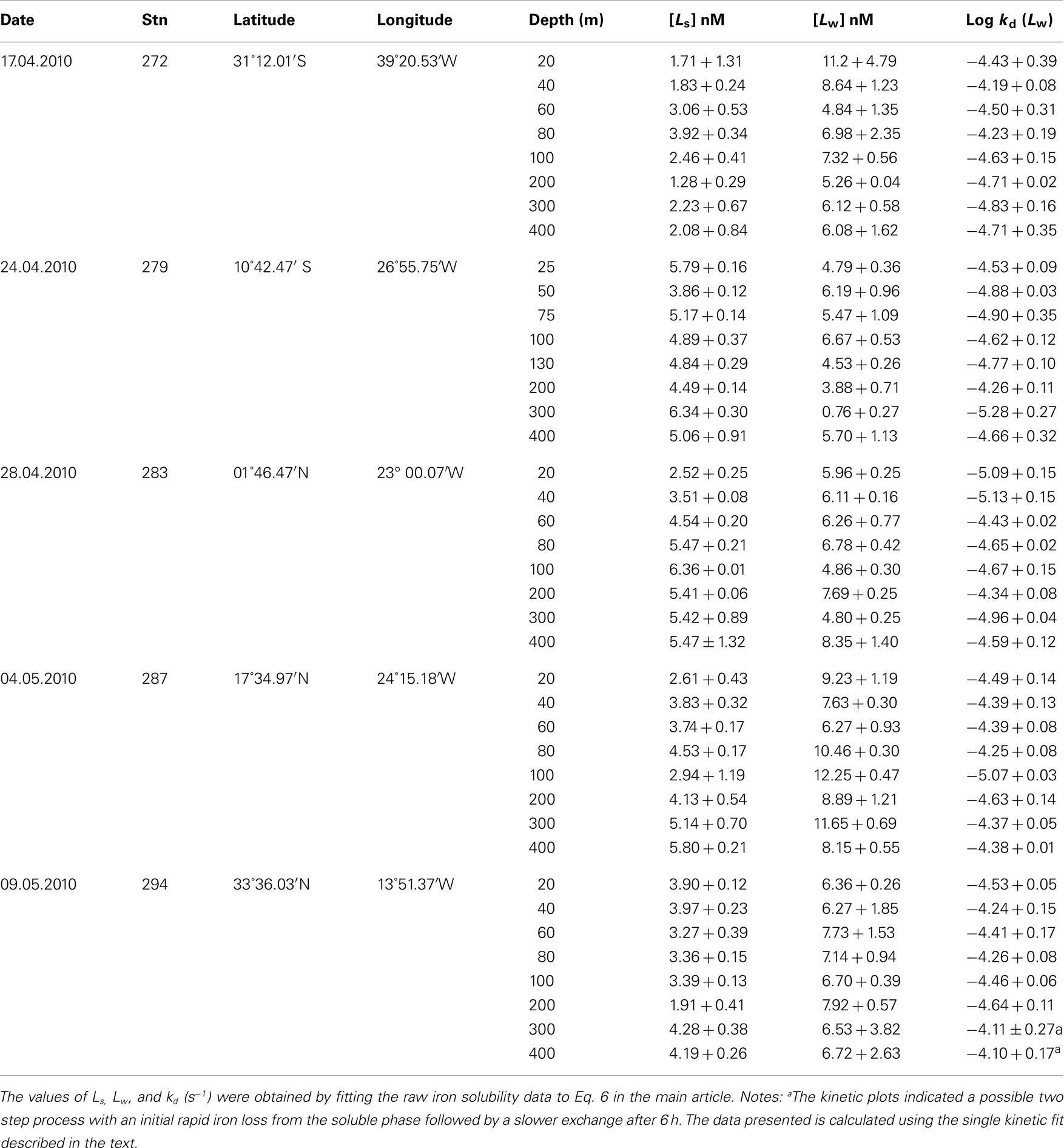
Experiments on the kinetics of soluble iron formation and loss were performed at five stations (Table A1 in Appendix) along a Atlantic meridional section during Polarstern expedition ANTXXVI-4 in April/May 2010. In all experiments the concentration of soluble Fe that passed through the Millipore MF filter decreased with time. Figure 5 shows the vertical distribution of soluble Fe over time after iron addition at station 294. Overall most data fitted the exponential decay model well and suggested the presence of a weaker Fe binding ligand which was exchanged over the course of the experiment into the colloidal/particulate phase and with any remaining strong ligand.
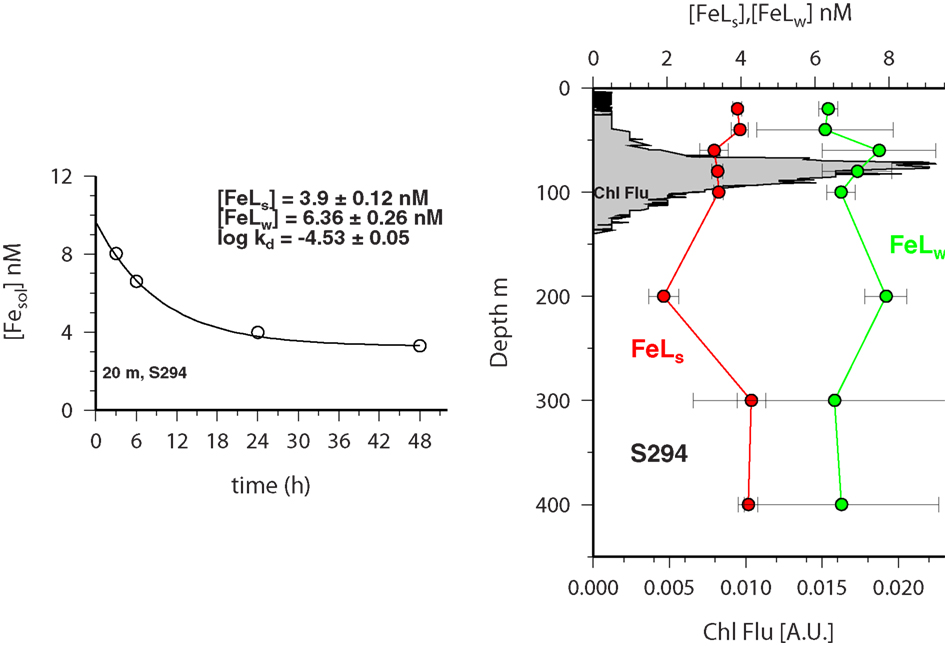
Figure 5. FESOL-KIN: (left) example of fitting equation to Fe solubility (<0.025 μm) data for sample from 20 m depth at S294. (Right) Vertical distribution FeLS and FeLW (see text for details of how determined) in the top 400 m of the water column at station 294 during ANTXXVI-4. The chlorophyll fluorescence profile is also shown (gray shading; right).
The measured dissociation rates for the weak ligands are slightly slower than the values obtained by CSV (see above and Table 2), and this may suggest that the dissociation of the weak iron binding ligands is slightly accelerated in the presence of TAC due to an adjunctive pathway in addition to the disjunctive pathway seen in the radiotracer experiments (see also the electronic appendix to this manuscript). Overall this data indicates the importance of weak ligands in the soluble size range for maintaining iron in solution over short timescales. This finding is particularly relevant to the processes occurring during atmospheric deposition (Baker and Croot, 2010; Duggen et al., 2010) of iron and would help to solubilize iron at the surface and increase the transport of soluble iron throughout the mixed layer and into pycnocline. The estimated lifetime for the retention of iron by weak ligands is from 1 to 2 days, which is significantly shorter than the residence time for dissolved iron in surface waters (weeks to months) of the same region (Croot et al., 2004). This strongly suggests that weakly complexed iron plays an important role in the exchange between soluble and colloidal iron fractions and that colloidal iron is important over longer time scales for maintaining dissolved iron levels (Wu et al., 2001; Bergquist and Boyle, 2006; Bergquist et al., 2007).
Comparison with the CSV data also suggests that TAC can rapidly remove iron from the weaker complexes as solubility measurements with radiotracers indicate that the concentration of soluble iron decreases with time to a constant value while Figure 3 illustrates that FeL measured by CSV increases with time to a constant value. Thus it appears that the weak ligands that solubilize iron also react within the time scale of the CSV measurement (i.e., minutes) to exchange their iron with TAC suggesting a rapid adjunctive mechanism accelerated by the presence of 10 μM TAC. In the case of the natural ligands this process is considerably slower due to the much lower concentrations of ligands encountered. The rate of exchange between the natural ligands and TAC is slightly faster than that observed with 55Fe and suggests a significant adjunctive reaction is occurring in the presence of TAC (see the appendix to this manuscript for details) but it is assumed that the dissociation kinetics (Tables 1 and 2) for the iron complexes in the absence of TAC is of a predominantly disjunctive character.
Our modeling approach is similar to that used recently by Schlosser et al. (2011), with the exception that we focus solely on the soluble Fe and not Fe adsorbed to the bottle walls or retained as colloids or particulates on the filter. We also make the assumption that initially most of the added Fe is complexed by soluble weak ligands which slowly exchange with colloidal sized ligands (Schlosser et al., 2011). Wall adsorption however is believed to be a significant sink for added iron in these experiments and is important to consider in the choice of equipment and experimental design (Fischer et al., 2007).
Impact of on iron solubility
The suggestion that can dissolve particulate sources of iron, is still very much under debate. Voelker and Sedlak (1995) found in their pulse radiolysis studies that did not react with colloidal Fe(III). They observed that at pH values greater than 6 the Fe(II) concentration decreased due to formation of unreactive amorphous Fe(OH)3. More recently Fujii et al. (2006) suggested from their work that can reduce Fe(III) present in amorphous ferric oxides. In our own work, we examined the effect of on dissolved Fe formed upon direct addition of Fe to seawater, and found no increase in soluble Fe (Heller and Croot, 2011) or in the loss rate of (Heller and Croot, 2010c). We also used a thermal source of (Heller and Croot, 2010a) that allows a first order controlled release of to follow the induced dissolution of iron from atmospheric dust. This work was performed in the presence of 1 mM of the strong Fe(II) chelator Ferrozine (FZ) in order to trap any Fe(II) formed during the experiment. Performed under close to natural conditions our results strongly suggested that is not a significant pathway for the dissolution of dust in the ocean (Heller and Croot, 2011). However may still play be important for redox cycling between soluble and colloidal phases of iron in dust impacted regions.
In the present work we obtained data for the influence of on the solubility of Fe at three stations (279, 287, and 292) along a meridional transect in the Atlantic (ANTXXVI-4). At station 279 a full depth profile in the top 400 m was investigated whereas at station 287 and 292 only one depth was sampled in the mixed layer to address this issue in the surface ocean. In the single samples from station 287 and 292 the solubility of iron increased in the bottles to which had been added in the samples which were filtered after 3 and 6 h and showed almost identical values after 24 h, this can be seen in Figure 6 where we plot the ratio of the experimental sample (i.e., seawater with SOTS-1 added) over the control sample (i.e., seawater without SOTS-1 added). Our results are consistent with the flux from SOTS-1 which decays exponentially (Heller and Croot, 2010a) with time (Figure 6) to almost negligible fluxes after 24 h. It should be noted that while the production flux of is known as a function of time in this case, the pseudo steady state concentration will vary proportionally to the decay rate of in the sample which is itself dependent on reactivity with Cu, Fe, Mn, and some organic species (e.g., quinones; Heller and Croot, 2010c). Interestingly the apparent maximum for the soluble iron was found at the 6 h time point at both stations indicating that a transient species such as Fe(II) may have been responsible for this result and required time to accumulate in the initial stages but decayed away under lower flux conditions. Reactivity with appears to be related to the availability of an accessible coordination site on the Fe complex, which is also related to the stability of the complexes (Dhungana and Crumbliss, 2005) thus the weaker FeEDTA complex is significantly more reactive than the stronger complexes ferrioxamine B and FeDTPA (Fisher et al., 2004). This suggests that most likely reacts with weakly bound iron and facilitates its release, while strongly bound iron is inert. Once released the Fe(II) may also react with leading to a rapid redox cycle between inorganic Fe(II) and Fe(III) whose turn over rate is related to the flux. The lag time before achieving the maximum soluble Fe may then be related to a slow reactivity between the weak iron binding ligand relative to Fe′. Further work is needed however to fully elucidate this mechanism.
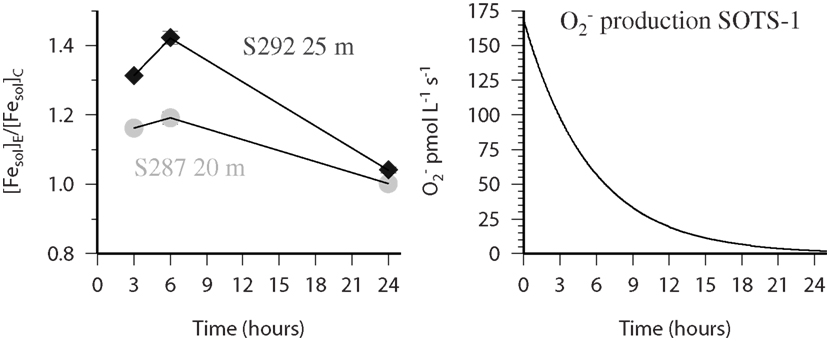
Figure 6. FESOL-KIN: (left) near surface samples from Station 287 (gray circles) and 292 (black diamonds) during ANTXXVI-4 which were spiked with 55Fe and (SOTS-1). Shown is the ratio ([Fesol]El/[Fesol]C) of the data obtained from paired bottles where the soluble Fe was measured in both the presence (experimental-E) and absence (control-C) of the thermal source SOTS-1. (Right) Time course of the production flux of from the thermal decay of SOTS-1 in the experimental treatment (see text for more details).
For the vertical profile collected at station 279 there was no statistically significant variation (paired t-test) from unity for the ratio between the soluble iron determined in the SOTS amended treatment and the control for samples below 100 m. However in the upper 100 m (Figure 7) there were significant differences observed. Initially all samples in the upper 100 m had ratios lower than 1 and with time the deeper samples (75 and 100 m) converged toward a ratio of 1. Interestingly the sample from 25 m continued to decrease with time to be at 0.46 after 48 h. The sample from 50 m however behaved very differently with the ratio increasing with time to 1.18 after 48 h. The reasons for these differences may be related to vertical differences in redox reactions initiated by the presence of ; previous work has shown that predominantly reacts with Cu in surface waters to form Cu(I) (Heller and Croot, 2010c, 2011), though reactions with CDOM may also be important in Tropical regions(Heller and Croot, 2010b) and as the redox cycling of Mn is also influenced by (Hansard et al., 2011) reactions with Mn may also be important in dust impacted regions where Mn is high (Shiller, 1997), such as here at S279. Superoxide reactions with CDOM may create or destroy iron binding ligands while reactions with other trace metals will reduce the amount of available to react with iron but may additionally provide other oxidants or reductants that react with iron. Further work is on-going to determine the critical processes at work here in the Tropical ocean and at present we lack key data on the cross reactivity between metals and Mn redox cycling in particular.
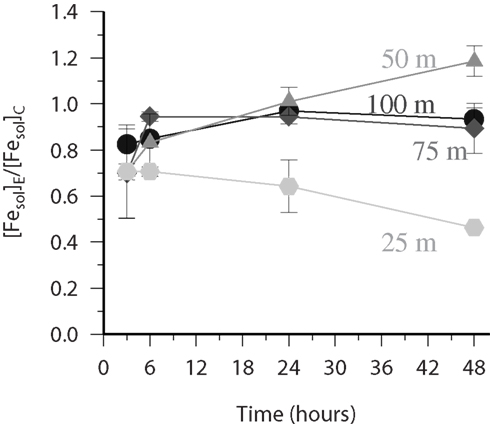
Figure 7. FESOL-KIN: experiment at S279 during ANTXXVI-4 to which a thermal source of (SOTS-1) was added. Time variation of the ratio ([Fesol]E/[Fesol]C) of the data obtained from paired bottles where the soluble Fe was measured in both the presence (experimental-E) and absence (control-C) of the thermal source SOTS-1 for samples from the upper 100 m (25 m hexagons, 50 m triangles, 75 m diamonds, 100 m circles). There was no statistical significant variation (as assessed by paired t-test) in the ratio for samples below 100 m.
The initial fluxes from the decay of SOTS-1 in the experiments was estimated to be 4 (Experiment at S279) to 10 times (all other experiments) higher than would be found in situ based on measured photochemical production rates in the open ocean (Heller and Croot, 2010a). The higher flux of may have also influenced the results by altering the balance between redox cycling and complexation reactions so that a more intense redox cycle was initiated. As the fluxes decrease exponentially with time typical surface open ocean midday fluxes would have been reached after 6–12 h and continued to decrease with time in essence simulating the decrease in the flux after midday or midday fluxes at deeper depths in the water column. Future experiments with an increased sampling frequency would allow a better estimation of these processes at natural levels, as the first order decay of SOTS allows for a range of flux concentrations to be evaluated over the course of a single experiment.
Author Contributions
Peter L. Croot performed the voltammetric analysis, and Maija I. Heller undertook the radiotracer work, both authors contributed equally to the writing of this manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like to express their deep thanks and appreciation to the crews of the R. V. Polarstern (ANTXXVI-4) and Meteor. This work was in part supported by grants awarded to Peter L. Croot as part of the BMBF Verbundsprojekt SOPRAN2 (IG03) and the DFG project ADIOS-BAO (CR145/18-1). This work is a contribution to German SOLAS (SOPRAN). This work is a contribution of the Sonderforschungsbereich 754 “Climate – Biogeochemistry Interactions in the Tropical Ocean” (www.sfb754.de). Financial support for this work was provided by the Deutsche Forschungsgemeinschaft (DFG) via grants to Peter L. Croot (CR145/2-1, CR145/7-1 CR145/15-1, and SFB754 B5).
References
Baker, A. R., and Croot, P. L. (2010). Atmospheric and marine controls on aerosol iron solubility in seawater. Mar. Chem. 120, 4–13.
Batchelli, S., Muller, F. O. L. L., Chang, K.-C., and Lee, C.-L. (2010). Evidence for strong but dynamic iron-humic colloidal associations in humic-rich coastal waters. Environ. Sci. Technol. 44, 8485–8490.
Bergquist, B. A., and Boyle, E. A. (2006). Dissolved iron in the tropical and subtropical Atlantic Ocean. Global Biogeochem. Cycles 20, 247–278.
Bergquist, B. A., Wu, J., and Boyle, E. A. (2007). Variability in oceanic dissolved iron is dominated by the colloidal fraction. Geochim. Cosmochim. Acta 71, 2960–2974.
Boyd, P. W., Watson, A., Law, C. S., Abraham, E., Trull, T., Murdoch, R., Bakker, D. C. E., Bowie, A. R., Buesseler, K. O., Chang, H., Charette, M., Croot, P. L., Downing, K., Frew, R., Gall, M., Hadfield, M., Hall, J., Harvey, M., Jameson, G., Laroche, J., Liddicoat, M., Ling, R., Maldonado, M., Mckay, R. M., Nodder, S., Pickmere, S., Pridmore, R., Rintoul, S., Safi, K., Sutton, P., Strzepek, R., Tannenberger, K., Turner, S., Waite, A., and Zeldis, J. (2000). Mesoscale iron fertilisation elevates phytoplankton stocks in the polar Southern Ocean. Nature 407, 695–702.
Boye, M., Nishioka, J., Croot, P., Laan, P., Timmermans, K. R., Strass, V. H., Takeda, S., and De Baar, H. J. W. (2010). Significant portion of dissolved organic Fe complexes in fact is Fe colloids. Mar. Chem. 122, 20–27.
Boye, M., Van Den Berg, C. M. G., De Jong, J. T. M., Leach, H., Croot, P. L., and De Baar, H. J. W. (2001). Organic complexation of iron in the Southern Ocean. Deep Sea Res. A 48, 1477–1497.
Butler, A., and Theisen, R. M. (2010). Iron(III)-siderophore coordination chemistry: reactivity of marine siderophores. Coord. Chem. Rev. 254, 288–296.
Croot, P. L., Bluhm, K., Schlosser, C., Streu, P., Breitbarth, E., Frew, R., and Van Ardelan, M. (2008). Regeneration of Fe(II) during EIFeX and SOFeX. Geophys. Res. Lett. 35, L19606.
Croot, P. L., Bowie, A. R., Frew, R. D., Maldonado, M., Hall, J. A., Safi, K. A., La Roche, J., Boyd, P. W., and Law, C. S. (2001). Retention of dissolved iron and FeII in an iron induced Southern Ocean phytoplankton bloom. Geophys. Res. Lett. 28, 3425–3428.
Croot, P. L., Heller, M. I., Schlosser, C., and Wuttig, K. (2011). “Utilizing radio-isotopes for trace metals speciation measurements in seawater,” in Radioisotopes – Applications in Physical Sciences, ed. N. Singh (Intech), 247–278.
Croot, P. L., and Johansson, M. (2000). Determination of iron speciation by cathodic stripping voltammetry in seawater using the competing ligand 2-(2-Thiazolylazo)-p-cresol (TAC). Electroanalysis 12, 565–576.
Croot, P. L., Streu, P., and Baker, A. R. (2004). Short residence time for iron in surface seawater impacted by atmospheric dry deposition from Saharan dust events. Geophys. Res. Lett. 31, L23S08.
de Baar, H. J. W., Boyd, P. W., Coale, K. H., Landry, M. R., Tsuda, A., Assmy, P., Bakker, D. C. E., Bozec, Y., Barber, R. T., Brzezinski, M. A., Buesseler, K. O., Boye, M., Croot, P. L., Gervais, F., Gorbunov, M. Y., Harrison, P. J., Hiscock, W. T., Laan, P., Lancelot, C., Law, C. S., Levasseur, M., Marchetti, A., Millero, F. J., Nishioka, J., Nojiri, Y., Van Oijen, T., Riebesell, U., Rijkenberg, M. J. A., Saito, H., Takeda, S., Timmermans, K. R., Veldhuis, M. J. W., Waite, A. M., and Wong, C.-S. (2005). Synthesis of 8 iron fertilization experiments: from the iron age to the age of enlightenment. J. Geophys. Res. 110, C09S16.
Dhungana, S., and Crumbliss, A. (2005). Coordination chemistry and redox processes in siderophore-mediated iron transport. Geomicrobiol. J. 22, 87–98.
Duggen, S., Olgun, N., Croot, P., Hoffmann, L., Dietze, H., Delmelle, P., and Teschner, C. (2010). The role of airborne volcanic ash for the surface ocean biogeochemical iron cycle: a review. Biogeosciences 7, 827–844.
Fischer, A. C., Kroon, J. J., Verburg, T. G., Teunissen, T., and Wolterbeek, H. T. (2007). On the relevance of iron adsorption to container materials in small-volume experiments on iron marine chemistry: Fe-55-aided assessment of capacity, affinity and kinetics. Mar. Chem. 107, 533–546.
Fisher, A. E. O., Maxwell, S. C., and Naughton, D. P. (2004). Superoxide and hydrogen peroxide suppression by metal ions and their EDTA complexes. Biochem. Biophys. Res. Commun. 316, 48–51.
Fujii, M., Rose, A. L., Waite, T. D., and Omura, T. (2006). Superoxide-mediated dissolution of amorphous ferric oxyhydroxide in seawater. Environ. Sci. Technol. 40, 880–887.
Gerringa, L. J. A., Herman, P. M. J., and Poortvliet, T. C. W. (1995). Comparison of the linear van den Berg/Ruzic transformation and a non-linear fit of the Langmuir isotherm applied to Cu speciation data in the estuarine environment. Mar. Chem. 48, 131–142.
Gerringa, L. J. A., Rijkenberg, M. J. A., Wolterbeek, H. T., Verburg, T. G., Boye, M., and Baar, H. J. W. D. (2007). Kinetic study reveals weak Fe-binding ligand, which affects the solubility of Fe in the Scheldt estuary. Mar. Chem. 103, 30–45.
Gran, H. H. (1931). On the Conditions for Production of Plankton in the Sea. Rapports et Proces-Verbaux des Reunions Conseil International pour l’Exploration de la Mer, Copenhague, 75, 37–46.
Grant, M., and Jordan, R. B. (1981). Kinetics of solvent water exchange on iron(III). Inorg. Chem. 20, 55–60.
Hansard, S. P., Easter, H. D., and Voelker, B. M. (2011). Rapid reaction of nanomolar Mn(II) with superoxide radical in seawater and simulated freshwater. Environ. Sci. Technol. 45, 2811–2817.
Heller, M. I., and Croot, P. L. (2010a). Application of a superoxide (O2-) thermal source (SOTS-1) for the determination and calibration of O2- fluxes in seawater. Anal. Chim. Acta 667, 1–13.
Heller, M. I., and Croot, P. L. (2010b). Kinetics of superoxide reactions with dissolved organic matter in tropical Atlantic surface waters near Cape Verde (TENATSO). J. Geophys. Res. 115, C12038.
Heller, M. I., and Croot, P. L. (2010c). Superoxide decay kinetics in the southern ocean. Environ. Sci. Technol. 44, 191–196.
Heller, M. I., and Croot, P. L. (2011). Superoxide decay as a probe for speciation changes during dust dissolution in tropical Atlantic surface waters near Cape Verde. Mar. Chem. 126, 37–55.
Helm, L., and Merbach, A. E. (1999). Water exchange on metal ions: experiments and simulations. Coord. Chem. Rev. 187, 151.
Hering, J. G., and Morel, F. M. M. (1990a). “The kinetics of trace metal complexation: implications for metal reactivity in natural waters,” in Aquatic Chemical Kinetics: Reaction Rates of Processes in Natural Waters, ed. W. Stumm (New York: John-Wiley & Sons).
Hering, J. G., and Morel, F. M. M. (1990b). Kinetics of trace metal complexation: ligand exchange reactions. Environ. Sci. Technol. 24, 242–252.
Hiemstra, T., and van Riemsdijk, W. H. (2006). Biogeochemical speciation of Fe in ocean water. Mar. Chem. 102, 181–197.
Hove, M., Van Hille, R. P., and Lewis, A. E. (2007). Iron solids formed from oxidation precipitation of ferrous sulfate solutions. AIChE J. 53, 2569–2577.
Hove, M., Van Hille, R. P., and Lewis, A. E. (2008). Mechanisms of formation of iron precipitates from ferrous solutions at high and low pH. Chem. Eng. Sci. 63, 1626–1635.
Hudson, R. J. M., Covault, D. T., and Morel, F. M. M. (1992). Investigations of iron coordination and redox reactions in seawater using 59Fe radiometry and ion-pair solvent extraction of amphiphilic iron complexes. Mar. Chem. 38, 209–235.
Hudson, R. J. M., and Morel, F. M. M. (1990). Iron transport in marine phytoplankton: kinetics of cellular and medium coordination reactions. Limnol. Oceanogr. 35, 1002–1020.
Hudson, R. J. M., and Morel, F. M. M. (1993). Trace metal transport by marine microorganisms: implications of metal coordination kinetics. Deep Sea Res. A 40, 129–150.
Ingold, K. U., Paul, T., Young, M. J., and Doiron, L. (1997). Invention of the first azo compound to serve as a superoxide thermal source under physiological conditions: concept, synthesis, and chemical properties. J. Am. Chem. Soc. 119, 12364–12365.
Jickells, T. D., An, Z. S., Andersen, K. K., Baker, A. R., Bergametti, G., Brooks, N., Cao, J. J., Boyd, P. W., Duce, R. A., Hunter, K. A., Kawahata, H., Kubilay, N., Laroche, J., Liss, P. S., Mahowald, N., Prospero, J. M., Ridgwell, A. J., Tegen, I., and Torres, R. (2005). Global Iron connections between desert dust, ocean biogeochemistry, and climate. Science 308, 67–71.
Johnson, K. S., Coale, K. H., Elrod, V. A., and Tindale, N. W. (1994). Iron photochemistry in seawater from the equatorial Pacific. Mar. Chem. 46, 319–334.
Johnson, K. S., Gordon, R. M., and Coale, K. H. (1997). What controls dissolved iron concentrations in the world ocean? Mar. Chem. 57, 137–161.
Kuma, K., Katsumoto, A., Kawakami, H., Takatori, F., and Matsunaga, K. (1998a). Spatial variability of Fe(III) hydroxide solubility in the water column of the northern north Pacific ocean. Deep Sea Res. 45, 91–113.
Kuma, K., Katsumoto, A., Nishioka, J., and Matsunaga, K. (1998b). Size-fractionated iron concentrations and Fe(III) hydroxide solubilities in various coastal waters. Estuar. Coast. Shelf Sci. 47, 275–283.
Kuma, K., Katsumoto, A., Shiga, N., Sawabe, T., and Matsunaga, K. (2000). Variation of size-fractionated Fe concentrations and Fe(III) hydroxide solubilities during a spring phytoplankton bloom in Funka Bay (Japan). Mar. Chem. 71, 111–123.
Kuma, K., Nakabayashi, S., and Matsunaga, K. (1995). Photoreduction of Fe(III) by Hydroxycarboxylic acids in seawater. Water Res. 29, 1559–1569.
Kuma, K., Nishioka, J., and Matsunaga, K. (1996). Controls on iron(III) hydroxide solubility in seawater: the influence of pH and natural organic chelators. Limnol. Oceanogr. 41, 396–407.
Luther, G. W., and Wu, J. (1997). What controls dissolved iron concentrations in the world ocean? – a comment. Mar. Chem. 57, 173–179.
Martin, J. H., Coale, K. H., Johnson, K. S., Fitzwater, S. E., Gordon, R. M., Tanner, S. J., Hunter, C. N., Elrod, V. A., Nowicki, J. L., Coley, T. L., Barber, R. T., Lindley, S., Watson, A. J., Van Scoy, K., Law, C. S., Liddicoat, M. I., Ling, R., Stanton, T., Stockel, J., Collins, C., Anderson, A., Bidigare, R., Ondrusek, M., Latasa, M., Millero, F. J., Lee, K., Yao, W., Zhang, J. Z., Friederich, G., Sakamoto, C., Chavez, F., Buck, K., Kolber, Z., Greene, R., Falkowski, P., Chisholm, S. W., Hoge, F., Swift, R., Yungel, J., Turner, S., Nightingale, P., Hatton, A., Liss, P., and Tindale, N. W. (1994). Testing the iron hypothesis in ecosystems of the equatorial Pacific ocean. Nature 371, 123–129.
Martin, J. H., and Fitzwater, S. E. (1988). Iron deficiency limits phytoplankton growth in the north-east Pacific subarctic. Nature 331, 341–343.
Mies, K., Wirgau, J., and Crumbliss, A. (2006). Ternary complex formation facilitates a redox mechanism for iron release from a siderophore. Biometals 19, 115–126.
Morel, F. M. M., and Hering, J. G. (1993). Principles and Applications of Aquatic Chemistry. New York: Wiley-Interscience.
Nakabayashi, S., Kuma, K., Sasaoka, K., Saitoh, S., Mochizuki, M., Shiga, N., and Kusakabe, M. (2002). Variation in iron(III) solubility and iron concentration in the northwestern north Pacific ocean. Limnol. Oceanogr. 47, 885–892.
Nakabayashi, S., Kusakabe, M., Kuma, K., and Kudo, I. (2001). Vertical distributions of iron(III) hydroxide solubility and dissolved iron in the northwestern north Pacific ocean. Geophys. Res. Lett. 28, 4611–4614.
Nowostawska, U., Kim, J. P., and Hunter, K. A. (2008). Aggregation of riverine colloidal iron in estuaries: a new kinetic study using stopped-flow mixing. Mar. Chem. 110, 205.
Okumura, C., Hasegawa, H., Mizumoto, H., Maki, T., and Ueda, K. (2004). Size fractionation of iron compounds in phytoplankton cultures in the presence of chelating ligands. Bunseki Kagaku 53, 1215–1221.
Roy, E. G., Wells, M. L., and King, D. W. (2008). Persistence of iron(II) in surface waters of the western subarctic Pacific. Limnol. Oceanogr. 53, 89–98.
Rue, E. L., and Bruland, K. W. (1995). Complexation of iron(III) by natural organic ligands in the central north Pacific as determined by a new competitive ligand equilibration/adsorptive cathodic stripping voltammetric method. Mar. Chem. 50, 117–138.
Schlosser, C., and Croot, P. (2009). Controls on seawater Fe(III) solubility in the Mauritanian upwelling zone. Geophys. Res. Lett. 36, L18606.
Schlosser, C., De La Rocha, C. L., and Croot, P. L. (2011). Effects of iron surface adsorption and sample handling on iron solubility measurements. Mar. Chem. 127, 48–55.
Schneider, W. (1988). Iron hydrolysis and the biochemistry of iron – the interplay of hydroxide and biogenic ligands. Chimia (Aarau) 42, 9–20.
Shiller, A. M. (1997). Manganese in surface waters of the Atlantic Ocean. Geophys. Res. Lett. 24, 1495–1498.
Stockdale, A., Tipping, E., Hamilton-Taylor, J., and Lofts, S. (2011). Trace metals in the open oceans: speciation modelling based on humic-type ligands. Environ. Chem. 8, 304–319.
van den Berg, C. M. G. (2006). Chemical speciation of iron in seawater by cathodic stripping voltammetry with dihydroxynaphthalene. Anal. Chem. 78, 156–163.
Voelker, B. M., and Sedlak, D. L. (1995). Iron reduction by photoproduced superoxide in seawater. Mar. Chem. 50, 93–102.
Vraspir, J. M., and Butler, A. (2009). Chemistry of marine ligands and siderophores. Annu. Rev. Mar. Sci. 1, 43–63.
Witter, A., and Luther, G. W. (1998). Variation in Fe-organic complexation with depth in the northwestern Atlantic ocean as determined using a kinetic approach. Mar. Chem. 62, 241–258.
Witter, A. E., Hutchins, D. A., Butler, A., and Luther, G. W. (2000). Determination of conditional stability constants and kinetic constants for strong model Fe-binding ligands in seawater. Mar. Chem. 69, 1–17.
Wu, J., Boyle, E., Sunda, W., and Wen, L.-S. (2001). Soluble and colloidal iron in the oligotrophic north Atlantic and north Pacific. Science 293, 847–849.
Wu, J., and Luther, G. W. (1995). Complexation of Fe(III) by natural organic ligands in the northwest Atlantic ocean by a competitive ligand equilibration method and a kinetic approach. Mar. Chem. 50, 159–177.
Appendix
Methods
Kinetic method for Fe speciation
Calculation of kd (rate of dissociation for recovery of Fe from FeL). Two conditions may result after the recovery period: 100% recovery of added Fe, or <100% recovery of added Fe (i.e., equilibrium is established between Fe, natural ligands and TAC). The solutions described here are adapted from earlier works (Wu and Luther, 1995; Witter and Luther, 1998). For an alternative derivation of the rate laws see the later sections of this appendix.
Weak ligands – all added Fe recovered. The overall reaction for the recovery of Fe3+ [as Fe(TAC)2] from Fe3+L (which is abbreviated FeL) is given in A1 as an associative reaction. It was previously assumed (Wu and Luther, 1995; Witter and Luther, 1998) that this process can be described by an associative reaction and that Fe3+ does not accumulate in solution as Fe′.
The overall reaction rate is pseudo first order in [TAC] due to the large excess of this ligand and can be expressed as:
Integrating gives the following solution:
A1 can be broken into two elementary reaction steps; the dissociation of the natural organic ligand complex to form Fe′ (A4), where Fe′ represents the inorganic forms of Fe at ambient pH; and the reaction of Fe′ with TAC (A5):
The overall reaction A5 is comprised of two sequential steps with the first step (A51) being the rate limiting step:
As [TAC] is greatly in excess over [L] ([TAC] = 1 × 10−5 M compared to [L] ∼ 1 − 4.0 × 10−9 M), any Fe′ formed will react faster with TAC than with [L], and the product Fe(TAC)2 will not revert to Fe′ and TAC during the timescale of the experiment. The overall reaction rate for A5 will be pseudo first order in [TAC] due to its large excess. Since TAC forms complexes with Fe′ very rapidly (k2 ∼ 1 × 106 M s−1), there will be no accumulation of Fe′ and/or subsequent formation of particulate iron. Therefore, the Fe′ concentration will always be very small (steady state approximation) and we can conclude:
We can write the rate eq. for Fe′ by applying the steady state approximation:
Solving for Fe′:
A9 is the rate law for the formation of Fe(TAC)2 from Fe′ (A5):
Substituting A8 into A9 gives A10:
In Wu and Luther (1995), two possibilities to simplify A10 were discussed. First, assuming kf[L] < < k2[TAC] because [TAC] (1 × 10−5 M) is much larger than [L] then A10 reduces to:
Integrating A11, and comparing it to A3 gives A12–A13:
The dissociation rate constant, kd, can be calculated when 100% recovery is achieved using A12. A plot of ln[FeL] (M) versus time (s−1) allows calculation of kd (M−1 s−1). The conditional stability constant, KFe3+L, can then be calculated from A 14 to 15.
The inorganic side reaction coefficient for Fe used in this work, aFe′ = 1010, was determined previously by Hudson et al. (1992).
The second possible solution (Wu and Luther, 1995) arises from the observation that the uptake rate of iron by the natural ligands and TAC are indistinguishable:
then A10 simplifies to:
Gerringa et al. (2007) previously estimated the value of k2 for Fe(TAC)2 formation to vary between 1.14 × 107 and 34 × 108 M−1 s−1 with the highest values found at lower salinities. These values are higher however than the water loss rate of Fe′ under these conditions (Hudson et al., 1992) and must be considered an artifact of the modeling scheme they employed. Our own estimates (unpublished) indicate a value of k2 for Fe(TAC)2 ∼ 1 × 106 M−1 s−1. Using this value in A10, no assumptions are necessary in calculating kd. The difference in KFe′L calculated based on A10 with and without assumptions based on the relative magnitude of kf[L] to k2[TAC] is 100.3, and is not considered as significant.
<100% recovery of added Fe3+ (full equilibrium is established). If less than 100% recovery of added Fe occurs, the conditional stability constant for Fe complexation can be determined by considering that the system has reached equilibrium. In seawater with natural organic ligands present, Fe3+ shifts from being complexed by organic ligands as Fe3+L to Fe(TAC)2 through an associative type mechanism so Fe′ never forms. A4 can then be expressed in equilibrium form as:
and a stability constant for the reaction can be calculated. Substituting A19 for Fe3+L in A18 above and rearrangement to A23 allows calculation of KFe3+L, since Krec is related to the conditional stability constant with respect to Fe3+ (KFe3+L).
The stability constant for KFe(TAC)2 has been determined experimentally at pH 8.0 to be 1022.4 (Croot and Johansson, 2000). Finally a conditional stability constant with respect to Fe′ can be calculated by considering:
In this study, we used an αFe′ at pH 8.0 of 1010 (Hudson et al., 1992). The dissociation rate constant, kd, can then be calculated from A23 using the values for kf and KFe′L obtained by experiment (see the methods section in the main text for details).
Alternative derivation of the kinetic method for iron speciation:
The approach used by Luther and colleagues (Wu and Luther, 1995; Witter and Luther, 1998) considers the overall reaction to be adjunctive (associative) but the rate determining step for the dissociation of FeL is a purely disjunctive mechanism (A4). The dependence on the competing ligand arises from inclusion of a kinetic term incorporating the formation of the electroactive species in solution. This is therefore in many regards not a strictly adjunctive mechanism as no ternary intermediate complex (e.g., M-L-TAC) is postulated. An alternative derivation of the rate equations is developed here which considers that a disjunctive (kdis) and adjunctive (kadj) pathway are occurring simultaneously.
Disjunctive mechanism. Formation and dissociation of FeL
The formation of Fe(TAC) and the electroactive complex Fe(TAC)2
For completeness we include the other reactions that are important in the formation of the assumed electroactive species Fe(TAC)2 (though we neglect the reactions with the individual components that make up Fe′).
Adjunctive mechanism. Formation of ternary complex FeL(TAC) from FeL and TAC
Formation of ternary complex FeL(TAC) from Fe(TAC) and L
In the present case we assume that there is no reaction between Fe(TAC)2 and L. The overall reaction is then the same as that described in A1:
The loss rate of FeL can then be described by the following using the equations described above:
In the context of the present work, the terms involving k1 can be omitted as the concentrations of Fe′, L will always be small compared to [FeL] and [TAC]. If it is assumed that [FeL(TAC)] ≪ [FeL] (see below) then B7 reduces to:
Rearranging leads to:
As above we assume that FeL, Fe(TAC)2 ≫ Fe′, FeL(TAC), and Fe(TAC). A not unreasonable assumption given the stability of these complexes under the analytical conditions, then the following rate law can be postulated from mass balance considerations:
Then the loss rate of formation of the natural ligands can thus be described by the following relationship:
Where
In this formulation kdis = k−1 and kadj = k4.
Integrating Eq. B11 and applying the appropriate initial and final conditions results in the following relationship:
Where the subscripts 0 and ∞ represent the initial and final time points and the subscript t indicates the time since the experiment started.
Case I: 100% recovery of FeL
In this case B13 reduces to the following:
Thus a plot of ln[FeL]t against time has slope kobs. B14 is thus analogous to A12, though in this case kobs includes both an adjunctive and disjunctive term.
Case II: <100% recovery of FeL
In this case B13 rearranges to the relationship:
Thus a plot of ln([FeL]t − [FeL]∞) against time has slope kobs. This approach uses kinetic data to determine the value of kobs from which the values of kdis and kadj can be calculated, and is an alternative to the thermodynamic approach employed by Luther and co-workers (see above).
Is there a significant adjunctive mechanism using TAC?
Unfortunately due to logistical constraints we have no data as yet with the following; (i) where different concentrations (multiple detection windows) of TAC have been employed or (ii) simultaneous radiotracer and CSV measurements have been performed on the same water sample. This excludes then a direct assessment of the significance of an adjunctive mechanism in Fe(TAC) formation and this is clearly a goal for future work. However comparison of the maximum and minimum rates measured in the CSV experiments (TAC present) with the radiotracer experiments (TAC absent) gives estimates of kdis = 10−4.1 to 10−5.3 s−1 and kadj = 5.8 to 17.2 M−1 s−1. This suggests then that the adjunctive mechanism is a significant reaction (70–90% of the overall rate) even at 10 μM TAC.
Note on Ternary Complex Formation: Central to the derivation above is the premise that the concentration of [FeL(TAC)] is always low, thermodynamically this is likely given that [TAC] ≫ [L] but the kinetics of this reaction have yet to be investigated thoroughly. There is growing evidence for the formation of such ternary iron complexes, with a recent example being the investigation of a series of iron-desferrioxamine B – citric acid complexes (Ito et al., 2011). In the case of TAC, or other ligands used for CSV, it is not yet known if any of the ternary complexes formed might also be electroactive.
Special Case I: When reactions B4a and B4b are in pseudo-equilibrium (steady state approximation) then the following equilibrium applies:
B7 then reduces to the following:
In this case the reaction is only disjunctive in character. That is the adjunctive mechanism, while occurring, is not rate determining.
Results
References
Keywords: iron biogeochemistry, iron solubility, redox kinetics, complexation kinetics
Citation: Croot PL and Heller MI (2012) The importance of kinetics and redox in the biogeochemical cycling of iron in the surface ocean. Front. Microbio. 3:219. doi: 10.3389/fmicb.2012.00219
Received: 31 October 2011; Accepted: 29 May 2012; Published online: 19 June 2012.
Edited by:
Benjamin Twining, Bigelow Laboratory for Ocean Sciences, USAReviewed by:
Benjamin Kocar, Stanford University, USAJochen Nuester, Bigelow Laboratory for Ocean Sciences, USA
Copyright: © 2012 Croot and Heller. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Peter L. Croot, Earth and Ocean Sciences, School of Natural Sciences, National University of Ireland Galway, Galway, Ireland.