Balanced plasticity and stability of the electrical properties of a molluscan modulatory interneuron after classical conditioning: a computational study
- 1 Department of Computer Science, University of Warwick, Coventry, UK
- 2 School of Life Sciences, University of Sussex, Brighton, UK
- 3 Institute of Higher Nervous Activity and Neurophysiology, Russian Academy of Sciences, Moscow, Russia
The Cerebral Giant Cells (CGCs) are a pair of identified modulatory interneurons in the Central Nervous System of the pond snail Lymnaea stagnalis with an important role in the expression of both unconditioned and conditioned feeding behavior. Following single-trial food-reward classical conditioning, the membrane potential of the CGCs becomes persistently depolarized. This depolarization contributes to the conditioned response by facilitating sensory cell to command neuron synapses, which results in the activation of the feeding network by the conditioned stimulus. Despite the depolarization of the membrane potential, which enables the CGGs to play a key role in learning-induced network plasticity, there is no persistent change in the tonic firing rate or shape of the action potentials, allowing these neurons to retain their normal network function in feeding. In order to understand the ionic mechanisms of this novel combination of plasticity and stability of intrinsic electrical properties, we first constructed and validated a Hodgkin-Huxley-type model of the CGCs. We then used this model to elucidate how learning-induced changes in a somal persistent sodium and a delayed rectifier potassium current lead to a persistent depolarization of the CGCs whilst maintaining their firing rate. Including in the model an additional increase in the conductance of a high-voltage-activated calcium current allowed the spike amplitude and spike duration also to be maintained after conditioning. We conclude therefore that a balanced increase in three identified conductances is sufficient to explain the electrophysiological changes found in the CGCs after classical conditioning.
Introduction
The Cerebral Giant Cells (CGCs) of the snail Lymnaea, like their homologs in other mollusks (Weiss and Kupfermann, 1976 ), play an important modulatory role in the neural control of feeding (Yeoman et al., 1996 ; Straub and Benjamin, 2001 ). A recent finding is that the CGCs become persistently depolarized after single-trial food-reward classical conditioning (Kemenes et al., 2006 ). This depolarization is delayed by 16–24 h with respect to acquisition and early memory formation, but concomitant with the formation and duration of long-term memory. The depolarized CGCs recruit command neurons that activate the feeding motor circuit to produce the conditioned response (Kemenes et al., 2006 ). Membrane potential manipulation and calcium imaging experiments suggest that this recruitment occurs by calcium-dependent facilitation of sensory pathways to the feeding command neurons (Kemenes et al., 2006 ). Surprisingly, the depolarization of the CGCs occurs without significant changes in the firing rate or shape of action potentials (Kemenes et al., 2006 ). This observation has raised interesting questions about the ionic mechanisms supporting both a long-lasting depolarization and stable spike frequency in the same neuron. Frequency stabilization is necessary in the feeding network because the CGCs need to fire within a narrow frequency range (between ∼ 0.6 and 1 Hz in the type of isolated CNS preparation we used in the present study) to carry out their normal (non-learning) modulatory role in supporting feeding motor output (Yeoman et al., 1994 ). Membrane potential depolarization already has been linked to a learning-induced increase of the persistent sodium current (INaP) of the CGCs (Nikitin et al., 2008 ), but the mechanism of spike frequency stabilization remained unknown.
To facilitate our understanding of the electrical mechanisms underlying this novel combination of plasticity and stability of key electrical properties in the same neuron, here we used voltage- and current-clamp data as inputs to parameter estimation in a single-compartment Hodgkin-Huxley-type model of the CGCs. The parameterized model is then validated against different data and its behavior correlated to that observed in the CGCs after conditioning.
Our main specific aim was to replicate the complex electrophysiological effects of behavioral conditioning by simulating changes in INaP and the delayed rectifier potassium current (ID) of the CGCs (Staras et al., 2002 ). The inclusion of ID in the modeling was justified by the finding that this current is also increased following conditioning (see Results). This new finding allowed us to formulate the hypothesis that a balanced increase in the conductances of ID and INaP underlie spike frequency stabilization during learning-induced persistent depolarization. However, while this hypothesis was being tested, the model revealed that an increase in the conductance of the also previously identified high-voltage-activated calcium current (IHVA, Staras et al., 2002 ) was required for the stabilization of spike amplitude and duration after conditioning. Our work therefore establishes a theoretical framework for relating multiple ion channel properties to the expression of cellular correlates of conditioning.
Materials and Methods
General Description of the Model
The model of the CGCs took the form of a single-compartment Hodgkin-Huxley-type neuron. We used a single- instead of a two- or multi-compartment model (e.g., Golowasch et al., 1999 ; Vavoulis et al., 2007 ), because the basic electrical properties (mean firing frequency, action potential shape, resting membrane potential, etc.) of the cell body in the CGCs after axotomy did not differ significantly from recordings made from the intact neuron in the absence of axotomy (Staras et al., 2002 ; Nikitin et al., 2006 ). Moreover, molluscan neurons have no dendritic processes on their cell bodies, so compartments modeling these processes did not need to be included. The model includes all the ionic currents previously identified in the CGCs from two-electrode voltage-clamp recordings (Staras et al., 2002 ; Nikitin et al., 2006 ), namely: (1) a transient TTX-sensitive sodium current (INaT), (2) a persistent TTX-resistant sodium current (INaP), (3) a persistent TEA-sensitive potassium current (ID), (4) a transient 4-AP-sensitive potassium current (IA), (5) a transient low-voltage-activated T-type calcium current (ILVA) and (6) a transient high-voltage-activated calcium current (IHVA). An SK-type Ca2+-dependent potassium current, rarely found in the CGCs and not characterized in detail, was not included in the model.
A detailed mathematical description of the model and the parameter estimation methods we used is given as Materials and Methods in Supplementary Material. The model for each current follows the Hodgkin-Huxley formalism, as described in Willms et al. (1999) . It includes a number of activation and, in the case of transient currents, inactivation gates, which exist in either an open or close state. The opening and closing of the gates in each channel type in response to changes in the membrane potential was modeled by a set of differential equations obeying first-order relaxation kinetics. The equilibrium states and associated relaxation times of this kinetics were respectively described as sigmoid and Gaussian functions of the membrane potential (Eq. S9 and S10 in Section Materials and Methods in Supplementary Material).
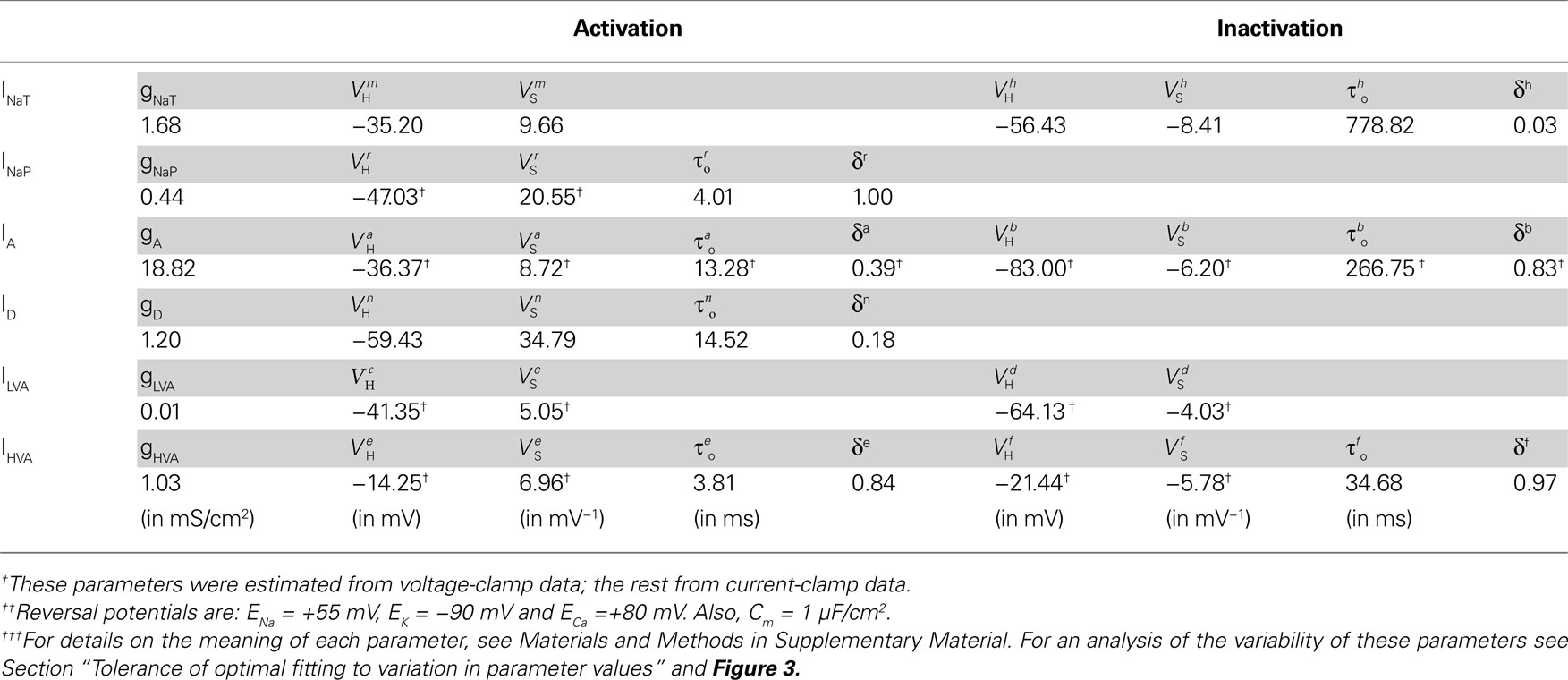
For the estimation of the maximal conductances, reversal potentials and the parameters governing the response of the currents to voltage (a total of 43 free parameters), we fitted the model against a combination of voltage- and current-clamp data (Staras et al., 2002 ; Nikitin et al., 2006 ) using an efficient optimization method, which permitted the fitted model to mimic the spike shape, spontaneous tonic firing activity and current-frequency response of the biological CGCs with high accuracy (for a more detailed description, see Materials and Methods in Supplementary Material). The fitting process was repeated for a large number of randomly selected initial values of the unknown parameters providing information on the uniqueness of the estimated values and the error associated with their estimation. Furthermore, the contribution of identified ionic currents to the electrical properties of the fitted CGCs model was estimated by simulating the application of specific pharmacological agents in the biological cells.
Simulations
The fitted CGC model took the form of an 8-dimensional system of Ordinary Differential equations (ODEs; see Materials and Methods in Supplementary Material), which were encoded using custom code in the programming language ANSI C and solved in MATLAB®. All simulations were realized on a number of Intel Core 2 Duo desktop computers with 2 or 4 GB of memory and the Linux operating system. The coupled ODEs were solved using an adaptive Runge-Kutta-Fehlberg (4,5) algorithm with absolute error tolerance 10−6 and relative error tolerance 10−3.
Electrophysiology
All the data on ionic currents used in the present study were obtained in previous experiments using standard two-electrode voltage-clamp methods. A variety of commonly used modified salines (containing TEA, 4-AP, nickel, etc.) were used to isolate specific ionic currents, as described in the same previous papers (Staras et al., 2002 ; Nikitin et al., 2006 , 2008 ).
To test predictions from the model regarding the CGCs’ electrical responses to increasing amounts of injected depolarizing current, we carried out new experiments using standard two-electrode current clamp methods in normal physiological saline (see details in Staras et al., 2002 ; Kemenes et al., 2006 ; Nikitin et al., 2006 ). CGCs (n = 5) in isolated CNS preparations from laboratory-bred Lymnaea stagnalis were impaled with two microelectrodes (filled with 4-M KAc, tip resistance: 8–15 MΩ), one to inject current and another to record voltage responses from the cell. The CGCs were identified on the basis of their size, position in the ganglia and characteristic tonic firing pattern (McCrohan and Benjamin, 1980a ,b ). At the beginning of each experiment, the membrane potential of the CGC was set at −80 mV by injecting an appropriate amount of steady current. To measure spike frequency increases in response to current injection, we injected increasing amounts of depolarizing current into the cells in the range 0 to 2 nA. Each period of current injection lasted for 10 s with 60 s intervals between successive stimulations to allow the CGC to fully recover from the effect of the preceding test. The average spike frequency (in Hz) at each test current level was calculated from the total number of spikes generated by the cell during the 10 s stimulation period.
Results
The model includes all the previously identified voltage-gated ionic currents in the biological CGCs. For each current, the maximal conductance, reversal potential and activation/inactivation kinetics were estimated from existing voltage- and current-clamp electrophysiological data (Staras et al., 2002 ; Nikitin et al., 2006 ). In a first stage, the estimation of 18 of the 43 parameters governing the activation and inactivation kinetics of most currents in the model was possible from voltage-clamp data (Table 1 ). In a second stage, the remaining parameters, including the maximal conductance and reversal potential for each current, were estimated by fitting the whole-cell model against current-clamp data, while most of the parameters estimated from voltage-clamp data in the previous step were kept fixed, as explained below. The final values of all parameters in the model are given in Table 1 along with information on whether their estimation was based on voltage- or current-clamp data. Information on the variability of parameter values is given in Section “Tolerance of optimal fitting to variation in parameter values” and Figure 3 .
Estimation of Model Parameters from Voltage-Clamp Data
Parameter estimation in the model from voltage-clamp data is summarized in Figure 1 . Beginning with the persistent sodium current (INaP), we utilized information from current traces induced by 800 ms-long voltage steps to membrane potentials in the range from −90 to +30 mV from a holding potential of −110 mV (see Nikitin et al., 2006 for details of methods). The induced current persisted without significant inactivation for the duration of each step. The equilibrium current at the end of each step was modeled as a function of voltage (Eq. S11 in Materials and Methods in Supplementary Material) and it was fitted to the experimental data (Figure 1 Ai). From the fitted model, the steady-state activation of the persistent-sodium current (r∞) was derived as a sigmoid function of the membrane potential (Figure 1 Aii).
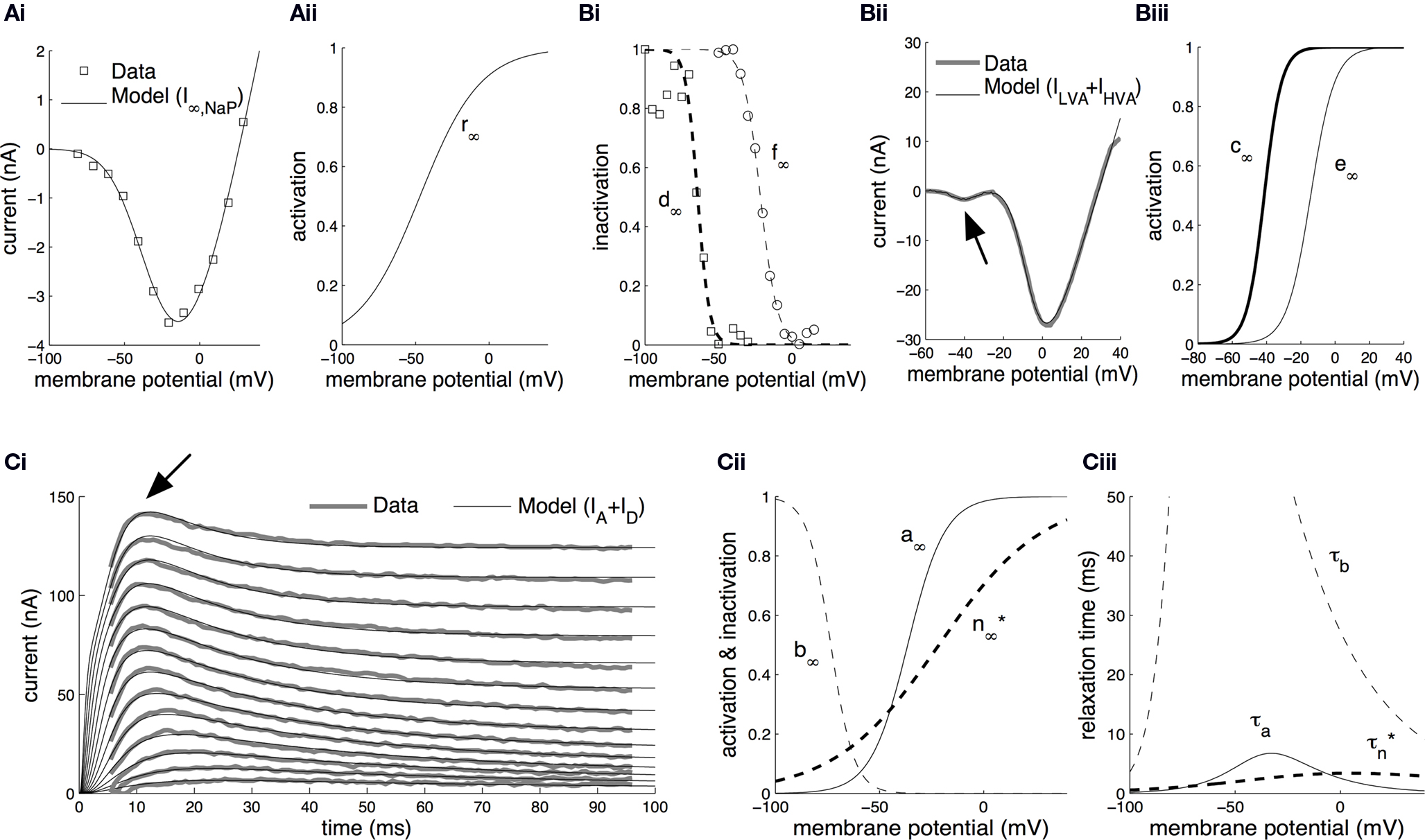
Figure 1. Parameter estimation from voltage-clamp data. (A) Estimation of the steady-state activation of the persistent sodium current. Persistent sodium currents at equilibrium, I∞,NaP, were measured at the end of 800 ms-long voltage steps to membrane potentials in the range from −90 to +30 mV from a holding potential of −110 mV (Ai, open squares; Nikitin et al., 2006
). The model for I∞,NaP (Eq. S11 in section Materials and Methods in Supplementary Material) was fitted against this data (Ai, solid line) permitting the estimation of the steady-state activation of the current, r∞, as a sigmoid function of the membrane potential (Aii). (B) Estimation of the steady-state activation and steady-state inactivation of the low-voltage-activated and high-voltage-activated calcium currents. The steady-state inactivation for ILVA, d∞, was computed by fitting a sigmoid curve to normalized peak currents recorded during voltage steps to −50 mV from holding membrane potentials between −100 mV and −30 mV (Bi, open squares; Staras et al., 2002
). Similarly, for the steady-state inactivation of IHVA, f∞, we fitted a sigmoid curve to normalized peak currents recorded during voltage steps to 0 mV from holding membrane potentials between −60 mV and +15 mV (Bi, open circles; Staras et al., 2002
). Subsequently, the model in Eq. S12 in Supplementary Material was fitted against the total calcium current induced during a voltage-ramp protocol changing the membrane potential from −100 mV to +30 mV over a time interval of 120 ms (Bii; Staras et al., 2002
). The arrow in Bii indicates the low-voltage-activated component corresponding to ILVA. From the fitted model, we derived the steady-state activation for ILVA and IHVA (c∞ and e∞, respectively) as sigmoid functions of the membrane potential (Biii). (C) Estimation of the activation and inactivation kinetics for the transient (IA) and delayed-rectifier (ID) potassium currents. The model for the total potassium current under voltage-clamp (Eq. S13–S16 in Supplementary Material) was fitted to current traces induced during 100 ms-long voltage steps from a holding membrane potential of −90 mV to steps from −20 to +35 mV (Ci; Staras et al., 2002
) using the full trace method (Willms et al., 1999
). The arrow in Ci indicates the early transient component corresponding to IA. The fitted model permitted the estimation of the steady-state activation, a∞, and inactivation, b∞, for the transient potassium current IA, and the steady-state activation, n∞*, for the delayed rectifier as illustrated in Cii. The corresponding relaxation times, τa, τb and 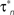 , were also derived from the fitted model (Ciii). The estimated kinetic parameters for ID are marked with an asterisk, because they are further modified and receive their final values based on current clamp data.
, were also derived from the fitted model (Ciii). The estimated kinetic parameters for ID are marked with an asterisk, because they are further modified and receive their final values based on current clamp data.
For the low-voltage-activated (ILVA) and high-voltage-activated (IHVA) calcium currents, we first computed the steady-state inactivation curves (Figure 1 Bi; d∞ and f∞ respectively) by fitting sigmoid functions of voltage (Eq. S9 in Supplementary Material) to normalized peak currents recorded during voltage steps to 0 mV from holding membrane potentials between −60 mV and +15 mV in the case of IHVA and to −50 mV from holding membrane potentials between −100 mV and −30 mV in the case of ILVA (Figure 1 Bi, open squares and open circles respectively; Staras et al., 2002 ). Subsequently, we used the current recorded during a voltage-clamp ramp protocol (voltage change from −100 mV to +30 mV over a time interval of 120 ms; see Staras et al., 2002 for details). The induced current trace had two components (Figure 1 Bii): (a) one activating at ∼ −60 mV and reaching a peak at ∼ −45 mV and (b) one activating at ∼ −30 mV and peaking at ∼0 mV. From the fitted model (Eq. S12 in Supplementary Material; Figure 1 Bii), we derived the steady-state activation for ILVA and IHVA, c∞ and e∞ respectively, as functions of membrane potential (Figure 1 Biii).
In the case of the delayed rectifier (ID) and transient potassium (IA) currents, we utilized the current traces recorded during a voltage step protocol from a holding membrane potential of −90 mV to steps from −20 to +35 mV over a period of 100 ms (Figure 1
Ci; Staras et al., 2002
). This protocol revealed an early transient current corresponding to IA and a second sustained one, which persisted for the duration of the step (ID). The model for the total potassium current (Eq. S13–S16 in Materials and Methods in Supplementary Material) was fitted simultaneously to the whole set of potassium data using the full trace method (Willms et al., 1999
), as illustrated in Figure 1
Ci. From the fitted model, we derived estimations for the steady-state activation and inactivation of IA (Figure 1
Cii, a∞ and b∞ respectively), the steady-state activation of ID (Figure 1
Cii, n∞*), the activation and inactivation relaxation times for IA (Figure 1
Ciii, τa and τb respectively) and the activation relaxation time for ID (Figure 1
Ciii, 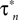 ).
).
Estimation of Model Parameters from Current-Clamp Data
The results from fitting the whole CGC model against current-clamp data are presented in Figure 2
. This data took the form of a 1.9 s-long voltage trace recorded using a two-electrode current-clamp protocol from CGCs in the intact nervous system of unconditioned animals in the absence of external stimulation (Figures 2
Ai, ii). We chose to fit a recording interval with only one spike, because consecutive spikes in the same recording are not exactly the same in terms of amplitude and duration, thus fitting simultaneously all of them using the present method would be problematic. However, the voltage trace we used is representative of the spontaneous CGCs activity and it contains information on both the spike shape and long interspike intervals that characterize this activity. The model was fitted to the data using an iterative method (see Materials and Methods in Supplementary Material for details), during which the parameter values estimated from voltage-clamp data in the previous stage were kept fixed, with the exception of those controlling the activation kinetics of ID (i.e. 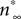 and
and 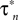 in Figures 1
Cii,iii). These were further adjusted at this stage, which was necessary for obtaining a sufficiently good fit to the experimental data. These and the remaining unknown parameters were left free to vary during the optimization process and progressively attained optimal values, as illustrated by the gradual convergence of the model to the experimental data (Figures 2
Ai,ii). The estimated parameters at this stage were the maximal conductances for each current (gNaP, gNaT, gA, gD, gLVA and gHVA), the activation and inactivation kinetics of INaT (m∞, h∞ in Figure 2
Bi; τh in Figure 2
Bii), the activation relaxation time for INaP (τr in Figure 2
Biii), the activation and inactivation relaxation times for IHVA (τe and τf in Figure 2
Biv) and the final parameter values for the activation kinetics of ID (n∞ in Figure 2
Bi and τn in Figure 2
Bii). The reversal potentials for each group of currents were given standard values at this stage (sodium, ENa =+55 mV; potassium, EK = −90 mV; calcium, ECa = + 80 mV), but they were left free to vary during the optimization at a later stage (see Figure 3
).
in Figures 1
Cii,iii). These were further adjusted at this stage, which was necessary for obtaining a sufficiently good fit to the experimental data. These and the remaining unknown parameters were left free to vary during the optimization process and progressively attained optimal values, as illustrated by the gradual convergence of the model to the experimental data (Figures 2
Ai,ii). The estimated parameters at this stage were the maximal conductances for each current (gNaP, gNaT, gA, gD, gLVA and gHVA), the activation and inactivation kinetics of INaT (m∞, h∞ in Figure 2
Bi; τh in Figure 2
Bii), the activation relaxation time for INaP (τr in Figure 2
Biii), the activation and inactivation relaxation times for IHVA (τe and τf in Figure 2
Biv) and the final parameter values for the activation kinetics of ID (n∞ in Figure 2
Bi and τn in Figure 2
Bii). The reversal potentials for each group of currents were given standard values at this stage (sodium, ENa =+55 mV; potassium, EK = −90 mV; calcium, ECa = + 80 mV), but they were left free to vary during the optimization at a later stage (see Figure 3
).
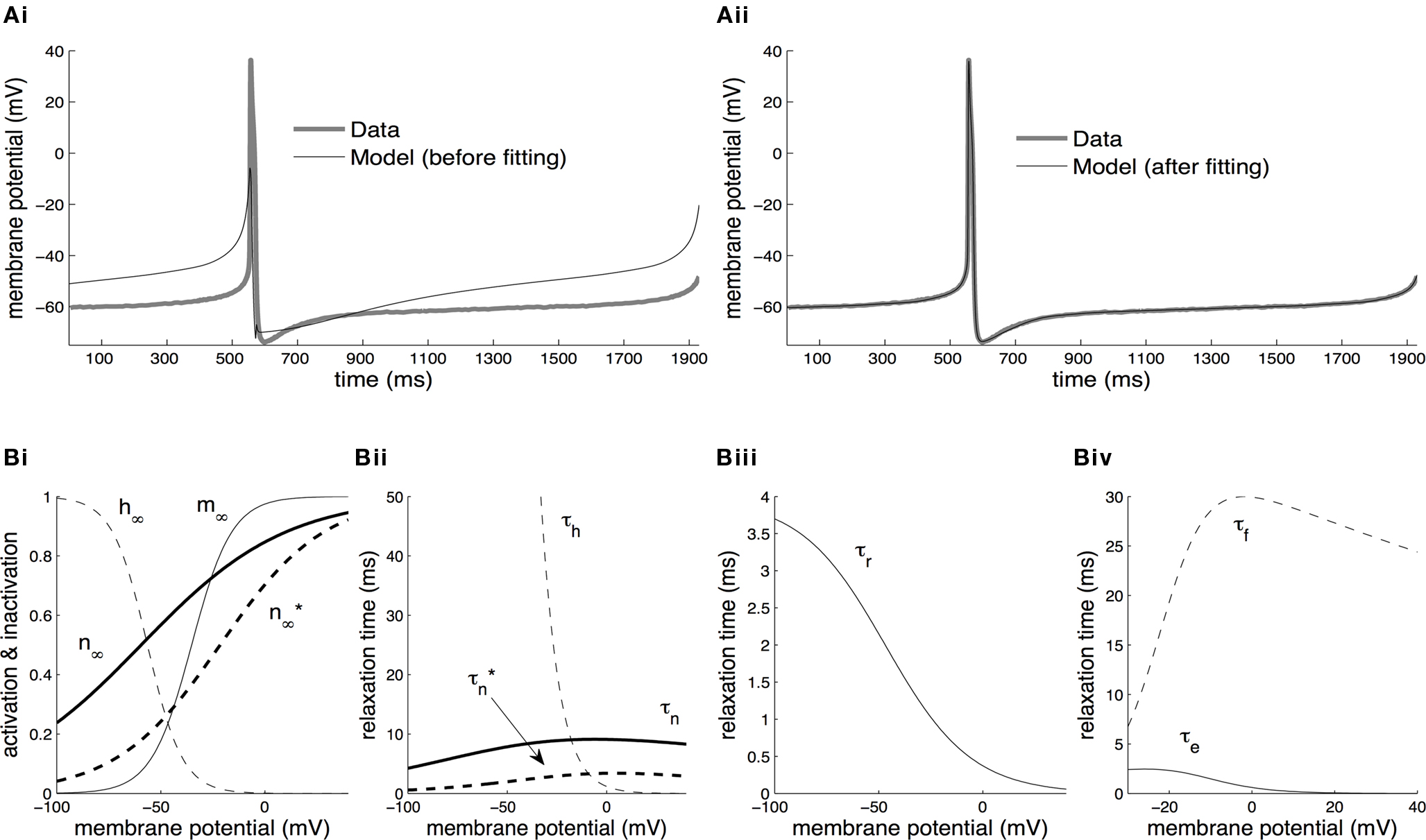
Figure 2. Parameter estimation from current-clamp data. (A) The whole-cell model was fitted against a two-electrode current-clamp recording of duration ∼1.9 s from CGCs in the intact nervous system of unconditioned animals. The parameters estimated at the previous stage from voltage-clamp data were kept fixed, with the exception of those referring to the activation kinetics of the delayed rectifier, ID. During the optimization process, the free parameters in the model progressively attained optimal values, as indicated by the gradual convergence of the model to the data (Ai, ii). (B) The steady-state activation, m∞, and inactivation, h∞, of the transient sodium current were derived from the fitted model at this stage as sigmoid functions of the membrane potential (Bi). The relaxation times for the inactivation of the transient sodium current, τh, for the activation of the persistent sodium current, τr, and for the activation, τe, and inactivation, τf, of the high-voltage-activated calcium current were also derived from the fitted model at this stage as functions of the membrane potential (Bii–iv). Also, the parameters for the steady-state activation of the delayed rectifier, n∞, and for the associated relaxation time, τn, received their final values at this stage (Bi, ii). The dashed lines illustrating 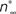 and
and 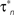 in the same panels are as in Figures 1
Cii,iii.
in the same panels are as in Figures 1
Cii,iii.
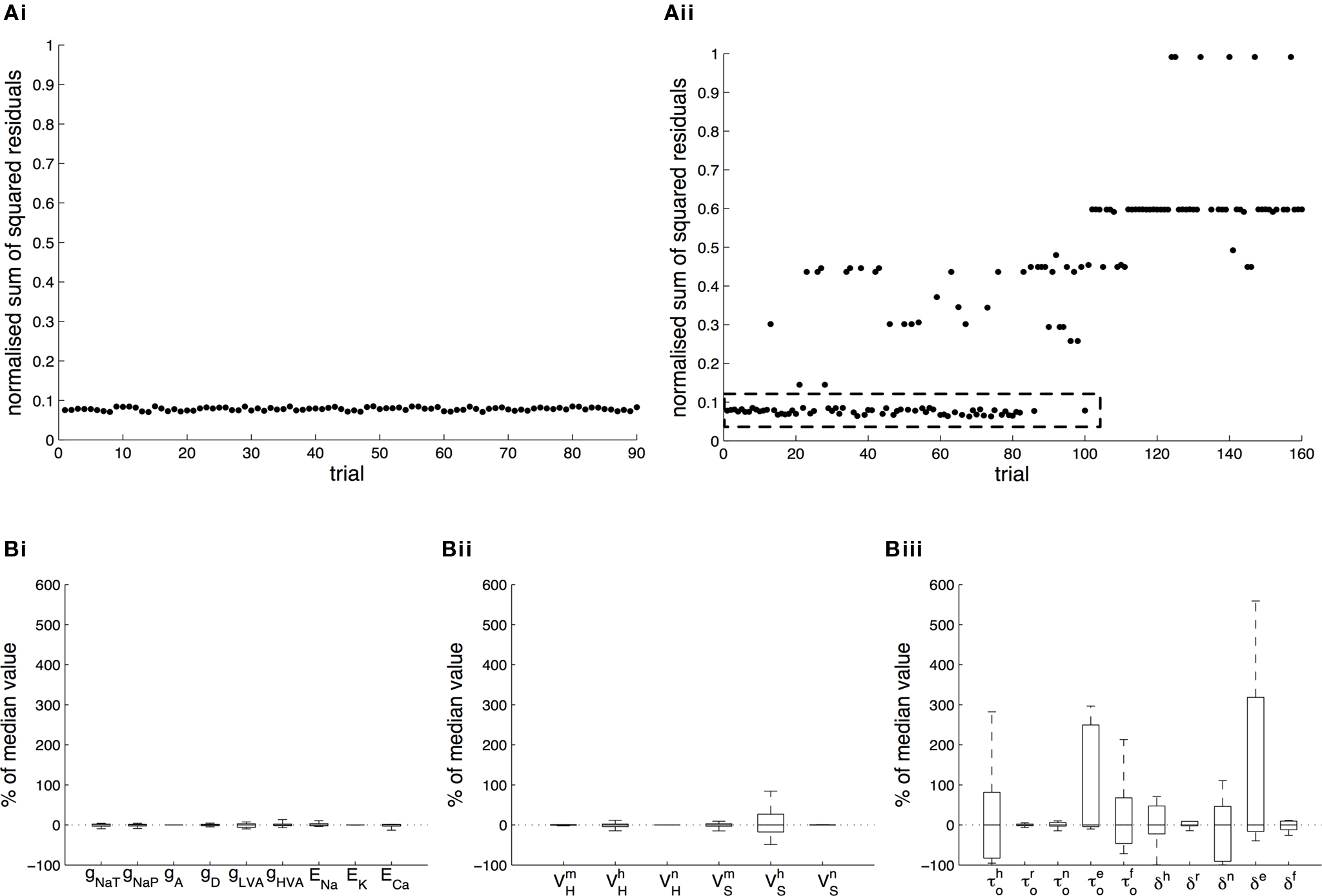
Figure 3. Tolerance of optimal fitting to variation in parameter values. (A) Optimization against current-clamp data was repeated from a large number of randomly selected initial values for the maximal conductances and reversal potentials in the model, while the rest of the parameters were kept fixed to their previously estimated values. A total of 90 different initial values for each free parameter were tested, all of which converged to the same equally good fit to the data at the end of the optimization (Ai). Similarly, the optimization based on current-clamp data was repeated for parameters 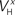 and
and 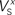 (x = m,h,n) and
(x = m,h,n) and 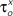 and δx (x = h,r,n,e,f), while the rest of the parameters in the model, including maximal conductances and reversal potentials, were kept fixed to their previously estimated values. We tested 140 randomly distributed initial values for each of the parameters
and δx (x = h,r,n,e,f), while the rest of the parameters in the model, including maximal conductances and reversal potentials, were kept fixed to their previously estimated values. We tested 140 randomly distributed initial values for each of the parameters 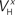 (x = m,h,n) and
(x = m,h,n) and 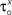 (x = h,r,n,e,f), among which only 63 (45%) converged to a sufficiently good fit to the current-clamp data (Aii, dashed rectangular region). All 230 points illustrated in Ai and Aii were normalized by dividing with the largest sum of squared residuals found in these simulations. (B) Examination of the estimated maximal conductance and reversal potential values corresponding to the optimal points illustrated in Ai revealed that these values were tightly constrained around the median, not exceeding 15% of this value (Bi). Similarly, the optimal values for parameters
(x = h,r,n,e,f), among which only 63 (45%) converged to a sufficiently good fit to the current-clamp data (Aii, dashed rectangular region). All 230 points illustrated in Ai and Aii were normalized by dividing with the largest sum of squared residuals found in these simulations. (B) Examination of the estimated maximal conductance and reversal potential values corresponding to the optimal points illustrated in Ai revealed that these values were tightly constrained around the median, not exceeding 15% of this value (Bi). Similarly, the optimal values for parameters 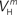 ,
, 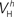 ,
, 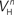 ,
, 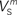 and
and 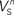 (i.e. those corresponding to the points inside the rectangular dashed region in Aii) were tightly constrained around the median with the exception of the values for
(i.e. those corresponding to the points inside the rectangular dashed region in Aii) were tightly constrained around the median with the exception of the values for 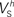 (a parameter controlling the steady-state inactivation of INaT; see Eq. S9 in section Materials and Methods in Supplementary Material), which were dispersed within 80% of the median value (Bii). On the other hand, the optimal values for most of the examined parameters
(a parameter controlling the steady-state inactivation of INaT; see Eq. S9 in section Materials and Methods in Supplementary Material), which were dispersed within 80% of the median value (Bii). On the other hand, the optimal values for most of the examined parameters 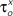 and δx (x = h,r,n,e,f) were rather broadly distributed around the median (Biii). All parameters in Bi–iii were centered and normalized with respect to the median. The lower and upper edges of each box in the same plots correspond to the 25th and 75th percentiles, respectively, while the whiskers above and below each box indicate the most extreme parameter values.
and δx (x = h,r,n,e,f) were rather broadly distributed around the median (Biii). All parameters in Bi–iii were centered and normalized with respect to the median. The lower and upper edges of each box in the same plots correspond to the 25th and 75th percentiles, respectively, while the whiskers above and below each box indicate the most extreme parameter values.
Tolerance of Optimal Fitting to Variation in Parameter Values
In order to assess the uniqueness and accuracy of the parameter values that were estimated from current-clamp data, the optimization process against this data was repeated starting from a large number of random initial values of the relevant parameters. First, we examined the maximal conductances and reversal potentials for all currents in the model, while the remaining parameters were kept fixed at their previously estimated values. The random initial values for the maximal conductances were uniformly distributed within the rather broad interval of 0.001–120 mS/cm2. Similarly, the reversal potentials for each group of ionic currents were again uniformly distributed within the following intervals: ENa, +25 to +60 mV; EK, −95 to −75 mV; ECa, 25 to 85 mV. A total of 90 random initial values for each of these parameters (10 × number of free parameters) were examined and for each of them, the model converged to an optimal solution (normalized sum of squared residuals 0.0782 ± 0.0004 s.e.m. Figure 3 Ai). Examination of the maximal conductance and reversal potential values estimated after the end of the process revealed that they were tightly confined, within 15% of their median value (Figure 3 Bi).
At a second stage, the same process was repeated, but this time the maximal conductances and reversal potentials were kept fixed to their previously estimated values, while the rest of the estimated-from-current-clamp-data parameters (indicated in Figures 3
Bii,iii) were left free to vary during the optimization. The random initial values were generated by letting parameters 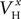 (x = m,h,n) and
(x = m,h,n) and 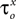 (x = h,r,n,e,f) be uniformly distributed within ±10 mV and ±50% of their previously estimated values, respectively. A total of 140 different initial values for each of these parameters were tested (10 × number of free parameters), among which only 63 (45%) converged to the same sufficiently good solution (normalized sum of squared residuals 0.0749 ± 0.0008 s.e.m. Figure 3
Aii, dashed rectangular region). Examination of the optimal values obtained after the end of the fitting process revealed that the estimated values for parameters
(x = h,r,n,e,f) be uniformly distributed within ±10 mV and ±50% of their previously estimated values, respectively. A total of 140 different initial values for each of these parameters were tested (10 × number of free parameters), among which only 63 (45%) converged to the same sufficiently good solution (normalized sum of squared residuals 0.0749 ± 0.0008 s.e.m. Figure 3
Aii, dashed rectangular region). Examination of the optimal values obtained after the end of the fitting process revealed that the estimated values for parameters 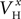 (x = m,h,n),
(x = m,h,n), 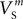 and
and 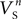 were confined narrowly around the median, with only the values for
were confined narrowly around the median, with only the values for 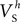 (a parameter controlling the steady-state inactivation of the transient sodium current) showing a broader dispersion (Figure 3
Bii). The estimated values for parameters
(a parameter controlling the steady-state inactivation of the transient sodium current) showing a broader dispersion (Figure 3
Bii). The estimated values for parameters 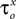 and δx (x = h,r,n,e,f) showed a broad distribution (Figure 3
Biii) indicating that tightly constraining these parameters was not critical for optimally fitting the model against the current-clamp experimental data.
and δx (x = h,r,n,e,f) showed a broad distribution (Figure 3
Biii) indicating that tightly constraining these parameters was not critical for optimally fitting the model against the current-clamp experimental data.
Overview of the Model Neuron Activity and Contribution of Identified Ionic Currents to Membrane Excitability
An overview of the spike shape and firing activity of the fitted model is given in Figure 4 . The model was compared to an intracellular current-clamp recording from axotomized cells, which demonstrated a close agreement in the spontaneous tonic firing activity (Figure 4 A), spike shape (Figure 4 B) and current-frequency response (Figure 4 C) between the model and the biological neuron. In the absence of synaptic or experimentally applied input both the biological and the model CGCs fire at a mean frequency of ∼0.7 Hz (∼42 spikes/min; Figure 4 A). Typically, an action potential starts as a gradual depolarization of the cell membrane that becomes very rapid after a threshold (∼−50 mV) is crossed (Figure 4 B). The spike reaches a peak of approximately +40 mV, which is followed by a repolarization phase with a pronounced “shoulder” (indicated by an arrow in Figure 4 B). At its most hyperpolarized state, immediately after the spike, the membrane potential reached a value of about −75 mV, before returning gradually to its baseline value (∼−60 mV). The spike had a total duration of ∼17 ms (measured at −20 mV). Furthermore, when injected with constant currents of increasing amplitude, the model responded with an increase in its firing frequency, which was in close agreement with the response of the biological neuron (Figure 4 C).
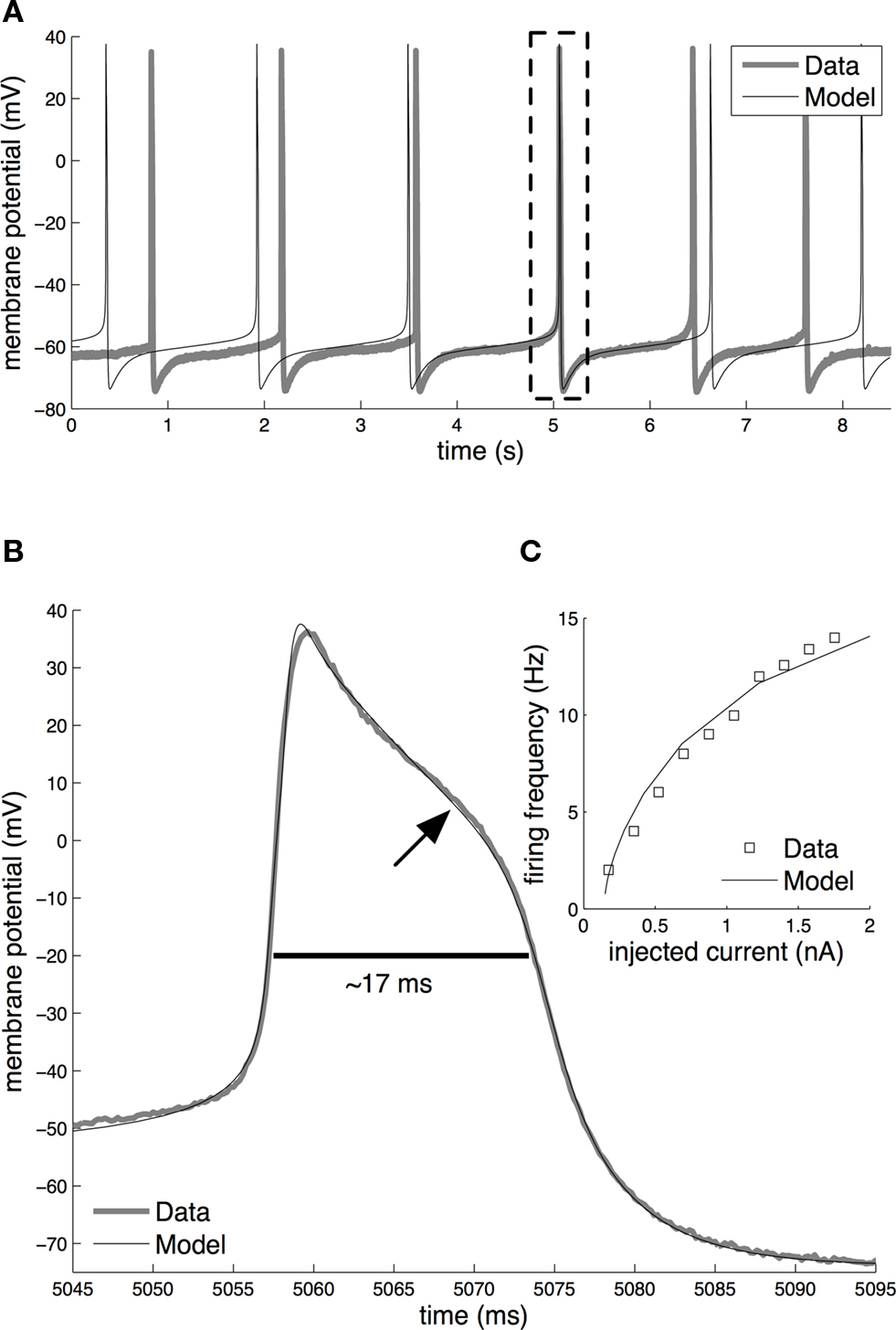
Figure 4. Basic electrical activity in the model and biological CGCs. (A) Spontaneous tonic firing in the fitted model and the biological neuron (Data). In the absence of external or synaptic input, both fire at approximately 0.7 Hz. Dashed rectangle indicates the overlapping real and simulated spike, respectively, shown on an expanded voltage and time scale in (B). (B) Shape of the action potential in the model and biological CGCs. In both the model and biological neuron, the shape of the action potential is very similar, with the duration being approximately 17 ms (measured at −20 mV) and amplitude being approximately 115 mV. The arrow indicates the characteristic “shoulder” of the action potential during its repolarisation phase. (C) Current-frequency response in the model and the biological neuron. In both, externally injected currents in the range 0–2 nA induce spikes at frequencies up to approximately 15 Hz. To aid clarity, the frequency data shown for the biological neuron come from a single experiment where the same CGC was tested with increasing amounts of current injected into the soma through one electrode while recording spike activity through a second electrode. The same test was repeated with 4 more CGCs in different preparations. The membrane potential of all five neurons tested this way was set at −80 mV prior to each test and so the frequency responses to the same amount of current showed very little variance between the individual neurons.
In a next stage, we performed a set of simulations in which we examined the effect of selectively blocking identified ionic currents on the electrical properties of the model cell, thus mimicking the application of specific pharmacological agents in the biological neurons during a series of independent electrophysiological experiments (Staras et al., 2002 ).
As a first example, we examined the effect of removing the persistent and transient sodium currents from the model. In the intact nervous system, bathing the preparation in zero-Na+ saline caused the CGCs to stop firing and hyperpolarize to a very negative potential (Figure 5 Ai; also see Staras et al., 2002 ; Nikitin et al., 2008 ). Artificially repolarizing the cell above the firing threshold failed to evoke action potentials, but washing back into normal saline caused the CGCs to start firing again, with no apparent change in the spike shape (Staras et al., 2002 ).
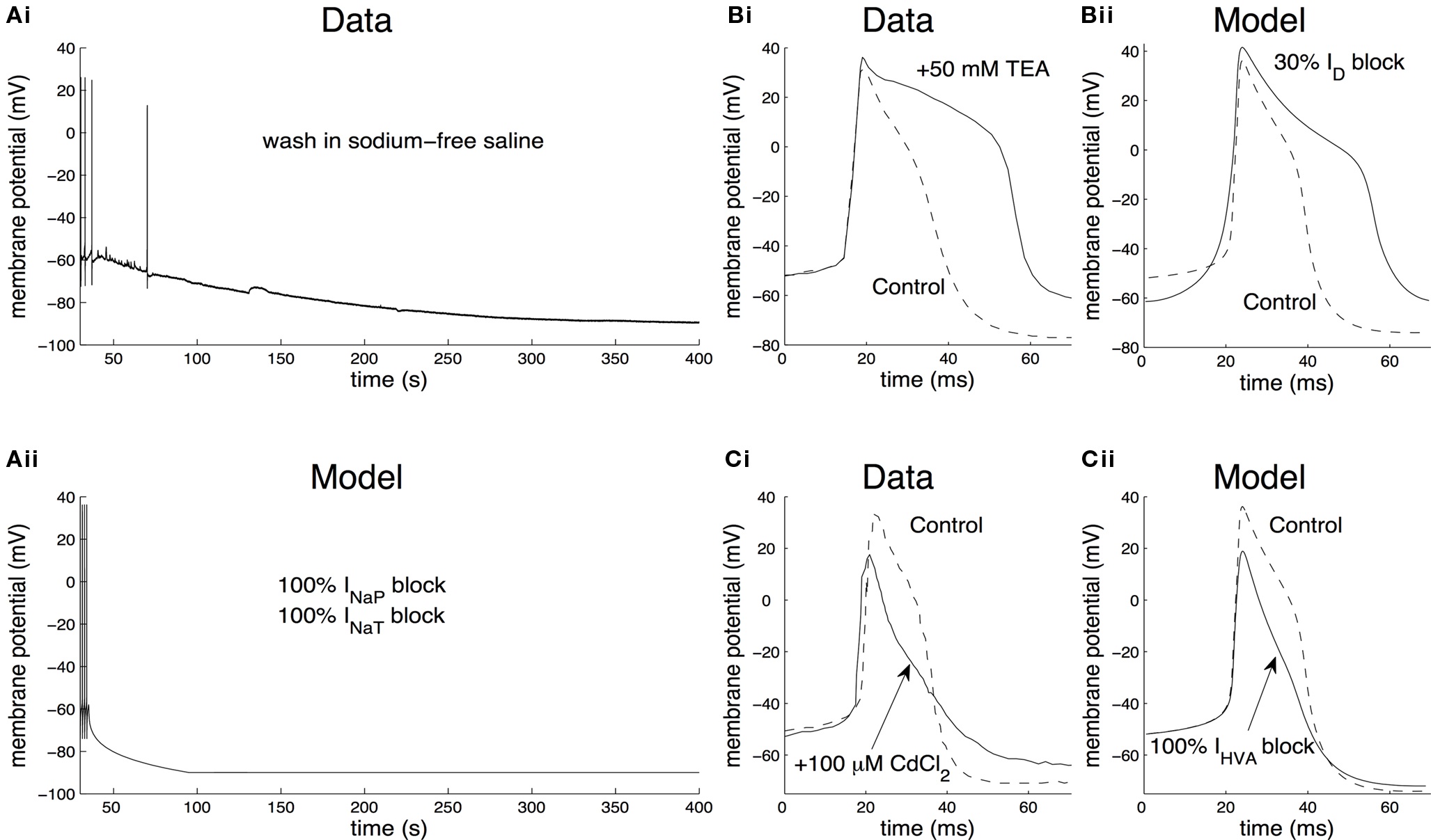
Figure 5. Contribution of identified ionic currents to the electrical properties of the CGCs. (A) Contribution of the total sodium current. When washing the preparation into sodium-free saline, CGCs from the intact nervous system cease to fire and the membrane potential is significantly hyperpolarized (Ai; also see Staras et al., 2002 ). In the model, washing into sodium-free saline was simulated by gradually setting the maximal persistent and transient sodium conductances (gNaP and gNaT, respectively) to zero over a time interval of 60 s (Aii). This is equivalent to completely removing the transient and persistent sodium currents from the model, inducing the cell to stop firing and the membrane potential to settle at a very negative value (∼−90 mV), similarly to the biological neuron. (B) Contribution of the delayed rectifier potassium current to spike shape. When blocking ID by washing the preparation in 50 mM TEA (tetraethylammonium chloride), the duration of the action potentials recorded from CGCs in the intact nervous system increased significantly (Bi; also see Staras et al., 2002 ). Also, the after-hyperpolarization following each spike was reduced in amplitude. In the model, this situation was simulated by blocking the maximal conductance of the delayed rectifier, gD, by 30% (Bii). This resulted in spikes of longer duration by ∼17 ms and a smaller spike after-hyperpolarization by ∼12 mV, similarly to washing the biological neuron into saline containing TEA. (C) Contribution of the high-voltage-activated calcium current to spike shape. When blocking IHVA by washing the preparation into 100-μM CdCl2, the spikes recorded from CGCs in the intact nervous system became shorter and narrower and the spike after-hyperpolarization was reduced in amplitude (Ci; Staras et al., 2002 ). In the model, blocking IHVA by CdCl2 was simulated by setting gHVA, the maximal conductance of the high-voltage-activated calcium current, equal to zero (Cii). This resulted in spikes losing their characteristic “shoulder” and becoming narrower and shorter by ∼6 ms and ∼17 mV respectively, similarly to recordings from the biological neuron after the application of CdCl2.
We simulated the removal of Na+ ions in our model by gradually setting the maximal conductance of the persistent and transient sodium currents (gNaP and gNaT, respectively) to zero over a time interval of 60 s. Under these conditions, the model neuron immediately ceased firing and the membrane potential hyperpolarized at a very negative value (∼−90 mV), as in the biological neuron (Figure 5 Aii). In addition, when the model was artificially repolarized above −50 mV by external current injection, the action potentials did not recover, similarly to the biological neuron (data not shown). This result suggests that the total sodium current plays an important role in the generation of action potentials (a function traditionally attributed to its transient component) in both the model and biological neurons. In addition, it constitutes a significant depolarizing force, sufficient to bring the membrane potential above its firing threshold even from a very negative value, thus sustaining spontaneous tonic firing in both the model and the biological CGCs.
Next, we examined the effect of blocking the delayed rectifier potassium current, ID, to the electrical properties of the neuron. In the intact nervous system, washing the preparation in 50-mM TEA (tetraethylammonium chloride) resulted in a significant depolarization of the membrane potential, the individual spikes became broader and the amplitude of the after-hyperpolarization following each spike became smaller (Figure 5 Bi). These effects were completely reversed, when the preparation was washed back into control saline (Staras et al., 2002 ).
In the model, application of TEA was mimicked by reducing the maximum conductance of the delayed rectifier, gD, by 30% (Figure 5 Bii). Under these conditions, the model neuron became significantly depolarized, with a spike after-hyperpolarization smaller by ∼12 mV and an increased spike duration by ∼17 ms. Completely blocking the delayed rectifier in the model by setting its maximal conductance equal to zero resulted in ceasing firing, the membrane potential failed to repolarize and settled at a very positive value (>50 mV; data not shown). These effects are comparable to those recorded from the biological neuron when TEA is present in the saline and they suggest that, in agreement with the role typically attributed to this current, the delayed rectifier is important in repolarizing the membrane during an action potential in both the biological and the model neuron.
As a final example, we examined the effect of blocking the high-voltage-activated calcium current, IHVA, on the electrical properties of the membrane. In neurons from the intact nervous system, washing the preparation into 100-μM CdCl2, a non-specific blocker of the high-voltage-activated calcium current, resulted in the cell becoming depolarized (from −63 mV to −59 mV) and a characteristic narrowing and shortening of the action potential (Figure 5 Ci), which reversed to normal, when the preparation was washed back to control saline (Staras et al., 2002 ).
In the model, the application of CdCl2 was mimicked by setting the maximal conductance of the high-voltage-activated calcium current, gHVA, to zero. Similarly to the biological neuron in the presence of CdCl2 in the saline, the spike lost its characteristic “shoulder”, becoming narrower and shorter by ∼6 ms and ∼17 mV respectively (Figure 5 Cii). Also, the after-hyperpolarization following each spike became smaller in amplitude by ∼2 mV, similarly to the biological neuron. These results suggest that IHVA contributes to the generation of action potentials resulting in higher and broader spikes, in both the model and the biological CGCs.
Blocking ILVA did not have any apparent effect on the firing frequency or spike shape of the model neuron, but enhancing ILVA had a weak effect on the firing frequency, which started becoming significant after a 10-fold increase in the maximal conductance of this current. On the other hand, blocking IA in the model resulted in increasing both the width and height of the spontaneous spikes. However, these effects were not consistent across different instantiations of the CGC model, i.e., when different parameter combinations were tested. In the absence of a systematic experimental analysis on the effects of blocking IA or ILVA under current-clamp conditions, which could serve for validating the model, we do not report these results in the present study.
Overall, the effects of blocking identified sodium, potassium and calcium currents on the electrical properties of the CGCs are similar in both the model and the biological cells. These results, in combination with the ability of the model to reproduce accurately the spike shape, spontaneous tonic activity and current-frequency response of the biological CGCs suggest that the model successfully captures essential aspects of the electrophysiological properties of the biological cells and justify its use in a predictive setting.
Simulating the Effects of Classical Conditioning on the Electrical Properties of the CGCs
During appetitive classical conditioning using a single-trial protocol (Alexander et al., 1984 ), the resting membrane potential of the CGC soma in trained animals is significantly depolarized at 24 h after conditioning (mean membrane potential increase, 2.5 mV; merged data from left and right CGCs), when compared to measurements taken from unpaired or naïve controls (Figures 6 Ai,ii; see Nikitin et al., 2008 for more details). However, no significant differences were found in the firing frequency of spontaneously generated CGC spikes between trained and control animals (Figure 6 Ai). Other spike parameters, such as duration, amplitude and after-hyperpolarization also remained unchanged after conditioning (Kemenes et al., 2006 ; Nikitin et al., 2008 ).
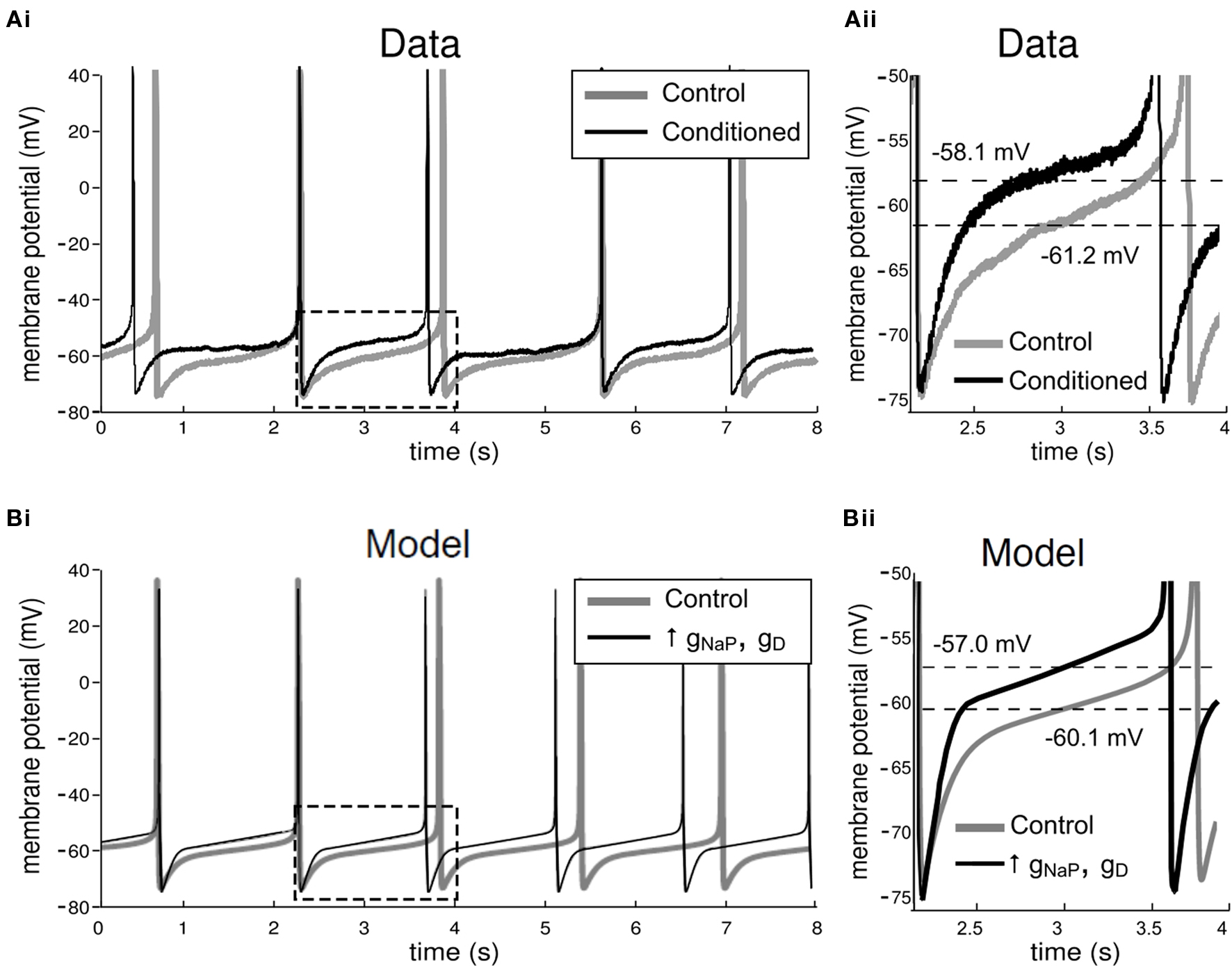
Figure 6. Electrophysiological effects of conditioning in the biological and model CGCs. (A) Effects of conditioning in the biological CGCs. Recordings from CGCs in animals trained using a single-trial classical appetitive conditioning protocol do not show any significant differences in the frequency of the spontaneous firing activity of the cell, when compared to recordings from cells in non-conditioned animals (Example traces shown in Ai, also see Kemenes et al., 2006 ). However, the membrane potential of CGCs from conditioned animals (measured midway between consecutive spikes and averaged for the whole trace shown) was depolarized, when compared to CGC recordings from non-conditioned control animals (section of Ai in dashed rectangle shown in Aii). (B) Effects of conditioning in the model CGCs. Conditioning in the model was simulated by a balanced increase in gNaP and gD, the maximal conductances of the persistent sodium and delayed rectifier potassium currents respectively. For example, when gNaP was increased by 50%, increasing gD by approximately the same proportion stabilized the spontaneous firing frequency in the model cell at the value it had before increasing the two conductances, i.e., ∼0.7 Hz (Bi). A closer inspection of the model CGCs revealed that the membrane potential after the increase was depolarized by 3.1 mV (section of Bi in dashed rectangle shown in Bii). This increase is comparable to the values measured from the biological cells after conditioning (example in Aii).
An interesting question raised during these experiments concerned the ionic mechanisms of the experience-induced changes in the electrical properties of the CGCs, namely the persistent depolarization of the somal membrane potential and the concomitant stabilization of spike frequency and other spike parameters. Here, we have utilized the model developed in the previous sections to test whether specific changes in identified ionic currents are sufficient to explain the electrophysiological effects of conditioning on the membrane of CGCs from trained animals. We initially focused on two ionic currents of the CGC, the persistent sodium current, INaP, and the delayed rectifier potassium current, ID (Staras et al., 2002 ). Previous work already has shown that conditioning enhances INaP (Nikitin et al., 2008 ). A statistical comparison of the areas under the full I-V curves of ID in CGCs from trained versus control animals has shown that there was no significant global decrease in ID that could have contributed to the learning-induced membrane potential depolarization (Nikitin et al., 2008 ) but in this previous work ID was not examined in more detail. We therefore now performed pairwise comparisons of discrete ID amplitude data from our original voltage-clamp experiments (Nikitin et al., 2008 ). This more detailed analysis revealed a consistent learning-induced increase in ID in response to voltage steps from −60 mV to ≥0 mV, reaching statistical significance at +30 mV (n = 10 in each group, unpaired t-test, df = 18, t = 2.43, p < 0.03), indicating a learning-induced increase in the maximal conductance of ID.
In the model, the electrophysiological effects of conditioning were simulated by a balanced increase in the maximal conductances of the persistent sodium and delayed rectifier potassium currents (gNaP and gD, respectively), such that the firing frequency of the cell before and after the increase remained approximately the same (∼0.7 Hz), as was observed experimentally when CGCs from trained and naïve animals were compared (Kemenes et al., 2006 ; Nikitin et al., 2008 ). For example, increasing only gNaP by 50% induced a dramatic increase in the firing frequency of the model cell (∼15 Hz; data not shown), far beyond the normal operating frequency range of the CGCs. However, if gD was increased simultaneously by approximately the same proportion, the mean firing frequency of the cell remained stable at ∼0.7 Hz (5 spikes over 7 s; Figure 6 Bi), i.e., within the narrow frequency range between 0.6 Hz and 1 Hz, which is characteristic for CGCs in the type of isolated preparation we used in this study. A closer comparison of the model before and after the enhancement of these two currents revealed that the membrane potential of the model after the enhancement was depolarized by 3.1 mV (Figure 6 Bii), similarly to biological neurons from trained animals (Nikitin et al., 2008 ).
The changes in the membrane potential, spike amplitude, spike duration and amplitude of the spike after-hyperpolarization induced by systematically increasing both the persistent sodium and delayed rectifier maximal conductance values in the model are summarized in Figure 7 . The two conductances were both increased in the range 5% to 50% of their initial values, such that the firing frequency of the cell remained stable at ∼0.7 Hz, as explained above (Figure 7 A). Overall, simulating conditioning by artificially enhancing gNaP and gD by up to 50% in the model was sufficient to depolarize the membrane by more than 2.5 mV (Figure 7 Bi), the experimentally measured mean depolarization in axotomized CGCs in isolated CNS preparations from conditioned animals (Nikitin et al., 2008 ).
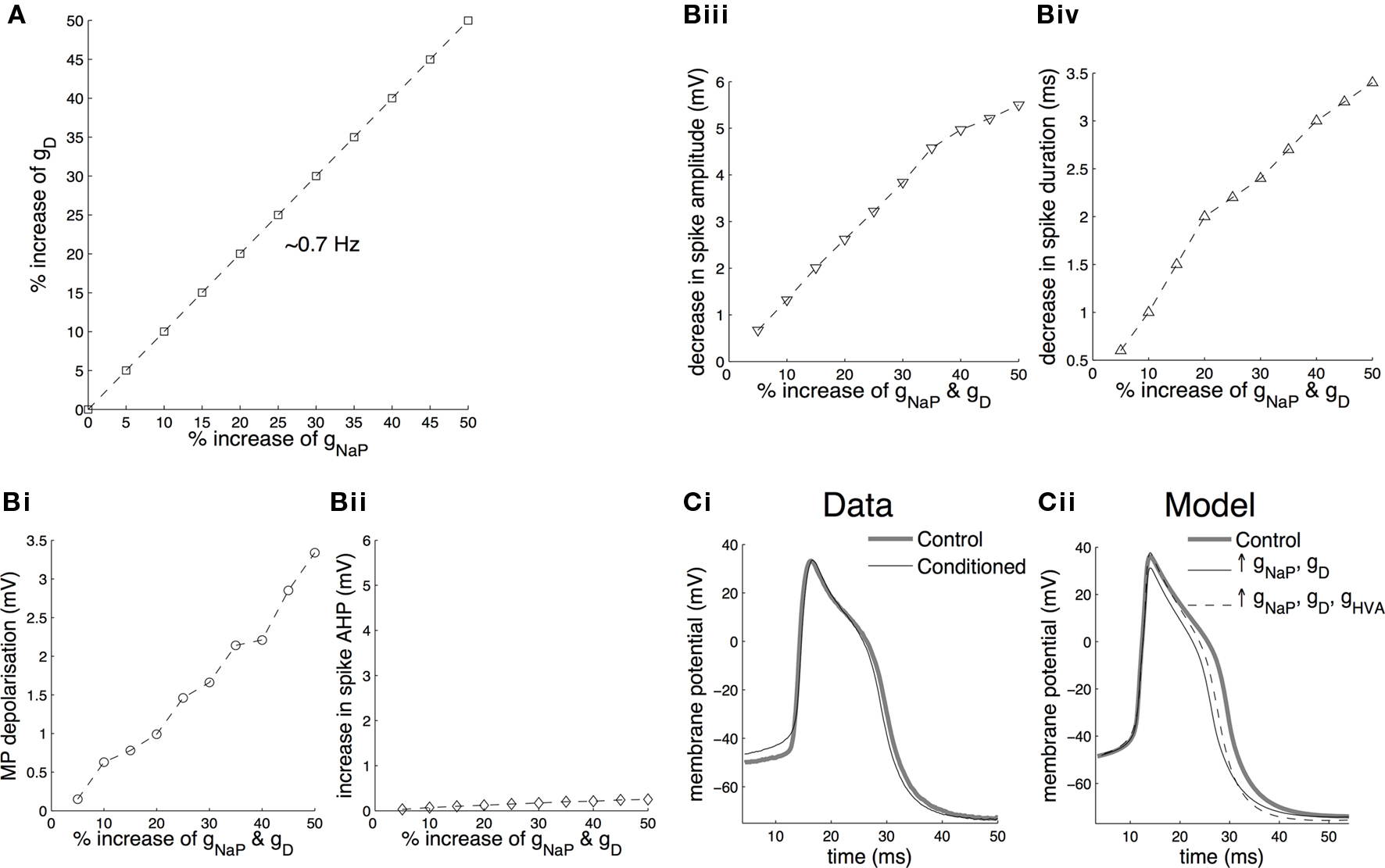
Figure 7. Effects of simulating conditioning on membrane potential and spike shape in the model CGCs. (A) The effect of conditioning in the model CGCs was simulated by a balanced increase in gNaP and gD such that the spontaneous firing frequency before and after the increase remained approximately the same (∼0.7 Hz). Stabilization of the firing frequency after increasing gNaP between 5% and 50% of its initial value required increasing gD by approximately the same proportion. (B) A balanced increase of gNaP and gD between 5% and 50% of their initial values resulted in a persistent membrane depolarization by more than 2.5 mV (the experimentally observed mean depolarization in axotomized CGCs in isolated CNS preparations; Nikitin et al., 2008 ) (Bi), virtually no increase in the amplitude of the spike after-hyperpolarization (Bii), a decrease in spike amplitude by ∼6 mV (Biii) and a decrease in spike duration by ∼3.5 ms (Biv). (C) Changes in spike amplitude and duration, however, do not occur after classical conditioning (example traces in Ci, also see Kemenes et al., 2006 ). These changes were fully (spike amplitude) or partially (spike duration) reversed by an appropriate increase (20%) of gHVA (Cii).
The model also faithfully replicated the lack of any significant effect of conditioning on the afterhyperpolarization of CGCs when gNaP and gD were increased together (Figure 7 Bii). However, unlike the electrophysiological experiments on CGCs from conditioned and control animals (Figure 7 Ci, also see Kemenes et al., 2006 ; Nikitin et al., 2008 ), when gNaP and gD were increased together in the model, both the duration and amplitude of the spikes decreased in an approximately linear manner (Figures 7 Biii,iv). We therefore set up the testable hypothesis that a change in a conductance other than gNaP and gD may compensate for the changes in spike amplitude and duration caused by these two conductances. When this new hypothesis was tested using the model (Figure 7 Cii), we found that the change in spike amplitude was completely reversed and the change in spike duration was partially reversed by an appropriate increase (20%) of the identified high-voltage-activated calcium conductance, gHVA, of the CGC (Staras et al., 2002 ), without affecting the membrane potential (Figure 7 Cii) or firing frequency of the cell (data not shown).
In summary, the above results demonstrate that our model is able to replicate the conditioning-induced persistent membrane depolarization and concomitant stabilization of the firing frequency in the CGCs by a balanced increase of the persistent sodium and delayed rectifier potassium currents. This, in combination with previously published experimental data (Nikitin et al., 2008 ) and the results of the new analysis described in the Results in Supplementary Material, suggests that there is a causal link between experience-induced changes in these two conductances and the electrical properties of the CGCs that underlie the formation of long-term associative memory in Lymnaea during conditioning. Importantly, the application of the model resulted in setting up the hypothesis that the high-voltage-activated calcium current, IHVA, also needs to be modified to fully stabilize the shape of the spike.
Discussion
Although a number of previous papers have already demonstrated learning-induced intrinsic changes in ionic conductances in both vertebrate and invertebrate preparations (Debanne et al., 2003 ; Magee and Johnston, 2005 ; Zhang and Linden, 2003 ), none of them addressed the issue of stability of key neuronal functions after learning, and specifically, after classical conditioning. Here, we established how a neuron can undergo learning-induced intrinsic plasticity of some of its key electrical properties (e.g. membrane potential) without consequent changes in other equally important electrical properties (e.g. spike frequency) essential for its basic network functions. To achieve this goal, we used a computational modeling approach based on both voltage- and current-clamp data obtained in the same identified neuron type in preparations from both classically conditioned and control animals. The CGC neuron of Lymnaea was a highly suitable model system to use for this analysis because (i) to fulfill its key modulatory role in the snail feeding network it has to fire in a particular frequency range (between ∼ 0.6 and 1 Hz in isolated CNS preparations (Yeoman et al., 1994 ) and (ii) this firing frequency is retained even after the neuron has undergone plastic changes affecting its membrane potential (Kemenes et al., 2006 ). Our new work provides the first mechanistic explanation of how this difficult task is achieved by balanced learning-induced changes in specific ionic conductances.
Analysis of the Hodgkin-Huxley-type model of the CGCs we have built revealed that plastic changes in two identified currents, INaP and ID, were sufficient to mimic the previously recorded modifications of the intrinsic electrical properties of these neurons during single-trial behavioral conditioning experiments, i.e., a persistent membrane depolarization with a parallel stabilization of the firing frequency (Kemenes et al., 2006 ). In addition, the model predicted that the high-voltage-activated calcium current, IHVA, is also likely to be enhanced in the CGCs as a result of conditioning. However, we found that if the simulated increase in IHVA exceeded 20%, when it compensated for around 40% of the spike narrowing effect of the enhancement of INaP and ID, it also started to affect spike amplitude. It will therefore need to be investigated whether changes in other currents might also contribute to further compensatory spike broadening after increasing IHVA, as well as INaP and ID. One possible candidate mechanism is a learning-induced decrease in a putative calcium-activated TEA-insensitive potassium current of the CGC (IK(Ca)), which only shows a significant activation at high voltage step levels (from –60 mV to –20 mV and above; Staras et al., 2002 ). Because of the rare occurrence of this current, it was not characterized in further detail in previous work (Staras et al., 2002 ) and therefore was not incorporated in our model. Whether IHVA and IK(Ca) are actually modified by classical conditioning, will be tested in future experiments, which can also lead to further refinement of the current model.
There are a number of important previous examples where long-lasting depolarization occurs after in vitro or in vivo training or activation of second messenger cascades with no underlying net change in input resistance (e.g., Swandulla and Lux, 1984 ; Kemenes et al., 1993 ; Ross and Soltesz, 2001 ; Jones et al., 2003 ). A lack of a change in input resistance also was observed in the depolarized Lymnaea CGCs after behavioral classical conditioning (Kemenes et al., 2006 ). Our recent voltage clamp studies (Nikitin et al., 2008 ) and the computational modeling described in this paper showed that in the CGCs the depolarization is predominantly driven by an enhanced persistent sodium current with increases in potassium and calcium conductances preventing changes in spike frequency and spike shape, respectively. Swandulla and Lux (1984) showed that a cAMP-induced increase in a sodium conductance in Helix neurons is compensated for by a decrease in a potassium conductance leading to no net change in input resistance near the resting potential. This is clearly not the case in the CGCs after learning. We therefore have to speculate that a so far unidentified conductance decreases after learning and this decrease compensates for the increase in the persistent sodium conductance. For example, there may be a learning-induced decrease in a chloride conductance resulting from the previously observed depolarization-induced increase in baseline levels of intracellular calcium in the CGC (Kemenes et al., 2006 ). Previous work already has linked a depolarization-induced rise in intracellular calcium levels in Lymnaea neurons to decreases in a chloride conductance (Vulfius et al., 1998 ) but further experiments will need to be performed to establish if this also happens in the CGCs after classical conditioning.
In the biological CGCs the learning-induced depolarization can be quite variable depending on the type of preparation used and time of test after training. Kemenes et al., (2006) used semi-intact preparations with all the lip chemosensory structures and nerves intact. In these preparations the shift at 24 h after training was ∼ 5 mV (with a stable CGC firing rate), whereas in isolated CNS preparations tested at 24 h post-training it was ∼ 2.5 mV (the paper that provided the learning-related voltage-clamp data for the model).Nikitin et al., 2008 ; Figures 7 A,Bi together show that a balanced change in INaP and ID can explain stable firing even when the membrane potential is shifted by more than 2.5 mV. We cannot rule out however that in the semi-intact preparations and indeed, in the intact animals, external modulatory inputs from the chemosensory pathways also contribute to both membrane potential depolarization and spike frequency stabilization. This is particularly likely to be the case at 14 days after training when in semi-intact preparations the shift was in the range of 10 mV (Kemenes et al., 2006 ).
An important issue in the construction of biologically realistic neuronal models is estimating the values of the various parameters that appear in the model, based on available electrophysiological data (Prinz et al., 2003 ; Huys et al., 2006 ; Haufler et al., 2007 ; Hobbs and Hooper, 2008 ). In the present paper, we successfully used a combination of voltage- and current-clamp recordings for estimating a large number of unknown parameters in our model, including maximal conductances, reversal potentials and the parameters governing the activation and inactivation kinetics of all the voltage-gated ionic currents that have been identified in the CGCs. The parameter estimation method we applied permitted the construction of a model capable of reproducing the spike shape, spontaneous firing activity and current-frequency response of the biological neurons with high accuracy. In addition, the model simulated successfully the effects of various pharmacological agents on the electrical properties of these cells by selectively blocking identified ionic currents in the model and comparing the results of these simulations to independent experimental data (Staras et al., 2002 ). These results confirm that the model captures essential aspects of the electrophysiology of the biological CGCs, thus being a useful predictive/analytical tool in mechanistic analyses of neuronal plasticity.
The only other examples of realistic modeling in the Lymnaea nervous system refer to the feeding CPG interneurons (Vavoulis et al., 2007 ) and a feeding motoneuron type, B1 (Vehovszky et al., 2005 ). In the first case (Vavoulis et al., 2007 ), two-compartment models of three important feeding CPG interneurons (N1M, N2v and N3t) and an identified modulatory interneuron, the Slow Oscillator (SO), were constructed. These models were then organized into a network that resembled important aspects of the Lymnaea feeding CPG, both in terms of network topology and function. In this network model, the individual cells were of the Hodgkin-Huxley type and mimicked sufficiently well the electrical properties of their biological counterparts, but unlike the CGC model presented here, the ionic currents included in these neuronal models were not, in most cases, the result of direct observation (e.g., through voltage-clamp experiments), but rather were inferred from the analysis of an extensive set of current-clamp recordings capturing the characteristic patterns of electrical activity expressed by the biological neurons.
In the case of the B1 motorneuron, the model was constructed in order to study the effects of the biogenic amine octopamine on neuronal excitability (Vehovszky et al., 2005 ). From a methodological point of view, both the B1 and the CGC models are single-compartment and they follow a similar mathematical formalism. One difference is that the B1 model contained three voltage-gated ionic currents (a persistent potassium current, a transient potassium current and a transient sodium current), which were the major ionic currents found in the B1 motoneurons (Vehovszky et al., 2005 ). Importantly, in the B1 model the parameters for the individual ionic currents were estimated mainly from analysis of voltage-clamp data, while in the case of the CGC model, we used a combination of voltage-clamp and current-clamp data. This made it possible to replicate the shape of the action potentials and the spontaneous firing activity of the biological neuron with very high fidelity.
Comparison with other Systems and Limitations of the Model
One of the early examples of biophysical neuronal modeling in invertebrates was a mathematical model of the lateral pyloric (LP) neuron in the crustacean stomatogastric ganglion (Buchholtz et al., 1992 ; Golowasch et al., 1992 ). The model contained all the major ionic currents identified through electrophysiological (voltage-clamp) analysis (Golowasch and Marder, 1992 ) and it mimicked successfully the basic activity of the biological neuron. A more recent modeling study (Nowotny et al., 2008 ) employed an automatic optimization method to fit a model of the LP neuron against a rich set of current-clamp data, enabling the simulation of the dynamic behavior of the biological neuron over a wide range of conditions. In the present paper, we first optimized the model against extensive voltage-clamp data, and then fitted a single spike from current clamp data. The ability of our model to reproduce the dynamic behavior of the biological neuron, e.g., its response to injected current and pharmacological agents and classical conditioning, emerged as a result of this initial optimization process against a combination of voltage- and current-clamp recordings.
In vertebrates, detailed computational models were used to study the contribution of a persistent sodium current to membrane excitability in CA1 hippocampal pyramidal cells (Vervaeke et al., 2006 ) and small dorsal root ganglion neurons (Herzog et al., 2001 ). In the latter study, the computer simulation showed that the persistent TTX-resistant sodium current, which is very similar to INaP in the CGCs, had a strong depolarizing influence on the resting membrane potential. Both our computational model and previous experimental work (Nikitin et al., 2008 ), have demonstrated a similar link between INaP and membrane potential in the CGCs. These observations suggest that a causal relationship between persistent sodium conductances and membrane potential is conserved between invertebrate and vertebrate neurons.
An important limitation is that the CGC model does not include at the moment any second-messenger cascades or intracellular calcium dynamics. A consideration of these processes will have to be included in further modeling in order to fully understand the mechanisms involved in the more dynamic properties of the CGCs, such as the ability of these cells to keep their firing frequency relatively stable in the face of external and internal perturbations. We hypothesize that this homeostatic capability of the CGCs relies upon activity-dependent mechanisms, which typically employ the concentration of intracellular calcium as an indicator of the level of electrical activity in the neuron (Marder and Prinz, 2002 ). Also, it has been shown that injection of cAMP in the CGC soma induces prolonged (lasting several hours) plastic changes of the electrical properties of the CGCs, including a significant enhancement of the persistent sodium current, increased bursting, a significant depolarization of the somatic potential and decreased input resistance (Nikitin et al., 2006 ). Thus, it is likely that processes dependent on the cAMP second-messenger cascade are implicated in the expression of long-term neuronal plasticity in the CGCs. It follows that modeling intracellular calcium dynamics and cAMP-dependent second-messenger pathways, as well as their interactions with ionic currents in the cell membrane will improve the realism of the CGC model and, therefore, should be the subject of future model development.
Conflict of Interest Statement
The authors declare that this research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Dimitris V. Vavoulis was supported by the U.K. Biotechnology and Biological Sciences Research Council and by the Future and Emerging Technologies (FET) European Commission program BION (number 213219). György Kemenes, Paul R. Benjamin, Eugeny S. Nikitin and Ildikó Kemenes were funded by the U.K. Biotechnology and Biological Sciences Research Council. György Kemenes was also funded by the U.K. Medical Research Council. Eugeny S. Nikitin was also supported by the Russian Foundation for Basic Research and the Russian Academy of Sciences (Molecular Cell Biology).
Supplementary Material
The Supplementary Material for this article can be found online at http://www.frontiersin.org/behavioralneuroscience/paper/10.3389/fnbeh.2010.00019/
References
Alexander, J., Audesirk, T. E., and Audesirk, G. J. (1984). One-trial reward learning in the snail Lymnea stagnalis. J. Neurobiol. 15, 67–72.
Buchholtz, F., Golowasch, J., Epstein, I. R., and Marder, E. (1992). Mathematical-model of an identified stomatogastric ganglion neuron. J. Neurophysiol. 67, 332–340.
Debanne, D., Daoudal, G., Sourdet, V., and Russier, M. (2003). Brain plasticity and ion channels. J. Physiol. Paris 97, 403–414.
Golowasch, J., Buchholtz, F., Epstein, I. R., and Marder, E. (1992). Contribution of individual ionic currents to activity of a model stomatogastric ganglion neuron. J. Neurophysiol. 67, 341–349.
Golowasch, J., Casey, M., Abbott, L. F., and Marder, E. (1999). Network stability from activity-dependent regulation of neuronal conductances. Neural. Comput. 11, 1079–1096.
Golowasch, J., and Marder, E. (1992). Ionic currents of the lateral pyloric neuron of the stomatogastric ganglion of the crab. J. Neurophysiol. 67, 318–331.
Haufler, D., Morin, F., Lacaille, J. C., and Skinner, F. K. (2007). Parameter estimation in single-compartment neuron models using a synchronization-based method. Neurocomputing 70, 1605–1610.
Herzog, R. I., Cummins, T. R., and Waxman, S. G. (2001). Persistent TTX-resistant Na+ current affects resting potential and response to depolarization in simulated spinal sensory neurons. J. Neurophysiol. 86, 1351–1364.
Hobbs, K. H., and Hooper, S. L. (2008). Using complicated, wide dynamic range driving to develop models of single neurons in single recording sessions. J. Neurophysiol. 99, 1871–1883.
Huys, Q. J. M., Ahrens, M. B., and Paninski, L. (2006). Efficient estimation of detailed single-neuron models. J. Neurophysiol. 96, 872–890.
Jones, N. G., Kemenes, I., Kemenes, G., and Benjamin, P. R. (2003). A persistent cellular change in a single modulatory neuron contributes to associative long-term memory. Curr. Biol. 13, 1064–1069.
Kemenes, G., Rózsa, K. S., and Carpenter, D. O. (1993). Cyclic-AMP mediated excitatory responses to leucine enkephalin in Aplysia neurons. J. Exp. Biol. 181, 321–328.
Kemenes, I., Straub, V. A., Nikitin, E. S., Staras, K., O’Shea, M., Kemenes, G., and Benjamin, P. R. (2006). Role of delayed nonsynaptic neuronal plasticity in long-term associative memory. Curr. Biol. 16, 1269–1279.
Magee, J. C., and Johnston, D. (2005). Plasticity of dendritic function. Curr. Opin. Neurobiol. 15, 334–342.
Marder, E., and Prinz, A. A. (2002). Modeling stability in neuron and network function: the role of activity in homeostasis. Bioessays 24, 1145–1154.
McCrohan, C. R., and Benjamin, P. R. (1980a). Patterns of activity and axonal projections of the cerebral giant-cells of the snail, Lymnaea stagnalis. J. Exp. Biol. 85, 149–168.
McCrohan, C. R., and Benjamin, P. R. (1980b). Synaptic relationships of the cerebral giant-cells with moto-neurons in the feeding system of Lymnaea stagnalis. J. Exp. Biol. 85, 169–186.
Nikitin, E. S., Kiss, T., Staras, K., O’Shea, M., Benjamin, P. R., and Kemenes, G. (2006). Persistent sodium current is a target for cAMP-induced neuronal plasticity in a state-setting modulatory interneuron. J. Neurophysiol. 95, 453–463.
Nikitin, E. S., Vavoulis, D. V., Kemenes, I., Marra, V., Pirger, Z., Mitchel, M., Feng, J. F., O’Shea, M., Benjamin, P. R., and Kemenes, G. (2008). Persistent sodium current is a non-synaptic substrate for memory. Curr. Biol. 18, 1221–1226.
Nowotny, T., Levi, R., and Selverston, A. I. (2008). Probing the dynamics of identified neurons with a data-driven modeling approach. PLoS ONE 3, e2627. doi:10.1371/journal.pone.0002627.
Prinz, A. A., Billimoria, C. P., and Marder, E. (2003). Alternative to hand-tuning conductance-based models: construction and analysis of databases of model neurons. J. Neurophysiol. 90, 3998–4015.
Ross, S. T., and Soltesz, I. (2001). Long-term plasticity in interneurons of the dentate gyrus. Proc. Natl. Acad. Sci. U.S.A. 98, 8874–8879.
Staras, K., Gyori, J., and Kemenes, G. (2002). Voltage-gated ionic currents in an identified modulatory cell type controlling molluscan feeding. Eur. J. Neurosci. 15, 109–119.
Straub, V. A., and Benjamin, P. R. (2001). Extrinsic modulation and motor pattern generation in a feeding network: a cellular study. J. Neurosci. 21, 1767–1778.
Swandulla, D., and Lux, H. D. (1984). Changes in ionic conductances induced by cAMP in helix neurons. Brain Res. 305, 115–122.
Vavoulis, D. V., Straub, V. A., Kemenes, I., Kemenes, G., Feng, J. F., and Benjamin, P. R. (2007). Dynamic control of a central pattern generator circuit: a computational model of the snail feeding network. Eur. J. Neurosci. 25, 2805–2818.
Vehovszky, A., Szabo, H., and Elliott, C. J. H. (2005). Octopamine increases the excitability of neurons in the snail feeding system by modulation of inward sodium current but not outward potassium currents. BMC Neurosci. 6, 70.
Vervaeke, K., Hu, H., Graham, L. J., and Storm, J. F. (2006). Contrasting effects of the persistent Na+ current on neuronal excitability and spike timing. Neuron 49, 257–270.
Vulfius, C. A., Ryazansky, V. D., Krasts, I. V., and Ilyasov, F. E. (1998). Intracellular Ca2+ modulates Cl- current evoked by acetylcholine in lymnaea neurons. Neurosci. Lett. 249, 5–8.
Weiss, K. R., and Kupfermann, I. (1976). Homology of giant serotonergic neurons (metacerebral cells) in Aplysia and Pulmonate mollusks. Brain Res. 117, 33–49.
Willms, A. R., Baro, D. J., Harris-Warrick, R. M., and Guckenheimer, J. (1999). An improved parameter estimation method for Hodgkin-Huxley models. J. Comput. Neurosci. 6, 145–168.
Yeoman, M. S., Brierley, M. J., and Benjamin, P. R. (1996). Central pattern generator interneurons are targets for the modulatory serotonergic cerebral giant cells in the feeding system of Lymnaea. J. Neurophysiol. 75, 11–25.
Yeoman, M. S., Kemenes, G., Benjamin, P. R., and Elliott, C. J. H. (1994). Modulatory role for the serotonergic cerebral giant-cells in the feeding system of the snail, Lymnaea. 2. photoinactivation. J. Neurophysiol. 72, 1372–1382.
Keywords: parameter estimation in Hodgkin-Huxley-type models, classical conditioning, intrinsic plasticity, persistent sodium current, delayed rectifier potassium current, high-voltage-activated calcium current, Lymnaea stagnalis
Citation: Vavoulis DV, Nikitin ES, Kemenes I, Marra V, Feng J, Benjamin PR and Kemenes G (2010) Balanced plasticity and stability of the electrical properties of a molluscan modulatory interneuron after classical conditioning: a computational study. Front. Behav. Neurosci. 4:19. doi: 10.3389/fnbeh.2010.00019
Received: 22 February 2010;
Paper pending published: 12 March 2010;
Accepted: 07 April 2010;
Published online: 05 May 2010
Edited by:
Martin Giurfa, Université Paul Sabatier-Toulouse III, FranceReviewed by:
Romuald Nargeot, Universités Bordeaux, FrancePeter Andras, University of Newcastle, UK
Copyright: © 2010 Vavoulis, Nikitin, Kemenes, Marra, Feng, Benjamin and Kemenes. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Dimitris V. Vavoulis, Department of Computer Science, University of Warwick, Coventry CV4 7AL, UK. e-mail: d.vavoulis@warwick.ac.uk; György Kemenes, School of Life Sciences, University of Sussex, 1 Lewes Road, Brighton, East Sussex, BN1 9QG, UK. e-mail: g.kemenes@sussex.ac.uk