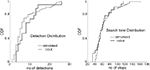1
CORTEX Research Team, Laboratoire Lorrain de Recherche en Informatique et ses Applications, Nancy, France
2
Advanced Concepts Team, European Space Research and Technology Centre, European Space Agency, Noordwijk, Netherlands
3
Unité Mixte de Recherche 1272, Physiologie de l’Insecte Signalisation et Communication, Institut National de la Recherche Agronomique, Versailles, France
Tracking scents and locating odor sources is a major challenge in robotics. The odor plume is not a continuous cloud but consists of intermittent odor patches dispersed by the wind. Far from the source, the probability of encountering one of these patches vanishes. In such dilute conditions, a good strategy is to first ‘explore’ the environment and gather information, then ‘exploit’ current knowledge and direct toward the estimated source location. Infotactic navigation has been recently proposed to strike the balance between exploration and exploitation. Infotaxis was tested in simulation and produced trajectories similar to those observed in the flight of moths attracted by a sexual pheromone. In this paper, we assess the performance of infotaxis in dilute conditions by combining robotic experiments and simulations. Our results indicate that infotaxis is both effective (seven detections on average were sufficient to reach the source) and robust (the source is found in presence of inaccurate modeling by the searcher). The biomimetic characteristic of infotaxis is also preserved when searching with a robot in a real environment.
Olfactory cues are employed by many forms of life to locate food or find mates with a high degree of precision. Moths and bacteria are the most illustrative and well documented examples of navigation strategies under real world conditions. The later rely on local concentration gradients to direct toward the source of a nutrient (Berg, 1975
). Male moths on the other hand are guided by pheromonal cues to locate their female (Baker et al., 1985
; Birch et al., 1990
; Mafra-Neto and Carde, 1994
). Upon sensing an odor signal, they surge upwind, since a good estimate of the source direction is provided by the direction of the flow. When odor information vanishes, they exhibit an extended cross-wind casting to perform a local search until the plume is reacquired. Considerable research has been carried out in an attempt to unravel the biological mechanisms that control some of these behaviors and apply them to robotics (Murlis et al., 1992
; Vickers, 2000
).
Computer or robot-based implementations of biomimetic strategies are relevant not only for testing hypotheses about animal behavior (Belanger and Arbas, 1998
), but also for tackling practical problems for which pure engineering solutions are still missing, e.g., finding dangerous substances such as explosives or drugs, or exploring inhospitable environments. Previous robotic attempts have been mainly based on plume tracking – performing a local search within the plume – or chemotaxis – climbing a concentration gradient (Kowadlo and Russell, 2008
). Even if shown to work for large environments (Farrell et al., 2005
), these strategies are truly effective in dense conditions only, i.e., close to the source where the odor plume can be considered as a continuous cloud. Far from the source, odor dispersal occurs mainly through advection and turbulence dominates. The local concentration gradient hence fluctuates constantly in magnitude and direction and does not always point to the source. The fine-scale structure of the chemical distribution consists of sparse, dispersed and sporadic patches of odors surrounded by wide voids, and the probability of encountering one of these patches decays exponentially with distance (Schraiman and Siggia, 2000
). Tracking scents and locating odor sources in such dilute conditions is a major challenge in current robotics.
Recently, Vergassola et al. (2007)
proposed a strategy, named ‘infotaxis’, for searching in turbulent environments. Infotaxis relies on Bayesian inference to maximize information gain, and exploits the scarcity of odor encounters. It involves a period of exploration during which the agent (robot) builds a probabilistic map of the source location, in a similar way to Pang and Farrell (2006)
. As the agent accumulates information, the map becomes sharper and its entropy – which reflects the uncertainty about the location of the source – decreases. Because the expected search time is determined by the uncertainty of the belief, the robot navigates to maximize the expected reduction in entropy, and therefore the rate of information acquisition. Maximizing information gain entails a competition between two conflicting terms. The exploitative term drives the robot toward locations where the probability of finding the source is high. The explorative term favors motion to regions with lower probabilities of source discovery but high rewards in terms of information gain. Interestingly, although animal patterns such as ‘casting’ or ‘zigzagging’ are not pre-programmed or imposed through explicit rules of movement, these behaviors do actually emerge naturally from the trade-off between exploration and exploitation at the core of the model (Martinez, 2007
).
Promising results were achieved with infotaxis in simulation, even for environmental conditions that consider turbulence. Nevertheless, matching the complexity of the world in simulation has been shown to be extremely difficult (Webb, 2000
). A formal description of the instantaneous structure of the plume in a turbulent flow may for instance require simplifications or assumptions to make the problem tractable. The use of a robot, on the contrary, compels to consider and confront all factors in the environment, yielding complete results. We present hereafter a successful solution for implementing infotaxis within a real robotic system, and we assess its performance in terms of effectiveness and robustness under turbulent conditions. This framework is employed as a testbed to assert complete and rigorous evaluations under real conditions. In addition, we confront infotaxis in simulation to time-varying environments such as the ones used in biological experiments, and thereby further evaluate the biomimetic characteristics pointed out by Vergassola et al. (2007)
. Our evaluation is twofold, and consists of both quantitative analyses of the agent’s propensity to surge upwind or to cast cross-wind, and qualitative interpretations of what compels him to exhibit such behaviors.
Although infotaxis is fully described in Vergassola et al. (2007)
, for the sake of completion the algorithm is sketched in Appendix. Infotaxis relies on the capacity to exploit the finest characteristics of the turbulent medium, i.e., discontinuous odor cues dispersed by the flow. A pre-requisite is that odor ‘cues’ are detected. They may refer either to brief and discrete odor patches or to odor filaments with extended spatiotemporal characteristics.
We tested extensively several gas sensors that are commercially available and none of them suited our needs in terms of response time and sensitivity. They saturate at medium concentrations and require a long-lasting phase of degassing before they can react again. To circumvent the problem, we used a temperature sensor that reacts quickly and does not saturate easily. Note that the transport model of heat is identical to the one of smell in environments where advection clearly dominates over diffusion (high Peclet numbers; Schraiman and Siggia, 2000
) so that the statistical model of the turbulent medium (only the time- averaged concentration is used) described in Vergassola et al. (2007)
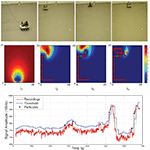
may be used for updating the source distribution map. Such a model considers independent detections over time, regardless of previous events. Yet in reality an odor patch or filament covers a certain volume and generates correlated hits as it passes in front of the sensor. In order to ensure that consecutive detections are not overcounted, the posterior probability distribution of the source is derived from a modified model of turbulent medium which accounts for correlated hits (see Appendix). The model is built from the time intervals of no-detection and from the transitions from no-detection to detection. In our implementation, the transitions occur whenever the sensor signal exceeds an adaptive threshold, whose role is to filter noisy oscillations due to wind or sensor fluctuations. The threshold is derived by averaging sensor readings over two time-steps (40 samples), and adding a constant term established empirically in the absence of stimuli (set to 25 under our environmental conditions – Figure 1
, bottom). Note nevertheless that since the duration of the detections is not taken into account, all the patches are equally considered, irrespective of their size.
Robot infotactic experiments were done with a Koala robot designed by K-Team SA, Switzerland and equipped with an on-board low-level CPU for motion control. The sensor output is sampled at 10 Hz, amplified (Amplifier LMC6462 from National Semiconductor) and quantized with the analog to digital converter available on the robot (10 bits of resolution, 5 V of dynamic range). The heat source had a power of 2000 W and a fan created a wind speed of 2.5 m/s. The wind is assumed to be constant and in the same direction at any time, i.e., local wind speed and direction needed not to be measured by the robot. In order to limit corruption of the temperature sensor by the additional airflow created from the movement of the robot, the motion was implemented as consecutive discrete steps and sensor readings were taken while the robot staying still. Steps of 20 cm were used so as to minimize the effect of discontinuities. The navigation experiments were performed in an arena of 5 m long by 4 m large resulting in a grid-based model of the environment of 25 × 20 points. In order to obtain statistically comparable results, all trials reported hereafter are initialized with the robot located at (10,2) and the source at (9,24). At every step, the agent updates its belief (probability map of the source distribution) according to the history of detection and non-detection events and chooses the best strategy in terms of entropy minimization among the five possible actions, i.e., making a move to one of the four neighboring steps or staying still. The robot is assumed to have reached its goal at one step from the source.
Figure 1. Robot infotaxis in action. Top: Snapshot of the robot at particular times during its path. Middle: Corresponding source distribution maps (belief functions). The blue (resp. red) color code corresponds to low (resp. high) probabilities. The path of the robot from start to current time is superimposed to the map as consecutive red dots when there is no detection, a green dot indicating a detection. Wind blows downwards. The source is at location (9,24), the robot starting point is (10,2). Bottom: Detection procedure. The sensor signal, recorded at 10 Hz during the robot path, is shown in red. An adaptive detection threshold, in blue, is derived from the smoothing average, in green. The five detected patches are indicated as black dots.
Complementary infotactic simulations were performed in Python. Continuous and pulsed sources were considered (see Appendix). For the continuous case, the parameters are: diffusivity D = 1, life-time of particle τ = 1.5 and emission rate of the source R = 2, expressed in arbitrary units. Wind speed is set to V = −2.5 m/s and the size of the sensor is a = 1 cm. These parameter values were established empirically to match the real robotic environment. For the pulsed case, the same values of parameters were used and the source frequency was set to 0.2 Hz for slow pulses (pulse duration = 0.2 s, air gap between pulses = 1.3 s) and 0.67 Hz for fast pulses (pulse duration = 0.2 s, air gap = 4.8 s).
To test the effectiveness of robot infotaxis for searching in dilute conditions, we performed 21 robot runs (see one example in Figure 1
) and compared them with 150 simulations of Infotaxis. For 20 trials out of 21, the robot was able to reach the source within a reasonable time limit of 150 steps, above which the robot is considered to be lost. This case occurred in one trial only, during which too many detections persuaded the agent that the source was already found, i.e., exploitation was predominantly compelling the robot to stay in its current location rather than exploring further and gather information. For the successful runs, the number of detections was low (7.53 ± 6.42, mean ± SD), reflecting the dilution condition of the experiments. The cumulative distribution of the number of detections for robot infotaxis, plotted in Figure 2
(left), is not statistically different from the one obtained with simulated infotaxis (8.59 ± 5.85, mean ± SD; two-sample Kolmogorov–Smirnov test p = 0.26). The search time cumulative distributions between simulated and robot infotaxis were also not different (Figure 2
, right, two-sample Kolmogorov–Smirnov test p = 0.73). The search time distribution is well described by a gamma distribution with shape and scale parameters 8.5 and 7.5 respectively. From Figure 3
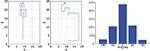
(left), we note that robot trajectories are similar to those obtained in simulations, e.g., biomimetic patterns such as ‘extended crosswind casting’ or ‘zigzagging upwind’ typical of moth flight emerge naturally from the trade-off between exploration and exploitation (Vergassola et al., 2007
). The track angle histogram of robot infotaxis shown in Figure 3
(right) presents a peak at 0° (p = 0.001, Rao’s circular test of non-uniformity), indicating a predominance of the robot to move upwind. Unimodal track angle histograms with mode at 0 are also representative of moths flying upwind in turbulent plumes (Mafra-Neto and Carde, 1994
; Lei et al., 2009
).
Figure 2. Robot vs simulated infotaxis. Left: Cumulative distributions of the number of detections for robot infotaxis (plain curve) and for simulated infotaxis (dashed curve). Right: Cumulative distributions of the number of steps (search time) for robot infotaxis (plain curve) and for simulated infotaxis (dashed curve).
Figure 3. Robot Navigation Patterns. Left: Examples of robot trajectories. The source is continuous and located at (9,24). The robot starting point is (10,2). Wind blows downwards. Right: track angle histogram. Track angles were computed as movement vectors with respect to the wind direction. A peak at 0° indicates a tendency to move upwind, as compared to movements perpendicular to the wind direction (±90°).
Infotactic simulations and robotic experiments described above were done with a continuous source. Females of several moth species however are known to rhythmically extrude their pheromone glands (Baker et al., 1985
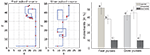
). To assess the capacity of infotaxis to cope with real conditions such as those faced in biology, we considered simulations with a pulsed source model that rhythmically releases odor patches in the environment. Note that there is a mismatch between the pulsed source generator and the continuous source model used to update the internal beliefs in Infotaxis. We performed 60 repeated simulation runs, 30 with fast pulses and 30 with slow pulses. For all trials, the agent was able to reach the source within a time limit of 200 steps. Typical infotactic trajectories under fast and slow pulsed conditions are shown in Figure 4
(left) and the percentage of wind-oriented movements per trajectory in the two regimes in Figure 4
(right). Percentages of downwind movements were low and not significantly different in both conditions, reflecting the high success rate of the searcher. We found however that the searcher moves mainly upwind in the fast pulsed condition and crosswind in the slow pulsed condition. We further investigated this behavioral difference by looking at the updates of the beliefs under both conditions. With fast pulses (Figure 5
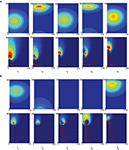
A), intervals of no-detection between pulses are short enough to keep the searcher on exploitation. Each update sharpens the posterior distribution. The high probability bump emerging in the wind direction induces the agent to move upwind. With slow pulses (Figure 5
B), ‘unexpected’ long periods of time with no odor encounter broaden the posterior distribution, hence compelling the agent to counterturn and explore the environment in large spirals.
Figure 4. Infotaxis confronted to a pulsed source. Left: Examples of simulated infotactic trajectories with incorrect modeling by the searcher. The searcher considers a continuous source model whereas the actual source is pulsed (fast and slow pulsed conditions). Source location indicated as a black dot is (20,49). The searcher initial location is (6,3). Detections are marked as red dots. Wind blows downwards. Right: Percent wind-oriented movements under the fast and slow pulsed conditions. Movements having no letters in common are significantly different at p < 0.05 (Kruskal–Wallis test followed by pairwise comparisons, n = 30 trials per condition).
Figure 5. Navigation patterns observed when infotaxis is confronted to a pulsed source (fast pulses in A, slow pulses in B). Top rows represent snapshots of the simulated environment at different times [pulsed source located in r0 = (25, 2), wind blows downwards] and bottom rows are for the corresponding source distribution (belief function). False blue and red colors correspond to low and high probabilities, respectively. The path of the robot is superimposed to the map as consecutive red dots when there is no detection, and green dots for detections. (A) High-frequency pulsed patches provoke new detections before the robot starts spiraling. High probabilities are frequently updated and assigned to upwind locations (at times t1, t3 and t5) hence pushing the agent forward. (B) Between pulses, long intervals of clean air – during which no detections arise – compel the agent to explore regions where previous detections were recorded. Probabilities updates take the form of concentric ellipses that spread as the robot navigates around them, as clearly seen at times t2′, t3′ and t4′. (Note that such behavior – although with much smaller radius – may also be recorded for the fast-pulsed case when the agent is close to the source, due to an excessive amount of detections that push him to switch to exploitation mode).
Three videos are appended as Supplementary Material and illustrate these evaluations. They cover the foundations of infotaxis, its robotic implementation and its efficiency when confronted to a pulsed source (infotaxis.mpeg, robot_infotaxis.mpeg, pulsed_infotaxis.mpeg).
The fundamental aspect of infotaxis is to exploit the finest characteristics of the turbulent medium, i.e., discontinuous odor patches dispersed by the flow. A requirement is thus to be capable of resolving single cues and to exploit them to guide the search. Output neurons in the pheromonal system of the moth have been shown to respond to pulses of pheromone delivered at a rate up to 10 Hz. When their capacity to follow pheromone pulses is pharmacologically disrupted, moths do not navigate successfully toward the source (Lei et al., 2009
). Likewise, robot infotaxis did not succeed in the search for odor sources because the transient response of gas sensors is too slow to track individual odor patches above 1 Hz (data not shown). As the diffusion model of heat is identical to the one of smell, we used instead a fast temperature sensor and a heat source. In our experiments, infotaxis led to effective searching and did not require fine tuning of parameters to work in the real environment. Seven detections on average and as few as three in many trials were sufficient to reach the source, reflecting the dilute condition of the experiments. The number of detections as well as the search time were not statistically different between simulated and robot infotaxis (see Figure 2
).
We found however that the search was influenced by the frequency at which the source was pulsed. The searcher moved mainly upwind in the fast-pulsed condition and crosswind in the slow-pulsed case (Figure 4
, right). Such a frequency modulated behavior is in agreement with biological observations. Experiments with a puffing device revealed that upwind flights of moths were sustainable in fast but not slow pulsed plumes (Mafra-Neto and Carde, 1994
; Vickers and Baker, 1994
). It has been emphasized that a tempo of cues above a certain frequency is needed to ensure odor encounters before the moth undertakes a counter-turning or casting behavior.
Our infotactic evaluations illustrate that the behavior of the searcher not only depends on the detections made in the past, but also on the expectations derived from his internal belief. Note from Figure 5
A that every single detection updates the agent’s belief in a way that pushes him forward as a first step. When the information provided by the cues cannot be further exploited to drive upwind, spiraling becomes a better strategy (as in Figure 5
B) unless a new cue is detected. The correlation between both the external detection rate and the internal expectations leads to efficient trajectories. Fast frequencies in Figure 5
A for instance bring new cues with a tempo that matches better the searcher’s internal expectations (i.e., before he switches to exploration mode), and iteratively updates his belief so that the behavior is targeted toward the goal. Resulting trajectories are mainly straight and upwind, except close to the source where too many detections persuade the agent that the source is already found, hence producing short-length zigzags and very localized spirals. On the contrary, in the slow-pulsed condition, unexpected long time-periods without odor encounters result from a mismatch which compels the agent to counter-turn and explore in large spirals as the probability map gets broadened. In both cases, a continuous belief model is assumed.
The question of whether moths do actually employ infotactic strategies as described is yet of a more delicate nature. The assumption that the agent constructs a detailed grid-based map of his environment is very computationally expensive, and requires the robot to be acquainted with the size and shape of the arena. Biological experiments have reported however that similar principles account for navigation strategies in rats. These mammals employ internal spatial maps that combine both a topographical description of the environment (encoded by ‘grid cells’) and location specific information (‘place cells’) (Hafting et al., 2005
), in a similar way to the grid-model of the arena used in Infotaxis which gets updated as localized cues are detected. Yet simpler descriptions of the environment could also be considered, for which infotactic strategies may prove equally efficient.
Previous experiments from the same laboratory revealed that a concentration gradient can be extracted from a turbulent plume in dense conditions when the robot moves slowly (2.5 cm/s) and near to the source (search area = 2.9 m2, see e.g., Figure 4
, left in Martinez et al., 2006
). To move the robot in the vicinity of the source, previous works considered the possibility of exploring the environment by using vision, in addition to olfaction (e.g., Martinez and Perrinet, 2002
). The main limitation is that odor source candidates need to be identifiable from visual features. Here we tackled the more difficult problem of searching in dilute conditions, for which only the information released by the source and wind direction were used. We implemented infotaxis on a real robot and considered a larger search area (20 m2) and faster robot speed (14 cm/s) than in our previous experiments.
The robustness of infotaxis was evaluated with respect to inaccurate modeling by the agent. The parameters employed internally to guide the search were not fine-tuned or adapted over time, and could differ from the instantaneous characteristics of the surrounding. Despite this discrepancy, the robot was able to reach the source within a reasonable time limit and produced very few downwind movements (Figure 4
, right). This emphasized the capability of the model to cope with the unpredictability imposed by real environments. Additional analyses with a pulsed source pointed out that frequencies at which cues are encountered account for the efficiency of the strategy followed, just as reported in the case of moths, which depends on how well detection rates match the internal map used by the searcher.
The extension of Infotaxis to cope with stereo sensing capabilities, just as in the case of insects, may prove beneficial in terms of effectiveness and ought to be considered as future work. Two sensors, employed in parallel to update the probability map, may indeed increase directionality. Further applications of Infotaxis to collective search have also been reported recently by Masson et al. (2009)
with impressive gains in search times.
Infotaxis is fully described in Vergassola et al. (2007)
. For completion, we detail its core modules in terms of probabilistic robotics (Thrun et al., 2005
) as employed in our robot implementation. The model combines a belief function – the robot internal knowledge about his environment, updated as cues are encountered – along with decision-making – execution of an action that maximizes a reward.
Statistical Model of the Odor Plume and Grid-Based Map of the Environment
In Infotaxis, the robot is provided with a statistical description of the odor plume that he uses to infer the probability that the source be located at any point of his internal grid-based probability map of the environment. The statistical description of the odor plume is derived from the resolution of the following advection-diffusion equation
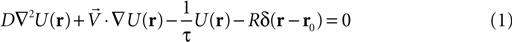
for an odor source located at r0 and emitting ‘particles’ or patches’ at a rate R. The particles propagate with diffusivity D, have a mean lifetime described by τ and are advected by a mean current or wind V. U(r) is the local concentration at location r and δ is the Dirac delta function. In such an environment, the mean frequency of odor encounters with a spherical sensor of radius ‘a’ follows the Smoluchowski’s (1917)
expression

This model provides a framework by which to take into consideration the geometry of the environment when navigating. It can be easily solved through numerical methods and makes it possible for autonomous robots to iteratively infer knowledge about their surrounding. In the continuous case, the solution to Eq. 1 writes:
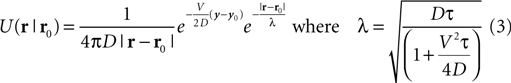
For the non-continuous case, i.e., under the influence of a pulsed odor source R(t) at location r0, we derived such function by solving the non-homogeneous diffusion-advection equation which, for the two-dimensional problem with mean vertical wind Vy, takes the form:
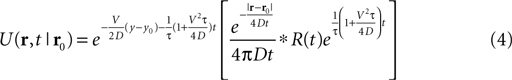
Belief Function
Let us consider the trace Γt = {(r1,t1), (r2,t2),…,(rn,tn)} of the hits (odor encounters) experienced by the searcher at locations x1,…,xn and times t1<,…,<tn<t during the path from its start to the current time t. The belief function is given by the posterior probability for the source to be located in r0 given the trace Γt

where ℒ(Γt|r0) is the likelihood of experimenting the trace Γt for a source in r0.
In our robot implementation of infotaxis, consecutive detections are not considered as they belong to a same patch and are correlated (see Section “Materials and Methods”). We therefore employ the following likelihood function (from Eq. 13 in supplementary materials of Vergassola et al., 2007
) instead of the one considered in the original algorithm
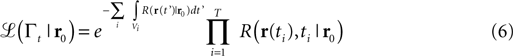
in which T represents the transitions from no-detection to detection, i.e., new patches, and the Vi’s are the time intervals of absence of detection. Note from Eq. 6 that the absence of correlations permits to update the probability map without storing the whole history. Indeed, Pt+∆t(r0) = Pt(r0) update δt (nparticles), where ‘nparticles’ is the number of detections that the searcher experienced during the short time interval δt. Memory requirements are therefore kept to a minimum.
Decision-Making
For the decision-making, the robot moves in the direction that minimizes its local uncertainty about the location of the source. The expected reduction of entropy – reward function – for the robot moving from ri to rj, consists of two terms:
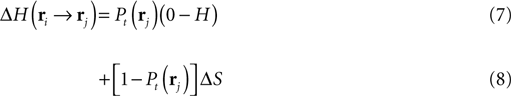
The first term (Eq. 7) evaluates the reduction of entropy if the source is found at the next step. Reaching the source in rj occurs with estimated probability Pt and the entropy goes from H to 0. The second term (Eq. 8) corresponds to the reduction of entropy if the source is not found. It occurs with probability 1 − Pt and δS represents the information gain in rj coming from expected odor encounters. The first term is seen as exploitative as it drives the searcher toward locations where the probability of finding the source is high. The second term is explorative as it compels the searcher toward regions with lower probabilities of source discovery but high information gains.
The expected reduction of entropy in the case where the source is not found derives from the probability sum of experiencing i new detections during the movement, where encounters are modeled by means of a Poisson-distributed random variable ρi

therefore accounting for all possible cases that new information is detected along the way (either 1, 2 or n encounters).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors acknowledge E. Villermaux for helpful discussions and for suggesting the use of a turbulent plume of heat in robotic experiments.
The Supplementary Material for this article can be found online at http://www.frontiersin.org/neurorobotics/paper/10.3389/fnbot.2010.00001/