Grounding the meanings in sensorimotor behavior using reinforcement learning

1. Introduction

One of the topics central to cognitive science is the representation of meanings related to language. Unlike the standard theories, that postulate the existence of amodal symbols, being the core of internal representations, the grounded theories of language acquisition and comprehension (Harnad, 1990; Barsalou, 1999; Jeannerod, 2001) claim that arbitrary symbols (of language) are grounded in some way in the world and body (Wilson, 2002). Thought is expressed not as a symbol manipulation, but as an inner simulation drawing on lower-level capacities of the sensorimotor cognition. A growing amount of empirical evidence serves in favor of grounded cognition (see, e.g., a review in Barsalou, 2008). The question of involvement of the motor modality in the comprehension of language was explored in various psycholinguistic and neuropsychological studies. For instance, Pulvermüller and colleagues (Pulvermüller et al., 2001; Hauk et al., 2004; Pulvermüller, 2005) measured the activity in motor areas of the brain during comprehension of simple action verbs connected to different effectors, namely “kick” executed with leg, “pick” with hand, and “lick” with mouth. Results from various experiments showed that during sole comprehension of language without movement, a somatotopic (map-like) activation appeared in the motor cortex, in accordance with the effector of the action verb. Glenberg and Kaschak (2002) studied this phenomenon on the basis of interference between motion execution and comprehension of so called “transfer” sentences (i.e., including motion from an agent to a patient). Results of experiments showed that the reaction time was significantly shorter when participants had to make a move congruent with the direction implied by the perceived sentence, in comparison with the incongruent direction. Interestingly, the significant difference was observed also in case of abstract sentences (Glenberg et al., 2008), which suggests that even high-level concepts may be somehow related to the sensorimotor behavior.

Despite the rich amount of empirical evidence on the nature of language comprehension, the actual mechanisms of grounding of concepts have not yet been clarified. Computational modeling has proved fruitful in the field of grounded cognition research. Some authors (e.g., Steels, 2008) claim that the problem of symbol grounding has been solved. This research direction of Steels (2003) and Steels and Belpaeme (2005) focuses on a basic method of grounding the language into sensorimotor cognition of the agent, and on the development of simple shared lexicon in a population of agents using language games. For instance, in the color naming domain, Steels and Belpaeme (2005) created a simple model of color categorization and naming, where agents play two types of games. First an agent plays a discrimination game to learn to distinguish color categories. Having acquired some basic categories, the agent is able to communicate randomly assigned names of those categories with other agents. Through such a negotiation process the agents are able to develop a shared lexicon of color names representing basic color categories qualitatively similar to human basic color categories. As the authors argue, the acquired meanings in the agents are grounded because they are autonomously generated in the world through a sensorimotor embodiment and perceptually grounded categorization methods, and the agents autonomously introduce and negotiate symbols invoking these meanings (Steels, 2008, p. 238). It appears though that the issue of grounding (referential) meanings is still a matter of vivid debate in the community (De Vega et al., 2008). Namely, some authors propose that the representation of meaning (e.g., in amodal or in perceptual symbols) is entirely independent from the question of whether meaning is grounded or not. Hence, the solution for symbol grounding could arise in a system using amodal symbols. The opposing argument holds that we truly need to avoid amodal symbols to guarantee the formation of meanings inherent to the agent. In their review, Taddeo and Floridi (2005) introduced zero semantical commitment condition as a criterion for valid solution to the symbol grounding problem, completely avoiding the designer’s approach. This criterion, however, appears unsatisfiable in artificial systems (Vavrečka, 2006).

Cognitive developmental robotics offers a stable platform to study the grounding in separate cognitive abilities (Asada et al., 2009). It uses physical and simulated robots operating in a simplified environment focusing on a concrete problem with a possible scalability to other skills and domains. Artificial neural networks are typically used as control architectures for these robots. Cangelosi and Riga (2006) examined how grounded meanings of words can be combined to form the meaning of a new word. This process is called the symbol grounding transfer, since the meaning is not grounded directly, but in its simpler components. For instance, words like “horse” and “horn” can be combined to a new concept “unicorn.” It is very likely that high-level abstract concepts, which cannot be directly associated with sensorimotor experience, are grounded using low-level concrete concepts (Barsalou and Wiemer-Hastings, 2005). The model of Cangelosi and Riga (2006) is based on learning through imitation, which has been considered fundamental for acquisition of language (Tomasello, 2003). In their experiment they used two robots simulated in open dynamics engine (ODE, www.ode.org), one pre-programmed demonstrator and one imitator endowed with a multi-layer perceptron neural controller trained using a standard back-propagation algorithm (Rumelhart et al., 1986). First the robot learns to comprehend and produce basic actions, in latter stages of development it learns to comprehend and produce composite actions based on a verbal command. In a subsequent work, Cangelosi et al. (2007) extended this simple architecture to not only comprehend, but also to produce verbal descriptions of actions. These important works, aimed to discover and describe the actual mechanism of learning abstract concepts, clearly demonstrate the importance of the cognitive robotics as a research method. However, a small drawback of this model is the learning procedure and the associated assumption about the availability of the required motor commands. It is not natural for the action to be literally forced to the agent, as if the instructor was dragging the child’s hand to learn to reach for an object.

One of the most intriguing recent connectionist models of embodied language acquisition is the Recurrent Neural Network with Parametric Biases (RNNPB, Tani, 2003; Tani and Ito, 2003). It is a Jordan-type recurrent neural network endowed with special parametric bias nodes, which enable it to recognize and categorize various spatio-temporal patterns and thus modulate its own dynamic function. The values of the PB nodes during the execution of concrete behaviors can be stored and subsequently (manually) fed as an input to the network, which will then produce the learned behavior, or to a twin RNNPB network (trained to acquire similar PB vectors for matching concepts) to produce recollection. An important feature of this model is, that the PB vectors are formed purely by self-organization, so they are self-determined by the network in an unsupervised manner. On the other hand, the general learning algorithm used in this architecture is the (supervised) back-propagation through time (BPTT) algorithm (Rumelhart et al., 1986). RNNPB was used in various setups where physical or simulated robots learned repertoires of actions, and/or action names (Tani et al., 2004; Sugita and Tani, 2005, 2008). A typical cognitive robotics methodology, used in experiments of Tani and Sugita comprises a simple perceptual categorization followed by a verbal command leading to the execution of a simple action. One particular experiment of Sugita and Tani (2005) served as a model setting for our experiments. It used a small mobile robot a task of which was to comprehend a two-word command indicating either a location or a color of one of the three objects in front of it (left, center, right, red, green, blue), and an action to be produced upon the object (push, point, hit).

Currently the most “accurate” prototype of a child robot is the iCub, a small-size humanoid robot created under the European project RobotCub (Metta et al., 2008). Designed to resemble a 2.5-year-old child, even in height and weight, the iCub is endowed with 53 degrees of freedom (DoF) in joints distributed all over its body in proportion similar to human effectors (e.g., 9 DoF for hands), movable eyes with color cameras, and various other sensors, providing a very accurate model of an actual child’s body. The platform includes a carefully designed virtual form of the iCub robot in the ODE, the iCub simulator (Tikhanoff et al., 2008), providing a safe, yet realistic, environment for testing the control architectures before implementing them to the real robot. Various computational models of cognitive capacities were created on the basis of the iCub simulator platform, many of which focus on sensorimotor cognition and grounded acquisition of language, the topic considered in this paper. For instance, Macura et al. (2009) propose a cognitive robotics model of grasping based on a hybrid neural network architecture, with Jordan recurrent neural network used as an executive component. In their experiments the iCub learns to execute various grasping sequences and to differentiate between them as different goals. Results of experiments showed that not only did the iCub learn to grasp successfully, but it also displayed similar stimulus–response compatibility effect (Simon, 1969) as human subjects, hence highlighting the model’s biological relevance.

Recently, Tikhanoff et al. (2011) created a neural network model for reaching and grasping, incorporating the linguistic component as well. The architecture encompasses a feed-forward network for reaching and a recurrent neural network for grasping. The reaching task, trained by error back-propagation (BP), is approached as one-step process, for which the training data is first acquired during the motor babbling stage when the required joint position are stored for various target positions in robot’s peripersonal space. In contrast, the grasping behavior is viewed as a sequential task and employs an associative reinforcement learning (RL) algorithm (Barto and Jordan, 1987), making the approach more ecologically plausible. This task is hence based on an appropriate design of the reward function that can drive successful grasp types for different objects. Marocco et al. (2010) proposed a model of direct grounding of language in action (motor control), inspired by Sugita and Tani (2005) and Cangelosi and Riga (2006), in which language and action are fully interconnected. Meanings in this model are specific exclusively to the robot (simulated iCub), not to the designer. Unlike less plausible input-target mapping pairs used in some of the previous models, the model of Marocco et al. (2010) learns dynamical sequences of input-output patterns as they develop in time. To achieve this, the model is trained using the BPTT algorithm, hence the procedure of the training data acquisition still requires the experimenter’s participation.

As an alternative to BP-based approach, some authors prefer the well-known self-organizing maps (SOMs; Kohonen, 1997) as core components of the cognitive architecture. For instance, Wermter and Elshaw (2003) propose a model of the self-organizing memory for a robot called MirrorBot, inspired by cortical assemblies and mirror-neurons. In this model, strongly influenced by neuropsychological findings of Pulvermüller and colleagues (e.g., Pulvermüller et al., 2001), verbally labeled actions are clustered according to the body parts they are associated with. It consists of multiple interconnected SOMs, each representing either a body part or an association area. First a map of the whole body projects to the maps for body parts, which, together with a linguistic module project to a higher-level association area on top. The model was trained on sensor readings from Mirror-neuron Robot Agent (MIRA; Wermter and Elshaw, 2003) using the standard Hebbian learning and was evaluated for some primary parts of the network. Unfortunately, Wermter and Elshaw (2003) do not provide results for the whole model, so its functionality has not been fully proved. Recently, Morse et al. (2010) proposed a cognitive robotics framework (ERA), based on hierarchically interconnected SOMs as well. In this model, one SOM represents a lower-level structure (for instance a sensory modality, some of its aspect, etc.) and is connected to a higher-level “hub” SOM. In ERA architecture, multiple SOM structures are hierarchically connected through the associative hubs. Morse et al. (2010) evaluated the architecture on a simple naming experiment with infants called the “modi” experiment (Smith and Samuelson, 2010). Here the child watches the experimenter showing two toys in particular locations (left and right). Later on, the child’s attention is brought to a specific location, and a name (for a toy) is uttered. Results from such experiments with children, as well as with a simulated iCub endowed with a body-posture hub architecture, showed that an infant (or iCub) could learn the names of objects accordingly to the object’s typical spatial location without the presence of the object.

An impressive piece of work related to grounding language in sensorimotor behavior has been done by Dominey and his colleagues (see, e.g., Dominey and Boucher, 2005; Lallee et al., 2010) and references therein). Dominey and Boucher (2005) developed a neural-network based system for language learning with a minimal pre-wired language-specific functionality. The meanings (of events and spatial relations) are extracted from video images in terms of low-level primitives, and are linked with descriptive sentence forms via learning grammatical constructions. The system was shown to reproduce various observations from developmental studies. Lallee et al. (2010) extend their framework for embodied language and action comprehension by including a teleological representation that allows goal-based reasoning for novel actions. This work demonstrates the advantages of a hybrid, embodied–teleological approach to action–language interaction, both from a theoretical perspective, and via results from human–robot interaction experiments with the iCub robot. The novelty of the teleological approach consists in the representation of the subcomponents of actions, which includes relations between initial enabling states and final resulting states for actions. The paper also explains how language comes to reflect the structure of action, and how it can subsequently be used as an input and output vector for embodied and teleological aspects of action.

The motivation for our work was to ground the meaning of action-related commands in robot’s sensorimotor behavior, using an approach in which the sensorimotor behavior is treated as inherently sequential and the learning is based on an ecologically justifiable feedback. Our model shares some features with the above mentioned models but its most distinguishing feature is the action learning module that is based on a continuous version of the RL paradigm (Sutton and Barto, 1998) that lends itself to generalization and moreover is biologically inspired. As explained below, the RL approach is based on a reward function that can lead to desired behavior by exploring the state space. The RL approach distinguishes our model from earlier models that are mainly restricted to the supervised learning paradigm, which requires a priori generation of the training data. The exception is the grasping module in Tikhanoff et al. (2011) where the data is generated online based on the feedback. Our task of action learning is inspired by Sugita and Tani (2005) which is neither reaching nor grasping but something in between (point, touch, and push actions). Details of our model are described below.

2. Materials and Methods

For our experiments we used the iCub simulator, activating 4 DoF in its right arm (the rest of robot’s body was motionless). The experimental setup involved the robot facing three objects in its peripersonal space (lying on a table), as displayed in Figure 1.

FIGURE 1

Figure 1. Example of a scene with the simulated iCub acting on objects.

Figure 2 displays the model. It comprises three neural network modules, which are trained for their respective subtasks. (1) Target localizer (TL) detects the position of the target object on the scene based on a low-level visual information about the scene and on the description of features of the target object. (2) Action learning (AL) module is responsible for motor control. Based on a command about action type and the information about the target object position, it produces a sequence of movements to execute the command. (3) Action naming (AN) module learns to generate the linguistic description of the executed action. TL and AN modules can be seen as “auxiliary,” whereas the AL module is the most distinguishing part of our model.

FIGURE 2

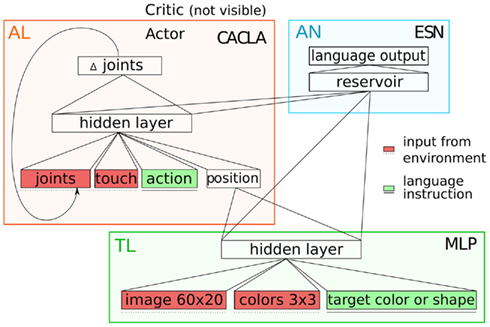
Figure 2. The scheme of the proposed model in terms of neural network modules (TL, target localizer, AN, action learning, AN, action naming).

2.1. Localization of Target Object

The TL module is a standard multi-layer perceptron with one hidden layer. It maps three groups of input – [IMAGE, COLOUR, TARGET] onto the target object POSITION. IMAGE is a bitmap displaying a selection retrieved from the original visual percept of the iCub, processed with the OpenCV library as described in the following text. TARGET encodes which object should be acted upon. Using a localist encoding with 6 neurons, TARGET can be represented either by its color (red, green, blue) or shape (box, cylinder, sphere), which can be seen as concepts, that the agent has in its mind. The whole input vector of the TL module is depicted in Figure 3.

FIGURE 3

Figure 3. The schema of the input vector for target localizer. In the simulations, the dimensionality of the object color and the target information was increased to counterbalance the effect of the high-dimensional image part.

Altogether, the input layer comprises 1200 neurons for image pixels (concatenated in a line), at least 9 neurons for coding colors, and 6 for the target (but see Section 3.1 regarding the multiplication of dimensions). The three output POSITION neurons have a sigmoid activation function with output values in the range 〈0, 1〉, and after winner-takes-all evaluation they encompass one-hot encoding of the target position (left, middle, right).

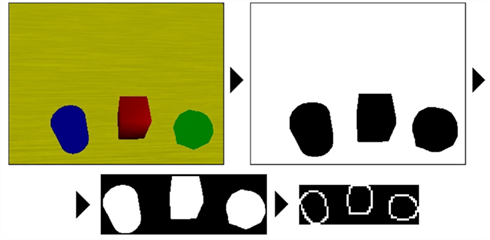
In our experiments, the standard visual output of 320 × 240 pixels from one of the iCub’s cameras encompasses a scene with three objects lying on the table, within the reach of the robot’s right arm. This image is then processed using the OpenCV library using a pre-programmed procedure (image processing is not the focus of our model), consisting of the following steps (see Figure 4): (1) conversion to black-and-white image, (2) cropping the objects as a group, (3) color inversion, and (4) edge extraction. The output of step 4 serves as (part of) input to the TL module.

FIGURE 4

Figure 4. Processing of the input image using the OpenCV library.

2.2. Action Learning

The AL module is based on the reinforcement learning paradigm (Sutton and Barto, 1998), which does not require prior exact knowledge about the sequences of joint positions leading to the target movement. It operates in a continuous space of states and actions, using the CACLA algorithm (Van Hasselt and Wiering, 2007). The AL module has an actor-critic architecture, consisting of two modules (function approximators). The actor’s task is to select optimal actions leading to the desired outcome (hence maximizing the reward). The critic’s task is to estimate the evaluation (reward) of the agent’s state. The actor is, unlike standard supervised learning with pre-given targets, adjusted on the basis of the adaptive critic’s evaluation.

Both actor and the critic consist of a two-layer perceptron. The actor maps the input [STATE, ACTION, POSITION] (together 11 neurons) onto STATE-CHANGE output (4 neurons). The critic maps the same input [STATE, ACTION, POSITION] into evaluation of the current state VALUE. Both networks contain the sigmoid activation function in all neurons.

The state vector of both actor and critic network is depicted in Figure 5. The STATE variables represent four joints of the robot’s arm (the hand remains still with fingers extended) and the hand’s touch sensor (which turns to 1 when the hand touches an object, otherwise it remains 0). The joint values are scaled from the degrees to the interval [−1, 1] using the formula

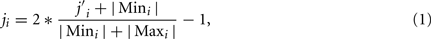
where Min_i and Max_i denote the minimal and maximal joint angles, respectively. These limit values, related to joints 1 through 4, determine the intervals [−95; 90], [0; 161], [−37; 100], [−6; 106], respectively.

FIGURE 5

Figure 5. The input vector for the AL module. The agent is in the state of making the push action on the middle object.

The ACTION input represents the pre-processed external linguistic input denoting which action should be taken, using three neurons (with localist encoding). Finally, POSITION denotes the output from the TL module, representing the position of the attended (target) object (left, center, right), together with ACTION input comprising the whole action command (e.g., “push red”).

2.2.1. Training the module

The value function V(s), computed by the critic, is updated based on temporal differences between agent’s subsequent states, using the equation

where δ_t = r_t+1 + γV_t(s_t+1) − V_t(s_t) is the temporal-difference (TD) error, 0 ≤ α_t ≤ 1 denotes the learning rate and 0 ≤ γ ≤ 1 is the discount factor. The reward r_t+1 is received by the agent immediately after executing the chosen action, which results in a state transition from s_t to s_t+1. It is known that using the update given by equation (2) for the discrete RL will result in convergence of the values to the actual expected rewards for a fixed policy (Sutton and Barto, 1998). CACLA extends the usability of this update in continuous RL by yielding accurate function approximators (of both the critic and the actor).

Critic’s parameters (weights), expressed by a vector 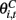are updated using a gradient-based learning rule

The actor chooses an action a_t(s_t) given by its parameters 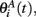but is also allowed to explore the environment by choosing a novel action 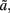taken from Gaussian distribution

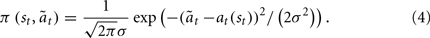
Then the update rule for the actor’s weights is applied if δ_t > 0:

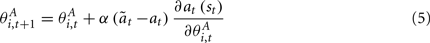
The training procedure for the AL module is summarized in Algorithm 1.

CACLA differs from other actor-critic architectures in some respect. Most other actor-critic methods use the size of the TD error and also the update in the opposite direction when its sign is negative. However, this is usually not a good idea for CACLA, since this is equivalent to updating toward some action that was not performed and for which it is not known whether it is better than the current output of the actor. An extreme case would be considering an actor that already outputs the optimal action in each state for some deterministic Markov decision processes. For most exploring actions, the temporal-difference error is then negative. If the actor were updated away from such an action, its output would almost certainly no longer be optimal (Van Hasselt, 2012, p. 238). Using only positive delta can hence be seen as a drive for improvement, and the improper behavior is implicitly unlearned by learning a new behavior.

So, CACLA only updates the actor when actual improvements have been observed. This avoids slow learning when there are plateaus in the value space and the TD errors are small. It was shown empirically that this can indeed result in better policies than when the step size depends on the size of the TD-error (Van Hasselt and Wiering, 2007). Intuitively, it makes sense that the distance to a promising action is more important than the size of the improvement in value. Overall, CACLA has been developed for continuous spaces but it has also been shown to compare favorably to commonly used discrete TD methods such as SARSA or Q-learning (Van Hasselt and Wiering, 2009).

2.2.2. Reward function

It appears that the design of the agent’s reward function plays an important role in learning the desired behavior. Learning should not be too complicated, otherwise it might be problematic for the critic to learn it. The first complication we encountered in this task was to make the agent distinguish between quite similar point and push actions. Therefore we designed a separate reward function for each action.

(1) During the push action the agent receives reward in the form of negative Euclidean distance of the palm from the original position of the target object, so in order to maximize the reward, the agent has to displace the object.

(2) For the touch action, the reward is again based on the negative Euclidean distance of the palm from the original position of the target object. Additionally, the agent receives a (constant) penalty if it touches another object during the movement (we used a value of −0.5). Somewhat counter intuitively, the agent was designed to receive a small penalty (−0.3) even when touching the target object, because this method yielded best results. The explanation is that in case of reward after touching the object, the agent would attempt to repeatedly touch the object which would tend to be displaced after each contact, because it has no knowledge about the absolute position of the objects. So when we introduce a small penalty factor for touching the object, the robot’s reward increases when it is getting closer and finally it stabilizes cyclically touching the object without displacing it. Another solution could be to use a recurrent network that would provide a memory for agent’s past positions, or include the object position into the agent’s state representation.

(3) The point action should be best rewarded when the robot’s hand is pointing at the target object, for which the above mentioned negative Euclidean distance turned out to be inappropriate. The reason is that the proximity of the palm to the target object does not guarantee the correct orientation of the fingers. Therefore, we first stored the information about the joint angles corresponding to fingers pointing to the desired position. Then the agent received a reward on the basis of negative Manhattan distance (i.e., in L1 norm) between the current joint configuration and the target joint configuration. This method enforced the correct orientation of the hand with respect to the target.

2.3. Action Naming

For implementation of the ANN module we chose an echo-state network (ESN; Jaeger, 2001) as an efficient recurrent network that can process sequences. The task of the AN module is to name the executed actions by learning the mapping of [M1-HID, M2-HID] to the output SENTENCE. M1-HID is the hidden-layer activation of the TL module, that allows to name the target property (color or shape). M2-HID is the hidden-layer activation of the actor of the AL module, that allows to predict and hence name the type of executed action. SENTENCE is the representation at the AN’s output layer comprising 3 units for action and 6 units for shape and color. The sentences consist of two words, so for each sentence two units (out of 9) are supposed to be active, one for action and the other for object identification.

The generic ESN architecture includes also weights from the input layer to the output layer, as well as feedback weights from outputs back to the reservoir, but we did not include these. Hence, the activation dynamics of the units in the reservoir is given by the equation

and the ESN output is computed as

At both layers, we experimented both with sigmoid (tanh) and linear activation functions f and f ^out; F and F^out are vectors of these functions, respectively. ESN requires proper initialization of recurrent weight in order to induce echo states as responses to input stimulation (Jaeger, 2001; Lukosevicius and Jaeger, 2009). This is achieved by proper scaling of recurrent weights such that the spectral radius of W is smaller than one. (The closer the radius to one from below, the slower is the signal attenuation.)

For training the ESN output weights, we applied the analytical approach, based on computing the matrix pseudoinverse. ESN is trained to map sequential data to static targets (representing two-word sentences). For each step in sequence, we computed the reservoir activations x which were concatenated (as column vectors), resulting in the matrix X. These were paired with appropriate targets d collected in the matrix D. The analytical method yields the output weight matrix in the form

where X⁺ is the pseudoinverse of X. The details of data preparation are described in the Results section.

3. Results

In all modules we systematically searched for optimal parameters. We used two thirds of data patterns for training and the remaining one third for testing, and the reported results of averages over 5 runs with a particular set of model parameters and random initial weights. The specificities of each module follow.

3.1. Target Localizer

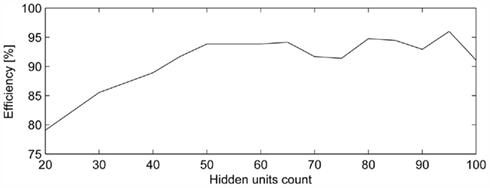
For training the TL module we used data from all 3 possible object locations, 3 possible object colors, and 6 target commands, making together 216 different configurations. The MLP was trained using standard back-propagation algorithm. The order of the inputs was shuffled for each run. The training of the displayed network took 600 epochs (i.e., sweeps through the training set) with the learning speed 0.1. Figure 6 depicts the network accuracy on the test data as a function of the number of hidden neurons. It can be seen that going beyond 50 neurons does not on average lead to further increase of accuracy above 95%. Further improvement depends more on the selected stopping criterion and the learning speed.

FIGURE 6

Figure 6. Network accuracy on the testing data as a function of the hidden-layer size.

Interestingly, these results were achieved with certain modifications of input encoding (without which the accuracy would not get over 75%). We observed that the MLP output was very sensitive to the variability of shape information (high-dimensional inputs), so we multiplied the number of neurons encoding the color and target by various factors (n) as shown in Figure 7. The best results, i.e., around 95% on testing data, were obtained for n = 20 (yielding the input dimensionality for TL module 1200 + 15 × 20 = 1500). However, higher values of n already lead to performance deterioration. The parameters revealed by our analysis used for final training of this modules are displayed in Table 1.

TABLE 1

Table 1. Final parameters for training of the TL module.

FIGURE 7

Figure 7. Network accuracy on testing data as a function of multiplication of non-visual units (for explanation see the text).

We trained the TL module for 500 epochs. The root-means-square-error (RMSE) tended to decrease significantly as early as during the first 50 epochs and then continued to decrease slowly. Since the testing error does not grow with time, the network with 50 hidden units did not show evident signs of over-training. The error on single output neurons in comparison with the desired value was 0.037 in average on the training data and 0.136 on the testing data.

We also briefly tested the robustness of the TL module with respect to noise. We ran some additional simulations with noisy inputs in which there was a 10% chance for each image pixel to be flipped. We observed that the training accuracy remained at 100% and the testing accuracy dropped to approximately 75% (probably due to overfitting).

3.2. Action Learning

In training the AL module, we first focused on finding optimal parameters (the learning rate and the hidden-layer size) for the critic and actor networks. Since the learning of AL module is a sequential task (unlike TL), we count its length in terms of episodes (one episode, related to an action type and the target, is a sequence of a number of time steps). The results for the critic trained for 500 episodes, each lasting 75 time steps (or iterations), for various learning rates, are displayed in Figure 8A. The best results were achieved with the discount factor γ = 0 and using the learning rate around 0.01. For smaller rates, the learning turned out to be too slow. Figure 8B shows the critic learning as a function of the hidden-layer size. For each size, the training was set to last 250 episodes, using the previously chosen learning rate 0.01. It can be seen that any size above 10 neurons leads to similar results. For the final configuration we used the critic with 20 hidden neurons.

FIGURE 8

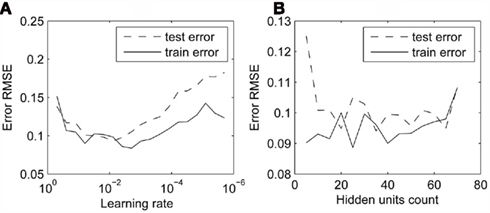
Figure 8. Error of the critic for various network parameters. RMSE as a function of (A) learning rate, (B) hidden-layer size.

We proceeded analogically in the case of the actor. Figure 9A reveals that the actor, trained for 200 episodes, learned best for a fairly wide range of rates between 0.01 and 0.0001. For subsequent tests, we chose the value of 0.001. Similarly, Figure 9B shows that setting the suitable number of hidden neurons is not critical. We chose 40 hidden neurons. The parameters revealed by our analysis used for final training of this modules are displayed in Table 2.

TABLE 2

Table 2. Final parameters for training of the AL module.

FIGURE 9

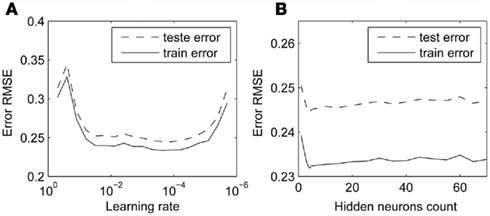
Figure 9. Error of the actor for various network parameters. RMSE as a function of (A) learning rate, (B) hidden-layer size.

We trained the AL module using the CACLA algorithm (Algorithm 1) in two phases. In phase 1, we trained the actor only in states resulting in higher rewards from the environment (r_t+1 > r_t), rather than reward estimates from the critic. The goal was, again, to speed up the training, because at the beginning of training, the critic is a very bad predictor. Interestingly, this modification led to the accelerated learning of the critic as well. After approximately 150 episodes we switched to phase 2, in which the training was based on the original CACLA algorithm during another 300 episodes.

Each episode represents the execution of one randomly chosen action-target pair. The length of one episode during the training consisted of 75 time steps (iterations, or movement instructions). If the agent touched and moved a wrong object, the episode was reduced to a few extra steps and terminated. In the remaining steps the agent should “figure out” which actions will lead to the increase in the reward, which was penalized by the previous movement. Since the agent has no specific knowledge about the changes in object positions, it was necessary to terminate the episode before its end to avoid learning an improper behavior.

For a randomly initialized agent at the beginning of training, the proposed actions are large (in terms of angle changes) and random in terms of direction. Since the exploration finds the right directions only randomly, we decided to reduce the “magnitude” of the proposed actions into one third of it. An even better solution could be to initialize the actor’s weights to smaller values (as commonly used in connectionist simulations) which would lead to smaller actions in terms of actor outputs.

In sum, we were able to successfully train the model to produce all three desired actions, having used various speed-up tricks. Figure 10 depicts the rewards during the execution of the trained actions for all positions of the objects. Typical characteristics for all positions is that actions are at first large in size and gradually they become smaller. The point action was executed perfectly. The reward grows during each episode, and the final joint angles perfectly match optimal values. The reward for touch action grows at first, until the agent touches the object. Afterward, the reward starts to oscillate which is due to repeated agent’s effort to touch it, combined with slight object displacement (caused by reward design). The magnitude of oscillations corresponds to the distance between palm and the target object. The magnitude could have been made smaller by decreasing the penalty upon touch. The execution of the push action was very good. As soon as the object was touched, the agent started to displace it. We can observe a minor decrease of the reward after touching which occurs because pushing the object makes it move away from the target position (the agent does not see the target object). If the object could have been moved without becoming an obstacle, the arm could have moved to the object target position where the reward is maximal.

FIGURE 10

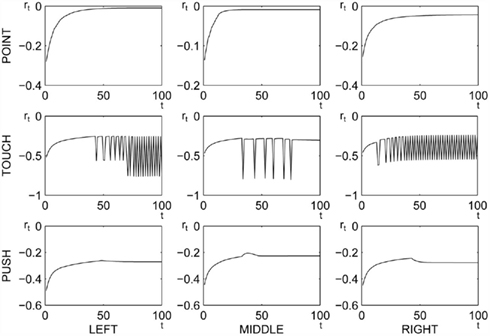
Figure 10. Reward obtained during the execution of learned actions, as a function of discrete time steps.

Figure 11 displays the generalization of the “point-left” action from five different starting positions. The starting point of the robot’s arm was the same for all training episodes, but after training the agent was able to perform the desired action from any other starting position. The graph on the left displays the changes in the joint angles. The graph on the right displays the values of the reward during the action. Interestingly, the agent chooses a correct trajectory even if the arm moves to another position during the action execution. The agent was observed to manifest similar behavior for other actions as well.

FIGURE 11

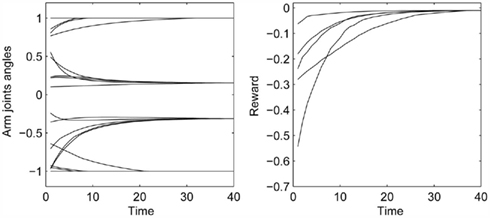
Figure 11. The joint angles and reward values during the execution of the “point-left” action from different starting positions, as a function of discrete time steps (iterations).

This generalization property also ensures the robustness of the robot’s behavior with respect to random noise. Indeed, if we initially induced a small amount of white noise into motor commands, this only had a negligible effect on correct performance, because noise only caused the arm shift in the (continuous) state space. Of course, large noise (reaching the magnitude of AL outputs) affected the arm dynamics and the compensation for noise was insufficient.

Next, in order to get insight into actor’s internal representations, we analyzed the activations on the actor’s hidden layer as action characteristics, and projected these high-dimensional data onto a 2D grid using a standard SOM with toroid topology (i.e., making the pairs of parallel borders of the map connected). The resulting SOM is displayed in Figure 12. It is the same map shown twice, with different labels shown (to increase transparency). The clearly identifiable spots of brighter color represent the concrete actions (left figure) and positions (right figure). The size of the spot reflects the number of respective activations. In each action spot there are some smaller and bigger marks, of which the largest ones represent the target position in which the arm of the robot remained already from the middle of an episode assigned for the testing action execution. The smaller marks indicate the trajectory of the arm during the execution of the action before reaching the target position. It can be seen, that in both displays of the SOM, each category (action type or target position) forms a compact cluster, reflecting the internal organization of actor’s hidden layer.

FIGURE 12

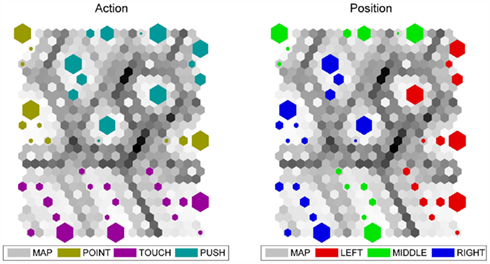
Figure 12. The visualization of the activations on the actor’s hidden layer using the self-organized map with toroid topology. The two plots correspond to the same SOM, with different labels shown.

We tested the behavior of the trained model in case of changing the action type and/or target position, to see whether the agent can react appropriately. Recall that the AL module has learned a kind of parametrized mapping toward the goal where the goal is kept active (and constant) at the AL input. Hence, we went systematically through all 3 actions and target positions (for 100 steps) and at step 20 we randomly changed action type or target position to another value. We measured the instantaneous reward (i.e., at the current step) of the model as an indicator of its performance. The results are shown in Figure 13. It can be seen that the reward always dropped at the moment of change and then started to increase toward the end of new action/target execution. Since the agent does not use any online visual feedback, it could bump into an obstacle, for instance when the change was made from the left to the right object (knocking down the middle object).

FIGURE 13

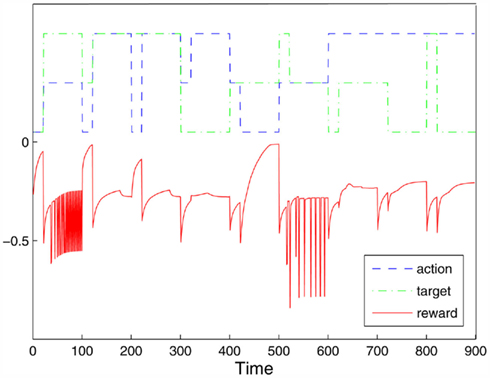
Figure 13. The behavior of the trained AL module (in terms of reward) in response to the sudden change of the action type or the target position. The growing value of the instantaneous reward, immediately after the change, serves as an indicator that the agent successfully responses to the new goal.

Last but not least, since the above learning scenario exploited various tricks to speed up and facilitate learning, we checked whether CACLA algorithm will succeed also without them, that is, in case of simultaneous learning of both AL components. Therefore, we ran a few simulations during which the actor only relied on critic’s value function from the very beginning. We observed that the model had learned the task and could generalize equally well, as with the sped-up scenario. The only disadvantage was the computing time: it took approximately four times longer to train (∼2000 episodes). Actions and the target position were chosen randomly for each episode. Figure 14 shows an example of the training procedure where each action occurred between 160 and 180 times (i.e., each point stands for one episode). The graph reflects the stochastic nature of learning, but the gradual increase of the cumulative rewards is discernible in all cases toward the end of training.

FIGURE 14

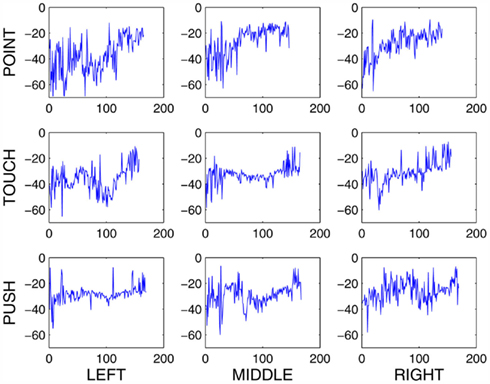
Figure 14. The development of rewards decomposed into action/target combinations. x-axis denotes episodes, y-axis denotes the cumulative rewards (during an episode).

3.3. Action Naming

As the AN module, the ESN was used with 50 units in the reservoir, with the spectral radius 0.9 and connectivity 20%. The matrix of input weights was initialized randomly from the interval [−1, 1]. ESN was designed to contain linear units at both the reservoir and the output layer. ESN behavior was observed to be quite robust with respect to model parameters. For training ESN we used a batch algorithm described in Section 2.3. Before training we prepared data (216 activations in total for all combinations of inputs) from the other two modules, i.e., 40-dimensional hidden-layer activations from the TL module and corresponding sequences of 50-dimensional hidden-layer activations of the actor network from the AL module of length 100 steps each. The parameters of the AN module are summarized in Table 3.

TABLE 3

Table 3. Final parameters for training of the AN module.

Each of the 216 hidden-layer activations of the TL module corresponds to a concrete target position that can be subject to three actions (yielding 3 × 100 hidden-layer activations). The input data for AN module is hence composed of 216 blocks of length 300. The blocks are serially concatenated and each hidden-layer activation vector of AN module is associated with one block (of length 300). As a result, each block contains 300 two-component activation vectors of length 90, whose first 40 components are dynamic (coming from the AL module, as a function of the just-executed action) and the remaining 50 components are static (coming from the TL module). For each input vector of the training set we stored the target output consisting of 2 active units.

We experimented with various ways of computing the matrix of output weights (see equation 8). The mapping task here involves the linking of dynamically changing reservoir activations with static targets. The choice could be made whether to concatenate all reservoir activation vectors during each episode (in columns of matrix X) or only a subset of them. The best results were obtained if we collected all activation vectors. In this way we achieved the accuracy on both the training and testing sets over 99%. During testing, AN module was always initialized at a random position. The outputs of the trained AN module tested on sphere-related actions are shown in Figure 15. The first row shows the graph of the output on the training set. The second row shows the action naming initiated at random positions. The graphs show that the linguistic output converges very rapidly (during a few steps) to desired activations. Actually, this should not be surprising, given that the AN module receives not only the information about the current action in terms of motor command, but also the high-level information about action type and the target position. As a result of AL learning, different actions operate in different subspaces of the actor state space, hence allowing the differentiation. In other words, the performing agent has access to its internal representations and hence knows from the very beginning what it is doing and is able to unambiguously name the action from the very beginning.

FIGURE 15

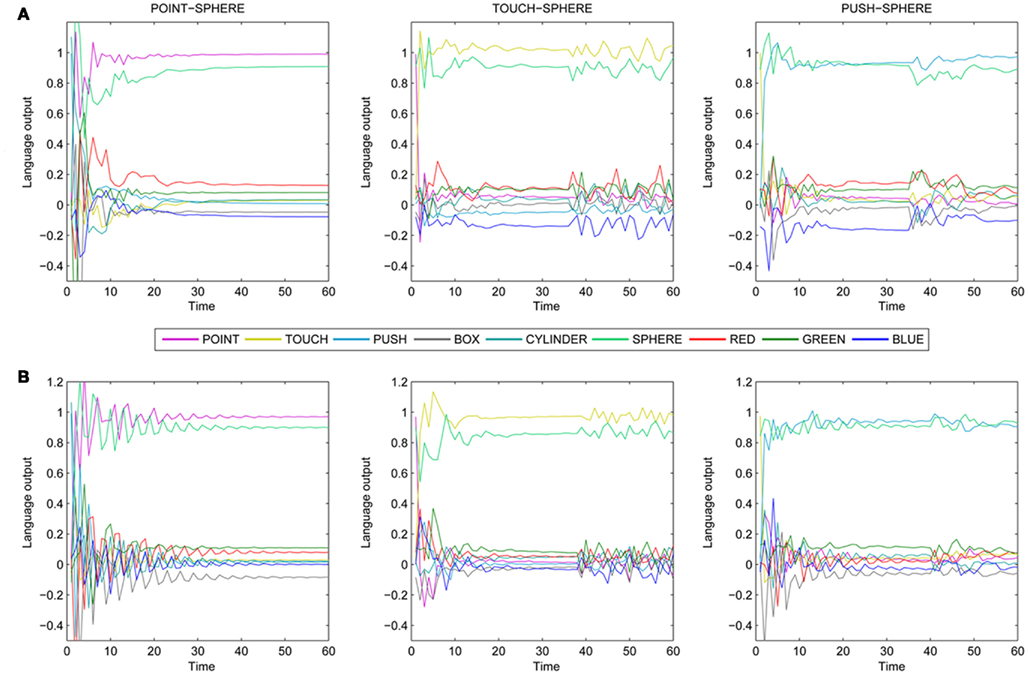
Figure 15. The linguistic output of AN module, during actions targeted at a sphere, as a function of discrete time steps (iterations). The actions start from (A) positions used during training, or (B) from random positions (B).

We can observe that for randomly initialized actions the settling process takes a bit longer, compared to the training sequences. For touch and push actions we observe at around the 40th step the contact with the target object. At this point the arm motion changes, which is reflected by slight oscillations not only at units coding the actions but also units coding the target object.

The situation would be different, though, for the observed actions. If we wanted to model the agent attempting to name the observed action, it could only have access to actor’s output of AL module, and only in the form of visual rather than proprioceptive information. In this case, the ability to name the action could be limited to the time step when the trajectory could already be differentiated visually. We could predict that the naming of the correct target position would precede the naming of the action type.

4. Discussion

We presented a connectionist model whose goal was to make the simulated iCub robot learn object-directed actions and to link this ability with language, hence grounding the linguistic meanings. The given task was learned with high accuracy. The model can be decomposed into three modules whose properties we will now discuss. The target localizer (TL) converts visual information to spatial information. It rests on a biologically relevant assumption that the shape and color of objects are processed separately in the visual system, so they are provided as parallel inputs. In our model the binding problem is avoided because during training, the MLP can learn to link the object shapes with corresponding colors (by associating the input components). The simplifying feature of our training data is the assumption that the target is always unambiguous (no two objects in the scene can have the same color or shape) so the target can be referred to by its color or its shape. On the other hand, any object of any color can be at any position in the visual field, which makes the task complexity somewhat higher than that used in Sugita and Tani (2005).

The feature of the target is assumed to be a high-level top-down information that serves as an additional (symbolic) input to the robot. Regarding the data dimensionality, from the computational perspective, it is an interesting observation, that we had to significantly extend the dimensionality of symbolic inputs to counterbalance the influence of the high-dimensional shape (contour) data. It is a question how biological systems, if understood in computational terms, solve the problem of merging data from multiple sources while maintaining the balance between them. The output of the TL module can be seen as the symbolic information (given by one-hot codes). The natural extension would be to use real-valued outputs that would allow the target to be placed anywhere in the robot’s visual field.

The action learning (AL) module is the main distinguishing part of our model. It takes two high-level (symbolic) inputs – action type and target location – that serve as fixed parameters of the motor behavior to be learned. The learning is based on RL which differs from supervised scenarios (e.g., RNNPB), which assume that target sensorimotor trajectories are available for the training. On the contrary, RL assumes a more realistic feedback available to the system. In our experiments, the robot was observed to learn required behaviors and to generalize well in the given task. Although during the training of this module the robot does not actually see (it has no direct visual input), it still is assumed to receive some visual information (at each step), reflected in the reward which is based on the distance between robot’s right hand and the target. What we reliably tested with our AL module, is that sudden change of the AL input parameters immediately led to a required change of the trajectory, either to a new target position, or resulting in a new target action.

It is clear that biological systems also evaluate the distance to the target, but they probably also use more detailed visual information (see, e.g., Oztop et al., 2004, for a model of grasping). The typical feature of these approaches is that they involve internal models for motor control (e.g., Kawato, 1999; Castellini et al., 2007). Such a step would be a natural extension of our model, giving it an ability to update the trajectory during execution, e.g., if the target moves (in our model the target is assumed to be static). This feedback could also be used for overcoming our difficulties in distinguishing between touch and push actions that would require even more fine-tuned motor actions to prevent the arm from oscillating when touching the target. Another improvement could include faster, “goal-oriented” learning rather than more-or-less blind search (at the initial phase) over the state space.

The action naming (AN) module learns to generate linguistic description of the performed action, taking information from the other two modules, about the action type (from AL) and the target (from TL). Both pieces of (input) information are pre-processed and become distributed (at the hidden layers), the former being sequential and the latter being static. The action naming task can be considered simple, since the ESN only needs to extract the (conceptual) information from AL and TL modules, and to map it onto the symbolic output (words). It is true that in our model the linguistic information (at AN output) is not sequential, as for instance in the case of twin RNNPBs (Tani et al., 2004). However, it could be made sequential with an appropriate change of the AN module architecture and the training scenario. In the current model, we did not consider this feature important.

The nature of conversion between subsymbolic sensorimotor information in both directions is hence qualitatively different, unlike the case of RNNPB, where the two modules are more-or-less symmetric both in terms of architecture and training (Sugita and Tani, 2005). In the behavior-to-language direction, we deal with mapping sequences to spatial patterns. In the language-to-behavior direction, the static symbolic information drives the appropriate sequence generation. Actually, our model mingles the linguistic information (words describing actions) with conceptual information (intended goals, given by action type and the target identity, presented as top-down inputs for AL and TL modules, respectively), both of which are coded localistically. Of course, in realistic systems these two types of information are different, without a one-to-one mapping between the two. In our model, this correspondence is hence simplified. We trained the three modules in our model separately in order to have a better control over the performance. It might be interesting to consider a more interactive scenario in which all modules would develop simultaneously, in which case we would be facing a more difficult task (can the robot learn actions that are not yet well parametrized/coded?).

One important feature of connectionist modeling is related to the training scenario. In our model, the learning of AN module following the AL module (which renders the former to be a posteriori categorizer of learned motor actions) differs from the synchronous action–language learning scenario used in RNNPB. The underlying motivation in RNNPB was to let the model converge to common “triggering” codes (via PB node learning) used for both action execution and action naming. This makes sense but on the other hand, we think that in this particular case this synchronous training is not necessary, nor justified. It is known from developmental psychology and neurophysiology (see, e.g., Jeannerod, 1997) that object recognition ability and object-related actions such as reaching and grasping are prelinguistic. For instance, reaching develops at around month three, early grasping and manipulation soon after, the hand is adjusted to the object’s size at around month nine and they are finally integrated in a single smooth action at around month 13 of age (Cangelosi et al., 2010). So, it is not unreasonable to assume that a child first acquires certain motor behaviors (at least to a certain level of proficiency) before it learns to name them, hence grounding the meaning of words. At the same time, we acknowledge that language can and does affect cognition as such also early in life, for instance in object categorization (see evidence in Waxman, 2003), and that the influence of language on cognition remains active throughout life (e.g., in spatial cognition; Landau et al., 2011). On the other hand, the TL and AL modules could be trained simultaneously, which would better correspond with infants’ scenario. The development of reaching and touching objects in infants overlaps significantly with learning the concepts and recognizing physical objects.

One interesting option that emerged in developmental robotics, concerns the type of feedback used for learning motor behavior. We argued that RL uses a biologically more plausible feedback (in terms of rewards), rather than required motor trajectories such as those used in RNNPB and some other models. Technically, one can use these trajectories in human–robot interaction, for example by manually controlling robot’s arms and storing the proprioceptive data to be used for training the robot later (as demonstrated with iCub in some works). It seems that this scenario could be sometimes adopted in AI to facilitate learning in robots. It depends on the goal of the effort (working technical solution or a model of child development). Actually, this practice is also usable to a limited extent in humans (for instance in teaching dance postures), but humans learn primarily by observation and self practicing. On the other hand, RL can be rather slow in convergence and becomes difficult in high-dimensional state spaces, so it is a remaining challenge to improve the existing algorithms or design new ones.

One drawback of our model, often present in similar works, is that in order to name the action, the agent has to execute it as well. On the other hand, in a real life one may need to name the action that is observed. To enhance the model with the capability to produce an action name when just observing it, a mirroring mechanism could be introduced. This could be based on the motor resonance (Van der Wel et al., in press), a partial activation of the neural circuitry for motor control during non-motoric tasks, which can be related to the functionality of the mirror-neuron system. From the computational point of view, the mirror-neurons were considered using various approaches, for instance by Tani et al. (2004), Chersi et al. (2010), or Wermter and Elshaw (2003). Our perspective, influenced by the common coding theory (Prinz, 1997; Hommel et al., 2001), is mostly similar to the model of Wermter and Elshaw (2003) described in the Introduction. To implement common coding, the activations on the hidden layers of the constituting modules could be, together with other perceptual information, projected onto a higher-level association area (using some kind of Hebbian learning), which could then influence the behavior of the modules by projecting back to the hidden layers. As we have already demonstrated, activations in the hidden layer of the AL module projected on a 2-dimensional SOM tend to form clusters characterizing various actions the agent is able to produce.

Another interesting issue worth discussing is the nature of reward. In the context of the RL approach, the reward is assumed to be the property of the environment, and the agent attempts to maximize it. Humans are also sensitive to rewards, but probably they can differ in what counts for them as a reward. The reward seems to be task-dependent and also agent-dependent. Related to our work, we assumed that the reward contains two generic components: the vision-related reward (the distance) and the haptic reward. This specification of reward can be seen as the designer’s intervention without which the robot could not learn. It could be interesting to look at the inverse RL whose goal is, based on agent’s behavior, to recover the underlying reward function that is maximized (Ng and Russell, 2000).

To conclude, we believe that cognitive robotics approach using neural networks is a promising path toward scalable cognitive architectures, embedded in simulated or real robots. The expected challenge could be to use ecologically plausible training algorithms and representations, with a goal to make the learning robots as autonomous as possible, hence minimizing the designer’s intervention.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank Martin Takáč and two anonymous reviewers for helpful comments. The research was supported by Slovak Grant Agency for Science, no. 1/0439/11.

References

Asada, M., Hosoda, K., Kuniyoshi, Y., Ishiguro, H., Inui, T., Yoshikawa, Y., Ogino, M., and Yoshida, C. (2009). Cognitive developmental robotics: a survey. IEEE Trans. Auton. Ment. Dev. 1, 12–34.

CrossRef Full Text

Barsalou, L. (1999). Perceptual symbol systems. Behav. Brain Sci. 22, 577–660.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Barsalou, L. (2008). Grounded cognition. Annu. Rev. Psychol. 59, 617–645.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Barsalou, L., and Wiemer-Hastings, K. (2005). “Situating abstract concepts,” in Grounding Cognition: The Role of Perception and Action in Memory, Language, and Thinking, eds D. Pecher, and R. Zwaan (New York: Cambridge University Press), 129–163.

Barto, A., and Jordan, M. (1987). “Gradient following without back-propagation in layered networks,” in Proceedings of the IEEE 1st International Conference on Neural Networks, San Diego, 629–636.

Cangelosi, A., Metta, G., Sagerer, G., Nolfi, S., Nehaniv, C., Tani, J., Belpaeme, T., Giulio, S., Fadiga, L., Wrede, B., Tuci, E., Dautenhahn, K., Saunders, J., and Zeschel, A. (2010). Integration of action and language knowledge: a roadmap for developmental robotics. IEEE Trans. Auton. Ment. Dev. 2, 167–195.

CrossRef Full Text

Cangelosi, A., and Riga, T. (2006). An embodied model for sensorimotor grounding and grounding transfer: experiments with epigenetic robots. Cogn. Sci. 30, 673–689.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cangelosi, A., Tikhanoff, V., Fontanari, J., and Hourdakis, E. (2007). Integrating language and cognition: a cognitive robotics approach. IEEE Comput. Intell. Mag. 2, 65–70.

CrossRef Full Text

Castellini, C., Orabona, F., Metta, G., and Sandini, G. (2007). Internal models of reaching and grasping. Adv. Robot. 21, 1545–1564.

Chersi, F., Thill, S., Ziemke, T., and Borghi, A. (2010). Sentence processing: linking language to motor chains. Front. Neurorobot. 4:4. doi: 10.3389/fnbot.2010.00004.

CrossRef Full Text

De Vega, M., Glenberg, A., and Graesser, A. (2008). “Reflecting on the debate,” in Symbols and Embodiment: Debates on Meaning and Cognition, eds M. De Vega, A. Glenberg, and A. Graesser (USA: Oxford University Press), 397–440.

Dominey, P. F., and Boucher, J. D. (2005). Developmental stages of perception and language acquisition in a perceptually grounded robot. Cogn. Syst. Res. 6, 243–259.

CrossRef Full Text

Glenberg, A., and Kaschak, M. (2002). Grounding language in action. Psychon. Bull. Rev. 9, 558.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Glenberg, A., Sato, M., Cattaneo, L., Riggio, L., Palumbo, D., and Buccino, G. (2008). Processing abstract language modulates motor system activity. Q. J. Exp. Psychol. 61, 905–919.

CrossRef Full Text

Harnad, S. (1990). The symbol grounding problem. Physica D 42, 335–346.

CrossRef Full Text

Hauk, O., Johnsrude, I., and Pulvermüller, F. (2004). Somatotopic representation of action words in human motor and premotor cortex. Neuron 41, 301–307.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hommel, B., Müsseler, J., Aschersleben, G., and Prinz, W. (2001). The theory of event coding (TEC): a framework for perception and action planning. Behav. Brain Sci. 24, 849–878.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jaeger, H. (2001). Short-term memory in echo state networks. Technical Report GMD Report 152. German National Research Center for Information Technology.

Jeannerod, M. (1997). The Cognitive Neuroscience of Action. Cambridge, MA: Blackwell.

Jeannerod, M. (2001). Neural simulation of action: a unifying mechanism for motor cognition. Neuroimage 14, S103–S109.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kawato, M. (1999). Internal models for motor control and trajectory planning. Curr. Opin. Neurobiol. 9, 718–727.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kohonen, T. (1997). Self-Organizing Maps. Berlin: Springer.

Lallee, S., Madden, C., Hoen, M., and Dominey, P. F. (2010). Linking language with embodied and teleological representations of action for humanoid cognition. Front. Neurorobot. 4:8. doi: 10.3389/fnbot.2010.00008.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Landau, B., Dessalegn, B., and Goldberg, A. M. (2011). “Language and space: momentary interactions,” in Language, Cognition and Space: The State of the Art and New Directions. Advances in Cognitive Linguistics Series, eds P. Chilton, and V. Evans (London: Equinox Publishing), 51–78.

Lukosevicius, M., and Jaeger, H. (2009). Reservoir computing approaches to recurrent neural network training. Comput. Sci. Rev. 3, 127–149.

CrossRef Full Text

Macura, Z., Cangelosi, A., Ellis, R., Bugmann, D., Fischer, M. H., and Myachykov, A. (2009). “A cognitive robotic model of grasping,” in Proceedings of the 9th International Conference on Epigenetic Robotics, Venice.

Marocco, D., Cangelosi, A., Fischer, K., and Belpaeme, T. (2010). Grounding action words in the sensorimotor interaction with the world: experiments with a simulated iCub humanoid robot. Front. Neurorobot. 4:7. doi: 10.3389/fnbot.2010.00007.

CrossRef Full Text

Metta, G., Sandini, G., Vernon, D., Natale, L., and Nori, F. (2008). “The iCub humanoid robot: an open platform for research in embodied cognition,” in Proceedings of the 8th Workshop on Performance Metrics for Intelligent Systems, Washington DC, 50–56.

Morse, A., de Greeff, J., Belpeame, T., and Cangelosi, A. (2010). Epigenetic robotics architecture (ERA). IEEE Trans. Auton. Ment. Dev. 2, 325–339.

CrossRef Full Text

Ng, A. Y., and Russell, S. (2000). “Algorithms for inverse reinforcement learning,” in Proceedings of the 17th International Conference on Machine Learning (ICML) (Standord, CA: Stanford University), 663–670.

Oztop, E., Bradley, N., and Arbib, M. (2004). Infant grasp learning: a computational model. Exp. Brain Res. 158, 480–503.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Prinz, W. (1997). Perception and action planning. Eur. J. Cogn. Psychol. 9, 129–154.

CrossRef Full Text

Pulvermüller, F. (2005). Brain mechanisms linking language and action. Nat. Rev. Neurosci. 6, 576–582.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pulvermüller, F., Härle, M., and Hummel, F. (2001). Walking or talking? Behavioral and neurophysiological correlates of action verb processing. Brain Lang. 78, 143–168.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rumelhart, D., Hinton, G., and Williams, R. (1986). Learning Internal Representations by Error Propagation, Vol. 1. Cambridge, MA: MIT Press, 318–362.

Simon, J. (1969). Reactions toward the source of stimulation. J. Exp. Psychol. 81, 174–176.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Smith, L., and Samuelson, L. (2010). “Objects in space and mind: from reaching to words,” in The Spatial Foundations of Language and Cognition, eds K. Mix, L. Smith, and M. Gasser (USA: Oxford University Press).

Steels, L. (2003). Evolving grounded communication for robots. Trends Cogn. Sci. (Regul. Ed.) 7, 308–312.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Steels, L. (2008). “The symbol grounding problem has been solved, so what’s next,” in Symbols and Embodiment: Debates on Meaning and Cognition, eds M. de Vega, A. Glenberg, and A. Graesser (USA: Oxford University Press), 223–244.

Steels, L., and Belpaeme, T. (2005). Coordinating perceptually grounded categories through language: a case study for colour. Behav. Brain Sci. 28, 469–489.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sugita, Y., and Tani, J. (2005). Learning semantic combinatoriality from the interaction between linguistic and behavioral processes. Adapt. Behav. 13, 33–52.

CrossRef Full Text

Sugita, Y., and Tani, J. (2008). “A sub-symbolic process underlying the usage-based acquisition of a compositional representation: results of robotic learning experiments of goal-directed actions,” in 7th IEEE International Conference on Development and Learning, Monterrey, 127–132.

Sutton, R., and Barto, A. (1998). Reinforcement Learning: An Introduction. Cambridge: MIT Press.

Taddeo, M., and Floridi, L. (2005). The symbol grounding problem: a critical review of fifteen years of research. J. Exp. Theor. Artif. Intell. 17, 419–445.

CrossRef Full Text

Tani, J. (2003). Learning to generate articulated behavior through the bottom-up and the top-down interaction processes. Neural Netw. 16, 11–23.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tani, J., and Ito, M. (2003). Self-organization of behavioral primitives as multiple attractor dynamics: a robot experiment. IEEE Trans. Syst. Man Cybern. A Syst. Hum. 33, 481–488.

CrossRef Full Text

Tani, J., Ito, M., and Sugita, Y. (2004). Self-organization of distributedly represented multiple behavior schemata in a mirror system: reviews of robot experiments using RNNPB. Neural Netw. 17, 1273–1289.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tikhanoff, V., Cangelosi, A., Fitzpatrick, P., Metta, G., Natale, L., and Nori, F. (2008). “An open-source simulator for cognitive robotics research: the prototype of the icub humanoid robot simulator,” in Proceedings of the 8th Workshop on Performance Metrics for Intelligent Systems, Gaithersburg, 57–61.

Tikhanoff, V., Cangelosi, A., and Metta, G. (2011). Integration of speech and action in humanoid robots: iCub simulation experiments. IEEE Trans. Auton. Ment. Dev. 3, 17–29.

CrossRef Full Text

Tomasello, M. (2003). Constructing a Language: A Usage-Based Theory of Language Acquisition. London: Harvard University Press.

Van der Wel, R., Sebanz, N., and Knoblich, G. (in press). “Action perception from a common coding perspective,” in Visual Perception of the Human Body in Motion, eds K. Johnson, and M. Shiffrar (New York: Oxford University Press).

Van Hasselt, H. (2012). “Reinforcement learning in continuous state and action spaces,” in Reinforcement Learning: State of the Art, eds M. Wiering, and M. van Otterlo (Berlin: Springer), 207–251.

Van Hasselt, H., and Wiering, M. (2007). “Reinforcement learning in continuous action spaces,” in IEEE International Symposium on Approximate Dynamic Programming and Reinforcement Learning (ADPRL), Honolulu, 272–279.

Van Hasselt, H., and Wiering, M. (2009). “Using continuous action spaces to solve discrete problems,” in Proceedings of the International Joint Conference on Neural Networks (IJCNN), Atlanta, 1149–1156.

Vavrečka, M. (2006). “Symbol grounding in context of zero semantic commitment (in Czech),” in Kognice a umĕ ýživot VI, eds J. Kelemen, and V. Kvasnicka (Opava: Slezská Univerzita), 401–411.

Waxman, S. (2003). “Links between object categorization and naming: origins and emergence in human infants,” in Early Category and Concept Development: Making Sense of the Blooming, Buzzing Confusion, eds D. Rakison, and L. Oakes (London: Oxford University Press), 213–241.

Wermter, S., and Elshaw, M. (2003). Learning robot actions based on self-organising language memory. Neural Netw. 16, 691–699.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wilson, M. (2002). Six views of embodied cognition. Psychon. Bull. Rev. 9, 625–636.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text