Theory of Connectivity: Nature and Nurture of Cell Assemblies and Cognitive Computation
- 1Brain and Behavior Discovery Institute and Department of Neurology, Medical College of Georgia at Augusta University, Augusta, GA, USA
- 2The Brain Decoding Center, Banna Biomedical Research Institute, Yunnan Academy of Science and Technology, Yunnan, China
Richard Semon and Donald Hebb are among the firsts to put forth the notion of cell assembly—a group of coherently or sequentially-activated neurons—to represent percept, memory, or concept. Despite the rekindled interest in this century-old idea, the concept of cell assembly still remains ill-defined and its operational principle is poorly understood. What is the size of a cell assembly? How should a cell assembly be organized? What is the computational logic underlying Hebbian cell assemblies? How might Nature vs. Nurture interact at the level of a cell assembly? In contrast to the widely assumed randomness within the mature but naïve cell assembly, the Theory of Connectivity postulates that the brain consists of the developmentally pre-programmed cell assemblies known as the functional connectivity motif (FCM). Principal cells within such FCM is organized by the power-of-two-based mathematical principle that guides the construction of specific-to-general combinatorial connectivity patterns in neuronal circuits, giving rise to a full range of specific features, various relational patterns, and generalized knowledge. This pre-configured canonical computation is predicted to be evolutionarily conserved across many circuits, ranging from these encoding memory engrams and imagination to decision-making and motor control. Although the power-of-two-based wiring and computational logic places a mathematical boundary on an individual’s cognitive capacity, the fullest intellectual potential can be brought about by optimized nature and nurture. This theory may also open up a new avenue to examining how genetic mutations and various drugs might impair or improve the computational logic of brain circuits.
Semon (1904) and Hebb (1949) are among the firsts to explore the concept of cell assembly: a group of neurons that fire transiently or sequentially, as the computational primitives to encode an object, concept, or memory engram (Figure 1A). This idea is now best summarized as “fire together, wire together” (Löwel and Singer, 1992). But in the real brain, neurons fire spontaneously, typically with huge variations even during resting periods. Such spontaneous firing variability make it nearly impossible to determine real-time sequential firing patterns while billions of neurons in the brain are not silent (Legendy, 1967; Palm, 1987; Harris et al., 2003; Harris, 2005; Dragoi and Buzsáki, 2006; Pastalkova et al., 2008; Takehara-Nishiuchi and McNaughton, 2008; Buzsáki, 2010).
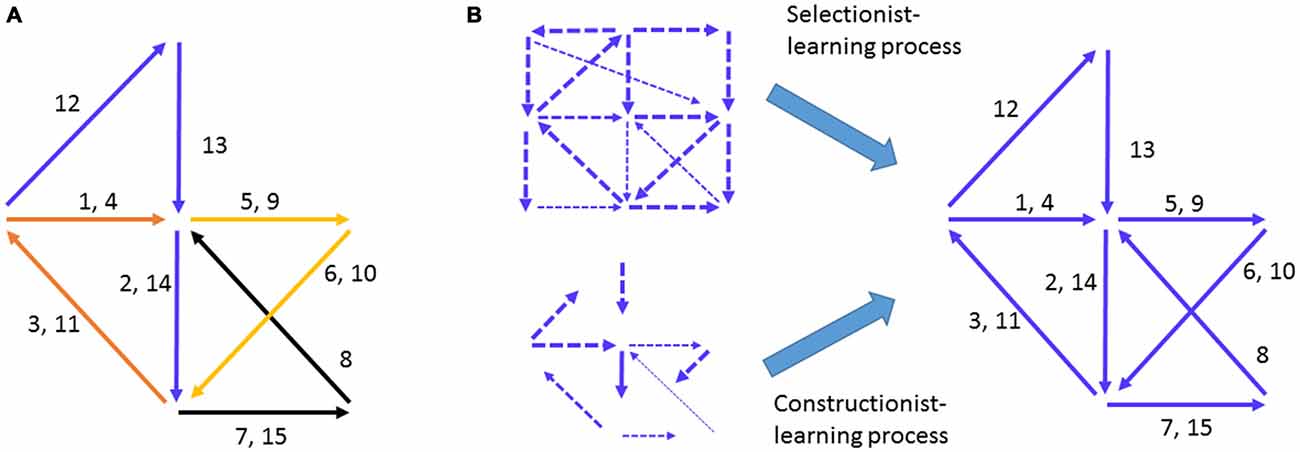
Figure 1. Hebbian cell-assembly and the proposed mechanisms of its formation. (A) Hebb illustrated his idea on the firing of the cell assembly as a way to represent concept or percept as follows: “Any frequently repeated, particular stimulation will lead to the slow development of a “cell-assembly,” a diffuse structure comprising cells in the cortex and diencephalon, capable of acting briefly as a closed system, delivering facilitation to other such systems and usually having a specific motor facilitation. …The theory is evidently a form of connectionism…” Different numbers represent the different neural pathways. Arrows represent a simple “assembly” of neural pathways and their firing chains or information flow. The drawing is adopted from Hebb (1949). (B) The mechanisms proposed to explain how Hebbian cell assembly may form. The Selectionist Theory of Learning vs. Constructionist Theory of Learning offered the two major ideas for the growth and maturation of cell assemblies, despite the fact that the internal organization of representational cell assembly was not defined.
Is Connectivity of Cell Assembly Randomized Or Organized?
Two influential theories have taken center stage in explaining how the brain may develop assembly-level mental representations of external worlds. One is termed the Selectionist Theory of Learning (Changeux and Danchin, 1976; Edelman, 1993). The idea is that during development, the genetic program initiates multiple waves of neural growth and synapse overproduction and is then subjected to regressive selection, or Neural Darwinism, during learning via synaptic pruning and stabilization (Figure 1B). The other complementary theory is the Constructivist Theory of Learning, which postulates that learning interplays with the growth of neural connections over the prolonged postnatal developmental period to gradually construct representational networks (Figure 1B; Quartz and Sejnowski, 1997). By either assuming random patterns or overlooking what the innate patterns should look like as Hebb had originally done, both theories focused on the requirement of learning to construct yet undefined “representational patterns”. However, models based on random connectivity face the difficulty of explaining the natural emergence of innate cognitive abilities in infants in the absence of apparent learning (Carruthers et al., 2005).
Theory of Connectivity: Canonical Computation of Cell Assemblies
How should cell assembly organize itself so that incoming information can be orderly and gradually converted into memory, concepts, and flexible motor behavior? We previously uncovered that CA1 cells used specific-to-general combinatorial strategy to encode three distinct fearful experiences (Lin et al., 2005, 2006; Tsien, 2007; Tsien et al., 2013). This seed of an idea led to the Theory of Connectivity that the specific-to-general combinatorial strategy may reflect the mathematical principle underlying the general organization of cell assemblies in the brain (Tsien, 2015). This theory described a “power-of-two” based, specific-to-general wiring logic, and predicts a series of pre-configured, conserved functional connectivity motifs (FCMs) capable of discovering specific features, as well as all possible relational patterns and abstract knowledge (Tsien, 2015, 2016).
This theory defines the size of a cell assembly: each FCM consists of neural cliques (N) made of principal neurons receiving specific afferent inputs, as well as those principal neural cliques receiving progressively more convergent inputs that are comprehensively and combinatorially arranged, following the formula of N = 2i−1 (i for numbers of distinct information inputs, N is the number of neural cliques with all possible combinatorial connectivity patterns; Figure 2A).
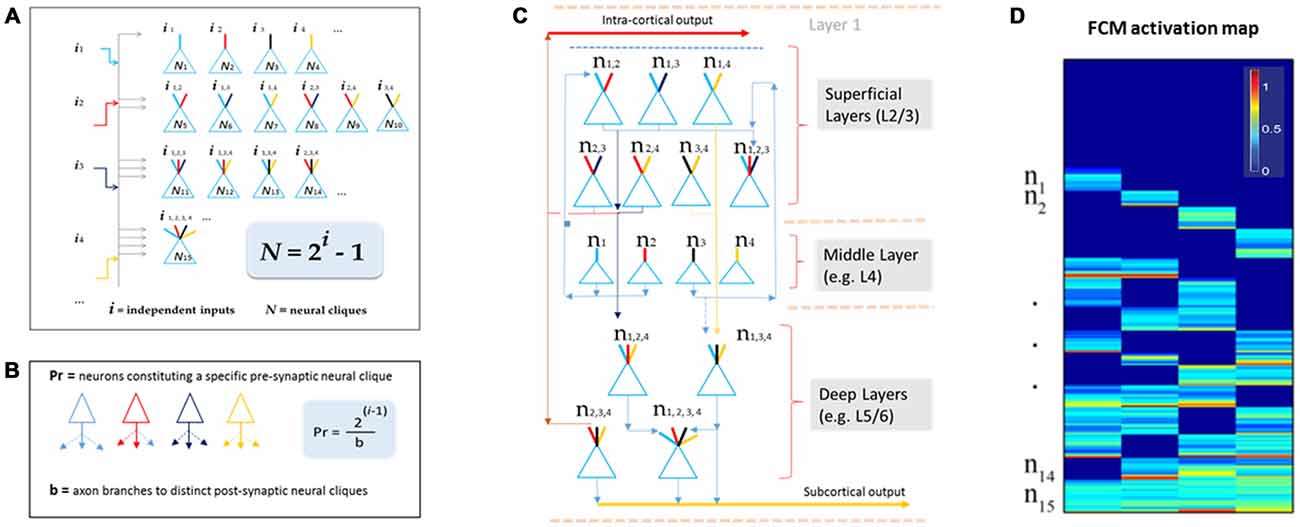
Figure 2. The Theory of Connectivity predicts the existence of specific-to-general, combinatorial wiring logic across the brain. (A) The proposed functional connectivity motif (FCM) is illustrated in a non-recurrent, feed-forward circuit. By following the proposed equation of N = 2i−1, the FCM exemplified here consists of 15 distinct neural cliques (N1...15), which cover all possible connectivity patterns in order to process four distinct inputs (i1, i2, i3, i4). The exponent i represents the number of distinct information inputs, and N is the number of neural cliques with all possible combinatorial connectivity patterns. (B) The number of presynaptic neurons (Pr) required to cover postsynaptic convergence can also be mathematically assessed (see the equation in the highlighted blue block, Pr = [2i−1]/b). For example, assuming a presynaptic neuron from the upstream FCM has only a single axon (branch number, b = 1) contacting a single postsynaptic neurons located in the downstream FCM containing 15 cliques (based on i = 4), the total number of such presynaptic specific-feature cells (providing input i1) required for comprehensively covering the specific-to-general, combinatorial-convergent postsynaptic cells in a non-recurrent downstream FCM would be eight. These eight postsynaptic neurons correspond to N1, N5, N6, N7, N11, N12, N14, N15 listed in the Panel A. On the other hand, if a single pre-synaptic neuron can have eight branches (b = 8; each making a contact with a unique postsynaptic neuron, respectively), this neuron is sufficient to provide inputs onto N1, N5, N6, N7, N11, N12, N14, N15 listed in Panel A. (C) The FCM-based computational logic can be mapped onto the multi-layered cortex as the general-purpose algorithm underlying canonical cortical computation. In the classic six-layered (L) cortex, L1 contains scattered interneurons and mainly dendrites and afferent axons from lower layers. L2 to L6 are the primary sites for canonical computation. The specific cliques occupy layer 4 (L4), which projects to L2/3 to form the initial set of combinatorial connectivity patterns (e.g., mostly two-featured combinations and some three-featured combinations). These subgeneral cliques then project downward to the deeper layers, L5/6, for generating even greater combinatorial connectivity. (D) Schematic “bar-code” illustrates the specific-to-general activation responses from the 15 distinct neural cliques (n1−15), processing four distinct inputs (i = 4). The warm color represents its activation level (% maximal activation). The cartoon illustration was adapted from Tsien (2015), TINS.
As the evolutionarily conserved cell-assembly wiring logic, it should exhibit: (1) Anatomical prevalence—to be prevalent across neural circuits, regardless of gross anatomical shapes; (2) Species conservancy—to be conserved across different animal species; and (3) Cognitive universality—to be used as a universal computational logic for processing various cognitive information, including appetitive, social and/or fearful events. It should be noted that in the natural world situation, as i become increasingly larger in more intelligent animal species, N in a given cell-assembly can approximate to 2i (e.g., ~90 or 95%) rather than rigidly calculated by the equation, this mathematical approximation would still preserve the essence of specific-to-general combinatorial logic.
FCM Implemented in the Non-Recurrent, Feed-Forward Circuits
The proposed connectivity logic can be used to examine biological and mathematical boundaries of wiring efficiency or computational capacities using modeling (McClelland and Rogers, 2003; Cutsuridis et al., 2010; Stevens, 2012), including recurrent and non-recurrent networks. In the non-recurrent feed-forward network (e.g., the CA1 region or dentate gyrus [DG]), specific-to-general combinatorial patterns can be established by combinatorial wiring of the presynaptic upstream inputs (Figure 2A). This wiring logic produces instantaneous pattern-separation and pattern-generalization by a cell assembly, which is radically different from pattern separation or pattern completion that was specifically or sequentially assigned to one of the hippocampal subregions (Marr, 1971; Yassa and Stark, 2011; Rolls, 2013). Furthermore, in the CA3 which is viewed as a completely auto-associative recurrent network, the traditional theories would predict the loss of the specific-to-general neural-clique connectivity logic, because any specific input into specific cliques would easily be taken over by feedback inputs from its subgeneral and general cliques.
One of the critical factors in building computational models based on this wiring logic is to determine how specific input-neurons (presynaptic neurons, whether pyramidal cells and long-range inhibitory projection cells) should project onto the non-recurrent networks. For instance, the number of presynaptic specific input-neurons (Pr) needed to cover all distinct postsynaptic neural cliques can be estimated by using the equation of Pr = [2i−1]/b (Figure 2B), whereas b represents numbers of axon branches. By assuming that the presynaptic neuron has one axon branch which projects to one postsynaptic cell, one would expect that the minimal number of cells from the pre-synaptic specific neural clique should be eight (Pr = 8) to ensure the specific-to-general combinatorial coverage in the postsynaptic FCM that deals with four distinct information input (i = 4). Obviously, most neurons have more than one axon and each can bifurcate at multiple points along its length to multiple terminal locations to form synapses with several postsynaptic target cells. For example, a single pre-synaptic cell can be modeled to have eight axon branches, each projecting to the eight distinct post-synaptic clique cells (Figure 2B, only three branches are drawn). In the real brain, the actual number of neurons per clique and their axon branching patterns would depend on molecular genetics and local cues during neural development. The connectome projects can prove to be highly valuable for this type of analysis.
Using Cortical Layers to Execute FCM-Based Canonical Computation
The cortex has a remarkably uniformed multi-layered architecture (usually with three or six layers; Barbas, 2015; Fournier et al., 2015). It has been shown that the cortex varies its surface area by a factor of 10,000 across a large number of surveyed mammalian species, while the thickness of cortical layers varies only by a factor of 10 (DeFelipe et al., 2002; Rakic, 2008). This finding has contributed to the search for a fundamental cortical “processing unit” (Hubel and Wiesel, 1977; Mountcastle, 2003). In literature, a variety of canonical neural computations have been proposed, including exponentiation, linear filtering, normalization, receptive field selectivity, gain control, etc. (Reichardt et al., 1983; Heeger, 1992; Bizzi et al., 1995; Hanes and Schall, 1996; Pouget and Snyder, 2000; Smith and Ratcliff, 2004; Carandini et al., 2005; Cisek, 2006; Kouh and Poggio, 2008; Carandini and Heeger, 2011; Miller, 2016). Despite these efforts in identifying operational components or neuronal properties, the core computational principles of the cortex remain elusive (Krubitzer, 2009).
Here, we would like to suggest that the universal canonical computation performed by cortical circuits is the power-of-two-based, specific-to-general computational logic (Tsien, 2015). This logic is implemented vertically across cortical layers (Figure 2C). Using the moderately recurrent cortical architecture, the locally disordered but canonically nonrandom cortical patterns can readily execute this proposed logic. For example, the input-cortical layer, such as layer 4 (L4), hosts specific neural cliques. These layers’ pyramidal cells typically project upwards to layers 2 and 3 where some recurrent connections are made. This would produce two-event or three-event subgeneral cells (binary or ternary cliques). These subgeneral cells would then project to the deep layers, such as layers 5 and 6, for further combinatorial feature discovery and extraction to generate more broadly tuned subgeneral and general neural cliques. It should be noted that variations can occur; for example, some of the L5 neurons are directly driven by thalamic inputs. This type of direct input would enable specific features to still be maintained in the deep layers. Regardless of such variations in wiring details, the fundamental power-of-two-based computational logic remains invariant.
Not all cortices have the classic six layers, rather some cortices only use a three-layered cortex (e.g., the prefrontal cortex, anterior cingulate cortex, piriform cortex, or retrosplenial cortex in mice, and the entire cerebral cortex in reptiles; Fournier et al., 2015). In such three-layered cortices, classic layers 2 and 3 are merged in the upper layer (L2/3), whereas layers 5 and 6 form the deep layer (L5/6). In this scenario, specific cliques and binary subgeneral cliques should be enriched in L2/3, whereas the general cliques should be mostly in L5/6. Therefore, the power-of-two-based computational logic is still preserved in such three-layered architecture. In short, we propose that evolution relies on the multi-layered cortical architecture to execute the power-of-two-based mathematical principle. This explains why scaling up cognitive capacity and intelligence is achieved by dramatically expanding the cortical surface areas, rather than by varying the cortical thickness.
To Test the Theory of Connectivity Experimentally
This theory can be tested initially by large-scale in vivo recordings, because structural connectivity is ultimately reflected by functional connectivity. One critical consideration is to identify the proper natural stimuli to which relevant cell assemblies in the higher cortex have been evolutionarily selected and developmentally programmed. Another consideration is to use multi-modality categorical stimuli (e.g., information i > 3), thereby allowing a more stringent testing of this power-of-two-of-two-based, specific-to-general computational logic in a given circuit. The proposed wiring and computational logic can be detected in the form of a brain activation “bar-code” (Figure 2D). This theory should be tested across many animal species—from fruit flies, zebra fish and songbirds, to rodents and primates (Gerber et al., 2004; Phillips et al., 2011; Beshel and Zhong, 2013; Shi et al., 2013; Tubon et al., 2013; Lin et al., 2014; Davis, 2015).
The theory further predicts that specific-to-general logic should be genetically programmed by evolution and during development and already takes its primitive shape, prior to learning, as the matured connectivity in the naïve unlearnt neural network. However, synaptic plasticity plays a crucial role in both neural development (Gao et al., 2014) and learning (Bliss and Collingridge, 1993; Frey and Frey, 2008). The critical question is how to distinguish the wiring logic set up by normal development vs. by learning and memory.
Because synaptic proteins are metabolically turned over within days or week(s), learning-induced synaptic connectivity will likely drift significantly over time (Shimizu et al., 2000; Wang et al., 2006). It has been shown that the NMDA receptor (NMDAR)-based synaptic reentry-reinforcement (SRR) is crucial for maintaining synaptic stability (Wittenberg and Tsien, 2002; Wittenberg et al., 2002). For example, inducible knockout of the NMDAR in the forebrain principal neurons for one-month (but not for one-week) caused a drift in the synaptic connectivity pattern, leading to the abolishment of remote fear memories (Cui et al., 2004). If the initial synaptic connectivity were random in the matured but unlearnt network, one should expect that deleting the NMDAR for a long period of time (e.g., 3 months) would eventually lead synaptic connectivity to drift all the way back to initial randomness. On the other hand, if one can still observe these non-random, specific-to-general neural cliques under such conditions, it would strongly suggest that this is a pre-configured logic and is independent of the NMDAR-dependent learning in adulthood.
Installing the Personalized Cognitive Algorithms by Nature and Nurture
Changes in gene expression underlie brain development and aging (Jiang et al., 2001; Mody et al., 2001; Förster et al., 2006; Langston et al., 2010; Wills et al., 2010; Gao et al., 2014; He et al., 2015). This provides a unique opportunity to investigate not only how computational logic emerges during the postnatal period and is affected by aging, but also how environment alters or enhances cognition (Rampon et al., 2000a,b; van Praag et al., 2000; Feng et al., 2001; Tang et al., 2001).
The pre-configured connectivity, as proposed by the Theory of Connectivity, would conceivably constrain or give rise to different intelligence. It also predicts that variable ratios among the specific, subgeneral and general cliques among individual brains can afford distinct cognitive abilities or unique talents. The larger the number of neurons devoted to specific neural cliques, the greater the ability of remembering episodic details would be expected. In contrast, if more neurons were devoted to the subgeneral and general neural cliques, such individuals may possess a greater ability for abstraction, generalization or flexible behavior.
Genetic mutations can also alter the basic computational algorithms of neural circuits. By examining such interactions in various genetically modified mice—including NMDAR1 conditional knockout mice and the memory-enhanced NR2B transgenic mice (Tang et al., 1999; Cui et al., 2004; Wang et al., 2009; Yu et al., 2009; Jin and Costa, 2010; Zhang et al., 2013; Jacobs and Tsien, 2014), one can obtain crucial insight into the precise relationships between genes, neural circuits and cognition. In addition, Reeler mice can be a particularly interest model because of their inverted cortex (D’Arcangelo and Curran, 1998). One prediction might be that Reeler mice still operate under the power-of-two-based computational logic but with the inverted anatomical distributions of specific-to-general cliques. On the other hand, it is also possible that the cortex of Reeler mice may host the specific-to-general clique arrangement in a similar manner to wild-type mice. This would suggest that histological and molecular characteristics critical for defining the different cortical layers are not essential for executing the power-of-two-based, specific-to-general computational logic.
Specific-To-General Cell Assembly for Representing Memory Engram
The study of memory engram has gained renewed interest. For example, using the C-fos promotor-based optogenetic approach, researchers reported a group of neurons in the DG or amygdala that were labeled during learning can be optogenetically reactivated during recall, leading to changes in freezing (see reviews by Josselyn et al., 2015; Tonegawa et al., 2015). Intriguingly, the same protocols and manipulation in the CA1 failed to produce a similar outcome produced by the DG (Xu Liu, personal communication), thereby raising the possibility that the artificial zapping of the amygdala loop by light may not truly alter memory engram per se. In general, methods using immediate-early-gene promoter to label memory engram are interesting, but it lacked the ability to distinguish categorical features and to obtain temporal dynamics essential for revealing the fundamental principles and encoding properties of memory engram (see Eichenbaum, 2016).
Memory is traditionally divided into episodic memory and semantic memory. Episodic memory refers to the memory of a specific event in a given time and context (Tulving, 1972), whereas semantic memory represents the memory of the conceptual knowledge of facts that are no longer ascribable to any particular occasion in life (Tulving, 1972; Cohen and Eichenbaum, 1993; Squire and Zola, 1998; Lin et al., 2007). This classical definition has led to intense search for the distinct network-mechanisms underlying the formation of episodic and semantic memory (Düzel et al., 1999; Maguire et al., 2005; Burianova and Grady, 2007; Ryan et al., 2008). Yet it remains unclear as to how semantic memory emerges from daily experiences, and what the relationship is between these two types of memories at the cell-assembly level.
The initial clue is provided by the revelation of specific-to-general neural clique assembly in the CA1 hippocampus (Lin et al., 2005, 2006; Tsien, 2007), which suggested that episodic memory and semantic memory are simultaneously generated within the same cell assembly. In other words, the computational logic used by memory engram follows the same power-of-two-based mathematical principle: the specific cliques extract specific features from sensory information to encode episodic traces of the memory engram, whereas the subgeneral and general cliques generate the relational knowledge and concepts of the memory engram (Tsien et al., 2013). Such simultaneous extractions of both episodic and semantic memory components by the same FCM offer a perfect solution to build the categorical and hierarchical organization of memory and knowledge in the brain. Encouragingly, large-scale neural recording experiments have begun to uncover critical insights and temporal patterns of real-time memory traces and fear memory engram in the normal brain as well as in the absence of synaptic plasticity (Chen et al., 2009; Oşan et al., 2011; Zhang et al., 2013).
General-To-Specific Combinatorial Logic for Motor Output Circuits
Gradually extracting perceptual information by sensory and memory circuits is what leads to generalized knowledge and concepts. In contrast, the motor output circuits may use the same specific-to-general computational logic—but in reverse. That is, cell assemblies in higher motor circuits (such as the motor-planning cortex) will be more general and abstract to begin with, then percolate to primary cortices and lower circuits, which become successively more specific. Motor-control circuits are crucial for a broad range of functions, spanning from movement planning and execution to imagined movement or motor cognition (Bizzi et al., 1995; Nicolelis et al., 1997; Moran and Schwartz, 1999; Fogassi et al., 2005; Georgopoulos and Carpenter, 2015; Stetson and Andersen, 2015). Overall, general-to-specific cliques in the FCM at the top of the hierarchy encode more abstract intent or decision-making for general motor execution, whereas the cliques in the lower FCMs encode less abstract motor command, with FCMs in spinal circuits commanding general-to-specific individual muscle activation. One can test these predictions by large-scale recording in the motor cortex, striatum, and spinal cord.
FCM as the Key Biomarker for Assessing Neurological and Psychiatric Disorders
The proposed theory should open a new avenue into examining the detrimental effects of brain disease and aging at the cell-assembly level. Characterizations of cell-assembly patterns in various diseased models—from Alzheimer’s to depression (D’Arcangelo and Curran, 1998; Hayashi et al., 2008; Feng et al., 2001)—can potentially lead to deeper insights into why gene mutations alter cognitive functions. In addition, examining the effects of various drugs on the proposed cell-assembly logic may provide new insights about their central mechanisms (Caine et al., 2007; Wang et al., 2010; Kong and Xu, 2011; Cao et al., 2015; Fuccillo et al., 2016), perhaps leading to further improvement for drug efficacy and safety (Slutsky et al., 2010; Liu et al., 2015).
In summary, the Theory of Connectivity postulates the power-of-two-based, specific-to-general wiring and computational logic for the organization of pre-configured cell assemblies in the brain. This prediction is radically different from local random connectivity currently assumed for cell assemblies in matured, but unlearnt, circuits. This theory also provides a new framework to investigate how learning and development interact to produce generative cognition and flexible behavior.
Author Contributions
JZT developed the idea and worked with ML and JL, as well as co-wrote the manuscript.
Funding
We would like to express our gratitude for the unique opportunity of working at the Brain Decoding Project Consortium organized by Banna Biomedical Research Institute of Yunnan Academy of Science and Technology and supported by Yunnan Science Commission (2014DG002). We also thank Georgia Research Alliance for its support of the Brain Decoding Project and National Institute of Health (R01NS079774) to JT.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Barbas, H. (2015). General cortical and special prefrontal connections: principles from structure to function. Annu. Rev. Neurosci. 38, 269–289. doi: 10.1146/annurev-neuro-071714-033936
Beshel, J., and Zhong, Y. (2013). Graded encoding of food odor value in the Drosophila brain. J. Neurosci. 33, 15693–15704. doi: 10.1523/JNEUROSCI.2605-13.2013
Bizzi, E., Giszter, S. F., Loeb, E., Mussa-Ivaldi, F. A., and Saltiel, P. (1995). Modular organization of motor behavior in the frog’s spinal cord. Trends Neurosci. 18, 442–446. doi: 10.1016/0166-2236(95)94494-p
Bliss, T., and Collingridge, G. (1993). A synaptic model of memory: long-term potentiation in the hippocampus. Nature 361, 31–39. doi: 10.1038/361031a0
Burianova, H., and Grady, C. L. (2007). Common and unique neural activations in autobiographical, episodic, and semantic retrieval. J. Cogn. Neurosci. 19, 1520–1534. doi: 10.1162/jocn.2007.19.9.1520
Buzsáki, G. (2010). Neural syntax: cell assemblies, synapsembles and readers. Neuron 68, 362–385. doi: 10.1016/j.neuron.2010.09.023
Caine, S. B., Thomsen, M., Gabriel, K. I., Berkowitz, J. S., Gold, L. H., Koob, G. F., et al. (2007). Lack of self-administration of cocaine in dopamine D1 receptor knock-out mice. J. Neurosci. 27, 13140–13150. doi: 10.1523/JNEUROSCI.2284-07.2007
Cao, V. Y., Ye, Y., Mastwal, S., Ren, M., Coon, M., Liu, Q., et al. (2015). Motor learning consolidates arc-expressing neuronal ensembles in secondary motor cortex. Neuron 86, 1385–1392. doi: 10.1016/j.neuron.2015.05.022
Carandini, M., Demb, J. B., Mante, V., Tolhurst, D. J., Dan, Y., Olshausen, B. A., et al. (2005). Do we know what the early visual system does? J. Neurosci. 25, 10577–10597. doi: 10.1523/JNEUROSCI.3726-05.2005
Carandini, M., and Heeger, D. J. (2011). Normalization as a canonical neural computation. Nat. Rev. Neurosci. 13, 51–62. doi: 10.1038/nrn3136
Carruthers, P., Laurence, S., and Stich, S. (2005). The Innate Mind: Structure and Contents. New York, NY: Oxford University Press.
Changeux, J. P., and Danchin, A. (1976). Selective stabilization of developing synapses as a mechanism for the specification of neuronal networks. Nature 264, 705–712. doi: 10.1038/264705a0
Chen, G., Wang, L. P., and Tsien, J. Z. (2009). Neural population-level memory traces in the mouse hippocampus. PLoS One 4:e8256. doi: 10.1371/journal.pone.0008256
Cisek, P. (2006). Integrated neural processes for defining potential actions and deciding between them: a computational model. J. Neurosci. 26, 9761–9770. doi: 10.1523/JNEUROSCI.5605-05.2006
Cohen, N. J., and Eichenbaum, H. (1993). Memory, Amnesia and the Hippocampal System. Cambridge, MA: MIT Press.
Cui, Z., Wang, H., Tan, Y., Zaia, K. A., Zhang, S., and Tsien, J. Z. (2004). Inducible and reversible NR1 knockout reveals crucial role of the NMDA receptor in preserving remote memories in the brain. Neuron 41, 781–793. doi: 10.1016/s0896-6273(04)00072-8
Cutsuridis, V., Cobb, S., and Graham, B. P. (2010). Encoding and retrieval in a model of the hippocampal CA1 microcircuit. Hippocampus 20, 423–446. doi: 10.1002/hipo.20661
D’Arcangelo, G., and Curran, T. (1998). Reeler: new tales on an old mutant mouse. Bioessays 20, 235–244. doi: 10.1002/(sici)1521-1878(199803)20:3<235::aid-bies7>3.0.co;2-q
Davis, R. L. (2015). Snapshot: olfactory classical conditioning of Drosophila. Cell 163, 524.e1–524.e1. doi: 10.1016/j.cell.2015.09.043
DeFelipe, J., Alonso-Nanclares, L., and Arellano, J. I. (2002). Microstructure of the neocortex: comparative aspects. J. Neurocytol. 31, 299–316. doi: 10.1023/A:1024130211265
Dragoi, G., and Buzsáki, G. (2006). Temporal encoding of place sequences by hippocampal cell assemblies. Neuron 50, 145–157. doi: 10.1016/j.neuron.2006.02.023
Düzel, E., Cabeza, R., Picton, T. W., Yonelinas, A. P., Scheich, H., Heinze, H. J., et al. (1999). Task-related and item-related brain processes of memory retrieval. Proc. Natl. Acad. Sci. U S A 96, 1794–1799. doi: 10.1073/pnas.96.4.1794
Edelman, G. M. (1993). Neural darwinism: selection and reentrant signaling in higher brain function. Neuron 10, 115–125. doi: 10.1016/0896-6273(93)90304-a
Eichenbaum, H. (2016). Still searching for the engram. Learn. Behav. doi: 10.3758/s13420-016-0218-1 [Epub ahead of print].
Feng, R., Rampon, C., Tang, Y. P., Shrom, D., Jin, J., Kyin, M., et al. (2001). Deficient neurogenesis in forebrain-specific presenilin-1 knockout mice is associated with reduced clearance of hippocampal memory traces. Neuron 32, 911–926. doi: 10.1016/s0896-6273(01)00523-2
Fogassi, L., Ferrari, P. F., Gesierich, B., Rozzi, S., Chersi, F., and Rizzolatti, G. (2005). Parietal lobe: from action organization to intention understanding. Science 308, 662–667. doi: 10.1126/science.1106138
Förster, E., Zhao, S., and Frotscher, M. (2006). Laminating the hippocampus. Nat. Rev. Neurosci. 7, 259–267. doi: 10.1038/nrn1882
Fournier, J., Müller, C. M., and Laurent, G. (2015). Looking for the roots of cortical sensory computation in three-layered cortices. Curr. Opin. Neurobiol. 31, 119–126. doi: 10.1016/j.conb.2014.09.006
Frey, S., and Frey, J. U. (2008). ’Synaptic tagging’ and ’cross-tagging’ and related associative reinforcement processes of functional plasticity as the cellular basis for memory formation. Prog. Brain Res. 169, 117–143. doi: 10.1016/s0079-6123(07)00007-6
Fuccillo, M. V., Rothwell, P. E., and Malenka, R. C. (2016). From synapses to behavior: what rodent models can tell us about neuropsychiatric disease. Biol. Psychiatry 79, 4–6. doi: 10.1016/j.biopsych.2015.02.009
Gao, P., Postiglione, M. P., Krieger, T. G., Hernandez, L., Wang, C., Han, Z., et al. (2014). Deterministic progenitor behavior and unitary production of neurons in the neocortex. Cell 159, 775–788. doi: 10.1016/j.cell.2014.10.027
Georgopoulos, A. P., and Carpenter, A. F. (2015). Coding of movements in the motor cortex. Curr. Opin. Neurobiol. 33, 34–39. doi: 10.1016/j.conb.2015.01.012
Gerber, B., Tanimoto, H., and Heisenberg, M. (2004). An engram found? Evaluating the evidence from fruit flies. Curr. Opin. Neurobiol. 14, 737–744. doi: 10.1016/j.conb.2004.10.014
Hanes, D. P., and Schall, J. D. (1996). Neural control of voluntary movement initiation. Science 274, 427–430. doi: 10.1126/science.274.5286.427
Harris, K. D. (2005). Neural signatures of cell assembly organization. Nat. Rev. Neurosci. 6, 399–407. doi: 10.1038/nrn1669
Harris, K. D., Csicsvari, J., Hirase, H., Dragoi, G., and Buzsáki, G. (2003). Organization of cell assemblies in the hippocampus. Nature 424, 552–556. doi: 10.1038/nature01834
Hayashi, F., Takashima, N., Murayama, A., and Inokuchi, K. (2008). Decreased postnatal neurogenesis in the hippocampus combined with stress experience during adolescence is accompanied by an enhanced incidence of behavioral pathologies in adult mice. Mol. Brain 1:22. doi: 10.1186/1756-6606-1-22
He, S., Li, Z., Ge, S., Yu, Y. C., and Shi, S. H. (2015). Inside-out radial migration facilitates lineage-dependent neocortical microcircuit assembly. Neuron 86, 1159–1166. doi: 10.1016/j.neuron.2015.05.002
Heeger, D. J. (1992). Normalization of cell responses in cat striate cortex. Vis. Neurosci. 9, 181–197. doi: 10.1017/s0952523800009640
Hubel, D. H., and Wiesel, T. N. (1977). Ferrier lecture: functional architecture of macaque monkey visual cortex. Proc. R. Soc. Lond. B Biol. Sci. 198, 1–59. doi: 10.1098/rspb.1977.0085
Jacobs, S. A., and Tsien, J. Z. (2014). Overexpression of the NR2A subunit in the forebrain impairs long-term social recognition and non-social olfactory memory. Genes Brain Behav. 13, 376–384. doi: 10.1111/gbb.12123
Jiang, C. H., Tsien, J. Z., Schultz, P. G., and Hu, Y. (2001). The effects of aging on gene expression in the hypothalamus and cortex of mice. Proc. Natl. Acad. Sci. U S A 98, 1930–1934. doi: 10.1073/pnas.98.4.1930
Jin, X., and Costa, R. M. (2010). Start/stop signals emerge in nigrostriatal circuits during sequence learning. Nature 466, 457–462. doi: 10.1038/nature09263
Josselyn, S. A., Köhler, S., and Frankland, P. W. (2015). Finding the engram. Nat. Rev. Neurosci. 16, 521–534. doi: 10.1038/nrn4000
Kong, H., and Xu, M. (2011). Exploring mechanisms underlying extinction of cue-elicited cocaine seeking. Curr. Neuropharmacol. 9, 8–11. doi: 10.2174/157015911795017173
Kouh, M., and Poggio, T. (2008). A canonical neural circuit for cortical nonlinear operations. Neural Comput. 20, 1427–1451. doi: 10.1162/neco.2008.02-07-466
Krubitzer, L. (2009). In search of a unifying theory of complex brain evolution. Ann. N Y Acad. Sci. 1156, 44–67. doi: 10.1111/j.1749-6632.2009.04421.x
Langston, R. F., Ainge, J. A., Couey, J. J., Canto, C. B., Bjerknes, T. L., Witter, M. P., et al. (2010). Development of the spatial representation system in the rat. Science 328, 1576–1580. doi: 10.1126/science.1188210
Legendy, C. R. (1967). On the scheme by which the human brain stores information. Math. Biosci. 1, 555–597. doi: 10.1016/0025-5564(67)90003-x
Lin, A. C., Bygrave, A. M., de Calignon, A., Lee, T., and Miesenböck, G. (2014). Sparse, decorrelated odor coding in the mushroom body enhances learned odor discrimination. Nat. Neurosci. 17, 559–568. doi: 10.1038/nn.3660
Lin, L., Chen, G., Kuang, H., Wang, D., and Tsien, J. Z. (2007). Neural encoding of the concept of nest in the mouse brain. Proc. Natl. Acad. Sci. U S A 104, 6066–6071. doi: 10.1073/pnas.0701106104
Lin, L., Osan, R., Shoham, S., Jin, W., Zuo, W., and Tsien, J. Z. (2005). Identification of network-level coding units for real-time representation of episodic experiences in the hippocampus. Proc. Natl. Acad. Sci. U S A 102, 6125–6130. doi: 10.1073/pnas.0408233102
Lin, L., Osan, R., and Tsien, J. Z. (2006). Organizing principles of real-time memory encoding: neural clique assemblies and universal neural codes. Trends Neurosci. 29, 48–57. doi: 10.1016/j.tins.2005.11.004
Liu, G., Weinger, J. G., Lu, Z. L., Xue, F., and Sadeghpour, S. (2015). Efficacy and safety of MMFS-01, a synapse density enhancer, for treating cognitive impairment in older adults: a randomized, double-blind, placebo-controlled trial. J. Alzheimers. Dis. 49, 971–990. doi: 10.3233/JAD-150538
Löwel, S., and Singer, W. (1992). Selection of intrinsic horizontal connections in the visual cortex by correlated neuronal activity. Science 255, 209–212. doi: 10.1126/science.1372754
Maguire, E. A., Frith, C. D., Rudge, P., and Cipolotti, L. (2005). The effect of adult-acquired hippocampal damage on memory retrieval: an fMRI study. Neuroimage 27, 146–152. doi: 10.1016/j.neuroimage.2005.04.006
Marr, D. (1971). Simple memory: a theory for archicortex. Philos. Trans. R. Soc. Lond. B Biol. Sci. 262, 23–81. doi: 10.1098/rstb.1971.0078
McClelland, J. L., and Rogers, T. T. (2003). The parallel distributed processing approach to semantic cognition. Nat. Rev. Neurosci. 4, 310–322. doi: 10.1038/nrn1076
Miller, K. D. (2016). Canonical computations of cerebral cortex. Curr. Opin. Neurobiol. 37, 75–84. doi: 10.1016/j.conb.2016.01.008
Mody, M., Cao, Y., Cui, Z., Tay, K. Y., Shyong, A., Shimizu, E., et al. (2001). Genome-wide gene expression profiles of the developing mouse hippocampus. Proc. Natl. Acad. Sci. U S A 98, 8862–8867. doi: 10.1073/pnas.141244998
Moran, D. W., and Schwartz, A. B. (1999). Motor cortical representation of speed and direction during reaching. J. Neurophysiol. 82, 2676–2692.
Mountcastle, V. B. (2003). Introduction. Computation in cortical columns. Cereb. Cortex 13, 2–4. doi: 10.1093/cercor/13.1.2
Nicolelis, M. A., Ghazanfar, A. A., Faggin, B. M., Votaw, S., and Oliveira, L. M. (1997). Reconstructing the engram: simultaneous, multisite, many single neuron recordings. Neuron 18, 529–537. doi: 10.1016/s0896-6273(00)80295-0
Oşan, R., Chen, G., Feng, R., and Tsien, J. Z. (2011). Differential consolidation and pattern reverberations within episodic cell assemblies in the mouse hippocampus. PLoS One 6:e16507. doi: 10.1371/journal.pone.0016507
Palm, G. (1987). Computing with neural networks. Science 235, 1227b–1228b. doi: 10.1126/science.235.4793.1227b
Pastalkova, E., Itskov, V., Amarasingham, A., and Buzsáki, G. (2008). Internally generated cell assembly sequences in the rat hippocampus. Science 321, 1322–1327. doi: 10.1126/science.1159775
Phillips, M. A., Colonnese, M. T., Goldberg, J., Lewis, L. D., Brown, E. N., and Constantine-Paton, M. (2011). A synaptic strategy for consolidation of convergent visuotopic maps. Neuron 71, 710–724. doi: 10.1016/j.neuron.2011.06.023
Pouget, A., and Snyder, L. H. (2000). Computational approaches to sensorimotor transformations. Nat. Neurosci. 3, 1192–1198. doi: 10.1038/81469
Quartz, S. R., and Sejnowski, T. J. (1997). The neural basis of cognitive development: a constructivist manifesto. Behav. Brain Sci. 20, 537–596; discussion 556–596. doi: 10.1017/s0140525x97001581
Rakic, P. (2008). Confusing cortical columns. Proc. Natl. Acad. Sci. U S A 105, 12099–12100. doi: 10.1073/pnas.0807271105
Rampon, C., Jiang, C. H., Dong, H., Tang, Y. P., Lockhart, D. J., Schultz, P. G., et al. (2000a). Effects of environmental enrichment on gene expression in the brain. Proc. Natl. Acad. Sci. U S A 97, 12880–12884. doi: 10.1073/pnas.97.23.12880
Rampon, C., Tang, Y. P., Goodhouse, J., Shimizu, E., Kyin, M., and Tsien, J. Z. (2000b). Enrichment induces structural changes and recovery from nonspatial memory deficits in CA1 NMDAR1-knockout mice. Nat. Neurosci. 3, 238–244. doi: 10.1038/72945
Reichardt, W., Poggio, T., and Hausen, K. (1983). Figure-ground discrimination by relative movement in the visual system of the fly. Part II. Towards the neural circuitry. Biol. Cybern 46, 1–30. doi: 10.1007/bf00595226
Rolls, E. T. (2013). The mechanisms for pattern completion and pattern separation in the hippocampus. Front. Syst. Neurosci. 7:74. doi: 10.3389/fnsys.2013.00074
Ryan, L., Cox, C., Hayes, S. M., and Nadel, L. (2008). Hippocampal activation during episodic and semantic memory retrieval: comparing category production and category cued recall. Neuropsychologia 46, 2109–2121. doi: 10.1016/j.neuropsychologia.2008.02.030
Shi, Z., Luo, G., Fu, L., Fang, Z., Wang, X., and Li, X. (2013). miR-9 and miR-140–5p target FoxP2 and are regulated as a function of the social context of singing behavior in zebra finches. J. Neurosci. 33, 16510–16521. doi: 10.1523/JNEUROSCI.0838-13.2013
Shimizu, E., Tang, Y. P., Rampon, C., and Tsien, J. Z. (2000). NMDA receptor-dependent synaptic reinforcement as a crucial process for memory consolidation. Science 290, 1170–1174. doi: 10.1126/science.290.5494.1170
Slutsky, I., Abumaria, N., Wu, L. J., Huang, C., Zhang, L., Li, B., et al. (2010). Enhancement of learning and memory by elevating brain magnesium. Neuron 65, 165–177. doi: 10.1016/j.neuron.2009.12.026
Smith, P. L., and Ratcliff, R. (2004). Psychology and neurobiology of simple decisions. Trends Neurosci. 27, 161–168. doi: 10.1016/j.tins.2004.01.006
Squire, L. R., and Zola, S. M. (1998). Episodic memory, semantic memory and amnesia. Hippocampus 8, 205–211. doi: 10.1002/(sici)1098-1063(1998)8:3<205::aid-hipo3>3.3.co;2-8
Stetson, C., and Andersen, R. A. (2015). Early planning activity in frontal and parietal cortex in a simplified task. J. Neurophysiol. 113, 3915–3922. doi: 10.1152/jn.00104.2014
Stevens, C. F. (2012). Brain organization: wiring economy works for the large and small. Curr. Biol. 22, R24–R25. doi: 10.1016/j.cub.2011.11.036
Takehara-Nishiuchi, K., and McNaughton, B. L. (2008). Spontaneous changes of neocortical code for associative memory during consolidation. Science 322, 960–963. doi: 10.1126/science.1161299
Tang, Y. P., Shimizu, E., Dube, G. R., Rampon, C., Kerchner, G. A., Zhuo, M., et al. (1999). Genetic enhancement of learning and memory in mice. Nature 401, 63–69. doi: 10.1038/43432
Tang, Y. P., Wang, H., Feng, R., Kyin, M., and Tsien, J. Z. (2001). Differential effects of enrichment on learning and memory function in NR2B transgenic mice. Neuropharmacology 41, 779–790. doi: 10.1016/s0028-3908(01)00122-8
Tonegawa, S., Liu, X., Ramirez, S., and Redondo, R. (2015). Memory engram cells have come of age. Neuron 87, 918–931. doi: 10.1016/j.neuron.2015.08.002
Tsien, J. Z. (2015). A postulate on the brain’s basic wiring logic. Trends Neurosci. 38, 669–671. doi: 10.1016/j.tins.2015.09.002
Tsien, J. Z. (2016). Principles of intelligence: on evolutionary logic of the brain. Front. Syst. Neurosci. 9:186. doi: 10.3389/fnsys.2015.00186
Tsien, J. Z., Li, M., Osan, R., Chen, G., Lin, L., Wang, P. L., et al. (2013). On initial brain activity mapping of episodic and semantic memory code in the hippocampus. Neurobiol. Learn. Mem. 105, 200–210. doi: 10.1016/j.nlm.2013.06.019
Tubon, T. C. Jr., Zhang, J., Friedman, E. L., Jin, H., Gonzales, E. D., Zhou, H., et al. (2013). dCREB2-mediated enhancement of memory formation. J. Neurosci. 33, 7475–7487. doi: 10.1523/jneurosci.4387-12.2013
Tulving, E. (1972). “Episodic and semantic memory,” in Organization of Memory, eds E. Tulving and W. Donaldson (New York, NY: Academic Press), 381–403.
van Praag, H., Kempermann, G., and Gage, F. H. (2000). Neural consequences of environmental enrichment. Nat. Rev. Neurosci. 1, 191–198. doi: 10.1038/35044558
Wang, D., Cui, Z., Zeng, Q., Kuang, H., Wang, L. P., Tsien, J. Z., et al. (2009). Genetic enhancement of memory and long-term potentiation but not CA1 long-term depression in NR2B transgenic rats. PLoS One 4:e7486. doi: 10.1371/journal.pone.0007486
Wang, H., Hu, Y., and Tsien, J. Z. (2006). Molecular and systems mechanisms of memory consolidation and storage. Prog. Neurobiol. 79, 123–135. doi: 10.1016/j.pneurobio.2006.06.004
Wang, L. P., Li, F., Shen, X., and Tsien, J. Z. (2010). Conditional knockout of NMDA receptors in dopamine neurons prevents nicotine-conditioned place preference. PLoS One 5:e8616. doi: 10.1371/journal.pone.0008616
Wills, T. J., Cacucci, F., Burgess, N., and O’Keefe, J. (2010). Development of the hippocampal cognitive map in preweaning rats. Science 328, 1573–1576. doi: 10.1126/science.1188224
Wittenberg, G. M., Sullivan, M. R., and Tsien, J. Z. (2002). Synaptic reentry reinforcement based network model for long-term memory consolidation. Hippocampus 12, 637–647. doi: 10.1002/hipo.10102
Wittenberg, G. M., and Tsien, J. Z. (2002). An emerging molecular and cellular framework for memory processing by the hippocampus. Trends Neurosci. 25, 501–505. doi: 10.1016/s0166-2236(02)02231-2
Yassa, M. A., and Stark, C. E. (2011). Pattern separation in the hippocampus. Trends Neurosci. 34, 515–525. doi: 10.1016/j.tins.2011.06.006
Yu, C., Gupta, J., Chen, J. F., and Yin, H. H. (2009). Genetic deletion of A2A adenosine receptors in the striatum selectively impairs habit formation. J. Neurosci. 29, 15100–15103. doi: 10.1523/jneurosci.4215-09.2009
Keywords: nature vs. nurture, theory of connectivity, cell assembly, memory engram, generalization, imagination, motor control, decision-making
Citation: Li M, Liu J and Tsien JZ (2016) Theory of Connectivity: Nature and Nurture of Cell Assemblies and Cognitive Computation. Front. Neural Circuits 10:34. doi: 10.3389/fncir.2016.00034
Received: 14 January 2016; Accepted: 11 April 2016;
Published: 29 April 2016.
Edited by:
Kuan H. Wang, National Institute of Mental Health, National Institutes of Health, USAReviewed by:
Vatsala Thirumalai, National Centre for Biological Sciences, IndiaYa-tang Li, California Institute of Technology, USA
Copyright © 2016 Li, Liu and Tsien. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution and reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Joe Z. Tsien, jtsien@augusta.edu
 Meng Li
Meng Li Jun Liu1
Jun Liu1  Joe Z. Tsien
Joe Z. Tsien