An inverse approach for elucidating dendritic function

Dendrites

Neurons possess two types of cellular appendages, axons and dendrites. While axons serve to deliver the output of their computations to other neurons via synapses, dendrites receive the synaptic inputs from other neurons.

The dendrites of neurons are highly diverse, both between and within classes of neurons (Soltesz, 2005; and see Figure 1). Furthermore, the distributions of voltage sensitive conductances (Migliore and Shepherd, 2002) and synapses of different polarity (excitatory/inhibitory) and presynaptic origin are distinct between different types of neurons (Stuart et al., 2008). What is the function of this great cellular diversity?

FIGURE 1

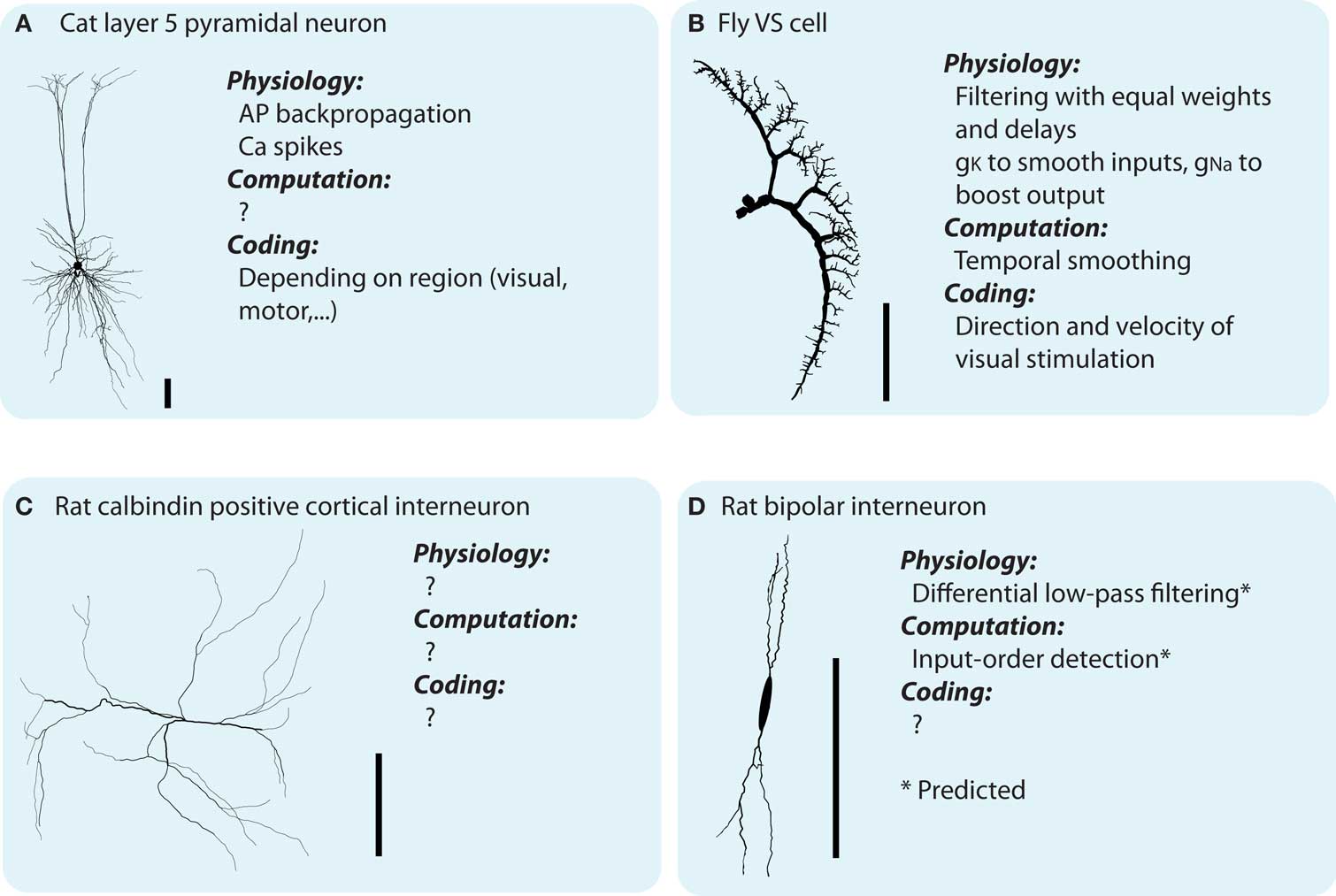
Figure 1. Dendritic morphologies exist in all sizes and shapes which are believed to parallel dendritic function. However, currently there is not much known about the neither synaptic integration in distinct neuronal types, nor the different types of integration taking place inside the dendrites (see main text). (A–D) Illustrates four different neuronal types, and, what is know about their physiology (with respect to synaptic integration), computation and coding function [soma shape of the bipolar interneuron modified for display purposes. Scale bar indicates 100 μm. The morphologies illustrated are all downloaded from NeuroMorpho.org (Ascoli et al., 2007) and originally coming from Borst and Haag, 1996; Contreras et al., 1997; Gulyás et al., 1999; Wang et al., 2002, for A–D, respectively).

Dendrites have been shown to support a diversity of physiological and computational processes, such as linear (Cash and Yuste, 1999) and location independent (Magee, 1999) synaptic integration, several types of dendritic spikes (Schiller et al., 2000; Harris et al., 2001) and back-propagation of axonal spikes (Markram et al., 1995), as well as plasticity of local conductance distributions (Hoffman et al., 1997). A multitude of theoretical studies have already dealt with the influence of the morphologies of dendrites on dendritic function (De Schutter and Bower, 1994; Mainen and Sejnowski, 1996; van Ooyen et al., 2002) and functions theoretically performed on dendrites (Koch and Segev, 2000; Segev and London, 2000). What can we add to this impressive body of work?

As long as physics is incomplete, and we are trying to understand the other laws, then the different possible formulations [of physical laws] may give clues about what might happen in other circumstances. In that case they are no longer equivalent, psychologically, in suggesting to us guesses about what the laws might look like in a wider situation. Richard Feynman in “The Character of Physical Law”.

What Feynman noted for physics is even more true for biology with its confusing zoo of phenomena, namely that a different perspective of a phenomenon can lead to novel insights. We have recently attempted to find a novel perspective on dendritic function–structure relationships (Stiefel and Sejnowski, 2007; Torben-Nielsen and Stiefel, 2009). Specifically, we are using an inverse approach where we pick a computational function and then use computer simulations to generate dendrites optimized for the chosen function. We thus go in the opposite direction of conventional studies, where the neural theorist starts with a known dendritic morphology and aims to find out the computational function: we start with the computational function and aim to find the corresponding morphology. This inverse approach can be used in two ways (Figure 2).

FIGURE 2

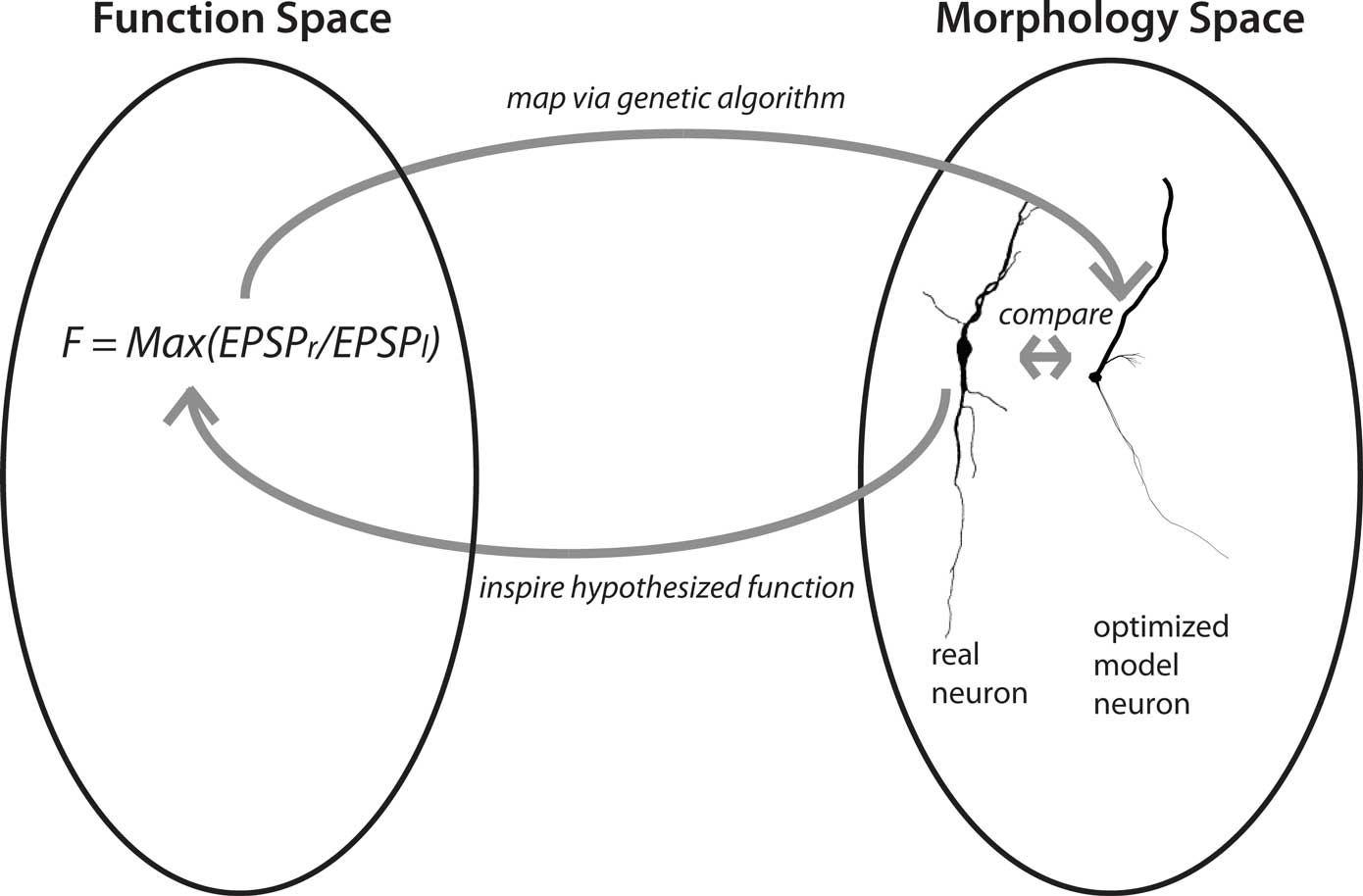
Figure 2. Concept of the inverse approach to elucidate dendritic function. Finding optimized model neurons for a given computational function corresponds to a mapping from function space to structure space. This mapping, from function to morphology, can be one-to-many; the mapping from morphology to function can be many-to-one. The “hypothesis generator” version of the approach starts with a function of general interest, such as input-order detection and proceeds to find a neuronal morphology optimized for that function. This morphology is then compared to the morphologies of real neurons, with similarities hinting at their functions. In the “function confirmation” variant of the approach, the cycle starts with a real neuron and a hypothesis about its computational function. The evolutionary algorithm then finds an optimized model neuron for this function, which in turn can be compared to the real neuron. Yet unmeasured features of the real neuron, such as conductance distributions, can be predicted from the optimized model neuron (neuron reconstruction from Furtak et al., 2007).

First, we can choose a computational function of neurobiological relevance, and find the optimized dendrites for performing that function. Then, by comparing the resultant artificial dendrites to the known dendritic morphologies of real neurons, we can gain novel hypotheses about the functions of their dendrites: If dendrites of a neural type resemble the artificial, optimized, dendrites, then they will likely fulfill a similar function. We call this approach the “hypothesis generator”.

Second, we can start our reasoning with a real neuron and its hypothesized computational function. We then optimize dendrites for that hypothesized function, and compare the outcome to the original neuron. If the dendrites are similar, this results provides additional support for the hypothesis that the neuron in fact performs that function. In addition, if the artificial dendrites have features which have not been determined yet in the biological system, such as distributions of conductances, these constitute predictions about these features in real neurons. We call this second approach the “function confirmation”.

Dendritic “Function”

At this point a short excursion on the use of the word “function” is warranted. How can we attribute a function, a concept originally applied to man-made tools, to a phenomenon in the natural world? We consult the theory of evolution. If we assume that an animal which does not perform activities necessary to gather nutrients and reproduce will fall to natural selection, then these are its functions on the organismic level. Any animal devoid of these functions will not leave offspring, and consequentially such animals will be eliminated from the population. The sub-components of the animal, such as individual neurons, will then have functions to subserve these organismic functions. This line of teleonomic reasoning (Mayr, 2004) justifies the concept of functionality in animate nature: an arm, wing, eye, or neuron came into existence because they fulfill a function for the survival and reproduction of an animal. For inanimate physical entities, such as a crystal, volcano, or sun-spot, this is not the case.

Now, it is furthermore useful to distinguish between three distinct uses of the word “function” in our context: a physiological, a computational and a sensory/motor coding use. Below we explain the three different aspects of “function” and demonstrate the meaning through the fly VS cell; a cell of which morphology, physiology, and input/outputs are well described (Borst and Haag, 1996; Strausfeld et al., 2006).

In the VS cells of the fly visual system, the physiological function of the dendrites is to low-pass filter the incoming synaptic potentials on their path from the synapses to the axon. Additionally, the synaptic potentials are conducted to the axon with roughly equal delays. Thus, the physiological functions are direct consequences of a neuron’s biophysics, its passive and active membrane properties. They are typically investigated with single neuron recordings (often, but not always in vitro) and single neuron model simulation (single- or multi-compartmental).

The computational function of the fly VS cell dendrites is to sum all synaptic potentials such that the voltage at the axon is proportional to the incoming mean signal. Furthermore, the dendrites reduce the voltage standard deviation and the power of the strongest frequency band in the input signal. Thus, the computational function is the signal processing performed by the dendrites. It describes the mathematical transformation the dendrites apply to their inputs. The computational function emerges from the sum of the physiological functions of a neuron plus the temporal and spatial structure of its inputs. The same dendrites, performing the same physiological functions, could carry out a different computational function if receiving different input patterns. Which of the many possible computational functions a neuron could carry out does it actually perform in ecologically relevant situations? We will come back to that question later.

The coding function of the fly VS cell dendrites is to calculate the direction and speed of the moving visual field based on the signals the neuron receives. Again, this function emerges from the previous function, the computational function plus the sensory meaning of the received signal, which represents small-field visual motion. Note that the same VS cell dendrites could calculate a completely different coding function, if their inputs would originate, for example, in the auditory system. Even with the same input structure, they would code for something completely different, like the average loudness of the auditory environment. Coding functions are investigated with in vivo recordings in animals engaged in sensory or motor tasks. Interestingly, in some cases (such as monkey visual cortical neurons) the coding function is known, while the physiological and computational function it emerges from are unknown. Only in a few cases of neurons (mostly in invertebrates; Michelsen et al., 1994; Strausfeld et al., 2006), where the cellular physiology is understood while the neurons are functioning in their sensory/motor role in vivo, are all three classes of function and their connections understood.

In summary, the physiological, computational, and coding functions are interrelated and emerge from the previous levels, together with the temporal and spatial structure of the inputs (physiological → computational) and the inputs’ sensory/motor coding meaning (computational → coding). There is an abundance of knowledge about the physiological functions of dendrites, which is often ill matched with an understanding of their computational and coding functions (Figure 1). With the inverse approach, we investigate the computational functions of dendrites, and how they emerge from their physiological functions.

The Inverse Approach

The inverse approach relies on three components: morphology generation, model construction, and the model optimization. Below we outline these components.

Morphology Generation

Dendritic morphologies are generated by a recursive algorithm (based on Burke’s algorithm; Burke et al., 1992). Starting from the soma, this algorithm adds dendritic segments piecewise to the neuron (Figure 3). After adding each new segment, the algorithm decides whether to terminate the dendritic tree, elongate it, or to introduce a bifurcation. It also decides on the new direction of the dendrite, on the thinning of the dendritic stems, and on the amount of active conductances inserted in that part of the dendrite. The algorithm makes this decision based on a set of probability functions. For instance, the termination probability is a cumulative gamma function dependent on the path length from the soma. These functions are created from parameter sets; each dendritic tree has its own parameter set. Thus, the distinct dendritic trees of an artificial neuron can look very different. The parameter sets are the subject of optimization (see below). For a detailed explanation of all parameters and how they guide the algorithm, see Torben-Nielsen and Stiefel (2009). This type of morphology-generation algorithm is very powerful and in earlier work we have used it to generate neurons that are statistically similar to real neurons (Torben-Nielsen et al., 2008). However, the drawback of describing dendrites with (unimodal) distributions is that the resultant neuron has similar features all over the dendrite. For instance, the branching angle is sampled from a single distribution and will be similar in the dendrite regardless the location in the dendrite. Hence, not every type of neuron can be reconstructed using this algorithm and the results of the inverse approach have to be interpreted while keeping in mind this constraint.

FIGURE 3

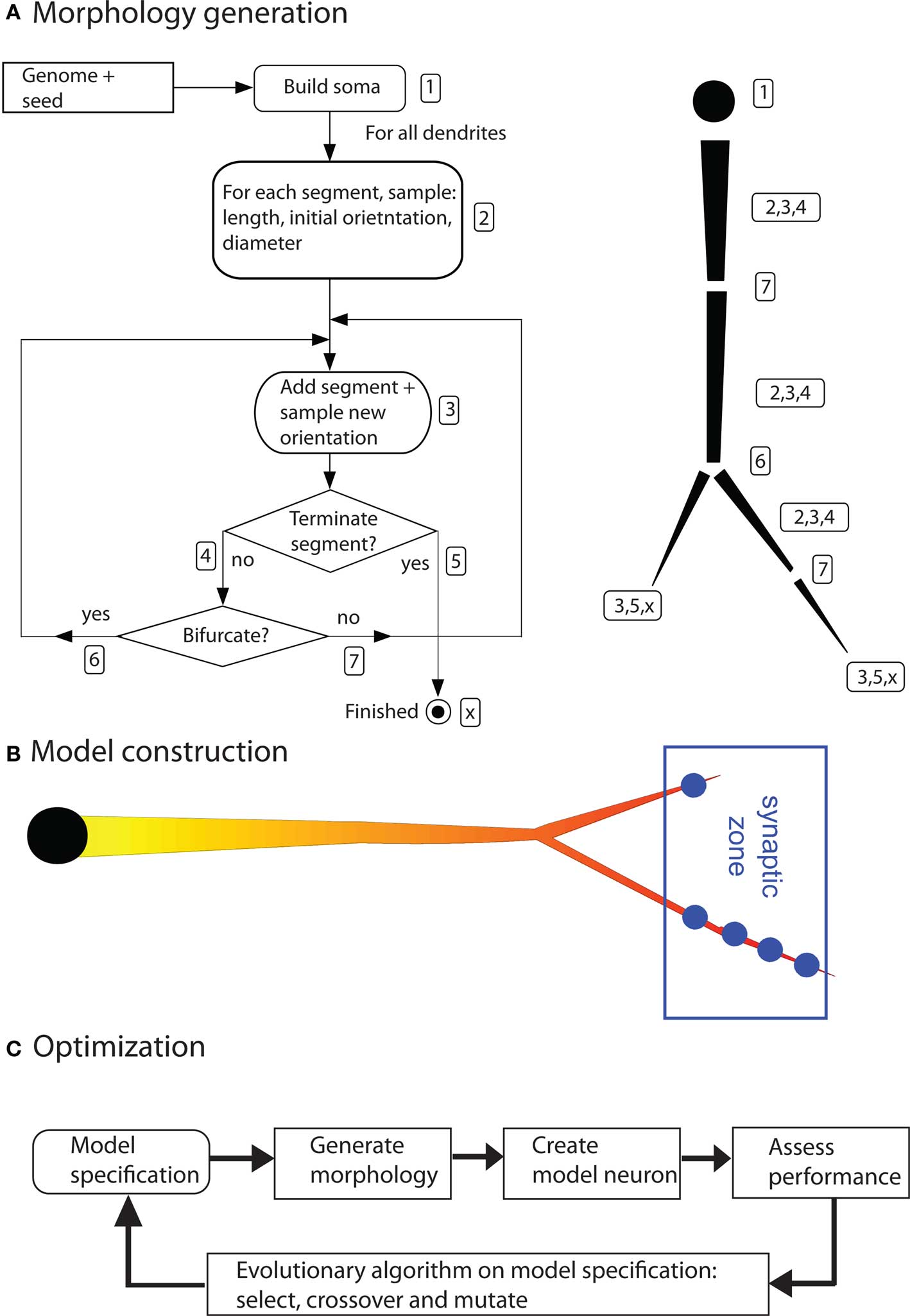
Figure 3. Components of the inverse approach. (A) Algorithm to generate dendritic morphologies. The exact geometry (segment length and orientation) are sampled from the model specification. Right side of (A) illustrates how a dendritic branch is generated according to the algorithm. The numbers in the left panel correspond to the numbered actions in the algorithm. (B) A neuron model is constructed by inserting (uniform) passive electrical properties, a distribution of voltage-gated ion channels (the shown gradient), and synapses at a predetermined location. (C) Optimization by means of an evolutionary algorithm (figures are modified from Torben-Nielsen and Stiefel, 2009).

Model Construction

So far the morphogenetic algorithm has generated a raw morphology. To simulate electrophysiological dynamics, a neuron model needs to be constructed from this morphology by inserting electrical properties and synapses. The electrical properties consist of passive electrical properties (membrane resistance, axial resistance and membrane capacitance) and active electric properties (voltage-gated conductances). The passive properties are constant and inserted uniformly across the whole morphology. The densities of the active conductances are specified by the morphogenetic algorithm (see above) and subject to optimization. Their kinetics were taken from models of hippocampal pyramidal neurons (Migliore and Shepherd, 2002) or fly VS cells (Haag et al., 1997), depending on the research question asked. Of course, the inverse approach can use a multitude of other channel kinetics.

The synapses are inserted in predetermined spatial areas relative to the soma, the “target zones”. The idea behind the target zones is to reflect afferent projection zones in the brain. Synapses are then inserted when a dendrite passes trough a target zone. One synapse is inserted (generally) for each 5 μm of dendrite inside a target zone. In this way, the absolute position of the dendrites becomes important; a rotation or translation of the whole neuron will move dendrites out of, or, into the target zones. The resultant model is then simulated in NEURON (Carnevale and Hines, 2006).

Model Optimization by an Evolutionary Algorithm

To optimize the constructed neuron models we use an evolutionary algorithm. The idea of evolutionary algorithms is inspired by biological evolution and the survival of the fittest. Initially, a population of individuals, in our case parameter sets specifying dendrites, is pseudo-randomly initiated. Subsequently, as described above, morphologies are generated from these parameter sets, and model neurons from the morphologies. The electrophysiological dynamics of the model neuron are then simulated, and, based on the outcome, the fitness of the models is judged according to the fitness function. The performance of each individual model neuron, and corresponding parameter set, is assessed in this way. Afterward, based on this performance assessment, a new population is made by selecting the best individuals and modifying them in a random fashion (by crossover and mutation, or random value changes in the parameter sets). Hence, the next-generation population consists of descendants of the best individuals of the previous generation. By iterating this process over many generations, the performance of the model neurons will improve, and, eventually converge to an optimal solution.

Crucial in evolutionary algorithms is the fitness function that assesses the performance of the individuals. In our inverse approach, the fitness function assesses the ability of the neuron model to perform the predetermined computational function. The fitness function is expressed in terms of features of the output signal, for instance as the amplitude of the membrane potential at the soma. Any such function is allowed as long as it can express the performance of a model in a single value. In the addition to the fitness function, we also use heuristics to guide the optimization process in finding desired solutions. In an analogy with skiing, the heuristics can be seen as the gates the skiers have to pass in a slalom competition and the fitness function is the finishing time. These heuristics reflect biological constraints and do not impose conceptual bias on the outcome. For instance, heuristics are used to ensure the neuron model receives synaptic inputs, or, that trivial solutions based on biologically unrealistic model responses are ruled out.

The advantage of evolutionary algorithms is that they can explore large solution spaces with relative ease. Crossover and mutation provide an efficient search strategy in a solution space where gradients are hard to determine (Schwefel, 1995; Back, 1996). A drawback which evolutionary algorithms share with all other numerical optimization procedures is that it is impossible to guarantee true optimality of a solution: the algorithm can be stuck in a local optimum, or, come close to a global optimum without actually reaching it. Performing different optimization runs with different initial conditions (i.e., random seeds) makes it less likely that non-global optima are found. We further elaborate on the issue of optimality later.

Another important issue is the search space the genetic algorithm acts in. The set of neural morphologies the genetic algorithm can sample from is smaller than the set of all possible neural morphologies. This is due to the fact that the morphogenetic algorithm we use, like any algorithm, will introduce a bias and will exclude the generation of certain morphologies. In the case of our algorithm, this, among other things, excludes dendrites with two separate domains, like the oblique and apical tuft dendrites of layer V pyramidal neurons in the cortex. This issue is an area of ongoing development of our method. While the inherent limitations of our (and any other) algorithm have to be kept in mind, the set of morphologies our algorithm can generate is nevertheless large; the computations we optimized dendrites for were highly satisfactorily solved by morphologically complex dendrites.

Now that we have described how we find model neurons optimized for chosen computational functions, we describe two applications of this method. In the first one, the computational function we chose was input-order detection, in the second one wide-field motion integration.

Application: Input-Order Detection

The first function we applied the inverse approach to is input-order detection (Torben-Nielsen and Stiefel, 2009). In this function, a neuron should respond as strongly as possible when two groups of synapses (red and blue in Figure 4) are activated in one temporal order (blue → red), but as weakly as possible when they are activated in the inverse temporal order (red → blue). The time between the activation of the red and blue synapses (Δt) was varied between 5 and 30 ms. Response was defined as maximal depolarization measured at the soma. We had no particular type of neuron in mind when we started optimizing dendrites for this function, thus this study was the “hypothesis generator” version of the inverse approach to dendritic function.

FIGURE 4

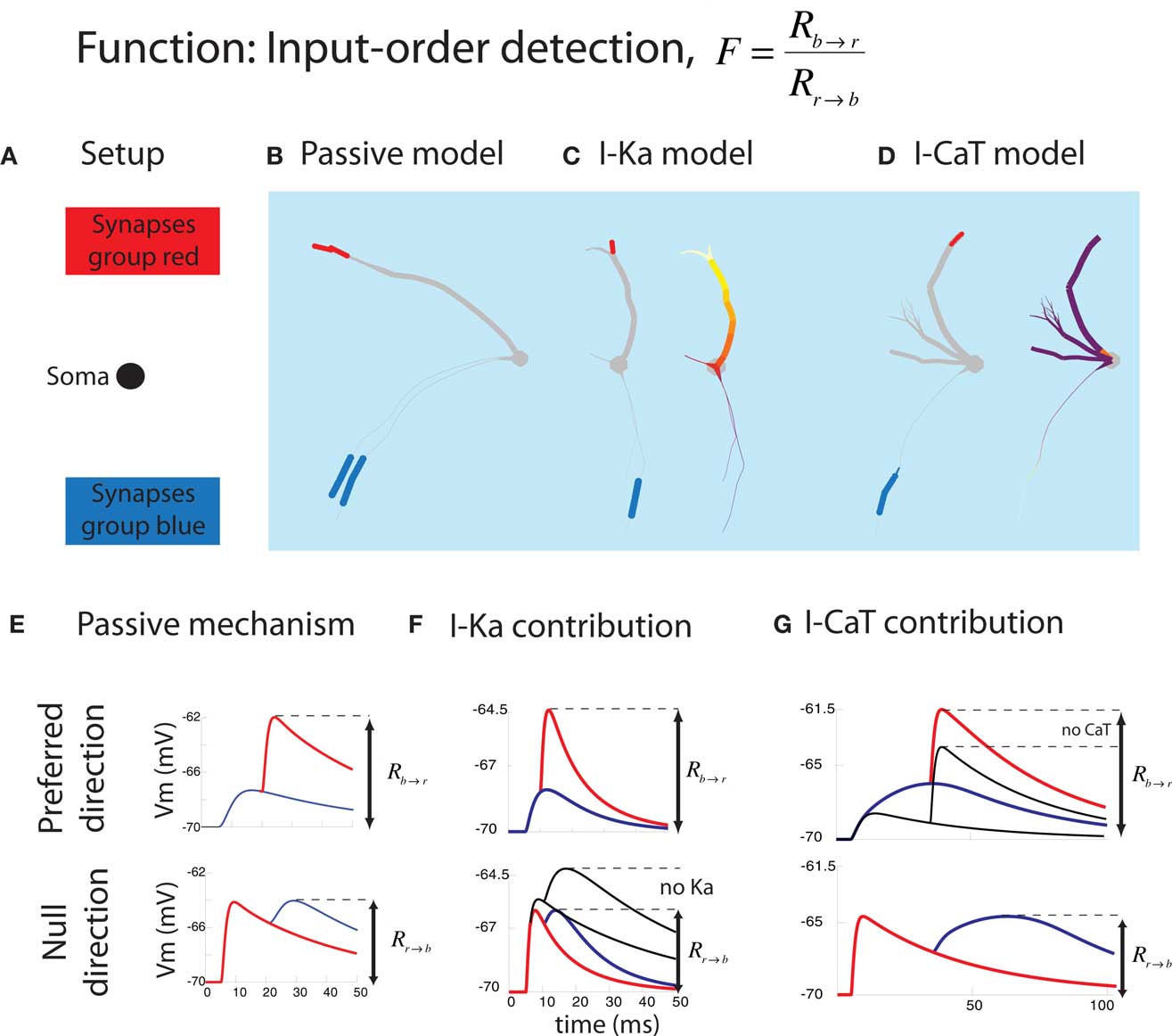
Figure 4. Summary of the result in the input-order detection function. (A) Experimental setup. The location of the soma and synapses are fixed. (B) Typical passive model optimized for Δt = 20 ms and having one thick branch and one (or here two) thin branch. The blue and red bars correspond to the colors from (A). (C) Typical model containing I_KA optimized for short Δt = 10 ms (illustrating both the synapses and the I_KA distribution). The density of the voltage-gated channel is heat-color coded; white represents the maximum allowed density while purple means 0. I_KA channels were always densely located in the thick branch while no I_KA channels were inserted in the thin branch. (D) Typical model containing I_CaT optimized for long Δt = 25 ms. An I_CaT hotspot was always found close to the blue synapses. (E) Two electrophysiological mechanisms underlying successful input-order detection. In the preferred direction, the second EPSP (red) should arrive at the soma at the peak of the first (blue) EPSP. In null-direction, the second EPSP (blue) should arrive at the soma when the first EPSP (red) is decayed as much as possible. (F) Contribution of I_KA to short Δt. It promotes faster decay of the first (red) EPSP in the null-direction. (G) Contribution of I_CaT to long Δt. I_CaT boosts the first (blue) EPSP in the preferred direction (figures are modified from Torben-Nielsen and Stiefel, 2009).

We found optimized neurons with one or more thin dendrites bearing the synapses activated first (blue) and a thick dendrite bearing the synapses activated second (red). This neural morphology lead to maximal summation of EPSPs in the preferred order via the following physiological functions: The EPSP originating at the synapses activated first were significantly low-pass filtered on their way to the soma by the thin dendrite. The waveform of this first EPSP thus decayed slowly, and the second EPSP waveform started at a voltage close to the peak of the first EPSP, and both EPSPs summed maximally (Figure 4E, top panel). If the EPSPs were evoked in the inverse order, the EPSP originating on the thick dendrite was evoked first. This EPSP was hardly low-pass filtered and decayed fast. Thus, the waveform of the EPSP originating on the thin dendrite started significantly further away from the peak of the first EPSP, and both EPSPs summed poorly (Figure 4E, bottom panel).

The active currents included in the simulations acted synergistically with the passive membrane properties in modifying the EPSP waveforms for the purpose of input-order detection. The thin dendrites contained I_CaT, an inactivating calcium conductance, which further broadened the already broad (low-pass filtered) EPSP waveform. The thick dendrites contained I_KA, an inactivating potassium conductance, which further sharpened the (weakly low-pass filtered) EPSP waveform. Two things were especially interesting about these conductance distributions: Firstly, while I_CaT was only located at the position of the synapses, I_KA was distributed along the dendrite in a gradient increasing from the soma outwards. These optimized distributions mirror the distributions found in nature, with hyperpolarizing conductances distributed along increasing gradients and depolarizing currents in “hot spots” (Migliore and Shepherd, 2002). Second, the role of the active currents showed a discontinuity between the neurons optimized for spike order detection for fast (Δt = 5–15 ms) and slow (Δt = 20–30 ms) time intervals between EPSPs. While in the neurons optimized for fast intervals I_KA was prominent, in the neurons optimized for slow intervals, a high density of I_CaT was found. Thus for performing the same computational function, with a quantitatively different parameter, different neurons were optimal.

In summary, by combining differential active and passive filtering with the geometry of summing waveforms, the artificial neurons our algorithm found were competent input-order detectors. We would like to note that even though a knowledgeable neuroscientist could have found this solution, they were completely emergent from our algorithm. No specification of any of the morphological features and current distributions described above was included in the fitness function. We only asked the optimization algorithm to produce model neurons optimized for input-order detection.

Finally, did the optimized artificial model neurons resemble real neurons? Yes, they resembled cortical bipolar interneurons in several important respects. Both the optimized input-order detectors as well as the bipolar interneurons have a thick and a thin primary dendrite and a similar number of end points (Furtak et al., 2007). As a result of our optimization studies we thus predict that cortical bipolar interneurons are input-order detectors and contain depolarizing conductances on their thin, and hyperpolarizing conductances on their thick dendrites – a testable consequence of the inverse approach not yet suggested as the function of the neurons in question.

Application: Wide-Field Motion Detection

Another function we applied the inverse approach to is wide-field motion integration (Torben-Nielsen and Stiefel, 2010). In this study, our starting point was the VS cell of the fly visual system. This was thus a use of the “function confirmation” variant of the inverse approach to investigate dendritic function. The VS cells are large neurons in the lobular plate, a central (downstream) structure in the fly visual system responsible for encoding visual motion. There are roughly 10 VS cells in each hemisphere of the fly brain, and they are specialized for detecting vertical motion (Haag et al., 1999; Egelhaaf, 2006). Each VS cell receives inputs from a series of small-field motion detectors (“Reichardt” detectors, covering ±4° of the visual field; Haag et al., 1999). It is generally believed that the VS cells act on these inputs to compute the global direction the visual field is moving relative to the fly, an operation termed “wide-field motion integration” (Franz and Krapp, 2000; Strausfeld et al., 2006).

We thus used our inverse approach to test the hypothesis that fly VS cells are wide-field motion integrators. In order to achieve this goal, we constructed a fitness function that capture the input–output transformation of VS cells in a phenomenological way. An existing model of fly wide-field motion detection (Haag et al., 1999) was used to provide the artificial dendrites with biologically plausible inputs. Then, we optimized the embedded model neurons to perform wide-field motion integration as formalized in our fitness function (Torben-Nielsen and Stiefel, 2010). Finally, we analyzed the resultant, optimized dendrites and found a morphological blueprint that shares crucial morphological features with real VS cells. Moreover, no optimized model neurons were found that did not comply with the found blueprint (Figure 5). In addition, the optimized model neuron’s responses to visual motion and intracellular current injection were very similar to data from real VS cells. We also observed the distributions of voltage-dependent conductances in the optimized model neurons: While voltage-dependent K⁺ conductances were located close to the synapses, the Na⁺ currents were located close to the axon. These conductance distributions have not yet been determined in real VS cells, and we predict that they will be similar to what we found in the optimized wide-field motion detectors.

FIGURE 5

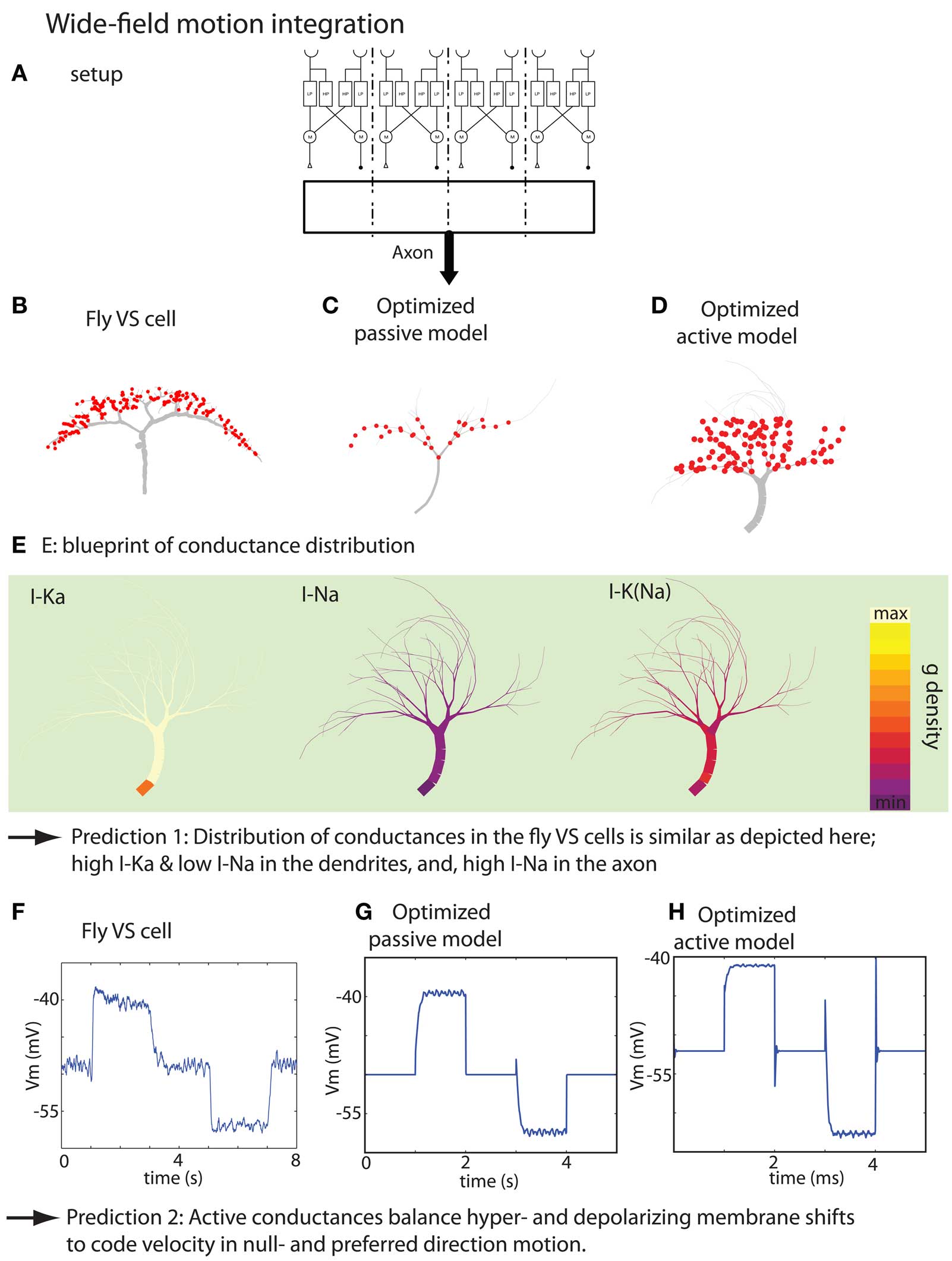
Figure 5. Summary of the result of the wide-field motion integration task. (A) Experimental setup depicting the stimulus, small-field motion detection by Reichardt detectors and the corresponding synaptic target zones where the optimized model receives the inputs. The real setup has 20 target zones instead of the 4 zones depicted here. (B) Morphology of a VS cell. (C,D) Morphology of optimized passive model neuron and active model neuron, respectively. (E) Blueprint for the distribution of the voltage-gated K, Na, and K (Na) channels. (F) Membrane potential measured at the initial axon segment of a VS cell (time-averaged over 10 runs). The stimulation protocol consist of the sequence: no motion, preferred-direction motion, no motion, null-direction motion and no motion. (G,H) Responses of the optimized passive and active model when stimulated with a similar protocol as in (F) (with thanks to H. Cuntz for providing the data displayed in F. Figures are modified from Torben-Nielsen and Stiefel, 2010).

Because passive neuron models could also perform the task fairly well, we set to investigate the role of the active conductances in wide-field motion integration. First, we established that the blueprint distribution of active conductances found by the inverse approach was significant by testing the optimized models without the active conductances, and, by inserting “random but plausible” distributions of the same active conductances. Both controls indicated that the particular distribution has a role in the performance of wide-field motion detection. Subsequently, we hypothesized that active conductances are required to balance for an inequality of the input strength. We tested this newly proposed hypothesis by optimizing dendrites for motion detection in which a much stronger response should be given to null-direction motion. We found that while model neurons with active conductances could perform this task, the purely passively optimized model could not. Therefore, we not only predict the distribution of the active conductances in VS cells, but also predict their role, namely balancing the output signal upon preferred- and null-direction motion.

Optimality

A recurring theme in the inverse approach described here is optimality. Do we obtain truly optimal or at least sufficiently close-to-optimal solutions? What assumptions regarding optimality are we making, and are they justified? Finally, what can optimality teach us?

With a numerical optimization algorithm it is in principle impossible to know if the determined solutions are in fact truly optimal. As mentioned earlier, the algorithm could be stuck in a local optimum, or be close, but not at the global optimum. In the absence of knowledge of the global optimum, it is not possible to rule out these cases. But how can we be at least reasonably sure that this is not the case? Evolutionary algorithms, by means of their jumps in parameter space, are some of the best optimization algorithms to tackle this problem. When optimizing neurons for input-order detection, we also determined the exact fitness landscapes (the performance of a model plotted against its parameters) for a simplified neuron model. This model only had two unbranched dendrites, which made it sufficiently simple so that its fitness can be expressed in a closed form (Torben-Nielsen and Stiefel, 2009). While the fitness landscape for this simplified model is not completely identical to the fitness landscape for the full model, we can expect a significant overlap. We thus plotted the optimized full models (found by the evolutionary algorithm) on the fitness landscapes, and found that they are in the vicinity of the global optima (Figure S1 in Supplementary Material). These numerical results, superimposed on the fitness landscapes, are indeed close to the global optima.

Another result which indicates that the optima found by our numerical optimization algorithm are close to the global optimum is that successive optimization runs lead to similar results. While the values of morphological parameters of the optimized dendrites, such as the path length, the number of branch points, or the area covered by dendrites varied, the basic blueprint of the dendrites remained the same. For the functions tested so far, the degree of freedom is large enough so that when certain morphological constraints are met (dendrites of different diameter in the input-order detection task), other morphological features can vary.

Given the large variability of real neurons to which we aim to compare the artificial optimized neurons, we argue that solutions close to the global optimum serve the purpose of comparison sufficiently well.

Having established that the optimized model neurons we obtain for different computational functions are most likely close to the optima for these functions, we next ask what conceptual assumptions go into these optimization procedures.

The main assumption we are making is that neuronal morphologies are determined to a large degree by their computational functions. Other possible determinants of neural morphologies are wiring efficiency and evolutionary history. We will now explain how these additional determinants are or can be accommodated by our inverse approach.

Brains have evolved to carry out their function while using the least amount of biological resources (cellular material used to assemble axons and dendrites) possible. Thus, wiring efficiency is a major constraint in brain architecture (Chen et al., 2006; Cuntz et al., 2007) and will partially determine dendritic architecture. For the whole brain, wiring schemes which minimize the total wiring length will be preferable. For individual neurons this means that the locations of their synapses will be at positions which are not only determined by necessities related to synaptic integration, but by axonal wiring efficiency. Furthermore, neurons with the smallest possible dendritic tree will be preferred. In our optimizations, we insert synapses on dendrites in spatial zones at predetermined positions relative to the soma (see above). These zones can be seen as axonal projection zones, which, when wisely chosen, will reproduce the axonal wiring efficiency constraints of the brains. We also include a heuristic selecting for small dendritic trees into our fitness functions (see above), which accommodates the dendritic wiring efficiency constraints. Hence, we believe that wiring efficiency constraints can be, and, are taken into account in our inverse approach to dendritic function. We argue that it is the interplay between wiring efficiency and necessities stemming from synaptic integration which shape dendritic function, and that both are accounted for in our optimizations.

In nature, neurons are not generated de novo at the beginning of the optimization like in our simulations, but are the products of long evolutionary histories. Thus, their structures will be the products of both current and past functional constraints. Just as a dolphin’s fin still reflects its past as a land mammal’s leg (Thewissen et al., 2009), a neuron’s dendrites will bear witness to computational functions it carried out in an ancestral brain. This aspect of neural function could be included in the inverse approach to dendritic function by starting not from a random population of dendritic morphologies, like now, but from a population believed to represent the neuron’s ancestral population.

Evolution can be seen as an optimization process constantly chasing a changing optimal setpoint. While the evolutionary algorithm used for optimization in our approach is infinitely less complex than the real evolutionary process, and not meant as a model of it, both processes give rise to optimized structures. In biological evolution, a structure will be optimized for the function it actually carries out; an argument that a certain neuron is performing a certain computational function is thus much stronger if it shows that the neuron is optimized for that function, not that it merely can compute it. Along this line of reasoning the inverse approach to dendritic function described here can contribute significantly to the understanding of neural function–structure relationships.

Future Directions

There are a multitude of possible uses for the inverse approach to studying dendritic function described here.

One interesting question is how different levels of input stochasticity will influence the dendritic morphologies and conductance distributions of neurons. How will the dendrites optimized for a certain computation change if they have to cope with an increasing amount of input variability? A second question is how the dendrites of neurons look which are optimized to perform more than one computational function. What compromises must be made, and which functions are more compatible with each other? Another interesting question is whether there exist “Gödel functions” for single neurons? We are referring to the insight by the mathematician Kurt Gödel (1906–1978), who found that for every axiomatic system in the realm of natural numbers there is a statement which is true, but can not be proven (computed). We do not pose this question in a strict mathematical sense, but we ask if there are functions which can not, or only very poorly, be computed by single neurons? Are there computational functions which necessitate a network of neurons?

We want to encourage the reader to think of interesting functions to optimize dendrites for. The code (in Python) for the inverse approach described here is freely available from us upon request.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank all our colleagues who contributed to the development of the research program described here with collaborations and inspiring discussions, especially Drs. Gordon Arboutnott, the late Theodore H. Bullock, Eugenia Chen, Cristina Domnisoru, Boris Gutkin, Terry Sejnowski, Eric O. Postma, Robert Sinclair, and Marylka Uusisaari.

References

Ascoli, G. A., Donohue, D. E., and Halavi, M. (2007). Neuromorpho.org: a central resource for neuronal morphologies. J. Neurosci. 27, 9247–9251.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Back, T. (1996). Evolutionary Algorithms in Theory and Practice: Evolution Strategies, Evolutionary Programming, Genetic Algorithms. New York, NY: Oxford University Press.

Borst, A., and Haag, J. (1996). The intrinsic electrophysiological characteristics of fly lobula plate tangential cells: I. Passive membrane properties. J. Comput. Neurosci. 3, 313–336.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Burke, R. E., Marks, W. B., and Ulfhake, B. (1992). A parsimonious description of motoneuron dendritic morphology using computer simulation. J. Neurosci. 12, 2403–2416.

Pubmed Abstract | Pubmed Full Text

Carnevale, N., and Hines, M. (2006). The Neuron Book. Cambridge, UK: Cambridge University Press.

Cash, S., and Yuste, R. (1999). Linear summation of excitatory inputs by ca1 pyramidal neurons. Neuron 22, 383–394.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chen, B. L., Hall, D. H., and Chklovskii, D. B. (2006). Wiring optimization can relate neuronal structure and function. Proc. Natl. Acad. Sci. U.S.A. 103, 4723–4728.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Contreras, D., Destexhe, A., and Steriade, M. (1997). Intracellular and computational characterization of the intracortical inhibitory control of synchronized thalamic inputs in vivo. J. Neurophysiol. 78, 335–350.

Pubmed Abstract | Pubmed Full Text

Cuntz, H., Borst, A., and Segev, I. (2007). Optimization principles of dendritic structure. Theor. Biol. Med. Model. 4, 21.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

De Schutter, E., and Bower, J. M. (1994). Simulated responses of cerebellar Purkinje cells are independent of the dendritic location of granule cell synaptic inputs. Proc. Natl. Acad. Sci. U.S.A. 91, 4736–4740.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Egelhaaf, M. (2006). “The neural computation of visual motion information,” in Invertebrate Vision, eds E. Warrant and D.-E. Nilsson (Cambridge, UK: Cambridge University Press), 399–461.

Franz, M. O., and Krapp, H. G. (2000). Wide-field, motion-sensitive neurons and matched filters for optic flow fields. Biol. Cybern. 83, 185–197.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Furtak, S. C., Moyer, J. R. Jr., and Brown, T. H. (2007). Morphology and ontogeny of rat perirhinal cortical neurons. J. Comp. Neurol. 505, 493–510.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gulyás, A. I., Megìas, M., Emri, Z., and Freund, T. F. (1999). Total number and ratio of excitatory and inhibitory synapses converging onto single interneurons of different types in the ca1 area of the rat hippocampus. J. Neurosci. 19, 10082–10097.

Pubmed Abstract | Pubmed Full Text

Haag, J., Theunissen, F., and Borst, A. (1997). The intrinsic electrophysiological characteristics of fly lobula plate tangential cells: II. Active membrane properties. J. Comput. Neurosci. 4, 349–369.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Haag, J., Vermeulen, A., and Borst, A. (1999). The intrinsic electrophysiological characteristics of fly lobula plate tangential cells: III. Visual response properties. J. Comput. Neurosci. 7, 213–234.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Harris, K. D., Hirase, H., Leinekugel, X., Henze, D. A., and Buzsáki, G. (2001). Temporal interaction between single spikes and complex spike bursts in hippocampal pyramidal cells. Neuron 32, 141–149.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hoffman, D. A., Magee, J. C., Colbert, C. M., and Johnston, D. (1997). K+ channel regulation of signal propagation in dendrites of hippocampal pyramidal neurons. Nature 387, 869.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Koch, C., and Segev, I. (2000). The role of single neurons in information processing. Nat. Neurosci. 3, 1171–1177.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Magee, J. C. (1999). Dendritic i_h normalizes temporal summation in hippocampal CA1 neurons. Nat. Neurosci. 2, 508–514.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mainen, Z. F., and Sejnowski, T. J. (1996). Influence of dendritic structure on firing pattern in model neocortical neurons. Nature 382, 363–366.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Markram, H., Helm, P. J., and Sakmann, B. (1995). Dendritic calcium transients evoked by single back-propagating action potentials in rat neocortical pyramidal neurons. J. Physiol. 485(Pt 1), 1–20.

Pubmed Abstract | Pubmed Full Text

Mayr, E. (2004). What Makes Biology Unique?: Considerations on the Autonomy of a Scientific Discipline. Cambridge: Cambridge University Press.

Michelsen, A., Popov, A. V., and Lewis, B. (1994). Physics of directional hearing in the cricket Gryllus bimaculatus. J. Comp. Physiol. A 175, 153–164.

CrossRef Full Text

Migliore, M., and Shepherd, G. M. (2002). Emerging rules for the distributions of active dendritic conductances. Nat. Rev. Neurosci. 3, 362–370.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schiller, J., Major, G., Koester, H. J., and Schiller, Y. (2000). NMDA spikes in basal dendrites of cortical pyramidal neurons. Nature 404, 285–289.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schwefel, H.-P. (1995). Evolution and Optimum Seeking. New York, NY: Wiley-Interscience.

Segev, I., and London, M. (2000). Untangling dendrites with quantitative models. Science 290, 744–749.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Soltesz, I. (2005). Diversity in the Neuronal Machine: Order and Variability in Interneuronal Microcircuits. New York, NY: Oxford University Press.

Stiefel, K. M., and Sejnowski, T. J. (2007). Mapping dendritic function onto neuronal morphology. J. Neurophysiol. 98, 513–526.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Strausfeld, N., Douglass, J., Cambell, H., and Higgins, C. (2006). “Parallel processing in the optic lobes of flies and the occurrence of motion computing circuits,” in Invertebrate Vision, eds E. Warrant and D.-E. Nilsson (Cambridge, UK: Cambridge University Press), 349–398.

Stuart, G., Spruston, N., and Hausser, M. (2008). Dendrites, 2nd Edn. Oxford: Oxford University Press.

Thewissen, J. G. M., Cooper, L. N., George, J. C., and Najpal, S. (2009). From land to water: the origin of whales, dolphins, and porpoises. Evol. Educ. Outreach 2, 272–288.

CrossRef Full Text

Torben-Nielsen, B., and Stiefel, K. M. (2009). Systematic mapping between dendritic function and structure. Netw. Comput. Neural Syst. 20, 69–105.

CrossRef Full Text

Torben-Nielsen, B., and Stiefel, K. M. (2010). Wide-field motion integration in fly vs cells: insights from an inverse approach. PLoS Comput. Biol. (in press).

Torben-Nielsen, B., Vanderlooy, S., and Postma, E. O. (2008). Non-parametric algorithmic generation of neuron morphologies. Neuroinformatics 6, 257–277.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

van Ooyen, A., Duijnhouwer, J., Remme, M. W. H., and van Pelt, J. (2002). The effect of dendritic topology on firing patterns in model neurons. Netw. Comput. Neural Syst. 13, 311–325.

CrossRef Full Text

Wang, Y., Gupta, A., Toledo-Rodriguez, M., Wu, C. Z., and Markram, H. (2002). Anatomical, physiological, molecular and circuit properties of nest basket cells in the developing somatosensory cortex. Cereb. Cortex 12, 395–410.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text