Robust Transient Dynamics and Brain Functions

Rabinovich, Mikhail I; Varona, Pablo

doi:10.3389/fncom.2011.00024

REVIEW article

Front. Comput. Neurosci., 13 June 2011
volume 5 - 2011 | https://doi.org/10.3389/fncom.2011.00024

Robust transient dynamics and brain functions

Mikhail I. Rabinovich¹* Pablo Varona²

¹ BioCircuits Institute, University of California San Diego, La Jolla, CA, USA
² Grupo de Neurocomputación Biológica, Departamento de Ingeniería Informática, Escuela Politénica Superior, Universidad Autónoma de Madrid, Spain

In the last few decades several concepts of dynamical systems theory (DST) have guided psychologists, cognitive scientists, and neuroscientists to rethink about sensory motor behavior and embodied cognition. A critical step in the progress of DST application to the brain (supported by modern methods of brain imaging and multi-electrode recording techniques) has been the transfer of its initial success in motor behavior to mental function, i.e., perception, emotion, and cognition. Open questions from research in genetics, ecology, brain sciences, etc., have changed DST itself and lead to the discovery of a new dynamical phenomenon, i.e., reproducible and robust transients that are at the same time sensitive to informational signals. The goal of this review is to describe a new mathematical framework – heteroclinic sequential dynamics – to understand self-organized activity in the brain that can explain certain aspects of robust itinerant behavior. Specifically, we discuss a hierarchy of coarse-grain models of mental dynamics in the form of kinetic equations of modes. These modes compete for resources at three levels: (i) within the same modality, (ii) among different modalities from the same family (like perception), and (iii) among modalities from different families (like emotion and cognition). The analysis of the conditions for robustness, i.e., the structural stability of transient (sequential) dynamics, give us the possibility to explain phenomena like the finite capacity of our sequential working memory – a vital cognitive function –, and to find specific dynamical signatures – different kinds of instabilities – of several brain functions and mental diseases.

Introduction: Transients vs. Attractors in Brain Functions

In 1896 William James wrote: We impute no mentality to sticks and stones, because they never seem to move for the sake of anything, but always when pushed, and then indifferently and with no sign of choice. In modern language we can rephrase these words as: mental activity involves not only the processing of external information but also, may be even more important, the generation of new information (i.e., information not present in the stimulus) that finally leads to a specific choice. This idea was formulated 20 years later by Thomas Graham Brown. In his view, brain operations mainly relate to the intrinsic maintenance of information for interpreting, responding, and predicting. Nowadays we can go a little bit further and affirm that the human brain is intrinsically organized into active, mutually interacting functional networks. On a coarse-grain level of description, mental brain activity can be represented by the dynamics of a complex self-organized system (Kelso, 1995; Port and van Gelder, 1995b). In spite of the fact the brain is a noisy place, i.e., the individual responses of single neurons to stimuli are highly variable, the cooperative activity of a large number of neurons is robust against noise and reproducible (Port and van Gelder, 1995b; Schurger et al., 2010).

Traditional efforts in modeling dynamical phenomena in the brain are predominantly based on the premise that dynamical systems tend to converge to stable fixed points or dynamical states (limit cycles or strange attractors – see Figures 1 and 2, row 1). Active neuronal networks in some specific conditions (with symmetric reciprocal interactions) give rise to a convergent mental activity involving multiple attractors (Hopfield, 1982; Cohen and Grossberg, 1983). There may be some cognitive activities, such as associative memory (Wills et al., 2005), which fits the attractor-oriented description. However, computing with attractors generally limits the use of complex dynamical networks. Once the attractor (or its vicinity) is reached, the “dynamical” nature of the brain becomes irrelevant. Furthermore, this scheme overlooks the informational qualities of the (transient) path from the initial condition to the attractor, an important phase where the brain could exploit its remarkable repertoire of behaviors. In this short review, we discuss an alternative/complementary paradigm, i.e., brain information processing based on robust transient dynamics which is observed in experiments as a sequential switching from one metastable state to another. Following the general perspective of liquid state (Maass et al., 2002) and echo-state models (Jaeger, 2003), we illustrate this paradigm with several examples that just point out the tip of an iceberg.

FIGURE 1

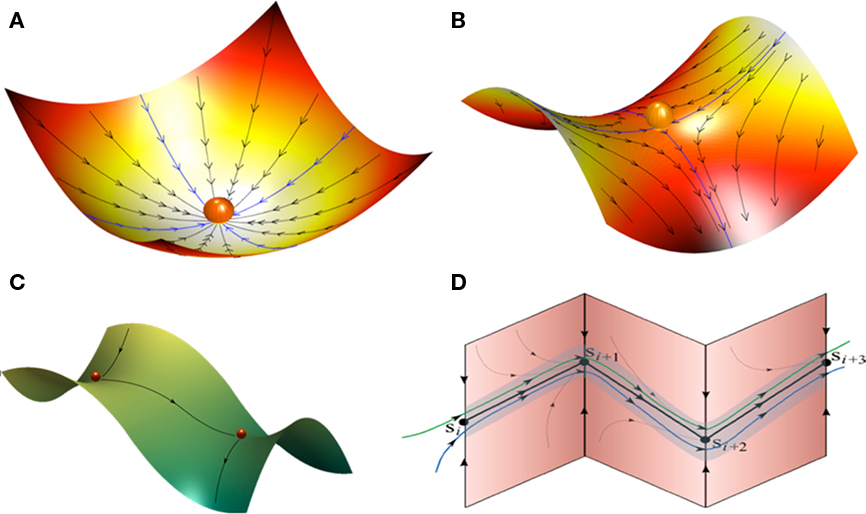
Figure 1. Landscape metaphors for brain dynamics (A–C). (A) Representation of a simple attractor (stable fixed point) in the phase space of a dynamical system. (B) Representation of a metastable state (saddle fixed point) with two stable and two unstable separatrices (a separatrix is a surface or curve that refers to the boundary separating two modes of behavior in the phase space of a dynamical system). (C) Representation of a simple heteroclinic chain with two connected metastable states. (D) Representation of a stable heteroclinic channel – robust sequence of metastable states.

FIGURE 2

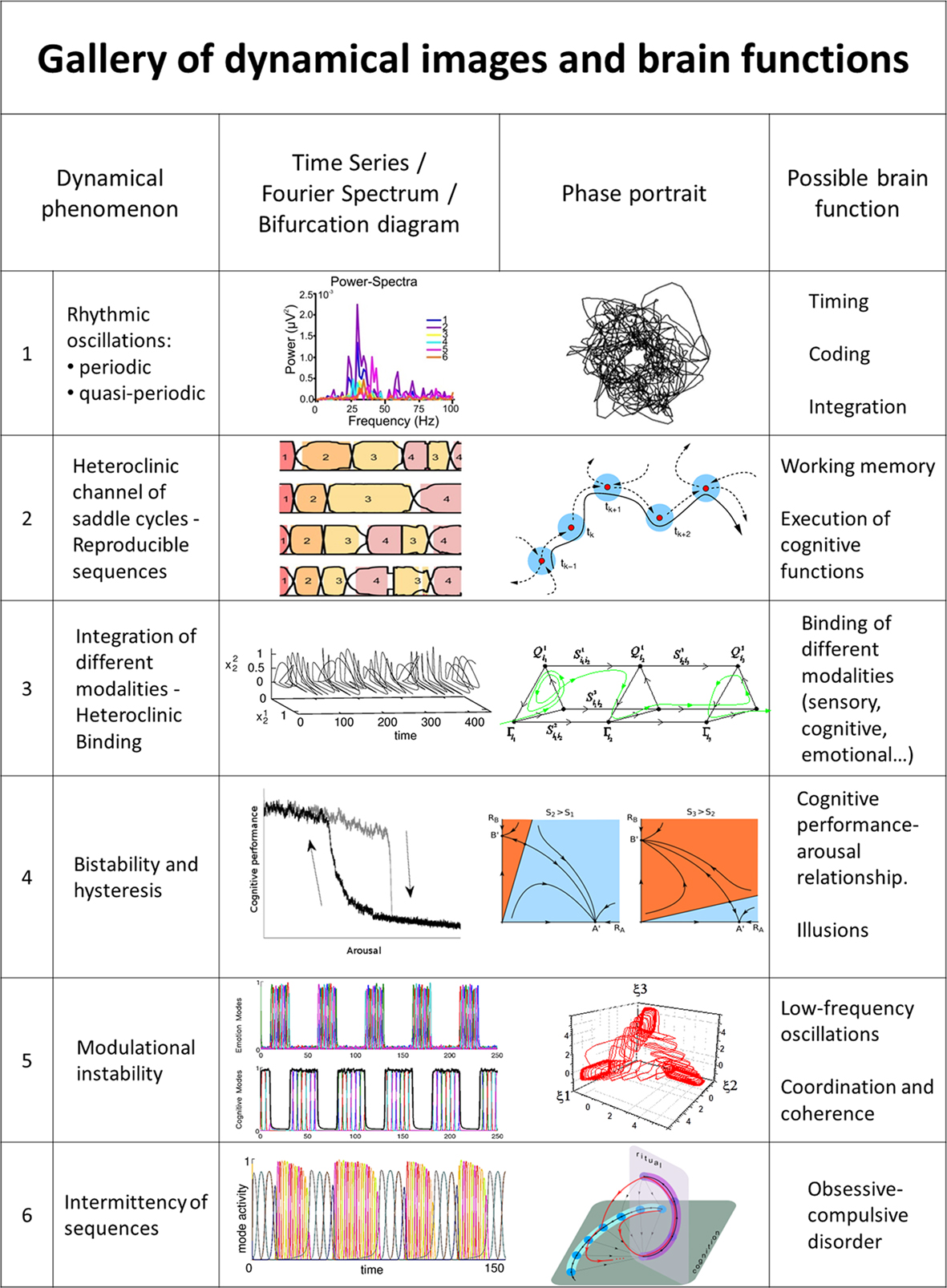
Figure 2. Representative examples of dynamical images of brain functions. (1) Rhythmic oscillations (adapted from Gloveli et al., 2005; Walling and Hicks, 2006). (2) Reproducible sequences of taste-specific switching patterns in the gustatory cortex (adapted from (Jones et al., 2007) and heteroclinic channel of saddle cycles (adapted from Rabinovich et al., 2008a). (3) Integration of different modalities – Heteroclinic Binding (Rabinovich et al., 2010a) for mutual modulation of coupled sequential dynamics. (4) Bistability and hysteresis (Jones and Hardy, 1990; Rabinovich et al., 2010b). (5) Low-frequency oscillations and modulational instability in a network with non-symmetric inhibition (WLC; Rabinovich et al., 2010b). (6) Intermittency of sequences (Rabinovich et al., 2010b).

Sequential Neural Switching in Experiments and Modeling

Nearly all kinds of mental activities, i.e., perception, cognition, and emotion are transient and sequential (Roelfsema et al., 2003; Zylberberg et al., 2010). Let us begin by discussing perception. The way sensory signals are processed in animals is through the activation of specific groups of neurons, which is determined by both the quality and the quantity of the stimulus. The intrinsic dynamics of neural networks produces firing patterns that encode informational inputs and relay them to further processing centers upstream. In general, this code is spatiotemporal and sequential, i.e., transient. Such encoding has been observed recently in experiments with olfactory and gustatory sensory systems (Jones et al., 2007; Rabinovich et al., 2008b; Fernandez et al., 2009).

An analysis of the response of a rat’s gustatory cortex to prototype tastes has revealed that reproducible taste-specific switching patterns are triggered shortly after the stimulus is presented (Jones et al., 2007; see Figure 2, row 2). Experimental observations in the olfactory systems of locusts (Stopfer et al., 2003), zebrafish (Friedrich and Laurent, 2001), and honeybee (Fernandez et al., 2009) reveal odor- and concentration-specific, reproducible, and transient patterns of activity in principal neurons. The odor representations are spatiotemporal successions of states, or trajectories, each corresponding to one odor identity and one concentration (Stopfer et al., 2003). The results of these experiments, in fact, demonstrate a stimulus-dependent switching dynamics that is based on the winnerless competition (WLC) principle (Rabinovich et al., 2001, 2006c, 2008b).

The dynamical image of WLC is a robust heteroclinic cycle or stable heteroclinic channel (SHC; see Figures 1 and 2). Winnerless competitive dynamics in neural systems can result from the presence of inhibitory connections among neurons or neuronal groups (ensembles). For example, inhibitory connected networks of interneurons in hippocampus and neocortex generate collective 40-Hz rhythms (gamma oscillations), when excited tonically (Jefferys et al., 1996). Here we use the term WLC principle for the non-autonomous transient dynamics of neural systems receiving external stimuli and exhibiting sequential switching among temporal winners – different neurons or neuronal groups whose activity is sequentially switching. Thus, the main point of the WLC principle is the transformation of incoming inputs into spatiotemporal outputs based on the intrinsic switching dynamics of the neuronal ensemble. Such switching dynamics can be represented by many metastable states – saddle equilibria or saddle cycles and many trajectories connecting them, i.e., many separatrices or heteroclinic orbits (Afraimovich et al., 2004a; Muezzinoglu et al., 2010; see Figure 1 for an intuitive representation of this dynamics). The sequence can serve as an attracting set when the metastable sets satisfy some conditions (see below and Afraimovich et al., 2004b; Ashwin and Timme, 2005; Rabinovich et al., 2006a, 2010b). The WLC network is able to solve the fundamental contradiction between robustness against noise and sensitivity to small informational signals because the metastable states – saddles – are determined by the stimulus signals (Rabinovich et al., 2008b). WLC dynamics can be described in the framework of different neuronal models. These could be rate models, Hodgkin–Huxley-type models, or even simple map models (Rabinovich et al., 2006c; see Figure 3 for an illustration of WLC dynamics in different models).

FIGURE 3

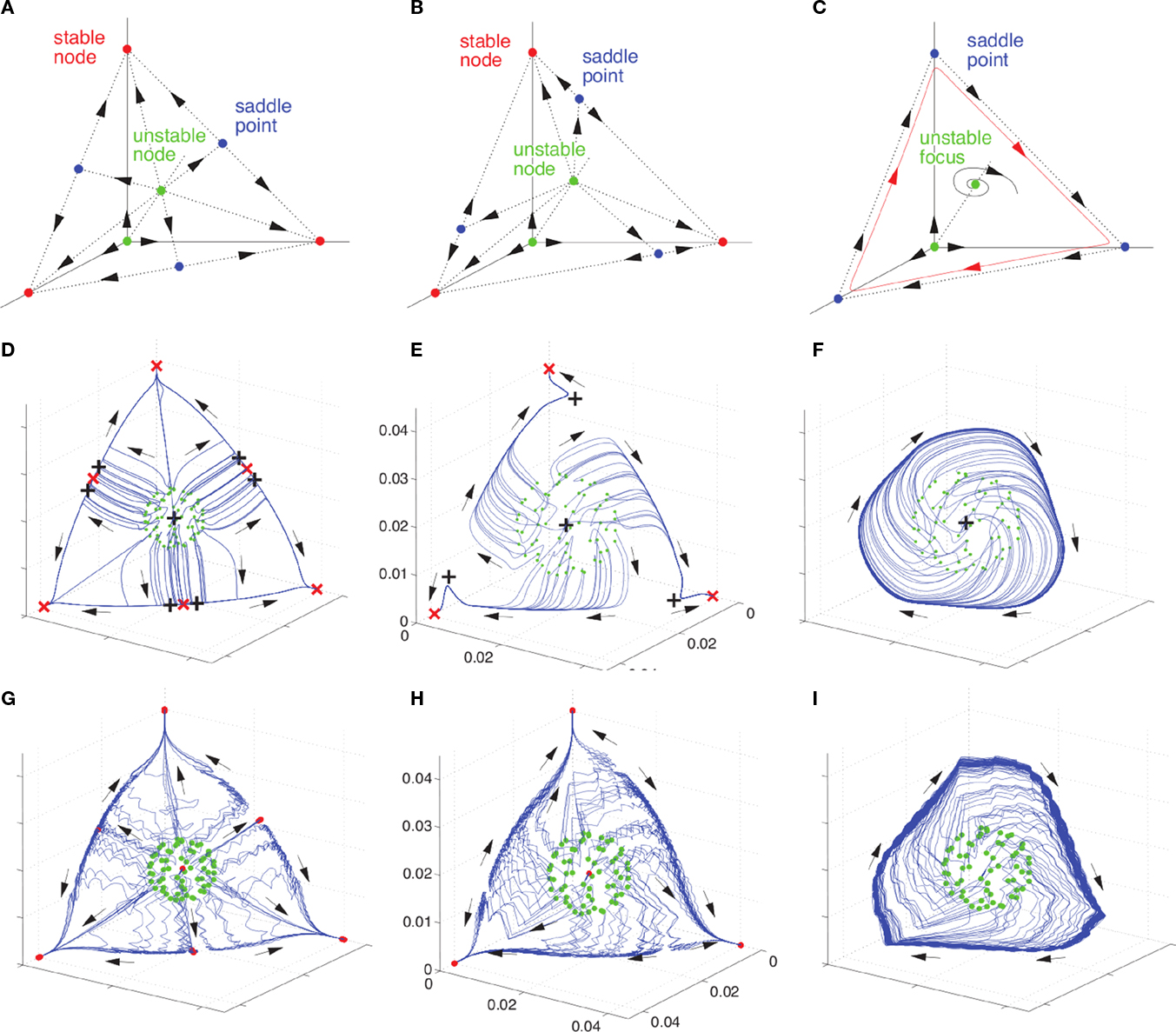
Figure 3. Transition from multistability to WLC with the connection asymmetry as the control parameter. Panels show the bifurcation toward a heteroclinic chain in different models: a Lotka–Volterra model, a H–H model, and a rate model. The Lotka–Volterra model with three units (A–C), undergoes a simultaneous saddle-node bifurcation in the three corners of the shown phase space simplex; with increasing asymmetry of the inhibitory connections (red points – stable fixed points (SFP), blue points – saddles, green points unstable SFP). Numerical evidence for a similar bifurcation can be found in a system of realistic Hodgkin–Huxley neurons (G–I) coupled by inhibitory synapses. This is confirmed by a systematic reduction of the biophysical Hodgkin–Huxley model to an equivalent rate model (D–F) and a subsequent numerical bifurcation analysis [red and black crosses in (D–F)] denote the calculated SFPs – red crosses are stable SFP and black markers are SFP with at least one unstable direction (saddles or unstable SFP). Adapted from Nowotny and Rabinovich (2011).

It is generally accepted that there is insufficient genetic information to account for all the synaptic connectivity in the brain. Then, how can the functional architecture of WLC circuits be generated in the process of development? One possible answer has been found by Huerta and Rabinovich (2004) using a circuit of 100 rate model neurons randomly connected with weak inhibitory synapses. The network demonstrated WLC dynamics after a period of Hebbian learning in the presence of weak noise. WLC can also be the result of local self-organization in networks of H–H model neurons that display STDP with inhibitory synaptic connections as shown in Rabinovich et al. (2006c).

As we already discussed, cognitive functions are usually executed through robust transient dynamics. For example, understanding language and speech processing relies on the concurrent activation of multiple areas within a distributed brain network. Internal representations of words are not symbols but locations in state space. The lexicon or dictionary is a structure in this space, and the processing rules are not symbolic specifications but the dynamics of the system which push the system state in a specific direction rather than in others (Port and van Gelder, 1995a). The general idea about the role of intrinsic transient brain dynamics for the execution of complex sequential behavior (such as playing a piece on the piano or delivering a speech) was formulated by Lashley (1951). He pointed out that such functions could not be executed solely by one response sending a proprioceptive signal back to the brain, which would then trigger the next response in the sequence. Behavior had to be controlled by a central, hierarchically organized program including multiple brain areas (Bornkessel and Schlesewsky, 2006).

An interesting example of possible applications of the WLC principle for understanding cognitive processes has been presented in the context of the study of the striatum (Ponzi and Wickens, 2010). The striatum is the main input structure of the basal ganglia (BG), receiving excitatory inputs from the entire cerebral cortex (McGeorge and Faull, 1989). This neural system plays an important role in planning, decision making, and modulation of movement pathways, but is also involved in a variety of other cognitive processes (Forstmann et al., 2008; Kubota et al., 2009). In humans the striatum is activated, for example, by stimuli associated with reward. Medium spiny neurons (MSNs), which account for 90% of striatal neurons, form inhibitory synapses with each other. This anatomy has been interpreted in the past as a winner-take-all (WTA) network. However, several experimental findings argue against this interpretation (Czubayko and Plenz, 2002; Tunstall et al., 2002; Koos et al., 2004; Taverna et al., 2004; Ponzi and Wickens, 2010): sparse connectivity with weak interactions, predominant one-way connections, and the presence of irregular firing (Wilson, 1993). A simulation of a striatal inhibitory network model composed of spiking neurons has shown that cells form assemblies that fire in sequential coherent episodes and display complex identity-temporal spiking patterns even when cortical excitation is simply constant or fluctuating noisily (Ponzi and Wickens, 2010; see Figure 4). These modeling results demonstrate a good qualitative agreement with experimental studies and support a view of endogenously generated robust sequential dynamics in the striatum.

FIGURE 4

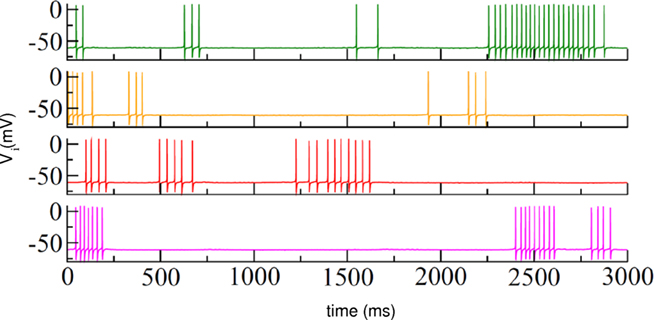
Figure 4. Irregular switching between firing and quiescent states in an inhibitory striatal network model of 500 neurons under a fixed excitatory input condition. Different colors correspond to randomly selected neurons in the network. Adapted with permission from Ponzi and Wickens (2010).

Mental Modes. Metastable States. Sequential Switching

The concept of mental modes was introduced by James (1950) and is a central point in brain transient dynamics theory. Because the term is widespread in different contexts, to use it in a constructive way we first need to explain our vision of this concept. As brain imaging shows (Friston, 2009), the execution of any mental function is based on the dynamical interaction of many different distributed functional networks of brain centers or neuronal groups. In general, these time-dependent distributed networks can be considered as mental modes. More specifically mental modes can be defined trough metastable states in the brain. Metastability imposes that there are semi-transient signals, which persist for a while and are different from the usual equilibrium state (Abeles et al., 1995). The metastable activity of the cortex can also be inferred from behavior (Bressler and Kelso, 2001). Metastability is a principle that describes the brain’s ability to make sense out of seemingly random environmental cues (Oullier and Kelso, 2006; Werner, 2007). The existence of mental metastable states is supported by interactions observed among diverse brain centers or neuron groups (Friston, 1997, 2000; Fingelkurts and Fingelkurts, 2006; Gros, 2007; Ito et al., 2007; Sasaki et al., 2007), and it is the result of self-organization in very complex neuronal systems (see Figure 5). The temporal order of metastable states is determined by the functional connectivity of the underlying networks and their causality structure (Chen et al., 2009). Each metastable state i is represented in neuronal space by a distributed ensemble of excited neurons. We denote this ensemble as U_i(k) where k is the index of the member of i-th ensemble.

FIGURE 5

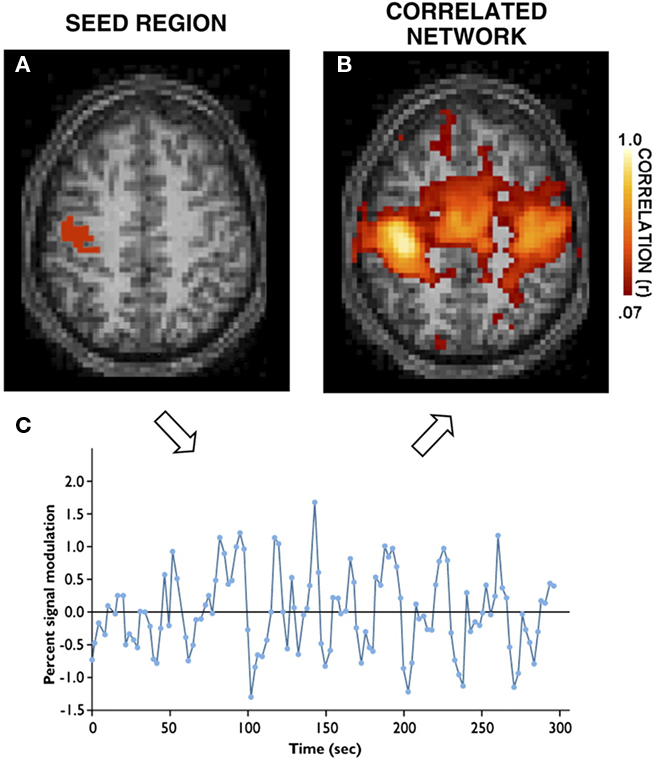
Figure 5. Example of resting-state modes in the brain. (A) Activity as measured from a MRI signal recorded at rest from an example seed region within the motor cortex. (B) Time series of intrinsic low-frequency oscillation activity fluctuations from the seed region. (C) The correlated network of regions reveals multiple cortical areas within the motor system as well as regions within the cerebellum (not shown). Adapted with permission from Buckner (2010); see also Tomasi and Volkow (2010).

For a coarse-grain description of mental dynamics, let us introduce the concept of mental mode formally: a spatiotemporal mental mode i is x_i(t)U_i(k), where x_i(t) ≥ 0 is the level of activity of i-th mode, in particular, it can be the average intensity of all voxels covering the spatial pattern U_i(k) in an fMRI image at time window t + Δt. Suppose that x_i(t) are the axes of the phase space of the dynamical model, then metastable states x_i = const > 0 are saddles on these axes. Thus, the mental cooperative activity related to these metastable states, i.e., the spatiotemporal mental field (perception, cognition, or emotion) can be represented as Σ_ix_i(t)U_i(k).

Below we wish to discuss mental mode competition. Why competition? It is well accepted that excitation in neural networks is responsible for the transduction of information to the right place at the right time and inhibition is responsible for non-trivial informational dynamics (see Buzsaki, 2006). As we know from many experiments (see above) this non-trivial dynamics is a competitive dynamics. In very complex systems, like the brain, the competition is hierarchical and related to a general “ecological” problem, i.e., the limited mental-attention and memory-(Kahneman, 1973; Banich et al., 2009; Martino et al., 2009; Slagter et al., 2010) and energy resources (for a review see Peters et al., 2004).

To describe mathematically the mental mode competition it is reasonable to separate two cases: (i) the intrinsic interaction inside the same modality (like odor, or gustatory encoding), and (ii) the interaction of mental fields corresponding to different modalities, i.e., perception, cognition, emotion, mental resources. In the simplest approximation these modalities have their own phase subspace. The simplest model – canonic equations – considering both interactions within a modality and among different modalities, which is able to describe robust transient dynamics, can be written in the form of generalized Lotka–Volterra equations:

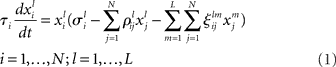
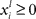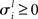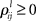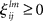where yes represents the instantaneous amplitude of the (i^l)-mode, τ_i is a time constant that depends on the specific problem described (e.g., for sensory systems can be around 100 ms, for working memory (WM) 1–5 s, for resting-state dynamics about 10 s), yes is the growth rate for the mode depending on the external stimulus, yes and yes are the interaction strengths between the modes. Here l, m indicate the modality and i, j indicate the modes within the same modality. 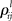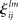The parameters yes and yes can also depend on the stimuli. In the case of a single family modality, i.e., L = 1 (for example, a single sensory processing) we have the traditional Lotka–Volterra model (see Muezzinoglu et al., 2010). The number of metastable states in this model is more or equal than N.

One of the remarkable features of such models is the existence in the phase space (for a wide range of control parameters) of a SHC that corresponds to robust sequential switching from one metastable state to other (Afraimovich et al., 2004b; Rabinovich et al., 2006b, 2010a; Bick and Rabinovich, 2009b).

In the case of interaction among modalities from different families (like cognition and emotion) we can write a phenomenological model in the form (Rabinovich et al., 2010b):

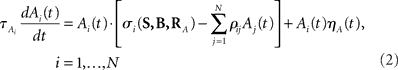
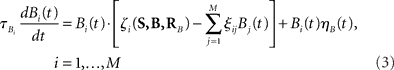
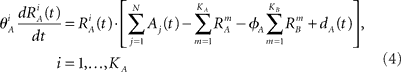
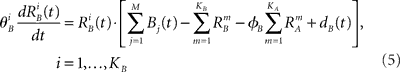
We introduce here the following notation for the variables that describe different modalities: A cognition, B emotion, R resources. The proposed model (2–5) reflects a mutual inhibition and excitation within and among different families of modes, and takes into account three types of interactions: (i) a competitive interaction within each family, (ii) the interaction through mutual excitation among families, and (iii) the competition for resources that are partially separated for different families. The mode dynamics depend on the inputs through parameter S (that may represent, for example, stress, cognitive load, physical state of the body). 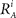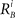The variables yes and yes characterize the K_A and K_B resource items that are allocated to different families, e.g., cognition and emotion (Banich et al., 2009; Martino et al., 2009). The vectors R _A and R _B are the collections of these items that gate the increments of the cognitive and emotional modes in competition. The characteristic times θ of the different resources may vary. The coefficients ɸ_A and ɸ_B determine the level of competition among different families for the “brain community resources.” Each process takes place in the presence of noise denoted by the η and d terms in the equations. The values of the increments σ_i and ζ_i depend on the stimuli and/or the intensity of the modes from different modalities. The only design constraint that we can impose on the increments σ_i and ζ_i is that they must stay positive.

The mathematical object that represents robust transient activity in the phase space of the corresponding model is a SHC, consisting of metastable states – saddle sets –, their vicinities, and the separatrices connecting them. A SHC is characterized by two properties: (i) a sufficiently strong convergence of the phase volume in the vicinity of each metastable state (saddle) with respect to the stretching along unstable separatrices in the case when these separatrices are one-dimensional; and (ii) the relatively long (but finite) passage (or exit) time that the system spends in the vicinity of a saddle in the presence of moderate noise.

To enlighten the conditions on the stability of one sequence of metastable states, we consider an elementary phase volume in the neighborhood of each saddle that is compressed along the stable separatrices and stretched along the unstable separatrix. Let us order the eigenvalues of saddle i as

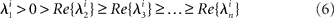
which imposes only one unstable manifold to each saddle. The number

is called the saddle value. If ν_i > 1, then the compression along the stable manifolds dominates the stretching along the unstable manifold, and the saddle is called as a dissipative saddle.

If 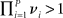yes (where P is the number of metastable states along the heteroclinic chain), the trajectories from the vicinity of a heteroclinic chain cannot escape from the channel, providing its robustness.

Sequential Working Memory Capacity

The analysis of the conditions for the structural stability of transient (sequential) dynamics allow us the possibility to explain phenomena like the finite capacity of our sequential WM. WM is the ability to transiently hold and manipulate several items in the mind, which are involved in the immediate information processing or actions such as thinking, planning, and eventually, behavioral output. Tasks involving WM include, for example, remembering a sequence of statements that we recently heard in a lecture or following driving directions to an unfamiliar place. Language, as sequential activity, is also based on WM. However, the capacity of WM is limited and that is one reason why the metaphor “blackboard of the mind” became popular to describe WM.

Information processing related to WM activity can be represented in an abstract space (the phase space of the network that implements the WM) as a continuous flow of “liquid phase” (Maass et al., 2002): the incoming information encoded in spatiotemporal manner excites the specific network with a functional reverberate loop that sustains the corresponding information item for a finite time (based on a transient attractor). The item networks are inhibitory interconnected with each other and build a macroscopic network that keeps the whole sequence of items. The cooperative dynamics of this macro-network can be based on the WLC principle and guarantee that the sequential items are recalled in the right order. Thus, all three processes – storing, maintaining, and retrieving sequential information, in fact, can be thought as continuous transient dynamical activity of hierarchically organized functional neuronal networks. This perspective has also been discussed in other models based on echo-state networks (Sussillo and Abbott, 2009; Pascanu and Jaeger, 2011).

As many experiments show (see for a review Jensen and Mazaheri, 2010), functional inhibition is reflected in oscillatory activity in the brain at the frequency band of 8–13 Hz (alpha rhythm). The alpha activity can facilitate sequential inhibition by reducing the activity of a given network. There are several models of WM based on the idea that all steps of WM information processing in the engaged distributed networks is reflected by neuronal synchronization in the gamma band (30–80 Hz) accompanied by a theta (5–8 Hz) or an alpha band (Lisman and Idiart, 1995; Roopun et al., 2008; Tort et al., 2008; Schroeder and Lakatos, 2009). It is reasonable to hypothesize that such synchronization leads to a temporal coordination between the fast one-item processing and the slow sequential item interaction.

One can expect that this coordination supports the robustness of information processing and contributes to a larger WM capacity (Palva et al., 2010). Now we show that sequential WM capacity in the context of our model is limited by conditions of the retrieval process stability (Bick and Rabinovich, 2009a).

The stability conditions of the models that we have discussed provide us with a very powerful tool to address and predict several dynamical aspects of brain activity. In particular, we can calculate how long a typical heteroclinic channel can be, i.e., how many steps the sequential switching can have. Note that we will not consider the time duration of the WM, this problem has been addressed in the context of several neuronal and synaptic mechanisms (Mongillo et al., 2008).

The capacity of sequential WM is defined as the number of items that can be recalled correctly after a WM task, and varies amongst different individuals, age and mental diseases. Numerous studies have led to the generally accepted view that the effective capacity for healthy subjects ranges between three to seven items (Swanson, 1999; Oberauer and Kliegl, 2006; Rouder et al., 2008; Edin et al., 2009). This limit has coined the term “magical number seven” (Miller, 1956) in conjunction with WM. In fact, this number is not strictly seven, but something in the range 3–7 depending on the subject.

The dynamical model for sequential WM that we would like to discuss here is based on WLC between informational items (Bick and Rabinovich, 2009a). These items are represented in the phase space by saddle fixed points and the mnemonic recall by a trajectory in a SHC (Rabinovich et al., 2008a,b). Note that there have also been several efforts to explain sequence generation with attractor networks based on synaptic delay and recurrent synaptic integration (Sompolinsky and Kanter, 1986; Rigotti et al., 2010).

Under certain simplifying assumptions, there is an upper bound on the number of items that can be stored in this sequential WM model when implemented by inhibitory-coupled neuronal clusters. Dynamics of such information items can be described by the model (1) with L = 1. The authors of Bick and Rabinovich (2009a) assumed that the relative connection strengths are sampled from uniform distributions and cannot exceed an order of magnitude. They found that the bound for the number of items is about seven. Let us explain this result. Sequential WM dynamics is separated into two stages: the storage of sensory information and its retrieval. Storage means initiation of a specific pattern in the phase space of the corresponding dynamical system by both sensory input and the contents of WM. Based on the hypothesis that WLC between different informational items is the main mechanism for the correct retrieval in sequential WM, the authors in Bick and Rabinovich (2009a) have analyzed the structural stability of sequential switching, i.e., the correct reproducibility of the sequence of the informational items (which is the key property for memory performance). The stability conditions require a strong enough inhibition in the WM random network and, what is a key point, the level of the inhibition increases exponentially with the WM capacity. If we suppose that the level of ρ_ij/ρ_ii is about 20 (large enough from the neurobiological point of view), the number of successfully recalled informational items, according to the exponential law, has to be between seven and eight. Recently, a functional magnetic resonance imaging (fMRI) study (Edin et al., 2009) has provided experimental evidence for the dependence of the capacity limitation for visual WM on the level of inhibition. WM capacity depends on the subject’s individuality that has to be reflected in the model’s architecture, i.e., the existence of subject-specific connections (parameters). WM capacity also depend on the environment - external inputs (S) that modulate the parameters, e.g. the connection strength that models the lateral inhibition ρ_ij = ρ_ij(S).It is very important to emphasize that the type of modulation by external stimuli also depends on the individuality. For example, the personal perception of the same pain stimulus depends on the level of cognitive control that is another modulator of the inhibition. If we assume the relationship between the level of pain and inhibition, the suggested model can be used to predict the dependence of working memory capacity in the presence of pain.

Mutual Modulation of Coupled Sequential Dynamics. Binding

Suppose we are testing a fine wine. Although the flavor of wine is typically perceived as a single perceptual experience, flavor perception reflects processing of inputs from multiple sensory systems: from gustation (through the stimulation of receptors on the mouth and tongue), smell (through the stimulation of receptors in the nose), and oral somato-sensation (through the stimulation of diverse receptors in the oral cavity, providing information about viscosity, temperature, pungency, spiciness, etc). Even though they derive from signals transmitted over several nerves, flavors often appear remarkably coherent in phenomenal perception. Integrating information across the senses enhance our ability to detect and classify objects in the environment. For example, to find flowers honeybees use the same multimodality approach – their sensory and central systems process in an integrative way at least three flows of sensory information, i.e., the color, odor, and taste of flowers. How does the brain do it?

As we discussed above, multi-electrode recordings from different areas of sensory systems in different animals have shown that sensory information on the first level of processing is encoded as spatiotemporal patterns by neural networks that implement a WLC interaction of different dynamical modes (variables). In the phase space, such dynamics is represented by a heteroclinic channel. Motivated by the multi-sensory dynamics observed in neural systems, authors in Rabinovich et al. (2010a) build a model that describes the heteroclinic integration of channels representing different modalities (binding dynamics). This model is described by model (1) with L > 1.

The main results of theoretical and computational analyzes in Rabinovich et al. (2010a) are the following: (i) for a wide range of control parameters, i.e., levels of excitation and inhibition, in the phase space of model (1) there exists an object that the authors named multimodality heteroclinic channel, and the trajectories in the vicinity/inside of this dynamical object represent an integrated (binded) information flow of different modalities (see Figure 2, row 3); (ii) the time series and spectrum of these multimodality-trajectories demonstrate new features – mutual modulation and regularization of the different modalities and, correspondingly, the appearance of new components in the power spectrum (see Figure 2, row 3). The properties displayed by the model can be key features for the next step of multimodality information processing, such as object recognition, speech generation etc. The proposed dynamical mechanism for binding accounts for different levels of temporal hierarchy, from milliseconds to minutes.

Emotion–Cognition Sequential Dynamics

The relationship between emotion (i.e., spontaneous motivation and subsequent implementation of a behavior) and cognition (i.e., complex problem solving by information processing) is very diverse and multidimensional. The main mechanisms of cognitive-emotional interaction are based on the involvement of multiple brain centers, e.g., amygdala and prefrontal cortex participate in both emotion and cognitive networks (Phelps, 2006; Adolphs, 2008), and the high degree of connectivity between different brain areas (Ranganath et al., 2005; Tomasi and Volkow, 2010). The strong influence of emotion to cognition is well known (some times the result of it is very unpleasant; Quartz, 2009). The more intriguing aspect of the interaction between emotion and cognition is the control of emotion by cognition. On the neurobiological level, this control is mainly due to prefrontal activity inhibiting relevant subcortical emotion processing regions.

Both emotion and cognition are sequential dynamic processes resulting from interactions of different brain subsystems in time (Scherer, 2001). Sequential transient dynamics of emotion–cognition interactions are directly relevant to action control, in terms of memory, decision making, reasoning, attention, and emotion regulation. As we illustrate below, the model (2)–(5) with hierarchical competition can be regarded as a normal or canonical form for the description and prediction of the temporal evolution of cognitive-emotional states. Crucially, some of the fundamental instabilities that arise in these coupled systems are remarkably similar to endogenous activity seen in the brain (Rabinovich et al., 2010b). Furthermore, by varying a small subset of the system’s parameters it is possible to produce bifurcations and changes in the metastable sequential dynamics, which can be a phenomenological explanation of pathological brain states seen in psychiatry. We discuss some examples below.

Possible Dynamical Origin of Low-Frequency Resting-State Oscillations

Let us discuss briefly the spontaneous mental dynamics in a stationary environment where the brain is not engaged in a particular cognitive function, i.e., resting-state brain dynamics (Lewis et al., 2009). The model (2)–(5) is very convenient for the analysis of such type of dynamics. We can choose the parameters of the model so that the basic dynamics of both cognitive and emotional modes demonstrate simple recurrent activity (pulsations with a characteristic time scale of 2–3 s). Such “independent” emotional and cognitive activity has been observed during weak competition between “cognitive” and “emotional” families. When competition passes the critical value, this simple independent activity becomes unstable due to a modulation instability that leads to stable low-frequency oscillations (LFO), as shown in Figure 2, row 5 (Rabinovich et al., 2010b). The averaged time series indicate that this robust modulation process is similar to the quasi-periodic LFO observed in Fox et al. (2005).

An increasing number of EEG and resting-state fMRI studies in both humans and animals confirm spontaneous LFO in cerebral activity at 0.01–0.1 Hz. This represents a fundamental component of brain functioning. However, the dynamical nature of LFO is unclear and has produced a lot of debates. In general, the LFO fluctuations observed with fMRI are not the same as the underlying neuronal fluctuations because they have been passed through a hemodynamic response function. Nevertheless some experiments (Biswal et al., 1995; Salvador et al., 2005; Schutter et al., 2006; Ben-Simon et al., 2008) support the hypothesis that LFO are correlated with the neural network’s activity, i.e., mode cooperative dynamics (e.g., due to their modulation or synchronization). The modulation instability that has been observed in Rabinovich et al. (2010b) discloses a plausible dynamical origin of LFO in the resting-states, possibly related to the “cortical–subcortical cross-talk” (Schutter et al., 2006).

Obsessive–Compulsive Disorder Transient Dynamics

The Obsessive–compulsive disorder (OCD) is a type of anxiety disorder that traps people in endless cycles of repetitive feelings, unwanted thoughts, and unwanted repetitive acts. The compulsive rituals (Huppert and Franklin, 2005; Hollander et al., 2007) are performed in an attempt to prevent obsessive thoughts or make them go away. To model OCD, authors (Rabinovich et al., 2010b) have introduced a sequence of metastable states (saddles), in the cognitive phase subspace, which have not one- but two-dimensional unstable separatrices, by construction. One of these dimensions forms the way leading to the next cognitive metastable state along a cognitive sequence, whereas the second unstable one targets the emotional saddle that represents the entry to the ritual, which is modeled as a different stable chain of the “emotional” metastable states. The ritual sequence terminates at a saddle that has many unstable separatrices, each yielding to a cognitive mode (see Figure 2, row 6). As a result, the OCD dynamics is represented by a (N + M) – dimensional transient, which qualitatively distinguishes itself from the normal behavior and from other psychiatric disorders characterized by a specific instability that leads to uncertainty.

Conclusion

The robustness and reproducibility of mental transients that we have discussed in this review are important features of global brain activities and functions. These features are based on several principles of brain dynamics that we would like to remind here: (i) the self-organization of a cooperative activity of different elements and, in particular, the formation of mental modes and metastable brain states; (ii) the limitation of mental and energy brain resources (ecological principle); and (iii) the hierarchy of the brain organization – structural, temporal, and functional. These principles are strongly related to each other, as one can see on the example of the hierarchical competition that we have discussed in this review. The models discussed in this paper are not intended to provide a quantitative description of mental processes. However, such models reflect the type of dynamics observed in many experiments, provide a theoretical framework to understand it, and some of them can lead to a more quantitative description of mental activity in the future.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Mikhail I. Rabinovich acknowledges support from ONR grant N00014-07-1-074. Pablo Varona was supported by MICINN BFU2009-08473.

References

Abeles, M., Bergman, H., Gat, I., Meilijson, I., Seidemann, E., Tishby, N., and Vaadia, E. (1995). Cortical activity flips among quasi-stationary states. Proc. Natl. Acad. Sci. U.S.A. 92, 8616–8620.