Visual representation determines search difficulty: explaining visual search asymmetries
- Department of Computer Science and Engineering and Centre for Vision Research, York University, Toronto, ON, Canada
In visual search experiments there exist a variety of experimental paradigms in which a symmetric set of experimental conditions yields asymmetric corresponding task performance. There are a variety of examples of this that currently lack a satisfactory explanation. In this paper, we demonstrate that distinct classes of asymmetries may be explained by virtue of a few simple conditions that are consistent with current thinking surrounding computational modeling of visual search and coding in the primate brain. This includes a detailed look at the role that stimulus familiarity plays in the determination of search performance. Overall, we demonstrate that all of these asymmetries have a common origin, namely, they are a consequence of the encoding that appears in the visual cortex. The analysis associated with these cases yields insight into the problem of visual search in general and predictions of novel search asymmetries.
1 Introduction
The past several decades of research surrounding visual search have produced a bounty of data on the relative difficulty of different experimental search paradigms. The richness of this data lies not only in its depth, but also in the range of target and distractor stimulus patterns that have been considered. Although much insight has been gained into the problem, the precise underpinnings of the mechanisms involved in determining search difficulty fall short of a comprehensive understanding.
Among the categories of search problems that have been addressed, one subset that lacks a satisfactory explanation are those that produce asymmetric search performance from an apparently symmetric experimental design (Wolfe, 2001). This class of problem has been discussed mostly as a peculiarity that arises under specific experimental conditions and in some instances existing claims of performance asymmetry have been attributed to experimental conditions that are not truly symmetric (Rosenholtz, 2001).
There exist many examples of unexpected behavioral phenomena that arise under very specific experimental conditions and are such that the unexpected behavior that arises is eminently useful in helping to tease apart the specific computational mechanisms underlying these phenomena. These conditions can be useful in hypothesis validation allowing certain otherwise plausible computational hypotheses to be ruled out. Visual search asymmetries correspond to unexpected asymmetric behavior in the context of a visual search task that is based on an apparently symmetrical design.
In the sections that follow we discuss distinct classes of search asymmetries that are shown to have a common rationale. The first of these classes is referred to as basic asymmetries, in which symmetric perturbations along a feature dimension (e.g., line orientation) yield asymmetric behavioral performance. The second of these is referred to as novelty asymmetries, in which novel stimuli give rise to asymmetric behavioral performance.
In each of these cases, we provide examples of the nature of asymmetries that appear in behavioral studies and the current thinking for the causation associated with observed behavior. We establish that virtually all of these asymmetries may be explained by a single underlying root cause, specifically, that they are emergent from the properties of efficient neural encoding when combined with mechanisms thought to underlie visual search behavior. Where possible, predictions of novel search asymmetries emergent from this principle are discussed. Moreover, this analysis and discussion casts the overall problem of visual search in a novel light yielding an explanation that extends to capture variations in visual search performance in general.
2 Materials and Methods
2.1 Determinants of Search Difficulty
To begin considering the problem of quantifying search difficulty, we require as a starting point a strongly plausible description of the computation underlying said determination. In the following we outline a handful of prevailing theories targeted at explaining search behavior in primates. We further demonstrate that all of these descriptions share a common thread which is one of the conditions necessary to justify the results that follow in this paper. The following outlines a variety of computational proposals targeted at defining the nature of visual saliency computation in the brain.
2.1.1 Koch and Ullman (1985)
Many computational models of visual search appeal to the notion of salience which aims at quantifying the extent to which stimuli draw an observers attention or gaze from a signal driven or bottom-up perspective. A classic model dealing with this problem is that of Koch and Ullman (1985) which models the problem of visual search by constructing a computational description of the cortical computation involved, inspired by the observed structure of the primate visual system. In this proposal, the visual input projects onto a number of topological maps that represent different features across the visual field (e.g., orientation, color, etc.). Different feature maps encode the conspicuity of individual features. These feature maps are combined to form an overall topologically organized saliency map upon which selection is based. Further details of this model are fleshed out in the work of Itti where operations of normalization (Itti et al., 1998) or iterative difference of Gaussians (DoG; Itti and Koch, 2000) operations serve to convert the feature level response to a measure of conspicuity. In the case of the DoG based normalization, conspicuity is determined by within feature (iso-feature) spatial competition.
2.1.2 Li (1999)
An additional influential model of visual salience is that of Li (1999) which posits local interaction among cells in visual area V1 as the basis for saliency computation. This interaction is implemented by way of excitatory principle cells and inhibitory interneurons, and is such that stimuli are subject to iso-orientation suppression, and collinear facilitation among stimuli that are aligned in a collinear fashion such that their arrangement forms a contour. The computation put forth in (Li, 1999) that is common to the other models discussed, is that of iso-feature suppression, and this suppression behaves in a similar manner to the other models discussed here in that suppression is strongest for matching orientation distractors in the surround and weakest or absent for orthogonal stimuli. The proposal discussed in (Li, 1999) also outlines a handful of asymmetries that can be explained by virtue of the local cellular interactions implemented by the model. The set of asymmetries considered in (Li, 1999) are distinct from those that appear in this paper, however, commonalities and differences are discussed in Section 3.1.1.
2.1.3 Attention by information maximization
In recent years, a number of novel models of visual salience have been proposed, motivated by quantitative principles alluding to the information content or discriminability of stimuli. In the model of Bruce and Tsotsos(2006, 2009), saliency is computed on the basis of the self-information corresponding to the response of a neuron in the context of neurons in its surround. The results presented in this paper build on our prior work and thus the attention by information maximization (AIM) model is the basis for the experimental results put forth in this paper. It should be noted that there is no loss of generality in the choice of saliency computation as the necessary properties exhibited by this model are common to the models described in this section. It is at the level of neural representation that the explanations for the observed behavioral effects appear. The computation of saliency in the context of the AIM model is as follows:
A local region of the image, of size (m × n × 3) in the case of an RGB image patch, may be represented by a vector L of dimensions (3mn × 1). Given a set of K basis functions represented by a K by |L| matrix M, one may project the local patch onto the set of basis functions by the matrix product ML. Performing this operation across all pixel locations (with the patch in question centered at the respective pixel locations) yields a set of K retinotopically organized feature maps. The matrix M corresponds to a set of basis functions learned via applying ICA to patches randomly sampled from an image set (a large varied set of natural images in prior work). The result then, given an input stimulus array, is a set of K feature maps that correspond roughly to the output of Gabor-like filters and color-opponent cells, in the case that M is learned from a large set of natural image patches. Let ak denote the K observed basis coefficients from the product ML. Given this representation, one may then compute the self-information as follows:
For each i, j pixel location in the image, the m × n neighborhood Ck centered at i, j and represented by L is projected onto the learned basis yielding a set of basis coefficients ai,j,k corresponding to the response of various cells whose receptive field center is at i, j. In order to evaluate the likelihood of any given coefficient p(ai,j,k), it is necessary to observe the values taken on by au,v,k, whereby u, v define cells that surround i, j providing its context. The values of au,v,k with u, v ∈ Sk (the surrounding context) define a probability density function that describes the observation likelihood on which the assessment of p(ai,j,k) is based.
To evaluate the likelihood of the content within any given neighborhood Ck, we are interested in the quantity p({ai,j}) evaluated for all k = 1…K features, or more specifically p(ai,j,1,…,ai,j,K). Owing to the independence assumption afforded by a sparse representation (ICA), we can instead evaluate the computationally tractable quantity 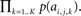 The self-information attributed to Ck is then given by −log
The self-information attributed to Ck is then given by −log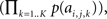 which may also be computed as
which may also be computed as 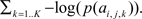
This yields for each location in the input stimulus array, a measure of the self-information of the response as defined by its surround. For computational parsimony, in the simulations carried out Sk is taken to be the entirety of the stimulus array. For further detail on the saliency computation involved in AIM, the reader is encouraged to consult (Bruce and Tsotsos, 2006, 2009).
2.1.4 Discriminant saliency
An alternative probabilistic definition based on the extent to which a region of the scene is distinct from its surround, is based on a discriminant definition (Gao et al., 2008). Saliency is defined by the power of a set of features to discriminate between center and surround regions, taking into account the statistical distribution of filter responses within the central and surround region. The computation involves considering the KL-Divergence conditioned on the class label as 1 (center) or 0 (surround). This yields a specific definition of feature contrast, akin to iso-feature surround suppression.
2.1.5 Bayes and ideal observer theory
An alternative approach to the problem, is to formulate the search task on the basis of an ideal observer (Torralba et al., 2006; Vincent et al., 2009). In this case, a Bayesian approach applies and the computation performed is formulated as P(T = 1|{rk}) where T = 1 denotes the presence of a target item, and {rk} is the set of neuronal firing rates involved in this determination. By Bayes rule, this expression can be rewritten as P({rk}|T = 1)P(T = 1)/P({rk}). As the salience of a stimulus is inversely proportional to the observation likelihood of its response (firing rate), there is as a consequence iso-feature suppression within feature maps involved in the representation.
2.2 Common Threads
Although the preceding models each present a different account of visual saliency attributed to stimuli in a target array, there are certain common conditions to all of the models discussed. These conditions are the central sufficient conditions that give rise to the myriad of search behaviors that appear in the balance of the paper. That said, the important common conditions are as follows:
1. All of these approaches prescribe mutual suppression (either explicit or implicit) among spatially distinct neurons within each of a number of distinct feature maps (i.e., within feature or iso-feature spatial competition as either lateral inhibition or normalization).
2. They all assume a decomposition of the image signal onto a set of disparate feature maps that form a decomposition or encoding of the input signal.
3. A third important condition not addressed explicitly by all of these models, but that factors into some of the discussion in the later sections of the paper is that of task bias, that is, the ability to modulate the response of units involved in representing the visual input is a property that clearly exists in the context of any visual computational modeling paradigm.
It is worth noting that there are many other important determinants of search difficulty for any task. For example, one might suggest that a backward 2 is more difficult to distinguish from a 5 than is a backward 7. A number of additional factors that are important in determining search difficulty include at least target–distractor similarity, distractor homogeneity, learning, and the role of noise, as well as additional local stimulus related modulation (e.g., collinear facilitation Li, 1999).
In the following sections we demonstrate how the body of visual search asymmetries that heretofore lack a consensus explanation can be explained by considering the implications of the conditions put forth in this section. In the simulation results we have applied the computational mechanism appearing in (Bruce and Tsotsos, 2009) and described in Section 2.1.3 owing to the explicit connection made to encoding natural image statistics that appears in the description of the model. While we have applied a particular strategy to quantify target salience this does not limit the generality of the results since as mentioned, the necessary conditions are common to prevailing theories concerning stimulus salience and we demonstrate that it is at the representational level that these effects appear.
2.3 Natural Image Statistics and Neural Coding
In the past decade, an active avenue of research has been the consideration of the relationship between neural representation and the statistics of the natural world. It has been shown explicitly that learning a sparse code for patches drawn from natural images produces filters with properties strongly reminiscent of early cortical cells (Olshausen and Field, 1996). Additional work has also shown this to be true of chromatic content (Atick et al., 1992, 1993; Tailor et al., 2000), spatiotemporal patterns (Dong and Atick, 1995; Li, 1996; van Hateren and van der Schaaf, 1998), and this strategy has also been established as a means of producing hierarchies involving more complex features (Hyvärinen and Hoyer, 2001) with properties that can be strongly tied to cortical computation.
In addition to the first condition outlined in Section 2.1, the nature of the decomposition of an input signal into an abstracted neural representation is the second important condition. Owing to the strong ties between sparse coding strategies and cortical representation, we have employed the strategy of sparse coding for the purposes of the demonstrations that form the subject matter of this paper.
In the simulation results that are presented, model cortical cells for either V1, or for the representation of handwritten digits were learned via extended infomax ICA (Lee et al., 1999). For details on the learning process employed, the reader is encouraged to consult (Lee et al., 1999). In the case of random natural image patches, the learning process results in a model set of basis functions that have been shown to have a close relationship with the encoding observed in the primate cortex and as such, is used as a model of early visual processing in our simulations. Patches were sampled randomly from approximately 2000 images drawn randomly from the Corel stock photo database for a total of 200,000 patches.
For the case of handwritten digits, the ICA learning resulted in a more complex set of basis filters that are optimal for encoding the characteristics associated with handwritten digits. These are intended to provide a cortical representation of a more complex pattern domain to allow the problem of stimulus novelty to be addressed. The details of the learned basis pertaining to the representation of handwritten digits is left to Section 3.2.
3 Results
3.1 Basic Asymmetries
There exists a handful of experimental paradigms wherein a symmetric perturbation of a stimulus results in asymmetric changes in behavioral performance (Treisman and Gormican, 1988; Wolfe, 2001). In the following, the discussion is focused upon two prominent and very basic stimulus conditions in order to shed further light on the source of these behaviors.
Perhaps the most prominent of visual search asymmetries derives from a task in which a search for a vertical bar among slightly tilted (e.g., 15° clockwise from vertical) bars is required, or the converse case. Behavioral experiments demonstrate that under these conditions, a search for a vertical bar among tilted bars is much more difficult than a search for a tilted bar among vertical bars.
This experimental paradigm naturally begs the question of what gives rise to the observed behavior. In early published work describing this effect, the explanation for this appeals to a coarse pre-attentive categorization of lines as steep, shallow, tilted left, or tilted right. In this account, the asymmetric behavior is thought to arise from the fact that the 15° from vertical bar is unique in its definition as tilted right, while the vertical and 15° from vertical bars are all categorized as steep (Wolfe et al., 1992; Wolfe and Horowitz, 2004). The vertical bar is then defined only by the absence of tilt, in line with other presence–absence asymmetries (Treisman and Gormican, 1988). Although this provides one possible explanation, the assumption that such a preattentive categorization exists is somewhat questionable.
In a recent effort Zhang et al. (2008) suggest an explanation that appeals directly to the observation likelihoods appearing in natural images in a general sense. That is, in this account target salience is based on the reciprocal of P({rk}) with this likelihood defined by the response of filters over the space of all natural images (Zhang et al., 2008).
In the following, we demonstrate that a probabilistic assessment of line orientation based on an explicit estimate of the observation likelihood of orientation statistics in natural images is unnecessary to observe this behavior. If one instead bases the assessment of P({rk}) on the search array under consideration as prescribed by the probabilistic models in Section 2.1, this yields iso-feature spatial competition not unlike models that prescribe this competition explicitly (Li, 1999; Itti and Koch, 2000). In the following, we demonstrate that the desired behavior emerges without appealing to a likelihood estimate based on ecological statistics but with this behavior instead tied to the underlying neural representation.
Figure 1 demonstrates an example of the aforementioned asymmetric pair of search stimuli (top). Also shown (bottom) is the output of the AIM model described in (Bruce and Tsotsos, 2009; and in Section 2.1.3) with a basis learned from randomly sampled patches from natural images via extended infomax ICA (Lee et al., 1999) and with P({rk}) based on the current stimulus array. Note that the model behavior that is produced is asymmetric and mirrors the behavior observed in human experiments.

Figure 1. Top: two cases in a visual search experiment that gives rise to asymmetric behavioral performance. Left: a bar oriented 15° from vertical results in an easy search among vertical distractors. Right: a vertical bar among tilted distractors results in a more difficult search. Bottom: an estimate of search difficulty or salience based on the method described in (Bruce and Tsotsos, 2009) with red indicating most visible and blue least visible.
How is it the case that this asymmetric behavior emerges from a symmetric mechanism determining stimulus salience? The answer lies within the properties of the model cells themselves. Specifically, the observation likelihood of natural image statistics implicitly factors into the response properties of the basis set in question. As a result of this, the suppressive effect among units is anisotropic with respect to orientation. While the suppression of a vertical target by tilted distractors is substantial, this is not true of the converse case. Note that there is recent support in the literature for such anisotropic orientation suppression (Essock et al., 2009). Therefore the effect emerges from within feature suppression in the context of a sparse representation of natural image statistics. Note that in contrast to the explanation of Zhang et al. (2008), it is at the representational level that the asymmetry emerges, and not at the level of likelihood estimation.
Some have argued that the notion that low level suppressive interactions are the impetus for these behavioral asymmetries is dubious, owing to the fact that surrounding the stimulus array with a tilted frame may cause a reversal of the performance asymmetry (Treisman and Gormican, 1988). The so called frame effect provides a potential challenge to the class of models that are outlined in Section 2.1 and suggests the possible involvement of top-down processes in this determination. One important study sheds light on this consideration (May and Zhaoping, 2009) revealing that both frame of reference derived from high-level configural cues and also bottom-up iso-orientation competition from the frame play a role. This study reveals two important display dependent effects that contribute to performance asymmetries within this paradigm. However, these orientation asymmetries also occur without a surrounding frame and with stimuli presented within a circular window (Treisman and Gormican, 1988; Marendaz, 1998; Doherty and Foster, 2001). Importantly, the results put forth in this paper provide an explanation for these basic performance asymmetries that are non-display-dependent. It is important to bear in mind that discussion of orientation bias is inherently oversimplified when considering purely visual encoding of orientation as there are invariably other factors that impact on the nature of the underlying representation including different frames of reference, and the contribution of vestibular influences to orientation processing (Marendaz et al., 1993; Marendaz, 1998; MacNeilage et al., 2008).
One such additional basic asymmetry that appears in (Treisman and Gormican, 1988) concerns asymmetries tied to color. The relationship between search asymmetries and color may be had in considering the corresponding image statistics. This is precisely what is examined in (Essock et al., 2009) which shows in general that distances to perceive a noticeable difference along various dimensions of color description are strongly predicted by their prevalence in natural images. The observation that a search for orange among red distractors is an easier search than red among orange distractors (Treisman and Gormican, 1988; Wolfe, 2001) is consistent with the observed statistics (having a strongly positive slope in the 635 to 700 nm range (See Figure 1 of Long et al., 2006).
3.1.1 Predictions for symmetric and asymmetric tasks
Taking the assumption that visual search asymmetries are emergent from a biased representation tied to natural image statistics, it is natural to consider what this assumption predicts with respect to visual search difficulty in general.
If one observes the power spectra derived from many natural images (or the average), there are some consistent observations concerning the relative prevalence of angular and radial frequencies represented (Field, 1987). Consistent with the vertical/15° from vertical experiment, a strong orientation bias exists in favor of vertically oriented structure. There is also a very strong bias in favor of structure oriented along the horizontal plane. There is considerable literature (e.g., Campbell et al., 1966; Mitchell et al., 1967) documenting orientation bias in primates (and ferrets Chapman and Bonhoeffer, 1998) toward oblique orientations, further supporting the notion that coding corresponds to an efficient representation of scene statistics (as argued by Hansen and Essock, 2004). On the basis of the statistical bias appearing in natural images and the corresponding encoding, one would then also expect that a near horizontal bar among horizontal distractors would be easier than the converse and this is indeed what is observed in behavioral experiments (Foster and Ward, 1991; Doherty and Foster, 2001).
In some cases, this analysis is made much more difficult by the fact that representation of visual content across the field of view is not isotropic. Foveation is bound to play an important role in both the perception of frequency and color. This is perhaps the reason that consistent basic behavioral asymmetries are more difficult to pin down than one might expect. Interestingly, in support of this point, the robustness of the vertical orientation asymmetry might be attributed to the fact that the relative dominance of orientation content corresponding to vertical observed in natural scenes, is a property that persists across the entire range of spatial frequencies.
As a whole, there are many predictions emergent from this analysis that might be tested with careful control of experimental conditions including foveation. This might include the behaviors emergent from small differences in radial frequency. A number of predictions for color asymmetries emerge in considering the results put forth in (Long et al., 2006) in light of the hypothesis put forth in this paper. One would expect on the basis of the statistics shown in (Long et al., 2006) to observe a few additional color asymmetries: blue (e.g., 490 nm) target among violet (e.g., 450 nm) distractors much easier than the converse, 580 nm (orange/yellow) and 500 nm (blue/green) among 550 nm (yellow/green) somewhat easier than the converse cases. Note that common categories of color only offer a crude description of the asymmetries expected compared with the more precise wavelength measurements given.
An important point emerges from this discussion: while as humans it is natural to talk about quantities such as color, orientation or size, what is important in describing search behavior is not these quantities, but the representation in the brain. For example, orientation and size (angular and radial frequency) are coded jointly and a stimulus that is unique only for a conjunction of these features is a pop-out target (Sagi, 1988), in contrast to say color and orientation. For this reason, in discussing symmetric experiments it is important to also consider the neural representation of these features which may not be at all symmetric.
It is interesting to also consider a handful of behavioral asymmetries that are considered in (Li, 1999). It is shown that local interactions at the level of V1 are sufficient to produce asymmetries for search arrays involving long versus short lines, parallel versus convergent line pairs, closed versus open contours, straight versus curved contours, and circles versus ellipses. While local iso-feature suppression is sufficient to explain some of this behavior (e.g., parallel versus convergent), there are other instances where the apparent involvement of other mechanisms we have not considered (e.g., collinear facilitation) play an important role. That said, viewed in the light of local iso-feature suppression involving a complex neural representation it is conceivable that iso-feature suppression may be implicated in some of the other cases as well. For example, one might expect that an efficient representation would have straight contours relatively over-represented compared with curved ones. In the instance of short versus long, or open versus closed contours, it is also conceivable that end-stopping cells play an important role, further emphasizing the importance of representation.
3.2 Novelty Asymmetries
A curious paradigm that falls under the envelope of asymmetric behavioral paradigms concerns visual search experiments in which novel stimuli are used. Specifically, this refers to the case where a search requires localizing a target that is a common pattern (e.g., the letter “A”) among unknown symbols (e.g., upside down A’s), or the converse case. The general finding within this sort of experimentation, is that a novel target among familiar distractors is much easier to locate than a familiar target among novel distractors (Frith, 1974; Reicher et al., 1976; Richards and Reicher, 1978; Hawley et al., 1994; Wang et al., 1994). This is perhaps counterintuitive, as one might expect that having an accurate mental representation of the target would be the most important factor in search performance. One question that naturally arises in regard to novel stimuli, is that of whether it is novelty itself that gives rise to pop-out, or some other confounding factor. One experiment that sheds light on this consideration, shows that in Slavic subjects who are familiar with N from the latin alphabet and a mirror-N from the Cyrillic alphabet (Malinowski and Hübner, 2001), the pop-out effect normally appearing for these stimuli is abolished. That is, the evidence that novelty is the characteristic that gives rise to pop-out associated with these stimuli, derives from the fact that when presenting the same search patterns to viewers for which neither the distractor or target are novel, these conditions do not elicit an efficient search (Wolfe, 2001). This has also been demonstrated in an experimental study featuring Chinese characters (Shen and Reingold, 2001). Figure 2 demonstrates some examples of this type of search stimuli as well as a related paradigm involving the form of animals (adapted from Wolfe, 2001).

Figure 2. An example of some search tasks in which target and distractor familiarity play a role in task difficulty. Top: relatively easier cases in which target is unfamiliar. Bottom: more difficult cases in which distractors are unfamiliar. Figures adapted from (Wolfe, 2001).
3.2.1 Novelty as a basic feature
A pervasive notion in the visual search literature involves the discussion of what constitutes a basic feature (Wolfe and Horowitz, 2004). A basic feature is generally equated to a stimulus characteristic that may give rise to a very efficient (or indeed pop-out) search. The surprising efficiency with which novel targets are found has led to discussion of whether novelty itself constitutes a basic feature (Wolfe, 2001; Wolfe and Horowitz, 2004). Examples of stimulus characteristics that are described undoubtedly as basic features include color, motion, and orientation (Wolfe and Horowitz, 2004).
While these concepts are easily defined in concrete and explicit terms, novelty as a feature remains a much more elusive conceptualization. In the absence of a concrete representation in which novelty can be addressed in explicit terms, the question of whether or not it constitutes a basic feature is perhaps misguided. Moreover there is no existing explanation of the impetus for novelty related asymmetries. It is with this in mind, that we have sought to investigate the nature of asymmetries attributed to novel stimuli with the primary goal of explaining the cause of these asymmetries and as a secondary goal, considering what this may tell us about visual search in general.
3.2.2 Experimenting with stimulus novelty
In order to further understand novelty related asymmetry, we have derived an experimental paradigm to demonstrate how novelty may play a role in determining search difficulty. This includes a demonstration of why novelty may give rise to efficient searches, why this is more true for some stimuli than others, and the importance of distractor representation in this process.
The demonstration of novelty related effects first requires that reasonable assumptions be made concerning the neural representation of stimuli involved. The experimentation presented here once again appeals to the notion that sparse coding is ubiquitous in the cortex. Since many of the more principled experiments pertaining to novelty have been performed on sets of forward facing and mirror imaged characters, a suitable starting point is to derive a simulated neural representation with characteristics that are a plausible match to the presumed encoding of these kinds of stimuli. This problem is non-trivial as presumably even for representing simple block letters the human brain carries a rich representation of characters that includes the observed variability in instances of these characters as they appear in the world.
For the purposes of experimentation, we have learned a sparse encoding of handwritten digits. The MNIST handwritten digit database was employed for the purposes of learning the desired representation (LeCun et al., 1998). This database consists of 60,000 instances of handwritten digits. Importantly this character set also has some variability in the appearance of specific instances and therefore allows a more plausible set of model cortical cells as a product. As was the case in the orientation experiments, the representation in question was learned using the Lee et al. (1999) extended infomax algorithm. Furthermore, an encoding was produced based on only the forward facing characters as one possible encoding, or with a 50/50 mix of forward and reverse facing digits as a control, in the same sense that a Slavic subject who is familiar with both the character N and the mirror image N is a control (Malinowski and Hübner, 2001). Examples of basis filters associated with these two stimulus sets appear in Figure 3A.

Figure 3. (A) Basis filters for an encoding of handwritten digits (left) and for a mix of forward facing and reversed digits (right). (B) Example of the type of search arrays used in the experimental simulation.
Steps involved in the simulated visual search experiments are as follows: first, a sample stimulus array was created by randomly sampling 16 28 × 28 images of handwritten digits from the set of 60,000. These images form a search array that consists of a 4 × 4 array of stimuli spaced evenly within a 392 × 392 pixel image. Examples of the sort of search arrays employed in the experiment appear in Figure 3B. The processed image is convolved with the basis filters yielding a 392 × 392 × 81 volume of feature maps. Note that 81 is the number of basis filters used to represent the 28 × 28 digits and this was produced by preceding the ICA step with PCA. Within feature map suppression and determination of stimulus salience is determined by applying the algorithm described in (Bruce and Tsotsos, 2009; remember that this result is not specific to this particular choice of algorithm). Finally, the resulting stimulus salience for the target is compared with that of the distractors as a measure of task difficulty. Ten thousand sample visual stimulus arrays and corresponding simulations of visual search difficulty were generated in this manner. Figure 4 demonstrates the ratio of target to distractor salience for four different sets of 10,000 experiments. These are (left to right) (i) basis based on forward facing letters, familiar distractors with unfamiliar target (ii) basis based on forward facing letters, unfamiliar distractors with familiar target (iii) basis based on both forward and reversed letters, familiar distractors with unfamiliar target (iv) basis based on both forward and reversed letters, unfamiliar distractors with familiar target. As can be seen from the results of this simulation, one expects a search task to be much easier for the case of a novel target among familiar distractors than the converse case. It is also worth noting that this asymmetry disappears if one is familiar with both forward and mirror imaged letters akin to the Slavic subjects familiar with both forward and reversed N’s.
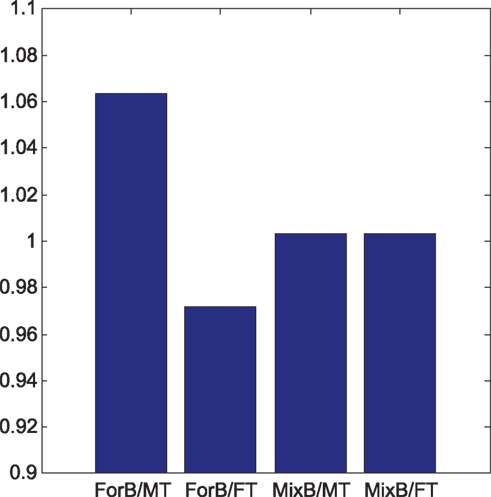
Figure 4. Average target to distractor salience across 10,000 simulated visual search trials for four search conditions. FT = forward facing target, MT = mirror imaged target, ForB = basis learned from forward facing letters. MixB = basis learned from forward and mirror imaged letters.
The nature of this behavior can be understood in considering the sparsity of the representation corresponding to forward and reversed digits respectively. Figure 6 (top) shows the response distribution of basis filters corresponding to the forward (blue) and reversed (red) digits as well as the combined stimulus set (green) for the basis learned from forward facing (left) and reversed (right) letters. The bottom row demonstrates for individual digits, the L1 norm as an approximation of sparsity. This demonstrates that the overall activation of model cells is greater in the case that the system views a novel stimulus only in the case that forward facing digits are familiar.
A second consideration is how this activity is distributed. Greater activity in itself is not necessarily predictive as it may be confined to a few mutually inhibitory cortical regions. To examine this issue, Figure 5 demonstrates the pairwise correlation of basis filters in representing forward (top right) and reversed (bottom left) digits corresponding to the basis learned from forward digits only (left) or a mix of forward and reversed digits (right). As may be seen, the novel stimuli give rise to a neural representation that is much more distributed, diminishing inhibitory interaction.

Figure 5. Correlation among basis filters learned from forward facing handwritten digits (left) and for a mix of forward and mirror image handwritten digits (right). The top right of each square corresponds to correlation among filter responses corresponding to the encoding of all forward facing digits from the data set and the bottom left to the encoding of mirror image digits. For improved contrast, white corresponds to a correlation greater than 0.3 and black to correlation of less than −0.3, with intermediate values scaled linearly between black and white.
One existing account of the novelty effect is put forth by Zhaoping and Frith(in press). In this effort, an experimental paradigm is put forth that considers the search for forward or mirror image N and Z targets among various combinations of forward facing and mirrored N and Z distractors. While the results of this study replicate some of the observations of prior experimentation, they also demonstrate that there is in fact a more complex interplay between the bottom-up stimulus driven direction of gaze that seeks the uniquely tilted bar, and the top-down confusion between target and distractor elements that share the same shape under a view-point invariant representation. While this account provides a convincing demonstration of the complex behavior that appears in this experimental paradigm, there are aspects of the general problem of novelty based search for letters that remain unexplained. In particular, in the studies of Reicher et al. (1976) and Richards and Reicher (1978), the novelty effect appears for an array that contains a mix of various different letters (See also Figure 3 in Wolfe, 2001) that do not share a common arrangement of features (even under viewpoint invariance) and for which there should be no apparent bottom-up local feature contrast assuming a standard Gabor-like model of V1 cells, as in the case for N and reverse N’s. Nevertheless, this behavior does appear in the simulation results that emerge from our model. The important property that gives rise to this behavior lies in the nature of the neural representation of the set of letters, which suggests that bottom-up guidance may be sufficient to produce these effects given an efficient representation of the set of digits, and also may imply involvement of cells that reside beyond V1. It is important to note that the nature of representation will also inevitably factor into the role of top-down deployment of attention on said representation.
3.2.3 Top-down guidance
While local iso-feature suppression is sufficient for novelty asymmetries to arise even in the case of the general letter array, the effect size remains small, and it is uncertain whether inhibitory connections among cortical units that encode these kinds of stimuli would have sufficient retinotopic extent. The study of (Zhaoping and Frith, in press) underscores the importance of considering the role of top-down involvement in determining search difficulty. For additional important discussion concerning the role of top-down guidance, see also (Wolfe, 2007; Wolfe et al., 1989). In light of the determinants of search difficulty that appear in Section 2 it is natural to consider other factors that may be important. It is conceivable that task bias plays an important role in determining search efficiency in the novelty task: response modulation of units that play a role in representing digits implies that activity corresponding to distracting stimuli may be suppressed. For this inhibition to reach units tied to a particular stimulus encoding, one requires a representation that is wired (directly or indirectly) to some central cognitive representation of the distracting stimuli. Given the highly distributed nature of the representation that arises from novel stimuli, it may be argued that no such representation exists. Moreover, it is easy to see that the combinatorics associated with connectivity to allow bias of arbitrary combinations of units would quickly exceed the capacity of the brain. By virtue of the representation associated with novel stimuli, efficient suppression is not possible and by extension task bias may also be implicated in the observed performance asymmetries.
These results give a sense of why novelty may result in an efficient search, and also why this effect is abolished if one has greater familiarity with the stimulus set. A less distributed representation of distracting stimuli implies greater suppression by way of mutual inhibition or task bias, in addition to greater overall activation. This yields an understanding of the novelty effect, or why dead elephants are hard to hide (Wolfe, 2001). It also raises an additional point of interest, namely that the discussion of whether novelty is a basic feature or not is misguided. In the same manner that the serial versus parallel distinction is an oversimplification in describing search difficulty, which exists on a continuum (Wolfe, 1998), the novelty paradigm is intimately related to, and parallels the serial–parallel distinction, corresponding to varying degrees of coding efficiency. There are no doubt other factors that play a role in search behavior as described in Section 2. Nevertheless, the coding argument made is sufficient to capture the rich array of peculiar behavior emergent from these asymmetric behavioral paradigms.
3.2.4 Why are some cases more asymmetric than others?
In (Wolfe, 2001) Wolfe notes that the effect size for asymmetries is variable and depends on the letters chosen. There are a few observations that can be made concerning this point. First, how well a mirror image digit is encoded by the representation learned for forward facing digits is a property that will be highly variable (i.e., how much overlap exists between constituent components of the mirror image of the target and components of forward facing letters that appear in the learned representation). This is seen in the poor correlation between the sparsity of respective forward and reversed digits that appears in Figure 6. The overlap in components involved in representing the target and distractor elements for a particular display is also an important factor in dictating the degree of mutual suppression among these elements. For most searches specific to one type of stimulus (e.g., forward 3 among reverse 3’s) one observes results similar to those that appear in Figure 4 albeit with most cases showing a stronger effect size due to greater overlap in the components representing distinct distractors. The important consideration to note is that while the problem is highly complex, one can appreciate how the nature of the representation involved can give rise to asymmetries and how the effect size can differ from one case to another.
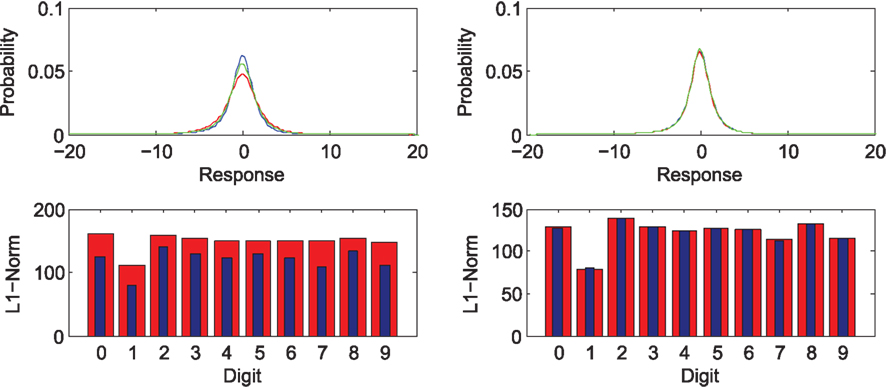
Figure 6. Top: probability density of activation across all cells for the encoding of forward facing (blue), reversed (red) digits, and a 50/50 mix of digits (green). Bottom: individual digit sparsity based on the L1-Norm for forward facing (blue) and reversed (red) digits. Left panels: representation learned from forward facing digits only. Right: based on representation learned from a 50/50 mix of forward and reversed digits.
4 Discussion
Rosenholtz (2001) discusses some interesting experimental asymmetries that appear to emerge from the fact that the experimental design is not truly symmetric. For example, the background color of a display is shown to play a role in determining task difficulty provided it shares neural machinery with the representation of target or distractors. In the cases presented here, it is by virtue of the nature of the neural machinery that the target and distractors elicit an asymmetric influence upon one another. This brings to light an interesting additional property that may be important to consider in experimental design. As the results of this paper establish, the nature of the neural representation or encoding of a stimulus is undoubtedly important in determining search behavior.
We have established that basic asymmetries, and those attributed to novelty may be explained by the combination of sparse coding and mechanisms of suppression. This is in effect the problem associated with discussion of search in such terms as serial versus parallel, basic features, or pop-out. In light of this, the notion of a basic feature is perhaps one that might be replaced by a more general statement concerning coding efficiency in the same manner that serial versus parallel is more accurately framed as inefficient versus efficient (Wolfe, 1998).
In addition, this sheds light on the problem of describing search difficulty in general which does not depend on variation along convenient descriptive dimensions that conform to human intuition concerning the world but rather depends on a complex and highly obscured neural representation.
5 Conclusion
The nature of neural representation may be implicated in many instances of asymmetric behavior in visual search paradigms, as revealed by demonstrations involving computational modeling and simulated visual search experiments.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Atick, J. J., Li, Z., and Redlich, A. N. (1992). Understanding retinal color coding from first principles. Neural Comput. 4, 559–572.
Atick, J., Li, Z., and Redlich, A. (1993). What does post-adaptation color appearance reveal about cortical color representation? Vis. Res. 33, 123–129.
Bruce, N. D. B., and Tsotsos, J. K. (2006). Saliency based on information maximization. Adv. Neural Inf. Process Syst. 18, 155–162.
Bruce, N. D. B., and Tsotsos, J. K. (2009). Saliency, attention, and visual search: an information theoretic approach. J. Vis. 9, 1–24.
Campbell, F., Kulikowski, J. J., and Levinson, J. (1966). The effect of orientation on the visual resolution of gratings. J. Physiol. 187, 437–445.
Chapman, B., and Bonhoeffer, T. (1998). Overrepresentation of horizontal and vertical orientation preferences in developing ferret area 17. Neurobiology 95, 2609–2614.
Doherty, L. M., and Foster, D. H. (2001). Reference frame for rapid visual processing of line orientation. Spat. Vis. 14, 121–137.
Dong, D. W., and Atick, J. J. (1995). Statistics of natural time-varying images. Network 6, 345–358.
Essock, E. A., Haun, A. M., and Kim, Y. J. (2009). An anisotropy of orientation-tuned suppression that matches the anisotropy of typical natural scenes. J. Vis. 9, 1–15.
Field, D. J. (1987). Relations between the statistics of natural images and the response profiles of cortical cells. J. Opt. Soc. Am. A 4, 2379–2394.
Foster, D. H., and Ward, P. A. (1991). Asymmetries in oriented-line detection indicate two orthogonal filters in early vision. Proc. Biol. Sci. 243, 75–81.
Frith, U. (1974). A curious effect with reversed letters explained by a theory of schema. Percept. Psychophys. 16, 113–116.
Gao, D., Mahadevan, V., and Vasconcelos, N. (2008). On the plausibility of the discriminant center-surround hypothesis for visual saliency. J. Vis. 8, 1–18.
Hansen, B. C., and Essock, E. A. (2004). A horizontal bias in human visual processing of orientation and its correspondence to the structural components of natural scenes. J. Vis. 4, 1044–1060.
Hawley, K. J., Johnston, W. A., and Farnham, J. (1994). Novel popout with nonsense strings: effects of predictability of string length and spatial location. Percept. Psychophys. 55, 261–268.
Hyvärinen, A., and Hoyer, P. O. (2001). A two-layer sparse coding model learns simple and complex cell receptive fields and topography from natural images. Vision Res. 41, 2413–2423.
Itti, L., Koch, C., and Niebur, E. (1998). A model of saliency-based visual attention for rapid scene analysis. IEEE Trans. Pattern Anal. Mach. Intell. 20, 1254–1259.
Itti, L., and Koch, C. (2000). A saliency-based search mechanism for overt and covert shifts of visual attention. Vision Res. 40, 1489–1506.
Koch, C., and Ullman, S. (1985). Shifts in selective visual attention: towards the underlying neural circuitry. Hum. Neurobiol. 4, 219–227.
LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998). Gradient-based learning applied to document recognition. Proc. IEEE 86, 2278–2324.
Lee, T., Girolami, M., and Sejnowski, T. (1999). Independent component analysis using an extended infomax alorithm for mixed subgaussian and supergaussian sources. Neural Comput. 11, 417–441.
Li, Z. (1996). A theory of the visual motion coding in the primary visual cortex. Neural Comput. 8, 705–730.
Li, Z. (1999). Contextual influences in v1 as a basis for pop out and asymmetry in visual search. Proc. Natl. Acad. Sci. U.S.A. 96, 10530–10535.
Long, F., Yang, Z., and Purves, D. (2006). Spectral statistics in natural scenes predict hue, saturation, and brightness. Proc. Natl. Acad. Sci. U.S.A. 103, 6013–6018.
MacNeilage, P. R., Ganesan, N., and Angelaki, D. E. (2008). Computational approaches to spatial orientation: from transfer functions to dynamic bayesian inference. J. Neurophysiol. 100, 2981–2996.
Malinowski, P., and Hübner, R. (2001). The effect of familiarity on visual-search performance: evidence for learned basic features. Percept. Psychophys. 63, 458–463.
Marendaz, C., Stivalet, P., Barraclough, L., and Walkowiac, P. (1993). Effect of gravitational cues on visual search for orientation. J. Exp. Psychol. Hum. Percept. Perform. 19, 1266–1277.
Marendaz, C. (1998). Nature and dynamics of reference frames in visual search for orientation: implications for early visual processing. Psychol. Sci. 9, 27–32.
May, K., and Zhaoping, L. (2009). Effects of surrounding frame on visual search for vertical or tilted bars. J. Vis. 9, 1–19.
Mitchell, D. E., Freeman, R. D., and Westheimer, G. (1967). Effect of orientation on the modulation sensitivity for interference fringes on the retina. J. Opt. Soc. Am. 57, 246–249.
Olshausen, B., and Field, D. (1996). Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature 381, 607–609.
Reicher, G. M., Snyder, C., and Richards, J. T. (1976). Familiarity of background characters in visual scanning. J. Exp. Psychol. Hum. Percept. Perform. 2, 522–530.
Richards, J., and Reicher, G. M. (1978). The effect of background familiarity in visual search: an analysis of underlying factors. Percept. Psychophys. 23, 499–505.
Rosenholtz, R. (2001). Search asymmetries? What search asymmetries? Percept. Psychophys. 63, 476–489.
Sagi, D. (1988). The combination of spatial frequency and orientation is effortlessly perceived. Percept. Psychophys. 43, 601–603.
Shen, J., and Reingold, E. M. (2001). Visual search asymmetry: the influence of stimulus familiarity and low-level features. Percept. Psychophys. 63, 464–475.
Tailor, D., Finkel, L., and Buchsbaum, G. (2000). Color opponent receptive fields derived from independent component analysis of natural images. Vision Res. 40, 2671–2676.
Torralba, A., Oliva, A., Castelhano, M., and Henderson, J. M. (2006). Contextual guidance of attention in natural scenes: the role of global features on object search. Psychol. Rev. 113, 766–786.
Treisman, A., and Gormican, S. (1988). Feature analysis in early vision: evidence from search asymmetries. Psychol. Rev. 95, 15–48.
van Hateren, J., and van der Schaaf, A. (1998). Independent component filters of natural images compared with simple cells in the primary visual cortex. Proc. Biol. Sci. 265, 359–366.
Vincent, B. T., Baddeley, R. J., Troscianko, T., and Gilchrist, I. D. (2009). Optimal feature integration in visual search. J. Vis. 9, 1–11.
Wang, Q., Cavanagh, P., and Green, M. (1994). Familiarity and pop-out in visual search. Percept. Psychophys. 56, 495–500.
Wolfe, J., Friedman-Hill, S., Stewart, M., and O’Connell, K. (1992). The role of categorization in visual search for orientation. J. Exp. Psychol. 18, 34–49.
Wolfe, J., and Horowitz, T. (2004). What attributes guide the deployment of visual attention and how do they do it? Nat. Rev. Neurosci. 5, 1–7.
Wolfe, J. M. (2007). “Guided search 4.0: current progress with a model of visual search,” in Integrated Models of Cognitive Systems, ed. W. Gray (New York, NY: Oxford), 99–119.
Wolfe, J. M., Cave, K. R., and Franzel, S. L. (1989). Guided search: an alternative to the feature integration model for visual search. J. Exp. Psychol. Hum. Percept. Perform. 15, 419–433.
Zhang, L., Tong, M., Marks, T., Shan, H., and Cottrell, G. (2008). Sun: a bayesian framework for saliency using natural statistics. J. Vis. 8, 1–20.
Keywords: visual search, visual representation, asymmetry, novelty, attention, attentional bias, natural image statistics
Citation: Bruce ND and Tsotsos JK (2011) Visual representation determines search difficulty: explaining visual search asymmetries. Front. Comput. Neurosci. 5:33. doi: 10.3389/fncom.2011.00033
Received: 22 February 2011;
Accepted: 24 June 2011;
Published online: 13 July 2011.
Edited by:
Klaus R. Pawelzik, University of Bremen, GermanyReviewed by:
Li Zhaoping, University College London, UKChristian Leibold, Ludwig Maximilians University, Germany
Copyright: © 2011 Bruce and Tsotsos. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Neil D. B. Bruce, Department of Computer Science and Engineering and Centre for Vision Research, 1003 CSEB, York University, 4700 Keele Street, Toronto, ON, Canada M3J 1P3. e-mail: neil@cse.yorku.ca