Sensory feedback, error correction, and remapping in a multiple oscillator model of place-cell activity

1. Introduction

Mammals maintain an internal representation of position by continually integrating their movements along a path and periodically reorienting to familiar environmental landmarks (Etienne et al., 1996; Etienne et al., 2000). The process of path integration necessarily accumulates errors due to variability in self-motion cues and must be corrected relative to an externally stable frame of reference (Etienne et al., 2004). The neural mechanisms of path integration, external cues, and their complementary interaction have not been fully characterized, such that any physiologically detailed model of navigation must rely on a large number of assumptions. Thus, it is critical to demonstrate generalized theoretical models that comport with what is currently known and that help to identify possible functional and anatomical substrates that can be assessed in future experiments.

In rodents, grid cells in medial entorhinal cortex (MEC; Hafting et al., 2005; Sargolini et al., 2006) and place cells in hippocampus (O’Keefe and Dostrovsky, 1971) carry, respectively, absolute and context-dependent spatial representations that support navigation and spatial memory (Knierim, 2006; Witter and Moser, 2006; Moser et al., 2008). The lateral entorhinal cortex (LEC) is functionally distinct from MEC and carries largely non-spatial activity (Hargreaves et al., 2005; Kerr et al., 2007; Monaco et al., 2007; Henriksen et al., 2010; Yoganarasimha et al., 2010), leading to theoretical suggestions that the context-dependence of hippocampal place-cell activity follows from the integration of information about external landmarks from LEC with the spatial metric provided by MEC (Redish, 2001; Knierim et al., 2006; Manns and Eichenbaum, 2006; Lisman, 2007; Hasselmo, 2008; Hayashi and Nonaka, 2010; Silkis, 2011). Spiking activity across both place fields (O’Keefe and Recce, 1993; Skaggs et al., 1996) and grid fields (Hafting et al., 2008) processes from late to early phases of successive cycles of the local theta (6–10 Hz) rhythm. This theta-related spiking activity may reflect a temporal code organizing hippocampal activity (Buzsáki, 2002, 2005; Harris et al., 2002; Maurer et al., 2006), however, LEC activity is only weakly theta-modulated compared to MEC (Deshmukh et al., 2010). Thus, navigation may require that asynchronous landmark information interacts with theta-synchronous spatial activity in the hippocampus. We explore this form of interaction in an abstract model of path integration and sensory feedback.

To help explain theta-phase precession, somato-dendritic interference models posit a frequency-modulated dendritic oscillation that interferes with a somatic hyperpolarizing theta oscillation (O’Keefe and Recce, 1993; Kamondi et al., 1998; Bose et al., 2000; Magee, 2001; Lengyel et al., 2003). The dendritic phase modulation in somato-dendritic models provides a potential carrier for path integration information. Oscillatory interference models of grid-cell activity extended this idea such that the temporal interference of several velocity-modulated oscillators (VMOs), supported by dendritic branches of grid cells or external oscillatory inputs to grid cells, produces the characteristic hexagonal grid patterns (O’Keefe and Burgess, 2005; Burgess et al., 2007; Hasselmo et al., 2007; Hasselmo, 2008). The relative phase differences between path-integrating oscillators in these models directly encode the current position.

While firing-rate mechanisms can transform the resulting grid-cell activity into place fields (McNaughton et al., 2006; Solstad et al., 2006; Blair et al., 2008; Hasselmo, 2009; Savelli and Knierim, 2010; Monaco and Abbott, 2011), we examine the alternative hypothesis that place fields may be generated directly by temporal interference (Blair and Zhang, 2009; Blair et al., 2010). To develop this hypothesis, we need to address the primary criticisms initially raised for oscillatory models of grid formation: that dendritically localized oscillators tend toward self-synchronization and lose independence (Remme et al., 2010), and that path integration based on precise neural timing will be rapidly overwhelmed by both cumulative noise in self-motion cues and intrinsic neuronal variability (Welinder et al., 2008; Zilli et al., 2009). Unlike grid cells, whose hexagonally periodic activity places geometric constraints on the directional modulation of input oscillations, the relative sparsity of place-cell activity may derive from the combinatorically rare synchronization of a large number of oscillators at a single location in the environment. Since it is unlikely that a pyramidal cell can intrinsically support large numbers of independent oscillations (Remme et al., 2010), we further hypothesize that the VMO population is an extrinsic layer of theta cells projecting to place cells (Blair et al., 2008; Blair and Zhang, 2009). Under this hypothesis, place cells individually compute the instantaneous amplitude envelope of their inputs, which is determined by the relative phase offsets of the oscillators, as the basis of place-field activity (Blair et al., 2010). These interference envelopes are stable, depending only on current spatial location and not on the particular movements of a trajectory. For this type of model, we distinguish two sources of error in the phase code: the large-scale systematic error that must be corrected upon introduction to a familiar environment, and the cumulative error due to phase noise that occurs continuously while path-integrating over behavioral time-scales.

In this modeling study, we simulate an extrinsic pool of VMOs with randomly oriented preferred directions and random feedforward projections to linear output units that generate place-cell activity. We show that randomly initializing VMO phases yields “complete remapping” similar to hippocampal remapping in which substantially novel environments evoke a statistically independent spatial representation (Bostock et al., 1991; Knierim, 2003; Leutgeb et al., 2005). We then introduce cue-associated phase-code feedback, which enables externally referenced calibration of the position encoded by the oscillators. We show that this phase resetting mechanism can correct for both systematic phase error and continuous phase noise. This feedback makes path integration robust to both intrinsic neuronal noise and noise in idiothetic cues, but also allows the simulation of discordant arrangements of external sensory cues. By rotating two sets of cues against each other around a circular track, we show that sensory feedback in our model produces “partial remapping” effects that resemble the hippocampal responses observed in cue-rotation experiments (Tanila et al., 1997; Brown and Skaggs, 2002; Knierim, 2002; Lee et al., 2004b).

2. Results

2.1. Path Integration Model

Temporal interference models of two-dimensional spatial activity require that VMO phases are modulated by the velocity vector of the animal exploring an environment (Burgess et al., 2007; Hasselmo, 2008; Blair et al., 2010). This modulation allows the phase code, consisting of the relative phase offsets between oscillators, to perform spatially stable path integration of a realistic trajectory. To model the activity of a population of place cells, we implemented a feedforward network (Figure 1) of VMOs driving a population of linear outputs that we call “place units.” Sparseness in the firing-rate output of the place units is enforced with feedforward inhibition modeled as a global activity threshold. Thus, place units here are linear thresholded readouts of the phase interference of their VMO inputs, and are not a biologically detailed representation of hippocampal place cells (see Section 3).

FIGURE 1

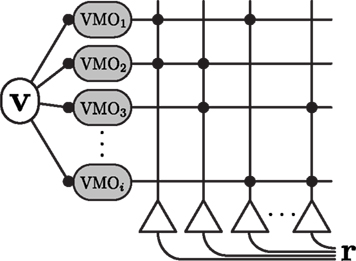
Figure 1. Schematic diagram of the path integration network, consisting of oscillatory inputs and place-unit outputs. The instantaneous velocity vector v of the simulated trajectory modulates the phases of the oscillators (Eq. 1). These velocity-modulated oscillators integrate distance traveled along independent and random preferred directions. Place-units (triangles) receive feedforward input from a random fixed-size subset of these oscillators. Phase interference produces a unique and spatially stable amplitude-modulated envelope of subthreshold activity for each place unit. The population firing-rate vector r is computed as a linear rectification of this spatial envelope for each place unit (Eq. 3). Unless otherwise specified, network simulations comprise 1000 oscillators driving 500 place units with 5% connectivity.

We define a population of N independently path-integrating VMOs as a phase vector θ evolving through time,

where f = 7 Hz is the theta carrier frequency, v = (v_x, v_y) is the instantaneous velocity vector (cm/s) of the trajectory, and M is a matrix specifying the velocity modulation of each oscillator (Burgess et al., 2007; Blair et al., 2008; Hasselmo, 2009). While running speed modulates local theta frequency in rats (McFarland et al., 1975; Geisler et al., 2007), our carrier wave has a constant frequency f. Since the carrier wave is shared across VMOs and the phase-code relies on relative phases, the addition of speed-dependence to the carrier frequency would not change our results. Unless we specify that phases are initialized to previous values, initial VMO phases are randomly sampled at the beginning of simulations presented here (see Section 4). Thus, the path integration parameters of each VMO are represented as a column of the matrix

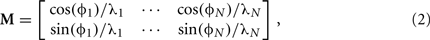
where Φ_i and λ_i specify the preferred direction and spatial scale (cm), respectively, of the ith oscillator. The phase modulation parameters are randomly and independently sampled. For the ith VMO, preferred direction Φ_i is sampled from 0 to 2π radians and spatial scale λ_i from 16 to 32 cm. The scale parameter λ determines the size of place fields and is the inverse of the slope of phase modulation along the preferred direction (Lengyel et al., 2003; Burgess et al., 2007; Blair et al., 2008). We chose a two-fold range of spatial scales with an upper bound commensurate with the radius of the track used in most simulations here (see below and Section 4), allowing for the formation of differently shaped place fields at distinct regions of the track. Further, the upper bound here matches the grid spacing (∼30 cm) of grid cells located dorsally in MEC and recorded in a larger 1 m² environment (Hafting et al., 2005). While larger scale ranges can be used to simulate larger environments with this model, the particular spatial scales used here are not determinative of our results. Based on Eq. 2, the relative phase of each VMO is positively modulated by velocities along its preferred direction, negatively modulated by velocities along the anti-preferred direction, and invariant along orthogonal directions. That is, the instantaneous effect of path integration can include either phase advance or phase delay. The amount of directional modulation is proportional to the cosine of the angle between the preferred and ongoing directions (see Section 3). For our simulations, the phase vector is numerically integrated by the first-order Euler method. Higher-order integration does not improve the quality of simulation results because phase evolution is predominantly linear.

Each place-unit receives unity-gain input from a fixed-sized random subset of the VMO population. The columns of the binary connectivity matrix J specify which VMOs provide fan-in input to each place unit. The connectivity in this model makes no assumption regarding the anatomical location of the VMOs beyond that they are an external input population shared by the place units. Unless specified otherwise, we simulate 1000 theta oscillators projecting to 500 place units with 5% connectivity (Figure 1). For every timestep, the synaptic drive to each place unit is the sum of the oscillations of its randomly chosen VMO inputs. That is, instantaneous place-unit excitation ξ is related to the VMO response vector 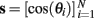by ξ = sJ so that ξ_i is an amplitude-modulated theta signal representing the total synaptic drive of the place unit i. The amplitude envelope of ξ_i reflects the degree of phase synchronization among the inputs to place unit i. Since transient synchronization among the ongoing oscillations of VMOs may represent some location in the environment (Hopfield and Brody, 2001), we define place-unit excitation as the amplitude envelope of ξ across time. We compute the envelope ξ^* = |ξ + iH(ξ)| as the magnitude of the analytic signal of the excitation time-series, where H(·) is the Hilbert transformation. It should be noted that this envelope is invariant to phase shifts such as those that may occur from one trial to the next or if the sign of the input oscillations were to be flipped. That is, simulation results here do not depend on whether the VMOs are excitatory or inhibitory (see Section 3). The output firing rate of the place unit i is computed as

where T is the global activity threshold, and brackets indicate half-wave rectification such that [x]₊ = 0 for x < 0 and [x]₊ = x otherwise. Thus, place-unit responses here are firing-rates computed as linear suprathreshold excitation. Future generalization to oscillatory spiking inputs (e.g., Hopfield and Brody, 2001) would allow the implementation of more biophysically realistic spiking outputs. While small numbers of oscillators are sufficient to produce periodic grid-cell activity (Burgess et al., 2007), larger numbers of randomly oriented VMOs are necessary to produce the unitary firing fields characteristic of hippocampal place-cell activity (Blair and Zhang, 2009). The sparsity of activity peaks across a simulated environment follows from the relative rarity of relatively strong synchronization among a larger set of oscillators. We did not fine-tune the connectivity for spatial specificity, but we found that this model produces place fields in open field environments (1 m²) using at least ∼50 VMO inputs. The threshold T is set to the median of the maximum excitation across place units. Applying place-field criteria (see Section 4), this threshold typically results in ∼40–45% activation of the place-unit population. This network sparsity is within the range of activity levels observed for ensembles of CA1 place cells (Wilson and McNaughton, 1993; Guzowski et al., 1999; Lee et al., 2004b; Leutgeb et al., 2004; Karlsson and Frank, 2008). Note that the phase-coding VMOs and rate-coding place units are independent populations: the only network interaction is the temporal interference performed by the place units. While the hippocampus comprises many different network types, the feedforward structure employed here allows consideration of the temporal coding mechanisms independent of network effects.

2.2. Circle-track Simulation

To enable comparison with the results of cue-rotation experiments (Tanila et al., 1997; Brown and Skaggs, 2002) on circular tracks (Knierim, 2002; Lee et al., 2004b), we simulated the model using an experimentally recorded trajectory (see Section 4). The time-series data for an example simulation of this 14-lap trajectory are shown in Figures 2A–C. The track angle (Figure 2A) shows predominantly forward locomotion around the track (clockwise, CW) with a small number of pauses. The instantaneous velocity vector (Figure 2B), which drives VMO phase modulation (Eq. 1), demonstrates both substantial short time-scale variability and longer time-scale periodicity due to the lap traversals (blue/green alternation in Figures 2B,C). The temporal interference patterns representing the synaptic drive of two example place units (Figure 2C) consist of cyclical peaks and valleys across the simulation. The oscillatory inputs of these two place-units synchronize to different degrees at different locations of the track. Within a single lap, their excitation envelopes are suprathreshold for different durations (Figure 2C, inset). The subthreshold activity exhibits increasing oscillatory amplitude up to the initial threshold crossing and through to the activity peak. The excitation envelopes, here analogous to the membrane voltage of a place cell, directly reflect the increase in oscillatory power. This subthreshold ramping of excitation and power in our path-integration simulation is consistent with similar observations based on intracellular recordings of CA1 place cells during place-field traversal (Harvey et al., 2009).

FIGURE 2

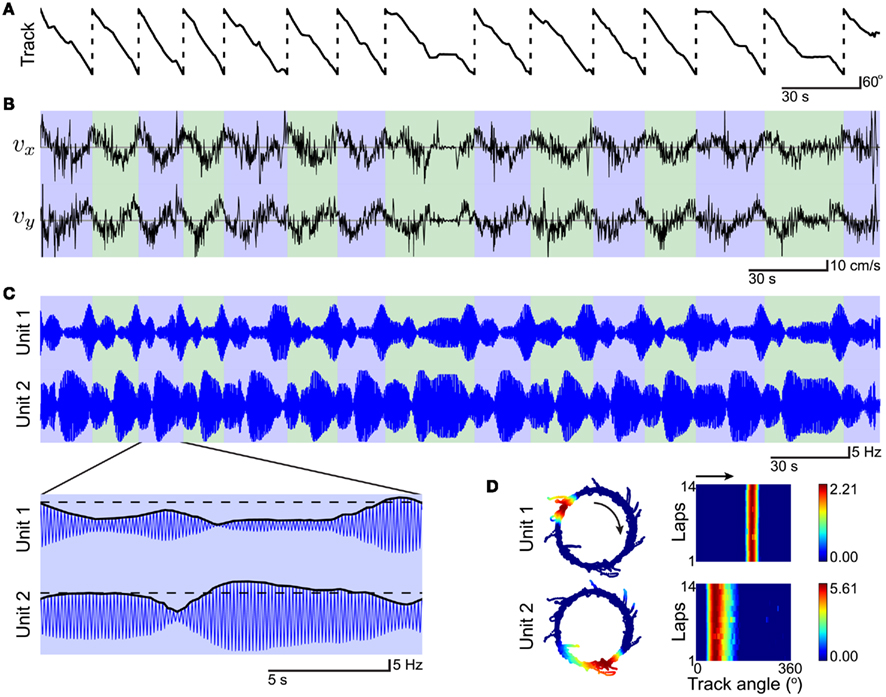
Figure 2. Example simulation of the path integration network for a 14-lap trajectory on a circular track. The input trajectory is actual position-tracking data from a previously published set of cue-rotation experiments (Lee et al., 2004b). Tracking data has been smoothed and interpolated (see Section 4) to be used as simulation input. (A) Position is converted to a track-angle relative to the track’s center (lap crossings, dashed lines) and shown for the duration of the simulation (t = 325 s). (B) The instantaneous velocity vector of the trajectory (x and y components: v_x, top; v_y, bottom) directly modulates the VMO phase vector (Eq. 1). Lap-to-lap (blue/green alternation) variation shows periodicity but also significant differences in traversal. (C) Interference patterns for two example place units with place fields. Inset: single lap with envelope (black lines) and threshold (dashed lines). (D) Firing-rates across time are mapped to position coordinates (left) to reveal distinct place fields. Linearized spatial responses (see Section 4) for each of the 14 completed laps (right) demonstrate the relative stability of VMO-based place fields. Black arrows indicate the running direction of the animal around the track.

To show the place fields, we mapped the resulting firing-rates across time to the spatial coordinates of the trajectory. The place fields of the two example outputs are distinct and unimodal (Figure 2D, left). The fields can be symmetrical (Unit 1) or asymmetrical (Unit 2) depending on the distribution of preferred directions of the component VMOs which synchronize to produce the fields. Response matrices of the individual laps show the high lap-to-lap stability of the place-unit activity [Figure 2D, right; population correlations of per-lap and pooled responses (see Section 4), N = 14 laps, r = 0.991 ± 0.002, mean ± SD] despite significant variability in the velocity signal (Figure 2B). Thus, temporal variability due to the details of the trajectory is counteracted by path integration to provide spatially stable responses for different runs around the track. For this simulation, 42% of the place-unit population had place fields: out of 500 place units, 182, 25, and 2 had 1, 2, or 3 place fields, respectively. Active place units (N = 209) had peak firing rates of 2.4 ± 1.7 Hz, a maximum rate of 9.9 Hz, and spatial information scores of 1.88 ± 3.78 bits (see Section 4). Place fields (N = 238) had track-angle sizes of 55 ± 24°, corresponding to lengths of 32 ± 14 cm assuming the track-center radius of 33 cm. The spatial scale of these simulated place-fields matches that of grid (Hafting et al., 2005; Fyhn et al., 2007) and place (Lee et al., 2004b; Maurer et al., 2005) cells recorded near the dorsal poles of entorhinal cortex and hippocampus.

Without retrieval of a previous representation, the ongoing phase code in a novel environment may interact with unfamiliar sensory inputs to produce a novel phase code. We demonstrate complete remapping of the population spatial code by randomizing the initial phase vector of the VMO population. The network is simulated as in Figure 2 but with two different random initial phase vectors corresponding to distinct environments A and B. Individual place-unit responses across environments (Figure 3, top) show a variety of remapping behaviors, including changes in firing rate, shifts in field location, and the appearance or disappearance of place fields. The place fields of environment A uniformly spanned the extent of the track (Figure 3, bottom left). The population responses (Figure 3, bottom), with place-units sorted by peak firing location in environment A, were fully remapped by the randomization of the initial VMO phases [population correlation between environments (see Section 4), r = -0.006, p < 0.01] without changing the spatial information scores of the place-unit responses [F(1,483) = 0.105, p > 0.5].

FIGURE 3

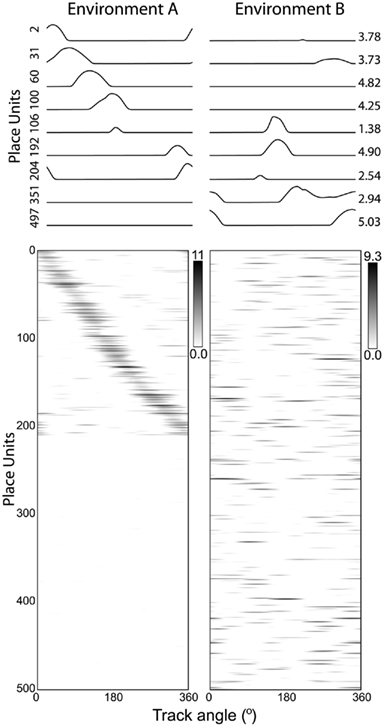
Figure 3. Complete remapping by randomized phase initialization. We compare responses from two simulations of the same path integration network: initialized with two different phase vectors representing environments A (left) and B (right). (Top) Individual place-unit responses (place-unit index, left) have place fields that variously appear, disappear, or remap their firing positions and/or rates (peak firing rate, right) between environments. (Bottom) Population response matrices show that place units, sorted by peak firing position along the track in environment A, exhibit primarily unimodal spatial activity that evenly spans the extent of the track. The population spatial representation randomly remaps between environments A and B.

2.3. Sensory Feedback from External Cues

We now introduce sensory cue inputs to our path integration model (Figure 4) that perform smooth and spatially extended phase resetting of the oscillators. Resetting the path integrator is a necessary condition for stable navigation in mammals (Etienne et al., 2004). The unit of this phase reset is an external cue whose interaction with the VMO population is described as a circular Gaussian centered at some position on the track. We define the cue interaction coefficient C_cue as a von Mises function,

FIGURE 4

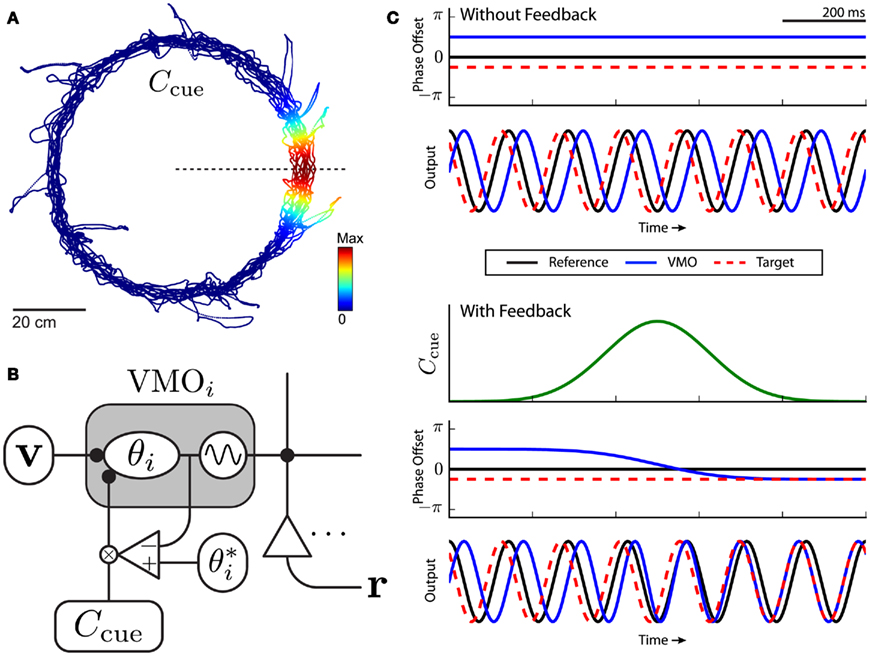
Figure 4. Sensory cue interaction as phase-code feedback. (A) The spatial profile of cue interaction C_cue is a circular Gaussian field (Eq. 4) oriented at some position on the track (dotted line). Example cue is 15° (SD) wide and centered at 0°. (B) Schematic circuit diagram of the abstract phase feedback mechanism (Eq. 5) for a single oscillator from the VMO population. The ith VMO is decomposed into its phase variable θ_i and output waveform. The phase of every oscillator receives the same velocity (v) and sensory (C_cue) inputs, and has an oscillator-specific feedback target depending on the current (closest) cue on the track. Phase targets are learned by path integration during the first lap. The phase difference between the ongoing (θ) and target (þeta*) phase offsets is gain modulated (×) by the strength of the cue. (C) Illustration of VMO synchronizing to a phase target. (Simplified for purposes of illustration, see Figure 5 for simulation and analysis output.) Top two panels: without feedback, constant phase offsets (top) yield out-of-phase oscillations (bottom). Bottom three panels: idealized cue interaction (top) modulates VMO phase offset (middle) so that its oscillation becomes phase synchronized with the target (bottom).

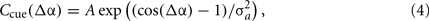
where Δα is the angle in radians between current track position and cue center, A is the peak gain of the cue, and σ_a is the cue size specified as the arc SD in radians of the cue interaction profile. An example 15° cue interaction centered at 0° is shown in Figure 4A. Though we refer to this interaction as an external cue, we are explicitly modeling only the spatially modulated influence (Eq. 4) of an environmental or sensory cue on the path integration mechanism. Here, cues directly control feedback to the oscillators (Figure 4B). The feedback targets are fixed points of the phase code, defined as a vector of phase angles relative to a shared carrier wave. Phase targets are acquired by path integrating the first lap of the trajectory (Eq. 1) and storing a vector of VMO phase offsets at the first crossing of each cue (see Section 4). There may be multiple cues, each of which is associated with a distinct phase target vector, but we initially consider single-cue simulations. Without modifying the output mechanism (Eq. 3), cue feedback is added to the phase equation (Eq. 1) so that

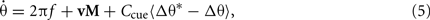
where Δθ is current phase offset vector; Δθ^* is the phase target vector associated with the cue; and 〈〉 signifies that phase differences are wrapped to the range [−π, +π). The wrapped phase differences provide a linear contribution to phase synchronization between the ongoing phase of VMOs and the phase targets associated with the cue. Thus, the cue interaction C_cue multiplicatively modulates the gain of a VMO-specific phase-code feedback signal (Figure 4B). Traversing an external cue independently impels each theta oscillator, either retarding or advancing its phase, toward a previously learned target. This is a not a perfect or instantaneous reset of all phases to the same angle (Burgess, 2008; Hasselmo, 2008), but a smooth approach to a point in the space of relative phases. An illustration of the effect of feedback on VMO activity (Figure 4C) shows the ongoing oscillation of a VMO gradually resetting toward its target phase defined relative to a reference theta wave. Note that while nearly perfect synchronization is shown for purposes of illustration (Figure 4C), a generalized solution for the phase reset is derived below and model simulations are shown in Figure 5.

FIGURE 5

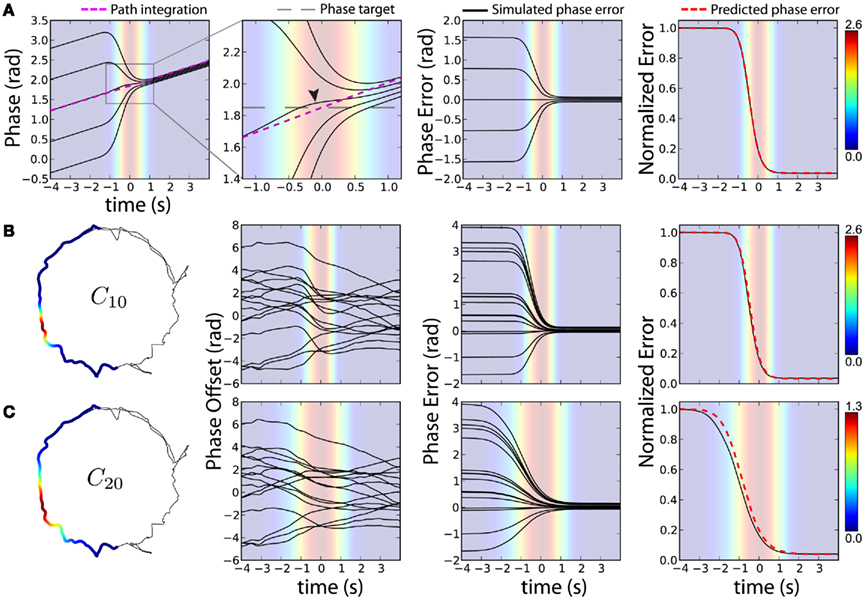
Figure 5. Correction of initial phase error during cue traversal. We show idealized simulations of a single oscillator (A) and circle-track trajectory simulations of a population of oscillators (B,C). Phase angles [first (A) and second (A–C) column], phase error (relative to cue interaction with 0 initial phase error, third column), and normalized error [simulated and predicted (Eq. 6, red dashed line), fourth column] show the time-course of error correction. Background color indicates cue modulation. (A) VMO is simulated for a linear constant-speed traversal of a 0.5-s SD cue. Phase angles for different initial phase errors (black lines) show modulation toward the phase target (thick dashed line, second panel) around the peak of the cue interaction (t = 0) and approach path integration (dashed magenta line) after the cue. Crop: second panel data same as within gray rectangle in first panel. (B,C) For cue sizes of 10 (B) and 20 (C) degrees SD, the 8-s time window around cue peak (shown as cue coefficients C₁₀ and C₂₀ on the first lap, left) is shown for 16 VMOs simulated with random initial phase errors on the first lap around the circle-track. Despite independent path integration, error correction for each oscillator follows the same time-course. The larger cue (C) evoked a temporally skewed sensory interaction, accounting for earlier correction than predicted by a symmetric interaction.

2.4. Phase-code Retrieval by a Single Cue

To understand the relationship between cue interaction and the resulting phase-code modulation, we consider a VMO integrating a straight line through a cue at constant speed. For this idealized cue traversal, path integration reduces to a linear function of time in which the slope of the phase depends on the running direction and the VMO parameters (Eq. 2). If Δθ₀ is the initial phase offset of the training lap, then we can introduce an initial phase error η₀ in a subsequent lap or simulation by initializing the VMO phase to Δθ₀ + η₀. With no cue present, this phase error will be constant; introducing cue-based feedback will change the magnitude of the phase error over time as the cue is traversed. To determine analytically the time-course of phase error for a linear traversal, we treat the cue interaction (Eq. 4) as a linear Gaussian function through time 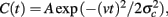where σ_c = Rσ_a, R = 35 cm is the track radius, v is the running speed, and the peak of the cue occurs at t = 0. We can then approximate the error correction performed by a cue by reformulating cue feedback (Eq. 5) with respect to phase error such that 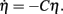Integrating this phase error approximation,

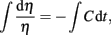
shows that phase error follows

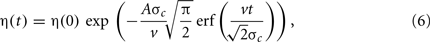
where η(0) is the remaining phase error at cue peak. This time-course describes a monotonically decreasing sigmoid function with the fastest correction occurring at cue peak. The fraction of the initial error remaining after the cue interaction, which we call the error tolerance, can be computed by evaluating the phase error at the limits:

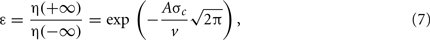
where η(−∞) and η(+∞) are initial and remaining amounts of phase error, respectively. We calculate the peak gain for any given cue interaction by solving (Eq. 7) for A by setting our desired error tolerance to ε = 0.05, the speed v = 13.3 cm/s to the average running speed of the trajectory, and σ_c to the parameterized cue size. Thus, simulated cue traversals will, on average, yield 95% total correction of phase error regardless of cue size.

To illustrate initial phase error correction, we simulated a single oscillator following an idealized cue traversal as described above (Figure 5A). This VMO had preferred direction Φ = π/3 radians and spatial scale λ = 32 cm. The running speed was a constant v = 10 cm/s along the positive x-axis. Path integration alone (Eq. 1) produced a linear phase modulation (Figure 5A, magenta dashed line) whose value at t = 0 provided the phase target Δθ^* = 1.84 radians (Figure 5A, gray dashed line). We then activated the cue feedback using a cue size of σ = 5 cm and simulated the same traversal with initial phase errors of 0, ±π/4, and ±π/2. The resulting phase trajectories smoothly approached the original path-integration phase code (Figure 5A, two left panels, black curves). Without initial phase error, the cue itself (Figure 5A, second panel, curve indicated by arrowhead) elicited a bidirectional phase modulation relative to path integration by advancing and retarding the phase prior to and after, respectively, the peak of the cue interaction. We computed phase error across time (Figure 5A, third panel) by subtracting this cue-only modulation. Phase errors, shown as both absolute and normalized phase differences, are reduced during cue traversal (Figure 5A, two right panels) following the predicted time dependence (Eq. 6; red dashed line).

Circle-track simulations of a population of randomly oriented VMOs (Figures 5B,C) show the same stereotyped error correction as the idealized cue traversals. We simulated 16 VMOs with random initial phase errors traversing 10° (Figure 5B, C₁₀) and 20° (Figure 5C, C₂₀) cues across the first 25 s of the trajectory. The resulting phase trajectories show temporal variability based on the spatiotemporal details of the behavioral trajectory. Phase errors, computed as in Figure 5A, show that the actual time-course of error correction was modulated by cue size even though the two cue sizes elicit similar overall error correction (median ε = 0.036 and 0.040 for C₁₀ and C₂₀, respectively). Interestingly, error correction for the larger cue appears to have been shifted earlier than predicted. The initial edge of C₂₀ (Figure 5C, left) overlapped a location where the trajectory momentarily slowed down, enhancing the amount of cue feedback at that location (Figure 5C, right) relative to predictions based on a temporally symmetric cue interaction (Eq. 6). These initial phase errors are the type of error that provoked complete remapping in Figure 3. By restoring the phase code at the appropriate location, we suggest that “familiar” sensory cues can retrieve a previous spatial representation.

2.5. Continuous Phase Noise

Independent, ongoing phase-noise rapidly destabilizes spatial activity in oscillatory interference models (Welinder et al., 2008; Zilli et al., 2009; Zilli and Hasselmo, 2010) as phases randomly drift apart. To examine the effects of such continuous phase noise, we simulated spatial responses of a place-coding network with (Eq. 5) or without (Eq. 1) a cue for various multiples mσ of a baseline phase dispersion σ = 0.05 radians. This dispersion is equivalent to σ(2πf)⁻¹ = 1.1 ms, which is low enough to provide 76 s of phase-code stability according to the metric derived by Zilli et al. (2009). The anatomical and physiological source of the VMO signals posited by this model is unknown (see Section 3), so we cannot easily estimate biologically realistic levels of phase noise. However, according to period variance measurements by Zilli et al. (2009) of several parahippocampal oscillators, the range of noise levels that we test here overlaps typical distributions of biological phase noise.

The cue for the simulations shown in Figure 6 is the same as C₁₀ in Figure 5B. For each simulation timestep of duration Δt, we sample a phase-noise vector from 𝒩(0, m²σ²Δt) and add it to the VMO phase vector. We computed the population spatial correlations (see Section 4) between each test condition and a reference simulation consisting of path integration with no noise or cue. Correlations are element-by-element Pearson product-moment coefficients between population rate matrices. The whole-session correlations (Figure 6A) show that 1σ dispersion produces moderate decorrelation (Pearson r = 0.664) while 4σ dispersion yields nearly uncorrelated spatial activity (r = 0.0546). The cue counteracts the effect of noise so that the 4σ (r = 0.850) and 8σ (r = 0.532) conditions show relatively strong spatial correlations. Correlations across individual laps (Figure 6B) show progressive decorrelation with high noise levels that is prevented by the presence of the cue. However, strong correlations tend to occur only near the location of the cue (Figure 6C), with the slope of decorrelation away from the cue dependent on the noise level. Multiple cues may be necessary to enable more frequent phase resets and prevent the decorrelation of spatial activity by phase noise.

FIGURE 6

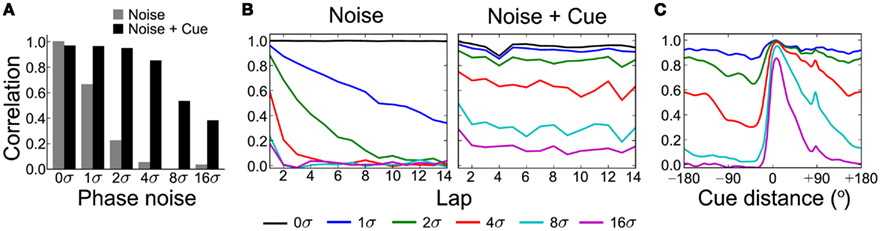
Figure 6. Continuous phase-noise decorrelation of spatial map counteracted by cue. We simulate full circle-track sessions with a single cue (same as Figure 6B) and varying levels of independent continuous noise injected into the VMO phase vector (see Section 4). The baseline noise level σ = 0.05 radians was chosen to produce moderate spatial decorrelation across the 325-s simulation (see Section 2 for details). Measurements are relative to the population response due to path integration (0σ, no cue). (A) Population spatial correlations (see Section 4) with (black) and without (gray) the cue present for multiples of σ. (B) Correlations are computed for each of the 14 individual laps around the track in the cue (right) and no-cue (left) simulations. Cue feedback prevents progressive decorrelation across laps. (C) Cue-centered average of population correlations across the track (see Section 4). The cue strongly but transiently restores local spatial correlations even at high levels of phase noise.

2.6. Partial Remapping

The double cue-rotation paradigm (Tanila et al., 1997; Knierim, 2002) differentially rotates two sets of external cues around the track to create an ambiguous or discordant sensory environment. In a cue-conflict configuration, local (track-based) and distal (room-based) cues are rotated counter-clockwise (CCW) and clockwise (CW), respectively, relative to a familiar configuration. We simulate double rotation (see Section 4) by coherently rotating the track-angle positions of cues within two independent cue sets (C_A and C_B; Figure 7, top). Each of the three cues in a set is active within a one-third sector of the track. We extend the cue feedback mechanism (Eq. 5) to two cue sets additively so that VMO phases follow

FIGURE 7

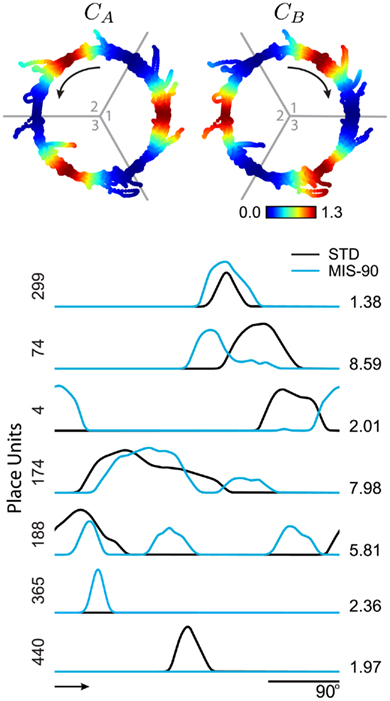
Figure 7. Double-rotation experiment simulated with a 90° cue mismatch. Two independent sets of cues (represented by cue interactions C_A and C_B) were simulated both in standard (STD, or “familiar”) and mismatch (MIS-90) configurations. Cue sets (STD configuration, top) consisted of three 20° cues that were each active on one-third of the track (enumerated areas) and were rotated 45° counter-clockwise (CCW arrow, left) or clockwise (CW arrow, right). Examples of simultaneous place-unit responses to the cue mismatch (bottom) include rate remapping, cue following in both CW and CCW directions, and on/off remapping. Arrow, bottom: CW running direction. Population responses for these data are shown in Figure 8.

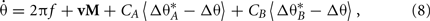
where C_A and C_B are the cue coefficients of the two sets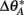, and and 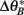are the phase targets of the active cues in each set. We show individual responses from a 90° cue mismatch (MIS-90; Figure 7, bottom) and population responses for a series of mismatch angles (Figure 8) simulated with the same place network and cues. Among the place-unit responses (Figure 7, bottom), there are examples of rate remapping (Unit 299), CCW (74) or CW (4) cue following, ambiguous responses (174 and 188), and place-field activation (365) or silencing (440). For each of four mismatch conditions, we compute the rotation angles and peak correlations (see Section 4) of all the place-unit responses. The distribution of responses across rotation and correlation are shown as two-dimensional histograms in Figure 8A. For the smallest mismatch angle (MIS-45), the singular response mode (rotation, 1.63 ± 0.45°, circular mean ± SEM; correlation, r = 0.95 ± 0.0038, mean ± SEM) is largely invariant to the mismatch. In contrast, the responses to MIS-90 are much more varied (cf Figure 7), consisting of cue-following modes in both rotation directions in addition to a large number of low-correlation responses. The larger mismatch angles elicit a stronger CCW cue-following mode and fewer ambiguous responses.

FIGURE 8

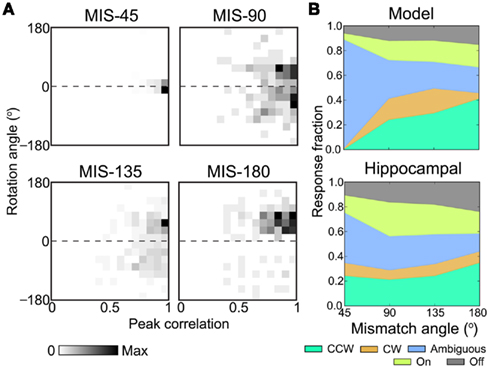
Figure 8. Population remapping response to various cue mismatch angles. For the same network in Figure 6, we simulated double-rotation mismatches of 45, 90, 135, and 180 total degrees between cue sets. Peak correlation and rotation angle (see Section 4) were computed for every place unit. (A) Two-dimensional 16 × 16 histograms of place-unit correlation and rotation (dashed line, no rotation) demonstrate different remapping modes across mismatch angles. MIS-45 was highly stable, while the population response to MIS-90 was dispersed. Histogram maxima: MIS-45, 112; MIS-90, 11; MIS-135, 26; and MIS-180, 14. (B) Individual responses were categorized (see Section 4) as cue following (CCW or CW) or remapping (On or Off) or neither (Ambiguous). Stacked category charts show response prevalence across mismatch angles for simulation results (top) and a hippocampal data set (bottom). The hippocampal data (spike times and position tracking from five rats, Lee et al., 2004b; J. Neunuebel, unpublished) has been re-analyzed here for visualization (see Section 4). No previous figures have been adapted.

We classified place-unit mismatch responses into remapping categories based on peak correlation and rotation angle (see Section 4). Coherently rotated responses were classified as cue following; the activation/deactivation of place units was classified as on/off remapping; the remaining responses were considered ambiguous. The distributions of response types (Figure 8B, top) highlight the decreasing proportions of ambiguous responses and increases in both coherent and on/off remapping responses with increasing mismatch angles. Notably, the simulated response distributions showing bias toward the CCW cues qualitatively resemble those of a hippocampal data set (Figure 8B, bottom; see Section 4). However, the simulated MIS-45 condition showed no coherent rotation and less remapping than the hippocampal data. Coherent rotation at small mismatch angles could be introduced by, for instance, increasing the number of CCW cues. Due to the minimal construction of this model, it is not instructive to fine-tune the configuration of the cue sets to more exactly match experimental data, but it is notable that CCW bias occurred despite the two cue sets having the same size and number of cues. To demonstrate that the amount and direction of cue bias depend on network parameters, we simulated 12 additional MIS-90 experiments with new VMO-place networks. Despite similar proportions of overall cue following (0.204 ± 0.014, mean ± SD), the cue mismatch produced CCW-to-CW ratios (1.02 ± 0.238) ranging from 0.729 to 1.57. The phase-code interaction between conflicting cues (Eq. 8) is able to produce heterogeneous mixtures of remapping responses consistent with the partial remapping observed in double cue-rotation experiments (Lee et al., 2004b).

2.7. Linear Phase Reset with a Spiking Neuron

While this study investigates effects of sensory feedback, our firing-rate model does not address the underlying neural mechanisms. To demonstrate a plausible phase feedback mechanism, we require, first, a more detailed oscillator model and, second, an input representation of the encoded phase target. We simulated a single theta oscillator as a leaky integrate-and-fire (LIF) neuron, allowing phase reset to be measured as a change in spike timing. The phase target is here represented as the relative timing of the sensory stimulus corresponding to an external cue (see Section 3). For the feedback to be effective, the phase reset evoked by the stimulus must reduce the phase difference between the stimulus and the oscillator. The phase resetting curve (PRC) representing the LIF phase response to stimulus timing can take different forms depending on the temporal profile of the stimulus. We are interested in the total effect of a stimulus on spike timing, whether the stimulus results in an advance or delay of the output spike relative to a control condition with no stimulus. Thus, we calculate the PRC (see Section 4 and Eq. 12) to include the effects of first and second order phase resetting (Oprisan et al., 2004). Here, we use the conventions that positive phase reset indicates a delay in spike timing and that 0-phase is defined by the control spike times.

Demonstrating that the sensory feedback from our firing-rate model can be implemented with a spiking oscillator requires both cue modulation (Eq. 4) and the linear feedback term that synchronizes the oscillator with a phase target (Eq. 5). The gain modulation induced by the cue can be implemented as the magnitude of the sensory stimulus. The feedback term is a phase difference wrapped to the range [−π, π] (Eq. 5). Thus, it must be shown that stimulus timing can produce a linear phase reset analogous to the phase difference term. That is, the phase at which a stimulus occurs must cause the spike timing to approach that same stimulus phase on later cycles, and the size of this phase reset should be linearly related to the stimulus phase. Additionally, the wrapped phase difference entails a discontinuity whereby differences larger than one half-cycle produce a change in sign. The essential requirement, however, is that each oscillator can be either advanced or delayed toward synchronization with the phase target. The spiking PRC must be bidirectional. By contrast, the linearity and discontinuity of the phase reset assumed in our firing-rate model are secondary features that are not strictly required for effective phase feedback, but they are consistent with the output of the spiking model below.

We simulated the LIF theta oscillator in a control condition with no stimulus and then in a series of stimulus conditions (see Section 4). We computed subthreshold membrane voltage V following

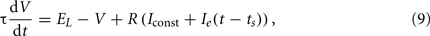
where membrane time constant τ = 40 ms and total membrane resistance R = 100 MΩ, and using 0.01 ms timesteps with forward Euler integration. Spikes occur when V reaches spike threshold V_th = −50 mV, and V is reset to the leak potential E_L = −70 mV. We solved analytically (Dayan and Abbott, 2001) for the constant input current I_const = 0.206 nA that provides a regular interspike-interval firing rate of 7 spikes/s. In the control condition, where the external input current I_e(t) = 0, the cell fires at regular theta rhythm (Figure 9A, black trace). In stimulus conditions, t_s defines the timing of stimulus occurrence and the external input follows a biphasic temporal profile,

FIGURE 9

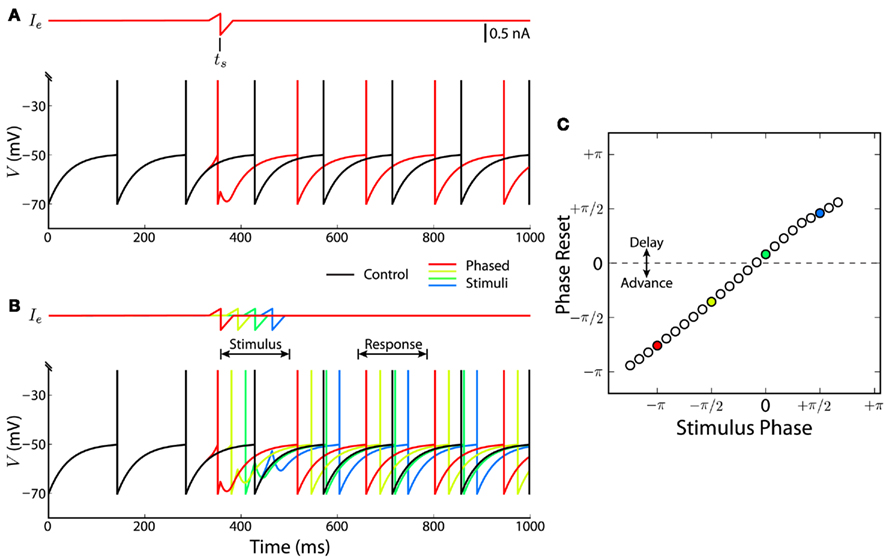
Figure 9. Spiking neuron demonstration of a bidirectional linear phase reset. We simulated a leaky integrate-and-fire model neuron (Eq. 9) spiking at a regular 7-Hz theta rhythm. Spike times are visualized as vertical lines superimposed on voltage traces. (A) We compare a control condition with constant input current (black trace) with a stimulus condition in which a biphasic sensory stimulus (I_e, Eq. 10) was injected centered at time t_s (red trace). (B) For a series of stimulus times within a theta cycle (“Stimulus”), we measured the resulting phase reset of the model neuron within a later theta cycle (“Response”). Voltage traces and spikes for four of these phased stimuli are shown, demonstrating phase advance or delay depending on the relative phase of the stimulus. (C) The phase resetting curve of the model neuron is shown [colored circles correspond to voltage traces in (B)]. Consistent with our cue-based feedback model (Eq. 5), the phase reset is bidirectional, linear, and discontinuous.

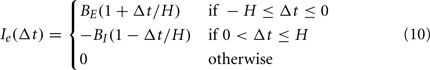
where the stimulus half-window H = 25 ms. This stimulus consists of a leading excitatory phase and a trailing inhibitory phase with gains of B_E = I_const and B_I = 2B_E, respectively. For computational convenience, the stimulus time t_s specifies the mid-point of these two phases for a given stimulus. A stimulus occurring halfway through a theta cycle (Figure 9A, red trace) noticeably draws the spike timing of the oscillator toward the middle of the reference theta cycle established by the control condition. The ordering of spikes from four example stimulus simulations (Figure 9B) matches the order of the stimuli, indicating that the oscillator is advancing or delaying based on stimulus timing. To evaluate the PRC (see Section 4), we simulated a series of stimulus times spanning a single theta cycle (Figure 9B, “Stimulus”) and measured the phase reset Eq. 12 during a subsequent theta cycle (Figure 9B, “Response”). Stimulus phase is measured as the phase difference between t_s and the control spike time at the center of the “Stimulus” theta cycle. The PRC, measured for 25 stimulus phases, shows that the spike phase response is bidirectional, highly linear, and discontinuous (Figure 9C). The subtraction used to compute the phase reset (Eq. 12) means that positive values correspond to delays in oscillator spike timing, and negative values correspond to advances in spike timing.

Whereas the slope and shape of the PRC depend on the temporal profile and magnitude of the stimulus, this particular stimulus at least serves to demonstrate that the bidirectional and linear phase reset assumed by our firing-rate model is plausibly implemented using a spiking model of a theta oscillator. The temporal profile that we chose reflects the hypothetical encoding of a sensory input sequence using spike timing-dependent plasticity (STDP; Abbott and Nelson, 2000; Kepecs et al., 2002). STDP can produce predictive coding, inhibitory tuning, and temporal compression of activity sequences within time-windows of tens of milliseconds in hippocampus (Abbott and Blum, 1996; Mehta et al., 2000) and sensory systems (Mu and Poo, 2006; Roberts and Leen, 2010). As an alternative mechanism, some type-II neuronal oscillators have intrinsic dynamics that allow both phase advance and phase delay (Hansel et al., 1995; Ermentrout, 1996; Oprisan et al., 2004; Tateno and Robinson, 2007) without using a biphasic stimulus. Nonetheless, our abstract firing-rate model, which may be regarded as a linear approximation to more complex phase resetting, provides a basis for understanding more detailed implementations of phase-code feedback.

3. Discussion

3.1. Temporal Interference Model with Sensory Feedback

We examined a temporal interference model of VMOs with sensory feedback as a way to integrate landmark-based navigation into path integration. We found that a spatiotemporally extended reset of the path integrators can provoke realistic partial remapping when familiar cues are put into conflict. There are distinct subregional differences in the hippocampal response to double cue rotation (Lee et al., 2004a,b), so several mechanisms may contribute to the observed mixture of coherent and remapping responses (Shapiro et al., 1997; Tanila et al., 1997; Knierim, 2002). We found that partitioning cues into independent sets can simultaneously produce coherent cue following in both directions, various ambiguous responses, and the appearance or disappearance of place fields. Thus, phase-code competition between conflicting sets of cues may help explain the heterogeneity of hippocampal response to environmental alteration. While previous models based on attractor networks (Touretzky et al., 2005) or partial realignment of MEC grid cells (Fuhs and Touretzky, 2006; Hayman and Jeffery, 2008) have been used to demonstrate partial remapping, theta-phase interference is a general temporal coding mechanism that may support hippocampal (Blair and Zhang, 2009; Blair et al., 2010) as well as entorhinal (O’Keefe and Burgess, 2005; Burgess et al., 2007; Burgess, 2008; Hasselmo, 2008) spatial representations.

The biological plausibility of our abstract firing-rate model requires neural implementations for reading out the interference of external oscillators. Our model place-units receive oscillatory inputs as sinusoidal signals that are integrated by linear summation. For a biological place cell, the inputs are pre-synaptic spikes that produce changes in post-synaptic transmitter concentrations, and the output is whether the cell spikes (or bursts). Assuming that input spike trains are at least theta-rhythmic, they can exhibit varying degrees of phase coherence. Non-coherent or asynchronous inputs may not produce a sufficient number of inputs within the integration time-window of the place cell to produce a dendritic spike or neuronal action potential. Thus, all else being equal, asynchronous oscillatory inputs can decrease the firing rate of (or silence) a place cell. Similarly, highly coherent oscillatory inputs can produce more spikes impinging on the post-synaptic membrane within the integration time-window, potentially resulting in suprathreshold excitation and spiking activity. This excitatory effect of input spike synchrony has been studied generally with biophysically detailed cortical neuron models (e.g., Wang et al., 2010) and integrate-and-fire models illustrating grid-cell integration of oscillatory inputs (Burgess, 2008). Thus, the mapping of VMO interference patterns to the place-unit firing-rate output in our model can be neurally implemented by the mapping of input spike synchrony to place-cell spiking activity. Equivalently, if we consider that the theta oscillators may be inhibitory cells, then the temporal details of integration may change, but the mechanism for reading out phase interference holds. Inhibitory theta-cell inputs would require baseline excitation to balance the inhibition from asynchronous inputs. Then, phase synchronization among the inhibitory inputs would produce a large amplitude post-synaptic oscillation consisting of alternating strong inhibition and strong disinhibition. The strong disinhibition coupled with the baseline excitation would produce theta-related spiking of the post-synaptic place cell. This form of excitatory–inhibitory balance has been experimentally and theoretically characterized on the basis of distinct dendritic and somatic oscillations in place cells (Kamondi et al., 1998; Magee, 2001; Lengyel et al., 2003; Losonczy et al., 2010).

A primary criticism of temporal interference models has been the sensitivity of the phase-code to noise (Welinder et al., 2008; Zilli et al., 2009). Any model of path integration loses accuracy with both intrinsic noise and noise in self-motion inputs (Welinder et al., 2008; Remme et al., 2010; Zilli and Hasselmo, 2010), but the accuracy of phase-code models additionally depends on temporal precision of neural activity on the order of tens of milliseconds. Several factors in the model explored here help to mitigate noise sensitivity of the positional code. Common-input sources of noise in the theta rhythm do not affect the positional code because it is based on relative phases between oscillators. Since our simulated VMOs are extrinsic to the place cells, they could be modeled separately as ring attractor networks that naturally maintain internal phase coherence (Blair et al., 2008) and avoid the potential for phase-locking between electrotonically coupled dendritic oscillators (Remme et al., 2010). However, intrinsic neuronal variability of theta cells and other sources of independent phase noise can rapidly degrade the positional code. We showed that representing familiar cues as a phase feedback process can counteract this type of noise. Multiple cues arrayed across an environment can continually recalibrate a noisy phase code to provide navigational stability.

We demonstrated that phase feedback, which addresses the noise sensitivity of the temporal code, can further act as a retrieval mechanism. Exposure to familiar cues impels randomly aligned oscillators to a previously learned point in-phase space represented as a phase target vector. Since all VMOs in our model are synchronized concurrently, the feedback we study is consistent with the all-or-none switching of spatial representations that occurs when animals are moved between distinct but familiar environments (Wills et al., 2005; Fyhn et al., 2007). However, we only implemented phase feedback phenomologically (as a wrapped phase-difference-minimizing term in the phase equation; Eq. 5), which raises the question of how independent synchronization of an oscillator population to a target vector may be implemented in a neural circuit. Phase targets may be learned based on landmark-related sensory information carried by LEC into the hippocampus (Hargreaves et al., 2005; Knierim et al., 2006; Kerr et al., 2007; Lisman, 2007; Monaco et al., 2007; Yoganarasimha et al., 2010). Since LEC activity is only weakly theta modulated (Deshmukh et al., 2010), it may be necessary for non-theta cue representations (Figure 4A) to become associated with specific theta-phase targets for each VMO. We showed that one way to encode the phase target is by locking the stimulus timing to the phase target (Figure 9). While we did not model the learning process that may perform this phase encoding, previous models have demonstrated encoding and recall in theta-modulated networks (Jensen et al., 1996; Wallenstein and Hasselmo, 1997; Hasselmo et al., 2002; Igarashi et al., 2007) using timing-based learning rules such as STDP (Lengyel et al., 2005; Câteau et al., 2008; Nolan et al., 2010). Additionally, our demonstration of stimulus timing-based phase-code retrieval using a spiking oscillator showed that effective encoding may rely on producing a stimulus representation with a trailing hyperpolarization. Further, if VMOs are independent, then the same phase-code retrieval process can operate in parallel so that for each VMO in the input population is concurrently synchronized to its specific target. It remains for future work to develop biologically realistic models of phase-code feedback in the path integration system.

3.2. Intrinsic versus Extrinsic Path Integrators

In oscillatory interference models (O’Keefe and Burgess, 2005; Burgess et al., 2007; Hasselmo, 2008) of grid-cell activity (Hafting et al., 2005; Sargolini et al., 2006), grid-cells compute path integration intrinsically and place-fields instantaneously reset the spatial phases of co-active grid cells by feedback that temporally synchronizes grid-cell oscillations (O’Keefe and Burgess, 2005; Burgess et al., 2007; Burgess, 2008; Hasselmo, 2008). The present model extends previous studies positing a parallel system of theta cells that project independently to grid cells and place cells (Blair and Zhang, 2009; Blair et al., 2010). The sensory feedback mechanism that we investigate here explores how phase reset could both calibrate path integration and enable various forms of remapping in this type of common-input and feedforward network. Importantly, the linear phase feedback that we implemented within the firing-rate model also emerges within an integrate-and-fire spiking model (Figure 9). This common-input approach to phase reset in the entorhinal–hippocampal system is consistent with the temporal simultaneity of hippocampal remapping and grid realignment (Fyhn et al., 2007). Further, we showed that phase-code calibration over behavioral time-scales allows for mixed and incremental spatial responses to environmental change that depend on the details of experience. Thus, network structure including extrinsic oscillators has potentially greater functional versatility than intrinsic temporal interference among, for example, dendritically localized oscillators within place cells. This versatility stems from the possibility of VMO-specific feedback targets and the synaptic integration of larger numbers of VMOs. However, because path integration in our abstract model allows for phase procession (delay) as well as precession (advance), theta-phase precession of spikes across place fields may be better explained by models of intrinsic dendritic dynamics (Kamondi et al., 1998; Magee, 2001) or by the restriction of VMO firing to preferred directions (Burgess, 2008).

Several lines of evidence suggest that the hippocampus may not directly inherit phase-coded information from entorhinal cortex. Extra-hippocampal theta sources (Buzsáki, 2002) may support phase precession within place fields during transient hippocampal silencing (Zugaro et al., 2005). Path integration performed intrinsically by place-cell phase precession would be disrupted by such a perturbation. Further, a pair of recent studies that disrupted the medial septal theta source (Koenig et al., 2011; Brandon et al., 2011) demonstrated the loss of grid-cell periodicity, but the directional selectivity of the head direction (HD) system (Brandon et al., 2011) and spatial modulation of hippocampal place fields Koenig et al. (2011) were largely preserved. The appearance of place-fields despite septal lesion indicates, in the context of our model here, that the VMOs may be located outside of the medial septum and other areas that depend on septal input for theta rhythmicity. Additionally, since the model only requires a common carrier wave, the VMOs could be operating at a non-theta frequency band. These functional dissociations of the temporal coding of spatial activity are consistent with the hypothesis of extra-hippocampal populations of theta cells with separable projections to hippocampus and entorhinal cortex (Blair et al., 2008; Blair and Zhang, 2009). These theta sources could be anatomically and/or functionally analogous to the subcortical ring attractor networks that have been proposed to explain the strong internal cohesiveness of the HD system (Skaggs et al., 1995; Zhang, 1996; Sharp et al., 2001; Yoganarasimha et al., 2006; Hargreaves et al., 2007; Blair et al., 2008).

3.3. Experimental Predictions

Oscillatory interference models (Burgess et al., 2007; Hasselmo, 2008; Blair and Zhang, 2009) require theta oscillators whose frequency is modulated by speed and the cosine of movement direction relative to preferred direction. The existence of such oscillators as potential inputs to the hippocampal formation has not been fully established. In freely behaving rats, preliminary recordings in anteroventral thalamus demonstrated cosine-tuning for movement direction (Blair et al., 2010). More recently, inspired by the finding that theta rhythmicity emerges in anterodorsal thalamus from bilateral lesions of lateral mammillary nucleus (Blair et al., 1999), a substantial population of “HD-by-theta” cells was also discovered in anteroventral thalamus (Tsanov et al., 2011). These HD-by-theta cells are characterized by conjunctive theta modulation and directional tuning. If these thalamic regions contain the VMO populations necessary to our model, then Papez’ circuit (Vertes et al., 2001) is a likely candidate for the anatomical substrate of the sensory feedback mechanism investigated here. Indeed, (Tsanov et al., 2011) found strong in-phase theta coherence between the local field potentials of hippocampal region CA3 and theta-rhythmic areas of anteroventral thalamus. This thalamo-hippocampal synchronization is consistent with the shared clock signal required for temporal phase coding and phase feedback.

Our findings point to several experimental predictions. The stability of path integration predicts that simultaneously recorded theta cells with the same preferred direction are strongly phase coherent. To account for the orienting of spatial activity based on global cues, the preferred directions of these cells should be anchored to distal landmarks; this cue control would be similar to that observed for HD cells in anterior thalamus (Goodridge et al., 1998; Yoganarasimha et al., 2006; Hargreaves et al., 2007). The spatiotemporally extended sensory reset predicts that a salient cue in a familiar environment elicits a bidirectional phase modulation (Figure 5A, second panel) that occurs simultaneously across theta cells. This signature could be assessed by removing a salient cue from a familiar environment and quantifying the difference in-phase modulation of theta cells. We would further predict increased phase coherence of spiking activity in simultaneously recorded theta cells and place cells while the animal is attending to external landmarks (perhaps during stopping or rearing behaviors). In addition, the prevalence of these signatures would be enhanced in familiar cue-rich environments relative to cue-sparse environments.

3.4. Conclusion

Many network mechanisms, including attractor network dynamics and temporal phase interference (Giocomo and Hasselmo, 2008; Burak and Fiete, 2009), may ultimately contribute to the diverse array of responses observed in hippocampus and entorhinal cortex in unfamiliar contexts. We have shown that one particular mechanism, an oscillatory interference model with phase-coded sensory feedback, is able to provide important hippocampal functions such as retrieval, navigational stability, complete remapping, and realistic partial remapping. Future modeling and experimental studies are necessary to refine these predictions and provide support for the various roles of temporal coding in navigation and spatial representation.

4. Materials and Methods

4.1. Software

Modeling and analysis code was developed as a custom Python software package, which is available for download from the ModelDB repository at http://senselab.med.yale.edu/ModelDB/ShowModel.asp?model = 137676.

4.2. Model Simulation

All simulations presented here used first-order forward Euler integration of the relevant phase modulation equation (Eqs. 1, 5, or 8) at timesteps of 2 ms (Figure 5) or 10 ms. Whole-session simulations of the circular track were computed for the full duration of the behavioral trajectory (see below). VMOs are defined at the simulation start by sampling uniformly random preferred orientations (Φ_i) on the range [0, 2π) and spatial scales (λ_i) on the range [16, 32] cm. Unless otherwise specified, VMOs are randomly initialized to phase offsets on the range [−π, π). At every timestep, the current spatial position and instantaneous velocity are computed from the trajectory data samples by linear interpolation. Based on the current position, the angular track position is determined along with, for cue simulations, the closest cue within each cue set according to track-angle differences. The phase targets associated with the closest cues become active in the feedback equations. (Simulations with a single cue have fixed phase targets.) Then, the current phase offsets of the VMOs are computed relative to a reference theta wave. During the first lap of a training session, these offsets are stored as the phase targets of each cue as its center position is first crossed by the trajectory. The feedback gain is computed for each active cue using Eq. 4. The VMO phases are then updated and the next timestep is simulated.

4.3. Hippocampal Data

For qualitative comparison with simulated responses, we present data from earlier studies of the cue double-rotation experimental paradigm (Figure 8B) consisting of five rats and 173 putative place-cells recorded from hippocampal regions CA3 and CA1 (J. Neunuebel, unpublished; Lee et al., 2004b). Within a recording session, we required single units to have >50 spikes and a spatial information score of >0.5 bits/spike (Skaggs et al., 1996) to be included in the analysis.

4.4. Behavioral Trajectory

Unless specified otherwise, simulations follow the spatiotemporal trajectory of an animal subject from a double-rotation experiment conducted on a circular track (Lee et al., 2004b). The track has inner and outer diameters of 56 and 76 cm, respectively. The position data were recorded during a cue-conflict condition on the first day of testing. The trajectory has a duration of 324 s and completes 14 clockwise laps with a forward running speed of 13.3 ± 7.4 cm/s (mean ± SD). To construct the velocity input for the phase equation (Eq. 1), we computed the velocity component time-series (Figure 2B) by first smoothing the 30 Hz head-position video tracking data with a four-sample boxcar filter. The smoothed tracking data was then differentiated and resampled by linear interpolation for each simulation timestep.

4.5. Place-field Analysis

We considered a simulated place unit to be active for purposes of computing place-field characteristics if its peak firing rate was >5% of the maximum rate of the population. We constructed linearized firing-rate maps by averaging responses across laps for each 1° bin in an angular partition of the track. For hippocampal spiking data (Figure 8B, bottom), we divided the total number of spikes across laps in each bin by the total occupancy time in the bin. We smoothed the resultant rate maps by circular convolution with a Gaussian kernel with a width (SD) of 4.3° (cf Lee et al., 2004b). Population response matrices were constructed by representing place-units across rows and track bins across columns. Lap response matrices were similarly constructed, except that response averages were restricted by lap and then represented along a third dimension. For simulated activity, a firing-rate variant of the spatial information score (Skaggs et al., 1996) was computed as

where p_i is the occupancy probability and r_i is the average rate, respectively, of the ith angular bin, and r is the average rate across the simulation. To assess field size, putative place fields were determined as contiguous segments of the linearized rate maps that respond at >20% of peak firing rate (Muller and Kubie, 1989). A place unit is considered active if it has at least one place field; network sparsity is determined as the fraction of inactive place units in a given simulation.

4.6. Correlation Analysis

To assess the effect of continuous phase noise on population responses (Figure 6), we compute the element-by-element Pearson correlation between population rate matrices for simulations of the same VMO-place network. Test condition simulation responses are compared to the whole-session average responses from a path-integration simulation with no noise or cue. Correlations for individual laps were computed using separate population rate matrices for the activity of each complete lap of the track. Cue-triggered population correlations were computed by averaging the Pearson correlation of the population rate vectors across laps for each angular bin around the track and then centering the averages on the cue position.

4.7. Double Cue Rotation

Cues in each set are mechanistically equivalent (Eq. 8) and are evenly distributed around the track. With the same number of cues in each set, cues from one set are interleaved with those of the other. In a mismatch simulation, one set coherently rotates CCW and the other CW. For the standard (STD, or “familiar”) cue configuration, CCW rotating cues are initially placed with no offset such that the first cue will be located at 0°; the first CW rotating cue is offset by half of the spacing between distal cues (Figure 7, top). The STD configuration is learned and simulated with cue feedback. Then, cue centers are rotated (one set CCW, the other CW) to produce mismatch (MIS) simulations for a series of mismatch angles: 45 (MIS-45), 90 (MIS-90), 135 (MIS-135), and 180 (MIS-180) degrees.

4.8. Remapping Analysis

To assess remapping due to cue conflict (for both model and hippocampal data), we examine spatial correlations for each place unit in a double cue-rotation simulation. We compute the linearized rate maps for the STD and MIS conditions. We rotate the MIS response around the track in 1° increments computing the Pearson correlations with the STD response. We determine the rotation angle of the response to be the MIS rotation that provides the peak spatial correlation. To categorize remapping responses, we set thresholds on rotation angle and peak correlation. If rotation is within ±50% of the cue-rotation angle of either set of cues and correlation is >0.4, then it is a cue-following response (either “CCW” or “CW”). Otherwise, it is “ambiguous.” Place units that are silent in STD but active in MIS are “on” responses, while the reverse are “off” responses.

4.9. Spiking neuron analysis

To quantify phase resetting in a spiking neuron model of a theta oscillator (Figure 9), we simulated 1000-ms responses with a constant current producing a single spike for each theta cycle. For our purposes, we are interested in the total effect of a stimulus on spike timing, which we measured relative to the spike timing for a baseline condition with no stimulus. We define 0/2π phase as the baseline spike times and consider theta cycles that range from one half-cycle before (−π) the spike to one half-cycle (+π) after the spike. We simulated repeated stimulus conditions in which a stimulus (Eq. 10) was injected at one of 25 different phases across a particular theta cycle. The oscillator phase was altered depending on the stimulus timing. We measured this phase response during a subsequent post-stimulus theta cycle, effectively summing the first and second order resetting (cf Oprisan et al., 2004). Each stimulus trial elicited a single spike within the theta cycle from which we derived the phase response. The phase reset values constituting the PRC (Figure 9C) were calculated by subtracting the baseline spike time t_theta from the stimulus-condition spike time ,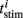

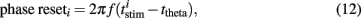
where i indexes the stimulus-condition trials, and f = 7 Hz is the spiking frequency. Thus, positive phase reset values indicate that the total effect of a stimulus was to delay spike timing; negative values indicate advance. To visualize the PRC, we wrapped the curve around its discontinuity to demonstrate its high degree of linearity.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was supported by NIH grants R01 NS039456 and P01 NS038310 to James J. Knierim and R01 MH079511 to H. T. Blair and Kechen Zhang. We thank H. T. Blair for helpful discussions, and Josh Neunuebel and Inah Lee for providing the hippocampal double rotation data sets.

References

Abbott, L. F., and Blum, K. I. (1996). Functional significance of long-term potentiation for sequence learning and prediction. Cereb. Cortex 6, 406–416.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Abbott, L. F., and Nelson, S. B. (2000). Synaptic plasticity: taming the beast. Nat. Neurosci. 3, 1178–1183.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Blair, H. T., Cho, J., and Sharp, P. E. (1999). The anterior thalamic head-direction signal is abolished by bilateral but not unilateral lesions of the lateral mammillary nucleus. J. Neurosci. 19, 6673–6683.

Pubmed Abstract | Pubmed Full Text

Blair, H. T., Gupta, K., and Zhang, K. (2008). Conversion of a phase- to a rate-coded position signal by a three-stage model of theta cells, grid cells, and place cells. Hippocampus 18, 1239–1255.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Blair, H. T., Welday, A., Shlifer, G., Bloom, M., and Zhang, K. (2010). Stationary envelope synthesis (SES): a universal method for phase coding by neural oscillators. Front. Neurosci. Conf. Abstr. Comput. Syst. Neurosci. doi:10.3389/conf.fnins.2010.03.00239

CrossRef Full Text

Blair, H. T., and Zhang, K. (2009). Place cells from theta rhythm: a many-oscillator model of path integration by phase interference. Soc. Neurosci. 192.27.

Bose, A., Booth, V., and Recce, M. (2000). A temporal mechanism for generating the phase precession of hippocampal place cells. J. Comput. Neurosci. 9, 5–30.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bostock, E., Muller, R. U., and Kubie, J. L. (1991). Experience-dependent modifications of hippocampal place cell firing. Hippocampus 1, 193–205.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brandon, M. P., Bogaard, A. R., Libby, C. P., Connerney, M. A., Gupta, K., and Hasselmo, M. E. (2011). Reduction of theta rhythm dissociates grid cell spatial periodicity from directional tuning. Science 332, 595–599.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brown, J. E., and Skaggs, W. E. (2002). Concordant and discordant coding of spatial location in populations of hippocampal CA1 pyramidal cells. J. Neurophysiol. 88, 1605–1613.

Pubmed Abstract | Pubmed Full Text

Burak, Y., and Fiete, I. R. (2009). Accurate path integration in continuous attractor network models of grid cells. PLoS Comput. Biol. 5, e1000291. doi:10.1371/journal.pcbi.1000291

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Burgess, N. (2008). Grid cells and theta as oscillatory interference: theory and predictions. Hippocampus 18, 1157–1174.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Burgess, N., Barry, C., and O’Keefe, J. (2007). An oscillatory interference model of grid cell firing. Hippocampus 17, 801–812.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Buzsáki, G. (2002). Theta oscillations in the hippocampus. Neuron 33, 325–340.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Buzsáki, G. (2005). Theta rhythm of navigation: link between path integration and landmark navigation, episodic and semantic memory. Hippocampus 15, 827–840.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Câteau, H., Kitano, K., and Fukai, T. (2008). Interplay between a phase response curve and spike-timing-dependent plasticity leading to wireless clustering. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 77(5 Pt 1), :051909.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dayan, P., and Abbott, L. F. (2001). Theoretical Neuroscience: Modeling of Neural Systems, Chapter 5. Computational Neuroscience Cambridge, MA: MIT Press.

Deshmukh, S. S., Yoganarasimha, D., Voicu, H., and Knierim, J. J. (2010). Theta modulation in the medial and the lateral entorhinal cortices. J. Neurophysiol. 104, 994–1006.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ermentrout, B. (1996). Type I membranes, phase resetting curves, and synchrony. Neural Comput. 8, 979–1001.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Etienne, A. S., Boulens, V., Maurer, R., Rowe, T., and Siegrist, C. (2000). A brief view of known landmarks reorientates path integration in hamsters. Naturwissenschaften 87, 494–498.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Etienne, A. S., Maurer, R., Boulens, V., Levy, A., and Rowe, T. (2004). Resetting the path integrator: a basic condition for route-based navigation. J. Exp. Biol. 207, 1491–1508.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Etienne, A. S., Maurer, R., and Séguinot, V. (1996). Path integration in mammals and its interaction with visual landmarks. J. Exp. Biol. 199, 201–209.

Pubmed Abstract | Pubmed Full Text

Fuhs, M. C., and Touretzky, D. S. (2006). A spin glass model of path integration in rat medial entorhinal cortex. J. Neurosci. 26, 4266–4276.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fyhn, M., Hafting, T., Treves, A., Moser, E. I., and Moser, M.-B. (2007). Hippocampal remapping and grid realignment in entorhinal cortex. Nature 446, 190–194.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Geisler, C., Robbe, D., Zugaro, M., Sirota, A., and Buzsáki, G. (2007). Hippocampal place cell assemblies are speed-controlled oscillators. Proc. Natl. Acad. Sci. U.S.A. 104, 8149–8154.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Giocomo, L. M., and Hasselmo, M. E. (2008). Computation by oscillations: implications of experimental data for theoretical models of grid cells. Hippocampus 18, 1186–1199.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Goodridge, J. P., Dudchenko, P. A., Worboys, K. A., Golob, E. J., and Taube, J. S. (1998). Cue control and head direction cells. Behav. Neurosci. 112, 749–761.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Guzowski, J. F., McNaughton, B. L., Barnes, C. A., and Worley, P. F. (1999). Environment-specific expression of the immediate-early gene Arc in hippocampal neuronal ensembles. Nat. Neurosci. 2, 1120–1124.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hafting, T., Fyhn, M., Bonnevie, T., Moser, M.-B., and Moser, E. I. (2008). Hippocampus-independent phase precession in entorhinal grid cells. Nature 453, 1248–1252.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hafting, T., Fyhn, M., Molden, S., Moser, M.-B., and Moser, E. I. (2005). Microstructure of a spatial map in the entorhinal cortex. Nature 436, 801–806.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hansel, D., Mato, G., and Meunier, C. (1995). Synchrony in excitatory neural networks. Neural Comput. 7, 307–337.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hargreaves, E. L., Rao, G., Lee, I., and Knierim, J. J. (2005). Major dissociation between medial and lateral entorhinal input to dorsal hippocampus. Science 308, 1792–1794.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hargreaves, E. L., Yoganarasimha, D., and Knierim, J. J. (2007). Cohesiveness of spatial and directional representations recorded from neural ensembles in the anterior thalamus, parasubiculum, medial entorhinal cortex, and hippocampus. Hippocampus 17, 826–841.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Harris, K. D., Henze, D. A., Hirase, H., Leinekugel, X., Dragoi, G., Czurkó, A., and Buzsáki, G. (2002). Spike train dynamics predicts theta-related phase precession in hippocampal pyramidal cells. Nature 417, 738–741.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Harvey, C. D., Collman, F., Dombeck, D. A., and Tank, D. W. (2009). Intracellular dynamics of hippocampal place cells during virtual navigation. Nature 461, 941–946.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hasselmo, M. E. (2008). Grid cell mechanisms and function: contributions of entorhinal persistent spiking and phase resetting. Hippocampus 18, 1213–1229.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hasselmo, M. E. (2009). A model of episodic memory: mental time travel along encoded trajectories using grid cells. Neurobiol. Learn. Mem. 92, 559–573.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hasselmo, M. E., Bodelón, C., and Wyble, B. P. (2002). A proposed function for hippocampal theta rhythm: separate phases of encoding and retrieval enhance reversal of prior learning. Neural Comput. 14, 793–817.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hasselmo, M. E., Giocomo, L. M., and Zilli, E. A. (2007). Grid cell firing may arise from interference of theta frequency membrane potential oscillations in single neurons. Hippocampus 17, 1252–1271.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hayashi, H., and Nonaka, Y. (2010). Cooperation and competition between lateral and medial perforant path synapses in the dentate gyrus. Neural Netw. 24, 233–246.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hayman, R. M., and Jeffery, K. J. (2008). How heterogeneous place cell responding arises from homogeneous grids: a contextual gating hypothesis. Hippocampus 18, 1301–1313.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Henriksen, E. J., Colgin, L. L., Barnes, C. A., Witter, M. P., Moser, M.-B., and Moser, E. I. (2010). Spatial representation along the proximodistal axis of CA1. Neuron 68, 127–137.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hopfield, J. J., and Brody, C. D. (2001). What is a moment? Transient synchrony as a collective mechanism for spatiotemporal integration. Proc. Natl. Acad. Sci. U.S.A. 98, 1282–1287.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Igarashi, J., Hayashi, H., and Tateno, K. (2007). Theta phase coding in a network model of the entorhinal cortex layer II with entorhinal–hippocampal loop connections. Cogn. Neurodyn. 1, 169–184.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jensen, O., Idiart, M. A., and Lisman, J. E. (1996). Physiologically realistic formation of autoassociative memory in networks with theta/gamma oscillations: role of fast NMDA channels. Learn. Mem. 3, 243–256.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kamondi, A., Acsády, L., Wang, X. J., and Buzsáki, G. (1998). Theta oscillations in somata and dendrites of hippocampal pyramidal cells in vivo: activity-dependent phase-precession of action potentials. Hippocampus 8, 244–261.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Karlsson, M., and Frank, L. (2008). Network dynamics underlying the formation of sparse, informative representations in the hippocampus. J. Neurosci. 28, 14271–14281.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kepecs, A., van Rossum, M. C. W., Song, S., and Tegner, J. (2002). Spike-timing-dependent plasticity: common themes and divergent vistas. Biol. Cybern. 87, 446–458.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kerr, K. M., Agster, K. L., Furtak, S. C., and Burwell, R. D. (2007). Functional neuroanatomy of the parahippocampal region: the lateral and medial entorhinal areas. Hippocampus 17, 697–708.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Knierim, J. J. (2002). Dynamic interactions between local surface cues, distal landmarks, and intrinsic circuitry in hippocampal place cells. J. Neurosci. 22, 6254–6264.

Pubmed Abstract | Pubmed Full Text

Knierim, J. J. (2003). “Hippocampal remapping: implications for spatial learning and memory,” in The Neurobiology of Spatial Behaviour, ed. K. J. Jeffery (Oxford: Oxford University Press), 226–239.

Knierim, J. J. (2006). Neural representations of location outside the hippocampus. Learn. Mem. 13, 405–415.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Knierim, J. J., Lee, I., and Hargreaves, E. L. (2006). Hippocampal place cells: parallel input streams, subregional processing, and implications for episodic memory. Hippocampus 16, 755–764.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Koenig, J., Linder, A. N., Leutgeb, J. K., and Leutgeb, S. (2011). The spatial periodicity of grid cells is not sustained during reduced theta oscillations. Science 332, 592–595.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lee, I., Rao, G., and Knierim, J. J. (2004a). A double dissociation between hippocampal subfields: differential time course of CA3 and CA1 place cells for processing changed environments. Neuron 42, 803–815.

CrossRef Full Text

Lee, I., Yoganarasimha, D., Rao, G., and Knierim, J. J. (2004b). Comparison of population coherence of place cells in hippocampal subfields CA1 and CA3. Nature 430, 456–459.

CrossRef Full Text

Lengyel, M., Kwag, J., Paulsen, O., and Dayan, P. (2005). Matching storage and recall: hippocampal spike timing-dependent plasticity and phase response curves. Nat. Neurosci. 8, 1677–1683.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lengyel, M., Szatmáry, Z., and Erdi, P. (2003). Dynamically detuned oscillations account for the coupled rate and temporal code of place cell firing. Hippocampus 13, 700–714.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Leutgeb, S., Leutgeb, J. K., Barnes, C. A., Moser, E. I., McNaughton, B. L., and Moser, M.-B. (2005). Independent codes for spatial and episodic memory in hippocampal neuronal ensembles. Science 309, 619–623.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Leutgeb, S., Leutgeb, J. K., Treves, A., Moser, M.-B., and Moser, E. I. (2004). Distinct ensemble codes in hippocampal areas CA3 and CA1. Science 305, 1295–1298.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lisman, J. E. (2007). Role of the dual entorhinal inputs to hippocampus: a hypothesis based on cue/action (non-self/self) couplets. Prog. Brain Res. 163, 615–625.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Losonczy, A., Zemelman, B. V., Vaziri, A., and Magee, J. C. (2010). Network mechanisms of theta related neuronal activity in hippocampal CA1 pyramidal neurons. Nat. Neurosci. 13, 967–972.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Magee, J. C. (2001). Dendritic mechanisms of phase precession in hippocampal CA1 pyramidal neurons. J. Neurophysiol. 86, 528–532.

Pubmed Abstract | Pubmed Full Text

Manns, J. R., and Eichenbaum, H. (2006). Evolution of declarative memory. Hippocampus 16, 795–808.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Maurer, A. P., Cowen, S. L., Burke, S. N., Barnes, C. A., and McNaughton, B. L. (2006). Organization of hippocampal cell assemblies based on theta phase precession. Hippocampus 16, 784–794.

CrossRef Full Text

Maurer, A. P., Vanrhoads, S. R., Sutherland, G. R., Lipa, P., and McNaughton, B. L. (2005). Self-motion and the origin of differential spatial scaling along the septo-temporal axis of the hippocampus. Hippocampus 15, 841–852.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

McFarland, W. L., Teitelbaum, H., and Hedges, E. K. (1975). Relationship between hippocampal theta activity and running speed in the rat. J. Comp. Physiol. Psychol. 88, 324–328.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

McNaughton, B. L., Battaglia, F. P., Jensen, O., Moser, E. I., and Moser, M.-B. (2006). Path integration and the neural basis of the ‘cognitive map’. Nat. Rev. Neurosci. 7, 663–678.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mehta, M. R., Quirk, M. C., and Wilson, M. A. (2000). Experience-dependent asymmetric shape of hippocampal receptive fields. Neuron 25, 707–715.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Monaco, J. D., and Abbott, L. F. (2011). Modular realignment of entorhinal grid cell activity as a basis for hippocampal remapping. J. Neurosci. 31, 9414–9425.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Monaco, J. D., Abbott, L. F., and Kahana, M. J. (2007). Lexico-semantic structure and the word-frequency effect in recognition memory. Learn. Mem. 14, 204–213.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Moser, E. I., Kropff, E., and Moser, M.-B. (2008). Place cells, grid cells, and the brain’s spatial representation system. Annu. Rev. Neurosci. 31, 69–89.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mu, Y., and Poo, M.-M. (2006). Spike timing-dependent LTP/LTD mediates visual experience-dependent plasticity in a developing retinotectal system. Neuron 50, 115–125.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Muller, R. U., and Kubie, J. L. (1989). The firing of hippocampal place cells predicts the future position of freely moving rats. J. Neurosci. 9, 4101–4110.

Pubmed Abstract | Pubmed Full Text

Nolan, C. R., Wyeth, G., Milford, M., and Wiles, J. (2010). The race to learn: spike timing and STDP can coordinate learning and recall in CA3. Hippocampus 21, 647–660.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

O’Keefe, J., and Burgess, N. (2005). Dual phase and rate coding in hippocampal place cells: theoretical significance and relationship to entorhinal grid cells. Hippocampus 15, 853–866.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

O’Keefe, J., and Dostrovsky, J. (1971). The hippocampus as a spatial map: preliminary evidence from unit activity in the freely-moving rat. Brain Res. 34, 171–175.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

O’Keefe, J., and Recce, M. L. (1993). Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus 3, 317–330.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Oprisan, S. A., Prinz, A. A., and Canavier, C. C. (2004). Phase resetting and phase locking in hybrid circuits of one model and one biological neuron. Biophys. J. 87, 2283–2298.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Redish, A. D. (2001). The hippocampal debate: are we asking the right questions? Behav. Brain Res. 127, 81–98.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Remme, M. W. H., Lengyel, M., and Gutkin, B. S. (2010). Democracy-independence trade-off in oscillating dendrites and its implications for grid cells. Neuron 66, 429–437.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Roberts, P. D., and Leen, T. K. (2010). Anti-hebbian spike-timing-dependent plasticity and adaptive sensory processing. Front. Comput. Neurosci. 4:156. doi: 10.3389/fncom.2010.00156

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sargolini, F., Fyhn, M., Hafting, T., McNaughton, B. L., Witter, M. P., Moser, M.-B., and Moser, E. I. (2006). Conjunctive representation of position, direction, and velocity in entorhinal cortex. Science 312, 758–762.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Savelli, F., and Knierim, J. J. (2010). Hebbian analysis of the transformation of medial entorhinal grid-cell inputs to hippocampal place fields. J. Neurophysiol. 103, 3167–3183.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shapiro, M. L., Tanila, H., and Eichenbaum, H. (1997). Cues that hippocampal place cells encode: dynamic and hierarchical representation of local and distal stimuli. Hippocampus 7, 624–642.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sharp, P. E., Blair, H. T., and Cho, J. (2001). The anatomical and computational basis of the rat head-direction cell signal. Trends Neurosci. 24, 289–294.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Silkis, I. G. (2011). Involvement of the trisynaptic hippocampal pathway in generating neural representations of object-place associations (an analytical review). Neurosci. Behav. Physiol. 41, 117–129.

CrossRef Full Text

Skaggs, W. E., Knierim, J. J., Kudrimoti, H. S., and McNaughton, B. L. (1995). A model of the neural basis of the rat’s sense of direction. Adv. Neural Inf. Process. Syst. 7, 173–180.

Pubmed Abstract | Pubmed Full Text

Skaggs, W. E., McNaughton, B. L., Wilson, M. A., and Barnes, C. A. (1996). Theta phase precession in hippocampal neuronal populations and the compression of temporal sequences. Hippocampus 6, 149–172.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Solstad, T., Moser, E. I., and Einevoll, G. T. (2006). From grid cells to place cells: a mathematical model. Hippocampus 16, 1026–1031.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tanila, H., Shapiro, M. L., and Eichenbaum, H. (1997). Discordance of spatial representation in ensembles of hippocampal place cells. Hippocampus 7, 613–623.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tateno, T., and Robinson, H. P. C. (2007). Phase resetting curves and oscillatory stability in interneurons of rat somatosensory cortex. Biophys. J. 92, 683–695.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Touretzky, D. S., Weisman, W. E., Fuhs, M. C., Skaggs, W. E., Fenton, A. A., and Muller, R. U. (2005). Deforming the hippocampal map. Hippocampus 15, 41–55.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tsanov, M., Chah, E., Vann, S. D., Reilly, R. B., Erichsen, J. T., Aggleton, J. P., and O’Mara, S. M. (2011). Theta-modulated head direction cells in the rat anterior thalamus. J. Neurosci. 31, 9489–9502.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Vertes, R. P., Albo, Z., and Viana Di Prisco, G. (2001). Theta-rhythmically firing neurons in the anterior thalamus: implications for mnemonic functions of Papez’s circuit. Neuroscience 104, 619–625.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wallenstein, G. V., and Hasselmo, M. E. (1997). GABAergic modulation of hippocampal population activity: sequence learning, place field development, and the phase precession effect. J. Neurophysiol. 78, 393–408.

Pubmed Abstract | Pubmed Full Text

Wang, H.-P., Spencer, D., Fellous, J.-M., and Sejnowski, T. J. (2010). Synchrony of thalamocortical inputs maximizes cortical reliability. Science 328, 106–109.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Welinder, P. E., Burak, Y., and Fiete, I. R. (2008). Grid cells: the position code, neural network models of activity, and the problem of learning. Hippocampus 18, 1283–1300.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wills, T. J., Lever, C., Cacucci, F., Burgess, N., and O’Keefe, J. (2005). Attractor dynamics in the hippocampal representation of the local environment. Science 308, 873–876.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wilson, M. A., and McNaughton, B. L. (1993). Dynamics of the hippocampal ensemble code for space. Science 261, 1055–1058.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Witter, M. P., and Moser, E. I. (2006). Spatial representation and the architecture of the entorhinal cortex. Trends Neurosci. 29, 671–678.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Yoganarasimha, D., Rao, G., and Knierim, J. J. (2010). Lateral entorhinal neurons are not spatially selective in cue-rich environments. Hippocampus. doi: 10.1002/hipo.20839. [Epub ahead of print].

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Yoganarasimha, D., Yu, X., and Knierim, J. J. (2006). Head direction cell representations maintain internal coherence during conflicting proximal and distal cue rotations: comparison with hippocampal place cells. J. Neurosci. 26, 622–631.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zhang, K. (1996). Representation of spatial orientation by the intrinsic dynamics of the head-direction cell ensemble: a theory. J. Neurosci. 16, 2112–2126.

Pubmed Abstract | Pubmed Full Text

Zilli, E. A., and Hasselmo, M. E. (2010). Coupled noisy spiking neurons as velocity-controlled oscillators in a model of grid cell spatial firing. J. Neurosci. 30, 13850–13860.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zilli, E. A., Yoshida, M., Tahvildari, B., Giocomo, L. M., and Hasselmo, M. E. (2009). Evaluation of the oscillatory interference model of grid cell firing through analysis and measured period variance of some biological oscillators. PLoS Comput. Biol. 5, e1000573. doi: 10.1371/journal.pcbi.1000573

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zugaro, M. B., Monconduit, L., and Buzsáki, G. (2005). Spike phase precession persists after transient intrahippocampal perturbation. Nat. Neurosci. 8, 67–71.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text