Emergent Properties of Interacting Populations of Spiking Neurons

Cardanobile, Stefano; Rotter, Stefan

doi:10.3389/fncom.2011.00059

ORIGINAL RESEARCH article

Front. Comput. Neurosci., 23 December 2011
volume 5 - 2011 | https://doi.org/10.3389/fncom.2011.00059

Emergent properties of interacting populations of spiking neurons

Stefano Cardanobile^1,2* Stefan Rotter^1,2

¹ Bernstein Center Freiburg, University of Freiburg, Freiburg, Germany
² Faculty of Biology, University of Freiburg, Freiburg, Germany

Dynamic neuronal networks are a key paradigm of increasing importance in brain research, concerned with the functional analysis of biological neuronal networks and, at the same time, with the synthesis of artificial brain-like systems. In this context, neuronal network models serve as mathematical tools to understand the function of brains, but they might as well develop into future tools for enhancing certain functions of our nervous system. Here, we present and discuss our recent achievements in developing multiplicative point processes into a viable mathematical framework for spiking network modeling. The perspective is that the dynamic behavior of these neuronal networks is faithfully reflected by a set of non-linear rate equations, describing all interactions on the population level. These equations are similar in structure to Lotka-Volterra equations, well known by their use in modeling predator-prey relations in population biology, but abundant applications to economic theory have also been described. We present a number of biologically relevant examples for spiking network function, which can be studied with the help of the aforementioned correspondence between spike trains and specific systems of non-linear coupled ordinary differential equations. We claim that, enabled by the use of multiplicative point processes, we can make essential contributions to a more thorough understanding of the dynamical properties of interacting neuronal populations.

Introduction

Dynamic neuronal networks represent an important new paradigm in neuroscience. The field has increasing impact in fundamental brain research, and it is relevant for some new branches of neural engineering. It is concerned with the analysis of biological neuronal networks and, at the same time, with the synthesis of artificial brain-like systems. Neuronal network models serve as mathematical tools to understand the function of brains, and they may develop into future tools to enhance brain function. Both analysis and synthesis of neuronal networks rely on a thorough understanding of the dynamical properties of neural populations. Currently, this understanding is episodic and elusive, and even the most basic questions about non-linear networks impose serious mathematical challenges.

In a previous paper (Cardanobile and Rotter, 2010) we introduced a framework that allows the concise analysis of dynamic activity patterns in structured networks of spiking neurons. Here, we exploit the new theory to analyze small meta-networks of neural populations (“networks of networks”), with a particular focus on functional properties that are considered relevant for biological brains.

Neural spike trains exhibit fluctuations of random appearance, which span different spatial and temporal scales, and which have both intrinsic and extrinsic causes (Marom, 2010). On the one hand, isolated neurons fire with limited reliability, depending on the circumstances of their stimulation (Mainen and Sejnowski, 1995). On the other hand, ongoing activity of unknown origin strongly modulates the activity of cortical networks that are part of an active brain (Arieli et al., 1996). It was also shown theoretically that balanced excitation and inhibition in large recurrent networks is bound to generate a very complex dynamics, resulting in strong intrinsic fluctuations of activity (van Vreeswijk and Sompolinsky, 1998; Jahnke et al., 2009). All this suggests the use of stochastic methods to model neuronal populations. In turn, it is possible that biological networks exploit such random effects to boost their computational properties, as, e.g., in stochastic resonance (Wiesenfeld and Moss, 1995; McDonnell and Abbott, 2009).

A useful framework to define and study stochastic dynamics for spiking neurons and networks is that of a Wiener cascade (Wiener, 1958; Rotter, 1996; Herz et al., 2006), which is related to the concept of escape noise or threshold noise (Plesser and Gerstner, 2000). Cascade models are characterized by linear input integration, and a non-linear transfer function, which specifies how the linear state variable (typically the membrane potential) is mapped onto the instantaneous firing rate of the neuron, see Figure 1.

FIGURE 1

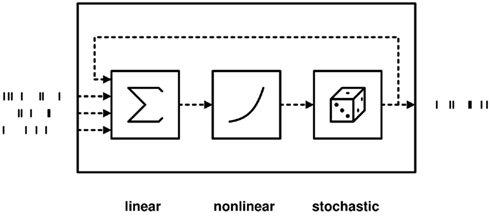
Figure 1. Schematic of cascade models. In a neural model with escape noise, the state variable (membrane potential) V is mapped to the instantaneous firing rate r via the transfer function f. The firing rate is used to generate a Poissonian spike train. Thus, the probability of firing a spike in a short interval (t, t + ε) is given by f(V(t))ε. Escape noise models have the advantage that the spike generation itself is stochastic, making the statistical analysis of such neurons more accessible than deterministic integrate-and-fire neurons with additive noise.

For exponential transfer functions, specifically, networks of cascade units have a predictable mean-field dynamics (Cardanobile and Rotter, 2010). The corresponding coupled non-linear differential equations for the ensemble firing rates turn out to be a competitive system of Lotka-Volterra type. A similar approach has been developed by Buice et al. (2010) starting from certain field equations (Wilson and Cowan, 1972). The long history of Lotka-Volterra equations in the mathematical literature, starting with Lotka (1910) and Volterra (1926), opens very interesting possibilities for the applications pursued here. In particular, it is possible to reversely engineer any prescribed Lotka-Volterra type competitive system, and to specify the connectivity pattern of the network of neuronal populations that have the given rate equations as a mean-field description. The suggested framework has two main advantages as compared to other models of networks of spiking neurons.

The first advantage is of practical nature: the essential behavior of spiking networks can be studied mathematically by analyzing the associated rate equations. Surprisingly, the rate equations provide an accurate description of the population dynamics not only in the case where the system converges to an attractive fixed point, but also if the rates undergo highly transient dynamics, even in the chaotic case. An important criterion for our choice of the examples was to demonstrate this feature in different situations. Moreover, the known mathematical properties of the non-linear rate equations can be exploited to construct networks of neural populations with prescribed behavior. In the sequel, we will give several examples for this modeling strategy. The second criterion for the choice of the examples was their relevance for better understanding biological spiking networks in the brain, and for designing artificial spiking networks in the emerging field of neural engineering, in which Lotka-Volterra equations already found application (Asai et al., 1999).

The second advantage offered by our framework is more of conceptual nature. Multiplicatively interacting point processes, i.e., cascade models with exponential transfer function, offer a framework to easily implement so-called “scaled-rate” models (Marom, 2010) for networks of spiking neurons. Marom suggests that

One good reason to bother with formulation of an abstract model is the hope that it will lead up to a mathematical construct that dramatically reduces the dimensionality of the problem at hand.

Multiplicatively interacting point processes offer an amazingly rich behavior already in low-dimensional cases, thus providing experimentalists and theoreticians with a powerful and innovative set of tools.

Materials and Methods

Comparison to Existing Population Rate Models

Rate-based descriptions of neural networks have a long tradition in neuroscience. To embed our work into this context we briefly review the most important approaches.

Temporal coarse-graining was introduced by Wilson and Cowan (1972) in their seminal paper. In this approach, the dynamic variables are given by the expected number of non-refractory cells receiving input above threshold in a (small) region. Averaging over times shorter than the time-scale of the population dynamics (which is assumed to be in the range of the refractory period) leads to non-linear rate equations. These equations take the form of a linear equation, complemented by a sigmoidal coupling function. These equations have recently been generalized to take fluctuations and higher-order moments into account (Buice and Cowan, 2007; Buice et al., 2010), as well as time-dependent inputs (Ledoux and Brunel, 2011). Already in the original paper by Wilson and Cowan arguments have been given that guarantee that fast dynamics on the time-scale of the refractory period does not affect the population dynamics. Different rate equations have been derived by resorting to ensemble averaging rather than temporal coarse-graining for the case of spiking neurons with refractoriness (Deger et al., 2010). Indeed, the refractory period was found to have a strong effect on the population dynamics.

A very successful, and by now classical theory for studying rate dynamics in homogeneous networks of integrate-and-fire neurons is based on a Fokker-Planck approach (Abbott and van Vreeswijk, 1993; Fusi and Mattia, 1999; Brunel, 2000; Knight et al., 2000). Some results about correlations arising from network interactions have recently been obtained, though (Ostojic et al., 2009). We will not follow this approach here, since the use of second-order partial differential equations makes the study of network dynamics difficult.

Ensemble averaging is the preferred approach for studying time-evolution of activity in neural networks. Ensemble averaging can be used to study neural dynamics both on the single cell and on the population level (Kriener et al., 2008; Deger et al., 2010; Pernice et al., 2011). In this manuscript, in particular, we assume that the instantaneous firing rate of a neuron is a function of its membrane potential, and we use ensemble averaging to obtain the average firing rate of a homogeneous population of independent units. For the transfer function, a common choice for population models is a threshold-linear non-linearity (Wilson and Cowan, 1972; Ledoux and Brunel, 2011). Such models have been used, for example, for the investigation of orientation selectivity in the early visual system (Carandini and Ringach, 1997; Ernst et al., 2001). Recently, a theory for the analytic derivation of transfer functions in the case of leaky integrate-and-fire neurons has been proposed (Ostojic and Brunel, 2011). In our manuscript, we chose an exponential transfer function (Jolivet et al., 2006). Both the reset and refractoriness are incorporated in the self-inhibition of neurons. The rate equations arising from this choice are of Lotka-Volterra type and have already been used in modeling neural activity (McCarley and Hobson, 1975; Fukai and Tanaka, 1997; Billock et al., 2001; Rabinovich et al., 2006; Cardanobile and Rotter, 2010). In some cases, Lotka-Volterra equations display the same attractor landscape as linear integrators complemented by a threshold-linear non-linearity (Hahnloser et al., 2003).

An important feature of our method is the correspondence between stability properties of the rate equation and of the underlying point process model. This correspondence goes far beyond the matching of attractive fixed points, and includes more complex attractors and associated bifurcations. The main aim of the present work is to demonstrate the correspondence between the point process model and the associated rate equations in different situations. We study feed-forward networks, but also recurrent networks both in the case of single (attractive or repulsive) fixed points, as well as in the multistable case. Finally, we show that stable limit cycles are also correctly mapped from the rate equation to the point process model.

Rate Equations

Here, we briefly recapitulate the model introduced in Cardanobile and Rotter (2010). In this model, a neuronal population is characterized by its mean membrane potential V(t). The mean membrane potential is assumed to obey a perfect integrator dynamics (Tuckwell, 1989).

where 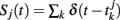yes represent the spike train of population j, and α_ij the net synaptic coupling from neurons in the population j to neurons in the population i. At this step, we have assumed that the populations are statistically homogeneous in the sense that the distribution of synaptic strengths from neurons of population j to neurons in population i is narrow. Action potentials are emitted according to a stochastic mechanism, as in escape noise models for single neuron dynamics (Gerstner and Kistler, 2002).

Such models rely on the assumption that the instantaneous firing rate λ(t) is only a function of the instantaneous value of the internal state variable V(t), which is the mean membrane potential in our case.

The interpretation of escape noise models is the following: the membrane potential as well as the spike threshold are subject to spontaneous fluctuations on very short time scales. These fluctuations are both due to internal noise (on the level of synapses and on the level of membrane) and to fluctuating input. Therefore, the probability of observing a spike in a small interval (t, t + Δt) is a non-linear function of the membrane potential V(t) at time t. This transfer function depends on the state of both the neuron and the network. A good choice for the transfer function for neurons is an exponential function (Rotter, 1996; Carandini, 2004; Jolivet et al., 2006). We have verified through simulations (data not shown) that this choice is also suitable for populations of integrate-and-fire neurons.

Under these assumptions, we can write, up to normalization constants

Inserting Eq. (2) into Eq. (1), rearranging, taking the ensemble mean, and ignoring covariances leads to the following non-linear dynamic equations

We refer to them as the rate equations of the system. They reflect the ensemble behavior of a homogeneous population of spiking neurons. We will use these equations exactly with this interpretation in mind. We would like to stress that the same type of dynamic equations has previously been employed in the neuroscientific literature (McCarley and Hobson, 1975; Fukai and Tanaka, 1997; Billock et al., 2001; Rabinovich et al., 2006), although without the biological motivation of the model offered here. We use the term homogeneous loosely, without a specific statistical framework in mind. Although the exact matching of spiking units to rate equations is a very interesting issue, the focus of this paper is to show that the rate equations offer a precise description of the expected behavior of multiplicatively interacting point process also in the time-dependent regime and to exploit the possibilities offered by this description.

In our firing rate equation, we have disregarded the leak term in the voltage dynamics. The question of whether leak terms can be consistently included into the equation is subject of current research.

The focus of the present work is to demonstrate with neuroscientifically relevant examples that the mapping from the spiking model to Lotka-Volterra equations holds for all stable regimes. The examples included here are multistable systems, and systems with stable limit cycles. We have verified the mapping also for chaotic attractors and Hopf bifurcations, but we have excluded these examples from the present manuscript for the sake of readability. The arguments given in this and our previous manuscript, and the examples of microcircuit design discussed here demonstrate unambiguously that the framework of Lotka-Volterra equations can indeed establish a solid connection between spiking dynamics of neural networks and their mean-field description.

Monte Carlo Simulations

All simulations of networks of spiking neurons were implemented in the programming language Python (van Rossum, 1995), the scripts are available upon request. We employed time-driven solvers, based on a fixed step size. Time steps were chosen between 0.5 and 5 ms, depending on the expected spike rates. The goal was to keep the probability of missing a spike as small as possible. In all cases, we have checked that our results are robust against a further decrease of step size (data not shown).

For the simulations, we resorted to a natural reformulation of the model in discrete time. Let S_i(t) again denote the spike train of neuron i, now with the convention that S_i(t) = 1 if neuron i fired a spike at time t, and S_i(t) = 0 otherwise. Due to the exponential transfer function, firing rates couple multiplicatively to incoming spikes such that

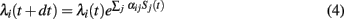
where dt is the step size of the simulation. In each time step

(i) a spike in neuron i is generated with probability 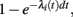yes and then

(ii) all spikes are propagated, and the rates are updated according to Eq. (4).

Simulations are quite effective, since only the state variables of those neurons must be updated that receive spikes. In addition, Python supports vectorized computations of using the numpy (Oliphant, 2006) module. For the for the estimation of the probability of observing an unstable network (Figure 4) and for the simulation of the spiking central pattern generator (Figure 5) we used an event-based solver for increased precision, based on the Doob-Gillespie algorithm (Doob, 1945; Gillespie, 1976).

Results

Power-Law Relaxation in Feed-Forward Systems

A specific strength of our approach is the possibility of determining the stationary response rate analytically, for a constant stimulus. To appreciate this result, it is instructive to first look at a very elementary “network,” composed of one input population and one output population (Figure 4). We assume that the input population fires at a constant rate λ_in ≥ 0. The strength of the connection is α_syn, which can be either positive (excitation) or negative (inhibition). We further assume that the output population is self-inhibiting with strength α_self < 0, implementing some sort of membrane potential reset after having produced a spike.

This population model describes a set of unconnected, independently firing neurons. Equivalently, it can be interpreted as the expected behavior of a single neuron, inferred from multiple independent observations (trials). This arrangement typically leads to an output spike train that is slightly more regular than a Poisson process (Softky and Koch, 1993; Shadlen and Newsome, 1998), and that has weak negative serial correlations between adjacent inter-spike intervals (Nawrot et al., 2008).

The system (3) of rate equations simplifies here to

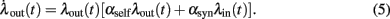
This non-linear ordinary differential equation governs the evolution of λ_out(t). Some elementary conclusions can be drawn right away: the output rate λ_out(t) remains always non-negative, provided the initial value is chosen non-negative. The two fixed points, which characterize the stationary solutions of Eq. (5), are 0 and 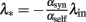yes . It is easy to verify that the more positive of the two fixed points is always globally attractive, and the other one is always globally repelling. That is, arbitrary non-negative initial output rates relax back to max {0, λ_*}. Considering α_synλ_in as the total signed input, a threshold-linear output characteristic (“half-wave rectifier”) results from this behavior, cf. also (Wilson and Cowan, 1972).

Apart from this simple non-linear response to stationary inputs, a feed-forward multiplicative unit also exhibits a power-law transient in its relaxation behavior, see Figure 2. Power-law relaxation to equilibrium has been described in real neurons (Lundstrom et al., 2008). In this paper fractional differentiation was used to model neuronal integration properties, with the aim describe slow time-scale dynamic properties.

FIGURE 2

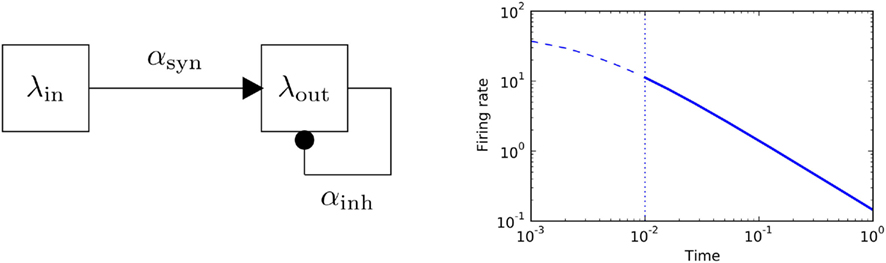
Figure 2. Feed-forward populations. Left panel: schematic of a two-population feed-forward circuit. Right panel: the decay of firing rate for a multiplicative process follows a power-law with exponent − 1. The analytic solution of the differential equation y′ = αy², y(0) = y₀ is given by 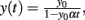yes plotted in blue for a particular choice of parameters (α = −3,y(0) = 50). Solid line marks the power-law region.

Input-Selective Response

If a unit has more than one input population, its total signed input is the sum of all input rates, weighted by the corresponding coupling constants. This suggests that the equilibrium dynamics of a multi-layer feed-forward network can be obtained by the following simple step-by-step procedure: first, one computes the equilibrium firing rates of the populations at the lowest level, induced by their respective inputs. The equilibrium rates of populations at higher levels are then obtained by the same method, treating the activity of all lower level populations as input.

As an example to illustrate the potential of such simple feed-forward networks, we demonstrate how to implement a system that is selective for inputs of strength within a prescribed range. This can be achieved with an arrangement of four populations, as depicted in Figure 3. Following the algorithm explained above, the output rate is given by

FIGURE 3

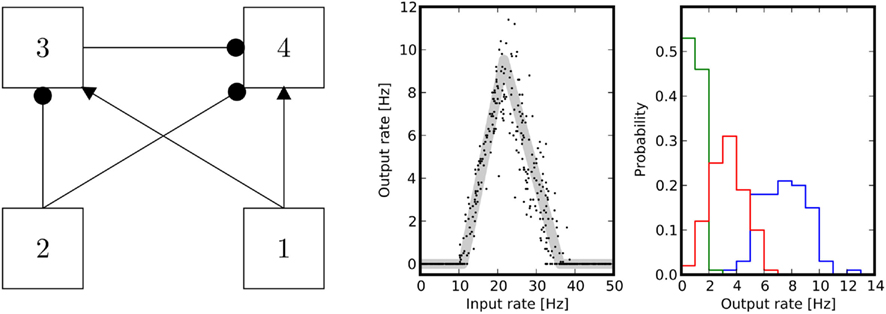
Figure 3. Band-pass filter. Left panel: population 1 is the input firing at λ_in, and population 4 is the output firing at λ_out. Population 2 provides a global inhibitory signal of rate λ_I that sets the point at which the circuit starts responding. Population 3 modulates the activity to adjust both the width and the slope of the filter. Center panel: the theoretical equilibrium response (light gray) was computed by determining the fixed points of Eq. (3). Simulations were performed by imposing Poissonian spike trains with different rates for the input population. The axes indicate input rate vs. output rate as extracted from single trials of 10 s duration. Right panel: normalized histograms of output rates measured during multiple trials, for three different input levels: onset (green), midpoint between onset and peak (red), peak (blue) of the tuning curve. The area under the ROC curve is always greater than 0.95. The parameters chosen for the simulation are w₄₁ = 1.1, w₃₁ = 1.05, w₃₂ = 0.9, w₄₂ = 0.9, w₃₃ = 0.7, w₄₄ = 0.9, λ₂ = 10.

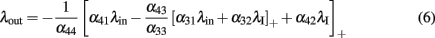
where we used the notation [λ]₊: = max{λ,0}. Furthermore, λ_I is a constant level of inhibition, and λ_in is the variable excitatory input.

For very strong input λ_in, the total excitation to the output unit is given only by the paths including the input, i.e., by 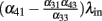yes . So, if the term in the brackets is positive, the output activity will increase for increasing input, whereas if it is negative, the output activity will be 0 for strong inputs. Since we want to construct a network selective for a certain range of inputs, we impose that

such that the output vanishes for high input rates. On the other hand, given that the input vanishes for high rates, the output is maximal at the point where the input rate to unit 3 overcomes the global inhibitory signal to unit 3, i.e., when

Inserting this value in Eq. (6) we obtain a maximal output of

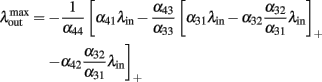
We now assume that 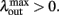yes Since α₃₁ > α₃₂ then 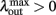yes if and only if

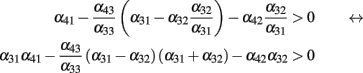
The only negative term in the sum is −α₄₂α₃₂. So we obtain a bound on the global inhibition level given by

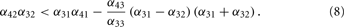
Under the conditions Eq. (7) and Eq. (8), the network is sensitive for rates in a certain range, given by the onset of the two threshold-linear functions. An example for a specific set of network parameters is given in Figure 3.

All computations in this network are performed on the level of mean firing rates of the neurons. Therefore, it is important to assess the behavior of the corresponding spiking network, e.g., its performance in a discrimination task. Results are given in Figure 3 and show, using ROC analysis, that different inputs can be well distinguished based on spike counts that are extracted from observations of finite duration.

Excitation-Inhibition Interplay

The situation for a recurrent network is typically more involved. The attractive regimes are not necessarily corresponding to stable fixed points. Depending on the number interacting units, competitive Lotka-Volterra systems can display a variety of different phenomena:

(i) continuous manifold of periodic trajectories in the classical two-dimensional case (Arnol’d, 1984);

(ii) periodic orbits with increasing periods, single and multiple limit cycles in three-dimensions (May and Leonard, 1975; Hofbauer and So, 1994; Rabinovich et al., 2006);

(iii) genuine chaotic dynamics in four dimensions (Wang and Xiao, 2010).

Here, we focus on one specific question of both theoretical and practical relevance: do the stability properties predicted by the rate Eq. (3) also determine the stability of the spiking system? Similar investigations have, in fact, been carried out for networks of integrate-and-fire neurons (Brunel, 2000; Mattia and Del Giudice, 2002; Ledoux and Brunel, 2011) as well as for binary neurons (van Vreeswijk and Sompolinsky, 1996, 1998).

We obtain a condition similar to the saddle-node bifurcation caused by a rate instability in LIF networks (Mattia and Del Giudice, 2004; Ledoux and Brunel, 2011).

To start our investigation, we recall that a sufficient condition for the dynamic stability of a non-linear equation can be derived from the existence of a so-called Lyapunov function for the system. Under certain conditions, such a function can be constructed for our networks. Specifically, if A_r denotes the recurrent part of the coupling matrix, then the system is stable, if all eigenvalues of A_r have a negative real part. With a slight abuse of terminology we will refer to such (not necessarily symmetric) matrices as negative definite. In this case, the total firing rate of all populations taken together is a Lyapunov function of the system, thus guaranteeing stability. This gives a handy sufficient (but not a necessary) condition for bounded rates in the system (Cardanobile and Rotter, 2010).

In two-dimensional systems describing mixed networks of homogeneous excitatory and inhibitory populations, dynamic stability can be assessed independently of a Lyapunov function. Such a system has dynamic variables λ_E(t) and λ_I(t), respectively, which are coupled by the two equations

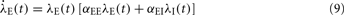
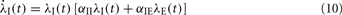
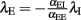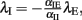where α_EE, α_IE > 0 and α_II, α_EI < 0. For such a system, the conditions for stability can be stated exactly, here made plausible using a simple heuristic argument. If the system was feed-forward and in equilibrium, the stationary rates of both populations would be yes and yes respectively. Inserting one expression into the other, we obtain

This is a self-consistency condition. The system has a transition when

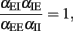
or, equivalently, when

We tested numerically the validity of this heuristic condition. Figure 4 shows simulation results that confirm the heuristic arguments made here. The condition given here is, in fact, a dissipativity condition which guarantees that the rate decays to 0 in absence of external input. Accordingly, if external input is present, the condition guarantees that the expected rate settles to an equilibrium value. It is interesting to mention that a linear system with the same coupling matrix has an additional stability condition. In fact, the condition given in Eq. (12) is a condition on the determinant of the connection matrix. The system is stable if and only if the determinant is larger than 0. For linear systems, one needs that additional constraints that the trace must be negative, which is not needed here.

FIGURE 4

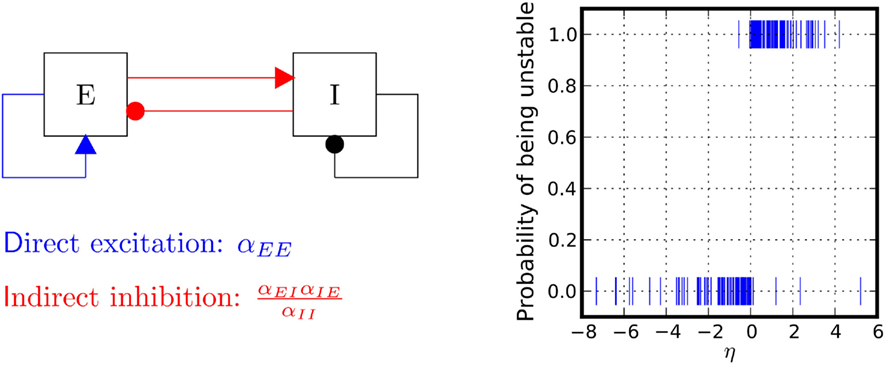
Figure 4. Stability properties. Shown is a Monte Carlo experiment that illustrates the condition for dynamic network stability derived in the main text. 200 Networks were initialized, with random couplings drawn from an exponential distribution with mean 1. For each network, a simulation was started and stopped whenever the total population rate would leave the range (10⁻¹⁰, 10²⁰⁰). If the total rate was small, the network was classified as stable, otherwise as unstable. For each network 1000 trials were performed. Plotted is the probability of being classified as unstable against the value of 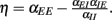yes This probability has a sharp transition from 0 to 1 at the value η = 0.

Spiking Central Pattern Generator

Central pattern generators have been studied on an abstract level by many authors, for a review see Rabinovich et al. (2006). Lotka-Volterra type equations have also been used as specific models (Venaille et al., 2005). However, no conclusive argument has been given why these systems would describe the mean-field dynamics of a neuronal network. In our framework, in contrast, using Eq. (3) and the exponential transfer function, one can map the parameters of the Lotka-Volterra oscillators onto the parameters of a spiking network, which is known to have the same mean-field dynamics. The main goal of this section is to demonstrate that the spiking networks behave according to the predictions of the rate equations also the latter have stable limit cycles, rather than attractive fixed points.

There are two fundamental alternatives to generate periodic patterns with Lotka-Volterra equations. Already the classical two-dimensional Lotka-Volterra system used in population dynamics predicts periodic orbits under certain conditions. More specifically, in that case a whole family of periodic orbits exists, surrounding a stable fixed point. This can be proven by using the fact that the system possesses a constant of motion with closed contour lines. As a consequence, oscillations can occur at different distances from the fixed point, and with possibly different frequencies (Arnol’d, 1984). Thus, due to intrinsic noise of the spiking system, these oscillations will not generate periodic patterns with a stable, precise frequency. Multiplicative point processes indeed exhibit periodic activity patterns with drifting frequencies, when connections are chosen according to the classical Lotka-Volterra system. However, we do not address this type of oscillator in this work.

Alternatively, it has been observed that higher dimensional Lotka-Volterra systems can have stable limit cycles (May and Leonard, 1975). In this case, the noise produced by the system is counterbalanced by the attractivity of the limit cycle. As a consequence, such oscillations have a stable frequency. Furthermore, since the limit cycle is attractive, the spiking network described by the rate equation is attracted to a periodic activity regime.

Mapping the parameters of such Lotka-Volterra systems back to its spiking counterpart allows to construct a spiking system generating precise periodic patterns of spiking. Figure 5 depicts an example of such behavior.

FIGURE 5

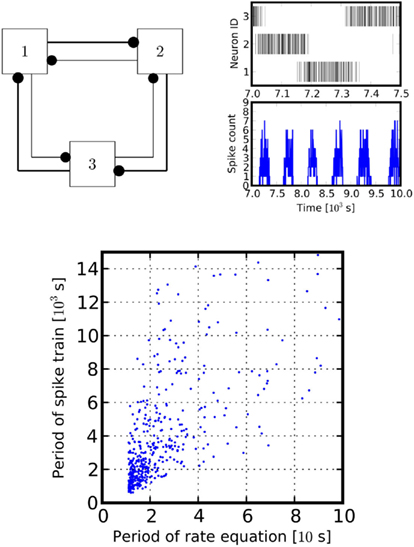
Figure 5. Central pattern generator. Left panel: a schematic of the connectivity of a simple central pattern generator. It involves three units with all-to-all inhibitory couplings (self-inhibition not shown), all provided with Poissonian input (not shown). Each unit sends inhibitory projections to its neighbors, one weak (inner, thin lines) and one strong (outer, thick lines). The asymmetric inhibition drives the network into an isolated periodic orbit, in which the three populations fire alternatingly. Right panel, upper box: raster plot for 500 s cycle length of the central pattern generator. Lower box: spike-time histogram of population 1. Spike counts are obtained in 30 s bins. Parameters for the raster plot were chosen as w = exp(−0.2 × 0.5) for weak inhibitory path, w = exp(−0.2 × 1.5) for the strong inhibitory path, w = exp(−0.2) for the self-inhibition. Poissonian input is at rate λ = 1. For the lower panel we randomized the coupling by drawing weights from a uniform distribution. Period length was estimated by taking the average distance between peaks of the autocorrelation of the simulated spike trains.

It is actually possible to design spiking networks that implement a given central pattern generator using spikes as signals. We have observed that, although strictly the firing rate description holds only for the mean-field model, periodic behavior is also exhibited in single trials, due to the absence of a competing stable regime. However, the spiking oscillator does not oscillate at exactly the same frequency as the rate equation. This is due to the intrinsically generated noise which continuously perturbs the system, continuously inducing transient behavior. Nevertheless, the oscillation frequencies of the rate equation and of the spiking counterpart are monotonically related, as it is shown in Figure 5, bottom panel.

A Linear Classifier Based on Winner-Take-All Dynamics

Networks with mutual inhibitory couplings that exhibit some kind of winner-take-all dynamics have long attracted the interest of neuroscientists in different contexts (Fukai and Tanaka, 1997; Wang, 2002). Fully connected inhibitory networks of multiplicative processes implement such winner-takes-all behavior, provided the total inhibitory output of each population exceeds its self-inhibition.

It can be shown that the probability of winning the competition is largest for the population which receives the strongest total input. According to the rate Eq. (3), the input to the ith population is given by

where λ_j denotes the firing rate of the jth population in the input layer, comprising K populations in total. Denote by

the vector of the synaptic strengths of the K input populations projecting to the ith unit. The total synaptic input to population i can thus be written as

Here, 〈v,w〉 denotes the standard scalar product between two vectors v and w. The population i_win receiving the strongest input maximizes 〈α_i,λ〉. Therefore, the highest probability of winning corresponds to the population for which the synaptic input vector is best-matching the input firing rates. In this sense, a completely connected inhibitory network of multiplicative processes performs a linear classification of input vectors.

The situation considered here is similar to the model described by Wang (2002). The network performs a decision (Figure 6), converging with high probability to the configuration where only the population with the best-matching input is firing. Additionally, the outcome of the (random) decision can be manipulated by adding a “bias” to one population (Figure 7). The performance of the classifier degrades if the input rate vectors are almost collinear, and it improves if they are close to orthogonal. This behavior imposes a limit to the number of patterns that can be linearly discriminated, but it also suggests that performance can be boosted by increasing the dimensionality of the input vector. Our results bear a similarity with the forbidden set theory developed by Hahnloser et al. (2003). The main difference is that we are concerned with the mapping of Lotka-Volterra equations to spiking systems.

FIGURE 6

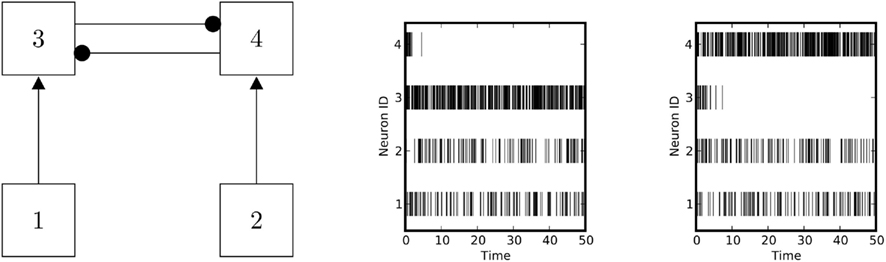
Figure 6. Decisions performed by a winner-takes-all network. Left panel: schematic of a winner-takes-all network. Right panel: the network performs a random decision between different alternatives. The probabilities for deciding between the different alternatives depend on the network parameters, on the initial states, and on the input levels.

FIGURE 7

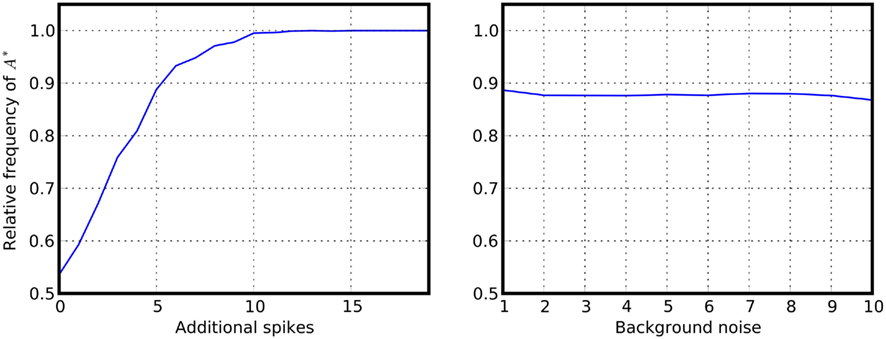
Figure 7. Providing a bias to winner-takes-all networks. Additional spikes are provided at the beginning of the simulation to one of the populations of a symmetric inhibitory network. Shown is the relative frequency that the primed alternative A^* is selected. Left panel: relative frequency for selecting A^*, displayed as a function of the number of additional spikes provided to one population at the beginning of the simulation. Right panel: reliability of the decision as a function of the background noise for a fixed number (n = 5) of additional spikes. Noise level was changed by increasing the synaptic strength while simultaneously decreasing the input firing rates.

Discussion and Outlook

In our study, we have demonstrated that multiplicative point processes (MPPs) provide a powerful new tool for the study of biological neuronal networks and their functional properties. We have constructed a number of previously unknown spiking network models with functional properties that can be predicted from the dynamics of the associated firing rate equations. In fact, the availability of a higher-level description of the spiking network dynamics in terms of population firing rates opens many new possibilities in terms of mathematical analysis, but also in terms of “engineering” spiking networks with desired properties. In particular, MPPs have the following features:

(i) They can be fitted to networks of homogeneous neural populations in terms of their first-order statistics (firing rates).

(ii) Their expected behavior (ensemble mean) can be precisely characterized in terms of coupled ordinary differential equations.

(iii) The mean-field rate equations give also useful information also about single trial spike statistics.

These features make our framework ideal for use in fundamental brain research, as well as in engineering applications. Specifically, a working theory for interacting neural populations could help in understanding the functional dynamics of interconnected brain areas. Inspired by considerations based on the rate description, research in modeling of the basal ganglia network has already been conducted by the authors (Kumar et al., 2011).

Biophysical Extensions

In this manuscript, we have addressed the construction of neural circuits with prescribed properties, using a first-order non-linear rate description. There are several directions in which the theory could be extended to a more detailed and more precise biophysical theory. In previous work, Toyoizumi et al. (2009) derived rate equations for leaky integrate-and-fire neurons based on a Markov process model combined with a noisy threshold. The Markov approximation is often combined with a Gaussian approximation of the membrane potentials. This method is mainly limited by the complexity of the resulting rate equations.

For multiplicatively interacting point processes, there are two possible directions in which the model could be extended. On the one hand, one could strive for more realistic models which include additional dynamic phenomena observed in the activity of neurons. Promising steps have been already performed by including refractoriness into dynamical models (Deger et al., 2010). The differential equations derived in this context could be easily adapted to describe also networks, for the price of increased mathematical complexity. Synaptic transmission delays can be also incorporated into the description, leading to systems of delay Lotka-Volterra equations. Such equations have been extensively studied in the mathematical literature (Bomze, 1983, 1995; Tainaka, 1988), also in a stochastic context (Mao et al., 2003; Cattiaux and Méléard, 2010) and with applications to neural networks (Yi and Tan, 2002).

To include more complex neuronal dynamics into the model one can use a relation connecting the derivative of the mean-field and the conditional derivative of a stochastic process (Nelson, 1987, Chap. 9)

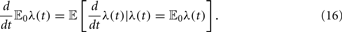
Here 𝔼₀ denotes the best prediction for λ(t) at time 0, the “mean–field.” Based on this relation, seems possible, at least in principle, to derive rate equations for any given neuronal dynamics, provided that the rate only couples to the membrane potential. The precise translation of this formalism into useful rate equations depends, of course, on the details of the neuron model under consideration.

Higher-Order Moments and Correlations

Another interesting question is whether the non-Gaussian approach we have adopted in this work can be adapted to study higher-order statistics of neural networks. Buice et al. (2010) introduced a path integral formulation of neuronal interactions with the aim of deriving expansions for higher-order moments. One limit of their approach is the intrinsic complexity of the path integral formalism.

For multiplicative processes one could attempt a similar treatment exploiting the following idea. Assuming that unit i has rate λ_i(0) at time 0, the rate at time t is given by

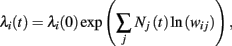
where N_j(t) denotes the number of spikes from unit j until time t. Differentiating, this expression leads to

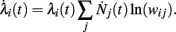
Since 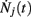yes is nothing but the spike train produced by unit j, taking expectations and ignoring covariances leads to Eq. (3). In fact, this is an alternative derivation of those equations. The advantage of this derivation is that now it becomes apparent that similar higher-order equations can be derived using the formula

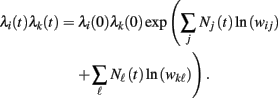
After differentiations, mixed third-order moments appear in the derivative of the rate product λ_i(t)λ_j(t). Unfortunately, it is not clear what are the terms that can be ignored. Further research will be needed to derive rate equations for higher moments.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Supported by the German Federal Ministry of Education and Research (BMBF 01GQ0420 to BCCN Freiburg; BMBF 01GW0730 Impulse Control).

References

Abbott, L. F., and van Vreeswijk, C. (1993). Asynchronous states in networks of pulse-coupled oscillators. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics 48, 1483.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Arieli, A., Sterkin, A., Grinvald, A., and Aertsen, A. (1996). Dynamics of ongoing activity: explanation of the large variability in evoked cortical responses. Science 273, 1868–1871.