Spike train auto-structure impacts post-synaptic firing and timing-based plasticity
- 1 Clinic for Anesthesia, Intensive Care Medicine and Pain Therapy, Johann Wolfgang Goethe University, Frankfurt am Main, Germany
- 2 Institute of Cognitive Science, University of Osnabrück, Osnabrück, Germany
- 3 Department of Neurophysiology, Max-Planck-Institute for Brain Research, Frankfurt am Main, Germany
- 4 Frankfurt Institute for Advanced Studies, Johann Wolfgang Goethe University, Frankfurt am Main, Germany
Cortical neurons are typically driven by several thousand synapses. The precise spatiotemporal pattern formed by these inputs can modulate the response of a post-synaptic cell. In this work, we explore how the temporal structure of pre-synaptic inhibitory and excitatory inputs impact the post-synaptic firing of a conductance-based integrate and fire neuron. Both the excitatory and inhibitory input was modeled by renewal gamma processes with varying shape factors for modeling regular and temporally random Poisson activity. We demonstrate that the temporal structure of mutually independent inputs affects the post-synaptic firing, while the strength of the effect depends on the firing rates of both the excitatory and inhibitory inputs. In a second step, we explore the effect of temporal structure of mutually independent inputs on a simple version of Hebbian learning, i.e., hard bound spike-timing-dependent plasticity. We explore both the equilibrium weight distribution and the speed of the transient weight dynamics for different mutually independent gamma processes. We find that both the equilibrium distribution of the synaptic weights and the speed of synaptic changes are modulated by the temporal structure of the input. Finally, we highlight that the sensitivity of both the post-synaptic firing as well as the spike-timing-dependent plasticity on the auto-structure of the input of a neuron could be used to modulate the learning rate of synaptic modification.
Introduction
The processing of information within the cortex crucially depends on the neuronal self-organization and structure formation of neuronal networks. While studying such networks and their structure formation, the spatiotemporal patterns of neuronal activity is often ignored and spike activity is modeled by Poisson-point processes. One argument for assuming Poissonian firing has been that neurons can receive input from up to several thousand pre-synaptic neurons (Destexhe et al., 2001; Faisal et al., 2008). With the further assumption that the firing of these pre-synaptic neurons is mutually independent, it has been argued that any auto-structure in the individual processes is washed out once the activity is integrated and forms a single so called compound process reaching the soma of the cell (original publication Hanson and Tuckwell, 1983; related publications please see Fellous et al., 2003; Ostojic et al., 2009). However, analytically it has been demonstrated that only the inter-spike interval (ISI) distribution and the ISI correlations of the compound process can be well approximated by a Poisson process (Lindner, 2006). The auto-correlation of the compound process, however, does not vanish in general (please note: a Poisson process has zero auto-correlation; Câteau and Reyes, 2006; Lindner, 2006). For the extreme case where all point processes are identically distributed, the auto-correlation of the compound process shows an overall reduction in amplitude compared to the auto-correlation of each individual process, with the shape being preserved (Lindner, 2006). Furthermore, it has been shown that individual non-Poissonian pre-synaptic activity might also result in a non-Poissonian compound activity, which holds true even if thousands of spike trains are added up (Pipa et al., 2008).
Structure formation due to synaptic plasticity has been discussed to be reliant on the precise timing of spiking events (Markram et al., 1997; Song and Abbott, 2001; Lazar et al., 2007, 2009). Since real neuronal activity typically deviates from Poisson processes (Smith, 1954a,b; Burns and Webb, 1976; Levine, 1991; Iyengar and Liao, 1997; Teich et al., 1997; Pipa et al., 2006; Nawrot et al., 2007, 2008; Averbeck, 2009; Maimon and Assad, 2009), the modeling of real neuronal firing and structure formation might require a more realistic assumption, including non-Poissonian pre-synaptic firing.
Here, the simulation of a conductance-based integrate and fire neuron is used to determine how deviations from a Poissonian structure of pre-synaptic spike trains affect the firing probability of a post-synaptic cell. We show that a non-Poissonian structure of pre-synaptic spike trains and the resulting changes in post-synaptic firing modulate structure formation in a network with synaptic plasticity modulated by spike-time-dependent plasticity (STDP). In particular, we show that even in the case of mutually independent inputs, both the equilibrium distribution of synaptic weights and the temporal evolution of the weight of individual synapses depend on the precise temporal auto-structure of pre-synaptic neurons. Finally, we discuss possible consequences of these results on structure formation in recurrent networks, as well as potential modulators of plasticity arising just by the sensitivity on the structure (i.e., regularity as well as rate distribution across pre-synaptic neurons).
Materials and Methods
Modeling the Pre-Synaptic Activity
We modeled pre-synaptic activity as a set of mutually independent renewal processes. The ISI (ξ) of each process followed a gamma distribution with an integer shape factor (γ)
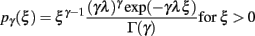
where γ = 1/〈ξ〉 stands for the rate of the point process. Note that a Poisson process is then a special case of a gamma process with a shape factor of γ = 1. In order to simulate spike trains, we sampled ISIs from the corresponding gamma distribution. To prevent correlations with respect to the initial condition, i.e., simulation time t0, we simulated a warm-up period containing 1000 spikes. For the simulation shown here, we used spikes subsequent to the warm-up period. To test whether spikes are equilibrated after the warm-up period, we performed a test on the homogeneity of the spiking probability in the first 100 ms after simulation start.
Modeling the Post-Synaptic Neuron
We simulated a conductance-based integrate and fire neuron (IF) which receives input from an excitatory and an inhibitory neuronal population, consisting of Ne and Ni spike trains, respectively. A detailed description of the model can be found in Salinas and Sejnowski (2001) and the exact values of the parameters are described on Table 1. The equation governing the membrane potential reads:
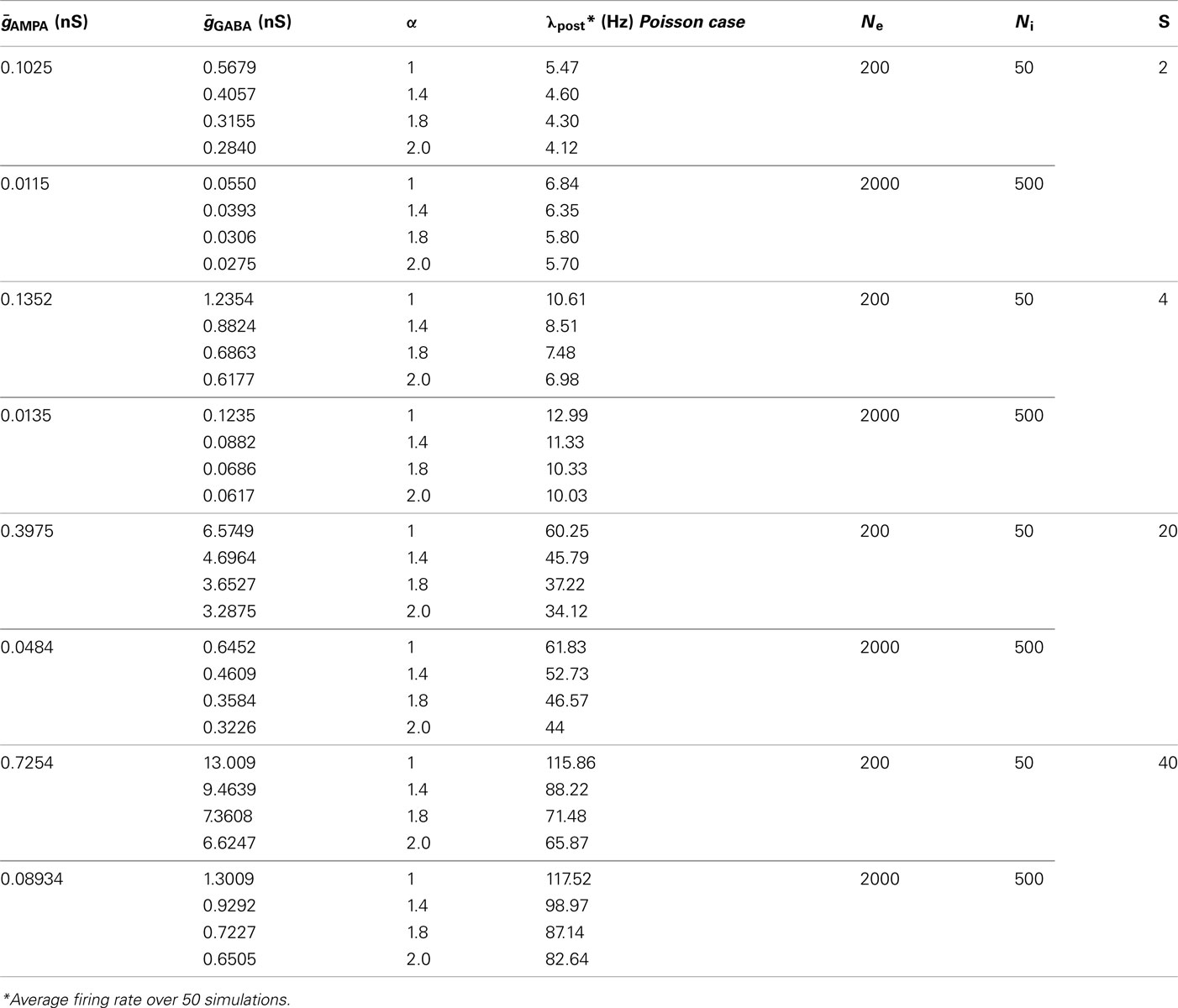
Table 1. Implementation details of the neural network model (as described in Nordlie et al., 2009).
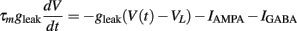
where
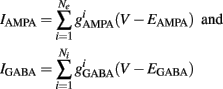
Additionally, when V(t) exceeds a threshold Vθ, an action potential is elicited. The membrane potential is then clamped to the value Vreset. The membrane time constant was set to τm = 20 ms. Numerical integration with forward Euler method was used to solve the differential equation (step size of 0.05 ms). AMPA and GABA mediated receptors were modeled by exponentially decaying synaptic conductances with time constants τAMPA = 2 ms and τGABA = 5.6 ms.
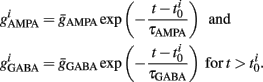
Maximal synaptic conductance strengths 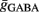 and
and 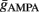 were chosen to be identical across all synapses of the same type.
were chosen to be identical across all synapses of the same type.
In this modeling study, we want to control four main criteria: First, we want to regulate the ratio between the leak conductance gleak and the total conductance contributed by both excitatory and inhibitory synapses gtotal (Destexhe and Paré, 1999). Second, we want to control the firing rate of the post-synaptic neuron. Third, we want to have an approximated balance between excitation and inhibition (average net synaptic drive approx. compensating the leak; Haider et al., 2006; Rudolph et al., 2007). Fourth, we want to control the input firing rate of both inhibitory and excitatory synapses so that we can control the auto-structure of the incoming activity. Regarding this last case, the ratio between the firing rate of the excitatory and inhibitory population is always described by:
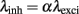
Next, we outline how these four constraints were met by choosing appropriate parameters. To control the ratio between the leak conductance gleak and the total conductance, we introduce the scaling factor S, so that gtotal = Sgleak (see Salinas and Sejnowski, 2001). Further simulation values of S = 2, 4, 20, 40 are used. However, motivated by experimental studies (e.g., Destexhe and Paré, 1999) for most parts of the simulations, we choose the total conductance to be four times higher than the leakage (S = 4), otherwise stated.
As follows, for controlling the post-synaptic firing rate, the average membrane potential and the sub-threshold fluctuations have to be considered. The average membrane potential in our model is determined by the balance between excitation and inhibition. The fluctuations are determined by the number of synapses and the average conductance 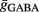 and
and 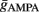 . Moreover, note that increasing the number of synapses while keeping the total conductance gtotal the same, leads to a reduction in the amount of membrane fluctuations and therefore to a reduction in the post-synaptic firing rate. Thus, to control the firing rate, given a certain number of pre-synaptic synapses and a certain S determining the total conductance, we adapted the balance of the average conductance
. Moreover, note that increasing the number of synapses while keeping the total conductance gtotal the same, leads to a reduction in the amount of membrane fluctuations and therefore to a reduction in the post-synaptic firing rate. Thus, to control the firing rate, given a certain number of pre-synaptic synapses and a certain S determining the total conductance, we adapted the balance of the average conductance 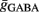 and
and 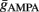 via numerical simulations such that the average post-synaptic firing rate was 10 spikes/s (pre-synaptic Poisson). Exact combinations of parameters can be taken from the Table 2.
via numerical simulations such that the average post-synaptic firing rate was 10 spikes/s (pre-synaptic Poisson). Exact combinations of parameters can be taken from the Table 2.
Modeling Spike-Time-Dependent Plasticity
Spike-time-dependent plasticity was modeled as originally introduced by Abbott and Nelson (2000) and Song and Abbott (2001). The synaptic connectivity between excitatory neurons is modified depending on the temporal difference δt between pre- and post-synaptic spikes. The synaptic modification, described by A+ and A−, is given by
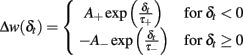
The exact values of the parameters are described in Table 1. This STDP curve describes the synaptic modification in pyramidal neurons of the layer 5 in neocortex as described in experiments by Markram et al. (1997). Although variable STDP learning curves have been found, such pair-based STDP models already represent the temporal causality relation between neurons. Moreover, it is widely used in theoretical studies, keeping results comparable across studies (Song and Abbott, 2001; Lazar et al., 2007; Morrison et al., 2008). For an efficient implementation, we keep track of the entire history that contributed to STDP at an individual synapse by defining an auxiliary Ppre and Ppost that satisfy:
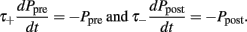
Every time an excitatory pre-synaptic terminal emits a spike, Ppre is increased by A+ otherwise, exponential decay with time constant τ−), resulting in a change in the conductances of excitatory neurons as follows:
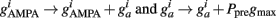
Thus, Ppre(t) determines how much a synapse is weakened if the pre-synaptic neuron fires an action potential at time t. Otherwise, Ppost is decreased by A− every time the post-synaptic neuron fires an action potential and 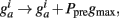 so that Ppost(t) determines how much the synapse is strengthened if the pre-synaptic terminal receives a spike at time t. Following Song and Abbott (2001), the conductances are a measure of the strengths of the weights. Finally,
so that Ppost(t) determines how much the synapse is strengthened if the pre-synaptic terminal receives a spike at time t. Following Song and Abbott (2001), the conductances are a measure of the strengths of the weights. Finally, 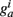 is bounded such that
is bounded such that 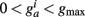 (hard bound).
(hard bound).
Results
First, we show that the auto-structure of pre-synaptic spiking can modulate the auto-structure of post-synaptic activity. In particular, we present the relation between pre- and post-synaptic firing for Poisson and gamma processes. In the last section of the results, we show the impact of non-Poissonian pre-synaptic activity on structure formation induced by spike-timing-dependent plasticity. Note that throughout the paper, when comparing results across different auto-structures of the pre-synaptic activity (different shape parameter of the ISI distribution γ), all other parameters are kept constant.
Impact of Pre-Synaptic Auto-Structure on Post-Synaptic Firing
To study how the temporal structure of either excitatory or inhibitory drive modulates the post-synaptic firing of a neuron, we simulated an Integrate and Fire neuron receiving inputs from Ne = 200 excitatory (AMPA) and Ni = 50 inhibitory (GABA) synapses. Each individual synapse transmits a spike train with mean firing rate λexci or λinh, depending on whether they are excitatory or inhibitory (see Materials and Methods for a more detailed description of the model). Throughout this paper, the temporal structure of each individual pre-synaptic train has been modeled as a gamma point-process with shape factor of either 1, corresponding to Poissonian activity (referred to as Poissonian) or γ = 100, which corresponds to oscillatory regimes (referred to as gamma). The impact of Poissonian and gamma processes for both excitatory and inhibitory activity will be addressed by comparing four different cases: Poissonian excitation and inhibition; gamma type excitation and Poissonian inhibition, Poissonian excitation and gamma type inhibition, and finally, gamma type excitation and inhibition.
We start by characterizing the relation between pre- and post-synaptic firing by means of the post-synaptic spike-triggered average of the pre-synaptic population activity (referred to as STA, Figure 1). The STA shows the pre-synaptic population activity, i.e., excitatory (black) and inhibitory (red), relative to the timing of a post-synaptic spike. For each of the combinations of Poissonian and gamma-process activity for inhibitory and excitatory neurons (Figure 1, row 1–4), there is a prominent increase of average excitatory activity and decrease of inhibitory population activity preceding a post-synaptic spike, since a post-synaptic spike is more likely to occur if inhibition is reduced (see red lines, Figure 1) and excitation increased (see black lines, Figure 1). For the gamma processes, we additionally find a repetitive structure, an increase/decrease of spiking density preceding and following the post-synaptic spike for excitatory/inhibitory populations, respectively. This reduction and increase of firing density are both occurring at a distance which corresponds to the individual average ISI of the pre-synaptic spike trains. Moreover, these peaks observed on the spiking density are a reflection of the modulation of the auto-correlation of the compound process (e.g., for excitatory neurons, see black lines in row 2 and 4 of Figure 1). The same modulation of pre-synaptic activity preceding a spike happens for the inhibitory population, but the direction of the modulation is opposite (see red lines in row 3 and 4 of Figure 1). In other words, the firing density of both excitatory and inhibitory populations is locked to a post-synaptic event. This could be explained by the fact that the neuron may fire if any relatively small subpopulation produces either a synchronized increase of excitatory activity or a synchronized decrease of inhibitory activity.
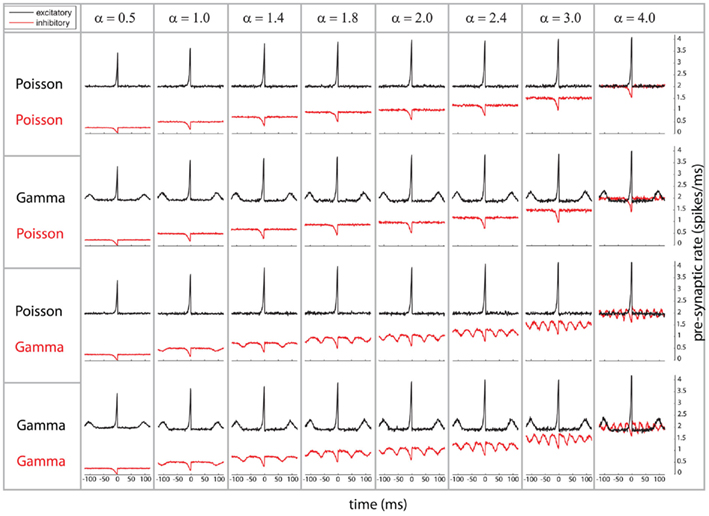
Figure 1. Spike-triggered average (STA) as relation between the compound process of 250 mutually independent pre-synaptic spike trains and post-synaptic firing. Variations of the relative firing rates of inhibitory/excitatory are reflected in α (columns), and different combinations of firing statistics (gamma γ = 100/Poisson γ = 1) are presented for the pre-synaptic excitatory (Ne = 200) and inhibitory (Ni = 50) population (rows). Total conductance was S = 4 and bin size 1 ms. Firing rates for excitatory neurons were kept at 10 Hz, whereas the firing rates of the inhibitory population was varied in the steps 5, 10, 14, 18, 20, 24, 30, and 40 Hz, corresponding to values of α = 0.5, 1.0, 1.4, 1.8, 2.0, 2.4, 3.0, and 40. Increasing the firing rates of the inhibitory pre-synaptic activity leads to a higher spike-triggered average. For a pre-synaptic gamma-process, the modulation in the STA shows peaks in a distance of the peaks representing the expected inter-spike interval.
In summary, as a first point, post-synaptic firing is sensitive to the pre-synaptic auto-structures of mutually independent spike trains. Secondly, post-synaptic firing is locked to periods with increases of excitatory firing and decreases of inhibitory firing. Third, in the case that either of the two types is composed of gamma processes, these increases and decreases reoccur with a temporal structure given by the auto-correlation of the compound process, which again is identical to an amplitude-reduced auto-correlation of the individual pre-synaptic processes.
After characterizing the relation between the pre- and post-synaptic firing, we now explore its implication on the auto-structure of the post-synaptic firing. To that end, we computed the auto-correlogram of the post-synaptic firing for the different combinations of excitatory and inhibitory pre-synaptic drives while modifying the relative firing rate between the two populations, the α factor (Figure 2). Therefore, note that the inhibitory rate is different for any column since α ranges from 0.5 to 4. The auto-correlation of the post-synaptic firing becomes flat (for time intervals larger than the refractory time of a few milliseconds) only when all of the pre-synaptic spike trains are Poissonian (Figure 2, row 1) or if α is large and only the inhibitory activity is temporally structured (Figure 2, row 3, last three columns). Otherwise, the auto-correlation of the post-synaptic firing is periodically modulated by at least one non-Poissonian pre-synaptic population (Figure 2). The period of the oscillatory modulation is determined by the expected ISI of the non-Poissonian processes (e.g., Figure 2, row 2, this modulation is 10 Hz (where Hertz stands for spikes per second) corresponding to an average ISI of 100 ms on the excitatory population). In the case where only the excitatory drive is temporally structured, the modulation of the auto-correlation has the same period as the expected ISI of the excitatory process (Figure 2, row 2). If both the excitatory and the inhibitory populations are composed of gamma processes with different rates, as shown in Figure 2 (row 4), the modulation of the post-synaptic auto-correlation is a mixture of modulations of both compound processes.
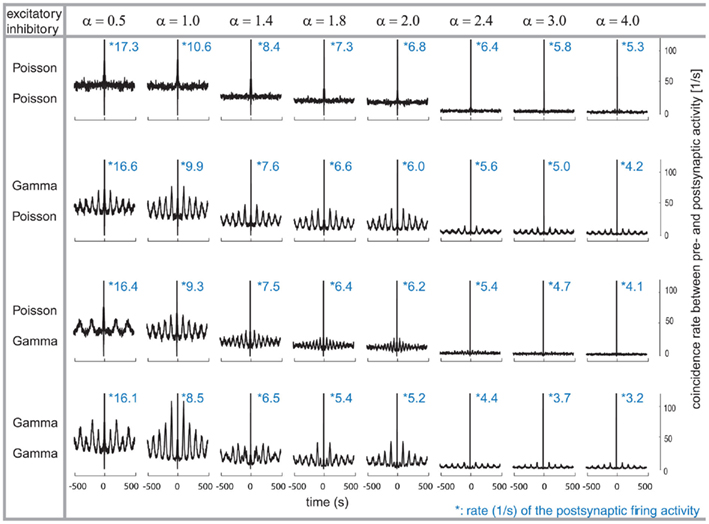
Figure 2. Correlograms and firing rates of the post-synaptic spiking activity. Variations of the relative firing rates of inhibitory/excitatory are reflected in α (columns), and different combinations of firing statistics (gamma γ = 100/Poisson γ = 1) are presented for the pre-synaptic excitatory (Ne = 200) and inhibitory (Ni = 50) population (rows). Total conductance was set to S = 4. With higher pre-synaptic inhibitory firing rates (α), the post-synaptic firing rates decrease. At each α, the post-synaptic firing rate decreases when the pre-synaptic firing is gamma-distributed, while the lowest post-synaptic firing rate is present when both pre-synaptic inhibitory and excitatory distributions are Poissonian. Modulations in the post-synaptic firing pattern are more prominent when the excitatory population is given a gamma-shaped firing modality, are missing when both inhibitory and excitatory firing show a Poisson-distributed pattern and is inhomogeneous in its appearance when the post-synaptic activity is driven by both inhibitory and excitatory gamma-shaped distributions.
Effect of different rates for individual pre-synaptic populations
Next, we investigate the effect of the excitatory and inhibitory input structure on the post-synaptic spike train while interacting at different firing rates. We model both excitatory and inhibitory populations by mutually independent gamma processes (γ = 100) and we vary the relative firing rate between them. The rate for the excitatory population is set to 10 Hz while the rate of the inhibitory population is varied systematically, based on the ratio between the firing rate of the inhibitory and excitatory population α. We explore a value of α = 1 and variations between 0.5 and 4.
In the case of α = 1, where excitatory and inhibitory neurons have the same firing rates, the interaction between the two auto-structures is restricted to a locked increase and decrease of activity in both populations (Figure 1, row 4 and column 2), as measured by the STAs. Nevertheless, the pre-synaptic spike-triggered average for regular gamma processes and different firing rates between populations shows a damped oscillation for all tested values of α, i.e.,α = 0.5, 1.4, 1.8, 2.0, 3.0, and 4.0 (Figure 1, row 4). Note that the STA of the excitatory population remains unchanged for different values of α, which is expected, since pre-synaptic activity is composed of mutually independent processes. The periods of the oscillatory modulations for both populations is determined by the expected ISI of the respective point processes.
Damped oscillations are also visible on the auto-correlation of the post-synaptic activity (Figure 2, row 4). In the case of α = 1 (Figure 2, row 1–4 and column 2), the post-synaptic auto-correlation function essentially reflects the auto-correlation of each of the individual processes, either excitatory or inhibitory. However, in the other cases of α, i.e.,α = 0.5, 1.4, 1.8, 2.0, 3.0, and 4.0, where the firing rates are not the same between excitation and inhibition, the interaction between both populations becomes more important. An α = 2 value induces a modulation with a strong component at 10 Hz coming from the excitatory expected ISI and a smaller component with 20 Hz arising by the inhibitory population (Figure 2, column 5). This modulation for α = 2 still leads to a clear damped periodic pattern of the auto-correlation. However, for other values of α the interaction is more complicated. For these values, the period length of the modulation in the STA of the excitatory and inhibitory drive does not follow as a simple n:m relation anymore, as for α = 0.5, 1, 2 corresponding to 1:2, 1:1, and 2:1 relation, respectively.
The cases of α (i.e.,α = 1.4, 1.8, 2.0, 3.0, and 4.0) induce more complex modulations, dominated by a rhythm of 10 Hz, arising by the expected ISI of the excitatory population. This becomes evident, for example, in the case of α = 1.4, for which the first side peak of the post-synaptic auto-correlation is lower than the second and the third (Figure 2, column 3).
Effect of population size
Additionally, we explored the effects of population size on the auto-structure of post-synaptic firing. In Figure 3, we show the STA and in Figure 5 the auto-correlation of the post-synaptic spike train for the same population size that was used in all other simulations previously discussed (Ne = 200 excitatory as gamma-process and Ni = 50 inhibitory Poisson process with rate λinh = λexci = 10 Hz, and a total synaptic weight S = 4 times the leak conductance). To assess the effect of the population size and the synaptic strength, we increased the population by a factor of 10 so that Ne = 2000 and Ni = 500 (STAs shown in Figure 4 and auto-correlogram shown in Figure 6). To distinguish the contribution of the increase in population size from that of the total synaptic weight, we scale at the same time the individual synaptic weights (different rows with S = 2, 4, 20 2, 4, 20, and 40 in the Figures 3–6). Note that the individual synaptic weight of a model with S = 2 and 250 synapses is equivalent to the model with S = 20 and 2500 synapses. The same holds true for S = 4 and S = 40 in the case of 250 and 2500 synapses, respectively. In contrast, other combinations of the number of synapses and S induce changes in the synaptic strength distribution. To identify the effect of an increase in the number of synapses keeping the individual strength of each synapse identical, one can compare the case S = 20 or 40 for the 250 synapses with the case S = 20 or 40 for 2500 synapses (compare row 1 and 2 from Figure 3 with row 3 and 4 from Figure 4). Irrespective of the choice of S and the number of synapses, all cases exhibit the same pattern, qualitatively. All show modulations with a frequency given by the ISI of the excitatory population. This indicates that the temporal structure of non-Poisson activity is modulating post-synaptic firing even for large pre-synaptic populations and rather small weights.
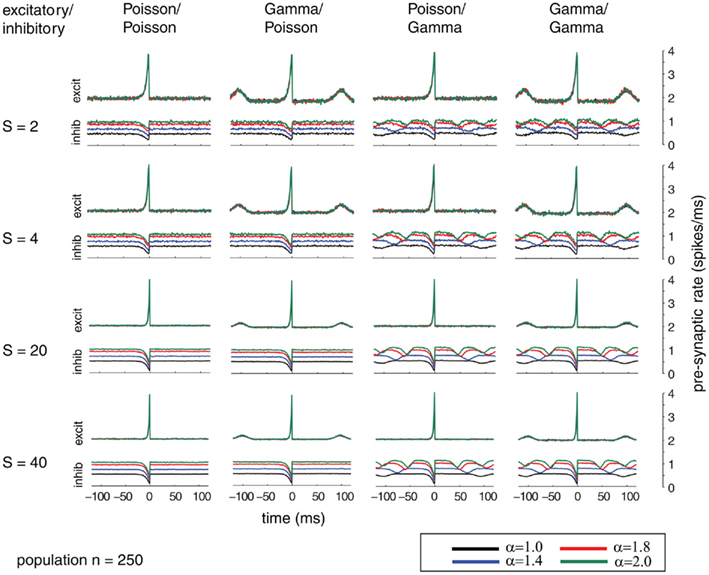
Figure 3. Spike-triggered average (STA) as relation between the compound process of 250 mutually independent pre-synaptic spike trains and post-synaptic firing. Variations of the relative firing rates of inhibitory/excitatory are reflected in α (color coded). Variable conductance of S (rows) is compared to different combinations of firing statistics (gamma γ = 100 and Poisson γ = 1) for the pre-synaptic excitatory (Ne = 200) and inhibitory (Ni = 50) population (columns). Firing rates for excitatory neurons were kept at 10 Hz, whereas the firing rates of the inhibitory population was varied in the steps 10, 14, 18, and 20 Hz, corresponding to values of α = 1.0, 1.4, 1.8, 2.0. Increasing the firing rates of the inhibitory pre-synaptic activity leads to higher values of the spike-triggered average. For gamma processes in the pre-synaptic activity, the modulation in the STA shows peaks with the distance of the peaks representing the expected inter-spike interval. The appearance of this modulation is irrespective of the conductance values S.
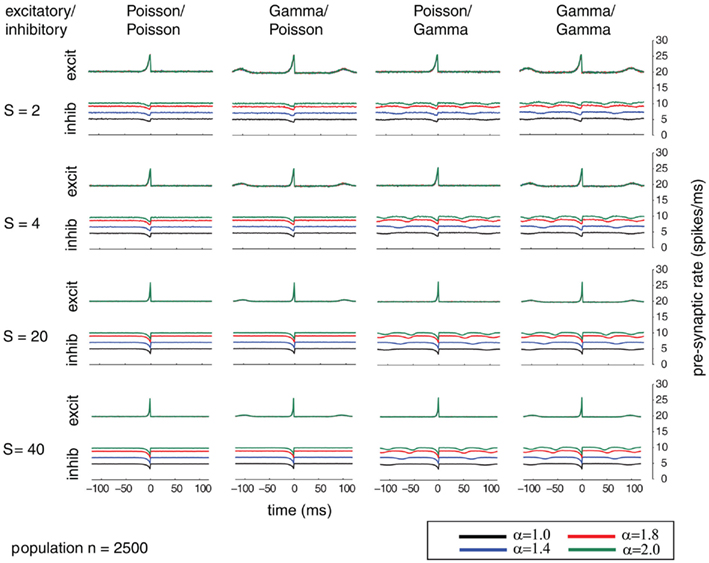
Figure 4. Spike-triggered average (STA) comparable to Figure 3 but for a population size of 2500 mutually independent spike trains. Figure 4 shows the dependence of varying relative firing rates for the inhibitory/excitatory spike trains α (color coded) and variable conductances S (rows) for the different combinations of firing statistics (gamma γ = 100 and Poisson γ = 1) for the excitatory (Ne = 2000) and inhibitory (Ni = 500) population. Firing rates for excitatory neurons were kept at 10 Hz, whereas the firing rates of the inhibitory population was varied in the steps 10, 14, 18, and 20 Hz, corresponding to values of α = 1.0, 1.4, 1.8, 2.0. Increasing the firing rates of the inhibitory pre-synaptic activity leads again to higher values of the spike-triggered average. For gamma processes in the pre-synaptic activity, the modulation in the STA shows peaks with the distance of the peaks representing the expected inter-spike interval. The appearance of the modulation is irrespective of the conductance values S.
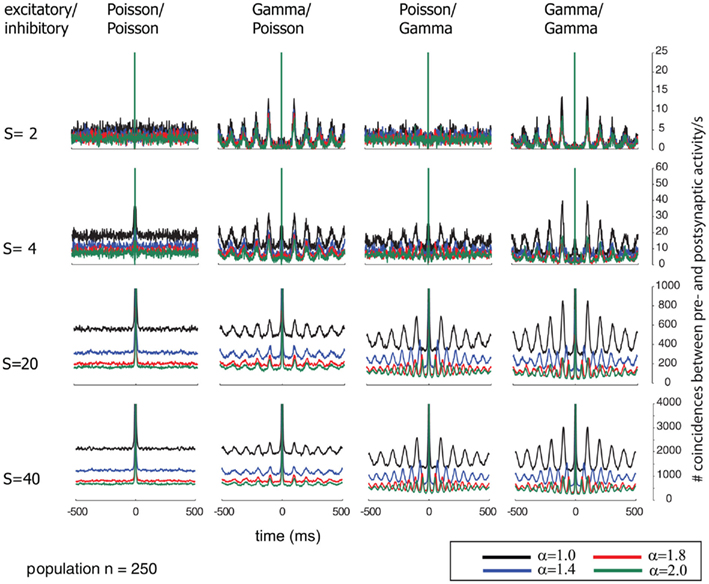
Figure 5. Correlograms of the post-synaptic spiking activity in dependence of varying relative pre-synaptic firing rates for the inhibitory/excitatory spike trains α (color coded) and variable conductances S (rows) for the different combinations of firing statistics (gamma γ = 100 and Poisson γ = 1) for the pre-synaptic excitatory (Ne = 200) and inhibitory (Ni = 50) population (columns).
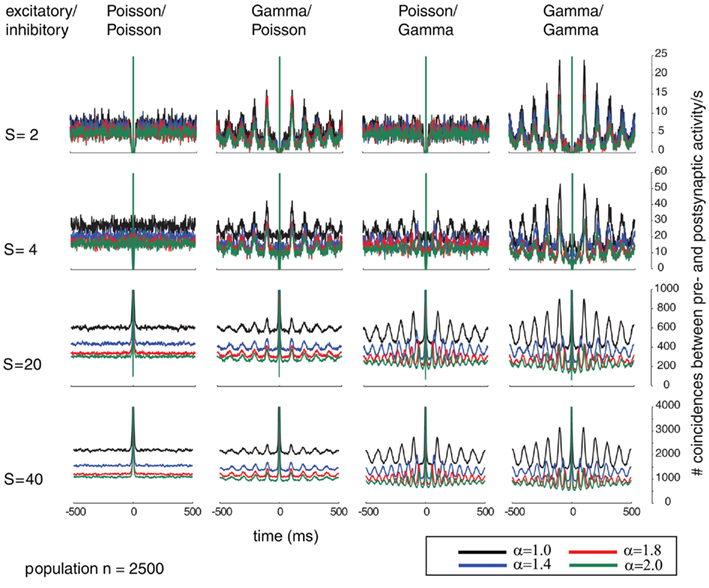
Figure 6. In analogy to Figure 5, This Figure shows the correlograms of the post-synaptic spiking activity in dependence of varying relative pre-synaptic firing rates for the pre-synaptic excitatory (Ne = 2000) and inhibitory (Ni = 500) population (columns for the inhibitory/excitatory spike trains α (color coded) and variable conductances S (rows) for the different combinations of firing statistics (gamma γ = 100 and Poisson γ = 1).
Effects of Non-Poissonian Input on Structure Formation due to STDP
After having evaluated the role of non-Poissonian pre-synaptic input in the firing properties of a post-synaptic neuron, we are now in a position to discuss the potential impact of non-Poissonian pre-synaptic activity on structure formation and learning via STDP. This form of plasticity has been applied to sequence learning and has been discussed to be involved in spontaneous and activity-driven pattern formation (Markram et al., 1997; Song et al., 2000; Lazar et al., 2007, 2009). STDP can strengthen potentially causal relations between pre-synaptic drive and post-synaptic activity by increasing the synaptic strength of all synapses that have been activated immediately before a post-synaptic spike is generated.
Equilibrium distribution of synaptic weights under STDP
We performed simulations on a single IF neuron (same as described above) with the addition of an exponential STDP rule to its excitatory synapses (see Materials and Methods). Inhibitory synapses were not involved in the plasticity dynamics and were initialized with the same synaptic strength. We then monitored, for each individual synapse, the temporal evolution of the changes on the synaptic strength for a period of 500 s. As in the previous sections, we used mutually independent renewal gamma processes as input. After ensuring that the distribution of synaptic strength was stable at the end of the simulation period, we used the last 50 s of the simulation time to estimate the equilibrium distribution of the synaptic conductances.
The cumulative equilibrium distributions of conductance for four combinations of Poissonian and gamma activity for the inhibitory and excitatory population are shown in Figure 7A. In general, the shape of the synaptic weight distribution is bimodal, as shown in Song and Abbott (2001). Remarkably, temporally structured and yet mutually independent activity of the excitatory population leads to different medians (corresponding to a value of 0.5 on the y axis in Figure 7A) and different shapes of the distributions. The median of the synaptic weight is typically larger for the case of excitatory Poisson processes, independent of the temporal structure of the inhibitory population. The difference in the median can be as large as ∼20%. For all tested cases, the tails of the bimodal distribution of weights became heavier in the case of excitatory Poisson processes regardless of the temporal structure of the inhibitory population. Both effects of the median and the shape are independent of the relative rate for the excitatory and inhibitory drives (compare different rows of Figure 7A). To test whether this difference is indeed caused by an interaction of the temporal structure of the pre- and post-synaptic spiking activity, we performed a control, for which we destroyed this interaction, while keeping the pre-synaptic temporal structure the same. To this end, we randomized the post-synaptic spike timing. Using this control, the cumulative distribution function (CDF) for temporally structured and unstructured pre-synaptic synapses became identical (CDFs were compared with a two-sample Kolmogorov–Smirnov test, test level 5%, see Figure 8), indicating that temporal structure in the pre-synaptic activity alone is insufficient to explain the differences observed in Figure 7.
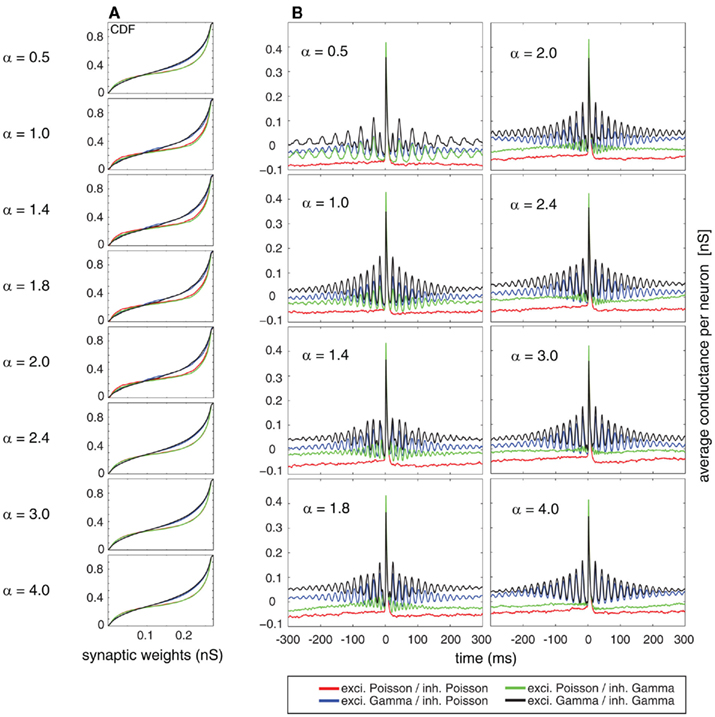
Figure 7. (A) Cumulative distribution function of the synaptic weights averaged on the stable period of simulation (last 50 s from a total simulation time of 300 s). (B) Spike-triggered average (STA) as a relation between the average synaptic weights of 250 mutually independent pre-synaptic spike trains Ne = 200 and Ni = 50) and the post-synaptic firing. Color coded for different combinations of firing statistics (gamma γ = 100 and Poisson γ = 1). Excitatory firing rate λexci was kept constant at 10 Hz and variations of inhibitory firing rate λinh correspond to values of α = 0.5, 1.0, 1.4, 1.8, 2.0, 2.4, 3.0, and 4.0 where λinh = αλexci.
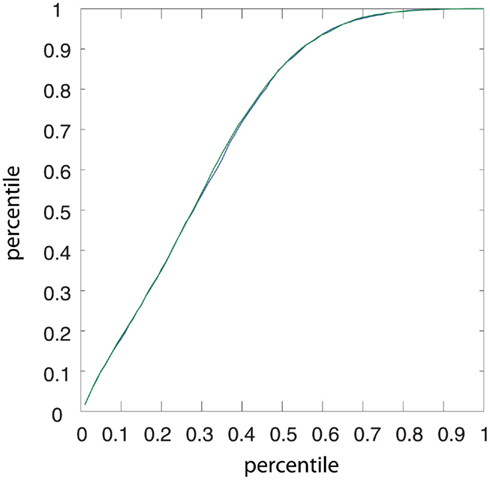
Figure 8. Quantile–Quantile plot of the CDFs of the surrogate STDP rule for Poisson and regular gamma pre-synaptic spiking activity. Two simulations were performed with identical parameters, but different auto-structure in the pre-synaptic activity. In one case, the excitatory drive was composed of regular gamma-spike trains (green), in the other case the excitatory activity was Poisson (blue). For both, the inhibitory activity was Poisson. For the surrogate STDP rule, the post-synaptic spike timing was randomized, i.e., a random Poisson process with fixed post-synaptic firing of 10 spikes/s. The result is a control showing that the CDFs for temporally structured and unstructured pre-synaptic activity become identical, indicating that temporal structure in the pre-synaptic activity alone is insufficient to explain the differences observed in Figure 7A.
In a second step, we studied the temporal structure of synaptic weight changes. In particular, we tested whether synaptic changes of the same synapse reoccur on a short time scale, as expected by the repetitive structure of the STAs (see Figures 1, 3, and 4). To this end, we performed a spike-triggered average of the synaptic changes of the STDP so that we could observe the averaged conductance changes triggered on the post-synaptic firing (Figure 7B). The analysis was performed for the same period (last 50 s) of the simulation as used for the CDFs where the total distribution of weights is already in a dynamic equilibrium. In the averaged STA of the conductances, we found a clear periodic component. The exact temporal structure of the synaptic is a function of both the temporal structure of the excitatory and the inhibitory activity. This was expected, based on the results regarding temporal structure of the post-synaptic firing (compare Figures 2, 5, and 6). If only either the excitatory or inhibitory activity is temporally structured (Figure 7B, blue and green curves, respectively), then the temporal structure of the post-synaptic changes is completely determined by the temporal structure of the non-Poissonian pre-synaptic process (notice the differences in the periodic component for variations of the inhibitory firing rate defined by α). However, if both the excitatory and inhibitory pre-synaptic drive is temporally structured, the temporal structure of the synaptic changes is a mix of the two pre-synaptic temporal structures (Figure 7B, black curve). Remarkably, the strength of repetitive changes, especially of the first satellite peaks in the STAs of the conductance, depends on α. For α = 1 (that corresponds to an n:m relation of 1:1) and still rather simple n:m relations of 1:2 and 2:1 for α = 0.5 and α = 2, the first side peak of the changes of the conductance are larger than for more complex n:m relations based on α = 1.4, 1.8, 2.4, 3.0 and 4.0. This indicates that synaptic modifications reoccur on a short timescale in the range of a few ISIs, which boost changes associated with the same reoccurring spiking pattern. It needs to be emphasized that this occurrence of the same spiking pattern is just caused by the temporal auto-structure of the pre-synaptic drive. This highlights that the auto-structure of pre-synaptic activity might be relevant for modulating synaptic learning.
Temporal evolution of weight changes caused by STDP
Next, we compared the temporal evolution of the distribution of individual synaptic weights as a function of the simulation time. In particular, we study whether the auto-structure of the pre-synaptic population also has an impact on the transient period of the distribution of weights and the speed of the weights’ changes. We compare the temporal evolution of weights for each case by means of observing the CDF. On the one hand, we present the CDF in the case where both pre-synaptic drives are Poisson processes (Figure 9A). This figure shows how the synaptic weight evolves over time due to STDP, from the initial point at t = 0, where all the weights are the same, up to a bimodal distribution at the end of the simulation (t = 100 s).
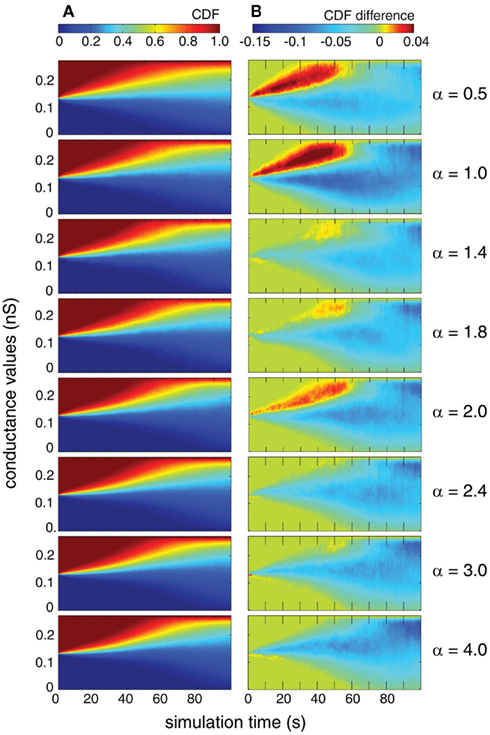
Figure 9. Distribution of synaptic weights of 250 mutually independent pre-synaptic spike trains (Ne = 200 and Ni = 50). Excitatory firing rate λexci was kept constant at 10 Hz and variations of inhibitory firing rate λinh correspond to values of α = 0.5, 1.0, 1.4, 1.8, 2.0, 2.4, 3.0, and 4.0 where λinh = αλecxi. (A) Time-resolved CDF of synaptic weights where the pre-synaptic firing statistics are Poissonian (γ = 1). (B) Time-resolved difference in the CDF of synaptic weights between the cases in which the pre-synaptic drive is gamma (γ = 100) and Poisson (γ = 1).
On the other hand, we present the differences between the CDF of synaptic weights between two cases: Poisson/Poisson and gamma/gamma (Figure 9B). Both measures were explored for different values of the relative firing rate α. We found that for identical rates (α = 1), synaptic weights change faster during the transition toward the equilibrium distribution. This effect is especially strong in the first 70 s of the simulation where the case of both populations being gamma leads to more extreme values, as indicated by the negative areas. Remarkably, we observe the same effect also for α = 0.5 and α = 2, which are both corresponding to a rather simple n:m relation of the period length of the modulation of the STAs (Figures 1, 3, and 4). For the more complicated relations, α = 1.4, 1.8, 2.4, 3.0, and 4.0, this faster change of the CDFs for temporally structured pre-synaptic activity disappears. This suggests that the temporal structure and the interaction between the rates of excitatory and inhibitory processes can modulate the speed with which synaptic weights are changing, which is the learning rate of the STDP. For simulation times longer than 100 s, the distributions are close to the equilibrium and consistent with the results reported in the previous section.
Comparison to gamma Processes with γ = 10
Further, we replicated the results mentioned in the case when the pre-synaptic activity has been modeled as a gamma point process where γ = 10. We first describe the impact of the pre-synaptic structure on the post-synaptic firing. Along this line, we observed that the effects were reduced but still present. The relation between the pre- and post-synaptic firing is characterized via the STA (Figure 10A1) and its implications can be observed on the auto-correlation function (Figure 10A2), which reflects the temporal structure of the post-synaptic firing. For that, we simulated the pre-synaptic activity with α = 1, so that the firing rate of both inhibitory and excitatory pre-synaptic neurons equals 10 Hz, and the overall conductances are scaled by S = 4. In the case where γ = 10, both STA and the auto-correlation are showing a modulation of the pre- and post-synaptic activity occurring at a distance which corresponds to the average ISI of the pre-synaptic spike trains. These peaks also reflect the modulation on the auto-correlation of the pre-synaptic compound process.
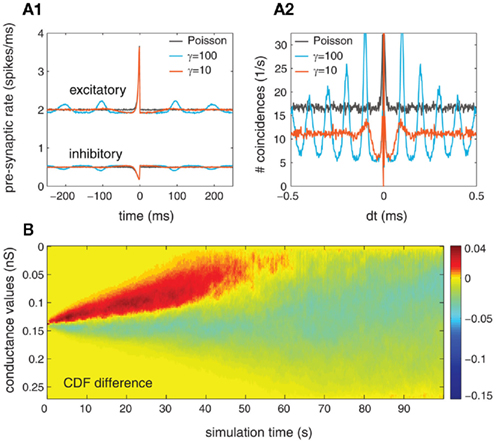
Figure 10. Exploring the effects of auto-structure in gamma processes where the ISI is drawn from a gamma distribution with a shape parameter γ = 10 for a population of 250 mutually independent pre-synaptic spike trains (Ne = 200, Ni = 50, and α = 1.0). In (A1, A2), the STA and auto-correlation of post-synaptic activity are presented, respectively. The different colors correspond to the comparison between three cases: gamma-spike trains γ = 10 (light blue), gamma-spike trains γ = 100 (red) and Poisson spike train γ = 1 (black). (B) Time-resolved difference in the CDF of synaptic weight distribution between the cases in which the pre-synaptic drive is gamma (γ = 10) and Poisson (γ = 1).
Second, we investigate the effects of non-Poissonian input on structure formation due to STDP. For that, the cumulative distribution of synaptic weights as a function of time was presented so that we could estimate the temporal evolution of synaptic weights caused by STDP. In Figure 10B, we present the differences between the CDF of synaptic weights between two cases: Poisson/Poisson and gamma/gamma (for γ = 10). Similar to the case where the gamma process was described by a shape factor of γ = 10 (see Figure 9B), we found that the synaptic weights change faster during the transition period (the first 70 s). Moreover, the synaptic weights shift toward more extreme values when both populations are modeled by gamma processes (with γ = 10). Note that the effects for both γ = 10 and γ = 100 are very similar regarding the strength and the temporal evolution of the synaptic weight distribution (compare Figure 10B with Figure 9B, row 2).
Discussion
We demonstrate that auto-structure, such as regularity and temporal structure of pre-synaptic activity, can induce temporal structure on the post-synaptic neuron, such as spatial temporal pattern of post-synaptic activity, even when spike trains are mutually independent. We also show that such a patterning can change the learning rates as well as the equilibrium distribution of synaptic weights in a model of synaptic plasticity, such as STDP. We will now discuss potential implications of these findings as well as their generalizability.
Interplay of Structure in Pre- and Post-Synaptic Spike Trains
A first step in understanding the interplay between pre- and post-synaptic activity is to describe the temporal structure of the compound process that is the overall input being delivered to the soma of the cell. From previous work (Câteau and Reyes, 2006; Lindner, 2006; Tetzlaff et al., 2008), it is known that the compound process of a set of spike trains has a remaining temporal structure, reflecting the temporal structure of the individual trains. Based on that, we study whether temporal structure in the inhibitory and excitatory drive of a neuron can affect the post-synaptic firing using numerical simulations of a leaky integrate and fire neuron model. We thus studied both the temporal structure of the post-synaptic spike train based on auto-correlograms and the interaction between the pre- and post-synaptic structure based on spike-triggered averages. We show that auto-structure of both the excitatory and inhibitory pre-synaptic population can induce temporal patterns in the post-synaptic activity (Figure 2). Even more, the impact of the temporal structure of the excitatory and inhibitory drive can lead to different post-synaptic firing patterns. This means that only if either excitatory or inhibitory activity is temporally structured (i.e., gamma-process), the post-synaptic spiking activity will reflect the same temporal modulation. For the case where both excitatory and inhibitory activities are gamma, the temporal structure of the post-synaptic activity is mainly determined by the excitatory drive for low and intermediate conductance values. For higher conductance values, both the structure of the excitatory and inhibitory population is relevant such that the temporal structure of the post-synaptic firing appears to be a superposition of both modulations.
Here, we studied a single neuron. However, there might be implications of our findings concerning temporally structured activity on the propagation of activity in large and recurrent networks. To this end, Câteau and Reyes (2006) studied feed-forward networks and the propagation of pulse packets as a function of different temporal structures of the spiking activity. Using the Fokker Planck approach and a leaky integrate and fire model, the authors demonstrate that temporal structure of excitatory gamma activity remains to be structured while propagating through layers of the network. Further evidence for the importance of auto-structure on the activity from a recurrent network is provided in the study by Tetzlaff et al. (2008). They first demonstrate the importance of auto-structure for individual neurons using an alternative approach based on the Fourier domain and second, they use numerical simulations to study the importance of auto-structure when neurons are embedded in a recurrent network. Combining the evidence presented by Câteau and Reyes (2006) and Tetzlaff et al. (2008), along with the results presented here, we suspect that temporal structure in excitatory and inhibitory activity is at least partially preserved through many layers.
Spike-Timing-Dependent Neuronal Plasticity and Temporal Structure
Neuronal plasticity links structure formation in recurrent neuronal networks with its spiking activity. Given the results that the temporal structure of pre-synaptic activity affects the post-synaptic firing (see first part of this publication) and therefore can propagate through a larger network (Câteau and Reyes, 2006), the question arises whether temporal structure of spiking can also effect neuronal plasticity. To study this question, we use a spike-timing-dependent type of neuronal plasticity (STDP) which uses the exact timing of the pre- and post-synaptic firing to change individual synaptic weights.
To test the impact of various pre-synaptic temporal structures of excitatory and inhibitory activity, we observe the equilibrium distribution of the synaptic weights. We find that at equilibrium the distribution of synaptic weights depends solely on the auto-structure of the excitatory population. One possible explanation could be the fact that the synapses of the excitatory population are the only ones subjected to STDP. However, auto-structure of the inhibitory population has an effect on the transient period of the synaptic changes. This can be explained by the fact that the auto-structure of the inhibitory population changes the firing pattern of the post-synaptic neuron. In particular, the interplay between pre-synaptic auto-structures can modulate the post-synaptic firing such that the structure formation also depends on the inhibitory firing patterns. We showed that not only the regularity of renewal processes, but also the rate of the individual processes, modulates the dynamics of the synaptic weights. For the case that rates of inhibitory and excitatory population match a simple n:m relation, i.e., 1:1, 1:2, 2:1, modulations of the auto-correlation of the post-synaptic firing are rather strong, while they are considerably reduced for other more complex relations.
In a next step, we test the temporal structure of synaptic modifications and the temporal evolution of the distribution of weights. As shown in the first part, temporal structure of even mutually independent spike trains induces temporal structure in the occurrence of spike patterns across neurons that take place just by chance. This temporal modulation can be repetitive, as observed for regular firing gamma processes. We find that such a repetitive pattern modulates the synaptic change by STDP. We additionally find that the auto-structure and the rate of the two types, i.e., excitatory and inhibitory pre-synaptic processes, interact and can both be used to regulate the speed with which STDP changes synaptic weights (Figure 9). There, the speed of changes in the weight distribution in the initial period between 0 and 70 s is strongest for a rate ratio between excitatory and inhibitory processes of 1:1 and 1:2. For other ratios between 1:1 and 1:2, this effect is strongly reduced. Such results highlight that both the rate and changes in the auto-structure can be used to modulate STDP.
Generalizability for Other Forms of Plasticity and Other Processes
Can the findings presented here be generalized to other STDP models as well as to different population sizes, point process models and models other than a conductance-based integrate and fire neuron?
In this study, we used a rather simple model of spike-timing-dependent plasticity. This form, also known as STDP with hard bounds, has an equilibrium weight distribution that is strongly bimodal with mainly weak or strong synapses. An alternative model is the soft-bound STDP which can lead to an equilibrium weight distribution that is uniform with most synapses having intermediate strength (Gütig et al., 2003). So the question is whether the results reported in this paper can be generalized for the soft-bound or other STDP models. We found that the auto-structure changes both the equilibrium distribution but also the evolution of the weight distribution over time. Especially the strong change in the first 70 s of the simulation (Figure 9), for which the weight distribution is still uniform, indicates that the auto-structure influences the structure formation based on STDP for both uniform and bimodal weight distribution. Since soft-bound STDP promotes unimodal distributions, we expect that also soft-bound STDP is sensitive to the auto-structure of pre-synaptic activity.
Similarly, this comparison could be made with other STDP models proposed. Modulations of synaptic weights due to STDP are observable, independent of the weight distribution. Structure formation depends on the temporal relations of the spiking activity rather than on the distribution of synaptic weights itself. Other STDP rules, such as the ones presented by van Rossum et al. (2000), Pfister and Gerstner (2006), Morrison et al. (2007), or Clopath et al. (2010), discuss the temporal relation among pre- and post-synaptic spike trains. Thus, we expect our model also to reflect the temporal structure of pre-synaptic spike trains.
We now address whether our findings are generalizable regarding population size and conductance strength. Based on the analytical results from Lindner (2006), it is known that the auto-correlation of a compound process of scaled point processes, i.e., scaled delta peaks δ(t)/N, is of order 1/N. In contrast, the auto-correlation of standard point processes, i.e., non-scaled delta peaks δ(t), grows linearly with N. However, it is important to note that the shape of the auto-correlation stays identical independent of N and whether the point processes are scaled or not. Especially in the case where synapses are weak, one could argue that the remaining auto-correlation is too small to drive the neuron. However, we know that neurons can be close to their threshold. This makes neurons sensitive, such that a small number of pre-synaptic events in a short temporal window can make a neuron fire. This highlights that it is not the total number of synapses but the number of pre-synaptic events that is necessary to drive the neuron, which determines the dampening of the auto-structure in a subpopulation of neurons. In other words, since the neuron is a thresholding device, it can receive noise inputs from a pre-synaptic population with no temporal structure, while being driven by a structured subset of such pre-synaptic neurons. Our results support this argumentation, since we found, for both a small and large population of the order of several thousand pre-synaptic events that the auto-structure of the pre-synaptic spike trains drives the post-synaptic neuron nearly equally well.
We next addressed the generalizability of our findings regarding the choice of the point process model. We chose gamma processes which are renewal processes and which can be entirely described by the ISI distribution. Here, we presented results for gamma processes that strongly deviate from Poissonian firing. Compared to data obtained from electrophysiology, the regularity used in the paper is rather high (Baker and Lemon, 2000; Nawrot et al., 2007, 2008). However, we chose this regime to demonstrate the rather strong impact auto-structure can have on structure formation based on neuronal plasticity. To test whether the effects are also existing for more biologically plausible ISI distribution, we used gamma processes with a shape parameter of γ = 10. We observed that the effects were reduced but still present (Figure 10). This demonstrates that the presented results can be generalized to less extreme deviations from Poissonian firing. However, we used renewal processes which are just a first step toward more realistic neuronal firing statistics. Such more realistic firing might also require to model serial correlation in between ISIs and therefore make the processes non-renewal. Analytically, one can show (Pipa et al., 2010), that the average frequency of spike patterns across neurons is independent of the exact ISI distribution of the renewal process, while deviation from this renewal property can also influence the average frequency of spike pattern across neurons. Since neuronal plasticity based on STDP is directly linked to the pattern frequency we expect that non-renewal point processes lead to even stronger changes of learning and structure formation as reported here.
Limitations
This study and neural model relies on three principle assumptions. First, that the membrane potential dynamics can be sufficiently described by a point neuron via an ordinary differential equation describing a conductance-based integrate and fire neurons. Second, that neural firing can be described by a gamma-renewal process which captures the neuron refractoriness on the ISI distribution. Third, that synaptic plasticity can be modeled by a rather simple additive STDP rule. Given that by definition such assumptions are wrong, we should raise the question to what degree can we expect these results to be generalizable for biological neurons?
The first assumption we made is that neurons can be modeled by a simple point neuron with conductance-based integrate and fire dynamics. That means that we ignored any non-linear dendritic computations. Predicting the effect of those non-linearities seems to be impossible in general since they depend on the very complex and specific topology of individual dendritic trees. However, it has been shown that non-linearities may act as coincidence detectors based on super-linear integration on local segments of the dendrites (London and Häusser, 2005). Since those effects are happening in a confined area with a relatively small number of synapses, and the modulations of auto-structure that we show here grow with decreasing population sizes, we therefore expect that non-linear properties of dendritic trees may boost the sensitivity to changes in the auto-structure. Further, such a conductance-based integrate and fire neuron is a simple one-dimensional model with a fixed threshold. More realistic neuronal models can manifest complex sub-threshold dynamics and may have thresholds that can depend on the state of the neuron (such as Hodkin-Huxley, Izhikevich or the exponential integrate and fire, see Izhikevich, 2003). For such neurons, we expect that structure imposed by the pre-synaptic activity and dynamics of the neuron model may interact. Therefore, we expect, as shown for example by Asai et al. (2008), that different neuronal models may lead to different results. However, we also expect that differences between Poissonian and non-Poissonian pre-synaptic activity survives in one way or the other.
Second, experimental studies indicate that gamma processes are better models that Poisson processes when describing the temporal structure of neuronal firing. Alternatively, the ISI distribution can be modeled by log-normal distributions. Common to both is that they are renewal processes, meaning that subsequent ISI are independent. Such assumption of independence on the ISI may be wrong (Farkhooi et al., 2009; Nawrot, 2010). Here, we did not test for the effect of non-renewal activity. Therefore, whether specific models of non-renewal processes can change the effect of STDP, still remains an open question for future research.
Finally, this study assumes that STDP can be modeled by a simple additive rule, while experimental findings show that this model oversimplifies the real spike-timing-dependent plasticity (Abbott and Nelson, 2000). Alternatively, multiplicative STDP rules or STDP rules which take patterns of spikes into account may be more biologically plausible (see Morrison et al., 2008 for review). However, it needs to be stressed that all these rules appear to be oversimplifications, if one considers that real neurons have multiple neuronal plasticity forms (i.e., homostatic plasticity, synaptic rescaling or short term modulations, like short term depression or facilitations), acting at the same time. Any of these interacting plasticity forms may change the reported results and may even lead to new emergent properties that cannot be predicted by any of the individual rules alone (Lazar et al., 2007, 2009). Despite these general complications which all modeling studies suffer from, it remains an issue whether the findings shown here can be generalized for other STDP rules mentioned before. We expect that most of the effects would be found when using other STDP rules, since all consider the exact temporal structure of the pre–post-synaptic firing. For example, one could argue that since different STDP rules would lead to different steady-state distributions of synaptic weights, it could destroy the effects reported on in this paper. However, we analyzed the changes in the strength of weights undergoing additive STDP in the early phase of learning (Figure 9B), where the weight distribution is still unimodal (i.e., period between 0 and 50 s of simulation time). We found that auto-structure-induced modulations in the effective strength of neuronal plasticity have been especially strong during this period. This suggests that the auto-structure modulates the effective strength of neuronal plasticity for both bimodal and unimodal weight distributions. Further, this indicates that the effects may be even stronger for multiplicative STDP.
Potential Implications for Structure Formation in Recurrent Networks
For learning in recurrent networks, a modulation of neuronal plasticity can be useful. Such modulation can be used to control self-organization via spontaneous structure formation of the network and the learning of certain trajectories of neuronal activities. One such mechanism for modulation was implemented as reward-modulated STDP, where a global teacher signal regulates the self-organization of the system (Florian, 2007; Izhikevich, 2007; Legenstein et al., 2008).
Here, we propose an alternative modulation of spontaneous structure formation based on the control of the auto-structure of the pre-synaptic activity. We showed that temporal structure in the pre-synaptic activity of both the excitatory and inhibitory activity can modulate the effective strength of neuronal plasticity as well as the speed with which synapses change their synaptic weights in the case of STDP. Therefore, this suggests that controlling the auto-structure of pre-synaptic activity can be used to control the effective strength of neuronal plasticity. For example, we showed that changes in the regularity of renewal processes and changes in the relation between the excitatory and inhibitory firing rates can be used to control the learning of structure in individual neurons. Alternative mechanisms of controlling the effective strength of neuronal plasticity via changes in the auto-structure could be making pre-synaptic activity non-renewal, e.g., by oscillatory firing or long-lasting temporal dependencies.
From a biological perspective, such control of the auto-structure could be realized by many intrinsic or extrinsic mechanisms. Potential intrinsic mechanisms are neuromodulator or top-down signals that shape the temporal structure of neuronal activity in the target population. Alternatively, temporal structure in the target population may be shaped by oscillatory activity emerging by synchronization of different populations. Extrinsic modulations may occur via stimulus-driven changes in the balance and rate relation of excitatory and inhibitory activity. Also, temporal structure induced by the stimulus may be a potential candidate to modulate the effective strength of neuronal plasticity.
In conclusion, our work suggests that variation in the auto-structure and the rate of activity in a recurrent network may be exploited by nature to modulate the sensitivity for spontaneous formation of structure and therefore learning.
Conclusion
Structure formation and neuronal self-organization in networks is crucial for information processing within the cortex. We demonstrate that both the speed and strength of structural changes induced by spike-timing-dependent plasticity can be modulated by the temporal structure of mutually independent spiking activity. This highlights the possibility that the modulation of auto-structure of larger groups of neurons could be used to modulate the sensitivity of spontaneous structure formation in networks. Especially the regularity in combination with the firing rates of the neurons seems to be a promising new concept for such a modulation of synaptic plasticity. Interestingly, changes in the firing rate and in the auto-structure of spiking activity are often modulated during cognitive tasks, such as attention and memory, which may indicate that nature exploits these mechanisms for modulation of structure formation and neuronal self-organization in neuronal circuits (Engel et al., 2001; Fries et al., 2001; Pesaran et al., 2002; Uhlhaas et al., 2009; Düzel et al., 2010).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Carl van Vreeswijk for his support and very constructive discussions. We also thank Sonja Grün and Markus Diesman who helped in developing the initial ideas of this paper. And finally, we would like to thank Larry Abbott who inspired Gordon Pipa during his time at Brandeis University. This work was partially financed by the Phocus EU project (FP7-ICT-2009-C).
References
Abbott, L. F., and Nelson, S. B. (2000). Synaptic plasticity: taming the beast. Nat. Neurosci. 3, 1178–1183.
Asai, Y., Guha, A., and Villa, A. E. P. (2008). Deterministic neural dynamics transmitted through neural networks. Neural Netw. 21, 799–809.
Averbeck, B. B. (2009). Poisson or not poisson: differences in spike train statistics between parietal cortical areas. Neuron 62, 310–311.
Baker, S. N., and Lemon, R. (2000). Precise spatiotemporal repeating patterns in monkey primary and supplementary motor areas occur at chance level. J. Neurophysiol. 84, 1770–1780.
Burns, B. D., and Webb, A. C. (1976). The spontaneous activity of neurones in the cat’s cerebral cortex. Proc. R. Soc. B Biol. Sci. 194, 211–223.
Câteau, H., and Reyes, A. (2006). Relation between single neuron and population spiking statistics and effects on network activity. Phys. Rev. Lett. 96, 1–4.
Clopath, C., Büsing, L., Vasilaki, E., and Gerstner, W. (2010). Connectivity reflects coding: a model of voltage-based STDP with homeostasis. Nat. Neurosci. 13, 344–352.
Destexhe, A., and Paré, D. (1999). Impact of network activity on the integrative properties of neocortical pyramidal neurons in vivo. J. Neurophysiol. 81, 1531–1547.
Destexhe, A., Rudolph, M., Fellous, J.-M., and Sejnowski, T. J. (2001). Fluctuating synaptic conductances recreate in vivo-like activity in neocortical neurons. Neuroscience 107, 13–24.
Düzel, M., Penny, W. D., and Burgess, N. (2010). Brain oscillations and memory. Curr. Opin. Neurobiol. 20, 143–149.
Engel, A. K., Fries, P., and Singer, W. (2001). Dynamic predictions: oscillations and synchrony in top–down processing. Nat. Rev. Neurosci. 2, 704–716.
Faisal, A. A., Selen, L. P. J., and Wolpert, D. M. (2008). Noise in the nervous system. Nat. Rev. Neurosci. 9, 292–303.
Farkhooi, F., Strube-Bloss, M., and Nawrot, M. (2009). Serial correlation in neural spike trains: experimental evidence, stochastic modeling, and single neuron variability. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 79, 1–10.
Fellous, J.-M., Rudolph, M., Destexhe, A., and Sejnowski, T. J. (2003). Synaptic background noise controls the input/output characteristics of single cells in an in vitro model of in vivo activity. Neuroscience 122, 811–829.
Florian, R. V. (2007). Reinforcement learning through modulation of spike-timing-dependent synaptic plasticity. Neural Comput. 19, 1468–1502.
Fries, P., Reynolds, J. H., Rorie, A. E., and Desimone, R. (2001). Modulation of oscillatory neuronal synchronization by selective visual attention. Science 291, 1560–1563.
Gütig, R., Aharonov, R., Rotter, S., and Sompolinsky, H. (2003). Learning input correlations through nonlinear temporally asymmetric Hebbian plasticity. J. Neurosci. 23, 3697–3714.
Haider, B., Duque, A., Hasenstaub, A. R., and McCormick, D. A. (2006). Neocortical network activity in vivo is generated through a dynamic balance of excitation and inhibition. J. Neurosci. 26, 4535–4545.
Hanson, F. B., and Tuckwell, H. C. (1983). Diffusion approximations for neuronal activity including synaptic reversal potentials. J. Theor. Neurobiol. 2, 127–153.
Iyengar, S., and Liao, Q. (1997). Modeling neural activity using the generalized inverse Gaussian distribution. Biol. Cybern. 77, 289–295.
Izhikevich, E. M. (2007). Solving the distal reward problem through linkage of STDP and dopamine signaling. Cereb. Cortex 17, 2443–2452.
Lazar, A., Pipa, G., and Triesch, J. (2007). Fading memory and time series prediction in recurrent networks with different forms of plasticity. Neural Netw. 20, 312–322.
Lazar, A., Pipa, G., and Triesch, J. (2009). SORN: a self-organizing recurrent neural network. Front. Comput. Neurosci. 3:23. doi:10.3389/neuro.10.023.2009
Legenstein, R., Pecevski, D., and Maass, W. (2008). A learning theory for reward-modulated spike-timing-dependent plasticity with application to biofeedback. PLoS Comput. Biol. 4, e1000180. doi:10.1371/journal.pcbi.1000180
Levine, M. W. (1991). The distribution of the intervals between neural impulses in the maintained discharges of retinal ganglion cells. Biol. Cybern. 65, 459–467.
Lindner, B. (2006). Superposition of many independent spike trains is generally not a Poisson process. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 73, 022901.
Maimon, G., and Assad, J. A. (2009). Beyond Poisson: increased spike-time regularity across primate parietal cortex. Neuron 62, 426–440.
Markram, H., Lubke, J., Frotscher, M., and Sakmann, B. (1997). Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science 275, 213–215.
Morrison, A., Aertsen, A., and Diesmann, M. (2007). Spike-timing-dependent plasticity in balanced random networks. Neural Comput. 19, 1437–1467.
Morrison, A., Diesmann, M., and Gerstner, W. (2008). Phenomenological models of synaptic plasticity based on spike timing. Biol. Cybern. 98, 459–478.
Nawrot, M. P. (2010). “Analysis and interpretation of interval and count variability in neural spike trains,” in Analysis of Parallel Spike Trains, Chap. 3, eds S. Grün and S. Rotter (Boston, MA: Springer US), 1–22.
Nawrot, M. P., Boucsein, C., Rodriguez Molina, V., Aertsen, A., Grün, S., and Rotter, S. (2007). Serial interval statistics of spontaneous activity in cortical neurons in vivo and in vitro. Neurocomputing 70, 1717–1722.
Nawrot, M. P., Boucsein, C., Rodriguez Molina, V., Riehle, A., Aertsen, A., and Rotter, S. (2008). Measurement of variability dynamics in cortical spike trains. J. Neurosci. Methods 169, 374–390.
Nordlie, E., Gewaltig, M.-O., and Plesser, H. E. (2009). Towards reproducible descriptions of neuronal network models. PLoS Comput. Biol. 5, e1000456. doi:10.1371/journal.pcbi.1000456
Ostojic, S., Brunel, N., and Hakim, V. (2009). How connectivity, background activity, and synaptic properties shape the cross-correlation between spike trains. J. Neurosci. 29, 10234–10253.
Pesaran, B., Pezaris, J. S., Sahani, M., Mitra, P. P., and Andersen, R. A. (2002). Temporal structure in neuronal activity during working memory in macaque parietal cortex. Nat. Neurosci. 5, 805–811.
Pfister, J. P., and Gerstner, W. (2006). Triplets of spikes in a model of spike timing-dependent plasticity. J. Neurosci. 26, 9673–6982.
Pipa, G., Riehle, A., and Grün, S. (2006). Validation of task-related excess of spike coincidences based on NeuroXidence. Neurocomputing 70, 2064–2068.
Pipa, G., van Vreeswijk, C., and Grün, S. (2010). Impact of spike-train auto-structure on probability distribution of joint-spike events. (Submitted).
Pipa, G., Vicente, R., and Tikhonov, A. (2008). Auto-structure of presynaptic activity defines postsynaptic firing statistics and can modulate STDP-based structure formation and learning. Lecture Notes in Comput. Sci. 5164, 413–422.
Rudolph, M., Pospischil, M., Timofeev, I., and Destexhe, A. (2007). Inhibition determines membrane potential dynamics and controls action potential generation in awake and sleeping cat cortex. J. Neurosci. 27, 5280–5290.
Salinas, E., and Sejnowski, T. J. (2001). Correlated neuronal activity and the flow of neuronal information. Nat. Neurosci. 2, 539–550.
Song, S., and Abbott, L. F. (2001). Cortical development and remapping through spike timing-dependent plasticity. Neuron 32, 339–350.
Song, S., Miller, K. D., and Abbott, L. F. (2000). Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nat. Neurosci. 3, 919–926.
Teich, M. C., Heneghan, C., Lowen, S. B., Ozaki, T., and Kaplan, E. (1997). Fractal character of the neural spike train in the visual system of the cat. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 14, 529–546.
Tetzlaff, T., Rotter, S., Stark, E., Abeles, M., Aertsen, A., and Diesmann, M. (2008). Dependence of neuronal correlations on filter characteristics and marginal spike train statistics. Neural Comput. 20, 2133–2184.
Uhlhaas, P. J., Pipa, G., Lima, B., Melloni, L., Neuenschwander, S., Nikolic, D., and Singer, W. (2009). Neural synchrony in cortical networks: history, concept and current status. Front. Integr. Neurosci. 3:17. doi:10.3389/neuro.07.017.2009
Keywords: spike train, auto-structure, STDP, temporal correlations, integrate and fire, non-Poissonian
Citation: Scheller B, Castellano M, Vicente R and Pipa G (2011) Spike train auto-structure impacts post-synaptic firing and timing-based plasticity. Front. Comput. Neurosci. 5:60. doi: 10.3389/fncom.2011.00060
Received: 17 November 2010;
Accepted: 29 November 2011;
Published online: 16 December 2011.
Edited by:
Hava T. Siegelmann, Rutgers University, USAReviewed by:
Markus Diesmann, RIKEN Brain Science Institute, JapanAlessandro Villa, University of Lausanne, Switzerland
Copyright: © 2011 Scheller, Castellano, Vicente and Pipa. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Gordon Pipa, Institute of Cognitive Science, University of Osnabrück, Albrechtstraße 28, 49069 Osnabrück, Germany. e-mail: mail@g-pipa.de
†Bertram Scheller and Marta Castellano have contributed equally to this work.