Establishing communication between neuronal populations through competitive entrainment
- Department of Computing, Imperial College London, London, UK
The role of gamma frequency oscillation in neuronal interaction, and the relationship between oscillation and information transfer between neurons, has been the focus of much recent research. While the biological mechanisms responsible for gamma oscillation and the properties of resulting networks are well studied, the dynamics of changing phase coherence between oscillating neuronal populations are not well understood. To this end we develop a computational model of competitive selection between multiple stimuli, where the selection and transfer of population-encoded information arises from competition between converging stimuli to entrain a target population of neurons. Oscillation is generated by Pyramidal-Interneuronal Network Gamma through the action of recurrent synaptic connections between a locally connected network of excitatory and inhibitory neurons. Competition between stimuli is driven by differences in coherence of oscillation, while transmission of a single selected stimulus is enabled between generating and receiving neurons via Communication-through-Coherence. We explore the effect of varying synaptic parameters on the competitive transmission of stimuli over different neuron models, and identify a continuous region within the parameter space of the recurrent synaptic loop where inhibition-induced oscillation results in entrainment of target neurons. Within this optimal region we find that competition between stimuli of equal coherence results in model output that alternates between representation of the stimuli, in a manner strongly resembling well-known biological phenomena resulting from competitive stimulus selection such as binocular rivalry.
1. Introduction
Oscillation in the gamma-band (approximately 30–100 Hz) is proposed to underlie a diverse range of high-level cognitive functions, including memory (Axmacher et al., 2006; Jensen et al., 2007), associative learning (Miltner et al., 1999), and sensory selection (Fries et al., 2002; Schroeder and Lakatos, 2009). Transient periods of synchronization and desynchronization or “phase-scattering” (Rodriguez et al., 1999; Womelsdorf et al., 2007) indicate a role for gamma oscillation in long-range cortical communication, and as a plausible mechanism for task-specific networks of functionally related neural areas to form dynamically in response to complex and changing cognitive demands (Varela et al., 2001; Fries, 2009).
Recent evidence supporting a functional role for gamma oscillation comes from a number of sources. Task-related changes in gamma synchronization (Montgomery and Buzsáki, 2007; Jutras et al., 2009; Popescu et al., 2009; van Vugt et al., 2010; Vinck et al., 2010), phase reset of cortical oscillation over multiple frequency bands during integration of sensory information (Lakatos et al., 2007, 2009) and changes in synchronization associated with selective attention (Brovelli et al., 2005; Womelsdorf and Fries, 2007; Doesburg et al., 2008) have all been the subject of experimental study. Several computational approaches have also been taken to establishing the link between oscillation and information transfer. It has been shown across a range of neuron models that a single neuron will selectively phase-lock with one of multiple oscillating inputs (Gielen et al., 2010). Application of information theoretic measures to inhibition-induced gamma oscillation demonstrate a relationship between the phase and the quantity and direction of information transferred between two excitatory neuronal populations (Buehlmann and Deco, 2010), and that one of multiple convergent stimuli can be recovered from the activity of a receiving population by switching that stimulus from an asynchronous to an oscillatory state (Akam and Kullmann, 2010). It is also worth mentioning the related study of coupled oscillators and the general properties of weakly coupled oscillator networks, where “chimera states” formed by subsets of phase-coherent oscillators have been shown to emerge from network dynamics (Kuramoto and Battogtokh, 2002; Abrams and Strogatz, 2004; Omel’chenko et al., 2008; Shanahan, 2010).
A theoretical framework for the mechanism underlying gamma mediated neuronal communication is provided by Communication-through-Coherence (CTC) (Fries, 2005), the idea that coherent phase relationships allow the effective transfer of information between oscillating neuronal populations. It is suggested that neurons undergoing oscillation open temporal windows for communication, where synaptic input arriving at or near the peak of oscillation has a greater likelihood of inducing a response in the receiving neuron. Convergent oscillating stimuli are effectively filtered by their relative phase to oscillation in the target neurons, a relationship subsequently modeled through correlated population firing rates (Masuda, 2009). Changes in the pattern of oscillation between neuronal populations thereby reflect changes in the flow of information in the brain.
The biological underpinnings of neuronal oscillation, and the process by which coherent relationships between populations are established and maintained, are key to any plausible explanation for flexible routing of neural information through phase coherence. The mechanisms underlying gamma oscillation (Whittington et al., 1995, 2011; Traub et al., 1996; Ritz and Sejnowski, 1997; Bartos et al., 2007; Tiesinga and Sejnowski, 2009; Wang, 2010), long-range synchronization (Roelfsema et al., 1997; Uhlhaas et al., 2009), and the role of different classes of inhibitory interneurons in generating and maintaining oscillation (Whittington and Traub, 2003; Middleton et al., 2008) have been extensively investigated. Inhibition and the action of locally connected networks of pyramidal neurons and inhibitory interneurons has been shown to be of fundamental importance in generating gamma oscillation (Whittington et al., 2000). Models of dynamic communication have focused particularly on Pyramidal-Interneuronal Network Gamma (PING), where synchronization is driven by a recurrent synaptic loop between excitatory and inhibitory neurons (Börgers et al., 2005). Excitatory pyramidal input to local interneurons results in alternating episodes of synchronized firing between excitatory and inhibitory populations, with synchronized volleys of spikes from inhibitory neurons temporarily suppressing excitatory activity. Gamma oscillation driven by this mechanism has been shown to increase the advantage of coherent excitatory stimuli over less coherent stimuli by raising the effective leakiness of target neurons (Börgers and Kopell, 2008).
Not all recent evidence supports the communication hypothesis however, and it remains unclear whether oscillation within biologically observed boundaries will support the efficient and reliable transfer of information (Ray and Maunsell, 2010). In this study we examine in detail a model of communication between neuronal populations that is driven by competition between oscillating stimuli. In particular we are interested in factors that allow inhibition-induced oscillation to gate the flow of population-encoded information when multiple sources are competing to entrain a single target. Our starting assumption is that the transmission of stimuli between communicating neuronal populations is enabled by phase-coherent oscillation, generated via interaction between networks of excitatory and inhibitory neurons, and that the absence of a coherent phase relationship between oscillation in connected populations should also inhibit the transfer of stimuli between them. We explore changes in the response of neurons receiving stimuli to variation in key parameters of the PING mechanism of gamma generation.
We first construct a model of stimulus selection that utilizes coherent oscillation to communicate one of two incoming spiking stimuli to a target neuronal population. We consider top-down control where target oscillation is driven by an external input to the model, and bottom-up control where the gamma oscillation is generated internally to the model in neurons receiving the stimuli through recurrent inhibition. In both cases entrainment of target neurons gates stimulus transmission. Information encoded in the entraining stimulus, a one-dimensional orientation embedded in the firing pattern of source neurons, is reproduced in the firing pattern of the target population, and the orientation encoded in the unentrained stimulus is filtered from target activity. In the bottom-up case we show that a competitive mechanism emerges whereby the target neurons are more likely to entrain to the stimulus of greater coherence.
A computational search of the model parameter space reveals the optimal region for stimulus selection to occur. We concentrate on parameters significant in defining the characteristics of PING oscillation, the weight, and delay of synapses within the recurrent excitatory-inhibitory loop, while other parameters remain fixed at biologically plausible values. We find a continuous region in the parameter space where the population response of target neurons is maximally correlated with a single stimulus. Parameters within this region yield model activity consistent with competitive transmission of stimuli. The search was carried out using both quadratic integrate-and-fire (QIF) and Hodgkin-Huxley neuron models, producing similar results. If the assumption of a functional role for gamma oscillation and particularly PING generated gamma in stimulus selection is correct, it is reasonable to suggest that biological networks should exhibit similar tuning of parameters in locally connected networks of excitatory and inhibitory neurons.
For synaptic parameters within the optimal region we found that the activity within our model resembles a well-known experimentally observed phenomenon, binocular rivalry, where two images presented to an observer compete for perceptual awareness (Andrews, 2001; Blake, 2001; Tong et al., 2006). When differing images are viewed exclusively by each eye, a single stimulus dominates perception such that only one of the images is seen by the observer at any time. While the images remain static the perceived image spontaneously flips between the two at irregular intervals. If either image is perturbed it is immediately brought forward into perception. When equally coherent stimuli are presented to our model, the output of target neurons exhibits a similar alternation between representation of each incoming stimulus. We show that the period and distribution of switching events within the model is a close to match experimentally observed results, and that changes in stimuli characteristics lead to realistic changes in model behavior.
2. Materials and Methods
We use two neuron models of differing complexity to establish the robustness of network behavior to changes in the underlying neuronal dynamics. Results were generated first using the QIF model and repeated using the Hodgkin-Huxley model.
2.1. Quadratic Integrate-and-Fire Neuron Model
The time evolution of the neuron membrane potential in the QIF neuron model (Latham et al., 2000) is given by
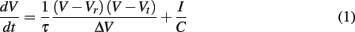
where Vr and Vt are the resting and threshold values of the membrane potential V, C is the capacitance of the cell membrane, ΔV = Vt − Vr, and τ = RC is the membrane time constant with resistance R. The value I represents a constant depolarizing current to the neuron. An action potential occurs when V reaches a value Vpeak at which point it is reset to value Vreset. The dynamics of the model are described by two fixed points, one stable and one unstable, which merge in a saddle-node bifurcation to produce an action potential. This corresponds to type I neuron dynamics (Ermentrout, 1996), hence the model supports arbitrarily low frequencies of firing and the phase response curve is strictly positive (Gutkin et al., 2005), excitatory input can only advance and not delay spike onset. For the reset condition Vpeak = ∞ and Vreset = −∞ the QIF model is equivalent to the theta neuron model described in (Ermentrout and Kopell, 1986). For all results relating to the QIF model we use values Vr = −65 mV, Vt = −55 mV, and τ = 50 ms.
2.2. Hodgkin-Huxley Neuron Model
The time evolution of the membrane potential in the classical Hodgkin-Huxley model (Hodgkin and Huxley, 1952) is described by the equations
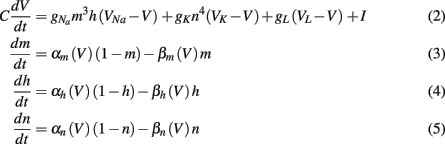
where V is the neuron membrane potential, C is the membrane capacitance, and g the conductance. Reversal potentials are set to VNa = 45, VK = −82, VL = −59.387 and maximum conductances to gNa = 120, gK = 36, gL = 0.3. The rate functions for each channel are given by
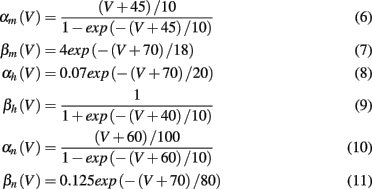
We take a spike to occur at time t when V(t) = 0 and dV/dt(t) > 0 (Börgers et al., 2010). In contrast to the QIF model, the Hodgkin-Huxley model displays type II dynamics. Action potentials are produced via a subcritical Hopf bifurcation (Mato and Samengo, 2008). The phase response curve displays both positive and negative regions, small depolarizing current may delay spike onset in the early phase of the firing cycle.
2.3. Synaptic Model
We include synaptic input via a standard conductance-based approach (Börgers and Kopell, 2003, 2005) with an additional parameter for synaptic delay. For each synapse connecting neurons i and j, a time dependent current is added to the right-hand side of Eq. 1
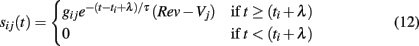
where t is the current simulation time, ti is the time of last firing of neuron i, λ is synaptic delay, gij is the maximum conductance of the synapse between neurons i and j, Rev is the synaptic reversal potential, and τ is the synaptic decay time constant. When a spike occurs the synaptic current jumps to value gij at the arrival time of the spike (ti + λ) and decays exponentially with rate τ.
For excitatory and inhibitory decay time constants we use values τ = 2 ms and τ = 10 ms respectively, based on the experimentally determined time constants of AMPA receptor mediated excitatory synapses and GABAA receptor mediated inhibitory synapses (Börgers and Kopell, 2005). For excitatory synapses we use reversal potential above the spiking threshold of the neuron model (Table 2). There are two cases to consider for inhibitory neurons. If the reversal potential is below the resting potential of the neuron the inhibition is hyperpolarizing, if it is near or above the resting potential it is termed shunting. Inhibitory input to hippocampal primary cells has been shown to undergo a coordinated transformation from shunting in early development to hyperpolarizing in mature cells (Ben-Ari, 2002), although there is evidence that certain classes of inhibitory synapse connecting interneurons remain shunting throughout development (Banke and McBain, 2006). In this study we take all inhibitory-to-excitatory synapses to be hyperpolarizing.
2.4. Network Architecture
We use a two-layer feedforward architecture, based on a common motif in the visual system of input from two neuronal populations converging on a third (Fries, 2009). The model consists of three populations of 1000 excitatory and a single population of 200 inhibitory neurons (Figure 1) each representing a local cortical network of excitatory pyramidal or inhibitory interneurons. Two excitatory populations in the source layer of the network project synaptic connections onto the target excitatory population, source populations generating separate stimuli that are received in the target layer. The source and target excitatory populations are connected topographically (S1, S2 in Figure 1) to preserve transmission of stimuli between the two layers of the network, each source excitatory neuron projecting a single synapse onto an opposing neuron in the target excitatory population. Simulation parameters are given in Table 1. We maintain the same network connectivity for both QIF and Hodgkin-Huxley neuron models with modified synaptic conductance. Delays for all synapses between any two populations within the model are constant, with the maximum conductance for each synapse sampled from a uniform random distribution (Table 2).
Table 1. Simulation parameters.
Table 2. Synaptic parameters.
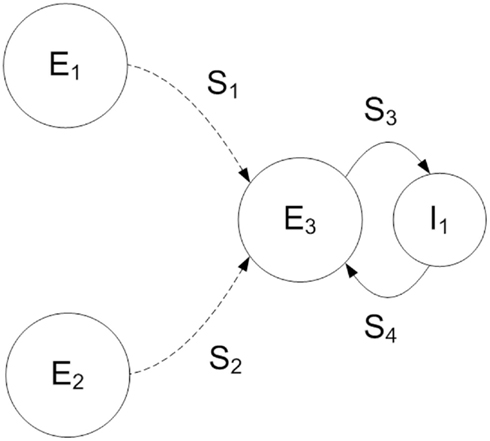
Figure 1. Schematic of the two-layer feedforward network model used in this study. The source layer consists of two populations of excitatory neurons (E1, E2). The target layer contains a single population of excitatory (E3) and a single population of inhibitory (I1) neurons. Each excitatory source layer neuron receives oscillating external current and Poisson spiking input, resulting in a random pattern of firing with the stimulus represented by elevated activity within the population at a preferred orientation. Excitatory neurons of the target layer (E3) receive both stimuli via a set of topographic synaptic connections (S1, S2). Within the target layer excitatory and inhibitory populations are fully connected (S3, S4).
We consider two variations of the model representing both top-down and bottom-up control of stimulus selection. Attention has been modeled previously as a top-down process (Buia and Tiesinga, 2006, 2008) where the top-down signal is assumed to represent some prior knowledge or goal. Imaging and neurophysiological studies indicate prefrontal and parietal areas as the source of top-down control in the brain (Buschman and Miller, 2007) in agreement with attentional deficits introduced by lesions to these areas, although much of the evidence is correlative (Miller and D’Esposito, 2005) and the nature of these signals remains unclear. Detection of behaviorally relevant but unexpected stimuli, such as the process of biased competition proposed to underlie visual attention (Desimone and Duncan, 1995; Reynolds and Desimone, 2003), is assumed to be bottom-up, i.e., driven by properties of the stimulus and not by prior expectation.
In the top-down case the model contains only excitatory populations (E1, E2, and E3 in Figure 1), there is no inhibitory synaptic input to excitatory target neurons. Subthreshold oscillation is generated in both source and target excitatory neurons via an external input of the form
where ε is the amplitude of oscillation, f is frequency, and θ is phase offset. Each neuron in the model additionally receives a unique noise term sampled from a Poisson distribution with scaling factor F, representing external synaptic input from the surrounding neural tissue. Every neuron within a single excitatory population receives input of the same parameter values (Table 1). By maintaining a constant frequency of oscillation within the gamma range of f = 40 Hz for all excitatory populations, while varying parameters ε and θ of Eq. 13 within the source layer of the network, we control the relative phase and coherence of oscillation between stimuli, and between stimuli and the target layer. We consider the effect of varying parameters of both synapses and of incoming stimuli on entrainment of target neurons and the resulting model output.
In the bottom-up case the model includes all excitatory and inhibitory populations (E1, E2, E3, and I1). Oscillation is generated in source excitatory populations (E1, E2) via an external input of the form given in Eq. 13, and all neurons in the model receive the same Poisson input with scaling factor F. We replace the external current supplied to the target excitatory population (E3) with the action of the inhibitory population (I1) and the PING mechanism of generating gamma oscillation. All-to-all synaptic connectivity between excitatory and inhibitory neurons in the target layer of the network (S3 and S4 in Figure 1) forms a recurrent excitatory-inhibitory loop, resulting in a sustained oscillation in the target neurons in response to activity generated by the incoming stimuli. This allows us to consider the relationship between the phase and coherence of the oscillating stimuli and the activity of receiving neurons. The frequency, phase, and coherence of oscillation are the result of interaction between target excitatory and inhibitory populations, and are strongly dependent on characteristics of synapses local to the target layer. For all results we assume equal delay on synapses in both directions of the excitatory-inhibitory loop.
2.5. Stimulus and Analysis of Population Response
We establish transmission of information between layers of the model by encoding a one-dimensional circular variable in the activity of each source layer excitatory population, and decoding the response of the target excitatory neurons in order to recover the angle of the transmitted stimulus. Each source layer excitatory neuron within a single population is assigned a preferred orientation varying between −π and π, with neurons arranged in a ring topology with equal spacing between them. Following (Seung and Sompolinsky, 1993) we represent the circular variable with the tuning curve generated by the function
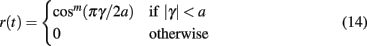
where m controls the rise, a controls the width, and γ controls the angle of the curve. The output of Eq. 14 is supplied as an additional input to each excitatory source population modulated by the oscillating current described in Eq. 13. This results in an elevated firing rate within the population where the angle is closest to the preferred orientation of the neuron, oscillating at frequency f with phase θ. The difference in angle supplied to each source layer excitatory population determines the spatial separation of the stimuli. Stimulus parameters are given in Table 1.
We use the cross-correlation of average binned spike counts to measure the similarity in activity of the target neuronal population to each incoming stimuli, with the correlation coefficient between a single source population si and target population t defined as
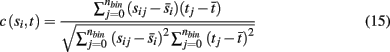
where nbin is the total number of bins, and each sij and tj is the average spike count across all neurons in a source population and target population for a single bin j. Each simulation was divided into a series of trials of equal length, where synaptic weights and the initial phase of stimuli were re-initialized with random values at the start of each trial. The average values over all bins for a single trial are denoted by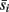 
and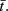 
We are interested in model parameter values that result in one of the stimuli being communicated to the target and the other being filtered out, where target activity is maximally correlated with one stimulus and decorrelated with the other. We measure this using the absolute difference in cross-correlation between stimuli and target
where large values indicate strong correlation between the target and a single stimulus, and low values correlation with both or neither stimuli.
Additionally in Section 1 we apply a template-based method to decode the response of the target layer excitatory network, where the template is a function fitted to the output of target cells estimating the population response to a single stimulus (Deneve et al., 1999; Quiroga and Panzeri, 2009). Following (Akam and Kullmann, 2010) the excitatory population is grouped into 20 bins of 50 neurons of adjacent preferred orientation. After each trial the total spike count in each bin is transformed to the frequency domain using a short-time Fourier transform (STFT) with binned spike counts filtered across a 1 s Hamming window. We use the normalized amplitude of the STFT at 0 Hz across bins, corresponding to the normalized average firing rate, as the output of the target layer of the network. The 40-Hz spectral component of the STFT represents power in output signal at the frequency of the stimuli. We base our template on the binned average firing rate however as biological implementation is clear, a plausible network for comparatively complex maximum-likelihood decoding of two-dimensional stimuli has been demonstrated previously (Deneve et al., 1999).
A template was generated for each stimulus over each variation of the model using training data generated independently of simulation results. The output of the network was first averaged over several presentations of a single stimulus to produce a mean amplitude across bins. A Von Mises distribution was then fitted minimizing the least-squares error to the normalized power in each bin, where the distribution is given by
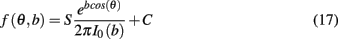
with parameters angle θ and concentration b, and where S is a scaling factor, C a constant, and I0 the modified Bessel function of order 0. The decoded output of the network is then taken to be the stimulus with minimal error between the template and normalized average binned firing rate on any given trial. We use the value Φ to denote the proportion of trials for any given set of model parameters corresponding to the first stimulus.
2.6. Numerics
All simulations using the QIF model were run over a fixed step size of 0.1 ms, with numerical integration of differential equations for all neurons carried out using a fifth-order Runge-Kutta method. The code for each simulation and the following analysis was written in C++,utilizing routines from the GNU Scientific Library (Galassi et al., 2009) for random number generation and frequency domain conversion of binned output. Visualization of results was carried out in MATLAB. The simulation framework, developed specifically for this study, is designed to allow search over multiple dimensions of a user-defined subsection of model parameter space with variable resolution per dimension. Computation can be carried out in parallel between cores of multiple CPUs on a distributed computing system when required. The workload run on each core is independent, giving a linear increase in performance for each additional core added to the system. Our simulation and analysis were accelerated with the aid of the Imperial College High Performance Computing (HPC) system.
The complete model contains 3200 QIF neurons and 4.02 × 105 conductive synapses. Generation of 1 s of simulation time at 0.1 ms resolution takes approximately 12 s of CPU time when run on a single core of one of the 3.6-GHz Intel Xeon nodes comprising the HPC system. Parallel execution using a large distributed cluster allowed us to explore the parameter space of the model over an area and resolution that would have been otherwise infeasible. Search over the space of excitatory-inhibitory synapses, comprising three parameters divided into a 41 × 41 × 41 grid with 100 iterations per data point, required 6.89 × 106 total iterations of the model, and approximately 6 h of real-world time per core when distributed over 5000 cores of the HPC system.
In Section 1 we present results with the QIF model replaced by the Hodgkin-Huxley model for all neurons. We used the same fifth-order Runge-Kutta method for integration of all differential equations involved in the model, with increased resolution of 0.01 ms per step. Search over the model parameter space was performed over a 41 × 41 × 41 grid with 10 iterations per data point for 6.89 × 105 total iterations. Each second of simulation time required approximately 200 s of CPU time to execute, the entire simulation requiring approximately 4 h per core when run over 10000 cores of the HPC system, or 4.5 years of total CPU time. Generating Figures 5E,F over a 101 × 101 grid with 100 iterations per data point required approximately 8 h per core over 10000 cores, or 9 years of total CPU time for each figure.
3. Results
3.1. Communication-through-Coherence
In this section we develop a model of stimulus selection through phase coherence. We consider both top-down selection, where the properties of target oscillation are determined by an external control signal applied to the target neurons, and bottom-up selection, where oscillation is driven by recurrent inhibition. Our network consists of three populations of excitatory neurons each receiving Poisson input and oscillating current. Two source populations generate stimuli which are sent to a third target population via a set of topographically connected synapses (Figure 1). In the bottom-up case oscillating drive to the excitatory target population is replaced by the action of a population of inhibitory neurons, with all-to-all recurrent target excitatory-inhibitory connectivity. The frequency and distribution of inhibitory spikes and resulting oscillatory dynamics of the target layer in response to excitatory input is dependent on parameters of the synaptic loop linking the two target layer neuronal populations. We aim to establish a competitive mechanism between source and target layers of the model where communication is the result of entrainment to one of the incoming stimuli, using stimulus coherence as the competitive characteristic driving selection.
When activity of the target population is unfiltered by an external input, with no top-down control signal applied to the network and target afferents restricted to synaptic and Poisson input, each stimulus is equally represented in the firing of the target neurons (Figure 2A). The average firing rate of target excitatory neurons exhibits two equal peaks at the preferred orientations of each stimulus (Figure 2B). With oscillation induced in the target excitatory population via an external control signal, the relative phase between the target oscillation and that of incoming stimuli determines representation of the stimuli in the firing of the target neurons. When the target oscillation is in-phase with a single arriving stimulus, the activity of the model in the top-down case is in agreement with the hypothesis that coherent oscillation aids transmission of information (Figure 2C). Coherent phase between target and stimulus results in elevated activity in the target neurons at the orientation of the in-phase stimulus and reduced activity at the orientation of the out-of-phase stimulus (Figure 2D).
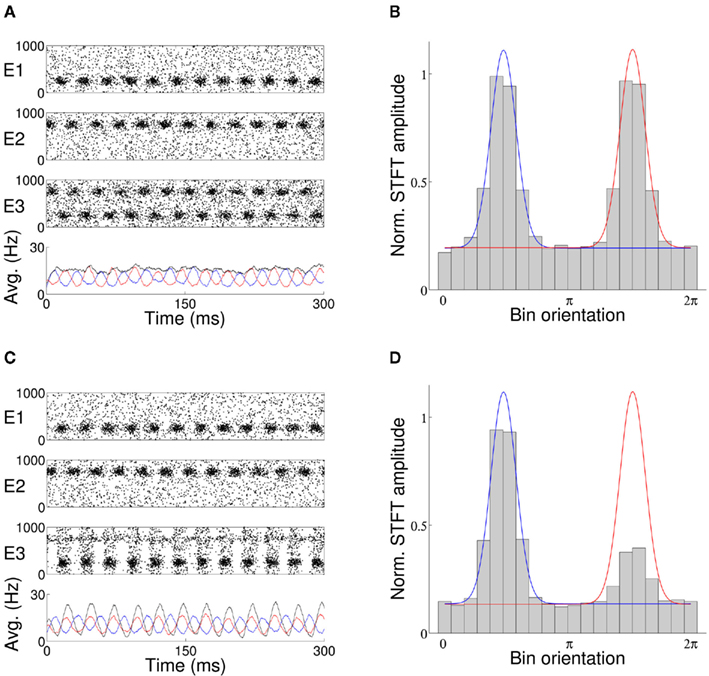
Figure 2. (A) With no external oscillation applied to the target layer of the top-down model of stimulus selection, both stimuli (E1, E2) are equally represented in the activity of the excitatory target population E3. The average activity in Hertz of the excitatory source (red/blue line) and target (black line) populations are shown in the lower panel of each plot. (C) An external top-down control signal applied to the target population in-phase with arrival of stimuli E1 results in elevated firing at the orientation of that stimulus and effective filtering of the out-of-phase stimulus E2. The average firing rate (bar) and fitted Von Mises template for activity of each stimulus (red/blue lines) are shown in (B,D), where each bar is the normalized average firing rate of a single bin of 50 neurons of consecutive preferred orientation.
The entrainment properties of neuronal models subject to oscillatory input have received extensive numerical and analytical treatment. The role of top-down attention in regulating the coherence of oscillation in a target neuron (Tiesinga et al., 2004; Tiesinga, 2005) and the selective response of a neuron to multiple oscillating inputs (Börgers and Kopell, 2008; Gielen et al., 2010) have been discussed in detail. We include two properties observed in biological networks in the present model to extend previous results. Single neurons recorded during cortical gamma rhythm have been shown to fire irregularly and at slower rate than the oscillation frequency of local field potential (LFP) (Pesaran et al., 2002; Geisler, 2005; Kondgen et al., 2007; Colgin et al., 2009), with the effect observed in both pyramidal and interneurons (Csicsvari et al., 1999), and individual neurons comprising the oscillating population displaying approximately Poisson interspike interval (ISI) distribution (Softky and Koch, 1993). The combination of coherent network oscillation and intermittent firing of single neurons has been shown to result from high levels of input noise coupled with strong recurrent inhibition (Brunel, 2000; Brunel and Wang, 2003). The effect is reproduced in the current model. Figure 4A shows the membrane potential and firing of a single excitatory and a single inhibitory neuron against normalized spiking activity of excitatory and inhibitory populations for the QIF model, and Figure 4B for the Hodgkin-Huxley model. Oscillation in both target populations is composed of the aggregate activity of a changing subset of neurons, with no single neuron firing regularly or with a fixed phase offset within the period of oscillation. The ISI distribution for a single excitatory neuron and fitted negative exponential is shown for both models in Figure 4C.
Additionally, each excitatory target neuron within the model receives as input an independent spike train with properties relative to its position within the population. Each input is highly random, with average coefficient of variation (CV) across spike trains comprising each source population greater that 0.9, and SD within ±0.15, for values of ε Eq. 13 in the range [0, 1.0]. This is consistent with the CV of experimentally observed neurons within the visual cortex (Softky and Koch, 1993). The synchronization of the population of neurons comprising the stimulus increases with ε however. Applying multivariate ISI-diversity (Kreuz et al., 2009) as a measure of population synchrony to neurons within ±0.3c of stimulus maximum results in decreasing values in the range [0.7, 0.45] over the same range [0, 1.0] of ε, indicating an increase in the coherence of firing within the population with increasing amplitude of oscillating input. Orientation selective cells are found widely throughout sensory areas of brain such as the visual and motor systems. It is reasonable that in a model of sensory selection between connected neuronal populations, such as converging areas of the visual cortex, input to each neuron is non-uniform and related to the stimuli being received. Entrainment of the target population to an individual oscillating stimulus within the current model then results from the aggregate activity of a population of target neurons receiving independent spatially encoded spiking input.
We start by considering the boundary cases for communication of a single stimulus to occur following CTC, specifically the dependence of transmission of stimuli between source and target on the phase relationship between the three oscillating populations. Given stimuli and target oscillating at the same frequency, we expect the relative phase of oscillation to be optimally aligned when one stimulus arrives close to the peak and the other close to the trough of target oscillation, i.e. when both stimuli arrive at the target neurons directly out-of-phase with a single stimulus in-phase with the target. We expect the corresponding worst-case to occur when the phase of both stimuli is directly aligned. Measures of correlation and decoding discussed in Section 5 are used to examine cases in between. An initial series of trials run with no sinusoidal modulation of stimuli resulted in low mean correlation between source and target excitatory populations (4.3 × 10−3 ± 0.02), confirming that results were not simply due to the presence of the control signal. Figure 3A shows the relationship between the relative phase of oscillation of the three excitatory populations and the cross-correlation of stimuli and target activity. Results are presented over a 41 × 41 grid with each data point the mean over 100 trials. Values over a single dimension are shown in Figure 3B. In-line with intuition, target activity is maximally correlated with a single stimulus when |θ1 − θ2| = π, where both stimuli oscillate directly out-of-phase (Figure 3B upper). For the case θ1 = θ2, where stimuli are directly aligned, both exhibit approximately equal correlation with target output regardless of the phase difference between model layers.
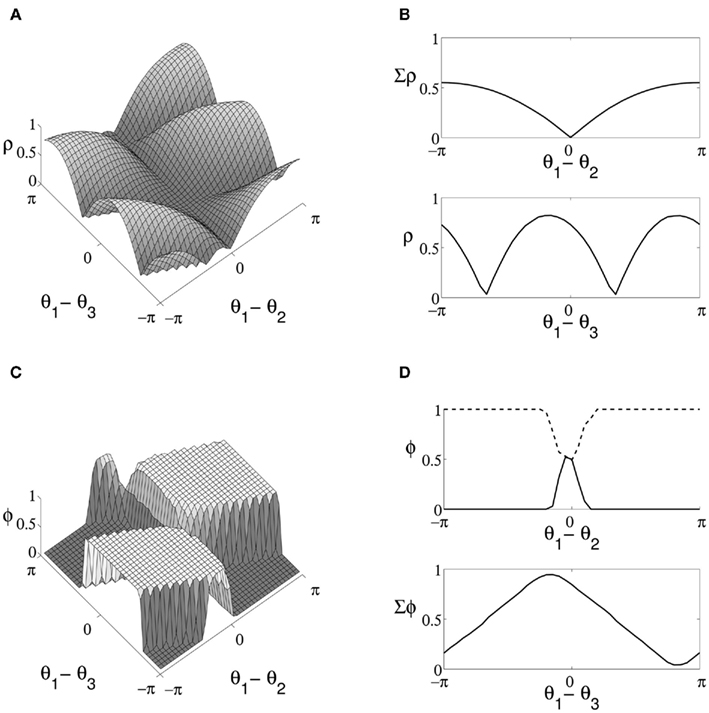
Figure 3. Properties of QIF model output for stimuli of equal coherence, where oscillation is driven in target neurons by a top-down control signal. (A) Difference in cross-correlation (indicated ρ) of stimuli and target activity enumerated over the range of relative phase values for oscillation in the three excitatory populations. Peaks indicate points of greatest correlation with a single stimulus, and θ1, θ2, and θ3 represent the phase of the two source and target populations respectively. (B) Cumulative values along the axis maintaining θ3 (upper) exhibit a single maxima where stimuli are directly out-of-phase. At this point, differences in source and target phase (lower) lead to two maxima at points where target oscillation is in-phase with either arriving stimulus accounting for delay. (C) The proportion of decoded trials corresponding to the first stimulus (indicated Φ) over the same range of relative phase values. (D) Cross-section taken at the optimal relative phase for selection of each stimuli (upper panel, the first stimulus shown by a solid line and the second by a dashed line) and cumulative values along the axis of varying stimulus phase (lower).
Results maintaining maximal phase offset between source populations and considering correlation relative to target oscillation are shown in the lower panel of Figure 3B, with peaks corresponding to the optimal phase offset between the target neurons and each stimulus for communication to occur accounting for the delay over synaptic connections linking model layers. In regions where the phase of target oscillation is unbiased relative to the phase of stimuli, top-down control is similarly of no benefit in filtering the stimuli in target activity. The results of decoding model output over the same parameters and dimensions are shown in Figure 3C, with areas where target neurons are highly correlated with a single source corresponding to consistent decoding to a single stimulus across trials. A cross-section of decoding results at points where correlation between source and target is maximal is shown in the upper panel of Figure 3D. Coherent oscillation between target neurons and a single stimulus produces reliable decoding results to within a small phase offset between stimuli, suggesting a wide margin within which decoding is unaffected by variation in relative stimulus phase. In the lower panel of Figure 3D we show cumulative results for decoding while varying source and target phase, with maxima and minima corresponding to points where correlation with a single stimulus is greatest.
Results for the bottom-up case are given in Figure 4D. We show correlation between activity of target neurons and stimuli, varying both the base and relative amplitude of oscillating input to source populations. Selection is competitive in that the stimulus displaying greater coherence of firing within the encoding population of neurons is more likely to entrain the target layer. In order to understand the sensitivity of this effect to changes in model parameters, a number of simulations were run with constant difference in stimulus coherence (ε1 = 3 mV, ε2 = 2.5 mV) for varying model parameters over both QIF (Figures 5A–C) and Hodgkin-Huxley (Figures 5D–F) variants of the bottom-up model. The range of potential parameters was constrained by fixing experimentally observed values such as the excitatory and inhibitory synaptic decay constants discussed in Section 3, while iterating over three synaptic variables, the weight of excitatory-to-inhibitory synapses, the weight of inhibitory-to-excitatory synapses, and synaptic delay within the excitatory-inhibitory loop. Results were generated via a computational search over the parameter space divided over a 41 × 41 × 41 grid, with 100 trials per data point and one variable per dimension. When viewed over all dimensions, synaptic parameters that result in high correlation to a single stimulus form a continuous region within the space of both models (Figures 5A,D). While the different characteristics of each neuron model lead to variation in the dimensions of this area, activity within the region is consistent in both cases with communication of a single stimulus through phase-coherent oscillation. Target neurons entrain to a single stimulus and the orientation encoded in that phase-locked stimulus is represented in the activity of the target excitatory population, with activity at the orientation of the unentrained stimulus greatly reduced.
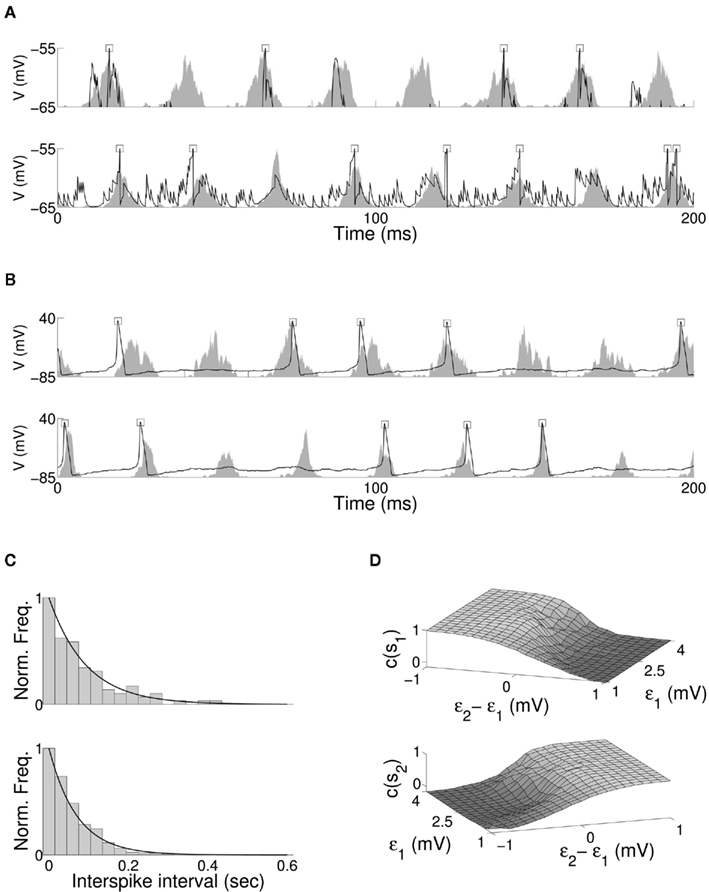
Figure 4. Membrane potential of a single excitatory (upper) and inhibitory (lower) neuron within the target excitatory (E3) and inhibitory (I1) populations, for the (A) QIF and (B) Hodgkin-Huxley bottom-up model of stimulus selection. Neuron firing is indicated by a square at the peak of membrane potential, and the normalized spiking activity of the entire excitatory or inhibitory neuronal population shown as a shaded area. In both cases firing of individual neurons within the model is irregular, with no single neuron firing regularly or at fixed phase offset within the period of oscillation. (C) The normalized distribution of interspike intervals with fitted negative exponential for a single target excitatory neuron, for QIF (upper) and Hodgkin-Huxley (lower) neuron models. (D) Cross-correlation of QIF excitatory target activity to the first (upper) and second (lower) stimulus for varying magnitude and relative stimuli coherence.
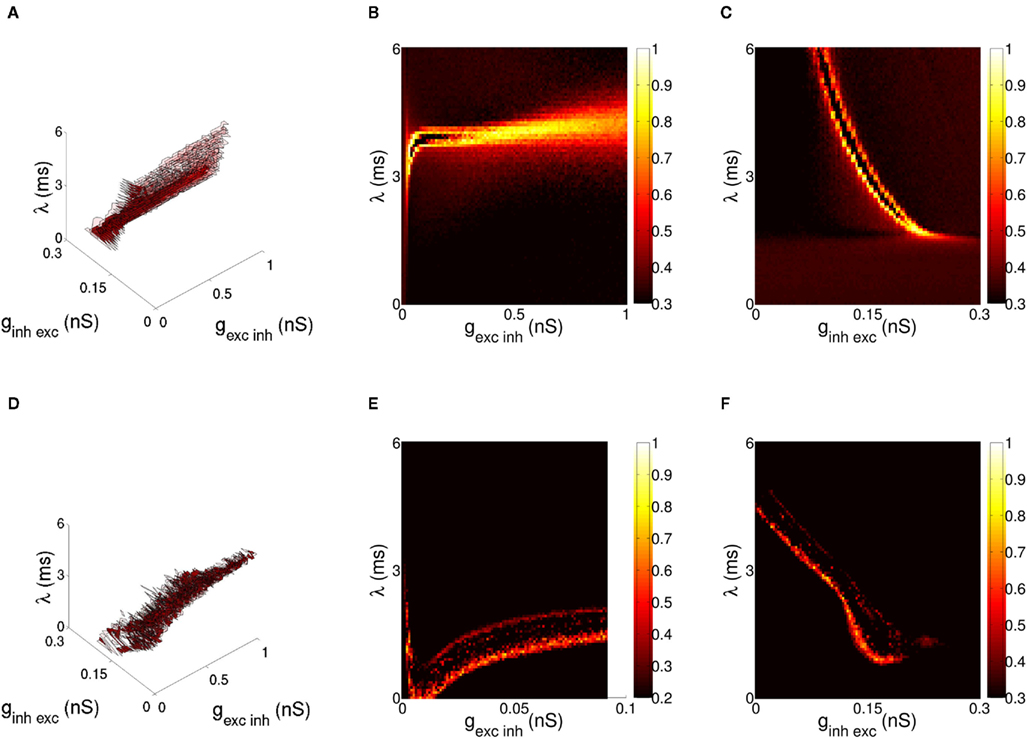
Figure 5. Enumeration of the synaptic parameter space for the bottom-up model of stimulus selection. The difference in cross-correlation (ρ) for the QIF neuron model is shown in (A–C), and Hodgkin-Huxley neuron model in (D–F). Hi-lighted regions in (A,D) indicate values of ρ > 0.7 (solid) and ρ > 0.5 (transparent) for the parameters excitatory-inhibitory weight, inhibitory-to-excitatory weight and synaptic delay local to the target later of the network. Delay was increased simultaneously for excitatory-inhibitory and inhibitory-excitatory synapses so both remained equal, the value (λ) indicating delay in a single direction of the recurrent synaptic loop. A cross-section of the difference in cross-correlation is shown in (B,E) for excitatory-to-inhibitory and (C,F) inhibitory-to-excitatory weight relative to synaptic delay. Within the hi-lighted region behavior of both variants of the model is consistent with communication of a single stimulus through phase-coherent oscillation.
3.2. Binocular Rivalry
We next consider whether the resulting activity within the model parallels experimentally observed results for binocular rivalry. The long-term activity of the model where both stimuli are of equal coherence is shown in Figure 7A. Entrainment of the target layer alternates between one source and the other in periods of unequal length, elevated activity in the excitatory target population switching between the two preferred orientations encoded in the stimuli. The distribution of switching events with equally coherent stimuli (Figure 6A) is both unimodal and skewed toward longer durations of mean within the range 1–2 s, in agreement with experimental data. We include fits for both the gamma distribution commonly used in studies of rivalry (Wade, 1975; Kovács et al., 1996) and more recently used log-normal distribution (Gomez et al., 1995; Lehky, 1995). The auto-correlation coefficients of dominance periods for the same data are shown in Figure 6B. The lack of significant correlation above zero lag is also in agreement with experimental observation (Walker, 1975; Lehky, 1995). Applying the Lathrop statistic (Fox and Herrmann, 1967; Logothetis et al., 1996), a measure of successive dependence between values in time series data, confirmed the lack of dependence between interval times generated by the model (
, σ = 0.05 with z-value −0.14).
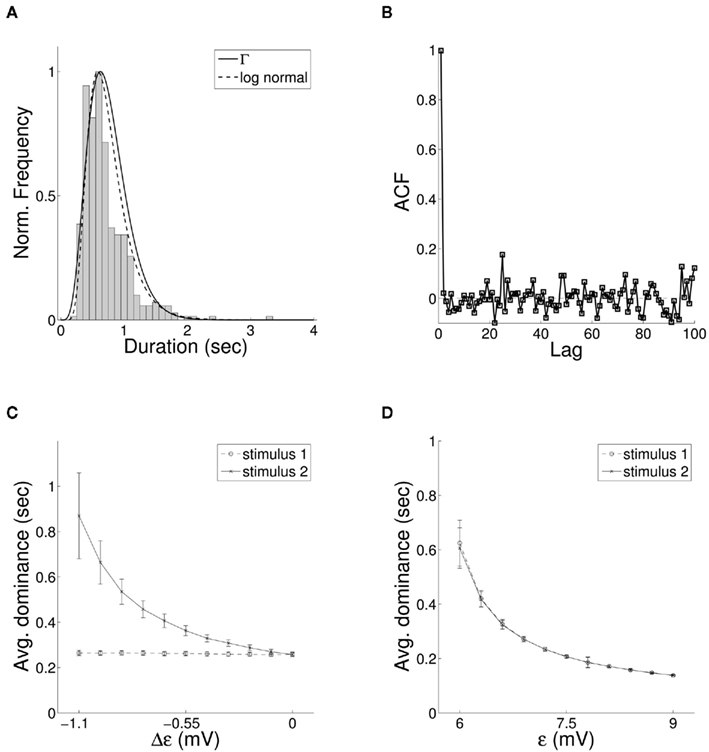
Figure 6. (A) The distribution of periods of entrainment of the bottom-up QIF model to a single stimulus with fitted gamma (solid) and log-normal (dashed) probability density functions and (B) auto-correlation of entrainment periods for the same data, both matching empirical results for binocular rivalry. (C) In accordance with Levelt “Proposition II,” when the strength of a single stimulus in the model is reduced, changes in relative duration of entrainment result mainly from a lengthening of periods of entrainment to the unchanged stimulus. (D) Similarly for Levelt “Proposition IV,” increasing the coherence of both stimuli simultaneously leads to an overall decrease in mean dominance time.
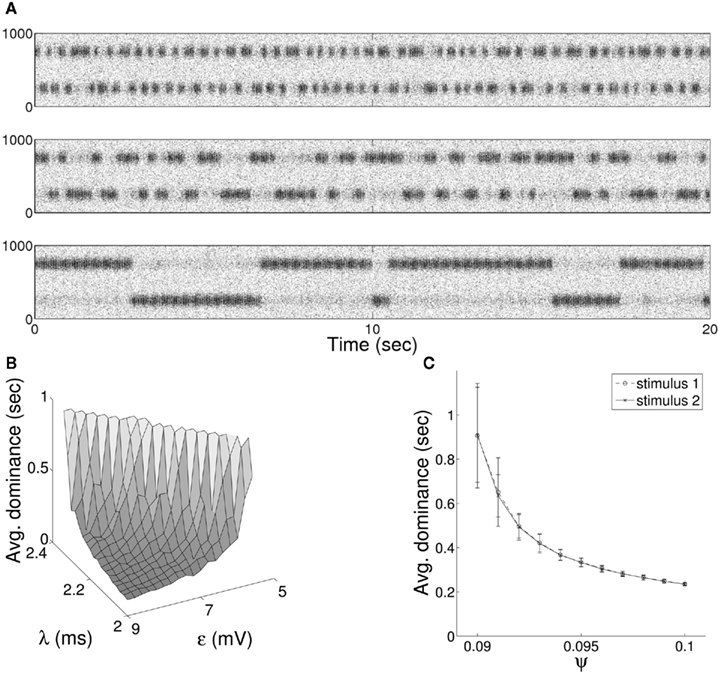
Figure 7. (A) Raster plot of alternation in entrainment of target neurons between incoming stimuli of equal coherence for the bottom-up QIF neuron model. Results are shown with synaptic delay (λ) connecting target excitatory and inhibitory populations of 2.2 ms (upper), 2.1 ms (middle), and 2.0 ms (lower) in either direction. (B) The mean duration of dominance intervals shows a non-linear dependence on both synaptic delay and stimulus coherence, while (C) increasing the level of input noise results in progressively faster switching times.
It is well-known that the rate and behavior of dominance intervals in episodes of binocular rivalry are influenced by variation in predominant stimuli characteristics such as luminance, contrast, and spatial frequency. The effect of modifying the contrast of visual stimuli on the alternation dynamics of rivalry is captured in a set propositions put forward by Levelt (Levelt, 1965). Of particular importance in constraining models of stimulus competition are Levelt “Proposition II,” increases in dominance times caused by weakening a single stimulus occur mainly through an increase in mean dominance duration of the unchanged stimulus, and “Proposition IV,” increasing the strength of both stimuli simultaneously increases the frequency of alternation. More recently it has been shown that changes in predominance produced through varying the strength of a single stimulus result largely from changes in the average dominance duration of the strongest stimulus (Brascamp et al., 2006; Klink et al., 2008) with a large non-linear increase in dominance duration of the unchanging stimulus coupled with a small decrease in the changing stimulus (Laing and Chow, 2002). Both effects are reproduced in the current model, where we treat varying coherence as analogous to a change in visual contrast. A non-linear increase in relative mean dominance duration was reproduced through a decrease in parameter ε to a single stimulus (Figure 6C), and model behavior consistent with proposition IV from a simultaneous increase in ε for both stimuli (Figure 6D). The model displays an additional dependence between mean dominance duration and the delay of synaptic connections within the recurrent excitatory-inhibitory loop (Figure 7A). In Figure 7B we show the effect of changing both synaptic delay and coherence on switching within the model, where traversal down either axis leads to non-linear variation in mean dominance times.
Models of binocular rivalry can be broadly categorized into those based on mutual inhibition and adaption (Blake, 1989; Kalarickal, 2000; Tong, 2001; Laing and Chow, 2002; Stollenwerk and Bode, 2003; Wilson, 2003; Lankheet, 2006), where pools of neurons representing alternate stimuli compete to inhibit one another and gradual adaptation allows switching, and models where alternation is driven by noise (Kim et al., 2006; Moreno-Bote et al., 2007). Given the mutually exclusive and stochastic nature of perceptual switching, we can consider all models of binocular rivalry to be consistent with a double-well potential framework with two marginally stable states (Suzuki and Grabowecky, 2002; Kim et al., 2006; Kang and Blake, 2011), where alternation between states is driven either by adaption or noise. The current model is consistent with a noise-based interpretation of stimulus rivalry, where the energy function is defined by model parameters and alternation driven by Poisson input. An increase in the level of noise to the system maintaining all other parameters should result in an increased rate of alternation between the two marginally stable states. The model behaves as expected, with increasing rate ψ of Poisson input to all neurons resulting in decreasing mean dominance intervals (Figure 7C). Many recent models of rivalry have been proposed that do not rely on oscillatory dynamics (Dayan, 1998; Freeman, 2005; Ashwin and Lavric, 2010; Laing et al., 2010), although there is evidence that perceptual switching is modulated by gamma-band oscillation (Doesburg et al., 2009) and oscillatory models have been put forward (Mishra et al., 2006; Zeitler et al., 2008). Ours differs from previous oscillatory models in that the influence of inhibitory connections is local and selection a function of entrainment of the target population to the incoming stimuli. The population of inhibitory neurons is connected only to the target excitatory neurons with no direct connections between the stimuli generating source neurons and inhibitory neurons of the target layer. The inhibitory neurons serve only as a mechanism of generating gamma oscillation in the local target excitatory population.
4. Discussion
The aim of the present study was to explore competitive selection of stimuli in networks of spiking neurons via oscillation, where transmission of a single relevant stimulus and filtering of irrelevant stimuli between multiple source and a single target neuronal population occurs through variation of stimulus characteristics. We build on previous work examining the CTC hypothesis and the role of neuronal oscillation in the dynamic routing of information in the brain. Recent studies have begun to address the phase dynamics of connected neuronal populations and the role of recurrent inhibition. It has been shown in a network consisting of a single bi-connected excitatory and inhibitory neuron that sinusoidal input across different neuron models gives rise to phase-locked firing suitable for coherent communication (Gielen et al., 2010) and that differences in the coherence of spiking input leads to predictable changes in entrainment (Börgers and Kopell, 2008). We have examined the transmission of population-encoded stimuli between oscillating neuronal populations and the competitive mechanisms that allow transmission of a single stimulus and filtering of a second stimulus to occur.
There is significant biological evidence for the stimulus-driven detection of unexpected but behaviorally relevant events in selective attention (Corbetta and Shulman, 2002). That a competitive mechanism exists is suggested by influential experiments in the macaque visual cortex (Moran and Desimone, 1985; Luck et al., 1997; Reynolds et al., 1999) demonstrating competition between multiple stimuli placed in the receptive field of visual primary cells. This has spawned a number of computational studies exploring the role of inhibition and gamma oscillation in the biased competition of stimuli (Tiesinga et al., 2004; Tiesinga, 2005; Börgers et al., 2008; Zeitler et al., 2008). Subsequent biological studies of macaque V4 provide evidence for increased gamma coherence associated with selective attention (Fries et al., 2001; Bichot et al., 2005). The underlying assumptions of our model are that competition between the stimuli is driven by relative coherence, where a stimulus of greater coherence is more likely to be attended, and that communication of the attended stimulus between oscillating populations is enabled by CTC. In the single neuron case (Börgers and Kopell, 2008) competition is generated through suppression of a less coherent input following firing of the excitatory neuron, where both the additional leakiness introduced by inhibitory synaptic input and timing of inhibition are important. The current model is similarly dependent on the timing and leakiness induced by recurrent inhibitory input, where the firing of each neuron is irregular and ISI times near Poisson. Oscillation, resulting from the aggregate activity of target neurons to independent spatially encoded spiking stimuli, results in filtering of the less coherent stimulus from target output. The relative coherence of the population of neurons encoding the stimuli determines entrainment of the target, and the phase difference between stimuli relative to target results in transmission of the entraining stimulus from source to target neurons.
A computational search of the bounds of this competitive process in relation to synaptic parameters linking target excitatory and inhibitory neuronal populations reveals the space within which those parameters are optimally tuned for selection of a single stimulus. Detailed exploration of even a few parameters of a model of several thousand neurons and tens of thousands of synapses requires significant computational resources, and the development of a framework for parallel simulation, collation, and analysis of results over a large distributed computing cluster was an essential component of this study. For parameters within the optimal region of our model, oscillation in target neurons entrains to the phase of incoming stimuli. Results of decoding model output over the complete range of relative phases between stimuli, and between stimuli and target oscillation, suggest that even a small difference in the phase of incoming stimuli is sufficient for the communication of a single entraining stimulus. That the same mechanism works for identical network connectivity using both QIF and Hodgkin-Huxley neuron models, which have significant differences in underlying dynamics and mechanism of action potential generation, supports the validity of the results.
A number of measures have been applied to the activity of connected oscillating neuronal populations, such as correlation (Masuda, 2009), phase coherence (Gielen et al., 2010), and information theoretic measures such as transfer entropy (Akam and Kullmann, 2010) and causal density (Shanahan, 2008). Given stimuli occupying distinct regions of coding space, we used the binned average firing rate as a basis for both correlation and template-based decoding. Ignoring additional information available in the frequency domain for distinguishing between oscillating and asynchronous stimuli allows for simple biologically plausible decoding of model output. A circuit for decoding the activity of target neurons based on binned average firing rate is not included in the model, but it is not difficult to imagine how this would be done.
It is interesting that the model displays alternation between transmission of stimuli analogous to binocular rivalry. That switching episodes in the model are well represented by gamma and log-normal distributions, the lack of correlation between successive dominance periods, and that model behavior is consistent with both Levelt Propositions II and IV, suggest competitive entrainment as a plausible basis for this type of stimulus rivalry. This is not the first model to draw a link between binocular rivalry, biased competition, and mechanisms of inhibition and oscillation, although we differ from previous models in that the effect of inhibition is local to the target population receiving the stimuli. Long-range connections between stimuli generating and receiving neurons in the model are entirely excitatory, with inhibitory neurons receiving no synaptic connections outside of the target layer of the network.
The assumption of a specific phase relationship between the oscillating populations requires some justification, forming the basis of not only the current model but as an underlying assumption of CTC and models of phase-coherent neuronal communication in general. Episodes of transient long-range phase-coherent synchronization in gamma and beta ranges have been shown to occur in frontal and visual areas during visual attention (Gross et al., 2004; Gregoriou et al., 2009), between hippocampal and prefrontal areas during learning (Benchenane et al., 2010; Colgin, 2011), and cross-frequency phase-coupling to occur during working memory tasks (Palva et al., 2005). Additionally there is direct evidence of oscillatory phase-encoding of stimuli in the insect olfactory system (Perez-Orive, 2002; Sivan and Kopell, 2004; Schnitzler and Gross, 2005) where odors induce precise and reproducible phase offsets in LFP oscillation between interacting neuronal areas. While it is not clear that similar phase-encoding mechanisms extend to the mammalian brain, methods for measuring phase-synchronization (Nolte et al., 2004; Stam et al., 2007; Hindriks et al., 2011; Pascual-Marqui et al., 2011; Vinck et al., 2011) and recovering structure from phase dynamics (Cadieu and Koepsell, 2010; Kralemann et al., 2011) remain active areas of research, and improved understanding is likely. It is reasonable to assume that generation of stimuli should result in reproducible if transient phase relationships occurring between the encoding regions.
Taken together these results suggest a plausible mechanism of competitive selection between stimuli through PING generated gamma oscillation. A combination of the entrainment of a population of oscillating excitatory neurons to spiking stimuli and CTC, where competition between stimuli is determined by relative coherence and CTC between source and target neurons by phase difference, allows both selection of a single salient stimulus and filtering of irrelevant stimuli. Stimuli of different orientation but equal coherence reproduce both the behavior and statistical properties of the well-known phenomena of stimulus rivalry. The results are robust to changes in the dynamical properties of the neuron model, and the underlying assumptions of model construction are consistent with biological evidence supporting both competition and changes in gamma frequency coherence in the bottom-up attentional selection of behaviorally relevant stimuli.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Abrams, D., and Strogatz, S. (2004). Chimera states for coupled oscillators. Phys. Rev. Lett. 93, 174102.
Akam, T., and Kullmann, D. M. (2010). Oscillations and filtering networks support flexible routing of information. Neuron 67, 308–320.
Andrews, T. J. (2001). Binocular rivalry and visual awareness. Trends Cogn. Sci. (Regul. Ed.) 5, 407–409.
Ashwin, P., and Lavric, A. (2010). A low-dimensional model of binocular rivalry using winnerless competition. Physica D 239, 529–536.
Axmacher, N., Mormann, F., Fernández, G., Elger, C. E., and Fell, J. (2006). Memory formation by neuronal synchronization. Brain Res. Rev. 52, 170–182.
Banke, T. G., and McBain, C. J. (2006). GABAergic input onto CA3 hippocampal interneurons remains shunting throughout development. J. Neurosci. 26, 11720–11725.
Bartos, M., Vida, I., and Jonas, P. (2007). Synaptic mechanisms of synchronized gamma oscillations in inhibitory interneuron networks. Nat. Rev. Neurosci. 8, 45–56.
Ben-Ari, Y. (2002). Excitatory actions of GABA during development: the nature of the nurture. Nat. Rev. Neurosci. 3, 728–739.
Benchenane, K., Peyrache, A., Khamassi, M., Tierney, P. L., Gioanni, Y., Battaglia, F. P., and Wiener, S. I. (2010). Coherent theta oscillations and reorganization of spike timing in the hippocampal-prefrontal network upon learning. Neuron 66, 921–936.
Bichot, N. P., Rossi, A. F., and Desimone, R. (2005). Parallel and serial neural mechanisms for visual search in macaque area V4. Science 308, 529–534.
Blake, R. (2001). A primer on binocular rivalry, including current controversies. Brain Mind 2, 5–38.
Börgers, C., Epstein, S., and Kopell, N. J. (2005). Background gamma rhythmicity and attention in cortical local circuits: a computational study. Proc. Natl. Acad. Sci. U.S.A. 102, 7002–7007.
Börgers, C., Epstein, S., and Kopell, N. J. (2008). Gamma oscillations mediate stimulus competition and attentional selection in a cortical network model. Proc. Natl. Acad. Sci. U.S.A. 105, 18023–18028.
Börgers, C., and Kopell, N. (2003). Synchronization in networks of excitatory and inhibitory neurons with sparse, random connectivity. Neural Comput. 15, 509–538.
Börgers, C., and Kopell, N. (2005). Effects of noisy drive on rhythms in networks of excitatory and inhibitory neurons. Neural Comput. 17, 557–608.
Börgers, C., and Kopell, N. J. (2008). Gamma oscillations and stimulus selection. Neural Comput. 20, 383–414.
Börgers, C., Krupa, M., and Gielen, S. (2010). The response of a classical Hodgkin–Huxley neuron to an inhibitory input pulse. J. Comput. Neurosci. 28, 509–526.
Brascamp, J. W., van Ee, R., Noest, A. J., Jacobs, R. H. A. H., and van den Berg, A. V. (2006). The time course of binocular rivalry reveals a fundamental role of noise. J. Vis. 6, 1244–1256.
Brovelli, A., Lachaux, J., Kahane, P., and Boussaoud, D. (2005). High gamma frequency oscillatory activity dissociates attention from intention in the human premotor cortex. Neuroimage 28, 154–164.
Brunel, N. (2000). Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J. Comput. Neurosci. 8, 183–208.
Brunel, N., and Wang, X. (2003). What determines the frequency of fast network oscillations with irregular neural discharges? I. Synaptic dynamics and excitation-inhibition balance. J. Neurophysiol. 90, 415–430.
Buehlmann, A., and Deco, G. (2010). Optimal information transfer in the cortex through synchronization. PLoS Comput. Biol. 6, e1000934. doi: 10.1371/journal.pcbi.1000934
Buia, C., and Tiesinga, P. (2006). Attentional modulation of firing rate and synchrony in a model cortical network. J. Comput. Neurosci. 20, 247–264.
Buia, C. I., and Tiesinga, P. H. (2008). Role of interneuron diversity in the cortical microcircuit for attention. J. Neurophysiol. 99, 2158–2182.
Buschman, T. J., and Miller, E. K. (2007). Top-down versus bottom-up control of attention in the prefrontal and posterior parietal cortices. Science 315, 1860–1862.
Cadieu, C. F., and Koepsell, K. (2010). Phase coupling estimation from multivariate phase statistics. Neural Comput. 22, 3107–3126.
Colgin, L. L. (2011). Oscillations and hippocampal-prefrontal synchrony. Curr. Opin. Neurobiol. 21, 467–474.
Colgin, L. L., Denninger, T., Fyhn, M., Hafting, T., Bonnevie, T., Jensen, O., Moser, M., and Moser, E. I. (2009). Frequency of gamma oscillations routes flow of information in the hippocampus. Nature 462, 353–357.
Corbetta, M., and Shulman, G. L. (2002). Control of goal-directed and stimulus-driven attention in the brain. Nat. Rev. Neurosci. 3, 201–215.
Csicsvari, J., Hirase, H., Czurkó, A., Mamiya, A., and Buzsáki, G. (1999). Oscillatory coupling of hippocampal pyramidal cells and interneurons in the behaving rat. J. Neurosci. 19, 274–287.
Deneve, S., Latham, P. E., and Pouget, A. (1999). Reading population codes: a neural implementation of ideal observers. Nat. Neurosci. 2, 740–745.
Desimone, R., and Duncan, J. (1995). Neural mechanisms of selective visual attention. Annu. Rev. Neurosci. 18, 193–222.
Doesburg, S. M., Green, J. J., McDonald, J. J., and Ward, L. M. (2009). Rhythms of consciousness: binocular rivalry reveals large-scale oscillatory network dynamics mediating visual perception. PLoS ONE 4, e6142. doi: 10.1371/journal.pone.0006142
Doesburg, S. M., Roggeveen, A. B., Kitajo, K., and Ward, L. M. (2008). Large-scale gamma-band phase synchronization and selective attention. Cereb. Cortex 18, 386–396.
Ermentrout, B. (1996). Type I membranes, phase resetting curves, and synchrony. Neural Comput. 8, 979–1001.
Ermentrout, G. B., and Kopell, N. (1986). Parabolic bursting in an excitable system coupled with a slow oscillation. SIAM J. Appl. Math. 46, 233.
Fox, R., and Herrmann, J. (1967). Stochastic properties of binocular rivalry alternations. Percept. Psychophys. 2, 432–436.
Fries, P. (2005). A mechanism for cognitive dynamics: neuronal communication through neuronal coherence. Trends Cogn. Sci. (Regul. Ed.) 9, 474–480.
Fries, P. (2009). Neuronal gamma-band synchronization as a fundamental process in cortical computation. Annu. Rev. Neurosci. 32, 209–224.
Fries, P., Reynolds, J. H., Rorie, A. E., and Desimone, R. (2001). Modulation of oscillatory neuronal synchronization by selective visual attention. Science 291, 1560–1563.
Fries, P., Schröder, J., Roelfsema, P. R., Singer, W., and Engel, A. K. (2002). Oscillatory neuronal synchronization in primary visual cortex as a correlate of stimulus selection. J. Neurosci. 22, 3739–3754.
Galassi, M., Davies, J., Theiler, J., Gough, B., Jungman, G., Booth, M., and Rossi, F. (2009). Gnu Scientific Library: Reference Manual. Surrey: Network Theory Ltd.
Geisler, C. (2005). Contributions of intrinsic membrane dynamics to fast network oscillations with irregular neuronal discharges. J. Neurophysiol. 94, 4344–4361.
Gielen, S., Krupa, M., and Zeitler, M. (2010). Gamma oscillations as a mechanism for selective information transmission. Biol. Cybern. 103, 151–165.
Gomez, C., Argandona, E. D., Solier, R. G., Angulo, J. C., and Vazquez, M. (1995). Timing and competition in networks representing ambiguous figures. Brain Cogn. 29, 103–114.
Gregoriou, G. G., Gotts, S. J., Zhou, H., and Desimone, R. (2009). High-frequency, long-range coupling between prefrontal and visual cortex during attention. Science 324, 1207–1210.
Gross, J., Schmitz, F., Schnitzler, I., Kessler, K., Shapiro, K., Hommel, B., and Schnitzler, A. (2004). Modulation of long-range neural synchrony reflects temporal limitations of visual attention in humans. Proc. Natl. Acad. Sci. U.S.A. 101, 13050–13055.
Gutkin, B. S., Ermentrout, G. B., and Reyes, A. D. (2005). Phase-response curves give the responses of neurons to transient inputs. J. Neurophysiol. 94, 1623–1635.
Hindriks, R., Bijma, F., van Dijk, B. W., Stam, C. J., van der Werf, Y. Y., van Someren, E. J., de Munck, J. C., and van der Vaart, A. W. (2011). Data-driven modeling of phase interactions between spontaneous MEG oscillations. Hum. Brain Mapp. 32, 1161–1178.
Hodgkin, A. L., and Huxley, A. F. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. (Lond.) 117, 500–544.
Jensen, O., Kaiser, J., and Lachaux, J. (2007). Human gamma-frequency oscillations associated with attention and memory. Trends Neurosci. 30, 317–324.
Jutras, M. J., Fries, P., and Buffalo, E. A. (2009). Gamma-band synchronization in the macaque hippocampus and memory formation. J. Neurosci. 29, 12521–12531.
Kalarickal, G. (2000). Neural model of temporal and stochastic properties of binocular rivalry. Neurocomputing 32–33, 843–853.
Kang, M., and Blake, R. (2011). An integrated framework of spatiotemporal dynamics of binocular rivalry. Front. Hum. Neurosci. 5:88. doi: 10.3389/fnhum.2011.00088
Kim, Y., Grabowecky, M., and Suzuki, S. (2006). Stochastic resonance in binocular rivalry. Vision Res. 46, 392–406.
Klink, P. C., van Ee, R., and van Wezel, R. J. A. (2008). General validity of Levelt’s propositions reveals common computational mechanisms for visual rivalry. PLoS ONE 3, e3473. doi: 10.1371/journal.pone.0003473
Kondgen, H., Geisler, C., Fusi, S., Wang, X., Luscher, H., and Giugliano, M. (2007). The dynamical response properties of neocortical neurons to temporally modulated noisy inputs in vitro. Cereb. Cortex 18, 2086–2097.
Kovács, I., Papathomas, T., Yang, M., and Fehér, Á. (1996). When the brain changes its mind: Interocular grouping during binocular rivalry. Proc. Natl. Acad. Sci. U.S.A. 93, 15508–15511.
Kralemann, B., Pikovsky, A., and Rosenblum, M. (2011). Reconstructing phase dynamics of oscillator networks. Chaos 21, 025104.
Kreuz, T., Chicharro, D., Andrzejak, R. G., Haas, J. S., and Abarbanel, H. D. (2009). Measuring multiple spike train synchrony. J. Neurosci. Methods 183, 287–299.
Kuramoto, Y., and Battogtokh, D. (2002). Coexistence of coherence and incoherence in nonlocally coupled phase oscillators. Nonlin. Phenom. Complex Syst. 5, 380–385.
Laing, C. R., and Chow, C. C. (2002). A spiking neuron model for binocular rivalry. J. Comput. Neurosci. 12, 39–53.
Laing, C. R., Frewen, T., and Kevrekidis, I. G. (2010). Reduced models for binocular rivalry. J. Comput. Neurosci. 28, 459–476.
Lakatos, P., Chen, C., O’Connell, M. N., Mills, A., and Schroeder, C. E. (2007). Neuronal oscillations and multisensory interaction in primary auditory cortex. Neuron 53, 279–292.
Lakatos, P., O’Connell, M. N., Barczak, A., Mills, A., Javitt, D. C., and Schroeder, C. E. (2009). The leading sense: supramodal control of neurophysiological context by attention. Neuron 64, 419–430.
Lankheet, M. J. M. (2006). Unraveling adaptation and mutual inhibition in perceptual rivalry. J. Vis. 6, 304–310.
Latham, P. E., Richmond, B. J., Nelson, P. G., and Nirenberg, S. (2000). Intrinsic dynamics in neuronal networks. I. Theory. J. Neurophysiol. 83, 808–827.
Logothetis, N. K., Leopold, D. A., and Sheinberg, D. L. (1996). What is rivalling during binocular rivalry? Nature 380, 621–624.
Luck, S. J., Chelazzi, L., Hillyard, S. A., and Desimone, R. (1997). Neural mechanisms of spatial selective attention in areas V1, V2, and V4 of macaque visual cortex. J. Neurophysiol. 77, 24–42.
Masuda, N. (2009). Selective population rate coding: a possible computational role of gamma oscillations in selective attention. Neural Comput. 21, 3335–3362.
Mato, G., and Samengo, I. (2008). Type I and type II neuron models are selectively driven by differential stimulus features. Neural Comput. 20, 2418–2440.
Middleton, S., Jalics, J., Kispersky, T., LeBeau, F. E. N., Roopun, A. K., Kopell, N. J., Whittington, M. A., and Cunningham, M. O. (2008). NMDA receptor-dependent switching between different gamma rhythm-generating microcircuits in entorhinal cortex. Proc. Natl. Acad. Sci. U.S.A. 105, 18572–18577.
Miller, B. T., and D’Esposito, M. (2005). Searching for “the top” in top-down control. Neuron 48, 535–538.
Miltner, W. H. R., Braun, C., Matthias, A., Witte, H., and Taub, E. (1999). Coherence of gamma-band EEG activity as a basis for associative learning. Nature 397, 434–436.
Mishra, J., Fellous, J., and Sejnowski, T. J. (2006). Selective attention through phase relationship of excitatory and inhibitory input synchrony in a model cortical neuron. Neural Netw. 19, 1329–1346.
Montgomery, S. M., and Buzsáki, G. (2007). Gamma oscillations dynamically couple hippocampal CA3 and CA1 regions during memory task performance. Proc. Natl. Acad. Sci. U.S.A. 104, 14495–14500.
Moran, J., and Desimone, R. (1985). Selective attention gates visual processing in the extrastriate cortex. Science 229, 782–784.
Moreno-Bote, R., Rinzel, J., and Rubin, N. (2007). Noise-induced alternations in an attractor network model of perceptual bistability. J. Neurophysiol. 98, 1125–1139.
Nolte, G., Bai, O., Wheaton, L., Mari, Z., Vorbach, S., and Hallett, M. (2004). Identifying true brain interaction from EEG data using the imaginary part of coherency. Clin. Neurophysiol. 115, 2292–2307.
Omel’chenko, O. E., Maistrenko, Y. L., and Tass, P. A. (2008). Chimera states: the natural link between coherence and incoherence. Phys. Rev. Lett. 100, 044105.
Palva, J. M., Palva, S., and Kaila, K. (2005). Phase synchrony among neuronal oscillations in the human cortex. J. Neurosci. 25, 3962–3972.
Pascual-Marqui, R. D., Lehmann, D., Koukkou, M., Kochi, K., Anderer, P., Saletu, B., Tanaka, H., Hirata, K., John, E. R., Prichep, L., Biscay-Lirio, R., and Kinoshita, T. (2011). Assessing interactions in the brain with exact low-resolution electromagnetic tomography. Philos. Transact. A Math. Phys. Eng. Sci. 369, 3768–3784.
Perez-Orive, J. (2002). Oscillations and sparsening of odor representations in the mushroom body. Science 297, 359–365.
Pesaran, B., Pezaris, J. S., Sahani, M., Mitra, P. P., and Andersen, R. A. (2002). Temporal structure in neuronal activity during working memory in macaque parietal cortex. Nat. Neurosci. 5, 805–811.
Popescu, A. T., Popa, D., and Paré, D. (2009). Coherent gamma oscillations couple the amygdala and striatum during learning. Nat. Neurosci. 12, 801–807.
Quiroga, R. Q., and Panzeri, S. (2009). Extracting information from neuronal populations: information theory and decoding approaches. Nat. Rev. Neurosci. 10, 173–185.
Ray, S., and Maunsell, J. H. (2010). Differences in gamma frequencies across visual cortex restrict their possible use in computation. Neuron 67, 885–896.
Reynolds, J. H., Chelazzi, L., and Desimone, R. (1999). Competitive mechanisms subserve attention in macaque areas V2 and V4. J. Neurosci. 19, 1736–1753.
Reynolds, J. H., and Desimone, R. (2003). Interacting roles of attention and visual salience in V4. Neuron 37, 853–863.
Ritz, R., and Sejnowski, T. J. (1997). Synchronous oscillatory activity in sensory systems: new vistas on mechanisms. Curr. Opin. Neurobiol. 7, 536–546.
Rodriguez, E., George, N., Lachaux, J., Martinerie, J., Renault, B., and Varela, F. J. (1999). Perception’s shadow: long-distance synchronization of human brain activity. Nature 397, 430–433.
Roelfsema, P. R., Engel, A. K., König, P., and Singer, W. (1997). Visuomotor integration is associated with zero time-lag synchronization among cortical areas. Nature 385, 157–161.
Schnitzler, A., and Gross, J. (2005). Normal and pathological oscillatory communication in the brain. Nat. Rev. Neurosci. 6, 285–296.
Schroeder, C. E., and Lakatos, P. (2009). Low-frequency neuronal oscillations as instruments of sensory selection. Trends Neurosci. 32, 9–18.
Seung, H. S., and Sompolinsky, H. (1993). Simple models for reading neuronal population codes. Proc. Natl. Acad. Sci. U.S.A. 90, 10749–10753.
Shanahan, M. (2008). Dynamical complexity in small-world networks of spiking neurons. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 78, 041924.
Shanahan, M. (2010). Metastable chimera states in community-structured oscillator networks. Chaos 20, 013108.
Sivan, E., and Kopell, N. (2004). Mechanism and circuitry for clustering and fine discrimination of odors in insects. Proc. Natl. Acad. Sci. U.S.A. 101, 17861–17866.
Softky, W. R., and Koch, C. (1993). The highly irregular firing of cortical cells is inconsistent with temporal integration of random EPSPs. J. Neurosci. 13, 334–350.
Stam, C. J., Nolte, G., and Daffertshofer, A. (2007). Phase lag index: assessment of functional connectivity from multi channel EEG and MEG with diminished bias from common sources. Hum. Brain Mapp. 28, 1178–1193.
Stollenwerk, L., and Bode, M. (2003). Lateral neural model of binocular rivalry. Neural Comput. 15, 2863–2882.
Suzuki, S., and Grabowecky, M. (2002). Evidence for perceptual trapping and adaptation in multistable binocular rivalry. Neuron 36, 143–157.
Tiesinga, P., and Sejnowski, T. J. (2009). Cortical enlightenment: are attentional gamma oscillations driven by ING or PING? Neuron 63, 727–732.
Tiesinga, P. H., Fellous, J., Salinas, E., José, J. V., and Sejnowski, T. J. (2004). Inhibitory synchrony as a mechanism for attentional gain modulation. J. Physiol. Paris 98, 296–314.
Tiesinga, P. H. E. (2005). Stimulus competition by inhibitory interference. Neural Comput. 17, 2421–2453.
Tong, F. (2001). Competing theories of binocular rivalry: a possible resolution. Brain Mind 2, 55–83.
Tong, F., Meng, M., and Blake, R. (2006). Neural bases of binocular rivalry. Trends Cogn. Sci. (Regul. Ed.) 10, 502–511.
Traub, R. D., Whittington, M. A., Colling, S. B., Buzsáki, G., and Jefferys, J. G. (1996). Analysis of gamma rhythms in the rat hippocampus in vitro and in vivo. J. Physiol. (Lond.) 493, 471–484.
Uhlhaas, P. J., Pipa, G., Lima, B., Melloni, L., Neuenschwander, S., Nikolic, D., and Singer, W. (2009). Neural synchrony in cortical networks: history, concept and current status. Front. Integr. Neurosci. 3:17. doi: 10.3389/neuro.07.017.2009
van Vugt, M. K., Schulze-Bonhage, A., Litt, B., Brandt, A., and Kahana, M. J. (2010). Hippocampal gamma oscillations increase with memory load. J. Neurosci. 30, 2694–2699.
Varela, F., Lachaux, J., Rodriguez, E., and Martinerie, J. (2001). The brain web: phase synchronization and large-scale integration. Nat. Rev. Neurosci. 2, 229–239.
Vinck, M., Lima, B., Womelsdorf, T., Oostenveld, R., Singer, W., Neuenschwander, S., and Fries, P. (2010). Gamma-phase shifting in awake monkey visual cortex. J. Neurosci. 30, 1250–1257.
Vinck, M., Oostenveld, R., van Wingerden, M., Battaglia, F., and Pennartz, C. M. A. (2011). An improved index of phase-synchronization for electrophysiological data in the presence of volume-conduction, noise and sample-size bias. Neuroimage 55, 1548–1565.
Wade, N. J. (1975). Binocular rivalry between single lines viewed as real images and afterimages. Percept. Psychophys. 17, 571–577.
Walker, P. (1975). Stochastic properties of binocular rivalry alternations. Percept. Psychophys. 18, 467–473.
Wang, X. (2010). Neurophysiological and computational principles of cortical rhythms in cognition. Physiol. Rev. 90, 1195–1268.
Whittington, M. A., Cunningham, M. O., LeBeau, F. E., Racca, C., and Traub, R. D. (2011). Multiple origins of the cortical gamma rhythm. Dev. Neurobiol. 71, 92–106.
Whittington, M. A., and Traub, R. D. (2003). Interneuron diversity series: inhibitory interneurons and network oscillations in vitro. Trends Neurosci. 26, 676–682.
Whittington, M. A., Traub, R. D., and Jefferys, J. G. R. (1995). Synchronized oscillations in interneuron networks driven by metabotropic glutamate receptor activation. Nature 373, 612–615.
Whittington, M. A., Traub, R. D., Kopell, N., Ermentrout, B., and Buhl, E. H. (2000). Inhibition-based rhythms: experimental and mathematical observations on network dynamics. Int. J. Psychophysiol. 38, 315–336.
Wilson, H. R. (2003). Computational evidence for a rivalry hierarchy in vision. Proc. Natl. Acad. Sci. U.S.A. 100, 14499–14503.
Womelsdorf, T., and Fries, P. (2007). The role of neuronal synchronization in selective attention. Curr. Opin. Neurobiol. 17, 154–160.
Womelsdorf, T., Schoffelen, J., Oostenveld, R., Singer, W., Desimone, R., Engel, A. K., and Fries, P. (2007). Modulation of neuronal interactions through neuronal synchronization. Science 316, 1609–1612.
Keywords: synchrony, stimulus competition, gamma oscillation, phase coherence
Citation: Wildie M and Shanahan M (2012) Establishing communication between neuronal populations through competitive entrainment. Front. Comput. Neurosci. 5:62. doi: 10.3389/fncom.2011.00062
Received: 05 May 2011; Accepted: 12 December 2011;
Published online: 12 January 2012.
Edited by:
Nicolas Brunel, Centre National de la Recherche Scientifique, FranceReviewed by:
Vincent Hakim, Centre National de la Recherche Scientifique, FranceStan Gielen, Radboud University Nijmegen, Netherlands
Copyright: © 2012 Wildie and Shanahan. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Mark Wildie, Department of Computing, Imperial College London, SW7 2AZ London, UK. e-mail: mark.wild05@imperial.ac.uk