Selectionist and evolutionary approaches to brain function: a critical appraisal

Edelman (1987) published a landmark book with Neural Darwinism and The Theory of Neuronal Group Selection as its title and subtitle, respectively. The view advocated in the book follows, in general, arguably a long tradition, ranging from James (1890) up to Edelman himself, operating with the idea that complex adaptations in the brain arise through some process similar to natural selection (NS). The term “Darwinian” in the title cannot be misunderstood to indicate this fact. Interestingly, the subtitle by the term “group selection” seems to refer to a special kind of NS phenomenon, called group selection [the reader may consult the textbook by Maynard Smith (1998) for many of the concepts in evolutionary biology that we use in this paper]. The expectation one has is then that the mapping between aspects of neurobiology and evolutionary biology has been clearly laid out. This is rather far from the truth, however. This is immediately clear from two reviews of Edelman’s book: one by Crick (1989), then working in neuroscience and another by Michod (1988, 1990), an eminent theoretical evolutionary biologist. The appreciation by these authors of Edelman’s work was almost diametrically opposite. Michod could not help being baffled himself. In a response to Crick he wrote; “Francis Crick concludes that ‘I have not found it possible to make a worthwhile analogy between the theory of NS and what happens in the developing brain and indeed Edelman has not presented one’ (p. 246). This came as a surprise to me, since I had reached a completely opposite conclusion” (Michod, 1990, p. 12). Edelman, Crick, and Michod cannot be right at the same time. But they can all be wrong at the same time. The last statement is not meant to be derogatory in any sense: we are dealing with subtle issues that do matter a lot! It is easy to be led astray in this forest of concepts, arguments, models, and interpretations. We are painfully aware of the fact that the authors of the present paper are by no means an exception. The aim of this paper is fourfold: (i) to show how all three authors misunderstood Darwinian dynamics in the neurobiological context; (ii) to show that at least two different meanings of the term “selection” are confused and intermingled; (iii) to propose that a truly Darwinian approach is feasible and potentially rewarding; and (iv) to discuss to what extent selection (especially of the Darwinian type) can happen at various levels of neurobiological organization.

We believe that a precondition to success is to have some professional training in the theory (at least) of both the neural and cognitive sciences as well as of evolution. Out of this comes a difficulty: neurobiologists are unlikely to follow detailed evolutionary arguments and, conversely, evolutionary biologists may be put off by many a detail in the neurosciences. Since the readership of this paper is expected to sit in the neurobiology/cognitive science corner, we thought that we should explain some of the evolutionary items involved in sufficient detail. It is hard to define in advance what “sufficient” here means: one can easily end up with a book (and one should), but a paper has size limitations. If this analysis were to stimulate a good number of thinkers in both fields, the authors would be more than delighted.

Some Issues with “Neural Darwinism”

Edelman argued for the applicability of the concepts of selection at the level of neuronal groups. Put simply, it is a group of neurons that have a sufficiently tightly knit web of interactions internally so that they can be regarded as a cohesive unit (“a set of more or less tightly connected cells that fire predominantly together,” Edelman, 1987, p. 198), demonstrated by the fact that some groups react to a given stimulus differentially, and groups that react better get strengthened due to plasticity of the synapses in the group, whereas others get weakened. There are two assumptions in the original Edelman model: synaptic connections are given, to begin with (the primary repertoire); and groups form and transform through the modifications of their constituent synapses. Where does selection come in?

As Crick (1989) noted: “What can be altered, however, is the strength of a connection (or a set of connections) and this is taken to be analogous to an increase in cell number in (for example) the immune system… This idea is a legitimate use of the selectionist paradigm… Thus a theory might well be called… ‘The theory of synaptic selection (TSS)’. But this would describe almost all theories of neural nets” (Crick, 1989, p. 241). We shall come back to this issue because in the meantime TSS has advanced. Let us for the time being assume that whereas a selectionist view of synapse dynamics might be trivially valid, such a view at levels above the synapse is highly questionable. Let us read Michod on the relation between NS and neuronal group selection (NGS): “We can now state the basic analogy between NS and NGS. In NS, differences in the adaptation of organisms to an environment lead to differences in their reproductive success, which, when coupled with rules of genetic transmission, lead to a change in frequency of genotypes in a population. In NGS, differences in receptive fields and connectivity of neuronal groups lead to differences in their initial responses to a stimulus, which, when coupled with rules of synaptic change, lead to a change in probabilities of further response to the stimulus.” Note that reproductive success (fitness) is taken to be analogous to the probability of responding to a stimulus. It should be clear that Michod thinks that the analogy is sufficiently tight, although neuronal groups (and normally their constituent neurons) do not reproduce. How can then NGS be Darwinian, one might ask? What is meant by selection here? We propose that sense can be made in terms of a special formalism, frequently used in evolutionary biology, that of the eminent Price (1970), who made two seminal contributions to evolutionary biology. One of them is the Price equation of selection.

If it is possible to describe a trait (e.g., activation of a neuronal group) and the covariance between that trait and its probability of it occurring again in the future, then Price’s equation applies. It states that the change in some average trait z is proportional to the covariance between that trait z_i and its relative fitness w_i in the population and other transmission biases E (e.g., due to mutation, or externally imposed instructed changes)…

$w\Delta z=cov\left(w_i,z_i\right)+E\left(w_i\Delta z_i\right)$(1)

where w is average fitness in the population. It is the first term that explains the tendency for traits that are positively correlated with fitness to increase in frequency. Note that there is no reference to reproduction here, except through implication by the term “fitness” that is not necessarily reproductive fitness in general. This is a subtle point of the utmost importance, without the understanding of which it is useless to read this paper further. The Price equation (in various forms) has been tremendously successful in evolutionary biology, one of Price’s friends: Hamilton (1975) used it also for a reformulation of his theory of kin selection (one of the goals of which is to explain the phenomenon of altruism in evolution). Approaches to multilevel selection (acting, for example, at the level of organisms and groups at the same time) tend to rely on this formulation also (Damuth and Heisler, 1988). Note that Michod is a former student of Hamilton, and that he is also an expert on the theory of kin selection. Although he does not refer to Price in the context of NGS, he does express a view that is very much in line with the Price equation of selection.

One might suspect, having gotten thus far, that there is some “trouble” with the Price equation, and indeed that is the case, we believe, and this unrecognized or not emphasized feature has generated more trouble, including the problems around NGS. Let us first state, however, where we think the trouble is not. Crick (1990) writes, responding to Michod: “It is very loose talk to call organisms or populations ‘units of selection,’ especially as they behave in rather different ways from bits of DNA or genes, which are genuine units of selection…” This is an interesting case when the molecular biologist/neurobiologist Crick teaches something on evolution to a professional evolutionary biologist. One should at least be a bit skeptical at this point. If one looks at models of multilevel selection, there is usually not much loose talk there, to begin with. Second, Crick (without citation) echoes Dawkins’ (1976) view of the selfish gene. We just mention in passing the existence of the famous paper with the title: “Selfish DNA: the ultimate parasite” by Orgel and Crick(1980, where the authors firmly tie their message to the view of the Selfish Gene; Orgel and Crick, 1980). We shall come back to the problems of levels of selection; suffice to say it here that we are not really worried about this particular concern of Crick, at least not in general.

Our concern lies with the algorithmic deficiency of the Price equation. The trouble is that it is generally “dynamically insufficient”: one cannot solve it progressively across an arbitrary number of generations because of lack of the knowledge of the higher-order moments: one ought to be able either to follow the fate of the distribution of types (as in standard population genetics), or have a way of calculating the higher moments independent of the generation. This is in sharp contrast to what a theoretical physicist or biologist would normally understand under “dynamics.” As Maynard Smith (2008) explains in an interview he does “not understand” the Price equation because it is based on an aggregate, statistical view of evolution; whereas he prefers mechanistic models. Moreover, in a review of Dennett’s, 1995 book “Darwin’s Dangerous Idea,” Maynard Smith writes: “Dennett’s central thesis is that evolution by NS is an algorithmic process. An algorithm is defined in the OED as “a procedure or set of rules for calculation and problem-solving” (Maynard Smith, 1996). The rules must be so simple and precise that it does not matter whether they are carried out by a machine or an intelligent agent; the results will be the same. He emphasizes three features of an algorithmic process. First, “substrate neutrality”: arithmetic can be performed with pencil and paper, a calculator made of gear wheels or transistors, or even, as was hilariously demonstrated at an open day at one of the authors son’s school, jets of water. It is the logic that matters, not the material substrate. Second, mindlessness: each step in the process is so simple that it can be carried out by an idiot or a cogwheel. Third, guaranteed results: whatever it is that an algorithm does, it does every time (although, as Dennett emphasizes, an algorithm can incorporate random processes, and so can generate unpredictable results)”. Clearly, Price’s approach does not give an algorithmic view of evolution. Price’s equation is dynamically insufficient. It is a very high level (a computational level) description of how frequencies of traits should change as a function of covariance between traits and their probability of transmission, and other transmission bias effects that alter traits. It does not constrain the dynamical equations that should determine transmission from one generation to another, i.e., it is not an algorithmic description.

In fact, Price’s aim was to have an entirely general, non-algorithmic approach to selection. This has its pros and cons. In a paper published well after his death, Price (1995) writes: “Two different main concepts of selection are employed in science… Historically and etymologically, the meaning select (from se-aside + legere to gather or collect) was to pick out a subset from a set according to a criterion of preference or excellence. This we will call subset selection… Darwin introduced a new meaning (as Wallace, 1916, pointed out to him), for offspring are not subsets of parents but new entities, and Darwinian NS… does not involve intelligent agents who pick out… These two concepts are seemingly discordant. What is needed, in order to make possible the development of a general selection theory, is to abstract the characteristics that Darwinian NS and the traditional subset selection have in common, and then generalize” (Price, 1995, p. 390). It is worth quoting Gardner (2008) who, in a primer on the Price equation, writes: “The importance of the Price equation lies in its scope of application. Although it has been introduced using biological terminology, the equation applies to any group of entities that undergoes a transformation. But despite its vast generality, it does have something interesting to say. It separates and neatly packages the change due to selection versus transmission, giving an explicit definition for each effect, and in doing so it provides the basis for a general theory of selection. In a letter to a friend, Price explained that his equation describes the selection of radio stations with the turning of a dial as readily as it describes biological evolution” (Gardner, 2008, p. R199). In short, the Price equation was not intended to be specific to biological selection; hence it is no miracle that it cannot substitute for replicator dynamics.

Before we move on we have to show how this generalized view of selection exactly coincides with the view of how the neuronal groups of Edelman are thought to increase or decrease in weight (Figure 1).

FIGURE 1

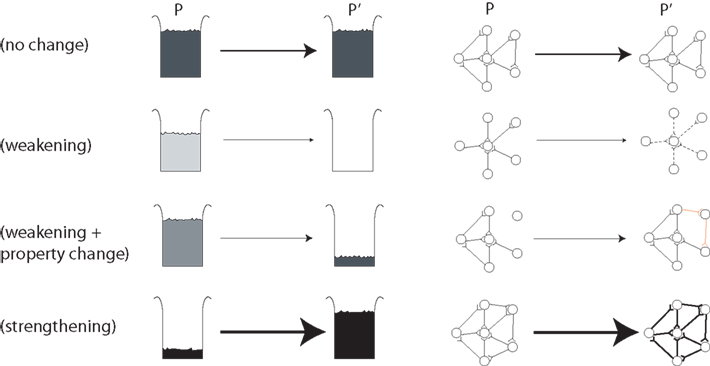
Figure 1. The general selection model of price (left) and its application to neuronal groups (right).

A population P of beakers contains amounts w_i of solution of varying concentrations x_i (dark = high concentration, light = low concentration). In standard selection for higher concentration liquid, low concentration liquids have a lower chance of transmission to the next generation P′ (top two rows). In “Darwinian selection” two elements are added. The first is the capacity for property change (or transmission bias), see row 3 in which the liquid is “mutated” between generations. The second is strengthening in which the offspring can exceed parents in number and mass, see row 4 in which the darkest liquid has actually increased in quantity. To quote Price (1995): “Selection on a set P in relation to property x is the act or process of producing a corresponding set P′ in a way such that the amounts w_i′ (or some function of them such as the ratios w_i′/w_i) are non-randomly related to the corresponding x_i values.” (p. 392). The right side of Figure 1 shows one interpretation of neuronal groups within the same general selection framework in which the traits are the pattern of connectivity of the neuronal group, and the amounts are the probability of activation of that neuronal group. In the top row there is no change in the neuronal group between populations P and P′. In the second row the neuronal group is weakened, shown as lighter synaptic connections between neurons, although the trait (connectivity pattern) does not change. In the third row the neuronal group is weakened (reduced probability of being activated) but is also “mutated” or undergoes property change (transmission bias) with the addition of two new synaptic connections in this case. In the final row a neuronal group with the right connectivity but a low probability of being activated gets strengthened. We conclude that Edelman’s theory of NGS is firmly selectionist in this sense of Price!

What is then the approach that is more mechanistic, suggestive of an algorithm that could come as a remedy? We suggest it is the units of evolution approach. There are several alternative formulations (itself a nice area of study); here we opt for Maynard Smith’s formulation that seems to us the most promising for our present purposes. JMS (Maynard Smith, 1986) defined a unit of evolution as any entity that has the following properties. The first property is multiplication; the entity produces copies of itself that can make further copies of themselves: one entity produces two, two entities produce four, four entities produce eight, in a process known as autocatalytic growth. Most living things are capable of autocatalytic growth, but there are some exceptions, for example, sterile worker ants and mules do not multiply and so whilst being alive, they are not units of evolution (Szathmary, 2000; Gánti, 2003; Szathmáry, 2006). The second requirement is inheritance, i.e., there must be multiple possible kinds of entity, each kind propagating itself (like begets like). Some things are capable of autocatalytic growth and yet do not have inheritance, for example fire can grow exponentially for it is the macroscopic phenomenon arising from an autocatalytic reaction, yet fire does not accumulate adaptations by NS. The third requirement is that there must be variation (more accurately: variability): i.e., heredity is not completely exact. If among the hereditary properties we find some that affect the fecundity and/or survival of the units, then in a population of such units of evolution, NS can take place. There is a loose algorithmic prescription here because the definition explicitly refers to operations, such as multiplication, information transmission, variation, fitness mapping, etc. We can conclude that neuronal groups are not units of evolution in this sense. It then follows that the picture portrayed by Edelman cannot be properly named neural Darwinism! This being so despite the fact that it fits Price’s view of general selection, but not specifically Darwinian natural selection. We shall see that this difference causes harsh algorithmic differences in the efficiency of search processes.

Now that we see what is likely to have been behind the disagreements, we would like to consider another aspect in this section: the problem of transmission bias (property change). In biological evolution this can be caused by, for example, environmental change, mutation, or recombination (whenever heredity is not exact). And this can create a problem. Adaptations arise when the covariance term in Eq. 1is significant relative to the transmission bias. One of Crick’s criticisms can again be interpreted in this framework: “I do not consider that in selection the basic repertoire must be completely unchanging, though Edelman’s account suggests that he believes this is usually true at the synaptic level. I do feel that in Edelman’s simulation of the somatosensory cortex (Neural Darwinism, p. 188 onward) the change between an initial confused mass of connections and the final state (showing somewhat distinct neuronal groups) is too extreme to be usefully described as the selection of groups, though it does demonstrate the selection of synapses” (Crick, 1990, p. 13). He also proposes: “If some terminology is needed in relation to the (hypothetical) neuronal groups, why not simply talk about ‘group formation’?” (Crick, 1989, p. 247). First, we concede that indeed there is a problem here with the relative weight of the covariance and transmission bias in terms of the Price formulation. There are two possible answers. One is that as soon as the groups solidify, there is good selection sensu Price in the population of groups. But the more exciting answer is that such group formation is not unknown in evolutionary biology either. One of us has spent by now decades analyzing what is called the major transitions in evolution (Maynard Smith and Szathmáry, 1995). One of the crucial features of major transitions is the emergence of higher-level units from lower level ones, or – to borrow Crick’s phrase – formation of higher units (such as protocells from naked genes or eukaryotic cells from separate microbial lineages). The exciting question is this one: could it be that the formation of Edelman’s groups is somehow analogous to a major transition in evolutionary biology? Surely, it cannot be closely analogous because neuronal groups do not reproduce. But if we take a Pricean view, the answer may turn out to be different. We shall return to this question, we just wet the appetite of the reader now by stating that in fact there is a Pricean approach to major transitions! Indeed, the recent formation of a secondary repertoire of neuronal groups arising from formation and selection of connectivity patterns between neuronal groups appears to be an example of such a transition. However, we note that whether we are referring to the primary repertoire of assemblies, or the secondary repertoire of super assemblies (Perin et al., 2011), there is no replication of these forms at either level in NGS.

A View of the Theory of Synaptic Selection

Although admittedly not in the focus of either Edelman or Crick, it is worthwhile to have a look at synaptic changes to have a clearer view on whether they are subject to selection or evolution, and in what sense. As we have seen, there is a view that selectionism at the level of the synapse is always trivial, but the different expositions have important differences. In this section we briefly look at some of the important alternatives; there is an excellent survey of this and related matters in Weiss (1994).

Changeux (1985), Changeux et al. (1973) in his TSS primarily focuses on how the connectivity of the networks becomes established during epigenesis within the constraints set by genetics, based on functional criteria. There is structural transformation of the networks during this maturation. There is a period of structural redundancy, where the number of connections and even neurons is greater than in the mature system (Figure 2). Synapses can exist in stable, labile, and degenerate form. Selective stabilization of functional connections prunes the redundancy to a considerable degree.

FIGURE 2

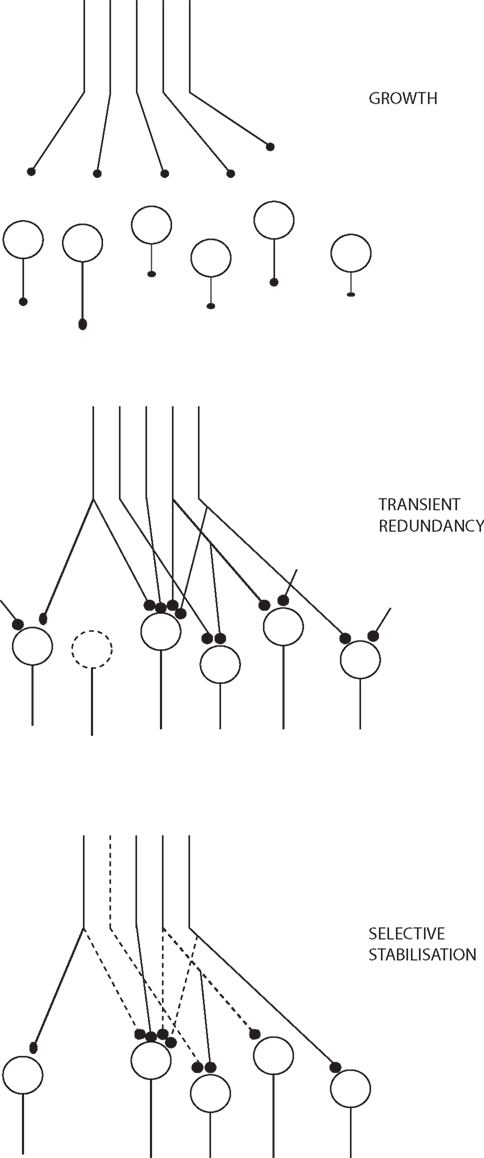
Figure 2. Growth and stabilization of synapses, adapted from Changeux (1985).

The question is again to what extent this is selection or a truly Darwinian process. One can readily object that as it is portrayed the process is a one-shot game. An extended period of redundancy formation is followed by an extended period of functional pruning. Since Darwinian evolution unfolds through many generations of populations of units, the original view offered by Changeux is selectionist, but not Darwinian. Again, the whole picture can be conveniently cast in terms of the Price formulation, however.

If it were not a one-shot game, and there were several rounds of synapse formation and selective stabilization, one could legitimately raise the issue of whether one is dealing with generations of evolutionary units in some sense. But this is exactly the picture that seems to be emerging under the modern view of structural plasticity of the adult brain (Chklovskii et al., 2004; Butz et al., 2009; Holtmaat and Sovoboda, 2009). We shall see in a later section that this view has some algorithmic benefits, but for the time being we consider a formulation of synaptic Darwinism that is a more rigorous attempt to build a mapping between some concepts of neuroscience and evolutionary theory. Adams (1998) proposes (consonant with several colleagues in this field) that synaptic strengthening (LTP) is analogous to replication, synaptic weakening (LTD) is analogous to death (disappearance of the copy of a gene), the input array to a neuron corresponds to the genotype, the specification of the output vector by the input vector is analogous to genotype–phenotype mapping, and a (modified) Hebb rule corresponds to the survival of the fittest (selection; Adams, 1998). There is some confusion, though, in an otherwise clear picture, since Adams proposes that something like an organism corresponds to the kind of bundling one obtains when “all neurons within an array receive the same neuromodulatory signal” (p. 434). Here one is uncertain whether the input vector as the “neuronal genotype” is that of these bundled group of axons, or whether he means the input vector of one neuron, or whether it is a matter of context which understanding applies.

We elaborate a bit on the suggestion that Darwin and Hebb shake hands in a modified Hebb rule. We have shown (Fernando and Szathmáry, 2010) that the Oja rule (a modified Hebb rule) is practically isomorphic to an Eigen equation describing replication, mutation, and selection a population of macromolecules. The Eigen (1971) equation reads:

$\frac{d{x}_i}{dt}=A_i{Q}_i{x}_i+\sum _{j\ne i}^{N_{}}{m}_{ij}{x}_j-\frac{x_i}{c}\sum _{j=1}^{N_{}}\sum _{k=1}^{N_{}}{m}_{ij}{x}_j,$(2)

where x_i is the concentration of sequence i (of RNA for example), m_ij is the mutation rate from sequence j to i, A_i is the gross replication rate of sequence i and Q_i is its copying fidelity, N is the total number of different sequences, and formally m_ij= A_iQ_i. The negative term introduces the selection constraint which keeps total concentration constant at the value of c (which can be taken as unity without loss of generality). The relation between the Oja rule and the Eigen equation is tricky. The Oja rule corresponds to a very peculiar configuration of parameters in the Eigen equation. For example, in contrast to the molecular case, here the off-diagonal elements (the mutation rates) are not by orders of magnitude smaller than the diagonal ones (the fitnesses). Moreover, mutational coupling between two replicators is strictly the product of the individual fitness values! In short, Eigen’s equation can simulate Hebbian dynamics with the appropriate parameter values, but the reverse is not generally true: Oja’s rule could not, for example, simulate the classical molecular quasispecies of Eigen in general. This hints at the more general possibility that although formal evolutionary dynamics could hold widely in brain dynamics, it is severely constrained in parameter space so that the outcome is behaviorally useful. A remarkable outcome of the cited derivation is that although there was no consideration of “mutation” in the original setting, there are large effective mutation rates in the corresponding Eigen equation: this coupling ensures correlation detection between the units (synapses or molecules). (Coupling must be represented somehow: in the Eigen equation the only way to couple two different replicators is through mutation. Hence if a molecular or biological population with such strange mutation terms were to exist, it would detect correlation between individual fitnesses.)

The formalistic appearance of synaptic weight change to mutation might with some justification be regarded as gimmickry, i.e., merely an unhelpful metaphor for anything that happens to change through time. So what could be analogous in the case of synapses to genetic mutations? We believe the obvious analog to genetic mutation is structural synaptic change, i.e., the formation of topologies that did not previously exist. Whereas the Eigen equation is a description of molecular dynamics, it is a deterministic dynamical system with continuous variables in which the full state space of the system has been defined at the onset, i.e., the vector of chemical concentrations. It is worth emphasizing that nothing replicates when one numerically solves the Eigen equation. There are no real units of evolution when one solves the Eigen equation, instead the Eigen equation is a model of the concentration changes that could be implemented by units of evolution. It is a model of processes that occur when replicators exist. Real mutation allows the production of entities that did not previously exist, i.e., it allows more than mere subset selection. For example this is the case where the state space being explored is so large that it can only be sparse sampled, e.g., as in a 100 nucleotide sequence, and it is also the case when new neuronal connectivity patterns are formed by structural mutation.

In Hebbian dynamics there are also continuous variables, but in the simplest case there is only growth and no replication of individuals. As Adams put it, “the synaptic equivalent of replication is straightforward… It corresponds to strengthening. If a synapse becomes biquantal, it has replicated” (Adams, 1998, p. 421). Yet this is different from replication in evolution where the two copies normally separate from each other. This aspect will turn out to be crucially important later when we consider search mechanisms.

Adams draws pictures of real replication and mutation of synapses (Figure 3) also. Clearly, these figures anticipate component processes of the now fashionable structural plasticity (Chklovskii et al., 2004). It is this picture that is closely analogous to the dynamics of replicators in evolution. In principle this allows for some very interesting, truly Darwinian dynamics.

FIGURE 3

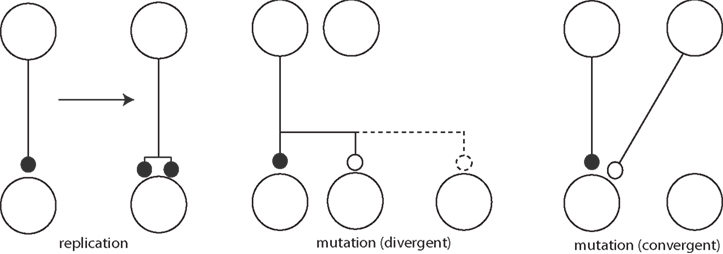
Figure 3. Synaptic mutation replication (left) and synaptic mutations (right), adapted from Adams (1998).

The last item in this section is the concept of a “hedonistic synapse” by Seung (2003). This hypothetical mechanism was considered in the context of reinforcement learning. The learning rule is as follows: (1) the probability of release is increased if reward follows release and is decreased if reward follows failure, (2) the probability of release is decreased if punishment follows release and is increased if punishment follows failure. Seung writes: “randomness is harnessed by the brain for learning, in analogy to the way genetic mutation is utilized by Darwinian evolution” (p. 1063) and that “dynamics of learning executes a random walk in the parameter space, which is biased in a direction that increases reward. A picturesque term for such behavior is “hill-climbing,” which comes from visualizing the average reward as the height of a landscape over the parameter space. The formal term is “stochastic gradient ascent” ” (p. 1066). This passage is of crucial importance for our discussion of search algorithms in this paper. The analogy seems to be crystal-clear, especially since it can be used to recall the notion of an “adaptive landscape” by Wright (1932), arguably the most important metaphor in evolution (Maynard Smith, 1988). We shall see later that Seung’s synapse may be hedonistic, but not Darwinian.

Selection in Groups of Neurons

We have already touched upon the functioning of the dynamics of neuronal groups as portrayed by Edelman (1987). We shall come back to one key element of NGS at the end of this section.

Now we turn to a complementary approach offered by Changeux (1985), the Theory of Selective Stabilization of Pre-representations (TSSP), which builds on TSS. TSSP elaborates on the question how somatic selection contributes to the functioning of the adult brain (Changeux et al., 1984; Heidmann et al., 1984), i.e., after transient redundancy has been functionally pruned. The first postulate of TSSP is that there are mental object (representations) in the brain, which is a physical state produced by an assembly (group) of neurons. Pre-representations are generated before and during interaction with the environment, and they come in very large numbers due to the spontaneous but correlated activity of neurons. Learning is the transformation, by selective stabilization, of some labile pre-representations into stored representations. Primary percepts must resonate (in space or time) with pre-representations in order to become selected. To quite him: “These pre-representations exist before the interaction with the outside world. They arise from the recombination of pre-existing sets of neurons or neuronal assemblies, and their diversity is thus great. On the other hand, they are labile and transient. Only a few of them are stored. This storage results from a selection!” (Changeux, 1985, p. 139). No explanation is given of how a beneficial property of one group would be transmitted when it is “recombined” with another group. The reticular formation is proposed to be responsible for the selection, by re-entry of signals from cortex to thalamus and back to cortex, which is a means of establishing resonance between stored mental objects and percepts.

Changeux assumes the formation of pre-representations occurs spontaneously from a large number of neurons such that the number of possible combinations is astronomical, and that this may be sufficient to explain the diversity of mental representations, images, and concepts. But how can such a large space of representations be searched rapidly and efficiently? Changeux addresses this by suggesting that heuristics act on the search through pre-representations, notably, he allows recombination between neuronal assemblies, writing “this recombining activity would represent a ‘generator of hypotheses,’ a mechanism of diversification essential for the geneses of pre-representations and subsequent selection of new concepts.” (Changeux, 1985, p167). However, no mechanism for recombination of functions is presented.

Changeux and Dehaene (1989) offer a unified account of TSS and TSSP and their possible contributions to cognitive functions. “The interaction with the outside world would not enrich the landscape, but rather would select pre-existing energy minima or pre-representations and enlarge them at the expense of other valleys.” (p. 89). In an elegant model of temporal sequence learning, Dehaene et al. (1987) show that “In the absence of sensory inputs, starting from any initial condition, sequences are spontaneously produced. Initially these pre-representations are quasirandom, although they partially reveal internal connectivity, but very small sensory weights (inferior to noise level) suffice to influence these productions.” (p. 2731). “The learnable sequences must thus belong both to the pre-representations and to the sensory percepts received” (pp. 2730–2731). Noise plays a role in the dynamics of the system.

Later models incorporate stabilization of the configurations in a global workspace by internal reward and attention signals (Dehaene et al., 1998). In a model of the Stroop task, a global workspace is envisaged as having a repertoire of discrete activation patterns, only one of which can be active at once, and which can persist independent of inputs with some stability. This is meant to model persistent activity of neurons in prefrontal cortex. These patterns constitute the selected entity (pre-representation), which “if negatively evaluated, or if attention fails, may be spontaneously and randomly replaced.” Reward allows restructuring of the weights in the workspace. The improvement in performance depends on the global workspace having sufficient variation in patterns at the onset of the effortful task, perhaps with additional random variability, e.g., Dehaene and Changeux (1997) write that “in the absence of specific inputs, prefrontal clusters activate with a fringe of variability, implementing a ‘generator of diversity’.” The underlying search algorithm is nothing more sophisticated than a random walk through pre-representation space, biased by reward! It truly stretches one’s imagination how such a process could be sufficient for language learning, for example, which is much more complex than the Stoop task but not effortful in the sense of Changeux and Dehaene.

A final note on a common element of the similar theories of Changeux and Edelman is in order. Sporns and Edelman (1993) present a tentative solution the Bernstein problem in the development of motor control. Besides the already discussed selective component processes of NGS, they state: “The ‘motor cortex’ generates patterns of activity corresponding to primary gestural motions through a combination of spontaneous activity (triggered by a component of Gaussian noise) and by responses to sensory inputs from vision and kinesthetic signals from the arm.” Thus noise is again a source of the requisite variety (p. 971).

So, again, “how much” Darwinism is there in these theories? Changeux and Dehaene (1989) insist: “the thesis we wish to defend in the following is the opposite; namely, that the production and storage of mental representations, including their chaining into meaningful propositions and the development of reasoning, can also be interpreted, by analogy, in variation–selection (Darwinian) terms within psychological time-scales.” We actually agree with that, but the trouble is that algorithmically the search mechanisms they present are very different from that of any evolutionary algorithm proper, and seem to correspond to stochastic gradient ascent, as explained by Seung (2003) for his hedonistic synapses, even if there is a population of stochastic hill-climbers. Something is crucially missing!

Combinatorial Chemistry Versus in vitro Selection of Functional Macromolecules

The reader might think that this is a digression. Not so, there are some crucial lessons to be learnt from this example. The production of functional molecules is critical for life and also for an increasing proportion of industry. It is also important that genes represent what in cognitive science has been called a “physical symbol system” (Fodor and Pylyshyn, 1988; Nilsson, 2007; Fernando, 2011a). Today, the genetic code is an arguably symbolic mapping between nucleotide triplets and amino acids (see Maynard Smith, 2000 for a characteristically lucid account of the concept of information in biology; Maynard Smith, 2000). Moreover, enzymes “know” how to transform a substrate into a product, much like a linguistic rule “knows” how to act on some linguistic constructions to produce others. How can such functionality arise? We must understand both, how the combinatorial explosion of possibilities (sequences) is generated, and how selection for adaptive sequences is implemented.

Combinatorial chemistry is one of the possible approaches. The aim is to generate-and-test a complete library of molecules up to a certain length. The different molecules must be tested for functionality, be identified as distinct sequences, and then amplified for lab or commercial production. It is easy to see that this approach is limited by combinatorial explosion. Whereas complete libraries of oligopeptides can be produced, this is impossible for polypeptides (proteins). The snag is that enzymes tend to be polymers. For proteins, there are 20¹⁰⁰ possible polypeptide sequences of length 100, which equal 10¹³⁰, a hyper-astronomically large number. In any realistic system an extremely tiny fraction of these molecules can be synthesized. The discrete space of possible sequences is heavily under-occupied, or – to use a phrase that should ring a bell for neuroscientists – sparsely populated. In order to look for functional sequences one needs an effective search mechanism. That search mechanism is in vitro genetics and selection. Ultimately, it is applied replicator dynamics. This technology yielded spectacular results. We just mention the case of ribozymes, catalytic RNA molecules that are very rare in contemporary biochemistry but may have been dominating in the “RNA world” before the advent of the genetic code (c.f. Maynard Smith and Szathmáry, 1995). An impressive list of such ribozymes has been generated by in vitro evolution (Ellington et al., 2009).

Of course, the mapping of RNA sequence to a functional 3D molecule is highly degenerate, meaning that many different sequences can perform the same function. But what does this mean in terms of the probability of finding a given function in a library of random RNA molecules? The number of random sequences in a compositionally unbiased pool of RNA molecules, 100 nucleotides long, required for a 50% probability of finding at least one functional molecule is, in the case of the isoleucine aptamer on the order 10⁹, and in case of the hammerhead ribozyme on the order of 10¹⁰ (Knight et al., 2005). This is now regarded as an inflated estimate, due to the existence of essential but not conserved parts (Majerfeld et al., 2010); thus the required numbers are at least an order of magnitude larger. Note that these are simple functionalities: the first case is just binding rather than catalysis, and the second case is an “easy” reaction to catalyze for RNA molecules. Simulation studies demonstrate that when mutation and selection are combined, a very efficient search for molecular functionality is possible: typically, 10,000 RNA molecules going through about a 100 generations of mutation and selection are sufficient to find, and often fix, the target (Stich and Manrubia, 2011).

The reason for us presenting the molecular selection/evolution case is as follows. Given the unlimited information potential of the secondary repertoire, configurations from which can only be sparsely sampled as in RNA sequence space, the advantages of Darwinian search are likely to also apply. Molecular technologies show that parallel search for molecular functionalities is efficient with replication with mutation and selection if the search space is vast, and occupation of sequence space is sparse. We shall return to the algorithmic advantages of this paradigm later.

Synapses, Groups, and Multilevel Selection

We have already raised the issue whether the developmental origin and consolidation of neuronal groups might be analogous in some sense to the major transitions in evolution. Based on the foregoing analysis this cannot apply in the Darwinian sense since while synapses can grow and reproduce in the sense of Adams (1998), neuronal groups do not reproduce. Yet, the problem is more tricky than this, because – as we have seen – selection does apply to neuronal groups in terms of the Price equation, and the Price equation has been used to describe aspects of multilevel selection (Heisler and Damuth, 1987; Damuth and Heisler, 1988), including those of the major transitions in evolution (Okasha, 2006). In concrete terms, if one defines a Price equation at the level of the groups, the effect of intra-group selection can be substituted for the transmission bias (see Marshall, 2011 for a technical overview), which makes sense because selection within groups effectively means group identity can be changed due to internal dynamics.

As Damuth and Heisler (1988) write: “A multilevel selection situation is one in which we wish to consider simultaneously selection occurring among entities at two or more different levels in a nested biological hierarchy (such as organisms within groups)” (p. 408). “There are two perspectives in this two-level situation from which we may ask questions about selection. First, we may be interested in the relative fitnesses of the individuals and in how their group membership may affect these fitnesses and thus the evolution of individual characters in the whole population of individuals. Second, we may be interested in the changing proportions of different types of groups as a result of their different propensities to go extinct or to found new groups (i.e., the result of different group fitnesses); of interest is the evolution of group characters in the population of groups. In this case, we have identified a different kind of fitness than in the first, a group-level fitness that is not simply the mean of the fitnesses of the group’s members. Of course, individual fitnesses and group fitnesses may be correlated in some way, depending on the biology. But in the second case we are asking a fundamentally different question that requires a focus on different properties – a question explicitly about differential success of groups rather than individuals” (p. 409). It is now customary to call these two perspectives multilevel selection I (MLS1) and multilevel selection II (MLS2) in the biological literature. In the view of Okasha (2006) major transitions can be mirrored by the degree to which these two perspectives apply: in the beginning there is MLS1, and in the end there is MLS2. In between he proposes to have intermediates stages where “collective fitness is not defined as average particle fitness but is proportional to average particle fitness” (p. 238).

It is tempting to apply this picture to the synapses → neuronal group transition, but one should appreciate subtle, tacit assumptions of the evolutionary models. Typically it is assumed that in MLS1 the groups are transient, that there is no population structure within groups, and that each generation of new groups is formed according to some probabilistic distribution. However, in the brain the process does not begin with synapses reproducing before the group is formed, since the topology and strength of synaptic connections defines the group. Synapses, even if labile, are existing connections not only topologically, but also topographically.

In sum, one can formally state that there is a major transition when neuronal groups emerge and consolidate in brain dynamics, and that there are two levels of selection, but only if one adopts a generalized (as opposed to strictly Darwinian) Pricean view of the selection, since neither neurons nor neuronal groups replicate. It is also worth saying that a formal analysis of synapses and groups in terms the Price equation, based on dynamical simulations of the (emerging) networks has never been performed. We might learn something by such an exercise.

Darwinian and Bayesian Dynamics

Many have drawn analogies between learning and evolution. Bayesian inference has proven a very successful model to characterize aspects of brain function at the computational level, as have Darwinian dynamics accounts for evolution of organisms at the algorithmic level. It is natural to seek a relationship between the two. A few people (Zhang, 1999; Harper, 2009; Shalizi, 2009) have realized the connection in formal terms. Here we follow Harper’s (2009) brief and lucid account. Let H₁, H₂ …, H_n be a collection of hypotheses; then according to Bayes’ theorem:

$P\left(H_i\text{|}E\right)=\frac{P\left(E\text{|}{H}_i\right)P\left(H_i\right)}{P\left(E\right)}\text{for}i=1,2,\dots n,$(3)

where the process iteratively adjusts the probability of the hypotheses in line with the evidence from each new observation E. There is a prior distribution [P(H₁), …, P(H_n)], the probability of the event given a hypothesis is given by P(E|H_i), P(E) serves as normalization, and the posterior distribution is [P(H₁|E), …, P(H_n|E)]. Compare this with the discrete-time replicator equation:

$x_i^{\prime }=\frac{x_i{f}_i\left(x\right)}{f\left(x\right)},\text{for}i=1,2,\dots ,n,$(4)

where x_i is the relative frequency of type in the population, prime means next generation, and f_i is its per capita fitness that in general may depend on the population state vector x. (Note that this is a difference to Eq. 3where the probability of a hypothesis does not depend on any other hypothesis). It is fairly straightforward to appreciate the isomorphism between the two models. Both describe at a purely computational (not algorithmic) level what happens during Bayesian reasoning and NS, and both equations have the same form. The following correspondences apply: prior distribution ←→ population state now, new evidence ←→ fitness landscape, normalization ←→ mean fitness, posterior distribution ←→ population state in the next generation. This isomorphism is not vacuously formalistic. There is a continuous-time analog of the replicator Eq. 4, of which the Eigen Eq. 2is a concrete case. It can be shown that the Kullback–Leibler information divergence between the current population vector and the vector corresponding to the evolutionarily stable state (ESS) is a local Lyapunov function of the continuous-time replicator equation; the potential information plays a similar role for discrete-time dynamics in that the difference in potential information between two successive states decreases in the neighborhood of the ESS along iteration of the dynamic. Moreover, the solutions of the replicator Eq. 4can be expressed in terms of exponential families (Harper, 2009), which is important because exponential families play an analogous role in the computational approach to Bayesian inference.

Recalling that we said that Darwinian NS that takes place when there are units of evolution is an algorithm that can do computations described by the Eigen equation, one feels stimulated to raise the idea: if the brain is computationally a Bayesian device, than it might be doing Bayesian computation by using a Darwinian algorithm (a “Darwin machine”; Calvin, 1987) containing units of evolution. Given that it is also having to search in a high dimensional space, perhaps the same benefits of a Darwinian algorithm will accrue? The isomorphisms do not give direct proof of this, because of the following reason. Whereas Eq. 3 is a Bayesian calculation, Eq. 4is not an evolutionary calculation, it is a model of a population doing, potentially, an evolutionary calculation.

Our recently proposed neuronal replicator hypothesis (NRH) states that there are units of evolution in the brain (Fernando et al., 2008, 2010). If the NRH holds any water, the brain must harbor real replicators, not variables for the frequencies of replicators. In other words, there must be information transfer between units of evolution. This is crucially lacking in Edelman’s proposal of Neural Darwinism. It is molecules and organisms that can evolve, not population counts thereof. Of course, based on the foregoing it must be true that replicating populations can perform Bayesian calculations with appropriate parameters and fitness landscapes. Is any advantage gained from this insight? The answer seems to be yes. Kwok et al. (2005) show the advantages of an evolutionary particle filter algorithm to alleviate the sample impoverishment problem; Muruzábal and Cotta (2007) present an evolutionary programming solution to the search for Bayesian network graph structures; Myers et al. (1999) report a similar study (see Figure 4); Strens (2003) shows the usefulness of evolutionary Markov-Chain Monte Carlo (MCMC) sampling and optimization; and Huda et al. (2009) report on a constraint-based evolutionary algorithm approach to expectation minimization that does not get trapped so often in local optima. Thus it seems that not only can evolutionary algorithms do Bayesian inference, for complex problems they are likely to be better at it. In fact, Darwinian algorithms have yet to be fully investigated within the new field of rational process models that study how optimal Bayesian calculations can be algorithmically approximated in practice (Sanborn et al., 2010).

FIGURE 4

Figure 4. Crossover operation for Bayesian networks. Adapted from Myers et al. (1999).

A burning question is how Bayesian calculations can be performed in the brain. George and Hawkins (2009) present a fairly detailed, but tentative account in terms of cortical microcircuits. Recent work by Nessler et al. (2009) shows that Bayesian computations can be implemented in spiking neural networks with first order spike-time-dependent plasticity (STDP). Another possibility is the implementation of Deep Belief Networks which carry out approximate hierarchical Bayesian inference (Hinton et al., 2006). The research program for NRH is to do the same for evolutionary computation, and to determine whether Bayesian inference may be carried out in a related way.

Darwinian Dynamics and Optimization

One could object to using NS in the neurobiological context that it is an imperfect search algorithm since there is no guarantee that the optimal solution can be found; the population might get stuck on a local instead of a global peak. This is true but by itself irrelevant. No search algorithm is perfect in this sense. The question is whether we on average gain something important in comparison with other search algorithms. “It is true that the optimization approach starts from the idea, already familiar to Darwin, Wallace, and Weismann… that adaptation is a pervasive feature of living organisms, and that it is to be explained by NS. It is not our aim to add to this claim that adaptation is perfect. Rather, the aim is to understand specific examples of adaptation, in terms of selective forces and the historical and developmental constraints operating. This requires that we have an explicit model, in each specific case, that tells us what to expect from a given assumption… We distinguish between general models and specific models, though in reality they form part of a continuum. General models have a heuristic function; they give qualitative insights into the range and forms of solution for some common biological problem. The parameters used may be difficult to measure biologically, because the main aim is to make the analysis and conclusions as simple and direct as possible” (Parker and Maynard Smith, 1990, p. 27).

Evolution by NS is an optimum-seeking process, but this does not guarantee that it will always find it. There are constraints on adaptation (which can be genetic, developmental, etc.) but the living world is full of spectacular adaptations nevertheless. And in many cases the solution is at, or very close to, the engineering optimum. For example, many enzymes are optimally adapted in the sense that the rate of catalysis is now constrained by the diffusion rates of substrates and products, so in practical terms those enzymes cannot be faster than they are. It is the same for senses (photon detection by the eye), or the boosted efficiency of photosynthesis by quantum entanglement. True, performance just has to be “good enough,” but good enough means relative to the distribution in the population, but as selection acts, the average is increasing, so the level of “good enough” is raising as well, as standard population genetics demonstrates (e.g., Maynard Smith, 1998). It is in this sense that we believe the applicability of evolutionary models of brain function warrant serious scrutiny, even if for the time being their exploration is at the rather “general” level.

A non-trivial aspect of neuronal groups is degeneracy (Edelman, 1987): structurally different networks can do the same calculations. Usually degeneracy is not a feature of minimalist models but it is certainly important for dynamics. Changeux and Dehaene (1989) called attention to this in their landmark paper: “In the course of the proposed epigenesis, diversification of neurons belonging to the same category occurs. Each one acquires its individuality or singularity by the precise pattern of connections it establishes (and neurotransmitters it synthesizes)… A major consequence of the theory is that the distribution of these singular qualities may also vary significantly from one individual to the next. Moreover, it can be mathematically demonstrated that the same afferent message may stabilize different connective organizations, which nevertheless results in the same input–output relationships… The variability referred to in the theory, therefore may account for the phenotypic variance observed between different isogenic individuals. At the same time, however, it offers a neural implementation for the often-mentioned paradox that there exists a non-unique mapping of a given function to the underlying neural organization.” (Changeux and Dehaene, 1989, p. 81).

The important point for NRH is that degeneracy plays a crucial role in the evolvability of replicators (Toussaint, 2003; Wagner, 2007; Parter et al., 2008). Evolvability has several different definitions; for our purposes here the most applicable approach is the measure of how fast a population can respond to directional selection. It is known that genetic recombination is a key evolvability component in this regard (Maynard Smith, 1998). It has been found that neutral networks also play a role in evolvability. Neutral networks are a web of connections in genotype space among degenerate replicators having the same fitness in a particular context. By definition two replicators at different nodes of such a network are selectively neutral, but their evolvability may be very different: one may be far, but the other may be close to a “promising” region of the fitness landscape; their offspring might then have very different fitnesses. Parter et al. (2008) show that under certain conditions variation becomes facilitated: random genetic changes can be unexpectedly more frequent in directions of phenotypic usefulness. This occurs when different environments present selective goals composed of the same subgoals, but in different combinations. Evolving replicator populations can “learn” about the deep structure of the landscape so that their variation ceases to be entirely “random” in the classical neo-Darwinian sense. This occurs if there is non-trivial neutrality as described by Toussaint (2003) and demonstrated for gene regulatory networks (Izquierdo and Fernando, 2008). We propose that this feature will turn out to be critical for neuronal replicators if they exist. This is closely related to how hierarchical Bayesian models find deep structure in data (Kemp and Tenenbaum, 2008; Tenenbaum et al., 2011).

Finally, an important aspect is the effect of population structure on the dynamics of evolution (c.f. Maynard Smith and Szathmáry, 1995; Szathmáry, 2011). Previously we (Fernando and Szathmáry, 2009) have noted that neuronal evolutionary dynamics could turn out to be the best field of application of evolutionary graph theory (Lieberman et al., 2005). It has been shown that some topologies speed up, whereas others retard adaptive evolution. Figure 5 shows an example of favorable topologies (selection amplifiers). The brain could well influence the replacement topologies by gating, thereby realizing the most rewarding topologies.

FIGURE 5

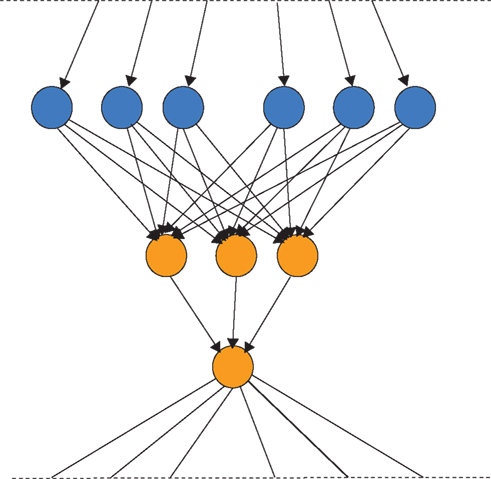
Figure 5. A selection amplifier topology from Lieberman et al. (2005). Vertices that change often, due to replacement from the neighbors, are colored in orange. In the present context each vertex can be a neuron or neuronal group that can inherit its state from its upstream neighbors and pass on its state to the downstream neighbors. Neuronal evolution would be evolution on graphs.

Reinforcement Learning

Thorndike (1911) formulated the “law of effect” stating that beneficial outcomes increase and negative outcomes decrease the occurrence of a particular type of behavior. It has been noted (Maynard Smith, 1986) that there is a similarity between the dynamics of genetic selection and the operant conditioning paradigm of Skinner (1976). Börgers and Sarin (1997) pioneered a formal link between replicator dynamics and reinforcement learning. It could be shown that in the continuous-time limit the dynamics can be approximated by a deterministic replicator equation, formally describing the dynamics of a reinforcement learner.

The most exciting latest development is due to Loewenstein (2011) who shows that if reinforcement follows a synaptic rule that establishes a covariance between reward and neural activity, the dynamics follows a replicator equation, irrespective of the fine details of the model. Let p_i(t) be the probability of choosing alternative i at time t. A simple expression of the dynamics of the probabilities postulates:

$\frac{d{p}_i}{dt}=\eta p_i\left(E\left[R\text{|}A=i\right]-E\left[R\right]\right),$(5)

where η is the learning rate A denotes the action, R is reward, and E[R] is the average return; and the form is that of a continuous-time replicator equation. Probabilities depend on the synaptic weight vector W(t), i.e.,

$p_i\left(t\right)=p_i\left(\mathbf{\text{W}}\left(t\right)\right).$(6)

The learning rule in discrete-time is:

$\Delta p_i\left(t+1\right)=p_i\left(\mathbf{\text{W}}\left(t+1\right)\right)-p_i\left(\mathbf{\text{W}}\left(t\right)\right),$(7)

and the change in synaptic strength in a trial is:

$\Delta \mathbf{\text{W}}=\phi R\left(N-\mathbf{\text{E}}\left[N\right]\right)$(8)

where φ is the plasticity rate and N is any measure of neural activity. The expectation value for this change can be shown to obey:

$\mathbf{\text{E}}\left[\Delta \mathbf{\text{W}}\right]=\phi \text{Cov}\left[R,N\right],$(9)

which is the covariance rule (the form of the synaptic weight change in Eq. 8can take different forms, while the covariance rule still holds). Using the average velocity approximation the stochastic dynamics can be replaced by a deterministic one:

$\frac{d\mathbf{\text{W}}}{dt}=\phi \text{Cov}\left[R,N\right].$

Now we can differentiate Eq. 6 with respect to time, and after several operations we obtain exactly Eq. 5, with a calculable learning rate! This is by definition a selectionist view in terms of Price, and arguably there are units of selection at the synapse level, but no units of evolution, since “mutation” in a sense of an evolutionary algorithm does not play a role in this elegant formulation. There is selection from a given stock, exactly as in many other models we have seen so far, but there is no generation and testing of novelty. NGS does provide a mechanism for the generation and testing of novelty, i.e., the formation of the secondary repertoire and stochastic search at the level of one neuronal group itself. Such dynamics can be seen during the formation and destruction of polychronous groups (Izhikevich, 2006; Izhikevich and Hoppensteadt, 2009) and can be modulated by dopamine based value systems (Izhikevich, 2007).

A relevant comparison is that of evolutionary computation with temporal-difference based reinforcement learning algorithms. Neural Darwinism has been formulated as a neuronal implementation of temporal-difference reinforcement learning based on neuromodulation of STDP by dopamine reward (Izhikevich, 2007). Neuronal groups are considered to be polychronous groups, where re-entry is merely recurrence in a recurrent neural network from which such groups emerge (Izhikevich et al., 2004). An elaboration of Izhikevich’s paper by Chorley and Seth considers extra re-entrant connections between basal ganglia and cortex, showing that further TD-characteristics of the dopaminergic signals in real brains can be captured with this model.

We have made the comparison between temporal-difference learning and evolutionary computation extensively elsewhere (Fernando et al., 2008, 2010; Fernando and Szathmáry, 2009, 2010) and we find that there are often advantages in adding units of evolution to temporal-difference learning systems in terms of allowing improved function approximation and search in the space of possible representations of a state–action function (Fernando et al., 2010). We would also expect that adding units of evolution to neuronal models of TD-learning should improve the adaptive potential of such systems.

Comparing Hill-Climbing and Evolutionary Search

We have argued informally above that in some cases Darwinian NS is superior compared to other stochastic search algorithms that satisfy the Price equation but do not contain units of evolution. Examples of search algorithms are reviewed in the table below.

The left hand column of Table 1 shows the simplest class of search algorithm, solitary search. In solitary search at most two candidate units are maintained at one time. Hill-climbing is an example of a solitary search algorithm in which a variant of the unit (candidate solution) is produced and tested at each “generation.” If the offspring solution’s quality exceeds that of its parent, then the offspring replaces the parent. If it does not, then the offspring is destroyed and the parent produces another correlated offspring. Such an algorithm can get stuck on local optima and does not require replicators for its implementation. For example, it can be implemented by a robot on a mountainous landscape for example. A robot behaving according to stochastic hill-climbing does the same, except that it stays in the new position with a certain probability even if it is slightly lower than the previous position. By this method stochastic hill-climbing can sometimes avoid getting stuck on local optima, but it can also occasionally lose the peak. Simulated annealing is a variant of stochastic hill-climbing in which the probability of accepting a worse solution is reduced over time. Solitary stochastic search has been used by evolutionary biologists such as Fisher to model idealized populations, i.e., where only one mutant exists at any one time in the population (Fisher, 1930). However, a real Darwinian population is a much more complex entity, and cannot be completely modeled by stochastic hill-climbing. Here we should mention Van Belle’s (1997) criticism of Neural Darwinism which makes a subtle point about stochastic search. He points out that replication (units of evolution) permits unmutated parental solutions to persist whilst mutated offspring solutions are generated and tested. If the variant is maladapted, the original is not lost. He claims that such replicators are missing in Neural Darwinism. He demonstrates through a variant of Edelman’s Darwin I simulation that if neuronal groups change without the capacity to revert to their previous form that they cannot even be properly described as undertaking hill-climbing because they cannot revert to the state they were in before taking the unsuccessful exploration step. However, Boltzmann networks (Duda et al., 2001) and other stochastic search processes such as Izhikevich’s (2007) dopamine stabilized reinforcement learning networks and Seung’s (2003) stochastic synapses show that even without explicit memory of previous configurations that optimization is possible. Therefore Van Belle has gone too far in saying that “The individuals of neural Darwinism do not replicate, thus robbing the process of the capacity to explore new solutions over time and ultimately reducing it to random search” because even without replicators, adaptation by stochastic search is clearly possible.

TABLE 1

Table 1. A classification of search (generate-and-test) algorithms of the Pricean and true Darwinian types.

Now consider column two of Table 1. What happens if more robots are available on the hillside for finding the global optimum, or more neuronal groups or synapses are available to explore the space of neural representations? What is an efficient way to use these resources? The simplest algorithm for these robots to follow would be that each one behaves completely independently of the others and does not communicate with the others at all. Each of them behave exactly like the solitary robot obeying whichever solitary strategy (hill-climbing, stochastic hill-climbing, etc.) it was using before. This is achieved by simply having multiple instances of the (stochastic) hill-climbing machinery. Multiple-restart hill-climbing is a serial implementation of this same process. It may be clear to the reader that such an algorithm is likely to be wasteful. If a robot becomes stuck on a local optimum then there would be no way of reusing this robot. Its resources are wasted. One could expect only a linear speed up in the time taken to find a global optimum (the highest peak). It is not surprising that no popular algorithm falls into this wasteful class.

Consider now the third column of Table 1. To continue the robot analogy of search on a fitness landscape, we not only have multiple robots available, but there is competition between robots for search resources (the machinery required to do a generate-and-test step of producing a variant and assessing its quality). In the case of robots a step is moving a robot to a new position and reading the altitude there. Such an assessment step is often the bottleneck in time and processing cost in a real optimization process. If such steps were biased so that the currently higher quality solutions did proportionally more of the search, then there would be a biased search dominated by higher quality solutions doing most of the exploration. This is known as competitive learning because candidate solutions compete with each other for reward and exploration opportunities. This is an example of parallel search with resource competition, shown in column 3 of Table 1. It requires no NS as defined by JMS, i.e., it requires no explicit multiplication of information. No robot communicates its position to other robots. Several algorithms fall into the above category. Reinforcement learning algorithms are examples of parallel search with competition (Sutton and Barto, 1998), see the discussion above about the Pricean interpretation of reinforcement learning. Changeux’s synaptic selectionism also falls into this class (Changeux et al., 1973; Changeux, 1985).

Do such systems of parallel search with competition between synaptic slots exhibit NS? Not according to the definition of JMS because there is no replicator; there is no copying of solutions from one robot to another robot, there is no information that is transmitted between synapses. Resources are simply redistributed between synapses (i.e., synapses are strengthened or weakened in the same way that the stationary robots increase or decrease their exploitation of their current location). Notice, there is no transmission of information between robots (e.g., by recruitment) in this kind of search. Similarly there is no information transfer between synapses in synaptic selectionism. Synaptic selectionism is selection in the Price sense, but not in the JMS sense. Edelman’s TNGS falls into this category also. In a recent formulation of Edelman’s theory of NGS, Izhikevich et al. (2004) shows that there is no mechanism by which functional variations in synaptic connectivity patterns can be inherited (transmitted) between neuronal groups. Neural Darwinism is a class of parallel search with competition but no information transfer between solutions, and is thus fundamentally different from Darwinian NS as defined by JMS.

This leads us to the final column in Table 1. Here is a radically different way of utilizing multiple slots that extends the algorithmic capacity of the competitive learning algorithms above. In this case we allow not only the competition of slots for generate-and-test cycles, but we allow slots to pass information (traits/responses) between each other. Returning to the robot analogy, those robots at the higher altitudes can recruit robots from lower altitudes to come and join them. This is equivalent to replication of robot locations. The currently best location can be copied to other slots. There is transmission of information between slots. Note, replication is always of information (patterns), i.e., reconfiguration by matter of other matter. This means that the currently higher quality slots have not only a greater chance of being varied and tested, but that they can copy their traits to other slots that do not have such good quality traits. This permits the redistribution of information between material slots. Crucially, such a system of parallel search, competition, and information transmission between slots does satisfy JMS’ definition of NS. The configuration of a unit of evolution (slot) can reconfigure other material slots. According to this definition, several other algorithms fall into the same class as NS, e.g., particle swarm optimization (Poli et al., 2007) because they contain replicators.

Algorithmic Advantages of Units of Evolution

Are there algorithmic advantages of the full JMS-type NS compared to independent stochastic hill-climbers or competitive stochastic hill-climbers without information transmission that satisfies only Price’s formulation of NS? We can ask: for what kinds of search problem is a population of replicators undergoing NS with mutation (but no crossover) superior to a population of independent hill-climbers or stochastic hill-climbers competing for resources?

Note, we are not claiming that Edelman’s Neural Darwinism is exactly equivalent to competitive learning or to independent stochastic hill-climbing It cannot be because Hebbian learning and STDP impose many instructed transmission biases that are underdetermined by the transmission bias term in the Price equation at the level of the neuronal group (and in fact, Hebb, and STDP have been interpreted above as Pricean evolution at the synaptic level thus). The claim is that it does not fall into the far right column of Table 1, but is of the same class as competitive learning algorithms that lack replicators.

So to answer first the question of when JMS-type NS is superior to independent stochastic hill-climbing, a shock to the genetic algorithm community came when it was shown that a hill-climber actually outperforms a genetic algorithm on the Royal Road Function (Mitchell et al., 1994). This was in apparent contradiction to the building-block hypothesis which had purported to explain how genetic algorithms worked (Holland, 1975). But later it was shown that a genetic algorithm (even without crossover) could outperform a hill-climber in a problem which contained a local optimum (Jansen et al., 2001). This was thought to be due to the ability for a population to act almost like an ameba at a local optimum, reaching down into a valley and searching the local solutions more effectively. The most recent explanation for the adaptive power of a Darwinian population is that the population is an ideal data structure for representing a Bayesian prior distribution of beliefs about the fitness landscape (Zhang, 1999). Another possible explanation is that replication allows multiple search points to be recruited to the region of the search space that is currently the best. The entire population (of robots) can acquire the response characteristics (locations) of the currently best unit (robot). Once all the robots have reached the currently best peak, they can all do further exploration to find even higher peaks. In many real-world problems there is never a global optimum; rather further mountain ranges remain to be explored after a plateau has been reached. For example, there is no end to science. Not every system that satisfies Price’s definition of selection can have these special properties of being able to redistribute a variant to all search points, i.e., for a solution to reach fixation in a population.

Here we carefully compare the simplest NS algorithm with independent hill-climbers on a real-world problem. Whilst we do not claim to be able to fully explain why NS works better than a population of independent hill-climbers balanced for the number of solution evaluations (no-one has yet fully explained this) we show that in a representative real-world problem, it does significantly outperform the independent hill-climbers.

Intuition and empirical evidence (Mitchell et al., 1994; McIlhagga et al., 1996a,b; Keane and Nair, 2005; De Jong, 2006; Harman and McMinn, 2007), suggest that selectionist, population based search (even without crossover) will often outperform hill-climbing in multimodal spaces (those with multiple peaks and local optima). However, in relatively well-behaved search spaces, for example with many smooth peaks which are easily accessible from most parts of the space, a random multi-start hill-climber may well give comparable or better performance (Mitchell et al., 1994; Harman and McMinn, 2007). But as the complexity of the space increases, the advantages of evolutionary search should become more apparent. We explored this hypothesis by comparing mutation-only genetic algorithms with a number of hill-climbing algorithms on a non-trivial evolutionary robotics (ER) problem. The particular ER task has been chosen because it provides a challenging high dimensional search space with the following properties: noisy fitness evaluations, a highly neutral space with very few widely separated regions of high fitness, and variable dimensionality (Smith et al., 2002a). These properties put it among the most difficult class of search problems. Finally, because it is a noisy real-world sensorimotor behavior-generating task, the search space is likely to share some key properties with those of natural brain-based behavior tasks. We should make it clear we do not believe this is how neural networks actually develop. The aim of this demonstration is to add to the molecular example an example of a problem which contains a realistic behavioral fitness landscape.

The task used in the studies is illustrated in Figure 6. Starting from an arbitrary position and orientation in a black-walled arena, a robot equipped with a forward facing camera must navigate under extremely variable lighting conditions to one shape (a white triangle) while ignoring the second shape (a white rectangle). The robot must successfully complete the task over a series of trials in which the relative position and size of the shapes varies. Both the robot control network and the robot sensor input morphology, i.e., the number and positions of the camera pixels used as input and how they were connected into the network, were under evolutionary control as shown in Figure 6. Evolution took place in a special validated simulation of the robot and its environment which made use of Jakobi’s (1998) minimal simulation methodology whereby computationally very efficient simulations are built by modeling only those aspects of the robot–environment interaction deemed important to the desired behavior and masking everything else with carefully structured noise (so that evolution could not come to rely on any of those aspects). These ultra-fast, ultra-lean simulations allow very accurate transfer of behavior from simulation to reality by requiring highly robust solutions that are able to cope with a wide range of noisy conditions. The one used in this work has been validated several times and transfer from simulation to reality is extremely good. The trade-off in using such fast simulations is that the search space is made more difficult because of the very noisy nature of the evaluations.

FIGURE 6

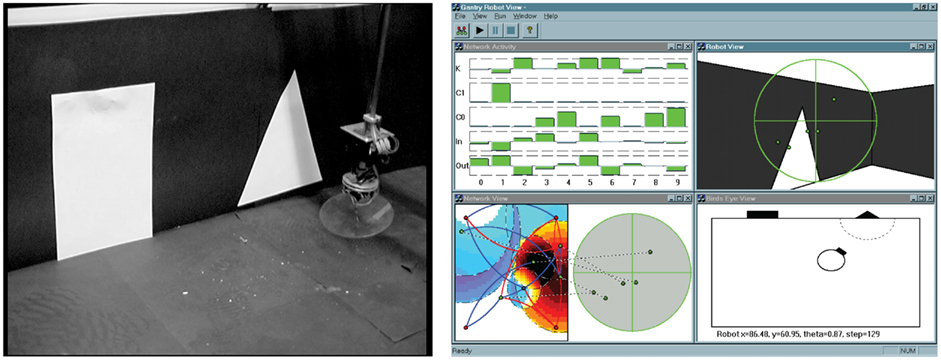
Figure 6. (Left): the gantry robot. A CCD camera head moves at the end of a gantry arm. In the study referred to in the text 2D movement was used, equivalent to a wheeled robot with a fixed forward pointing camera. A validated simulation was used: controllers developed in the simulation work at least as well on the real robot. (Right): the simulated arena and robot. The bottom right view shows the robot position in the arena with the triangle and rectangle. Fitness is evaluated on how close the robot approaches the triangle. The top right view shows what the robot “sees,” along with the pixel positions selected by evolution for visual input. The bottom left view shows how the genetically set pixels are connected into the control network whose gas levels are illustrated. The top left view shows current activity of nodes in the GasNet.

The robot nervous system consists of a GasNet. This form of non-standard neural network has been used as it has previously been shown to be more evolvable (in terms of evaluations required to find a good solution) and to produce search spaces with a high degree of neutrality (Husbands et al., 1998, 2010; Philippides et al., 2005). Hence the problem provides a very challenging but not impossibly difficult search space.

Details of the GasNet, the encoding used, and the fitness function are found in the Appendix. Table 2 summarizes the results of the comparison of search methods on the ER problem. The maximum fitness for the task is 1.0. The average fitness for a randomly generated solution (from which all methods start) is 0.0213 (from a random sample of 100,000). The statistics were gathered over sufficient runs of each method to require 8 million fitness evaluations, making the statistics particularly watertight.

TABLE 2

Table 2. Summary statistic for comparison of the search methods on the ER problem.

DEA and SEA are population based (mutation-only) evolutionary algorithms, RSHC, and its variants are random start stochastic hill-climbing algorithms, PS_SHC consists of a population of independent stochastic hill-climbers in which selection is operating in order to allocate search resources. It is exactly the same as the DEA algorithm except there is no replication. All the algorithms make use of the same set of mutation operators to generate new solutions (offspring). The search algorithms and mutation operators are fully described in the Appendix.

Many variations of all these algorithms were explored (by varying all algorithm parameters, e.g., mutation rates, maximum number of iterations, populations sizes etc.) but the results were not significantly different so only the main representative algorithms are shown here. The distributed population based evolutionary algorithm, DEA, found a solution with a perfect score on every run made (85 runs were needed to ensure the required 8 Million fitness evaluations). On many runs the evolutionary algorithm found perfect solutions in less than 200 generations (20,000 fitness evaluations). Although significantly worse than DEA, SEA was able to find perfect solutions on 55% of runs and reasonably good solutions on all runs. Each random start hill-climbing method required many restarts (often more than 10,000) to secure the 8 Million fitness evaluations needed for comparison. Still none of them were able to find a good solution. PS_SHC produced better solutions than the RSHC methods and in most runs rapidly moved to areas of moderate fitness but was never able to climb to high fitnesses. For further details of the statistical analysis of results see the Appendix.

As the evolutionary algorithms did not use crossover, and all methods used the same mutation functions to produce offspring (new candidate solutions), the advantage of the evolutionary algorithms must lie in their use of selection and replication within a population. This allows partial information on several promising search directions to be held at the same time. Selection allows an automatic allocation of search resources that favors the most promising directions, as represented by the fittest individuals in the population. This accounts for PS_SHC’s superior performance in comparison with the RSHC methods, in particular its rapid movement to moderate fitness areas of the search space. However, it is the combination of selection and replication that generates real search power. Selection pushes search resources toward the currently most promising search directions and replication, biased toward fitter individuals, magnifies this effect by spreading higher fitness fronts throughout the population. Such processes are particularly effective in the DEA where distributed parallel search is always going on at many fronts simultaneously. The geographical distribution, in which local neighborhoods overlap, allows information on promising search directions to rapidly diffuse around the grid on which the population operate, without the need for global control. Such processes are often at play in biological media, which are by nature spatially distributed, and could plausibly operate in neural substrates. The population based distributed nature of the evolutionary search was also instrumental in coping with the high degree of noise in the fitness evaluation. The population is able to “smooth out” the noisy evaluation signal and progress to the higher fitness regions (Arnold and Beyer, 2003; Jin and Branke, 2005). Hill-climbing, with its use of a solitary solution at any one time, could not cope with the noisy, unreliable feedback from the evaluation function (even though it involved averaging over several trials) and could never rise above the low-fitness foothills and neutral plains that occupy most of the search space.

Proposed Neuronal Units of Evolution

Having seen two examples (the molecular and the neural) of the relative efficiency of true evolutionary search, we are ready to pose the question: do units of evolution in the brain exist after all? The answer is that for the time being we do not know. Since neurons do not reproduce, any realization of true Darwinian dynamics beyond the synapse level must be subtle and easy to miss unless sought after with the right paradigm in mind. Here we review two candidate mechanisms for neuronal replication: one replicates local connectivity patterns, the other propagates activity patterns. These models are not for “fitting curves” at this stage; rather, they are meant to stimulate the development of specific models and then experimental tests. They have the status of “toy models” in that they are idealized and very simple.

Previously we have proposed a tentative outline of a means by which a higher-order unit of neuronal evolution above the synaptic level may be able to replicate. The method allows a pattern of synaptic connections to be copied from one such unit to another as shown in Figure 7 (Fernando et al., 2008). Several variants of the mechanism are possible, however the principle remains the same; a copy is made by one neuronal (offspring) region undertaking causal inference of the underlying connectivity of another (parental) neuronal region based on the spike trains the parent emits to the offspring region.

FIGURE 7

Figure 7. Outline of a mechanism for copying patterns of synaptic connections between neuronal groups. The pattern of connectivity from the lower layer is copied to the upper layer. See text.

In the brain there are many topographic maps. These are pathways of parallel connections that preserve adjacency relationships and they can act to establish a one-to-one (or at least a few-to-few) transformation between neurons in distinct regions of the brain. In addition there is a kind of synaptic plasticity called STDP, the same kind of plasticity that Young et al. (2007) used to explain the copying of receptive fields. It works rather like Hebbian learning. Hebb (1949) said that neurons that fire together wire together, which means that the synapse connecting neuron A to neuron B gets stronger if A and B fire at the same time. However, recently it has been discovered that there is an asymmetric form of Hebbian learning (STDP) where if the pre-synaptic neuron A fires before the post-synaptic neuron B, the synapse is strengthened, but if pre-synaptic neuron A fires after post-synaptic neuron B then the synapse is weakened. Thus STDP in an unsupervised manner, i.e., without an explicit external teacher, reinforces potential causal relationships. It is able to guess which synapses were causally implicated in a pattern of activation.

If a neuronal circuit exists in layer A in Figure 7, and is externally stimulated randomly to make its neurons spike, then due to the topographic map from layer A to layer B, neurons in layer B will experience similar spike pattern statistics as in layer A (due to the topographic map). If there is STDP in layer B between weakly connected neurons then this layer becomes a kind of causal inference machine that observes the spike input from layer A and tries to produce a circuit with the same connectivity, or at least that is capable of generating the same pattern of correlations. One problem with this mechanism is that there are many possible patterns of connectivity that generate the same spike statistics when a circuit is randomly externally stimulated to spike. As the circuit size gets larger, due to the many possible paths that activity can take through a circuit within a layer, the number of possible equivalent circuits grows. This can be prevented by limiting the amount of horizontal spread of activity permissible within a layer (Hasselmo, 2006). Our early models used simple error-correction neurons that undertook heterosynaptic depression to eliminate false-positive and false-negative inferences, and using these we found it was possible to evolve networks of 20–30 neurons in size to obtain a particular desired pattern of connectivity. The network with connectivity closest to the desired connectivity was allowed to replicate itself to other circuits. Recently we have shown that error-correction neurons are not needed if sub-threshold depolarization is used such that coincident spikes from the parent layer and the offspring layer are required to activate an offspring layer neuron, Section “Details of a Modified Model for Copying of Patterns of Synaptic Connectivity” in Appendix. Furthermore, use of heterosynaptic competition rules and first order STDP rules (Nessler et al., 2009) allows causal disambiguation (Gopnik and Schulz, 2004). Recently there has been evidence for this kind of copying in neuronal cultures and in the hippocampus of rats navigating routes in a maze (Isaac et al., 2009; Johnson et al., 2010). Further work is required to identify the fidelity of this copying operation in neuronal cultures and slices to determine the size of networks that may be copied by intra-brain causal inference.

Previously William Calvin had proposed that patterns of activity can replicate over hexagonal arrays that extend over the cortex; however there is no evidence for the donut of activation that is needed around each pyramidal cell for this mechanism to properly work, and indeed no model has been produced to demonstrate Calvin’s sketch (Calvin, 1987, 1996; Fernando and Szathmáry, 2009, 2010). This was remedied in our recent paper which proposed an even simpler method of activity replication using bistable neurons, inhibitory gating, and topographic maps (Fernando et al., 2010). This work combines Hebbian learning with the replication operation to allow learning of linkage disequilibrium in a way that would not be possible in genetic evolution. Aunger (2002) has also argued for true neuronal replication although has produced no model. Finally, John Holland in his development of Learning Classifier Systems had in mind a cognitive implementation, but had proposed no model of such an implementation (Holland, 1975; Holland and Reitman, 1977; Holland et al., 1986) although recent work in learning classifier systems has done so (Fernando, 2011a,b). Our latest work shows that paths taken by activity through a neuronal network can be interpreted as units of evolution that overlap and that exhibit mutation and crossover by activity dependent structural plasticity (Fernando et al., 2011). Such units of evolution are serial Darwinian entities rather than parallel ones in the sense that their phenotypes can only be expressed in series and not in parallel. In all other respects they share the characteristics of units of evolution.

Conclusion

Some circumstantial evidence for neuronal replicators exists. For example it has been shown that neuronal response characteristics can replicate. This involves the copying of a functional pattern of input connections from one neuron to another neuron and is a lower-boundary case of replication of synaptic connectivity patterns in small neuronal circuits (Young et al., 2007). Further work is required to examine to what extent more complex response characteristics can be copied. There is evidence that connectivity patterns can be entrained by stimuli (Johnson et al., 2010) and that this can also occur during behavior (Isaac et al., 2009). These mechanisms could be extended for copying of patterns of synaptic connectivity, and undertaking such experiments in neuronal slices and cultures could test the NRH. Our proposal for the evolution of neuronal paths is supported by increasing evidence for activity dependent structural plasticity (Chklovskii et al., 2004). In summary we have distinguished between selectionist and truly Darwinian theories, and have proposed a truly Darwinian theory of Darwinian Neurodynamics. The suggestion that true Darwinian evolution can happen in the brain during, say, complex thinking, or the development of language in children, is ultimately an empirical issue. Three possible outcomes are possible: (i) nothing beyond the synapse level undergoes Darwinian evolution in the brain; (ii) units of evolution will be identified that are very different from our “toy model” suggestions in this paper (and elsewhere); and (iii) some of the units correspond, with more complex details, to our suggested neuronal replicators. The potential significance of the last two options cannot be overrated.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We work was funded by an FP-7 FET OPEN Project E-Flux, and the Hungarian research project (NAP 2005/KCKHA005).

References

Adams, P. (1998). Hebb and Darwin. J. Theor. Biol. 195, 419–438.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Arnold, D., and Beyer, H. (2003). A comparison of evolution strategies with other direct search methods in the presence of noise. Comput. Optim. Appl. 24, 135–159.

CrossRef Full Text

Aunger, R. (2002). The Electric Meme: A New Theory of How We Think. New York: The Free Press.

Barnett, L. (2001). “Netcrawling-optimal evolutionary search with neutral networks,” in Congress on Evolutionary Computation CEC’01 (Seoul: IEEE Press), 30–37.

Bi, G.-Q., and Poo, M.-M. (1998). Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 15, 10464–10472.

Börgers, T., and Sarin, R. (1997). Learning through reinforcement and replicator dynamics. J. Econ. Theory 77, 1–14.

CrossRef Full Text

Buchanan, K. A., and Mellor, J. R. (2010). The activity requirements for spike timing-dependent plasticity in the hippocampus. Front. Synaptic Neurosci. 2:11. doi:10.3389/fnsyn.2010.00011

CrossRef Full Text

Bush, D., Philippides, A., Husbands, P., and O’Shea, M. (2010). Spike-timing dependent plasticity and the cognitive map. Front. Comput. Neurosci. 4:142. doi:10.3389/fncom.2010.00142

CrossRef Full Text

Butz, M., Worgotter, F., and van Ooyen, A. (2009). Activity-dependent structural plasticity. Brain Res. Rev. 60, 287–305.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Calvin, W. H. (1987). The brain as a Darwin machine. Nature 330, 33–34.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Calvin, W. H. (1996). The Cerebral Code. Cambridge, MA: MIT Press.

Changeux, J. P. (1985). Neuronal Man: The Biology of Mind. Princeton: Princeton University Press.

Changeux, J. P., Courrege, P., and Danchin, A. (1973). A theory of the epigenesis of neuronal networks by selective stabilization of synapses. Proc. Natl. Acad. Sci. U.S.A. 70, 2974–2978.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Changeux, J. P., and Dehaene, S. (1989). Neuronal models of cognitive functions. Cognition 33, 63–109.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Changeux, J. P., Heidmann, T., and Patte, P. (1984). “Learning by selection,” in The Biology of Learning, eds P. Marler and H. S. Terrace (New York: Springer), 115–133.

Chklovskii, D. B., Mel, B. W., and Svoboda, K. (2004). Cortical rewiring and information storage. Nature 431, 782–788.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Crick, F. H. C. (1989). Neuronal Edelmanism. Trends Neurosci. 12, 240–248.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Crick, F. H. C. (1990). Reply. Trends Neurosci. 13, 13–14.

CrossRef Full Text

Damuth, J., and Heisler, I. L. (1988). Alternative formulations of multilevel selection. Biol. Philos. 3, 407–430.

CrossRef Full Text

Dawkins, R. (1976). The Selfish Gene. Oxford, UK: Oxford University Press.

De Jong, K. A. (2006). Evolutionary Computation: A Unified Approach. Cambridge, MA: MIT Press.

Dehaene, S., and Changeux, J. P. (1997). A hierarchical neuronal network for planning behaviour. Proc. Natl. Acad. Sci. U.S.A. 94, 13293–13298.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dehaene, S., Changeux, J. P., and Nadal, J. P. (1987). Neural networks that learn temporal sequences by selection. Proc. Natl. Acad. Sci. U.S.A. 84, 2727–2731.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dehaene, S., Kerszberg, M., and Changeux, J. P. (1998). A neuronal model of a global workspace in effortful cognitive tasks. Proc. Natl. Acad. Sci. U.S.A. 95, 14529–14534.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dennett, D. C. (1995). Darwin’s Dangerous Idea. Simon & Schuster.

Duda, R. O., Hart, P. E., and Stork, D. G. (2001). Pattern Classification. New York: John Wiley and Sons, Inc.

Edelman, G., and Gally, J. (2001). Degeneracy and complexity in biological systems. Proc. Natl. Acad. Sci. U.S.A. 98, 13763–13768.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Edelman, G. M. (1987). Neural Darwinism. The Theory of Neuronal Group Selection. New York: Basic Books.

Eigen, M. (1971). Selforganization of matter and the evolution of biological macromolecules. Naturwissenschaften 58, 465–523.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ellington, A. D., Chen, X., Robertson, M., and Syrett, A. (2009). Evolutionary origins and directed evolution of RNA. Int. J. Biochem. Cell Biol. 41, 254–265.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fernando, C. (2011a). Symbol manipulation and rule learning in spiking neuronal networks. J. Theor. Biol. 275, 29–41.

CrossRef Full Text

Fernando, C. (2011b). Co-evolution of lexical and syntactic classifiers during a language game. Evol. Intell. 4, 165–182.

CrossRef Full Text

Fernando, C., Goldstein, R., and Szathmáry, E. (2010). The neuronal replicator hypothesis. Neural Comput. 22, 2809–2857.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fernando, C., Karishma, K. K., and Szathmáry, E. (2008). Copying and evolution of neuronal topology. PLoS ONE 3, e3775. doi:10.1371/journal.pone.0003775

CrossRef Full Text

Fernando, C., and Szathmáry, E. (2009). “Natural selection in the brain,” in Toward a Theory of Thinking, eds B. Glatzeder, V. Goel, and A. von Müller (Berlin: Springer), 291–340.

Fernando, C., and Szathmáry, E. (2010). “Chemical, neuronal and linguistic replicators,” in Towards an Extended Evolutionary Synthesis, eds M. Pigliucci and G. Müller (Cambridge, MA: MIT Press), 209–249.

Fernando, C., Vasas, V., Szathmáry, E., and Husbands, P. (2011). Evolvable paths: a novel basis for information and search in the brain. PLoS ONE 6, e23534. doi:10.1371/journal.pone.0023534

CrossRef Full Text

Fisher, R. A. (1930). The Genetical Theory of Natural Selection. Oxford: Clarendon Press.

Flajnik, M. F., and Kasahara, M. (2010). Origin and evolution of the adaptive immune system: genetic events and selective pressures. Nat. Rev. Genet. 11, 47–59.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fodor, J. A., and Pylyshyn, Z. W. (1988). Connectionism and cognitive architecture: a critical analysis. Cognition 28, 3–71.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Friston, K. J. (2000). The labile brain. I. Neuronal transients and nonlinear coupling. Proc. Trans. R. Soc. Lond. B Biol. Sci. 335, 215–236.

CrossRef Full Text

Friston, K. J., and Buchel, C. (2000). Attentional modulation of effective connectivity from V2 to V5/MT in humans. Proc. Natl. Acad. Sci. U.S.A. 97, 7591–7596.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gánti, T. (2003). The Principles of Life. Oxford, UK: Oxford University Press.

Gardner, A. (2008). The price equation. Curr. Biol. 18, R198–R202.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

George, D., and Hawkins, J. (2009). Towards a mathematical theory of cortical micro-circuits. PLoS Comput. Biol. 5, e1000532. doi:10.1371/journal.pcbi.1000532

CrossRef Full Text

Gopnik, A., Glymour, C., Sobel, D. M., Schulz, L. E., Kushnir, T., and Danks, D. (2004). A theory of causal learning in children: causal maps and bayes nets. Psychol. Rev. 111, 3–32.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gopnik, A., and Schulz, L. (2004). Mechanisms of theory formation in young children. Trends Cogn. Sci. (Regul. Ed.) 8, 371–377.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hamilton, W. D. (1975). “Innate social aptitudes of man: an approach from evolutionary genetics,” in ASA Studies 4: Biosocial Anthropology, ed. R. Fox (London: Malaby Press), 133–153.

Harman, M., and McMinn, P. (2007). “A theoretical and empirical analysis of evolutionary testing and hill climbing for structural test data generation in 2007,” in International Symposium on Software Testing and Analysis (London: ACM), 73–83.

Harper, M. (2009). The replicator equation as an inference dynamic. arXiv:0911.1763.

Hasselmo, M. E. (2006). The role of acetylcholine in learning and memory. Curr. Opin. Neurobiol. 16, 710–715.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hebb, D. O. (1949). The Organization of Behaviour: A Neuropsychological Theory. New York: John Wiley and Sons, 378.

Heidmann, A., Heidmann, T. M., and Changeux, J. P. (1984). Stabilisation selective de representations neuronales par resonance entre “presepresentations” spontanes du reseau cerebral et “percepts.” C. R. Acad. Sci. III Sci. Vie 299, 839–844.

Heisler, I. L., and Damuth, J. (1987). A method for analyzing selection in hierarchically structured populations. Am. Nat. 130, 582–602.

CrossRef Full Text

Hinton, G. E., Osindero, S., and Teh, Y. W. (2006). A fast learning algorithm for deep belief nets. Neural Comput. 18, 1527–1554.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hofbauer, J., and Sigmund, K. (1998). The Theory of Evolution and Dynamical Systems. Cambridge, UK: Cambridge University Press.

Holland, J. H. (1975). Adaptation in Natural and Artificial Systems. Ann Arbor: University of Michigan Press.

Holland, J. H., Holyoak, K. J., Nisbett, R. E., and Thagard, P. (1986). Induction: Processes of Inference, Learning, and Discovery. Cambridge, MA: MIT Press.

Holland, J. H., and Reitman, J. S. (1977). Cognitive systems based on adaptive algorithms. ACM SIGART Bull. 63, 43–49.

Hollander, M., and Wolfe, D. (1999). Non-Parametric Statistical Methods. New York, NY: Wiley.

Holtmaat, A., and Sovoboda, K. (2009). Experience-dependent structural plasticity in the mammalian brain. Nat. Rev. Neurosci. 10, 647–658.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Huda, S., Yearwood, J., and Togneri, R. (2009). A stochastic version of expectation maximization algorithm for better estimation of hidden Markov model. Pattern Recognit. Lett. 30, 1301–1309.

CrossRef Full Text

Husbands, P., Philippides, A., Vargas, P., Buckley, C. L., Fine, P., Di Paolo, E., and O’Shea, M. (2010). Spatial, temporal and modulatory factors affecting GasNet evolvability in a visually guided robotics task. Complexity 16, 35–44.

CrossRef Full Text

Husbands, P., Smith, T., Jakobi, N., and O’Shea, M. (1998). Better living through chemistry: evolving GasNets for robot control. Connect. Sci. 10, 185–210.

CrossRef Full Text

Isaac, J. T. R., Buchanan, K. A., Muller, R. U., and Mellor, J. R. (2009). Hippocampal place cell firing patterns can induce long-term synaptic plasticity in vitro. J. Neurosci. 29, 6840–6850.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Izhikevich, E. M. (2006). Polychronization: computation with spikes. Neural Comput. 18, 245–282.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Izhikevich, E. M. (2007). Solving the distal reward problem through linkage of STDP and dopamine signaling. Cereb. Cortex 17, 2443–2452.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Izhikevich, E. M., and Desai, N. S. (2003). Relating STDP to BCM. Neural Comput. 15, 1511–1523.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Izhikevich, E. M., Gally, J. A., and Edelman, G. M. (2004). Spike-timing dynamics of neuronal groups. Cereb. Cortex 14, 933–944.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Izhikevich, E. M., and Hoppensteadt, F. C. (2009). Polychronous wavefront computations. Int. J. Bifurcat. Chaos 19, 1733–1739.

CrossRef Full Text

Izquierdo, E., and Fernando, C. (2008). “The evolution of evolvability in gene transcription networks,” in Proceedings of the 11th International Conference on Artificial Life, eds S. Bullock, J. Noble, R. A. Watson, and M. A. Bedau (Southampton: MIT Press), 265–273.

Jakobi, N. (1998). Evolutionary robotics and the radical envelope of noise hypothesis. Adapt. Behav. 6, 325–368.

CrossRef Full Text

James, W. (1890). The Principles of Psychology. Dover Publications.

Jansen, T., Wegener, I., and Kaufmann, P. M. (2001). “On the utility of populations in evolutionary algorithms,” in Proceedings of the Genetic and Evolutionary Computation Conference (GECCO), San Francisco, 1034–1041.

Jin, Y., and Branke, J. (2005). Evolutionary optimization in uncertain environments – a survey. IEEE Trans. Evol. Comput. 9, 303–317.

CrossRef Full Text

Johnson, H. A., Goel, A., and Buonomano, D. V. (2010). Neural dynamics of in vitro cortical networks reflects experienced temporal patterns. Nat. Neurosci. 13, 917–919.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Keane, A. J., and Nair, P. B. (2005). Computational Approaches for Aerospace Design: The Pursuit of Excellence. London: John Wiley.

Kemp, C., and Tenenbaum, J. B. (2008). The discovery of structural form. Proc. Natl. Acad. Sci. U.S.A. 105, 10687–10692.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Knight, R., De Sterck, H., Markel, R., Smit, S., Oshmyansky, A., and Yarus, M. (2005). Abundance of correctly folded RNA motifs in sequence space, calculated on computational grids. Nucleic. Acids Res. 33, 5924–5935.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kwok, N. M., Fang, G., and Zhou, W. (2005). “Evolutionary particle filter: re-sampling from the genetic algorithm perspective,” in Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, 1053–1058.

Lieberman, E., Hauert, C., and Nowak, M. (2005). Evolutionary dynamics on graphs. Nature 433, 312–316.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Loewenstein, Y. (2011). Synaptic theory of replicator-like melioration. Front. Comput. Neurosci. 4:17. doi:10.3389/fncom.2010.00017

CrossRef Full Text

Majerfeld, I., Chocholousova, J., Malaiya, V., Widmann, J., McDonald, D., Reeder, J., Iyer, M., Illangasekare, M., Yarus, M., and Knight, R. (2010). Nucleotides that are essential but not conserved; a sufficient L-tryptophan site in RNA. RNA 16, 1915–1924.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Marshall, J. A. R. (2011). Group selection and kin selection: formally equivalent approaches. Trends Ecol. Evol. (Amst.) 26, 325–332.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Maynard Smith, J. (1986). The Problems of Biology. Oxford: Oxford University Press, 144.

Maynard Smith, J. (1988). Obituary Sewall Wright (1889–1988). Nature 332, 492–492.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Maynard Smith, J. (1996). Genes, Memes, and Minds. New York: The New York Review of Books.

Maynard Smith, J. (1998). Evolutionary Genetics. Oxford: Oxford University Press.

Maynard Smith, J. (2000). The concept of information in biology. Philos. Sci. 67, 177–194.

CrossRef Full Text

Maynard Smith, J. (2008). 45 – Price’s Theorem. How Scientists Think. Available at: http://www.webofstories.com/play/7297?o=S&srId=203622

Maynard Smith, J., and Szathmáry, E. (1995). The Major Transitions in Evolution. Oxford: Oxford University Press.

Mazzoni, A., Broccard, F. D., Garcia-Perez, E., Bonifazi, P., Ruaro, M. E., and Torre, V. (2007). On the dynamics of the spontaneous activity in neuronal networks. PLoS ONE 2, e439. doi:10.1371/journal.pone.0000439

CrossRef Full Text

McIlhagga, M., Husbands, P., and Ives, R. (1996a). “A comparison of search techniques on a wing-box optimisation problem,” in Fourth International Conference on Parallel Problem Solving from Nature, eds H. Voigt, H.-P. Schwefel, I. Rechenberg, and W. Ebeling (Berlin: Springer), 614–623.

McIlhagga, M., Husbands, P., and Ives, R. (1996b). “A comparison of optimisation techniques for integrated manufacturing and scheduling,” in Fourth International Conference on Parallel Problem Solving from Nature, eds H. Voigt, H.-P. Schwefel, I. Rechenberg, and W. Ebeling (Berlin: Springer), 604–613.

Michod, R. E. (1988). Darwinian selection in the brain. Evolution 43, 694–696.

CrossRef Full Text

Michod, R. E. (1990). Letter to the editor. Trends Neurosci. 13, 12–13.

CrossRef Full Text

Miles, R. (1990). Synaptic excitation of inhibitory cells by single CA3 pyramidal cells of the guinea pig in vitro. J. Physiol. 428, 61–77.

Pubmed Abstract | Pubmed Full Text

Mitchell, M., Holland, J. H., and Forrest, S. (1994). “When will a genetic algorithm outperform hill climbing?,” in Advances in Neural Information Processing Systems 6, eds J. D. Cowan, G. Tesauro, and J. Alspector (San Mateo: Morgan Kaufmann), 51–58.

Muruzábal, J., and Cotta, C. (2007). A study on the evolution of Bayesian network graph structures. StudFuzz 213, 193–213.

Myers, J. W., Laskey, K. B., and DeJong, K. A. (1999). “Learning Bayesian networks from incomplete data using evolutionary algorithms,” in Fifteen Conference on Uncertainty in Artificial Intelligence, Toronto.

Nadel, L., Campbell, J., and Ryan, L. (2007). Autobiographical memory retrieval and hippocampal activation as a function of repetition and the passage of time. Neural Plast. 2007. doi: 10.1155/2007/90472

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nadel, L., and Moscovitch, M. (1997). Memory consolidation, retrograde amnesia and the hippocampal complex. Curr. Opin. Neurobiol. 7, 217–227.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nadel, L., Samsonovich, A., Ryan, L., and Moscovitch, M. (2000). Multiple trace theory of human memory: computational, neuroimaging, and neuropsychological results. Hippocampus 10, 352–368.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nessler, B., Pfeiffer, M., and Maass, M. (2009). “STDP enables spiking neurons to detect hidden causes of their inputs,” in Proceedings of NIPS Advances in Neural Information Processing Systems (Vancouver: MIT Press).

Nilsson, N. (2007). “The physical symbol system hypothesis: status and prospects,” in 50 Years of AI, ed. M. Lungarella (Springer), 9–17.

Okasha, S. (2006). Evolution and the Levels of Selection. Oxford: Oxford University Press, 288.

Orgel, L. E., and Crick, F. H. C. (1980). Selfish DNA: the ultimate parasite. Nature 284, 604–607.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Parker, G. A., and Maynard Smith, J. (1990). Optimality theory in evolutionary biology. Nature 348, 27–33.

CrossRef Full Text

Parter, M., Kashtan, N., and Alon, U. (2008). Facilitated variation: how evolution learns from past environments to generalize to new environments. PLoS Comput. Biol. 4, e1000206. doi:10.1371/journal.pcbi.1000206

CrossRef Full Text

Perin, R., Berger, T. K., and Markram, H. (2011). A synaptic organizing principle for cortical neuronal groups. Proc. Natl. Acad. Sci. U.S.A. 108, 5419–5424.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Philippides, A., Husbands, P., Smith, T., and O’Shea, M. (2005). Flexible couplings: diffusing neuromodulators and adaptive robotics. Artif. Life 11, 139–160.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Poli, R., Kennedy, J., and Blackwell, T. (2007). Particle swarm optimization: an overview. Swarm Intell. 1, 33–57.

CrossRef Full Text

Price, G. R. (1970). Selection and covariance. Nature 227, 520–521.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Price, G. R. (1995). The nature of selection. J. Theor. Biol. 175, 389–396.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Prügel-Bennett, A. (2004). When a genetic algorithm outperforms hill-climbing. Theor. Comp. Sci. 320, 135–153.

CrossRef Full Text

Sanborn, A. N., Griffiths, T. L., and Navarro, D. J. (2010). Rational approximations to rational models: alternative algorithms for category learning. Psychol. Rev. 117, 1144–1167.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Seung, S. H. (2003). Learning in spiking neural networks by reinforcement of stochastic synaptic transmission. Neuron 40, 1063–1973.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shalizi, C. R. (2009). Dynamics of Bayesian updating with dependent data and mis-specified models. Electron. J. Stat. 3, 1039–1074.

CrossRef Full Text

Skinner, B. F. (1976). About Behaviourism. Vintage.

Smith, T., Husbands, P., Layzell, P., and O’Shea, M. (2002a). Fitness landscapes and evolvability. Evol. Comput. 1, 1–34.

CrossRef Full Text

Smith, T., Husbands, P., Philippides, A., and O’Shea, M. (2002b). Neuronal plasticity and temporal adaptivity: GasNet robot control networks. Adapt. Behav. 10, 161–184.

CrossRef Full Text

Smith, T. M. C., Husbands, P., and O’Shea, M. (2003). Local evolvability of statistically neutral GasNet robot controllers. Biosystems 69, 223–243.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Song, S., and Abbott, L. (2001). Cortical development and remapping through spike timing-dependent plasticity. Neuron 32, 339–350.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Song, S., Miller, K. D., and Abbott, L. (2000). Competitive Hebbian learning through spike-timing dependent synaptic plasticity. Nat. Neurosci. 3, 919–926.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sporns, O., and Edelman, G. M. (1993). Solving Bernstein’s problem: a proposal for the development of coordinated movement by selection. Child Dev. 64, 960–981.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sporns, O., and Kotter, R. (2004). Motifs in brain networks. PLoS Biol. 2, e369. doi:10.1371/journal.pbio.0020369

CrossRef Full Text

Stich, M., and Manrubia, S. (2011). Motif frequency and evolutionary search times in RNA populations. J. Theor. Biol. 280, 117–126.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Strens, M. J. A. (2003). “Evolutionary MCMC sampling and optimization in discrete spaces,” in Proceedings of the Twentieth International Conference on Machine Learning (ICML-2003), Washington, DC.

Sutton, S. R., and Barto, A. G. (1998). Reinforcement Learning: An Introduction. Cambridge, MA: MIT Press, 322.

Szathmary, E. (2000). The evolution of replicators. Philos. Trans. R. Soc. Lond. B Biol. Sci. 355, 1669–1676.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Szathmáry, E. (2006). The origin of replicators and reproducers. Philos. Trans. R. Soc. Lond. B Biol. Sci. 361, 1761–1776.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Szathmáry, E. (2011). Evolution. To group or not to group? Science 324, 1648–1649.

CrossRef Full Text

Tenenbaum, J. B., Kemp, C., Griffiths, T. L., and Goodman, N. D. (2011). How to grow a mind: statistics, structure, and abstraction. Science 331, 1279–1285.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Thorndike, E. L. (1911). Animal Intelligence: Experimental Studies. New York: Macmillan.

Toussaint, M. (2003). The Evolution of Genetic Representations and Modular Adaptation. Bochum: Department of Computer Science, Ruhr University of Bochum, 117.

Van Belle, T. (1997). Is neural Darwinism Darwinism? Artif. Life 3, 41–49.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wagner, A. (2007). Robustness and Evolvability in Living Systems. Princeton Studies in Complexity. Princeton: Princeton University Press.

Wallace, A. R. (1916). “Letter of July 2, 1866 to Charles Darwin,” in Alfred Russel Wallace: Letters and Reminescences, Vol. 1, ed. J. Marchant (London: Cassell), :170.

Weiss, A. P. (1994). A Theoretical Basis of Human Behaviour. London: Routledge/Thoemmes Press.

Wright, S. (1932). “The roles of mutation, inbreeding, crossbreeding and selection in evolution,” in Proceedings of the 6th International Congress of Genetics, Ithaca, 356–366.

Young, J. M., Waleszczyk, W. J., Wang, C., Calford, M. B., Dreher, B., and Obermayer, K. (2007). Cortical reorganization consistent with spike timing but not correlation-dependent plasticity. Nat. Neurosci. 10, 887–895.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zachar, I., and Szathmáry, E. (2010). A new replicator: a theoretical framework for analysing replication. BMC Biol. 8, 21. doi:10.1186/1741-7007-8-21

CrossRef Full Text

Zhang, B.-T. (1999). “A Bayesian framework for evolutionary computation,” in The 1999 Congress on Evolutionary Computation ZCEC99 (Washington: IEEE Press), 722–727.

Appendix

Details of Comparison of Evolutionary Search and Hill-Climbing Methods on a GasNet Evolutionary Robotics Task

GasNets

GasNets make use of an analog of volume signaling, whereby neurotransmitters freely diffuse into a relatively large volume around a nerve cell, potentially affecting many other neurons irrespective of whether or not they are electrically connected. By analogy with biological neuronal networks, GasNets incorporate two distinct signaling mechanisms, one “electrical” and one “chemical.” The underlying “electrical” network is a discrete-time step, recurrent neural network with a variable number of nodes. These nodes are connected by either excitatory or inhibitory links. In addition to this underlying network in which positive and negative “signals” flow between units, an abstract process loosely analogous to the diffusion of gaseous modulators is at play. Some units can emit virtual “gases” which diffuse and are capable of modulating the behavior of other units by changing their transfer functions. The networks occupy a 2D space; the diffusion processes mean that the relative positioning of nodes is crucial to the functioning of the network. A GasNet is illustrated in Figure A1.

FIGURE A1

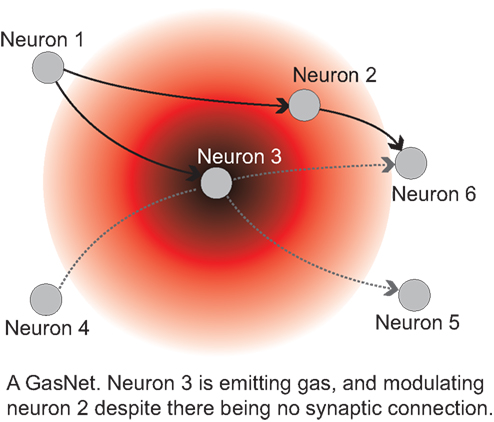
Figure A1. A basic GasNet showing excitatory (solid) and inhibitory (dashed) “electrical” connections and a diffusing virtual gas creating a “chemical” gradient.

The network architecture (including number of nodes and how/if they are connected) and all properties of the nodes and connections and gas diffusion parameters are set by the search algorithm, along with which camera pixels are used as input. Because of the noise and variation, and limited sensory capabilities (generally only very few pixels are used), this task is challenging, requiring robust, general solutions. The coevolution of network and sensor morphology and the fact that the network does not have a prespecified architecture makes this far from a simple “network tuning” type problem. The search space has other interesting properties that are often found in biological systems, particularly that of degeneracy, in the sense discussed by Edelman and Gally (2001). Analysis of GasNet solutions often reveals high levels of degeneracy, with functionally equivalent sub-networks occurring in many different forms, some involving gas and some not (Smith et al., 2002b). Their genotype to phenotype mapping (where the phenotype is robot behavior) is also highly degenerate with many different ways of achieving the same outcome (e.g., moving node positions, changing gas diffusion parameters, adding new connections, or deleting existing ones can all have the same effect). This is especially true considering variable length genotypes are used to efficiently sculpt solutions in a search space of variable dimensions. These properties partly explain the robustness and adaptability of GasNets in noisy environments as well as their evolvability (there are many paths to the same phenotypical outcome with reduced probabilities of lethal mutations; Philippides et al., 2005). See Husbands et al. (2010) for a detailed discussion of the properties of the networks and their resultant search spaces.

Network encoding

Networks were encoded on a variable sized genotype coding for a variable number of nodes. A genotype consisted of an array of integer variables, each lying in the range (0, 100). For continuous variables, the phenotype value is obtained by normalizing the genotype value to lie in the range (0.0, 1.0) and multiplying by the relevant variable range. For nominal values, such as whether or not the node has a visual input, the phenotype value = genotype value MOD N_nom, where N_nom is the number of possible nominal values, and MOD is the binary modular division operator. Each node in the network has 21 variables associated with it. These define the node’s position on a 2D plane; how the node connects to other nodes on the plane with either excitatory (weight = +1) or inhibitory (weight = −1) connections; whether or not the node has visual input, and if it does the coordinates of the camera pixel it takes input from, along with a threshold below which input is ignored; whether or not the node has a recurrent connection; whether and under what circumstances the node can emit a gas and if so which gas it emits; and a series of variables describing the gas emission dynamics (maximum range, rate of emission, and decay etc). All variables were under evolutionary control. Four of the nodes are assigned as motor nodes (forward and backward nodes for the left and right motor, with motor speeds proportional to the output of the relevant forward node minus the output of the relevant backward node). See Husbands et al. (1998, 2010) for further details.

Formally:

<genotype>::(<gene>)*

<gene>::<x><y><R_p><TH_1p><TH_2p><Rn><TH_1n>

    <TH_2n><vis_in><vis_r>

<vis_θ><vis_thr><rec><TE><CE><s><R_e><index⁰><bias>

Fitness function

Sixteen evaluations were carried out on an individual network, with scores f_i calculated on the fraction of the initial robot-triangle distance that the robot moves toward the triangle by the end of the evaluation; a maximum score of 1.0 is obtained by getting the robot center to within 10.0 cm of the triangle at any time during the evaluation (this requires the outside of the robot to get very close to the target). The controller only receives visual input; reliably getting to the triangle over a series of trials with different starting conditions, different relative positions of the triangle and rectangle, and under very noisy lighting, can only be achieved by visual identification of the triangle. The evaluated scores are ranked, and the fitness F is the weighted sum of the N = 16 scores, with weight proportional to the inverse ranking i (ranking is from 1 to N, with N as the lowest score):

$F=\frac{{\displaystyle {\sum }_{i=1}^{N}i{f}_i}}{{\displaystyle {\sum }_{i=1}^{N}i}}=\frac{2}{N\left(N+1\right)}{\displaystyle \sum _{i=1}^{N}i{f}_i}$

Note the higher weighting on the poorer scores provides pressure to do well on all evaluations; a solution scoring 50% on every evaluation has fitness nearly four times that of one scoring 100% on half of the evaluations and zero on the other half.

Mutation operators

The basic search operators available to all the search methods used in the study are the following mutation operators:

Gaussian mutation. Each integer in the genotype string had a x% probability of mutation in a Gaussian distribution around its current value with a variance of 10% of the range of the gene values. x is a control parameter for the algorithm and was typically set at 10.

Random uniform mutation. Each integer in the genotype string had a y% probability of mutation in a uniform distribution across the full range of the gene. y is a control parameter for the algorithm and was typically set at 2. The combination of Gaussian mutation at a relatively high rate and random uniform mutation at a relatively low rate is found to be very effective combination.

Neuron addition operator. An addition operator, with a z% chance per genotype of adding one neuron to the network by inserting a block of random gene values describing each of the new node’s properties. z is a control parameter for the algorithm and was typically set at 4.

Neuron deletion operator. A deletion operator, also with a z% chance per genotype of deleting one randomly chosen neuron from the network by removing the entire block of genes associated with it. The addition and deletion operators allowed exploration of a variable dimension space. The default starting number of nodes in a network was 10 which could then shrink (to a minimum of six) or grow (without limit) as the search proceeded. The search was always operating in a space of more than 100 dimensions and those good solutions that were found typically had 200–300 dimensions.

Each of the search algorithms generated new candidate solutions (offspring) by applying all the operators according to the probability distributions described.

Search methods

RSHC is a basic random start hill-climber. N random mutations of the current solution are created and the fittest of these is chosen as the new solution, unless no better solution is found. This is repeated until P cycles have run without any improvement in fitness. At that point the hill-climber starts again from a newly generated random point (a new “run” for generating the performance statistics). Various values of N and P were explored with very little difference in performance found as long as N > 50 and P > 100. The values in the table were generated for N = 100, P = 1000.

Greedy RSHC is similar to RSHC but with N = 1. Mutations are continually generated until a better solution is found. In this case P = 5000.

Neutral RSHC is the same as Greedy RSHC except that neutral moves are taken. If the fitness of the mutated copy is the same or better than the current solution, it is accepted as the new current solution. This allows neutral net crawling (Barnett, 2001). Because of the noisy nature of the fitness evaluation, statistical neutrality is used (fitnesses within a statistically defined band around the current fitness are accepted as “equal” fitness; Smith et al., 2003).

Neutral-50 RSHC is the same as Neutral RSHC except that there is now only a 50% chance of accepting a neutral move in the search space.

Kimura RSHC is a random start hill-climber that uses a probability of accepting a move based on a Kimura distribution: P(a) = 1 − e^2S/1 − e^2NKS, where P(a) is the probability of accepting a new solution as the next point to move to, S = (F_o − F_p)/F_p, F_o = fitness of offspring, F_p = fitness of parent, N = effective population size, K is a control parameter. Many different values for N and K were investigated, but there was no significant difference between them. The results in the table are for N = 100 and K = 1.

DEA is a geographically distributed mutation-only evolutionary algorithm with local selection and replacement. This parallel asynchronous algorithm uses a population size of 100 arranged on a 10 × 10 grid. Parents are chosen through rank-based roulette-wheel selection on the pool consisting of the eight nearest neighbors to a randomly chosen grid-point. A mutated copy of the parent is placed back in the pool using inverse rank-based roulette-wheel selection (De Jong, 2006). The algorithm is run until a perfect score (1.0) is achieved for 10 consecutive pseudo-generation or until 3000 pseudo-generation have passed. A pseudo-generation occurs every N mutation (offspring) events, where N is the population size. See Husbands et al. (1998) for full details.

SEA is a simple, generational genetic algorithm in which the entire population (except the fittest member) is replaced on each generation. Roulette-wheel selection is used to pick a parent which produces a mutated offspring for the next generation. A population size of 100 was used. The algorithm is run until a perfect score (1.0) is achieved for 10 consecutive generations or until 3000 generations have passed.

PS_SHC consists of a population of independent stochastic hill-climbers in which selection is operating in order to allocate search resources. It is exactly the same as the DEA algorithm except there is no replication and if an individual is selected (according to fitness) to be mutated (a single search move), and its offspring is fitter, the offspring replaces the parent (rather than another member of the population). This means there is no diffusion of genetic material around the population grid. Variations of this algorithm allowing neutral moves and (with a low probability) replacement of parents with lower fitness offspring were also tried. These variants did not produce significantly different results.

Statistical analysis of results

A statistical analysis of the comparative study summarized in Table 2 was carried out. A Kruskal–Wallis test performed on the whole data set revealed highly significant differences between the distributions (p < 10⁻¹⁸). Pair-wise Wilcoxon rank-sum tests, adjusted for multiple comparisons using the Dunn–Sidak procedure for controlling type-1 statistical errors (Hollander and Wolfe, 1999), were used to further probe the differences between the distributions. As can easily be seen from the table, DEA was significantly better than all other algorithms including SEA (p ≪ 10⁻⁶ in all cases), SEA was significantly better than all the hill-climbing algorithms (p < 10⁻⁶) and PS_SHC was significantly better than all other hill-climbers (p < 10⁻⁶) but significantly worse than both the evolutionary search algorithms. There was no significant differences between the RSHC methods except the one using the Kimura distribution which is significantly worse. The main difference between the random start hill-climbing methods was the length of typical individual hill climbs before a new random restart is triggered (due to lack of progress). Simple RSHC had the shortest individual climbs (typically 500 moves), while the neutral methods had the longest (typically 5,000 moves).

Details of a Modified Model for Copying of Patterns of Synaptic Connectivity

We demonstrate a novel mechanism for copying of topology that does not require explicit error-correction neurons. A causal network (Bayes net) is learned on the basis of spikes received from another causal network. Each node in the causal network consists of a group of neurons (unconnected within a group). Neurons are fully connected between groups. Each node is constituted by n = 5 stochastic neurons that are activated on the basis of a linear sum of weighted synaptic inputs put through a sigmoid (logistic) function. Directed synaptic connections between neurons will come to describe causal interdependencies between events. The probability that a neuron fires p_fire is given by Eq. A1.

$p_i=\frac{1}{1+{\text{e}}^{-\text{bias}+\sum w_{ji}{s}_j}}$(A1)

where s_j is the state of an afferent neuron j (i.e., 0 or 1) and w_ji is the synaptic weight from pre-synaptic neuron j to post-synaptic neuron i. The state of neurons is updated every millisecond based on this calculation. A neuron cannot fire for a refractory period of 10 ms after it has fired already.

Inputs to the network arise from perceptual processes or from other brain regions. Each distinct event type (shown in Figure A2) may activate a specific set of neurons in the causal network (top) via an input neuron (bottom), as assumed in previous models of STDP based Bayesian learning (Nessler et al., 2009). Each set of causal network neurons initially has weak connections to all other sets of causal network neurons, but has no connections to neurons within the same set. Why do we assume that many causal network neurons are used to represent one event? This allows the network to deal with low fidelity transmission from the input neuron (bottom) to each causal network neuron (top) because the probability that at least one causal network neuron fires when the input neuron fires will be 1 − (1 − p)ⁿ, where n is the number of neurons in the set of neurons that represents an event. The weak connections between sets of causal network neurons can be interpreted as representing the initial prior expectation of a causal relationship between events. To be specific, in the simulation this expectation is as follows; if a pre-synaptic neuron fires then there is a probability of 0.0009 that a post-synaptic neuron will fire. Activity can pass between neurons with delays ranging from 0 to 4 ms, as shown in Figure 1. That is, between any two neurons that represent two different events, a connection exists that links these events by a delay of either 0, 1, 2, 3, or 4 ms. The range of delays between sets is set up so that all possible delays exist between two sets of neurons. This range of delays is intended to match the characteristic delays between neurons in the CA3 region of the Hippocampus (Miles, 1990). The connectivity in Figure 1 is entirely plausible. It only assumes that there exist connections from the hippocampus to the cortex such that there is at least a disjoint set of neurons receiving inputs from hippocampal neurons that represent distinct events, and that there exists a range of delays between cortical neurons within the same region.

FIGURE A2

Figure A2. Overall structure of a two-cause causal network (above) and its inputs that represent two event types (below). The bias of causal network neurons is set to 9.5. As shown on the graph below, this means that external input alone (at fixed synaptic weight 5.25) causes a neuron in the causal network to fire with probability only 0.014. However, if external input is simultaneous with internal delay line input from another causal network neuron, then the neuron will fire with probability 0.15 (given the initial internal delay line synaptic weight of 2.5). If a causal delay line has been potentiated to its maximum (ACh depressed) weight of 4.0, then simultaneous external and internal inputs to a neuron will cause it to fire with probability 0.43. However, internal delay line activation alone (without simultaneous external input) is insufficient to make a neuron fire with any greater than probability 0.004 (even at the maximum internal ACh depressed weight of 4.0). This arrangement insures that simultaneous input from external events and internal delay lines is an order of magnitude more likely to cause a neuron to fire than unsynchronized inputs from either source alone. This non-linearity is essential in training of the causal network because it means that only connections that mirror the delays between received events are potentially strengthened.

In the simulation shown, the part of the neuronal network that entrains to form the causal network consists of 15 neurons arranged into three sets of five. Each set receives inputs from a separate input neuron from the input layer. Neurons from each set are connected all-to-all to neurons in the other two sets. Each neuron in a set sends connections with delays 0, 1, 2, 3, and 4 ms to the five neurons in each other set. This means that all possible configurations of delay from 0 to 4 ms in a three-node network are represented in the initial network.

A neuron in the causal network must be depolarized simultaneously by intrinsic causal network neurons and by extrinsic input neurons for it to have a high probability of firing a spike. As shown in Figure 1, external “perceptual” input from the input neuron to its set of causal network neurons is sub-threshold (5.25) which means that if the input neuron fires, there is only a low probability (0.014) that any causal network neuron within its set fires. Only when extrinsic spikes reach a causal network neuron at the same time as intrinsic spikes from another causal network neuron is the probability of the post-synaptic neuron firing increased to at least 0.15. This is an order of magnitude greater than with unsynchronized reception of intrinsic and extrinsic spikes. This principle of dependence on two sources of activation for firing is also to be found in more detailed neuronal models that simulate intrinsic synaptic connections within a population as fast inhibitory (GABA) and fast excitatory (AMPA) connections, but between-population connections as modulatory (NMDA) synapses (Friston, 2000). These later synapses are voltage-dependent such that they have no effect on the intrinsic dynamics in the second population unless there is already a substantial degree of depolarization. Whilst those models are intended to show attentional top-down modulation of bottom-up driving connections (Friston and Buchel, 2000), here we are concerned with how intrinsic connections (within a cortical region) are entrained by extrinsic inputs from the hippocampus (Nadel and Moscovitch, 1997; Nadel et al., 2000, 2007). We do not consider neuromodulation explicitly, although the addition of neuromodulation may well be expected to improve causal inference performance.

Next we describe the rules that determine synaptic weight change in the causal network. Three plasticity rules were modeled; first order STDP, first order long-term depression (LTD), and a (Rescorla–Wagner type) heterosynaptic competition rule. The use of first order rules was first considered by Nessler et al. (2009) and we are grateful to the group of Wolfgang Maass for suggesting the use of such rules.

The first plasticity rule is a subtle modification of STDP (Song and Abbott, 2001; Izhikevich, 2007). The modification made to STDP here is that the weight change is obtained by multiplying the current weight by the standard STDP term, i.e., the absolute extent of weight change is related to the current weight by a first order dependence such that the weight experiences exponential autocatalytic growth and decay in a manner identical to that observed in asexual biological replicators (Adams, 1998; Zachar and Szathmáry, 2010). This is until a maximum weight threshold is reached which can be interpreted as a equivalent to a carrying capacity in a population dynamic model. We are intentionally choosing to see the change in synaptic as a kind of unit of evolution or replicator (Fernando and Szathmáry, 2009, 2010). An alternative is to use a sub-exponential (e.g., parabolic) growth rule dw/dt = kw^p where p < 1 that does not result in survival of the fittest but survival of everybody, a modification which may allow preservation of synaptic diversity (Szathmary, 2000; Szathmáry, 2006). For the time being we use a simple exponential model with p = 1.

The second plasticity rule we simulate is a pair of first order long-term depression (LTD) rules that can work with neuronal network models that are sufficiently realistic to include explicit delays between a spike leaving the body of a neuron and reaching the synapse. Firstly, if the pre-synaptic neuron fires and if when the spike reaches the synapse the post-synaptic neuron does not fire, then the synaptic weight experiences first order depression, i.e., the weight is reduced by a fixed proportion of its current value. This embodies the intuitive notion that if event A occurs but event B does not occur when it should have occurred if event A were to have caused it, then event A is naturally less likely to have caused event B with that particular delay. Note that if the STDP rule were used alone then there would be no weight change because the STDP rule produces maximum weight change for spikes that co-occur close together in time, but not where only one spike occurs. Secondly when a post-synaptic neuron fires, those synapses that precisely at that time are not being reached by spikes from their respective pre-synaptic neurons have their weights depressed by a fixed proportion of their current values. This embodies the intuitive causal notion that if effect B occurs and yet putative cause A did not occur at the right time before B, then cause A is less likely to have caused effect B. In both cases the synapse experiences exponential decay. Both rules refine the STDP rule in the sophistication of causal assumptions they embody. Both causal assumptions seem entirely natural and intuitive at the cognitive level. Note again that if STDP were simulated as for example in Izhikevich (2007) then weight change would only occur when both pre- and post-synaptic neurons fired, in other words, changes to causal assumptions could only be made when both potential cause and effect were observed, but not when only one or the other was observed. It is LTD of the type described above that occurs when only one of the events occurs and it is essential for explaining the phenomenon of backward blocking (Gopnik and Schulz, 2004; Gopnik et al., 2004).

The third plasticity rule is a competitive rule that redistributes synaptic weights if two synapses are simultaneously active. This implements synaptic competition between simultaneously active synapses for weight resources, and it implements screening off behavior. If two pre-synaptic neurons activate a post-synaptic neuron simultaneously, they compete for synaptic resources, in a manner analogous to ecological competition dynamics between two species competing for the same food resource (Hofbauer and Sigmund, 1998). This rule embodies the natural causal assumption that if two potential causes occur together that they should compete for explanatory weight. In a sense, this is the synaptic implementation of Occum’s razor which prevents the needless multiplication of causal entities. Competition between simultaneously co-occurring events for causal influence, but in the two-cause condition there is no competition between events.

Finally, we assume that during the training phase there is a high level of ACh based neuromodulation that reduces the effective synaptic transmission between weights between neurons in the causal network. This is modeled simply by multiplying the weights in the causal network by a factor < 1, such that the maximum permissible weight is 4, which translates to the probability of 0.004 that a post-synaptic neuron fires given a pre-synaptic neuron has fired. This limit means that it is typically necessary for a post-synaptic causal network neuron to receive simultaneous activation from the input neuron, and from a causal network neuron in order for it to have a high probability of firing, i.e., there is a kind of associative control based on sub-threshold depolarization (Bush et al., 2010). In the simulation we implement an upper weight bound which suddenly cuts off further exponential growth, although a more realistic assumption may have been to implement resource limitation resulting in a sigmoidal synaptic growth function.

The details of the implementation are as follows. Initial synaptic weights within the causal network are all initialized at 2.5 mV which gives a very low probability that the post-synaptic neuron will fire if one pre-synaptic neuron fires, see Figure 1. The input weights to the causal network are fixed at 5.25 that corresponds to a probability of 0.014 that a post-synaptic neuron will fire if it receives input only from one external input neuron. However, if external input is simultaneous with internal delay line input from another causal network neuron, then the neuron will fire with probability 0.15 (given the initial internal delay line synaptic weight of 2.5). Synaptic weights are maintained in the range (0:w_max) where w_max = 4 mV during ACh depression, and 20 mV without ACh depression. If a causal delay line has been potentiated to its maximum (ACh depressed) weight of 4.0, then simultaneous external and internal inputs to a neuron will cause it to fire with probability 0.43. However, internal delay line activation alone (without simultaneous external input) is insufficient to make a neuron fire with any greater than probability 0.004 (even at the maximum internal ACh depressed weight of 4.0). The bias of causal network neurons is set to 9.5 mV that gives them a low probability of spontaneous firing.

First order STDP

The STDP rule works as follows: τ is the time difference in milliseconds between pre- and post-synaptic spiking. The standard STDP rule is to allow the weight of a synapse to change according to the standard implementation of additive STDP shown in Eq. A1 below (Song et al., 2000; Izhikevich and Desai, 2003).

$\begin{array}{c}\text{STDP}\left(\tau \right)=A_{+}{\left(1-\frac{1}{{\tau }_{+}}\right)}^{\tau }\text{for }\tau >\text{ 0}\\ \text{STDP}\left(\tau \right)=A_{-}{\left(1-\frac{1}{{\tau }_{-}}\right)}^{-\tau }\text{for }\tau \le \text{0}\end{array}$(A2)

The parameters A₊ and A₋ effectively correspond to the maximum possible change in the synaptic weight per spike pair, while τ₊ and τ₋ denote the time constants of exponential decay for potentiation and depression increments respectively. Typically τ₊ and τ₋ = 20 ms, and A₊ = 1.0 and A₋ = 1.5. If a pre-synaptic spike reaches the post-synaptic neuron (taking into account conduction delays) before the post-synaptic neuron fires, then STDP(τ) is positive. If a pre-synaptic spike reaches a post-synaptic neuron after it fires, then STDP(τ) is negative. This STDP rule is based on data from cultures of hippocampal pyramidal neurons (Bi and Poo, 1998). However, more complex activity dependent plasticity dynamics have been observed (Buchanan and Mellor, 2010).

The above rule is approximated by a simplified version of the STDP rule where for all values of −10 > τ < = 0, i.e., where the pre-synaptic neuron fires after the post-synaptic neuron, the weight is depressed by 0.8 multiplied by the current weight, i.e., the weight is decreased by 20% of its existing value. If 10 > τ > 0 then the existing weight is multiplied by 1.2, i.e., is increased by 20% of its current value.

First order LTD

Two types of first order short-term depression are simulated. The first reduces the synaptic weight by 2% of its current weight if the pre-synaptic neuron fires and post-synaptic neuron does not fire. The second reduces the synaptic weight by 0.2% if the post-synaptic neuron fires and the pre-synaptic neuron does not fire.

Heterosynaptic competition rule

If two pre-synaptic neurons i and j simultaneously activate a post-synaptic neuron p then the new weight w_jp = w_jp − 0.6w_ip and w_ip = w_ip − 0.6w_jp. That is, the existing weight is decreased by a first order term that is proportional to the weights of the other simultaneously active synapses to that post-synaptic neuron p.

Results

If the output of one neuronal network that is activated randomly by background neuronal noise can be observed by another network at another location in the brain, then it can be copied. Using our new mechanism, not only can the structure be copied, but the delays can also be copied. We show that this observing network, which we will call the “offspring” network, can undertake causal inference on the first network, which we will call the “parental” network. If we can successfully demonstrate the capacity for one neuronal network to copy the temporal and causal relationships that exist between other neurons elsewhere in the brain, then we have identified a novel potential substrate of neuronal information storage and transmission at the level above that of the synapse, i.e., the neuronal group.

The idea of copying of neuronal topology has been proposed before, however the authors were not able to demonstrate effective copying in the case where transmission between neurons involves non-uniform delays. Also even with uniform delays, error-correction neurons were needed to prevent false-positive and false-negative causal inferences (Fernando et al., 2008). The mechanisms described here are able to entrain networks to learn specific delays without the need for error-correction neurons. This represents a significant step in the development of the neuronal replicator hypothesis which proposes that units of evolution exist in the brain and can copy themselves from one brain region to another (Fernando et al., 2008).

The ability of one causal network to infer the connectivity of another causal network was demonstrated by randomly sparsely stimulating the parental causal network which is assumed to consist of only three neurons equivalent to the input neurons used in the previous experiments. Sparse stimulation means any uniform external stimulate rate of the parental network that does not impose significant correlation artifacts between neuronal firings, e.g., 10 Hz. Figure A3 shows the successful copying of common-cause, common-effect, and causal chain networks with all possible combinations of integer delays from 1 to 4 ms.

FIGURE A3

Figure A3. Successful copying of common-cause, common-effect, and causal chain networks with all delay combinations from 1 to 4 ms. The “parental” network is stimulated randomly and the resulting spikes are passed to the “offspring” network by a topographic map.

The same synaptic plasticity rules can be used to infer recurrent network structures, see Figure A4. One-cycles and two-cycles of delays up to 4 ms are not detected by the causal inference mechanism due to the refractory period of 10 ms. However, three-cycles of 4 ms are inferred correctly because by the time activation passes back to the initially stimulated neuron that neuron can again be activated.

FIGURE A4

Figure A4. One-, two-, and three-neuron cycles. Only if the cycle has a period greater than the refractory period of the neurons within it can the cycle be inferred. For example three-cycles with 4 ms delays can be inferred when the refractory period is 10 ms.

A motif thought to be of some significance is the feedforward “loop” (Sporns and Kotter, 2004). Again, due to the refractory period there are regions in delay space for the feedforward “loop” that are not correctly causally inferred, see Figure A5, however, in most cases it is possible to copy the “loop.” Altogether these results show that it is possible for the plasticity mechanisms described to not only infer acyclic graphs but cycling graphs with delays.

FIGURE A5

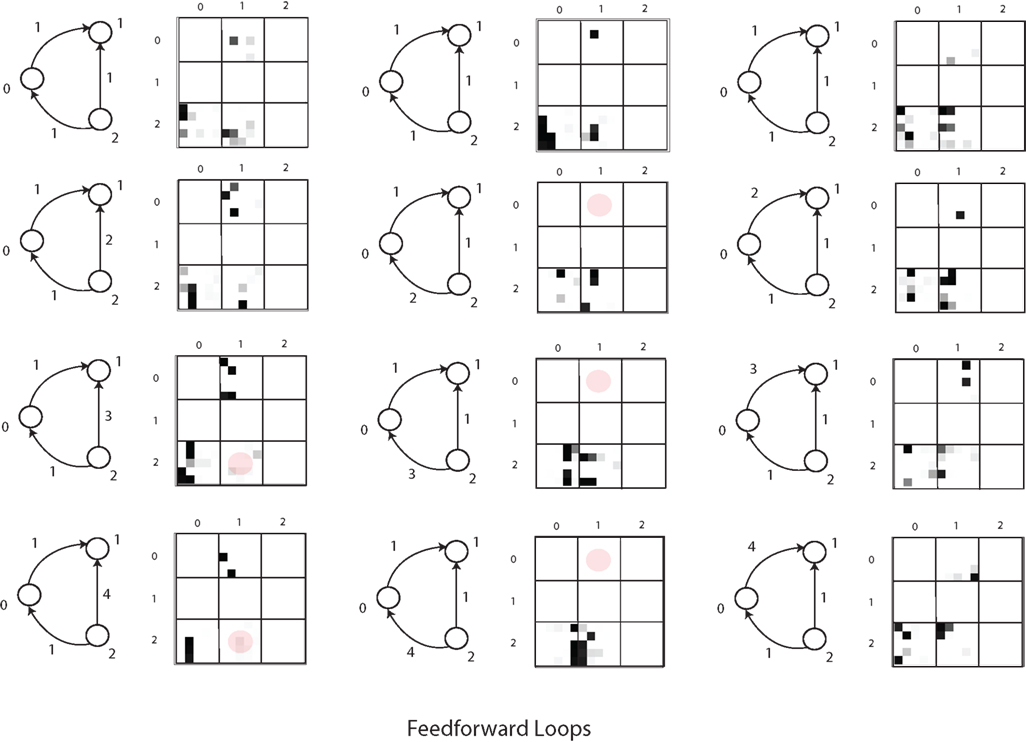
Figure A5. Feedforward loops (FFLs) with a sample of delays. Some regions in delay space cannot be properly inferred. Light red circles mark synapse sets that were not strengthened when they should have been, i.e., false-negatives.

The demonstration given here that causal inference between one brain region and another that can occur by one network observing the intrinsic dynamics that occurs during sparse stimulation suggests a new role for spontaneous activity in the brain (Mazzoni et al., 2007), i.e., allowing the replication of synaptic connectivity patterns within a neuronal group to other brain regions.