Intentional Communication: Computationally Easy or Difficult?

Van Rooij, Iris; Kwisthout, Johan; Blokpoel, Mark; Szymanik, Jakub; Wareham, Todd; Toni, Ivan

doi:10.3389/fnhum.2011.00052

ORIGINAL RESEARCH article

Front. Hum. Neurosci., 30 June 2011
Sec. Cognitive Neuroscience
volume 5 - 2011 | https://doi.org/10.3389/fnhum.2011.00052

Intentional communication: Computationally easy or difficult?

Iris van Rooij¹* Johan Kwisthout² Mark Blokpoel¹ Jakub Szymanik³ Todd Wareham⁴ Ivan Toni¹

¹ Donders Institute for Brain, Cognition and Behaviour, Radboud University Nijmegen, Nijmegen, Netherlands
² Institute for Computing and Information Sciences, Radboud University Nijmegen, Nijmegen, Netherlands
³ Department of Artificial Intelligence, University of Groningen, Groningen, Netherlands
⁴ Department of Computer Science, Memorial University of Newfoundland, St. John’s, NL, Canada

Human intentional communication is marked by its flexibility and context sensitivity. Hypothesized brain mechanisms can provide convincing and complete explanations of the human capacity for intentional communication only insofar as they can match the computational power required for displaying that capacity. It is thus of importance for cognitive neuroscience to know how computationally complex intentional communication actually is. Though the subject of considerable debate, the computational complexity of communication remains so far unknown. In this paper we defend the position that the computational complexity of communication is not a constant, as some views of communication seem to hold, but rather a function of situational factors. We present a methodology for studying and characterizing the computational complexity of communication under different situational constraints. We illustrate our methodology for a model of the problems solved by receivers and senders during a communicative exchange. This approach opens the way to a principled identification of putative model parameters that control cognitive processes supporting intentional communication.

Introduction

This paper introduces a formal methodology for analyzing the computational complexity of intentional communicative actions, i.e., actions designed to modify the mental state of another agent. The need for such a methodology is evident from the obvious discrepancies between intuitions on the complexity of human communication. Some neuroscientists have argued that intentional communication is easy: we have neural mechanisms that can directly extract communicative intentions from detectable sensory events through the filter provided by our motor abilities (Iacoboni et al., 1999, 2005; Rizzolatti et al., 2001). However, this non-inferential view of intentional communication seems at odds with a core feature of intention attributions, i.e., their context-dependency (Figure 1 presents a graphical illustration; see also Toni et al., 2008; Uithol et al., 2011). The animal world is bursting with examples of communicative phenomena in which a physical event conveys information by virtue of an interpretation made by a receiver according to the dominant statistical association, without any need for the interpreter to postulate a sender. Highly conventionalized forms of human communication may appear to fall into this category, and thereby within the explanatory power of neuronal mechanisms like those afforded by the mirror neuron system (Jacob and Jeannerod, 2005). Yet, even highly conventionalized signals – such as a thumbs up action – may take on different meanings (e.g., “move up” or “let him live”) depending on the communicative context in which they occur. Moreover, even in cases where a thumbs up action does signal the conventional “OK,” this apparently unequivocal mapping between sign and signified remains highly ambiguous. For instance, it could signal “OK, let’s have dinner,” or “OK, it is a deal,” or “OK, you can go ahead with what you were planning to do,” or an indefinite number of other things which could all be said to be “OK.” Accordingly, some theoreticians have argued that, in principle, human intentional communication forms an intrinsically intractable problem, as there is an indefinite number of possible intentions a communicator may entertain at any time and it is logically impossible for a recipient of a communicative signal to determine which intention motivated it (Levinson, 1995, 2006).

FIGURE 1

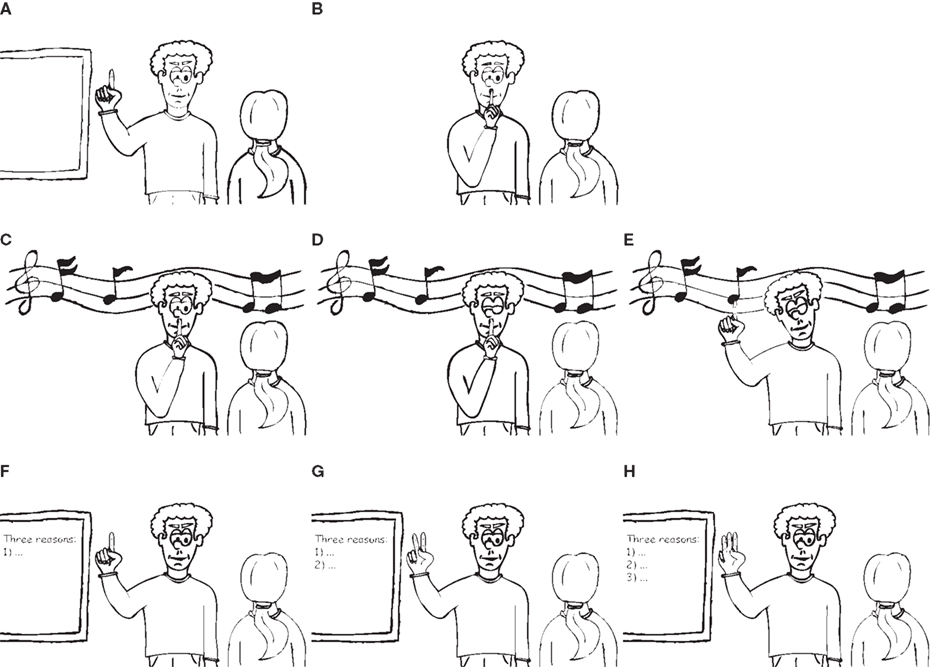
Figure 1. Motor acts (such as raising of the arm and/or extension of the index finger) can suggest different communicative intentions depending on the context in which they are performed. Context information can pertain to information about the concurrent state of the world. For instance, the presence of a school board may make it more likely (compared to other contexts) that a person standing in front of it (likely a teacher) intends to signal “pay attention” to a recipient [see e.g., (A)]. Context information can also pertain to information about other concurrently performed motor acts. For instance, a person raising his arm, extending his index finger, and moving the index finger to his (closed) lips will more likely (compared to other combinations of actions) intend to signal “be silent” [see e.g., (B)]. When this combination of motor acts is additionally combined with a context in which music is played and furthermore additionally acts are made such as closing the eyes, tilting the head and moving the finger away from the lips a combination of communicative intentions may be signaled [e.g., “be silent, pay attention, and listen” see (C–E)]. Importantly, identical actions, performed in different contexts, can signal qualitatively different communicative intentions. For instance, the act and posture of the communicator in (A) and (F) are identical, but the finger gesture in (F) likely does not signal (just) “pay attention” but instead (or also) “let’s consider the first reason …”, especially if this action is followed by those depicted in (G) and (H). (Illustrations by Bas Maes)

Evidently, human communication falls in between these two extremes. Trivial as well as intractable views of human communication fail to adequately characterize the complexity of communication problems solved by humans in everyday situations. After all, humans are often capable of communicating with each other with little or no error, and even when errors occur communicators are often quick to adapt their behaviors so as to resolve any ambiguities. This behavioral success suggests that humans are somehow able to quickly take contextual factors into account and use them to estimate the likely meanings of communicative behaviors in context. Yet, context-sensitive computations are notorious in cognitive computational science for the astronomical demands that they make on computation time (Pylyshyn, 1987; Haselager, 1997; Fodor, 2000; Lueg, 2004). It thus remains a real scientific challenge to explain the success of human communication in combination with its speed. We propose that a more fruitful research agenda is to characterize the conditions that mark boundaries of high and low computational complexity in human communication. This paper presents a conceptual framework and analytic methodology for fleshing out this research agenda.

The framework we propose builds explicit models of communicative problems in order to assess the computational (in)tractability of those problems under different situational constraints. Situational constraints that render communication tractable under the given models are then candidate explanations of the speed of everyday human communications. Crucially, these candidate explanations can then be empirically tested, assessing whether the same relation between situational constraints and computational demands predicted by the model fit with the behavior and cerebral processes observed in participants in the lab while solving the same communicative problems. This type of model-driven approach offers several benefits for cognitive neuroscience. First, it identifies putative model parameters that control the cognitive processes supporting intentional communication. Second, it provides a rigorous ground for empirical tests of those models. Third, it offers the possibility to test the neurophysiological plausibility and cognitive relevance of the model by comparing the predicted dynamics of relevant model parameters with the observed dynamics of communicators’ internal states (i.e., cerebral signals measured with neuroimaging methods).

Overview of the Paper

We will illustrate our proposed approach using one particular model of intentional communication as a case study. The model is an extension of the Bayesian inverse planning (BIP) model of goal inference proposed by Baker et al. (2007, 2009). In Section “A Probabilistic Model of Intentional Communication,” we will describe in detail the original BIP model of goal inference and our adaptations of this model in the form of a Receiver model and Sender model. In Section “Computational Complexity Results,” we will study the computational complexity of these Receiver and Sender models, observing that both are computationally intractable unless properly constrained. We then set out to identify constraints that render the models tractable. In Section “Implications and Predictions for Cognitive Neuroscience” we will discuss how the conditions of (in)tractability reported in Section “Computational Complexity Results” can inform critical empirical tests in cognitive neuroscience. In Section “Open Theoretical Questions and Future directions” we present a set of open questions and suggestions for future theoretical research. We close, in Section “Conclusion,” with a reflection on the general relevance of this analytic methodology for cognitive neuroscience of communication and other forms of social interaction.

A Probabilistic Model of Intentional Communication

Our model of communication builds on an existing model of how humans infer instrumental goals from observing someone’s actions, called the BIP model (Baker et al., 2007, 2009; see also Blokpoel et al., 2010). We extend this model to the domain of communication by making it apply to communicative goals as well. We first explain the BIP model (see Preliminaries: The BIP Model of Goal Inference), and then we explain how it can be adapted to the domain of intentional communication (see A BIP Model of Sender and Receiver).

Preliminaries: The Bip Model of Goal Inference

According to the BIP model, observers assume that actors are “rational” in the sense that they tend to adopt those actions that best achieve their goals. Here “best” may, for instance, be defined in terms of (expected or believed) efficiency of a set of actions for achieving a given (combination of) goal(s). Say, a person has a single goal of tying his shoe laces. Then this person could make the necessary moves of the fingers, or he could start the finger movements, pause to scratch his chin, and then continue making the finger movements until his shoe laces are tied. If “rationality” is defined in terms of efficiency then the latter sequence of actions would be considered less rational for the goal of “tying one’s laces” than the former sequence of actions. Be that as it may, the latter sequence of actions can of course be rational for a different goal, e.g., if the actor has two simultaneous goals “to tie the shoe laces” and “to get rid of that itch on the chin” (and an observer of the latter sequence of action will also likely attribute this combination of goals, over a single goal to the actor).

Given the assumption of rationality, (probabilistic) knowledge of the world and how actions are affected by it, and a measure of relative rationality of action–goal pairs, one can compute the probability that an agent performs an action given its goals, denoted

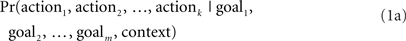
or in shorter format:

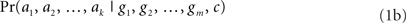
An important insight of researchers such as Baker et al. (2007, 2009) is that observers can use this probabilistic model of planning to make inferences about the most likely goals that actors are pursuing. The reason is that the probability in Eq. 1a/b can be inverted using Bayes’ rule to compute the probability of a given combination of goals, given observations of actions that an actor performs:

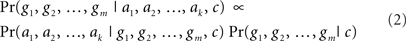
Of all the possible combinations of goals that an observer can (or does) entertain, the goal combination that maximizes the probability in Eq. 2 best explains why the observed actions were performed, and according to the BIP model it is this goal combination that an observer will infer¹. In sum, goal inference under the BIP model equals the computation of the following input–output mapping, informally stated.

Goal Inference (informal)

Input: A representation of the probabilistic dependencies between actions, goals, and states and how these dependencies change over time, and a sequence of observed actions and world states.

Output: A combination of goals that best explains the sequence of actions and world states against the background of the probabilistic dependencies between actions, goals, and world states and how these dependencies change over time.

To be able to analyze the computational complexity of the GOAL INFERENCE problem we need to define formal counterparts of all the notions and constructs introduced in the informal problem definition above. Following Baker et al. (2007, 2009), we use BIP-Bayesian networks to formally model the input representations in the GOAL INFERENCE problem (for a mathematical definition see Preliminaries from Bayesian Modeling in the Appendix). In these networks actions, goals, and world are modeled as value assignments to nodes in the network, and probabilistic dependencies are indicated by directed arcs connecting such nodes (see Figure 2 for an illustration). For each node in the network there is an associated prior probability of the node taking on a value (e.g., “true” or “false”). In addition, each node has an associated probability distribution, coding the conditional probability of the node taking on a value as a function of the probability of different possible value assignments for the nodes that are connecting to it (called, its “parents”). A set of observed actions and world states is modeled by a value assignment to a sequence of action and state nodes. A combination of goals is modeled as a truth assignment for the goal nodes. A combination of goals is said to “best” explain the observations of actions and world states if it maximizes the probability defined in Eq. 2.

FIGURE 2

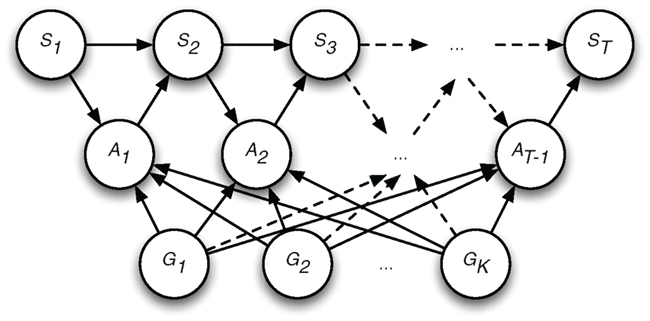
Figure 2. The BIP-Bayesian network with T time slices: S_t with t = 1, 2, … T, is a state variable at time t; A_t with t = 1, 2, … T, is an action variable at time t. The goal variables, G₁, G₂, … G_K are fixed over the different time slices. Arrows indicate probabilistic dependencies between variables in the network. Note that no direct dependencies exist between states and goals, but that any indirect dependencies between states and goals are mediated by action variables.

Having formalized all the relevant notions in the GOAL INFERENCE problem, we can now state the formal counterpart of the problem (for explanation of notation and mathematical concepts, refer to Preliminaries from Bayesian Modeling in Appendix).

Goal Inference (formalized)

Input: A BIP-Bayesian network B = (D, G), where D is a dynamic Bayesian network with time slices D₁…D_T, where each time slice contains an action variable A and a state variable S, and G = G₁…G_k denotes a set of instrumental goals. Further, a set of observed actions and states a ∪ s.

Output: The most probable joint value assignment g to the goals in G, i.e., argmax_g Pr(G = g | A = a, S = s), or ∅, if Pr(G = g | A = a, S = s) = 0 for all joint value assignments g (here the output ∅ can be read as meaning “no plausible goal attribution can be made”).

The computational complexity of this model has previously been analyzed by Blokpoel et al. (2010). Specifically, these authors presented a mathematical proof that the problem is computationally intractable (NP-hard) if no constraints are imposed on the input representations. They furthermore found that the problem is tractably computable under the constraint that the set of candidate goals (G) is small and/or the probability of the most probable goal assignment (p) is large. Here, we will use the GOAL INFERENCE problem as an inspiration for similarly explicit characterizations of the SENDER and RECEIVER problems solved by human communicators. As we will see, some (though not all) of the computational complexity results for GOAL INFERENCE apply also to the new SENDER and RECEIVER problems.

A Bip Model of Sender and Receiver

If indeed – as the BIP-model postulates – observers of actions infer goals from actions by means of an inference to the best explanation, then senders can use this knowledge to predict how a receiver will interpret their actions ahead of time. For instance, they could engage an internal simulation of a receiver’s inferences to the best explanation when considering the suitability of candidate actions (Noordzij et al., 2009). Such a simulation subroutine could be called multiple times during the planning of instrumental and communicative behaviors, allowing a sender to converge on an action sequence which is both efficient and is likely to lead a receiver (if properly simulated) to attribute the correct (i.e., intended) communicative goal to the sender. This conceptualization of the computational bases of sender signal creation can be summarized by the following informal input–output mapping².

Sender (informal)

Input: A representation of the probabilistic dependencies between actions, goals, and states and how these dependencies change over time, and one or more communicative and instrumental goals.

Output: A sequence of actions that will lead to the achievement of the instrumental goals and will lead a receiver to attribute the correct communicative goals to the sender.

Note that our model allows for the possibility that senders can have simultaneous instrumental and communicative goals as seems required for ecological validity. After all, in everyday settings communicative behaviors are typically interlaced with several sequences of instrumental actions – think, for instance, of a car driver signaling to another driver at night that his lights are off, while at the same time trying to drive safely and stay on route.

Building on the formalisms used in the GOAL INFERENCE model, the informal SENDER model yields the following formal input–output mapping (see Figure 3 for an illustrative example of a BIP-network for communicative goals).

FIGURE 3

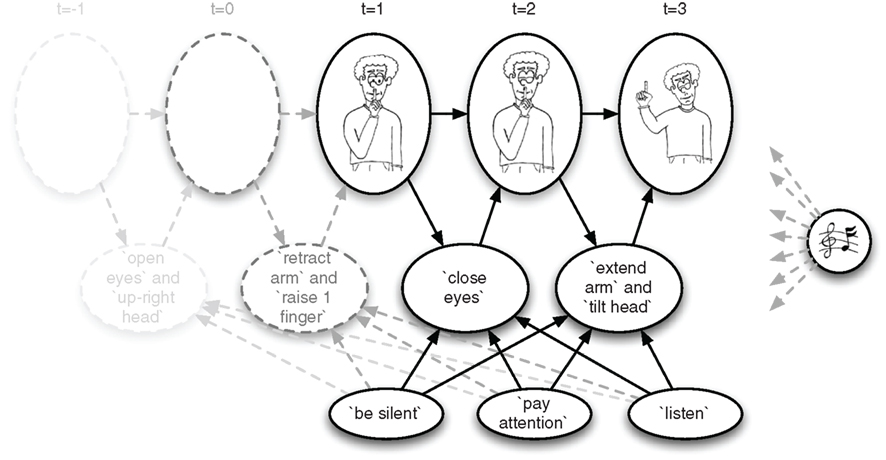
Figure 3. An illustration of how probabilistic knowledge about the scenarios depicted in Figures 1C–E can be encoded in a BIP-Bayesian network as probabilistic dependencies between goals, actions, and states.

Sender (formalized)

Input: A BIP-Bayesian network B = (D, G), where D is a dynamic Bayesian network with time slices D₁…D_T, such that each time slice contains an action variable A and a state variable S, G_I = G₁…G_k denotes a set of instrumental goals, and G_C = G_k+1…G_n denotes a set of communicative goals, and a set of goal assignments g_I ∪ g_C to G_I ∪ G_C.

Output: A joint value assignment a to the action variables such that a = argmax_aPr(A = a|G_I = g_I) and RECEIVER(B, a, s) = g_C, or ∅ if no such joint value assignment a is possible. Here s is argmax_s Pr(S = s | A = a), i.e., the most likely state s to follow from the actions.

Here the receiver function RECEIVER(.,.,.) is modeled after the GOAL INFERENCE function studied by Baker et al. (2007, 2009) and Blokpoel et al. (2010), but with an important difference: the receiver is presented with a sequence of actions that was purposely designed by a sender with the aim of making her communicative goals interpretable by a receiver, while concurrently trying to achieve one or more instrumental goals unknown to the receiver. This difference between the GOAL INFERENCE problem and the RECEIVER problem can have non-trivial consequences for the computational complexity of the RECEIVER problem, which is why we need to analyze it anew in this paper.

For completeness and clarity, we state the RECEIVER problem in both informal and formal format below.

Receiver (informal)

Input: A representation of the probabilistic dependencies between actions, goals, and states and how these dependencies change over time, and a sequence of observed actions and world states.

Output: A combination of communicative goals that best explains the sequence of actions and world states against the background of the probabilistic dependencies between actions, goals, and world states and how these dependencies change over time.

Receiver (formalized)

Input: A BIP-Bayesian network B = (D, G) as in the SENDER problem; a set of observed actions and states a ∪ s.

Output: The most probable joint value assignment g_C to the communicative goals in G_C, i.e., argmax_g Pr(G_C = g_C | A = a, S = s), or ∅, if Pr(G_C = g_C | A = a, S = s) = 0 for all joint value assignments g_C.

Having defined both the generic SENDER and RECEIVER problems, we are now in a position to analyze their computational complexity. We report on our analyses in the next section.

Computational Complexity Results

In this section we state all computational complexity results. Readers interested in full details on the mathematical proofs are referred to the Section “Computational Models and Computational Complexity Analyses” in the Appendix. This section assumes familiarity with concepts and methods from the field of computational complexity analysis (for a primer see Preliminaries from Complexity Theory in the Appendix). For instance, contrary to the suggestion that computationally intractable functions can be approximately computed efficiently (e.g., Love, 2000; Chater et al., 2003, 2006), computational complexity theory (cf. Kwisthout et al., 2011) has clearly shown that many intractable (e.g., NP-hard) functions cannot be efficiently approximated (Arora, 1998; Ausiello et al., 1999), and almost all are intractable to approximate if only a constant sized error is allowed (Garey and Johnson, 1979; van Rooij et al., 2010)³. Accordingly – although the analyses we provide work under the assumption that the models exactly predict the outputs of human computations – we conjecture that the obtained results also apply under the assumption that the models approximately predict the outputs of human computations. Here “approximate” means that the approximate prediction does not differ from the exact prediction by more than some small constant factor. For ideas on how approximation can be explicitly taken into account in fixed-parameter tractability analyses we refer the reader to Hamilton et al. (2007) and Marx (2008).

Intractability of Generic Communication

Our two main computational intractability results are:

Result 1. The RECEIVER problem is NP-hard.

Result 2. The SENDER problem is NP-hard.

These results establish that both RECEIVER and SENDER problems are computationally as hard to compute as a whole class of problems that are strongly conjectured to be intractable, called the NP-complete problems, and possibly even harder. This means that SENDER and RECEIVER problems cannot be computed efficiently (more precisely, in polynomial-time) unless all NP-complete problems can be (Garey and Johnson, 1979; Aaronson, 2005; Fortnow, 2009). As there is both theoretical and empirical evidence that no NP-complete problem allows for an efficient solution procedure we conclude that RECEIVER and SENDER problems, as we have defined them, are intractable. We note that our Results 1 and 2 are, to the best of our knowledge, the first formal proofs that are consistent with intuitive claims of intractability in the communication literature (Levinson, 1995, 2006; Pickering and Garrod, 2004; Barr and Keysar, 2005).

Identifying Conditions for Tractability

Importantly, our analyses do not stop at the intractability results (Results 1 and 2). On the contrary, we view such results as merely the fruitful starting point of rigorous analyses of the sources of complexity in human communication. For these further analyses we adopt a method for identifying sources of intractability in cognitive models developed by van Rooij and Wareham(2008; see also van Rooij, 2008; van Rooij et al., 2008). The method builds on concepts and techniques from the mathematical theory of parameterized complexity (Downey and Fellows, 1999), and works as follows.

First, one identifies a set of potentially relevant problem parameters K = {k₁, k₂,…, k_m} of the problem P under study (for us, the RECEIVER and SENDER problems). Then one tests if it is possible to solve P in a time that can grow excessively fast (more precisely: exponential or worse) as a function of the elements in the set K = {k₁, k₂, …, k_m} yet slowly (polynomial) in the size of the input⁴. If this is the case, then P is said to be fixed-parameter (fp-) tractable for parameter set K, and otherwise it is said to be fp-intractable for K. Observe that if a parameter set K is found for which P is fp-tractable then the problem P can be solved quite efficiently, even for large inputs, provided only that the members of K are relatively small. In this sense the “unbounded” nature of K can be seen as a reason for the intractability of the unconstrained version of P. Therefore, we also call K a source of intractability of P.

The RECEIVER and SENDER models have several evident parameters, each of which may be a source of the intractability inherent in the general problems postulated by these models. Table 1 gives an overview of the parameters that we consider here. Using the abovementioned methodology for fp-tractability analysis we have been able to derive a set of fp-(in)tractability results, which are summarized in Table 2. We will discuss these results and what they imply for the tractability of the RECEIVER and SENDER under different situational constraints.

TABLE 1

Table 1. Overview of parameters considered in our tractability analyses.

TABLE 2

Table 2. Overview of complexity results and open questions for RECEIVER problem (top) and SENDER problem (bottom).

We start by considering the fp-(in)tractability of the RECEIVER problem. We have two main fp-tractability results:

Result 3. The RECEIVER problem is fp-tractable for parameter set {|G_I|, |G_C|}.

Result 4. The RECEIVER problem is fp-tractable for parameter set {|G_I|, 1 − p}.

Note that, by definition, if a problem is fp-tractable for a parameter set K then it is also fp-tractable for any superset K′ ⊇ K. Hence, Results 3 and 4 imply all other fp-tractability results listed in Table 2 for the RECEIVER problem, including the fp-tractability of the problem for the combined parameter set {|G_I|, |G_C|, 1 − p}.

Result 3 establishes that it is possible to compute the input–output mapping defined by the RECEIVER problem in a time which grows fast (read: exponential) only in the two parameters |G_I| and |G_C|, and slow (read: polynomial) in the remainder of the input, regardless the size of other input parameters. Result 4 establishes that it is also possible to compute the input–output mapping defined by the RECEIVER problem in a time which grows fast only in the two parameters 1 − p and |G_I|, and slow in the remainder of the input, regardless the size of other input parameters (including |G_C|). Informally, this means that the inference task modeled by the RECEIVER problem can be performed fast, even for large networks of beliefs, if the number of possible instrumental goals that the receiver believes the sender may have (|G_I|) is relatively small and at the same time either the number of communicative goals is relatively small or the probability of the most likely communicative goal attribution (p) is relatively large.

These mathematical results lead to a clear prediction. A receiver is able to quickly attribute communicative intentions to a sender’s actions if the number of instrumental goals that the receiver assumes that the sender is pursuing in parallel to her communicative goals is small and the sender does not have many communicative goals she wishes to convey simultaneously, or otherwise she was able to construct a sequence of actions that leads to a signal of low ambiguity (captured by small 1 − p).

Importantly and perhaps counter intuitively, low ambiguity of the signal is by itself not sufficient for tractability, as we have the following intractability result.

Result 5. The RECEIVER problem is fp-intractable for parameter set {1 − p}.

Similarly, a small number of communicative goals is by itself not sufficient for tractability, as we also have the following fp-intractability result.

Result 6. The RECEIVER problem is fp-intractable for parameter set {|G_C|}.

However, if senders were to focus solely on communicating (and forgetting for the moment about any other instrumental goals they may also want to achieve), then |G_I| = 0, and hence low ambiguity (or small number of communicative goals) would by itself suffice to make the inference task easy for the receiver. The reason that low ambiguity (or small number of communicative goals) is not enough for tractability for |G_I| > 0 is that, in order to compute the probability of the most probable communicative goal assignment, the receiver needs to do this computation against the background of all possible instrumental goals a sender may have, as having one or more of those can affect the probability of the target communicative goals. The number of possibilities that the receiver needs to be taken into account grows, in this case, exponential in |G_I|, and therefore the computation is too resource demanding to be done efficiently for large |G_I|.

Having seen that neither large p nor small |G_C| are by itself sufficient for tractability of the RECEIVER problem, but that combining either with small |G_I| does yield tractability, one may ask if there are other combinations of constraints that are sufficient for tractability of the RECEIVER problem. As can be seen from the overview of fp-(in)tractability results in Table 2, no combination of parameters excluding {|G_I|, |G_C|} or {|G_I|, 1 − p} as subsets yields fp-tractability for the RECEIVER problem. This means that these two sets seem to fully characterize what makes the RECEIVER problem difficult or easy (at least, relative to the total set of parameters that we consider here and listed in Table 1).

As the parameter |G_I|, |G_C| and 1 − p all seem to be, to some extent, under the control of the sender, Results 3 and 4 raise the question of how computationally complex it is for senders to ensure these parameters (or pairs of them) are small, and thereby make the intention attribution task tractable for receivers. We will discuss a set of results that are relevant to this question, starting with the following:

Result 7. The SENDER problem is fp-intractable for parameter set {|G_I|, |G_C|}.

In other words, the RECEIVER problem being tractable is by itself not sufficient for the SENDER problem to be tractable (compare Result 3 and Result 7). Additional constraints need to be assumed to explain the tractability of the sender’s task. Result 8 shows that a low upper-bound on the length of the sequence of actions that needs to be planned can help make the sender’s task easier.

Result 8. The SENDER problem is fp-tractable for parameter set {|A|, |G_I|, |G_C|}.

Result 8 can be understood as a consequence of the ability of a sender to use the same fp-tractable algorithm that the receiver can use to tractably infer the sender’s communicative goals to predict the receiver’s interpretation of a given action sequence, and then search the space of action sequences (which is exponential only in |A|) for a sequence that yields the right receiver inference. This algorithmic strategy does not yield fp-tractability for the Sender problem for the parameter set {|A|, |G_I|, 1 − p}, because contrary to |G_C|, which is constant for all action sequences the sender may consider, the value of 1 − p is different for different candidate action sequences. As a result, 1 − p cannot generally be assumed to be small for all possible action sequences. Whether or not a different strategy exists that can exploit this combination of parameters for solving the SENDER problem in fixed-parameter tractable time is currently unknown:

Open question. Is the SENDER problem is fp-tractable for parameter set {|A|, |G_I|, 1 − p}?

What we do know is that no other combination of parameters excluding {|A|, |G_I|, |G_C|} as a subset suffices to render the SENDER problem fp-tractable. If future research were to reveal that the SENDER problem is fp-tractable for parameter set {|A|, |G_I|, 1 − p}, then this would indicate that given that the RECEIVER problem is tractable (e.g., Result 3 and 4) parameter a bound on |A| suffices for tractability of the SENDER problem. If, on the other hand, it would turn out that the SENDER problem is fp-intractable for parameter set {|A|, |G_I|, 1 − p}, then this would underscore the high complexity of the SENDER problem, as it is impossible for the input to the SENDER problem to be large when all three parameters |A|, |G_I|, and |G_C| are small at the same time.

Discussion

We analyzed the complexity of two models of senders and receivers in a communicative exchange. In Section “Implications and Predictions for Cognitive Neuroscience” we will discuss the implications of our findings for cognitive neuroscience, including a set of empirical predictions testable by cognitive neuroscience methods. All predictions made in this section must, of course, be understood relative to the models that we studied, which inevitably make some basic assumptions about properties of the mental representations of receivers and senders in the communication task. In Section “Open Theoretical Questions and Future directions” we will explicitly discuss these assumptions and give pointers for possible extensions or adaptations of the models. As such new model variants need not inherit all the (in)tractability results from our SENDER and RECEIVER models they naturally yield a set of open questions for future theoretical research.

Implications and Predictions for Cognitive Neuroscience

We presented two new models of the tasks engaging senders and receivers during a communicative exchange: see the RECEIVER and SENDER models in Section “A BIP model of Sender and Receiver.” As these models are situated at Marr’s (1982) computational level, they are not bound to particular assumptions about a specific algorithm that human brains would use to perform the postulated computations, nor about how these algorithms are exactly implemented in neural mechanisms. They merely state the hypothesized input–output mappings assumed to underlie the receiver and sender tasks in communication respectively. This high level of abstraction has the benefit of generalizability, i.e., the sources of intractability identified in the models are inherent in the problems that they describe, and not specific to particular algorithms for solving those problems or implementations thereof. As a consequence, our intractability results are proofs of impossibility: no algorithmic implementation of any type, in any neural mechanism, can ever compute the problems quickly if the input domain is unconstrained.

It could be argued that, since human communication is evidently tractable for real humans in the real world, the present results are useless. However, the mismatch between model and reality is informative for improving formal models of human communication, and for rejecting claims that intentional communication is computationally trivial to explain (Rizzolatti and Craighero, 2004; Iacoboni et al., 2005). The results can help to avoid trying to account for situations that are in fact impossibilities as far as efficient human communication is concerned. In other words, the generic RECEIVER and SENDER models considered here are too powerful, i.e., they describe situations that preclude tractable computation. Many models in cognitive neuroscience which are powerful enough to cover a wide variety of domains, such as models of reinforcement learning (Gershman and Niv, 2010) or decision-making (Dayan, 2008), appear to have this property. This can be understood by the inherent computational complexity introduced by the (unconstrained) domain generality of computations, an issue that has long been known in artificial intelligence and cognitive science (Fodor, 1983, 2000; Pylyshyn, 1987; Haselager, 1997).

A major advantage of the current approach lies in its ability to indentify, from first principles, which situational constraints render the generic RECEIVER and SENDER models tractable. Our fp-tractability results show that there exist algorithms for efficiently computing the problems if the situations that arise are constrained in specific ways. For instance, we found that if receiver assumes that senders do not pursue many instrumental goals concurrently to their communicative goals, and if they ensure that the most probable communicative goal assignment has high probability, then the receiver task is tractable. Similarly, we found that if senders do not pursue many instrumental and communicative goals, and use short action sequences for communication, then the sender task is tractable. Conditional on the validity of our assumptions, these findings are novel and important insofar that they describe those situations in which human communication could proceed efficiently. These results are testable in the context of novel experimentally controlled empirical approaches to communication, in particular those rapidly evolving in the new exciting domain of experimental semiotics (Galantucci and Garrod, 2011). This domain is focused on studying interactions that occur in the absence of pre-established communicative conventions, thereby allowing researchers an unprecedented level of experimental control over the communicative means and goals of the communicators. Accordingly, communicative interactions are studied in the context of non-verbal tasks. This approach allows one to disambiguate the ability to solve genuine communicative problems de novo, from the implementation of empirical generalizations from past experience. This approach also excludes that communicators simply exploit a pre-existing communicative system powerful enough to mutually negotiate new communicative behaviors, an obvious non-sequitur for understanding how human communicative abilities come into place. The communicative games designed according to these principles appear amenable to manipulation of the crucial parameters that have emerged from the present analysis of computational complexity, namely the number of instrumental goals that a sender needs to accomplish during a communicative exchange, or the number of actions afforded by a sender. Furthermore, bringing these present results to the level of empirical research will be beneficial for highlighting some of the simplifications inherent in developing a computational-level account of human communicative abilities. For instance, translating the present results into empirical studies will require non-trivial operationalization of abstractions like “actions” and “goals.”

The fp-tractability results are possibility proofs in the sense that there exist fp-algorithms that can perform the sender and receiver tasks quickly if certain situational parameters are constrained to take small values. Specifically, we proved the existence of an fp-tractable algorithm for the SENDER problem which exploits small values for parameters |A| (the number of to be planned sender actions), |G_I| (the number of sender instrumental goals), and |G_C| (the number of sender communicative goals). Furthermore, we proved the existence of an fp-tractable algorithm for the RECEIVER problem that can exploit the same set of parameters, or even a smaller set which does not include |A|. In addition, we proved the existence of an fp-tractable algorithm for the RECEIVER problem that can exploit the parameters |G_I| and 1 − p (where p is the probability of the most likely communicative goal attribution). Whether or not human brains actually use and implement such fp-tractable algorithms is an empirical question. Note that posing this question is only made possible by the type of complexity analysis described in this paper. We believe this is a relevant question, as it stems from a principled analysis rather than occasional observations. The cognitive neuroscience literature is replete with examples of cerebral responses being attributed to “task difficulty” on the basis of introspections. Here, we show how task difficulty could be formally parameterized. This approach opens the way for using cognitive neuroscience methods to test whether and how human brains exploit similar fp-tractable computations to efficiently solve communicative problems. The prediction to be tested is that resource demands during human communication should be extremely sensitive to the parameters identified as critical for tractability of the model. Recall that an fp-tractable algorithm for parameters {k₁, k₂, …, k_m} runs fast if and only if all the parameters k₁, k₂, …, and k_m are constrained to sufficiently small values in the current input (i.e., situation). If, in the lab, one were to create communication tasks in which the critical parameters can be systematically manipulated, then two critical predictions follow from the hypothesis that the senders use, say, the fp-tractable algorithm underlying Result 8, and receivers use the fp-tractable algorithm underlying Result 3 or 4:

(1) As long as |A|, |G_I|, |G_C|, and 1 − p remain small the task of communication should proceed efficiently.

(2) As soon as two parameters in the set {|G_I|, |G_C|, 1 − p} take on large values, the task of communication would start to consume an excessive amount of computational resources (for sender and/or receiver, depending in which the relevant parameters are large), which may be reflected in a decrease of speed, increase of communicative errors, and/or increased brain activities in certain brain areas underlying the relevant computations.

If these predictions were to be confirmed, then this result would provide evidence for both cerebral use of fp-tractable computations, and for the RECEIVER and SENDER models as defined above. A natural next question would then be how these algorithms are neurally implemented. If, on the other hand, the predictions were to be disconfirmed, then two interpretations are open. Either, the RECEIVER and SENDER models are not valid, and this would motivate new modeling directions; or RECEIVER and SENDER models are valid, but humans use different fp-tractable algorithms for computing them, exploiting parameters other than the ones that we have studied here. This latter option is not excluded, as there may be parameters of the problems outside the set described in Table 1. Constraining these additional parameters may render computation of these problems tractable as well. Both research directions appear highly informative.

We end this section by remarking that complexity results, such as we have derived here, also expand the ways in which computational-level models can be tested for input–output equivalence with human communicators. This form of testing involves presenting a participant with a situation that can be described as a particular input in the model’s input domain, computing the output that according to the model corresponds to that input, and testing if the responses of the participant match the predicted outputs. This test is quite common in cognitive science, and was also the method used by Baker et al. (2007, 2009) to test their computational-level model of (instrumental) goal inference. However, this methodology is often used within particular “toy-scenarios,” where the tested situations need to be exceedingly simple, such that inputs can be explicitly modeled and output computation is tractable for the researcher (see e.g., Oztop et al., 2005; Cuijpers et al., 2006; Erlhagen et al., 2006; Baker et al., 2007; Yoshida et al., 2008). Without a clear estimate of the complexity of the problem at hand, the results found within the boundaries of those toy-scenarios might easily fail to scale up to more complex and realistic domains. For instance, those computational models of goal inference that seem to work (i.e., that make plausible goal inferences without running into tractability issues) severely restrict the possible contexts and the number of possible actions and goals, keeping their application domain far removed from realistically complex situations. In contrast, the present results enable communication researchers to move away from trivial “toy domains,” using the fp-tractable algorithms identified here to expand the domains in which to compute predicted input–output mappings (for details on the algorithms see the Appendix). In cases where it is difficult or impossible to get an explicit model of the entire communicative setting, our proposed methodology of testing sources of tractability in the computational-level models of interest can be used instead.

Open Theoretical Questions and Future Directions

For our case study, we opted for analyzing the RECEIVER and SENDER models as defined in Section “A BIP model of Sender and Receiver.” By doing so, we made several commitments that may have affected our complexity results. We will briefly highlight those commitments known to affect the results, and those which we believe are unlikely to have had an effect. We will distinguish between model-specific commitments (such as the nature of the connectivity of the input networks and assumptions about the amount and type of information available to senders and receiver) and our choice of formalism (i.e., a probabilistic formalism).

The models that we defined make the strong commitment that there is no direct (probabilistic) dependency between states and goals, as all such dependencies are assumed to be mediated by actions (see Figures 2 and 3). This assumption seems problematic if one considers that states of the world may make certain goals of an actor more likely (e.g., if a cup is present and within reach, then a grasping action toward that cup is more likely to have as goal “grasp the cup,” as compared to a situation where the cup is not present, or out of reach). Although this commitment strictly speaking reduces the validity of the model, we know it has no effect on our complexity results (they would apply equally well to a model that allows for direct state-goal dependencies). The reason is that the model makes an additional assumption, namely the assumption that all relevant states and actions are observable by the receiver. This brings us to the point of validity of this assumption.

Although complete observability may hold true in some situations (and in those situations the models may thus apply without problem), it is likely that in many real-world situations not all relevant actions and states are observable. Think, for instance, of the possibility that part of a visual scene is occluded by nearby objects or even an eye blink. Then some actions and state changes may be observed directly, while others need to be inferred by an observer. Humans are often able to do this, and models of receivers should be able to explain how they can do so. Because our fp-tractability results reported in Section “Computational Complexity Results” heavily depend on the assumption of complete observability, we must admit that our analyses have not yet shed light on how communication can proceed efficiently under conditions of partial observability. Future research on the computational complexity of model variants that include the assumption of partial observability are thus called for.

Another important property of our models is that they assume that the sender and receiver know everything that is relevant to the context of the communicative exchange, including which action and goal variables are relevant, and their probabilistic interdependencies. Clearly, this assumption sweeps a considerable amount of computational complexity under the rug; after all, computing the set of relevant information itself may well be computationally very resource demanding. Be that as it may, our analyses apply in those cases where humans do have complete knowledge of everything relevant to the communication task, and this is a condition that can certainly be met in laboratory settings used to investigate sources of complexity in communication as suggested in Section “Implications and Predictions for Cognitive Neuroscience.” Also, our analyses show that even if there are not an indefinite number of intentions that senders and receivers may entertain (see our Introduction), communication under simpler models can still be intractable. In contrast, even in the case where sender and receiver have complete common ground on the set of possible sender goals, the planning biases of the sender (i.e., the probabilistic dependencies between sender’s goals and actions, and world, as well as how those dependencies change over time) and all events that are relevant to the interpretation of the sender’s actions, still the task of communication is computationally intractable. Future research may address the additional computational complexities introduced by establishing this common ground in the first place. This could be done by building an explicit model of that process and submitting it to the same sort of complexity analyses as we have performed here for the SENDER and RECEIVER models.

Last, we reflect on our choice of formalism: we opted for Bayesian networks as a formal representation of communicators’ situational knowledge and we used the mathematical notion of posterior probability to define the intuitive notion of “inference to the best explanation.” This choice of probabilistic formalism aligns our models with the current trend in cognitive neuroscience, which assumes that the brain implements its cognitive functions by means of probabilistic computations (Wolpert and Ghahramani, 2000; Ma et al., 2006), including the cognitive function of inferring people’s goals and intentions from their actions (Cuijpers et al., 2006; Baker et al., 2007, 2009; Kilner et al., 2007a,b). Importantly, our complexity results should not be seen as bound to this formalism. It is well known that knowledge structures can be represented using other formalisms, such as (non-classical) logics or as constraint networks (van Ditmarsch et al., 2007; Russell and Norvig, 2009). In those cases, “Inference to the best explanation” could be defined in terms of logical abduction (e.g., Bylander et al., 1991; Eiter and Gottlob, 1995; Nordh and Zanuttini, 2005, 2008) or constraint satisfaction (e.g., Thagard and Verbeurgt, 1998; Thagard, 2000). The present results would apply to those alternative formalisms, provided that the same basic structural information is encoded in the representations of those alternative formal languages. If models identical or similar to those analyzed in this paper get expressed in the different formalisms, chances are that all such formal model variants can be transformed into each other via mathematical reductions not unlike the one we used to prove that the Sender and Receiver models are of the same computational complexity as the known intractable logic problem called Satisfiability (see Computational Models and Computational Complexity Analyses). One would not want complexity predictions to depend on the formal language chosen to express a model, in the same way that one would not want a verbal theory to lead to different predictions if it is expressed in English or in Dutch.

Conclusion

Recent accounts of human communication have focused on the motoric abilities of individual agents (Iacoboni et al., 2005), as if the meaning conveyed by a pointing finger were an intrinsic property of that action. Others have correctly highlighted the fact that, when unconstrained, human communication is intractable (Levinson, 1995, 2006). Here we have tried to move our knowledge forward, showing that those positions are case limits of a continuum as a function of the constraints applicable to the inferences involved in human communication. We believe the approach exemplified in this paper has the potential to formally define sources of computational complexity, opening the way to tackle some hard problems in intentional communication. Acquiring this knowledge appears fundamental to generate a neurobiologically grounded formal account of the computational mechanisms supporting our communicative abilities, which is a necessary step to understand the biological and cognitive bases of human sociality.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would like to thank the reviewers for their valuable comments on an earlier version of this article. Johan Kwisthout was supported by the OCTOPUS project under the responsibility of the Embedded Systems Institute. Mark Blokpoel was supported by a DCC PhD grant awarded to Iris van Rooij and Ivan Toni. Todd Wareham was supported by NSERC Personal Discovery Grant 228104. Jakub Szymanik was supported by NWO (VICI grant #277-80-001). Ivan Toni was supported by NWO (VICI grant #453-08-002).

Footnotes

^In other words, in the BIP model, goal inference is conceptualized as a form of probabilistic inference to the best explanation, a.k.a. abduction (Charniak and Shimony, 1990). As this model is situated at Marr’s (1982) computational level, the theory is in principle consistent with a variety of hypotheses about the architecture that implements the postulated computations, ranging for instance from predictive coding or forward models (Miall and Wolpert, 1996; Oztop et al., 2005; Kilner et al., 2007a,b) to neural network models (Paine and Tani, 2004) or random sampling models (Vul et al., 2009).
^We remark that the computational-level SENDER and RECEIVER models that we propose are in one respect a simplification and in another an enrichment of the Shafto and Goodman (2008) model (see also Frank et al., 2009). Our models are a simplification in the sense that they do not assume infinite recursive reasoning by sender and receiver about each other, in contrast to the Shafto and Goodman model. Our model is an enrichment in the sense that we adopt the Bayesian network structure of the Baker et al. (2007, 2009) BIP model to have a more general characterization of the assumed dependencies between states, goals, and actions.
^We are aware of computer simulation studies in the cognitive science literature that seem to suggest that Bayesian models can be efficiently approximated (Vul et al., 2009; Sanborn et al., 2010). However, the intractability results for approximating Bayesian computations available in the computer science literature show that these “simulation-based approximability findings” cannot generalize to all types of inputs, but only to some that have special properties (cf. “parameters”) that can be exploited for tractable (exact or approximate) computation (Kwisthout et al., in 2011).
^More formally, this would be a time on the order of f(k₁, k₂, …, k_m)n^c, where f is an arbitrary computable function, n is a measure of the overall input size, and c is a constant.

References

Aaronson, S. (2005). NP-complete problems and physical reality. SIGACT News Complex. Theory Column 36, 30–52.