Equilibrium and response properties of the integrate-and-fire neuron in discrete time
- 1 RIKEN Brain Science Institute, Wako City, Japan
- 2 Bernstein Center Freiburg, Albert-Ludwig University, Freiburg, Germany
- 3 Computational Neuroscience, Faculty of Biology, Albert-Ludwig University, Freiburg, Germany
- 4 Institute for Neuroscience and Medicine (INM-6), Computational and Systems Neuroscience, Research Center Jülich, Germany
- 5 Brain and Neural Systems Team, Computational Science Research Program, RIKEN, Wako City, Japan
A generic property of the communication between neurons is the exchange of pulses at discrete time points, the action potentials. However, the prevalent theory of spiking neuronal networks of integrate-and-fire model neurons relies on two assumptions: the superposition of many afferent synaptic impulses is approximated by Gaussian white noise, equivalent to a vanishing magnitude of the synaptic impulses, and the transfer of time varying signals by neurons is assessable by linearization. Going beyond both approximations, we find that in the presence of synaptic impulses the response to transient inputs differs qualitatively from previous predictions. It is instantaneous rather than exhibiting low-pass characteristics, depends non-linearly on the amplitude of the impulse, is asymmetric for excitation and inhibition and is promoted by a characteristic level of synaptic background noise. These findings resolve contradictions between the earlier theory and experimental observations. Here we review the recent theoretical progress that enabled these insights. We explain why the membrane potential near threshold is sensitive to properties of the afferent noise and show how this shapes the neural response. A further extension of the theory to time evolution in discrete steps quantifies simulation artifacts and yields improved methods to cross check results.
1 Introduction
Understanding neural networks requires the characterization of how neurons transfer synaptic inputs to a sequence of outgoing action potentials. A basic feature of neuronal interaction is the emission of action potentials, each causing a small change of the membrane potential in the receiving cell. The integrate-and-fire neuron model has a long history in neuroscience (Lapicque, 1907; Gerstein and Mandelbrot, 1964; Stein, 1965) reviewed in Brunel and van Rossum (2007). Despite its simplicity the model successfully reproduces prominent features of neuronal dynamics, for example it qualitatively captures the relation between injected current and firing rate (Rauch et al., 2003; La Camera et al., 2004). Equipped with an additional adaptation mechanism, the model also reproduces with high accuracy the sequence of action potentials of a neuron subject to current injection (Jovilet et al., 2008).
The transmission properties of neuron models not only depend on the signal to be transmitted, but also on the activity of the remaining input channels of the cell. The remaining inputs can be regarded as noise with respect to the signal under consideration. If this background noise level is low, a population of neurons faithfully transmits an injected current stimulus up to high frequencies (Knight, 1972; Gerstner, 2000). Independent of the origin of the noise and the associated noise model, the framework of spike response models (Gerstner, 2000) shows that for increasing noise level the transmission becomes progressively more smooth. Often the impact of the signal on the neural dynamics can be assumed to be small compared to the entire synaptic barrage so that a linear approximation of the response is justified. Linear responses to arbitrary transient signals can be constructed as superpositions of responses to sinusoidal variations of the considered signal variable, such as the afferent firing rate. Since a neuron receives many synaptic afferents each having only a small impact, a common approach is to replace the total synaptic input by a Gaussian white noise in the so called diffusion approximation: only the mean μ and the variance σ2 of the total input are kept (Siegert, 1951; Johannesma, 1968; Ricciardi and Sacerdote, 1979; Lánský, 1984; Risken, 1996). In this approximation, the afferent spike trains to a neuron translate into – possibly time dependent – parameters μ(t) and σ(t) of the corresponding Gaussian white noise. Mean and variance can vary independently for example by different co-modulations of the rate of excitatory and inhibitory afferents. For the leaky integrate-and-fire neuron a modulation of the mean was found to cause a low-pass response, whereas modulations of the variance are transmitted instantaneously (Lindner and Schimansky-Geier, 2001) up to linear order. Experiments confirmed these transfer properties for Gaussian white noise currents injected into cells in vivo (Silberberg et al., 2004).
Realistic synaptic currents are extended in time, causing low-pass filtering and the suppression of fast fluctuations in the total input current. Given such filtered background noise, modulations of the mean are transmitted up to arbitrarily high frequencies (Brunel et al., 2001; Fourcaud and Brunel, 2002), equivalent to an immediate response. For more realistic onset dynamics of the action potential the neuron model becomes a low-pass (Fourcaud-Trocmé et al., 2003). However, the cutoff frequency increases with the speed of voltage change at action potential onset (Naundorf et al., 2005) and can reach very high frequencies.
The literature cited above rests on the assumption, that the sum of the synaptic inputs can be approximated as Gaussian white noise. However, synaptic inputs arrive as small impulses. Therefore, the work reviewed here (Helias et al., 2010a) reconsiders the integrate-and-fire model neuron, the simplest neuron model which allows us to study the impact of finite and identical synaptic impulses on the stationary and transient neural properties. The analysis of such neural dynamics is complicated, because it comprises two qualitatively different processes. On the one hand, the membrane voltage continuously changes in time in a deterministic way due to ionic currents through the membrane. On the other hand, the incoming synaptic impulses typically arrive at discrete, unpredictable time points and cause rather sudden changes of the voltage. Very recently, for the case of finite synaptic amplitudes drawn randomly from an exponential distribution at each incoming impulse, an exactly solvable framework was presented (Richardson and Swarbrick, 2010). The firing rate, the membrane potential distribution and the response properties are in qualitative agreement with the results for identical synaptic amplitudes, focused on in the present review.
In Section 2 we illustrate that the frequently invoked diffusion approximation causes artifacts and we show how to remedy them by the recently developed theory (Helias et al., 2010a). As a result, in Section 3 we show how neurons can employ the pulse-like synaptic interaction in order to foster fast signal transfer and to perform non-linear operations on short transient signals. In the presence of many synaptic afferents, a single synaptic impulse is intuitively lost in the total synaptic barrage. In Section 4 we show, however, why the reverse is true: in the presence of a certain number of synaptic inputs a neuron operates optimally. The issue of artifacts by shortcomings of neural simulation tools and how they can theoretically be addressed (Helias et al., 2010) is the topic of Section 5. Finally, in Section 6 we summarize our results, put them into the context of the existing literature and provide an outlook.
2 Shishi Odoshi – The Deer Scarer
In this review we illustrate recent conceptual advances in the theory of neuronal dynamics using a model reduced to the fundamental mechanisms. The model is not an abstract equation but has a concrete analogy. The shishi odoshi, as it is depicted in Figure 1A is frequently found in Japanese gardens and used to chase away deers (or birds) and please humans. A bamboo tube, open at one end, accumulates water. Once the tube is filled, the shishi odoshi tilts and the water drains (Figure 1C). Returning into the initial position the shishi odoshi starts over again. The basic operation of a neuron is very similar: Each incoming excitatory synaptic impulse from other neurons causes the membrane potential to depolarize by a small amount, like the shishi odoshi in the rain (Figure 1B). Once a threshold value Vθ is reached, the neuron fires an action potential, the voltage returns to the reset potential Vr, and the process begins from the start. This analogy has probably been made several times before; just recently we found the work by Misonou (2010). Technically, the equation describing both the shishi odoshi and the above reduction of neuronal dynamics is called the perfect integrator. Despite its simplicity, the dynamics still captures some properties that remained unexplained by contemporary theory. For illustration, we decided to resort to the analogy of the shishi odoshi, because it allows an intuitive understanding of the concepts underlying the mathematical formulation (Helias et al., 2010a; Richardson and Swarbrick, 2010).
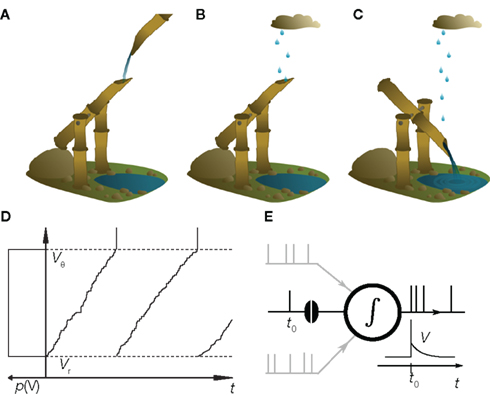
Figure 1. The shishi odoshi is analogous to a neuron. (A) Water, traditionally from a steady source, accumulates in a bamboo tube. (B) Raindrops that hit the opening are a better analogy for the synaptic impulses received by the neuron. (C) Once the water level reaches a critical value, the shishi odoshi tilts, releases the accumulated water, and returns to its original position causing the characteristic knocking sound when the bamboo hits the stone. (D) Similarly, a neuron integrates synaptic input until the membrane potential V reaches a threshold voltage Vθ (upper dashed line). Then the neuron generates an action potential (a spike, vertical marking) and the membrane potential is reset to Vr (lower dashed line). If the neuron receives random excitatory input pulses, the probability distribution p(V) of the membrane potential is uniform (sketched to left of the vertical axis). (E) In the presence of many synaptic afferents (gray) p(V) determines how an additional synaptic impulse (black spike at t0) influences the neuron’s time dependent firing rate ν(t).
Consider a shishi odoshi in persistent, heavy rain (Figure 1B). If we watched the level of water V(t) in the tube, we would see a typical time course as shown in Figure 1D. The same holds for a neuron receiving a bombardment of excitatory synaptic impulses. The membrane voltage V(t) increases until it reaches the threshold value Vθ and the neuron emits an action potential (indicated by the markings at the top of Figure 1D). After such an event, both in case of the shishi odoshi and the neuron, V is reset to Vr. On the left side of the figure the probability of the perfect integrator to assume a particular value of V is shown. Since V travels through the range Vr to Vθ with constant speed on average, the probability density is the same for all values in the range. The number of raindrops falling into the tube within a time interval varies from interval to interval, so a frequently made approximation of the total input is a constant current with some fluctuations, as opposed to many individual inputs. Formally, this replacement is achieved by considering the effect of each input to vanish as the rate of arrival goes to infinity (see Lánský, 1984, for a rigorous derivation). The stationary properties of a neuron in this so called diffusion approximation or Fokker–Planck theory (Risken, 1996; Ricciardi et al., 1999) are known since long (Siegert, 1951; Johannesma, 1968; Ricciardi and Sacerdote, 1979; Risken, 1996). For the special case of individual excitatory synaptic impulses the steady state probability density can still be obtained analytically (Sirovich et al., 2000; Sirovich, 2003). If the amplitude of excitatory and inhibitory synaptic impulses are drawn randomly from an exponential distribution, the stationary firing rate is known analytically (Jacobsen and Jensen, 2007). For this case, a recently presented analytical framework also allows to calculate the membrane potential distribution and the response properties up to linear order (Richardson and Swarbrick, 2010).
Before we delve into the theory let us pause for a moment and consider what happens in the vicinity of the threshold in the diffusion approximation in contrast to the situation in the model. In this region, shaded in Figure 2A, random fluctuations of the input cause a threshold crossing the more likely the closer V gets to Vθ. At Vθ, the system immediately crosses the threshold, or fluctuates to a slightly smaller value, since it is impossible to have no fluctuation at all. Hence in the diffusion approximation, the probability p(V) has to drop to zero at Vθ (Brunel et al., 2001) as shown in Figure 2A. However, this is not what happens in the real system where the input is composed of many small input events, drops of water or excitatory synaptic impulses respectively. Here inputs are not received continuously, but rather at specific points in time. Upon reception of such an input event V(t) jumps to a new, slightly larger value. These little jumps happen often, and drive V(t) up close to the threshold. Contrary to the diffusion case, the probability p(V) does not have to approach 0 close to threshold. Instead V(t) jumps over the threshold when the next input event is received, so for all voltages below threshold the picture is just the same. Thus in the actual system, p(V) is flat all over the range from Vr to Vθ, in particular also in the shaded area in Figure 2B. This fact has been known for deterministic input since the work of Knight (1972) and here we extended the argumentation to the arrival of input pulses at random points in time. So apparently the description of the system in the diffusion approximation leads to discrepancies in the probability distribution of V close to the threshold Vθ. Formally, the value p(Vθ) at threshold is called the boundary condition.
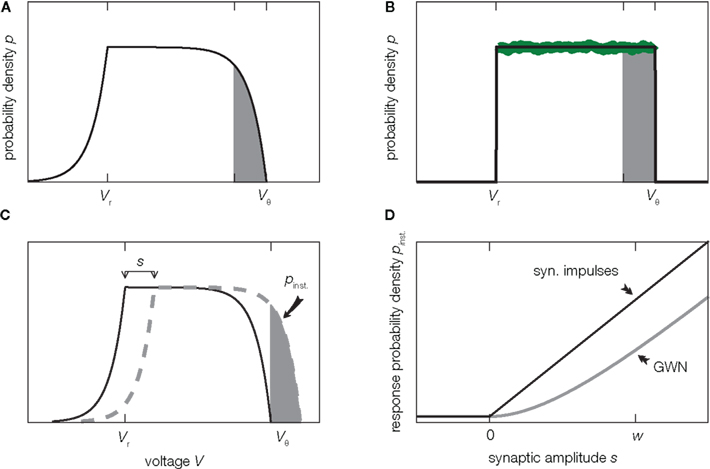
Figure 2. Background shapes equilibrium density and response. (A) Probability density of voltage V of a perfect integrator driven by Gaussian white noise (2). (B) Probability density of a perfect integrator driven by excitatory synaptic impulses of finite size w causing the same drift and fluctuations as in (A) given by (3). The green curve shows the collective histogram of a direct simulation of a population of 20,000 model neurons with random initial conditions observed for 1 s (bin size (Vθ − Vr)/100 same as line width of black curve). The density near threshold most strongly differs on the scale of the synaptic amplitude w (gray shaded region). (C) An additional excitatory impulse of amplitude s shifts the density (here for Gaussian white noise background input), so that the gray shaded area exceeds the threshold. (D) The probability Pinst. to respond with an action potential corresponds to the area of density above threshold in (C). Pinst. depends on the shape of the density near threshold and hence on the type of background input (black: background of synaptic impulses of size w given by (5), gray: Gaussian white noise background (4). Further parameters used for this and all other figures are specified in Section 7.
As indicated above, the preceding argumentation is based on simplifications in order to explain the concepts. First of all, real neurons do not stay depolarized, but any deviation of the membrane potential from its resting value will decay in the absence of further input because of leak currents through the membrane. In the analogy of the shishi odoshi, such a leak corresponds to a small hole at the lower end of the bamboo tube. Furthermore here we considered excitatory input alone. In case of neurons in the brain, there are both excitatory and inhibitory synaptic inputs from other cells. The original publications deal with the leaky integrate-and-fire model (Helias et al., 2010, 2010a), including leak and inhibition in order to derive a general theory. Qualitatively, however, the above arguments apply just in the same manner. The correction provided by the theory becomes most important for the case of strong mean drive, as in the illustrative example presented here Figure 1. For excitation and inhibition of comparable strength (balanced regime), the deviation of the density from the diffusion approximation is typically smaller.
3 The Fast Response of Neurons
Depending on what is considered the “code” by which neurons communicate with each other, different aspects of the transformation of the synaptic input signal to the outgoing sequence of action potentials are of interest. Assuming action potentials to appear stochastically, their activity is well described by a time varying firing rate. In this view neurons communicate with a rate code and their transfer properties are determined by the stationary firing rate ν0. This rate obviously depends on the size of the postsynaptic potentials w elicited by an incoming synaptic impulse and by the frequency λ of their arrival. For the perfect integrator, the firing rate is ν0 = λw/(Vθ − Vr), because (Vθ − Vr)/w impulses are needed to bring the membrane voltage from reset to threshold. In this particular case the diffusion limit yields exactly the same firing rate. For more realistic neuron models, however, the firing rate differs from the diffusion approximation. In Helias et al. (2010a) we derive an analytical approximation correcting for these deviations for small impulses w, which is simpler than the iterative analytical solution (Cope and Tuckwell, 1979). For exponentially distributed synaptic amplitudes an analytically exact result for the firing rate became available recently (Richardson and Swarbrick, 2010).
Many studies investigating recurrent networks rest on the assumption that a population of neurons can be described by a time varying firing rate and that the barrage of synaptic impulses is well approximated in the diffusion limit, or equivalently, as an effective Gaussian white noise. The time varying firing rate then translates into continuously changing mean and variance of the corresponding Gaussian noise current (Brunel and Hakim, 1999; Lansky and Sacerdote, 2001; Mattia and Del Guidice, 2002, 2004). For small modulations of the population rate the modulation of the neural firing rate can be obtained in linear approximation (Brunel and Hakim, 1999; Brunel et al., 2001; Lindner and Schimansky-Geier, 2001). Non-linear neuron models require numerical solutions (Omurtag et al., 2000; De Kamps, 2003; Richardson, 2007, 2008) and neuron models with several dynamical variables, like synaptic currents, can be treated in the framework of the refractory density approximation (Chizhov and Graham, 2008). The approximation of neural transfer properties by linear response in the diffusion approximation has been proven to successfully capture the global features of recurrent network dynamics (Brunel and Hakim, 1999; Brunel, 2000; Mattia and Del Guidice, 2002, 2004) as well as qualitative properties of the transmission of correlated activity by pairs of neurons (De la Rocha et al., 2007; Shea-Brown et al., 2008). In this section we illustrate which features of neural transfer are missed by neglecting that neurons communicate by synaptic impulses. To this end, we focus on the firing rate of a neuron triggered on the arrival of an incoming synaptic impulse of amplitude s, as illustrated in Figure 1E, assuming the other afferents are active irregularly.
Although the differences in the membrane potential distribution for Gaussian noise input and for finite synaptic jumps are most pronounced within a narrow range of voltages below threshold (Figures 2A,B, shaded area), these differences noticeably affect the transmission of transient signals by a population of neurons. The reason is, that the width of the range is comparable to the amplitude w of a postsynaptic potential of the background activity. A single synaptic impulse of amplitude s can elicit an action potential in the cell, if the membrane potential is closer to threshold than s. This means that the fraction Pinst. of cells that fire a spike in direct response to this impulse is equal to the shaded area in Figure 2C. The shape of the density close to threshold (Figures 2A,B) determines the size of this area. Since for Gaussian white noise background input the density goes to zero at threshold, the response probability to lowest order grows quadratically for small synaptic amplitudes s, as shown in Figure 2D. Synaptic background input of finite impulses causes a finite, positive value of the density at threshold. So there are more neurons ready to fire and the response probability is larger and grows linearly in the amplitude s. Similar arguments have been invoked to explain the fast component in the presence of filtered Gaussian noise (Brunel et al., 2001) and in the spike response model at low noise (Gerstner, 2000).
In the example of the perfect integrator, the response to an incoming synaptic impulse is instantaneous in time. The fraction Pinst. of neurons in the population fires a spike in direct succession to the received input impulse. Also the diffusion approximation yields an instantaneous response for an excitatory impulse, because the event causes an impulse-like co-modulation of the mean and of the variance. The response to modulations of the variance is instantaneous in neurons (Silberberg et al., 2004) and in the integrate-and-fire model (Lindner and Schimansky-Geier, 2001), giving rise to an impulse in the firing rate response.
In the perfect integrator the firing rate immediately returns to its baseline value after the instantaneous response (Figure 3C). The reason is that the probability density remains effectively unchanged by the extra excitatory input: all neurons that where shifted across threshold are reinserted at the lower end of the density as illustrated in Figure 3A. For an inhibitory incoming input, however, the density is shifted away from threshold toward negative voltages. Consequently, after the impulse has been received, the firing rate of the population is zero, since there are no neurons with a voltage close enough to threshold, as shown in Figure 3B. Only gradually, as the neurons receive excitatory background spikes, will the gap in the density below threshold be reoccupied so the population reapproaches its equilibrium firing rate, as shown in Figure 3D. Hence, the responses to excitatory and inhibitory synaptic impulses are asymmetric, as recently observed in somatosensory cortex in vivo (London et al., 2010). In particular, the inhibitory response does not exhibit a fast component. This is in contrast to the prediction of the diffusion approximation, because here an inhibitory impulse causes the same impulse-like perturbation of the variance as an excitatory impulse, so the same fast response is expected in both cases. For exponentially distributed synaptic background pulses, this asymmetry persists. Richardson and Swarbrick (2010) showed that sinusoidal modulations of the rate of excitatory incoming impulses are transmitted in the limit of arbitrary high frequencies, while the modulation of inhibition is suppressed in this limit. The reason is the same as in the case of impulses illustrated in Figure 2C: excitatory synaptic impulses cause jumps over the threshold, whereas inhibitory impulses do not. The diffusion approximation would yield a symmetric result for excitation and inhibition. In motor neurons, Fetz and Gustafsson (1983) found that the integral of the firing rate response follows the time course of the EPSP on its rising flank, but not when the voltage decays. For the integrate-and-fire model neuron, where the EPSPs jump abruptly, this observation directly translates to the impulse-like response present for EPSPs but not for IPSPs. In more realistic models which include a rise time of the EPSP, this immediate response is dispersed over the rising flank of the voltage deflection. Earlier studies pointed out that this sharpening of the response is due to voltage trajectories crossing the threshold on the upstroke of the EPSP and correspondingly found a dependence on the rate of change of the voltage (Herrmann and Gerstner, 2001; Chizhov and Graham, 2008; Goedeke and Diesmann, 2008). Spike response models fitted to simulations of integrate-and-fire models provide a quantitative numerical solution for the non-linear asymmetric response in this case (Herrmann and Gerstner, 2001).
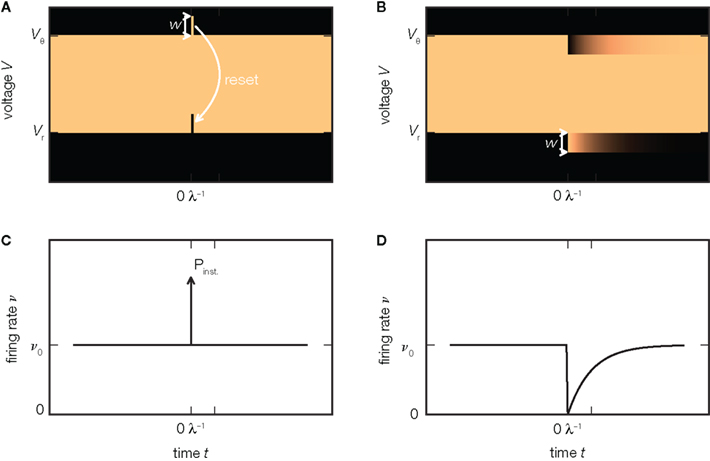
Figure 3. Asymmetry of response. (A) An additional excitatory impulse of amplitude w shifts the probability density (luminance coded, bright colors indicate high density) upward, so that a small part of the density exceeds the threshold. This leads to an instantaneous spiking response, visible as a δ-shaped deflection in the firing rate ν (C). The reset of the membrane voltage to Vr after the spike moves the excess density down, so that the density equals the state before the impulse. (B) An additional inhibitory impulse of amplitude −w deflects the density downward (7). It does not evoke a response concentrated at the time of the impulse (D). Instead, the firing rate ν drops and exponentially reapproaches its equilibrium value ν0 (D) as the density gradually relaxes to its steady state on a time scale 1/λ, with λ the rate of synaptic background impulses (6).
A similar observation is made in the leaky integrate-and-fire model (Helias et al., 2010a). In this case, however, the response to an excitatory impulse not only has an instantaneous component, but the firing rate is also slightly elevated thereafter over a time-span of milliseconds. The reason is the non-uniform probability density between reset and threshold. The shift due to the extra impulse deflects the population from its stationary state and it only gradually relaxes back.
4 Stochastic Resonance of Fast Response
A neuron in the cortex receives synaptic afferents from numerous presynaptic sources. The activity of these inputs often shows only small correlations (Ecker et al., 2010; Hertz, 2010; Renart et al., 2010). Intuitively one would suspect that the presence of the other synaptic inputs acts like noise (indicated as σ in Figure 4A), so that the effect of the single synaptic pulse at t0 becomes the more negligible, the stronger this noise is. One can therefore ask the question, whether the sequence of action potentials generated by the neuron still contains information about the spike timing of a particular incoming synaptic impulse (London et al., 2010). For some non-linear systems, like neurons, it is known that the transfer of a signal from input to output becomes optimal at a certain level of background noise. The effect is called stochastic resonance (reviewed in McDonnell and Abbott, 2009). Experimentally it has been found in mechanoreceptors of crayfish (Douglass et al., 1993), in the cercal sensory system of crickets (Levin and Miller, 1996), and in human muscle spindles (Cordo et al., 1996). Thresholded Gaussian processes are simple theoretical models exhibiting this phenomenon (Boven and Aertsen, 1990). For the leaky integrate-and-fire neuron in linear approximation stochastic resonance has been reported for sinusoidal periodic input currents (Lindner and Schimansky-Geier, 2001). Also for non-periodic signals which are slow compared to the dynamics of the neuron, an adiabatic approximation reveals stochastic resonance (Collins et al., 1996). Neither approximation, however, is valid for a synaptic impulse, which is a fast non-periodic signal. In (Helias et al., 2010, 2010a) we demonstrate that the non-linear fast response of the leaky integrate-and-fire model exhibits pronounced stochastic resonance.
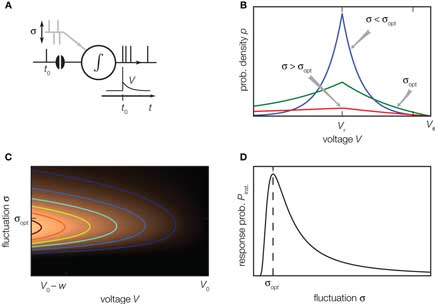
Figure 4. Stochastic resonance. (A) A neuron receives balanced excitatory and inhibitory background input (gray spikes). The probability of eliciting an immediate response to a particular synaptic impulse (black spike at t0) depends on the amplitude σ of the fluctuations caused by the other synaptic afferents. (B) The spread of the probability density of the voltage depends on the amplitude σ of the fluctuations caused by all synaptic afferents (8). At low fluctuations (σ < σopt, blue) it is unlikely to observe the voltage near threshold, the density there is negligible. At intermediate fluctuations (σopt, green), the density below threshold is elevated. Increasing the fluctuations beyond this point (σ > σopt, red) spreads out the density to negative voltages, effectively depleting the range near threshold. (C) Probability density (8) near threshold (luminance coded with equal-density lines) over voltage V (horizontal axis) as a function of the fluctuation σ (vertical axis). At the optimal level of fluctuations σopt, the density near threshold becomes maximal. (D) The voltage integral of this density determines the probability of eliciting a firing response and has a single maximum at σopt (9).
The intuitive explanation of stochastic resonance in neurons rests on the observation that a single synaptic impulse cannot depolarize the neuron sufficiently to cause an action potential on its own, as a single raindrop will not tilt an empty shishi odoshi. In the presence of many synaptic afferents, or when the shishi odoshi is in torrential rain, there is at each point in time a certain probability that the system is already close to its threshold so that a single additional impulse suffices to ultimately cause an action potential, a single additional raindrop turns the bamboo tube. This explains why the response increases with increasing background noise. In order to understand why the response decreases again when there is too much noise, we need to specify the model a bit more carefully. We consider an integrator as before, but with balanced excitatory and inhibitory synaptic inputs, so that the mean voltage does not change over time. For simplicity, in the following we assume that the mean value corresponds to the reset potential Vr. In the perfect integrator the presence of inhibition causes the problem that the membrane potential might become arbitrarily negative. In neurons this is prevented by the leak current, driving the voltage back to the mean and by the finite value of the inhibitory reversal potential. For the case of V above the mean Vr, we follow Fusi and Mattia (1999), Mattia and Del Guidice (2002) and introduce a constant negative current, so that in the absence of any synaptic input (noise σ = 0), the membrane potential rests at Vr. In their model, arbitrary negative voltages cannot occur because the membrane potential is constrained to V > Vreversal, mimicking the inhibitory reversal potential. In contrast, we imagine the mean potential between reversal and threshold and therefore introduce a current that is constant and positive, if the membrane voltage V is below its mean level Vr. In our operating range we expect the model of Fusi and Mattia (1999) to exhibit qualitatively the same results. Gradually increasing the noise, the probability of finding the neuron at voltages larger than Vr increases; the membrane potential distribution becomes wider, as shown in Figure 4B (blue curve). The density right below threshold grows as well, as indicated in Figure 4C. Here a single additional impulse of size w is sufficient to cause a threshold crossing. For even higher noise the density near threshold ultimately decreases again. The threshold prevents the density to spread beyond, so for larger σ the density is effectively pushed toward negative voltages, as shown in Figure 4B (red curve). Consequently the probability density below threshold assumes a maximum at an optimal noise level σopt (Figure 4C) which directly translates into the maximum of the instantaneous response (Figure 4D).
The classical notion of stochastic resonance considers the signal-to-noise ratio in the output to exhibit a maximum at a certain level of noise in the input. In the system at hand, the absolute value of the instantaneous response probability shows a maximum. In this sense, we use the term stochastic resonance in its broader meaning, as recently suggested (McDonnell and Abbott, 2009). The leaky integrate-and-fire neuron exhibits a mechanism in complete analogy to the simple example presented here (Helias et al., 2010, 2010a).
5 Effect of Time Discretization on Probability Density and Response Properties
In simulations of recurrent neuronal networks, time is customarily discretized into an equidistant grid (for example Gerstein and Mandelbrot, 1964; MacGregor and Lewis, 1977), see Brette et al. (2007) for a recent review. The spacing of the grid is called the computation step size h. This approach enables the simulation of large neuronal networks on laptop computers and high-performance clusters in an efficient manner. In traditional implementations, the evolution of the membrane potential progresses in steps of h and the times of action potentials are constrained to the time grid. This, however, may cause artificial synchronization in neural networks (Hansel et al., 1998), which can be avoided by resetting the membrane potential at a continuous time threshold crossing found by interpolating between two points on the grid (Hansel et al., 1998; Shelley and Tao, 2001). The accuracy required in a simulation depends on the scientific question. In simulations in discrete time, the error of spike timing drops only linearly with the simulation step size (Morrison et al., 2007). Therefore recently developed algorithms combine the representation of spikes in continuous time with the efficient progression of time in discrete steps (SMorrison et al., 2007; Hanuschkin et al., 2010; ee Figure 5B). Nevertheless, many simulations still rely on time discretization and if only a low accuracy in spike timing is required grid constrained implementations commonly have shorter run times. This is particularly relevant for simulations involving synaptic plasticity which typically run over long periods of biological time. It is, however, important to distinguish between the accuracy of the mathematical model of nature and the accuracy of the solver used to integrate the equations. Otherwise the researcher cannot decide whether the observed discrepancies with nature are just due to a technical problem or whether the model fails to represent a relevant aspect.
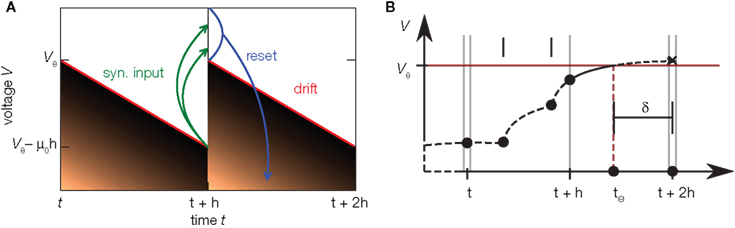
Figure 5. Time discretization and continuous time simulation. (A) Time evolution of the probability density (density plot) of the membrane voltage in an integrator with constant drift −μ0 in discrete time steps of duration h. Within one step the density moves away from the threshold due to the drift, such that the highest possible voltage is indicated by the red line. Synaptic impulses are taken into account at the end of the time step at t + h, so the voltage jumps by a random amount as indicated by the green arrows. This again inflates the density, also populating states above threshold Vθ. By subsequent thresholding (blue) each neuron above Vθ emits a spike and is reset, so the density above threshold vanishes. In the stationary state, after one cycle of duration h the density is identical again. This allows to derive an effective time-discrete Fokker–Planck equation describing the stationary density. (B) Schematic of continuous spike timing in discrete time simulations. The membrane potential of a neuron (dashed curve) evolves in time, driven by synaptic impulses (black dots). The membrane potential crosses the threshold in (t + h, t + 2h). The exact location tθ is determined and this information is passed to the target neurons as an offset value δ with respect to the subsequent point on the temporal grid. Adapted from Hanuschkin et al. (2010).
In Helias et al. (2010) we observed that time discretization changes the shape of the membrane potential density. In particular the probability density near threshold increases with coarser time discretization. We have seen above that the shape of the membrane potential distribution determines the response properties of the model. Let us therefore assess the artifacts caused by the discretization of time. Here we characterize the artifacts using the model with constant restoring force introduced in Section 4. A treatment of the full leaky integrate-and-fire model is given in Helias et al. (2010). Figure 5A illustrates the time evolution of the membrane potential density in one cycle of the simulation. The time evolution in neural simulators is typically divided into three different phases (Morrison and Diesmann, 2008): (1) Starting at t, the deterministic neural dynamics evolves. As in the example of the last section, this evolution is a drift of the membrane potential away from threshold, so that the density contracts and a gap emerges between the highest observable voltage (red) and the threshold Vθ. (2) At the end of the time step at t + h the incoming synaptic events are taken into account. Each such event causes a jump of the voltage, indicated by the green arrows in the diagram. This way the synaptic input again spreads the density and the voltage might exceed the threshold, indicated by the narrow stripe of density above threshold at t + h. (3) Due to the firing threshold of the neuron, these supra-threshold states are immediately reset to the reset potential. As a result, the density observed at the end of the third step has a finite value at threshold which is elevated compared to the model in continuous time because all spikes arriving in the interval h are projected to grid position t + h. For the leaky integrate-and-fire neuron, discretization of time slightly lowers the stationary firing rate, while the transient response properties experience only minor changes (Helias et al., 2010). The division of the time evolution operator into three subsequent steps allows us to extend the Fokker–Planck theory to processes evolving in discrete time steps. Next to this approximation, Helias et al. (2010) presents a numerical scheme to obtain the stationary properties of such processes with arbitrary precision.
6 Conclusion
6.1 Key Findings
The work reviewed in this article (Helias et al., 2010, 2010a) extends the theory of integrate-and-fire neuron models to capture the effect of synaptic pulse coupling. We demonstrate that the pulsed nature of synaptic afferents changes both the stationary properties of neurons and their dynamical response to transient inputs. In particular, we obtain more accurate expressions for the equilibrium firing rate (cf. Siegert, 1951) and the membrane potential distribution (cf. Brunel, 2000). We find that approximating the total synaptic current by a Gaussian white noise qualitatively changes the observed properties. The reason is that this diffusion approximation neglects threshold crossings by finite jumps. Mathematically, our approach amounts to a novel boundary condition for the Fokker–Planck equation (Risken, 1996). The importance of the type of noise for the boundary condition has previously been highlighted (Hanggi and Talkner, 1985). Our hybrid theory combines the diffusion approximation with a description of the finite synaptic impulses and enables us to quantitatively explain the increased probability of finding a neuron’s membrane potential closely below threshold. A similar effect has been observed in the case of synaptic currents with slow temporal dynamics (Brunel et al., 2001; Fourcaud and Brunel, 2002; Moreno-Bote and Parga, 2006; Chizhov and Graham, 2008). However, the underlying mechanisms are different. While in our case the probability flux over threshold is limited by the finite rate of excitatory synaptic events, in the earlier studies the flux is limited by the slower fluctuations caused by the low-pass filtered synaptic Gaussian noise. In the presence of synaptic filtering the effect of non-vanishing synaptic amplitudes on the probability density remains. The simplest case to realize this is a perfect integrator driven by excitatory positive current pulses of some waveform and finite duration. The total input current is positive I(t) > 0 at any time point, so the membrane potential is monotonously increasing, except at threshold crossings when the reset to a lower voltage takes place. Identifying the threshold value with the reset, the voltage always moves in the same direction along the voltage axis, now forming a ring. All points on the ring are equivalent, so the resulting membrane potential density must reflect this symmetry and hence is uniform. For filtered Gaussian noise, however, the density is not uniform (cf. Fourcaud and Brunel, 2002, their Figure 4) not even for purely excitatory drive. This demonstrates that the effect of finite synaptic amplitudes is a general phenomenon and not an artifact of the simple integrate-and-fire dynamics. For balanced excitatory and inhibitory input, however, we found that the deviations from the diffusion approximation are smaller.
Obtaining simple analytical expressions for the stationary probability density of the membrane voltage also leads to new insights into the time dependent transfer of information by neurons. The characterization of their input–output relation is required to understand which operations neurons are able to perform and to analyze the dynamics of recurrent networks of such neurons. The prevailing theory to address the latter question employs in addition to the above mentioned diffusion approximation a linearization of the transfer function (Brunel and Hakim, 1999; Brunel et al., 2001; Lindner and Schimansky-Geier, 2001). Going beyond both of these approximations, we discover novel features of neuronal transfer even in the simple leaky- and perfect integrate-and-fire models.
The higher density near threshold due to non-zero synaptic amplitudes increases the fraction of neurons in a population that responds rapidly to afferent signals. Moreover, a neuron’s response to an excitatory incoming impulse has an immediate component, but an inhibitory impulse just delays the next firing, an inherent asymmetry due to the rectifying property of the threshold. A simple geometric argument allows us to transcend the linear approximation and to uncover the full non-linear dependence of the fast component of the neuronal response on input amplitude. The nature of the background activity shapes this non-linearity. Even in the presence of substantial background noise, often assumed to linearize transfer, we still find the threshold of the neuron to impose this asymmetry. The asymmetry is a generic non-linearity present in any excitable system. This finding is in contradiction to the prevalent diffusion approximation. This limit predicts a symmetric fast response for excitatory and inhibitory impulses alike, because both modulate the fluctuations in the input at high frequencies (Lindner and Schimansky-Geier, 2001). For realistic EPSPs, the excitatory response is concentrated in the short time interval of the rise time. Experimentally, these response properties have first been documented a long time ago for neurons of cat motor cortex (Fetz and Gustafsson, 1983) and an even earlier theory made according qualitative predictions (Knox and Poppele, 1977). The theory of spike response models yields a formal framework which quantitatively explains the asymmetry of the response and the sharpening with respect to the postsynaptic potential (Herrmann and Gerstner, 2001).
The geometric consideration explaining the instantaneous response also elucidates why a certain amount of additional uncorrelated synaptic input promotes the fast spiking response. The dependence on the noise amplitude of this so called stochastic resonance is more pronounced than for the previously known linear transfer of sinusoidal currents (Lindner and Schimansky-Geier, 2001). This means that the neuron optimally transmits fast changes in its input to the output if it receives a certain well defined amount of unrelated background activity.
Many theoretical studies focused on the transfer of sinusoidal modulations of some parameter of the input to a neuron model up to linear response. In early sensory areas, such as the visual system or the auditory system, however, transient inputs are frequently observed. These transient signals often evoke responses that depend non-linearly on a parameter of the input. Cells in primary visual cortex show non-linear responses depending on the local contrast (Geisler et al., 2007). In the auditory system of the locust the probability of response increases non-linearly with the sound pressure (Gollisch and Herz, 2005). The responses in the latter system occur with sub-millisecond precision, but single action potentials appear unreliably with a probability that grows non-linearly with the membrane depolarization. These findings are in line with the increasing and saturating non-linearity of the fast response discussed here. The dispersion of the membrane potential distribution in the auditory cell is due to subthreshold fluctuations by cell-intrinsic noise (Gollisch and Herz, 2005). Functionally these fluctuations promote the response at low stimulus intensities through stochastic resonance (Collins et al., 1996). Our analytical results render this transient processing amendable to theoretical analysis using integrate-and-fire dynamics.
For synaptic impulses which are not small compared to the distance between reset voltage and threshold, the presented theory cannot be employed because it still relies on the diffusion approximation as long as the voltage is sufficiently far away from threshold. However, the recently developed theory for excitatory and inhibitory synaptic jumps with exponentially distributed amplitudes (Richardson and Swarbrick, 2010) confirms that even for large synaptic jumps the altered response properties are governed by the same mechanisms reviewed here. Also for a particular class of exactly solvable integrate-and-fire models the transfer of correlations by pairs of neurons was recently shown to be sensitive to the spiking nature of the input (Rosenbaum and Josic, 2011). A limitation of current theories is the assumption of a hard threshold defined by an exact value Vθ. We presume that a more realistic soft threshold (Naundorf et al., 2005), which captures the action potential onset dynamics like, e.g., in the exponential integrate-and-fire model (Fourcaud-Trocmé et al., 2003), leads to qualitatively similar results. We imagine a population of such neurons receiving stationary input for a long period of time, such that the membrane potential distribution over the ensemble is stationary. An additional excitatory pulse impinging on the population shifts this distribution to higher voltages within the rise time of the EPSP, thus populating the region beyond the separatrix. Neurons with a membrane voltage above the separatrix emit an action potential after a further short delay, constituting a fast population response. This response appears within a short time interval of the order of the sum of the rise time of the EPSP and the time for action potential initiation and corresponds to the immediate response reported here. Future work needs to address the dynamics in more detail to obtain quantitative results.
6.2 Simulation Technology and Theory
The last two decades have brought accelerated progress in the technology to simulate neuronal networks. Both hardware and software development have made tools available that are easily capable of simulating networks of 100,000 neurons and more with realistic synaptic connectivity. With the increased complexity of the simulation experiments, however, understanding and interpreting the results becomes more challenging. In the classical sense, a model is an abstraction of the real biological system that reproduces experimentally observed phenomena. The reduced complexity allows to draw conclusions about the necessary features that lead to the phenomenon. The possibility to perform simulations that take into account biological features in great detail bears the possibility to subsequently check whether the approximations and assumptions entering the simplified model are justified. However, such simulations bring the danger of producing results comparable in complexity to experimental data. A particular result may leave us puzzled about whether we observe an interesting effect, a shortcoming of the simulation technique, or even an error in the computer program. For example, in grid constrained simulations of the leaky integrate-and-fire model supplied with random input spikes we consistently observed lower stationary spikes rates than predicted by the classical theory of Siegert (1951). In Helias et al. (2010) we addressed this problem by the construction of a new theory taking into account the discretization of time and the finite amplitude of synaptic impulses. The predicted spike rate is in good agreement with the simulation results. While this verifies that the simulation program works correctly it remained unresolved whether the result of Siegert (1951) or our simulation is closer to the true spike rate of the model because the new theory incorporates a technical detail of the software implementation; the discretization of time. Furthermore, the new theory predicts a fast response of the model neuron to time varying signals (see Section 3) observed in the grid constrained simulations. As a rapid response has also been observed experimentally this raises the question whether the theoretical result is an artifact of time discretization or an inherent property of the integrate-and-fire model. Fortunately, in the mean time the technology became available to efficiently simulate integrate-and-fire type neuron models in continuous time (Morrison et al., 2007; Hanuschkin et al., 2010). Thus we repeated our earlier simulations using the new technology and established that the rapid response persists. Motivated by the observation we extended the theory for finite synaptic impulses to the case of continuous time. The theoretical description of the response properties and the stationary spike rate are in good agreement with the simulation results. As the continuous time implementation is an exact computer representation of the model, the theory delivers the true spike rate of the model, bounded only by the order of the approximation used in the derivation. The spike rate is generally slightly higher than in grid constrained simulations but still lower than predicted by the theory of Siegert (1951). The latter results are published as Helias et al. (2010a) and constitute the first neuroscientific discovery employing the capability of the simulation software NEST (Gewaltig and Diesmann, 2007; Hanuschkin et al., 2010) to simulate spike interaction in continuous time.
6.3 Future Directions
The generic feature of a fast component of the neuronal response reviewed in the present work has implications for the emergence and propagation of synchronized activity in neural networks. For example in auditory cortex, the firing of neurons has been shown to be driven by simultaneous activation of several of their synaptic afferents (DeWeese and Zador, 2006). Synchronized activity, as it occurs, e.g., in primary sensory cortex (Poulet and Petersen, 2008), easily drives a neuron beyond the range of validity of the linear response. The convex increase of firing probability generic to leaky integrate-and-fire model neurons (Goedeke and Diesmann, 2008) is of advantage to obtain output spikes closely locked to the input, thus propagating the spike timing information. But even for small synaptic impulses does the fast component contribute to the transmission of synchronous activity by groups of neurons (Tetzlaff et al., 2003; De la Rocha et al., 2007; Renart et al., 2010; Rosenbaum and Josic, 2011). This is promoted by the presence of noise from uncorrelated synaptic afferents through stochastic resonance. Whether neurons in the cortex are in the right regime to employ the fast response to transfer and process information depends on its relative contribution to the total response probability. Recently, the response probability has been quantified experimentally in vivo (London et al., 2010). The observed slight quadratic dependence on the impulse amplitude indicates a noticeable contribution of the fast non-linear component. Its relative contribution can be estimated experimentally by intracellularly recording the membrane potential distribution and the size of a postsynaptic potential and applying the methods presented in our work. The total response is approximated by the expression 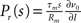 with the slope ∂ν0/∂I of the firing rate curve for stationary current injection, the membrane resistance Rm, the membrane time constant τm and the amplitude of a postsynaptic potential s. The ability of a neuron to perform non-linear operations on fast activity transients may enable neural networks to perform non-trivial computations (Herz et al., 2006), such as performing categorization tasks with high memory capacity (Poirazi and Mel, 2001). Also Hebbian synaptic plasticity mechanisms (Hebb, 1949) like spike timing dependent plasticity (Morrison et al., 2008) are sensitive to the correlation between afferent activity and the outgoing action potentials of a neuron. This correlation has so far been approximated by the linear response kernel (Kempter et al., 1999; Helias et al., 2008; Morrison et al., 2008; Gilson et al., 2009a,b,c,d). Synaptic plasticity typically reacts most sensitively to pairs of afferent and efferent spikes that are closely locked in time, as facilitated by the fast response. Its non-linear dependence on the synaptic efficacy in turn may give rise to multiple stable fixed points of the synaptic weight promoting pattern formation in plastic recurrent networks. The results covered in this review may render some of the effects his outlined above more accessible for analytical treatments.
with the slope ∂ν0/∂I of the firing rate curve for stationary current injection, the membrane resistance Rm, the membrane time constant τm and the amplitude of a postsynaptic potential s. The ability of a neuron to perform non-linear operations on fast activity transients may enable neural networks to perform non-trivial computations (Herz et al., 2006), such as performing categorization tasks with high memory capacity (Poirazi and Mel, 2001). Also Hebbian synaptic plasticity mechanisms (Hebb, 1949) like spike timing dependent plasticity (Morrison et al., 2008) are sensitive to the correlation between afferent activity and the outgoing action potentials of a neuron. This correlation has so far been approximated by the linear response kernel (Kempter et al., 1999; Helias et al., 2008; Morrison et al., 2008; Gilson et al., 2009a,b,c,d). Synaptic plasticity typically reacts most sensitively to pairs of afferent and efferent spikes that are closely locked in time, as facilitated by the fast response. Its non-linear dependence on the synaptic efficacy in turn may give rise to multiple stable fixed points of the synaptic weight promoting pattern formation in plastic recurrent networks. The results covered in this review may render some of the effects his outlined above more accessible for analytical treatments.
7 Methods
7.1 Stationary Solution of Perfect Integrator with Excitation
The membrane potential V of the perfect integrator (Tuckwell, 1988) evolves according to the stochastic differential equation 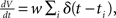 where ti are random time points of synaptic impulses generated by a Poisson process with rate λ. If V reaches the threshold Vθ the neuron emits an action potential. After the threshold crossing, the voltage is reset to V ← V − (Vθ − Vr). This reset preserves the overshoot above threshold and places the system above the reset value by this amount. We consider a population of equivalent neurons and assume a uniformly distributed membrane voltage between Vr and Vθ initially. In what follows we apply the formalism outlined in Helias et al. (2010a). The detailed calculations with intermediate steps can be found in a separate note (Helias et al., 2010b). The first and second infinitesimal moments (Ricciardi et al., 1999) of the diffusion approximation are
where ti are random time points of synaptic impulses generated by a Poisson process with rate λ. If V reaches the threshold Vθ the neuron emits an action potential. After the threshold crossing, the voltage is reset to V ← V − (Vθ − Vr). This reset preserves the overshoot above threshold and places the system above the reset value by this amount. We consider a population of equivalent neurons and assume a uniformly distributed membrane voltage between Vr and Vθ initially. In what follows we apply the formalism outlined in Helias et al. (2010a). The detailed calculations with intermediate steps can be found in a separate note (Helias et al., 2010b). The first and second infinitesimal moments (Ricciardi et al., 1999) of the diffusion approximation are 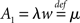 and
and 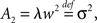 respectively. The model in diffusion limit hence obeys the stochastic differential equation dV/dt = μ + σξ(t), with a zero mean Gaussian white noise ξ, 〈ξ(t)ξ(t + s)〉t = δ(s). The probability flux operator is
respectively. The model in diffusion limit hence obeys the stochastic differential equation dV/dt = μ + σξ(t), with a zero mean Gaussian white noise ξ, 〈ξ(t)ξ(t + s)〉t = δ(s). The probability flux operator is 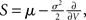 which, after normalization of the stationary probability density p(V) by the as yet unknown flux ν0 as
which, after normalization of the stationary probability density p(V) by the as yet unknown flux ν0 as 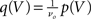 yields the stationary Fokker–Planck equation
yields the stationary Fokker–Planck equation

Here 1expr. equals 1 if expr. is true, and 0 else. The homogeneous solution is 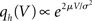 and the particular solution which vanishes at V = Vθ for V < Vr < Vθ follows by variation of constants as
and the particular solution which vanishes at V = Vθ for V < Vr < Vθ follows by variation of constants as 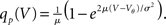
We first consider the case of Gaussian white noise input of mean μ and variance σ. A finite probability flux in this case requires continuity at the threshold, implying q(Vθ) = 0. Thus we obtain the full solution continuous at reset (Abbott and van Vreeswijk, 1993)
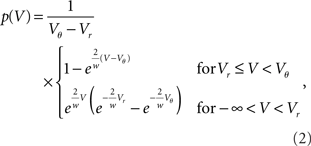
where we used μ/σ2 = 1/w and the firing rate ν0 = λw/(Vθ − Vr) is determined by the normalization 1 = ν0 ∫q(V)dV. We next take into account the finite amplitude of the synaptic jumps to obtain a modified boundary condition (Helias et al., 2010a) at the threshold. For Vr < V < Vθ the n-th derivative of the solution of (1) fulfills the recurrence relation q(n) = cn + dnq, with dn = (2μ/σ2)n and 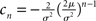 , for n ≥ 1 and c0 = 0, d0 = 1. Applying eq. (8) of Helias et al. (2010a), summing up to n ≤ 2, determines the boundary value q(Vθ) = μ−1. In the case of finite jumps, the region below reset will never be entered, hence q(V) = 0 for V < Vr. For the solution to fulfill the boundary value at threshold the homogeneous solution
, for n ≥ 1 and c0 = 0, d0 = 1. Applying eq. (8) of Helias et al. (2010a), summing up to n ≤ 2, determines the boundary value q(Vθ) = μ−1. In the case of finite jumps, the region below reset will never be entered, hence q(V) = 0 for V < Vr. For the solution to fulfill the boundary value at threshold the homogeneous solution 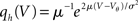 needs to be added to the particular solution qp, so the complete stationary density is
needs to be added to the particular solution qp, so the complete stationary density is
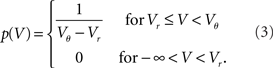
The normalization 1 = ν0 ∫ q(V)dV yields the same firing rate ν0 = λw/(Vθ − Vr) as in the case of Gaussian white noise in agreement with intuition, because (Vθ − Vr)/w input impulses are needed to cause an output spike. The illustrations in Figures 2A–C use w = 3 mV, Vr = 0, Vθ = 15 mV, and λ = 200(1/s).
7.2 Instantaneous and Time Dependent Response
The probability Pinst.(s) that a neuron in the population instantaneously emits an action potential in response to a single synaptic input of postsynaptic amplitude s equals the probability mass 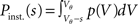 crossing the threshold. In the case of Gaussian white noise, with p(V) from (2) we obtain
crossing the threshold. In the case of Gaussian white noise, with p(V) from (2) we obtain
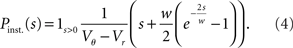
This expression grows quadratically like 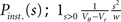 for small synaptic amplitudes s. In the case of finite synaptic jumps with (3) we obtain
for small synaptic amplitudes s. In the case of finite synaptic jumps with (3) we obtain
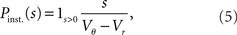
growing linear in the amplitude s. A linear approximation of the integral response can be obtained from the slope of the equilibrium rate with respect to μ as 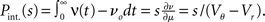 For positive s this expression equals the integral instantaneous response (5) so the complete response is instantaneous in this case. For s < 0 we only consider the special case of a synaptic inhibitory pulse with the same magnitude s = −w as the excitatory background pulses. Now the density is shifted away from threshold by w and the firing rate drops to 0. The density reaches threshold again if at least one excitatory pulse has arrived, which occurs within time t with probability Pk≥1 = 1− e−λτ. Given this event, the hazard rate of the neuron is λw/(Vθ − Vr), so the time dependent response is
For positive s this expression equals the integral instantaneous response (5) so the complete response is instantaneous in this case. For s < 0 we only consider the special case of a synaptic inhibitory pulse with the same magnitude s = −w as the excitatory background pulses. Now the density is shifted away from threshold by w and the firing rate drops to 0. The density reaches threshold again if at least one excitatory pulse has arrived, which occurs within time t with probability Pk≥1 = 1− e−λτ. Given this event, the hazard rate of the neuron is λw/(Vθ − Vr), so the time dependent response is
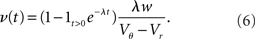
The density following the inhibitory event is a superposition of the shifted density and the equilibrium density with the relative weighting given by the probabilities 1 − Pk≥1 and Pk≥1, respectively.
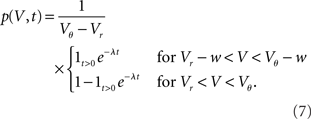
The integrated response probability 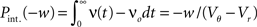 is the same as for an excitatory spike and agrees with the linear approximation. The illustrations Figure 2D and Figures 3A,B,D use w = 3 mV, Vr = 0, Vθ = 15 mV, and λ = 200(1/s).
is the same as for an excitatory spike and agrees with the linear approximation. The illustrations Figure 2D and Figures 3A,B,D use w = 3 mV, Vr = 0, Vθ = 15 mV, and λ = 200(1/s).
7.3 Stochastic Resonance
In order to observe stochastic resonance, the fluctuation in the input must be varied. We therefore assume a zero mean Gaussian white noise input current σξ(t). Adding a constant drift term μ(V) = −μ0sign(V − Vr), μ0 > 0 assures that the voltage trajectories do not diverge to −∞ and approach Vr in absence of synaptic input. The homogeneous solution of the stationary Fokker–Planck equation, analog to (1), therefore is 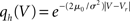 . The particular solution for V > Vr fulfilling the boundary condition q(Vθ) = 0 can be found by variation of constants as
. The particular solution for V > Vr fulfilling the boundary condition q(Vθ) = 0 can be found by variation of constants as 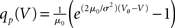 . The complete density, demanding continuity at reset Vr, is
. The complete density, demanding continuity at reset Vr, is
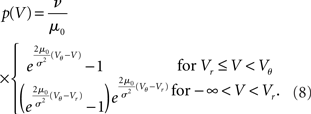
where the normalization 1 = ν0 ∫ q(V)dV yields the equilibrium rate
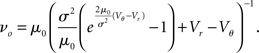
In the limit of large fluctuations σ2 ≫ μ0 the density decreases proportional to 1/σ2 between reset and threshold and falls off linearly toward threshold
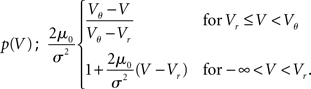
The response to an incoming impulse of amplitude s is
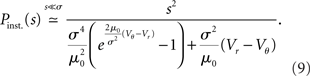
The illustrations use Vr = 0, Vθ = 15 mV, μ0 = 5.0 mV/s in Figures 4C,D and in addition σ = 5.5, 11, 16.5 mV for the {blue, green, red} curves in Figure 4B.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Johanna Derix for the idea of using the shishi odoshi as an analogy for neural dynamics and are especially grateful to Susanne Kunkel for creating the artwork in Figures 1A–C. We thank Petr Lansky, and Laura Sacerdote for comments on an earlier version of the manuscript and acknowledge fruitful discussions with Nicolas Brunel, Benjamin Lindner, Carl van Vreeswijk, and our colleagues in the NEST Initiative. Partially funded by BMBF Grant 01GQ0420 to BCCN Freiburg, EU Grant 15879 (FACETS), EU Grant 269921 (BrainScaleS), DIP F1.2, Helmholtz Alliance on Systems Biology (Germany), and Next-Generation Supercomputer Project of MEXT (Japan).
Key Concepts
For input signals that only weakly affect a non-linear system, a linear approximation of the system suffices to explain the signal transfer. The response to a brief (Dirac δ) impulse completely characterizes the dynamics. The response to a sum of inputs is the sum of the single responses (superposition principle). The responses to positive and negative impulses are identical with opposite sign.
Integrate-and-fire model neuron, perfect integrator
A neuron model with membrane voltage V as dynamical variable. If V exceeds the threshold Vθ an action potential occurs and V is reset to a lower value Vr. An incoming synaptic impulse causes a jump in V describing the amplitude of the postsynaptic potential. In the leaky integrate-and-fire model the leak current through the membrane causes V to approach a resting level in absence of inputs.
In an ensemble of identical neurons each neuron has a voltage V, which may be different due to random synaptic input. The probability density p(V) describes the fraction p(V)•∆V of neurons with a voltage in the small interval between V and V + ∆V.
Diffusion approximation or Fokker–Planck theory
In this limit the effect of a single synaptic impulse vanishes, but the rate of impulses diverges, so that the fluctuations caused by the total input remain the same. The resulting membrane dynamics is equivalent to the diffusive motion of a particle. The Fokker–Planck equation describes how the probability density p(V,t) of an ensemble of such systems evolves over time t.
The stationary solution p(V) of the Fokker–Planck equation requires the specification of p(Vθ), the value at the boundary of the domain, here firing threshold Vθ. The boundary condition determines the firing rate and the probability to respond with spike emission to synaptic inputs. The present work derives the boundary condition for the case of synaptic voltage jumps.
A phenomenon exhibited by some non-linear, stochastic systems transferring input to output (like neurons). The transfer of the input signal becomes optimal (in absolute amplitude or the signal-to-noise ratio of the output) if a certain amount of noise is added to the input. In the integrate-and-fire neuron model the non-linearity is provided by the threshold and the noise by uncorrelated synaptic input.
References
Abbott, L. F., and van Vreeswijk, C. (1993). Asynchronous states in networks of pulse-coupled oscillators. Phys. Rev. E 48, 1483–1490.
Boven, K.-H., and Aertsen, A. (1990). “Dynamics of activity in neuronal networks give rise to fast modulations of functional connectivity,” in Parallel Processing in Neural Systems and Computers, eds R. Eckmiller, G. Hartmann, and G. Hauske (Amsterdam: Elsevier), 53–56.
Brette, R., Rudolph, M., Carnevale, T., Hines, M., Beeman, D., Bower, J. M., Diesmann, M., Morrison, A., Goodman, P. H., Harris, F. C. Jr., Zirpe, M., Natschläger, T., Pecevski, D., Ermentrout, B., Djurfeldt, M., Lansner, A., Rochel, O., Vieville, T., Muller, E., Davison, A., El Boustani, S., and Destexhe, A. (2007). Simulation of networks of spiking neurons: a review of tools and strategies. J. Comput. Neurosci. 23, 349–398.
Brunel, N. (2000). Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J. Comput. Neurosci. 8, 183–208.
Brunel, N., Chance, F. S., Fourcaud, N., and Abbott, L. F. (2001). Effects of synaptic noise and filtering on the frequency response of spiking neurons. Phys. Rev. Lett. 86, 2186–2189.
Brunel, N., and Hakim, V. (1999). Fast global oscillations in networks of integrate-and-fire neurons with low firing rates. Neural Comput. 11, 1621–1671.
Brunel, N., and van Rossum, M. C. W. (2007). Lapicque’s 1907 paper: from frogs to integrate-and-fire. Biol. Cybern. 97, 337–339.
Chizhov, A. V., and Graham, L. J. (2008). Efficient evaluation of neuron populations receiving colored-noise current based on a refractory density method. Phys. Rev. E 77, 011910.
Collins, J. J., Chow, C. C., Capela, A. C., and Imhoff, T. T. (1996). Aperiodic stochastic resonance. Phys. Rev. E 54, 5575–5584.
Cope, D. K., and Tuckwell, H. C. (1979). Firing rates of neurons with random excitation and inhibition. J. Theor. Biol. 80, 1–14.
Cordo, P., Inglis, J. T., Sabine, V., Collins, J. J., Merfeld, D. M., Rosenblum, S., Buckley, S., and Moss, F. (1996). Noise in human muscle spindles. Nature 383, 769–770.
De Kamps, M. (2003). A simple and stable numerical solution for the population density equation. Neural Comput. 15, 2129–2146.
De la Rocha, J., Doiron, B., Shea-Brown, E., Kresimir, J., and Reyes, A. (2007). Correlation between neural spike trains increases with firing rate. Nature 448, 802–807.
DeWeese, M. R., and Zador, A. M. (2006). Non-gaussian membrane potential dynamics imply sparse, synchronous activity in auditory cortex. J. Neurosci. 26, 12206–12218.
Douglass, J. K., Wilkens, L., Pantazelou, E., and Moss, F. (1993). Noise enhancement of information transfer in crayfish mechanoreceptors by stochastic resonance. Nature 365, 337–340.
Ecker, A. S., Berens, P., Keliris, G. A., Bethge, M., and Logothetis, N. K. (2010). Decorrelated neuronal firing in cortical microcircuits. Science 327, 584–587.
Fetz, E., and Gustafsson, B. (1983). Relation between shapes of postsynaptic potentials and changes in firing probability of cat motoneurones. J. Physiol. (Lond.) 341, 387–410.
Fourcaud, N., and Brunel, N. (2002). Dynamics of the firing probability of noisy integrate-and-fire neurons. Neural Comput. 14, 2057–2110.
Fourcaud-Trocmé, N., Hansel, D., van Vreeswijk, C., and Brunel(2003). How spike generation mechanisms determine the neuronal response to fluctuating inputs. J. Neurosci. 23, 11628–11640.
Fusi, S., and Mattia, M. (1999). Collective behavior of networks with linear (vsli) integrate-and-fire neurons. Neural Comput. 11, 633–652.
Geisler, W. S., Albrecht, D. G., and Crane, A. M. (2007). Responses of neurons in primary visual cortex to transient changes in local contrast and luminance. J. Neurosci. 27, 5063–5067.
Gerstein, G. L., and Mandelbrot, B. (1964). Random walk models for the spike activity of a single neuron. Biophys. J. 71, 41–68.
Gerstner, W. (2000). Population dynamics of spiking neurons: fast transients, asynchronous states, and locking. Neural Comput. 12, 43–89.
Gilson, M., Burkitt, A. N., Grayden, D. B., Thomas, D. A., and van Hemmen, J. L. (2009a). Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks. I. Input selectivity – strengthening correlated input pathways. Biol. Cybern. 101, 81–102.
Gilson, M., Burkitt, A. N., Grayden, D. B., Thomas, D. A., and van Hemmen, J. L. (2009b). Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks. II. Input selectivity – symmetry breaking. Biol. Cybern. 101, 103–114.
Gilson, M., Burkitt, A. N., Grayden, D. B., Thomas, D. A., and van Hemmen, J. L. (2009c). Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks III. Partially connected neurons driven by spontaneous activity. Biol. Cybern. 101, 411–426.
Gilson, M., Burkitt, A. N., Grayden, D. B., Thomas, D. A., and van Hemmen, J. L. (2009d). Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks IV. Structuring synaptic pathways among recurrent connections. Biol. Cybern. 101, 427–444.
Goedeke, S., and Diesmann, M. (2008). The mechanism of synchronization in feed-forward neuronal networks. New J. Phys. 10, 015007.
Gollisch, T., and Herz, A. V. M. (2005). Disentangling sub-millisecond processes within an auditory transduction chain. PLoS Comput. Biol. 3, e8. doi: 10.1371/journal.pbio.0030008
Hanggi, P., and Talkner, P. (1985). First-passage time problems for non-Markovian processes. Phys. Rev. A 32, 1934–1937.
Hansel, D., Mato, G., Meunier, C., and Neltner, L. (1998). On numerical simulations of integrate-and-fire neural networks. Neural Comput. 10, 467–483.
Hanuschkin, A., Kunkel, S., Morrison, A., and Diesmann, M. (2010). A general and efficient method for incorporating precise spike times in globally time-driven simulations. Front. Neuroinform. 4:113. doi: 10.3389/fninf.2010.00113
Hebb, D. O. (1949). The Organization of Behavior: A Neuropsychological Theory. New York: John Wiley & Sons.
Helias, M., Deger, M., Diesmann, M., and Rotter, S. (2010). Equilibrium and response properties of the integrate-and-fire neuron in discrete time. Front. Comput. Neurosci. 3:29. doi: 10.3389/neuro.10.029.2009
Helias, M., Deger, M., Rotter, S., and Diesmann, M. (2010a). Instantaneous non-linear processing by pulse-coupled threshold units. PLoS Comput. Biol. 6, e1000929. doi: 10.1371/journal.pcbi.1000929
Helias, M., Deger, M., Rotter, S., and Diesmann, M. (2010b). The perfect integrator driven by poisson input and its approximation in the diffusion limit. arXiv.org 1010.3537.
Helias, M., Rotter, S., Gewaltig, M., and Diesmann, M. (2008). Structural plasticity controlled by calcium based correlation detection. Front. Comput. Neurosci. 2:7. doi: 10.3389/neuro.10.007.2008
Herrmann, A., and Gerstner, W. (2001). Noise and the psth response to current transients: I. general theory and application to the integrate-and-fire neuron. J. Comput. Neurosci. 11, 135–151.
Hertz, J. (2010). Cross-correlations in high-conductance states of a model cortical network. Neural Comput. 22, 427–447.
Herz, A. V. M., Gollisch, T., Machens, C. K., and Jaeger, D. (2006). Modeling single-neuron dynamics and computations: a balance of detail and abstraction. Science 314, 80–84.
Jacobsen, M., and Jensen, A. T. (2007). Exit times for a class of piecewise exponential markov processes with two-sided jumps. Stoch. Proc. Appl. 117, 1330–1356.
Johannesma, P. I. M. (1968). “Diffusion models for the stochastic activity of neurons,” in Neural Networks: Proceedings of the School on Neural Networks Ravello, June 1967 ed. E. R. Caianiello (Berlin: Springer-Verlag ), 116–144.
Jovilet, R., Kobayashi, R., Rauch, A., Naud, R., Shinomoto, S., and Gerstner, W. (2008). A benchmark test for a quantitative assessment of simple neuron models. J. Neurosci. Methods 169, 417–424.
Kempter, R., Gerstner, W., and van Hemmen, J. L. (1999). Hebbian learning and spiking neurons. Phys. Rev. E 59, 4498–4514.
Knight, B. W. (1972). Dynamics of encoding in a population of neurons. J. Gen. Physiol. 59, 734–766.
Knox, C. K., and Poppele, R. E. (1977). Correlation analysis of stimulus-evoked changes in excitability of spontaneously firing neurons. J. Neurophysiol. 40, 616–625.
La Camera, G., Rauch, A., Luscher, H., Senn, W., and Fusi, S. (2004). Minimal models of adapted neuronal response to in vivo-like input currents. Neural Comput. 10, 2101–2124.
Lansky, P., and Sacerdote, L. (2001). The ornstein-uhlenbeck neuronal model with signal-dependent noise. Phys. Lett. A 285, 132–140.
Lapicque, L. (1907). Recherches quantitatives sur l’excitation electrique des nerfs traitee comme une polarization. J. Physiol. Pathol. Gen. 9, 620–635.
Levin, J. E., and Miller, J. P. (1996). Broadband neural encoding in the cricket cereal sensory system enhanced by stochastic resonance. Nature 380, 165–168.
Lindner, B., and Schimansky-Geier, L. (2001). Transmission of noise coded versus additive signals through a neuronal ensemble. Phys. Rev. Lett. 86, 2934–2937.
London, M., Roth, A., Beeren, L., Häusser, M., and Latham, P. E. (2010). Sensitivity to perturbations in vivo implies high noise and suggests rate coding in cortex. Nature 466, 123–128.
MacGregor, R. J., and Lewis, E. R. (1977). Neural Modeling, Electrical Signal Processing in the Nervous System. New York: Plenum Press.
Mattia, M., and Del Guidice, P. (2002). Population dynamics of interacting spiking neurons. Phys. Rev. E 66, 051917.
Mattia, M., and Del Guidice, P. (2004). Finite-size dynamics of inhibitory and excitatory interacting spiking neurons. Phys. Rev. E 70, 052903.
McDonnell, M. D., and Abbott, D. (2009). What is stochastic resonance? definitions, misconceptions, debates, and its relevance to biology. PLoS Comput. Biol. 5, e1000348. doi: 10.1371/journal.pcbi.1000348
Misonou, H. (2010). Homeostatic regulation of neuronal excitability by k+ channels in normal and diseased brains. Neuroscientist 16, 51–64.
Moreno-Bote, R., and Parga, N. (2006). Auto- and crosscorrelograms for the spike response of leaky integrate-and-fire neurons with slow synapses. Phys. Rev. Lett. 96, 028101.
Morrison, A., and Diesmann, M. (2008). “Maintaining causality in discrete time neuronal network simulations,” in Lectures in Supercomputational Neuroscience: Dynamics in Complex Brain Networks, Understanding Complex Systems, eds P. Beim Graben, C. Zhou, M. Thiel, and J. Kurths (Berlin: Springer), 267–278.
Morrison, A., Diesmann, M., and Gerstner, W. (2008). Phenomenological models of synaptic plasticity based on spike-timing. Biol. Cybern. 98, 459–478.
Morrison, A., Straube, S., Plesser, H. E., and Diesmann, M. (2007). Exact subthreshold integration with continuous spike times in discrete time neural network simulations. Neural Comput. 19, 47–79.
Naundorf, B., Geisel, T., and Wolf, F. (2005). Action potential onset dynamics and the response speed of neuronal populations. J. Comput. Neurosci. 18, 297–309.
Omurtag, A., Knight, B. W., and Sirovich, L. (2000). On the simulation of large populations of neurons. J. Comput. Neurosci. 8, 51–63.
Poirazi, P., and Mel, B. W. (2001). Impact of active dendrites and structural plasticity on the memory capacity of neural tissue. Neuron 29, 779–796.
Poulet, J., and Petersen, C. (2008). Internal brain state regulates membrane potential synchrony in barrel cortex of behaving mice. Nature 454, 881–885.
Rauch, A., La Camera, G., Lüscher, H., Senn, W., and Fusi, S. (2003). Neocortical pyramidal cells respond as integrate-and-fire neurons to in vivo like input currents. J. Neurophysiol. 90, 1598–1612.
Renart, A., De La Rocha, J., Bartho, P., Hollender, L., Parga, N., Reyes, A., and Harris, K. D. (2010). The asynchronous state in cortical cicuits. Science 327, 587–590.
Ricciardi, L. M., Di Crescenzo, A., Giorno, V., and Nobile, A. G. (1999). An outline of theoretical and algorithmic approaches to first passage time problems with applications to biological modeling. Math. Japonica 50, 247–322.
Ricciardi, L. M., and Sacerdote, L. (1979). The Ornstein-Uhlenbeck process as a model for neuronal activity. Biol. Cybern. 35, 1–9.
Richardson, M. J. E. (2007). Firing-rate response of linear and nonlinear integrate-and-fire neurons to modulated current-based and conductance-based synaptic drive. Phys. Rev. E 76, 1–15.
Richardson, M. J. E. (2008). Spike-train spectra and network response functions for non-linear integrate-and-fire neurons. Biol. Cybern. 99, 381–392.
Richardson, M. J. E., and Swarbrick, R. (2010). Firing-rate response of a neuron receiving excitatory and inhibitory synaptic shot noise. Phys. Rev. Lett. 105, 178102.
Rosenbaum, R., and Josić, K. (2011). Mechanisms that modulate the transfer of spiking correlations. Neural Comput. doi:10.1162/NECO_a_00116. [Epub ahead of print].
Shea-Brown, E., Josic, K., de la Rocha, J., and Doiron, B. (2008). Correlation and synchrony transfer in integrate-and-fire neurons: basic properties and consequences for coding. Phys. Rev. Lett. 100, 108102.
Shelley, M. J., and Tao, L. (2001). Efficient and accurate time-stepping schemes for integrate-and-fire neuronal networks. J. Comput. Neurosci. 11, 111–119.
Silberberg, G., Bethge, M., Markram, H., Pawelzik, K., and Tsodyks, M. (2004). Dynamics of population codes in ensembles of neocortical neurons. J. Neurophysiol. 91, 704–709.
Sirovich, L. (2003). Dynamics of neuronal populations: eigenfunction theory; some solvable cases. Network 14, 249–272.
Sirovich, L., Omurtag, A., and Knight, B. W. (2000). Dynamics of neuronal populations: the equilibrium solution. SIAM J. Appl. Math. 60, 2009–2028.
Keywords: leaky integrate-and-fire model, perfect integrator, diffusion approximation, non-linear response, shot noise
Citation: Helias M, Deger M, Rotter S and Diesmann M (2011) Finite post synaptic potentials cause a fast neuronal response. Front. Neurosci. 5:19. doi: 10.3389/fnins.2011.00019
Received: 23 October 2010;
Accepted: 07 February 2011;
Published online: 24 February 2011.
Edited by:
Wulfram Gerstner, Ecole Polytechnique Fédérale de Lausanne, SwitzerlandReviewed by:
Wulfram Gerstner, Ecole Polytechnique Fédérale de Lausanne, SwitzerlandMagnus Richardson, University of Warwick, UK
Nicolas Brunel, CNRS, France
Copyright: © 2011 Helias, Deger, Rotter and Diesmann. This is an open-access article subject to an exclusive license agreement between the authors and Frontiers Media SA, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Moritz Helias is a research scientist whose main interests are the dynamics of recurrent spiking neural networks, in particular how correlations are shaped by dynamical properties of neurons and the mutual interplay with synaptic plasticity. Since his graduation in theoretical physics at the University of Hamburg, he works at the interface of numerical simulations and theoretical descriptions. During his PhD studies of neuroscience at the Bernstein Center Freiburg he became a developer of the neural simulation software NEST. Currently he is a postdoc at the RIKEN Brain Science Institute. helias@brain.riken.jp
