A Ca2+-based computational model for NMDA receptor-dependent synaptic plasticity at individual post-synaptic spines in the hippocampus
- 1 Department of Engineering Mathematics, Bristol Centre for Complexity Sciences, University of Bristol, University Walk, Bristol, UK
- 2 Department of Engineering Mathematics, Bristol Centre for Applied Nonlinear Mathematics, University of Bristol, University Walk, Bristol, UK
- 3 Department of Mathematics, Bristol Centre for Complexity Sciences, University of Bristol, University Walk, Bristol, UK
- 4 Department of Anatomy, Medical Research Council Centre for Synaptic Plasticity, University of Bristol, University Walk, Bristol, UK
Associative synaptic plasticity is synapse specific and requires coincident activity in pre-synaptic and post-synaptic neurons to activate NMDA receptors (NMDARs). The resultant Ca2+ influx is the critical trigger for the induction of synaptic plasticity. Given its centrality for the induction of synaptic plasticity, a model for NMDAR activation incorporating the timing of pre-synaptic glutamate release and post-synaptic depolarization by back-propagating action potentials could potentially predict the pre- and post-synaptic spike patterns required to induce synaptic plasticity. We have developed such a model by incorporating currently available data on the timecourse and amplitude of the post-synaptic membrane potential within individual spines. We couple this with data on the kinetics of synaptic NMDARs and then use the model to predict the continuous spine [Ca2+] in response to regular or irregular pre- and post-synaptic spike patterns. We then incorporate experimental data from synaptic plasticity induction protocols by regular activity patterns to couple the predicted local peak [Ca2+] to changes in synaptic strength. We find that our model accurately describes [Ca2+] in dendritic spines resulting from NMDAR activation during pre-synaptic and post-synaptic activity when compared to previous experimental observations. The model also replicates the experimentally determined plasticity outcome of regular and irregular spike patterns when applied to a single synapse. This model could therefore be used to predict the induction of synaptic plasticity under a variety of experimental conditions and spike patterns.
Introduction
Hebbian synaptic plasticity is the cellular and molecular correlate of associative learning in the brain. During presentation of information that needs to be retained for future use, specific synapses are subjected to activity patterns that induce a long-term change in synaptic strength. For Hebbian synaptic plasticity at Schaffer collateral synapses in the hippocampus, these patterns require coincident activity in pre- and post-synaptic neurons to activate NMDA receptors (NMDARs) present on the membrane of the post-synaptic dendritic spine. The resulting Ca2+ influx through NMDARs is the critical trigger for induction of synapse specific plasticity (Lisman, 1989).
Classically, high frequency synaptic stimulation induces long-term potentiation (LTP) whereas low frequency stimulation induces long-term depression (LTD) suggesting that brief high concentrations of Ca2+ in the post-synaptic spine induce LTP whereas prolonged lower concentrations of Ca2+ induce LTD (Bear et al., 1987; Hansel et al., 1996). This hypothesis is supported by measurements of Ca2+ concentration during plasticity induction (Hansel et al., 1997; Cho et al., 2001; Cormier et al., 2001; Ismailov et al., 2004; Gall et al., 2005) and by plasticity induction protocols designed to vary Ca2+ influx through NMDARs by fixing the post-synaptic membrane potential during low frequency synaptic stimulation (Isaac et al., 1995; Daw et al., 2000).
Spike timing-dependent plasticity (STDP) is a form of Hebbian synaptic plasticity that incorporates a temporal specificity to coincident pre- and post-synaptic activity. In the hippocampus, STDP was originally thought to be induced by single pairs of pre- and post-synaptic action potentials such that if the pre-synaptic action potential occurs before the post-synaptic action potential LTP is induced whereas if the order of action potentials is reversed then LTD is induced (Bi and Poo, 1998; Debanne et al., 1998; Nishiyama et al., 2000; Campanac and Debanne, 2008; Kwag and Paulsen, 2009). Other data have proposed this model should include a requirement for bursts of post-synaptic action potentials for the induction of LTP although LTD may be induced by single pairs (Pike et al., 1999; Wittenberg and Wang, 2006; Buchanan and Mellor, 2007) reviewed in (Buchanan and Mellor, 2010). This is a divergence from the situation at cortical synapses where single pairs of action potentials can induce both LTP and LTD (Sjostrom et al., 2001; Sjostrom and Nelson, 2002; Froemke et al., 2006, but see Nevian and Sakmann, 2006).
Since Ca2+ influx through NMDARs is pivotal for LTP and LTD, this suggests the induction of synaptic plasticity can be predicted by NMDAR opening kinetics in response to pre-synaptic glutamate release and post-synaptic depolarization. This approach has been adopted for the modeling of post-synaptic calcium dynamics in response to synaptic stimulation or back-propagating action potentials (Franks et al., 2002; Grunditz et al., 2008; Keller et al., 2008) and to STDP induction protocols (Shouval et al., 2002; Rubin et al., 2005; Graupner and Brunel, 2007; Helias et al., 2008; Urakubo et al., 2008; Castellani et al., 2009). However, these STDP models are limited by the experimental data used to determine their parameters and, in addition, ought to accurately predict the plasticity outcomes of a variety of induction protocols. Recent advances in dendritic spine imaging provide data on spine depolarization and Ca2+ concentrations in response to pre- and post-synaptic action potentials (Sabatini et al., 2002; Nevian and Sakmann, 2006; Bloodgood and Sabatini, 2007; Canepari et al., 2007; Palmer and Stuart, 2009) that potentially greatly increase the accuracy of such models of plasticity induction.
We have developed a computational model of synaptic plasticity induction based on one originally described by Shouval et al. Our model incorporates the latest experimental data on dendritic spine depolarization and Ca2+ dynamics. We also test the predictive power of our model on many plasticity induction protocols by calculating continuous Ca2+ concentrations during long induction periods. We find that our model accurately predicts the experimental data tested and we hypothesize that it can thus be used to search for instances of synaptic plasticity induction during continuous activity at Hebbian synapses in the hippocampus.
Materials and Methods
We use a physiologically plausible model based on intracellular Ca2+ dynamics caused by NMDAR activation during the induction of synaptic plasticity to predict the plasticity outcome of any set of pre- and post-synaptic activity patterns that occur at the Schaffer collateral synapse in the hippocampus. Since we are interested in studying experimental spike trains we modify a model originally proposed by Shouval et al. (2002) to allow us to carry out such analysis. We make a number of critical modifications to analyze the Ca2+ dynamics in individual dendritic spines during long periods of irregular spiking activity. This is illustrated using short epochs of overlapping hippocampal place cell activity (Figure 1) (Isaac et al., 2009).
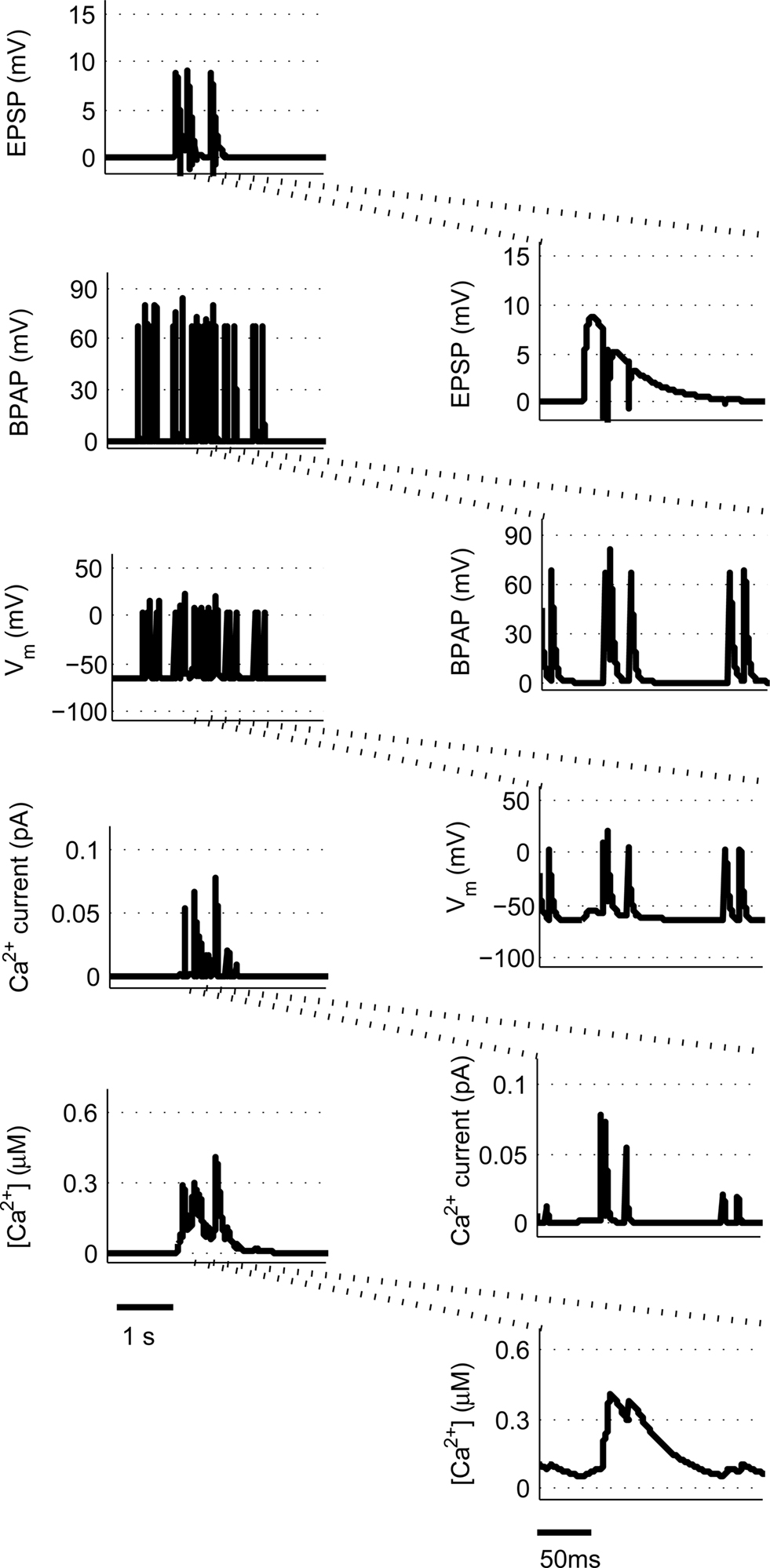
Figure 1. Calculating [Ca2+] in dendritic spines during continuous pre- and post-synaptic activity. The model initially calculates the membrane potential during continuous activity by summating the membrane potential changes due to EPSPs and BPAPs from a resting membrane potential of −65 mV. The Ca2+ current passing through synaptic NMDARs is then calculated from the membrane potential and glutamate binding kinetics. Finally spine [Ca2+] is calculated from Ca2+ buffering and diffusion kinetics. Left hand panels show the post-synaptic responses to an epoch of place cell activity spanning 3500 ms. Right hand panels show a 200 ms excerpt from this epoch.
Essential components of the experimental spike trains for the activation of NMDARs and therefore the induction of synaptic plasticity are (i) the pre-synaptic release of glutamate that dictates the binding of glutamate to the NMDARs and (ii) the post-synaptic membrane potential that determines the relative blockade of NMDARs by Mg2+. For the purposes of this model, we have assumed the two events that determine the post-synaptic membrane potential within an individual dendritic spine are excitatory post-synaptic potentials (EPSPs) and back-propagating action potentials (BPAPs). We start by modeling the BPAPs as follows:
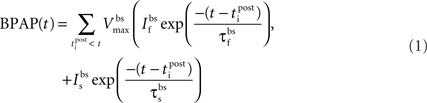
where 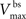 is the maximum depolarization due to the BPAP,
is the maximum depolarization due to the BPAP, 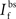 , and
, and 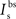 are the relative magnitudes of the fast and slow components of the BPAP, respectively, that sum to one, and the integration time step δ is 0.1 ms. Due to the slower (and much smaller) after-depolarizing potential, if two spikes happen near enough to each other that the first spike is still decaying, the effect of the BPAPs is additive. Since we are modeling the BPAP at the spine
are the relative magnitudes of the fast and slow components of the BPAP, respectively, that sum to one, and the integration time step δ is 0.1 ms. Due to the slower (and much smaller) after-depolarizing potential, if two spikes happen near enough to each other that the first spike is still decaying, the effect of the BPAPs is additive. Since we are modeling the BPAP at the spine 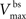 is set at 67 mV in line with experimental data measuring membrane potential in spines with voltage-sensitive dyes (Canepari et al., 2007; Palmer and Stuart, 2009). This is smaller than the maximum BPAP amplitude found at the soma used by Shouval et al. An example of the modeled BPAP during place cell activity can be seen in Figure 1.
is set at 67 mV in line with experimental data measuring membrane potential in spines with voltage-sensitive dyes (Canepari et al., 2007; Palmer and Stuart, 2009). This is smaller than the maximum BPAP amplitude found at the soma used by Shouval et al. An example of the modeled BPAP during place cell activity can be seen in Figure 1.
The equation that governs the behavior of AMPAR-mediated EPSPs in the model is similar to (1) having a slow and a fast exponential component:
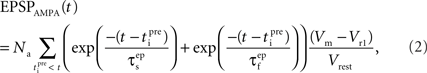
where the parameter Na reflects the maximum effect that a single AMPAR-mediated EPSP can have. The value of Na can vary depending on the number of synapses activated. Activation of a single synapse results in a membrane depolarization in the spine of approximately 10 mV (Palmer and Stuart, 2009). Again this deviates from the value of 1 mV recorded at the soma and used by Shouval et al. Assuming that the maximum depolarization that a single EPSP can generate is 10 mV we define Na in the following way:
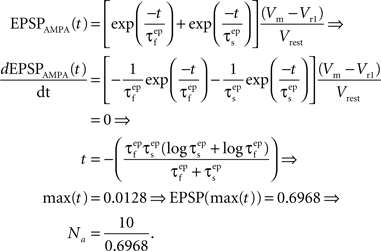
EPSPAMPA also depends on the membrane potential, Vm. This dependence is represented by the term (Vm−Vr1)/Vrest where Vr1 is the reversal potential for AMPARs (0 mV) and Vrest is the resting membrane potential (−65 mV).
The equation that governs the behavior of NMDA-mediated EPSPs in the model has the following form:
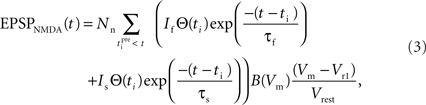
where the parameter Nn reflects the maximum effect of the NMDAR-mediated component of the EPSP. This is calculated in a similar fashion to Na for EPSPAMPA using a value of 5 mV for the NMDAR-mediated EPSP at −65 mV in the absence of Mg2+ measured by dendritic recordings (Fernandez de Sevilla et al., 2007).
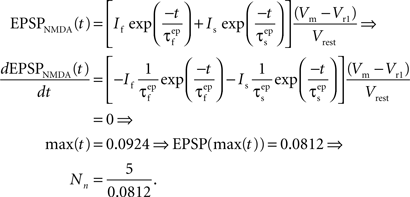
 and
and 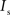 are the relative magnitudes of the fast and slow component of the NMDAR current as a result of glutamate binding, respectively, that sum to one, and Θ is the Heaviside (unit) step function. The voltage dependence of the current that takes into account Mg2+ block of the receptor (Jahr and Stevens, 1990) is represented by the term B(Vm)(Vm−Vr1)/Vrest, where (Vm−Vr1) is the driving force determined by the reversal potential, Vr1 (0 mV), and
are the relative magnitudes of the fast and slow component of the NMDAR current as a result of glutamate binding, respectively, that sum to one, and Θ is the Heaviside (unit) step function. The voltage dependence of the current that takes into account Mg2+ block of the receptor (Jahr and Stevens, 1990) is represented by the term B(Vm)(Vm−Vr1)/Vrest, where (Vm−Vr1) is the driving force determined by the reversal potential, Vr1 (0 mV), and
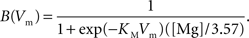
We then calculate the spine membrane potential as the summation of BPAP and EPSPAMPA and EPSPNMDA:
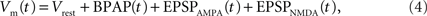
where Vrest is set at −65 mV unless otherwise stated. An example of the predicted spine voltage can be seen for a sample epoch of overlapping place cell activity in Figure 1.
Since NMDARs provide the major source of Ca2+ influx into post-synaptic dendritic spines (Bloodgood and Sabatini, 2007), we incorporate in our model the Ca2+ current through NMDAR that takes the following form (Shouval et al., 2002):
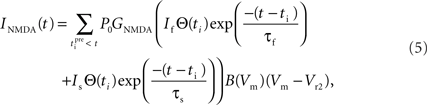
This is similar to Eq. 3 except for the terms P0 and GNMDA that represent the open channel probability and NMDAR Ca2+ conductance respectively and Vr2 is the reversal potential for calcium (130 mV).
Next, the rate of change of the [Ca2+] inside the post-synaptic spine is governed by:

where α is a factor that converts current to flux and τCa is the calcium passive decay time constant. An example of the Ca2+ current flow through NMDARs and the resulting predicted [Ca2+] in the spine can be seen in Figure 1.
Finally, we assume that spine [Ca2+] is the trigger for synaptic strength change. For the purposes of our study the continuous model for synaptic strength used in Shouval et al. is modified to act as a Ca2+-gated function based on local peaks in [Ca2+] as follows:
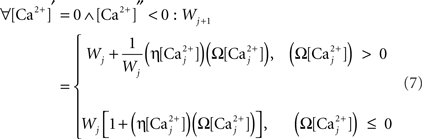
where
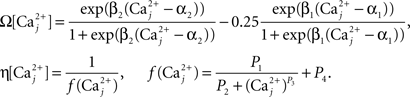
The critical target for Ca2+ influx through NMDARs is the enzyme CAMKII. Due to its ability to autophosphorylate, the activation of this molecule can be long lived and the level is determined by local peak [Ca2+]. Thus, synaptic weight change is determined at local peak [Ca2+] (Miller et al., 2005; Graupner and Brunel, 2007; Helias et al., 2008; Urakubo et al., 2008; Castellani et al., 2009). Since there is no noise associated with our model, these peaks are measured instantaneously without smoothing. Experimentally, increases in synaptic weight tend towards saturation as synaptic weight increases. In addition, decreases require synaptic weight to always be >0. These constraints explain the form of Eq. 7.
Numerical integration was performed using forward Euler method implemented in MATLAB.
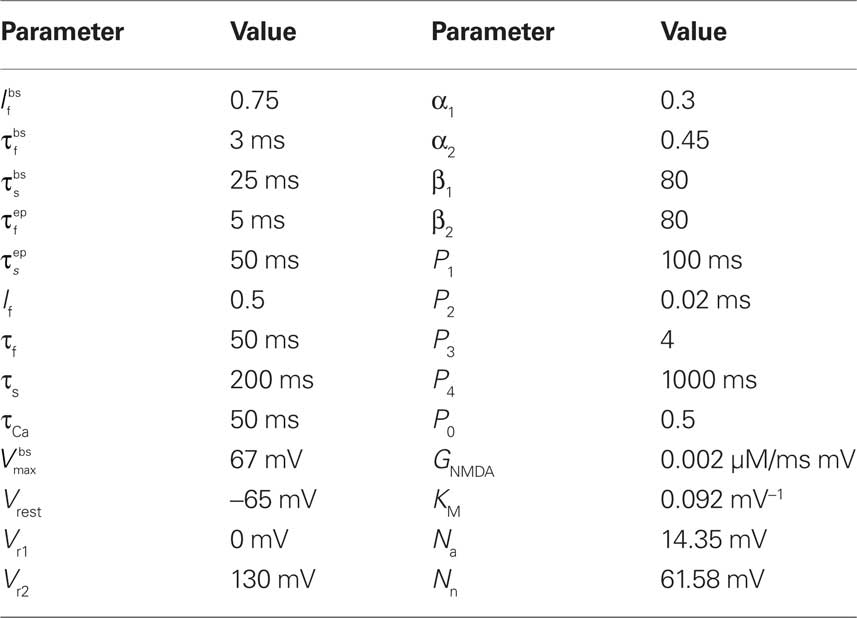
The parameter values used in the simulations are given for completeness in Table 1.
Results
Our starting point for developing a model for the induction of synaptic plasticity was to incorporate the most recent and accurate measurements of voltage changes within dendritic spines using data from measurements of voltage-dependent dyes (Canepari et al., 2007; Palmer and Stuart, 2009). We model the membrane potential at the spine rather than the soma because this is the site of the NMDARs critical for the induction of synaptic plasticity. This shifts the determination of membrane depolarization away from BPAPs and towards EPSPs since the former attenuate as they pass along the dendrite and the latter are now measured at their site of origin. This is a departure from previous models that used values for BPAPs and EPSPs recorded at the soma (Shouval et al., 2002). With this change, our model predicts that an EPSP resulting from the activation of a single synapse is sufficient to cause a significant Ca2+ influx through NMDARs (Figure 2A) in line with experimentally observed data (Bloodgood and Sabatini, 2007; Canepari et al., 2007; Sobczyk and Svoboda, 2007). The pairing of a BPAP with a single EPSP with a time delay of 10 ms produces 3–4 times the Ca2+ influx (Figure 2A) that again agrees qualitatively with experimentally observed data (Bloodgood and Sabatini, 2007). For comparison we changed the maximal EPSP and BPAP amplitudes to those known to occur at the soma (∼1 and ∼100 mV respectively). With these parameters, a single EPSP produces limited Ca2+ influx whereas pairing an EPSP with a BPAP produces a large Ca2+ influx (Figure 2B).
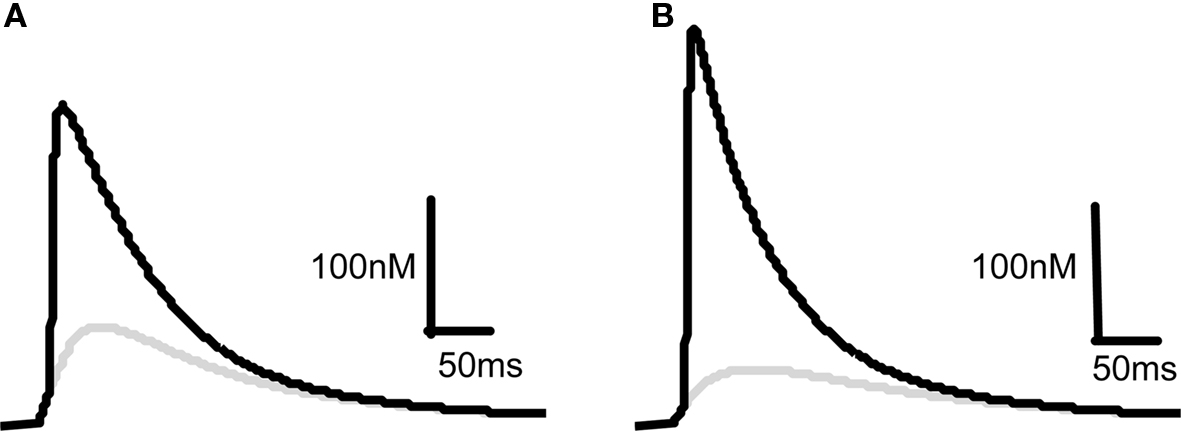
Figure 2. Comparison of predicted [Ca2+] dynamics in dendritic spines and in the soma. [Ca2+] profiles in response to a 10 mV EPSP at the spine (A) or a 1 mV EPSP at the soma (B) on their own (gray) or in combination with a BPAP (black) of amplitude 60 mV at the spine (A) or 100 mV at the soma (B). The delay between EPSP and BPAP initiation is 10 ms.
Having validated our model for the observed Ca2+ influx at dendritic spines we next asked the question if the model could replicate experimental data for the induction of synaptic plasticity using a variety of protocols. We have restricted our model to comparisons with experimental data from the Schaffer collateral synapse of the hippocampus and not considered other synapses in other brain regions.
Spike Timing-Dependent Plasticity with Pairs of Pre- and Post-Synaptic Spikes
To model STDP with pairs of pre- and post-synaptic spikes we initially assumed single synaptic activation and varied Δt between −20 and + 100 ms at intervals of 0.1 ms measuring the peak [Ca2+] at each value of Δt (Figure 3A). [Ca2+] rose from its baseline of 72 nM (the peak [Ca2+] attained for a single EPSP in isolation) to a peak of 230 nM at Δt ≈10 ms (Figure 3B). Experiments such as these have been shown to generate no significant synaptic plasticity (Buchanan and Mellor, 2007) whereas those using larger amplitude EPSPs have been shown to generate LTD (Wittenberg and Wang, 2006). We estimated the activation of multiple synapses at the same time would increase the depolarization within a single dendritic spine during an EPSP from 10 to 20 mV based on experimental predictions (Palmer and Stuart, 2009). Thus we have estimated that the activation of other spines will contribute an additional 10 mV of depolarization within an activated spine above and beyond the experimentally determined 10 mV for activation of a single synapse. This doubling of the EPSP amplitude resulted in an increase in peak [Ca2+] at all values of Δt with a peak of 279 nM occurring at Δt ≈10 ms (Figure 3C).
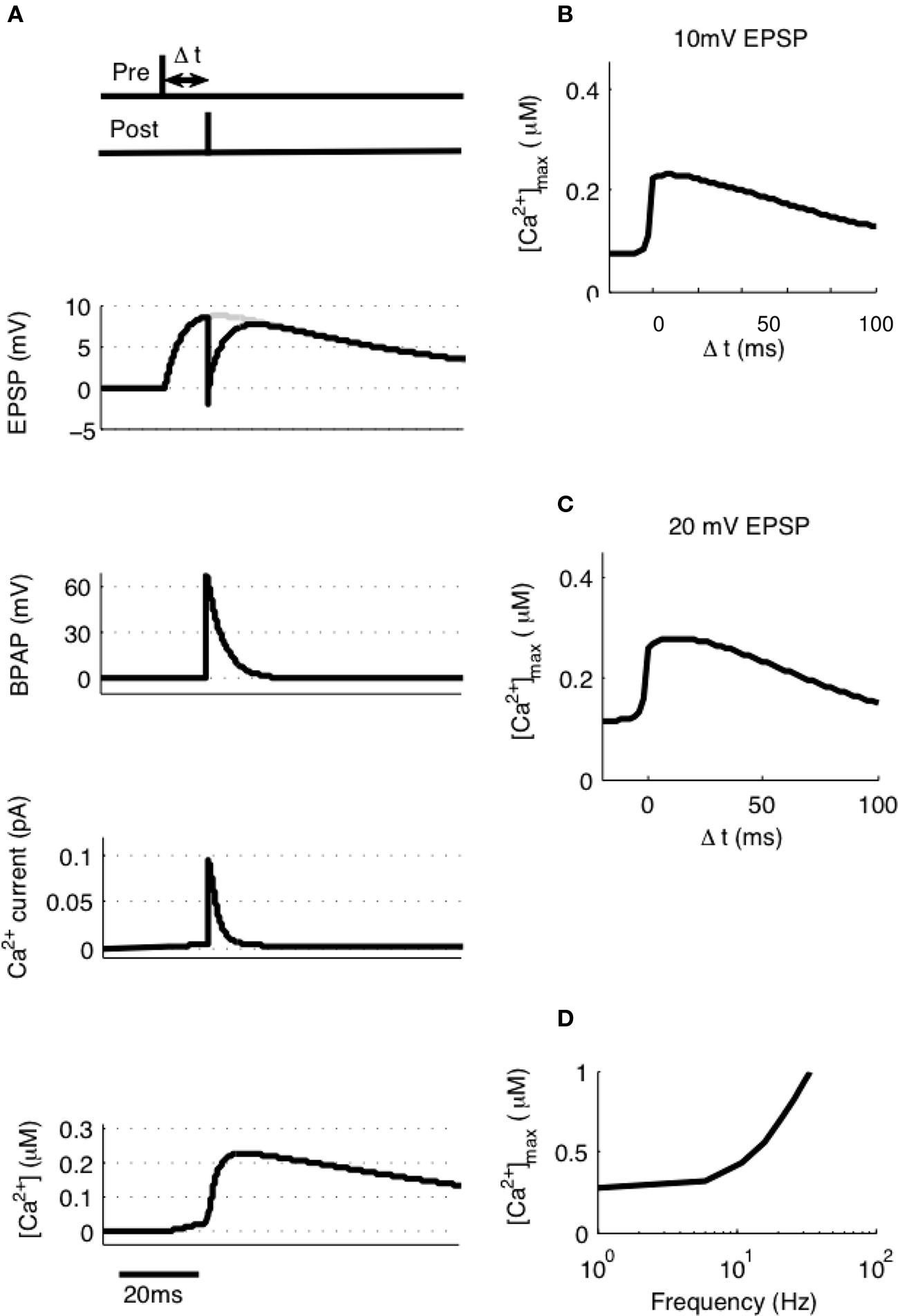
Figure 3. [Ca2+] dynamics in response to paired pre- and post-synaptic spikes. (A) The model calculates [Ca2+] within a spine from the membrane potential resulting from a pair of pre- and post-synaptic spikes. Gray line shows EPSP in the absence of BPAP. Varying Δt shows that [Ca2+]max is greatest when 0 ≤ Δt ≤ 30 ms for 10 mV (B) or 20 mV (C) EPSPs. (D) The frequency of spike pairings given at Δt = 10 ms determines [Ca2+]max.
It has also been shown that the frequency of spike pairing is important for the induction of plasticity such that at higher frequencies (>5–10 Hz) LTP can be induced (Wittenberg and Wang, 2006; Buchanan and Mellor, 2007). We varied the frequency of spike pairings in our model for 10 mV EPSPs over a range of frequencies from 1 to 100 Hz (Figure 3D). Summation of Ca2+ transients was found to occur at frequencies greater than ∼5 Hz indicating that increasing the frequency will shift the STDP protocol towards larger [Ca2+] and therefore LTP in line with the experimental data.
Spike Timing-Dependent Plasticity with Triplets of Spikes
Post-synaptic burst firing has been shown to be important for the induction of LTP at Schaffer collateral synapses in the hippocampus where burst firing in this instance refers to any number of spikes greater than one (Pike et al., 1999; Wittenberg and Wang, 2006; Buchanan and Mellor, 2007). We tested this on our model using triplets of spikes composed of one pre-synaptic spike and two post-synaptic spikes where Δt is the time between the pre-synaptic spike and the first post-synaptic spike and Δs is the delay between the two post-synaptic spikes (Figure 4A). We first used 10 mV EPSPs with a constant Δs of 10 ms and varied Δt between −20 and +100 ms. This produced a peak [Ca2+] of 420 nM at Δt = 4 ms which increased to a peak [Ca2+] of 475 nM when 20 mV EPSPs were used (Figure 4B) confirming that spike triplets produce higher peak [Ca2+] than spike pairs and therefore are more likely to induce LTP.
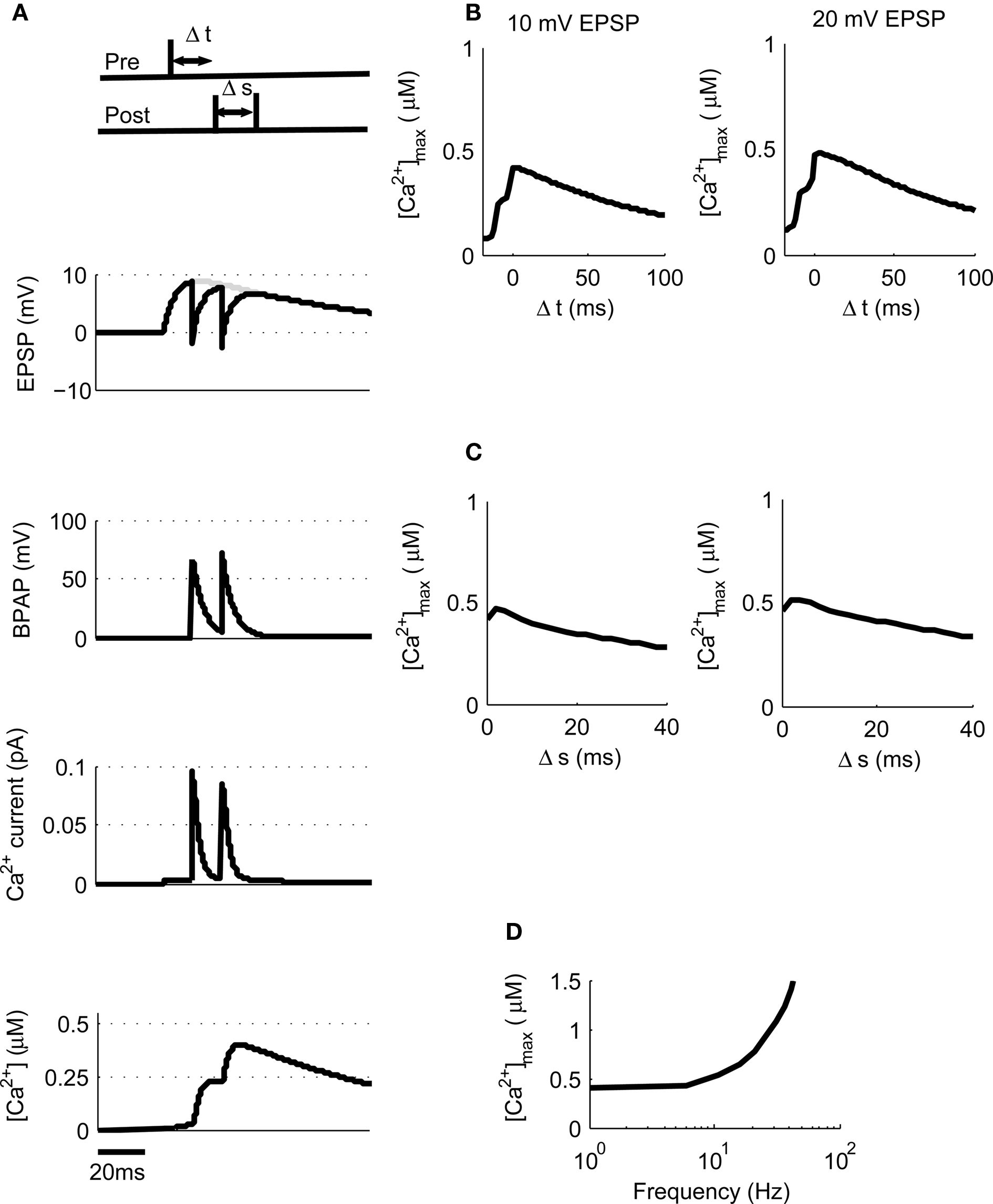
Figure 4. [Ca2+] dynamics in response to triplets of one pre- and two post-synaptic spikes. (A) The model calculates [Ca2+] within a spine from the membrane potential resulting from a triplet of pre- and post-synaptic spikes. Gray line shows EPSP in the absence of BPAP. (B). Varying Δt shows that [Ca2+]max is greatest when 0 ≤ Δt ≤ 30 ms for 10 or 20 mV EPSPs for Δs = 10 ms. (C) Varying Δs shows that [Ca2+]max decreases as Δs increases for 10 or 20 mV EPSPs and Δt = 10 ms. (D) The frequency of spike pairings given at Δt = 10 ms and Δs = 10 ms determines [Ca2+]max.
We next varied Δs whilst maintaining Δt constant at 10 ms for both 10 and 20 mV EPSPs revealing a decrease in peak [Ca2+] as Δs increases (Figure 4C). Finally, we varied the frequency of triplets for 10 mV EPSPs over a range of frequencies from 1 to 100 Hz whilst keeping Δt and Δs constant at 10 ms each (Figure 4D). Summation of Ca2+ transients was found to occur at frequencies greater than ∼4 Hz.
Theta Burst Plasticity
We now moved away from STDP to look at other common synaptic plasticity induction protocols. The theta burst protocol was developed to mimic the activity patterns believed to occur at hippocampal synapses during learning and consists of bursts of four or five spikes at 100 Hz with an interburst interval of 200 ms. These can either be applied to the pre- and post-synaptic neuron coincidentally (Frick et al., 2004) or to just the pre-synaptic neuron (Larson et al., 1986). The latter then leads to post-synaptic spikes through EPSP summation if the initial EPSP amplitude is sufficiently large (Buchanan and Mellor, 2007). We used our model to mimic coincident theta burst activity in pre- and post-synaptic neurons using 10 mV EPSPs and found that this type of synaptic stimulation produces very large peak [Ca2+] within dendritic spines (Figure 5) indicating that this protocol is very efficient at producing LTP in agreement with experimental data. Experimental data also shows when theta burst stimulation is given to only the pre-synaptic neuron without initiating action potentials then no plasticity is induced (Buchanan and Mellor, 2007). When we used theta burst stimulation with five stimuli to only the pre-synaptic input, the model predicted peak [Ca2+] within the spine to be 325 nM (Figure 5) and with four stimuli 250 nM. The value for four stimuli is more physiologically relevant since the probability of neurotransmitter release at any one Schaffer collateral synapse is considerably less than 1. Therefore it is highly unlikely that an experimental theta burst will ever generate five EPSPs at an individual synapse.
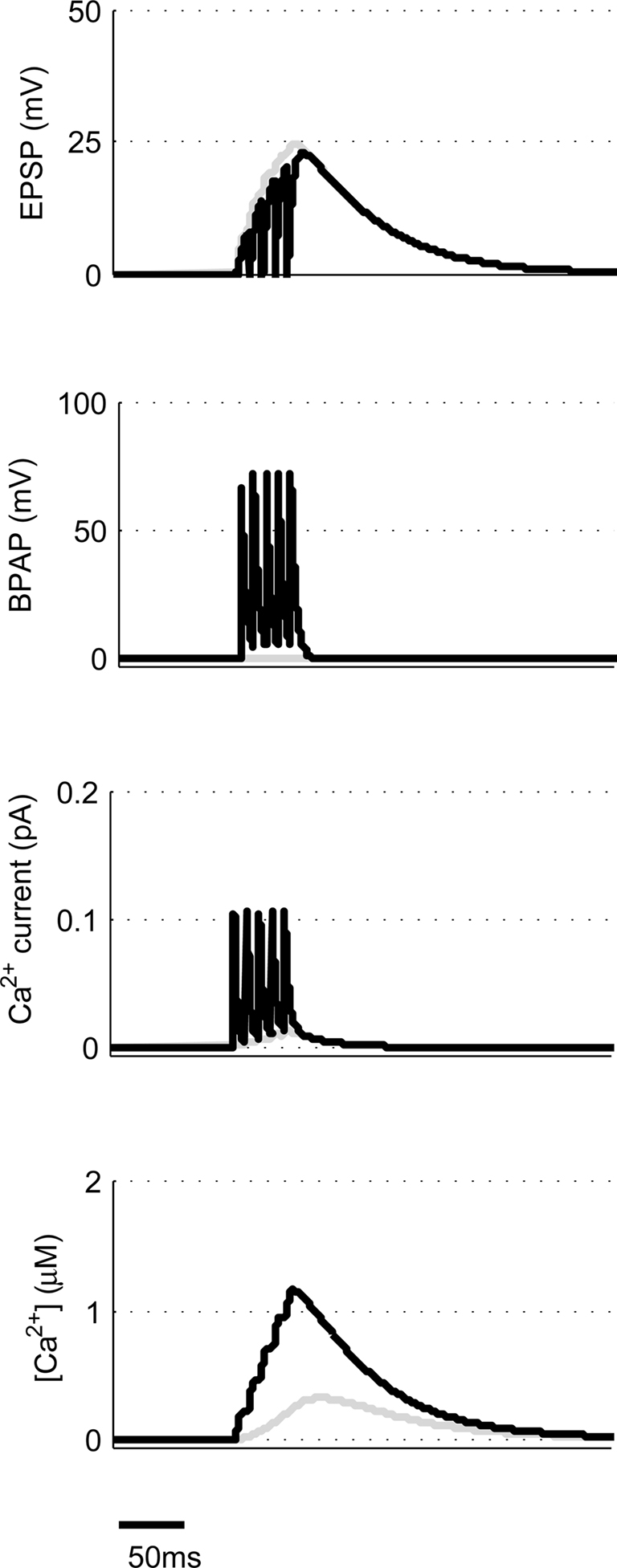
Figure 5. Theta burst pairing produces large spine [Ca2+]. The model calculates [Ca2+] within a spine from the membrane potential resulting from coincident theta burst stimulation of pre- and post-synaptic neurons (black) or only pre-synaptic neuron (gray).
Pairing Post-Synaptic Depolarization with Pre-Synaptic Stimulation
Other common synaptic plasticity induction protocols have dispensed with the need for post-synaptic spikes altogether and use voltage clamp to depolarize the post-synaptic membrane and allow NMDAR activation. This technique neatly demonstrates the bidirectional nature of NMDAR-dependent plasticity since depolarization to moderate levels (−40 mV) produces LTD whereas higher depolarization (0 mV) produces LTP (Isaac et al., 1995; Daw et al., 2000). We tested this with our model by clamping the membrane potential (Vm) at either −40 or 0 mV (Figure 6). Peak [Ca2+] in response to EPSPs were 336 nM and 2.43 μM respectively, which when compared to peak [Ca2+] produced by other protocols would be expected to induce LTD and LTP respectively in agreement with experimental data.
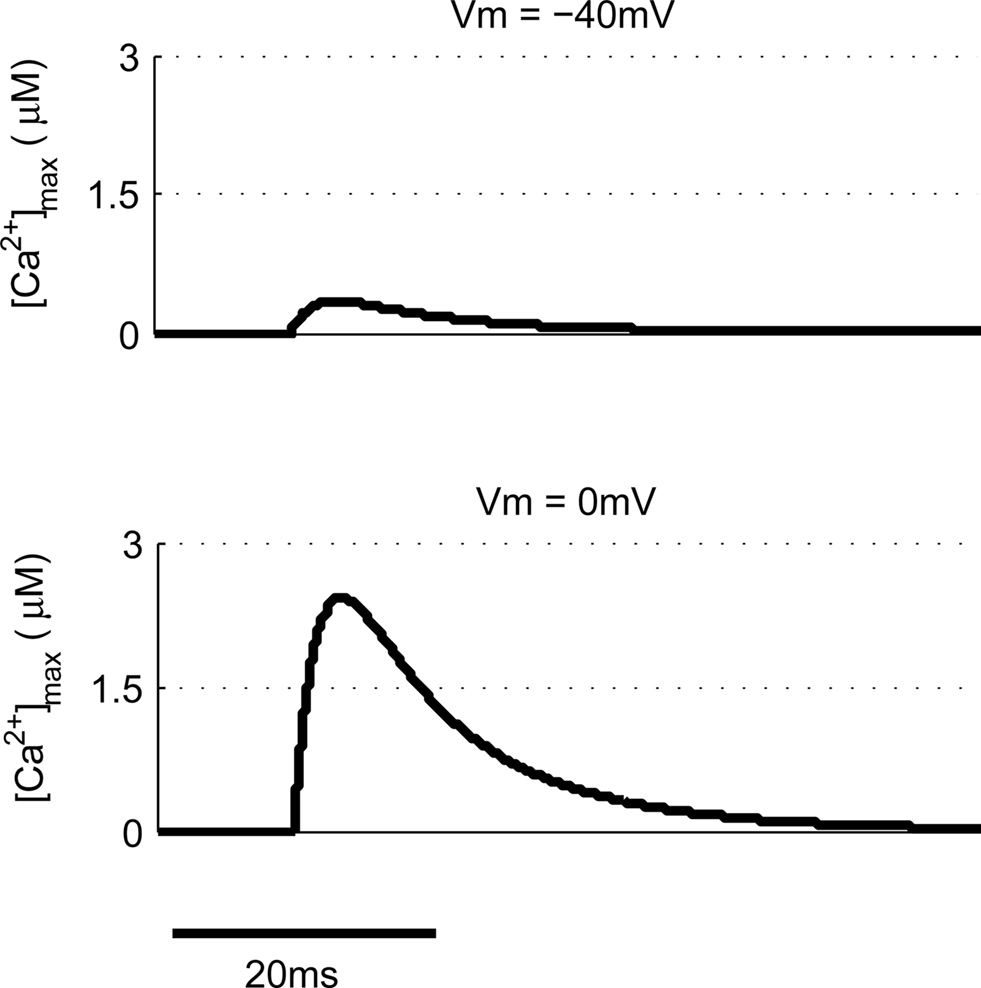
Figure 6. Post-synaptic voltage clamp paired with pre-synaptic stimulation determines spine [Ca2+]. The model predicts that voltage clamp of the post-synaptic membrane potential at −40 mV produces a much smaller spine [Ca2+] than 0 mV when paired with a single pre-synaptic stimulation.
The Ca2+ Hypothesis can Explain Previous Experimental Data
The Ca2+ hypothesis states that brief high concentrations of Ca2+ in the post-synaptic spine induce LTP whereas prolonged lower concentrations of Ca2+ induce LTD (Bear et al., 1987; Hansel et al., 1996). This is expressed graphically in Figure 7. Points are indicated representing the predicted [Ca2+] from our model for specific plasticity inducing protocols. STDP with single pairs of BPAPs and small EPSPs do not induce plasticity (Buchanan and Mellor, 2007) but when large EPSPs are used LTD is induced (Wittenberg and Wang, 2006) and STDP with triplets of single EPSPs and bursts of BPAPs produces LTP (Pike et al., 1999; Wittenberg and Wang, 2006; Buchanan and Mellor, 2007). When the post-synaptic membrane potential is set at −40 mV during pre-synaptic stimulation LTD is induced (Daw et al., 2000) whereas at 0 mV LTP is induced (Isaac et al., 1996). Theta burst pairing also induces LTP (Frick et al., 2004; Buchanan and Mellor, 2007) whereas theta burst to only pre-synaptic inputs does not (Buchanan and Mellor, 2007). In this instance the absolute [Ca2+] values predicted by the model are not as important as the relative magnitudes between plasticity induction protocols. However, it is interesting to note that the absolute [Ca2+] values predicted by the model broadly agree with those measured experimentally for the induction of synaptic plasticity at Schaffer collateral synapses on CA1 pyramidal neurons (Cormier et al., 2001). Thus the predictions from our model support the Ca2+ hypothesis for synaptic plasticity induction.
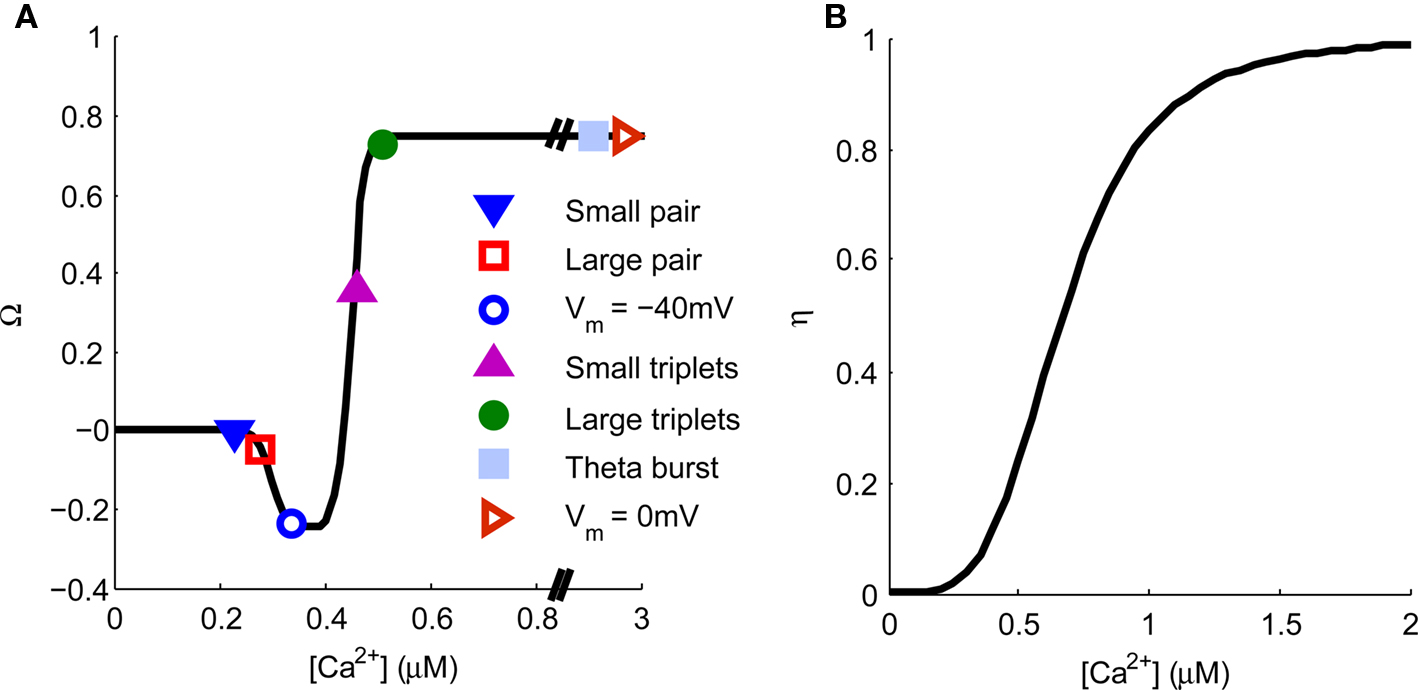
Figure 7. Spine [Ca2+] determines the direction and magnitude of synaptic weight change. (A). The Ω−function describes the relationship between peak spine [Ca2+] and synaptic weight change. Symbols represent the peak [Ca2+] produced by a single application of the plasticity induction protocols shown in Figures 3–6 and indicate the resulting predicted synaptic weight change. (B) The η-function describes the learning rate for synaptic weight change as a function of peak spine [Ca2+].
Induction of Synaptic Plasticity by Hippocampal Place Cell Firing Patterns
One of the main purposes for developing a model that is capable of continuously monitoring [Ca2+] in spines and therefore predicts changes in synaptic strength is to scan long periods of neuronal activity for epochs that would be expected to induce plasticity without having to directly measure synaptic strength. To test if the model could perform this task we used data from experiments where long sections of hippocampal place cell activity were replayed into single hippocampal synapses to test the plasticity outcome (Isaac et al., 2009).
We first took an ∼16-min period of activity from a pair of place cells (1A and 1B) that had overlapping place fields and therefore would be expected to fire at approximately the same time (Isaac et al., 2009). During the ∼16-min period short coincident bursts of activity could be seen in the two place cells that the model predicted would produce large [Ca2+] sufficient to induce LTP (Figures 1 and 8). This LTP was initiated in the first few minutes of activity and eventually reached a plateau.
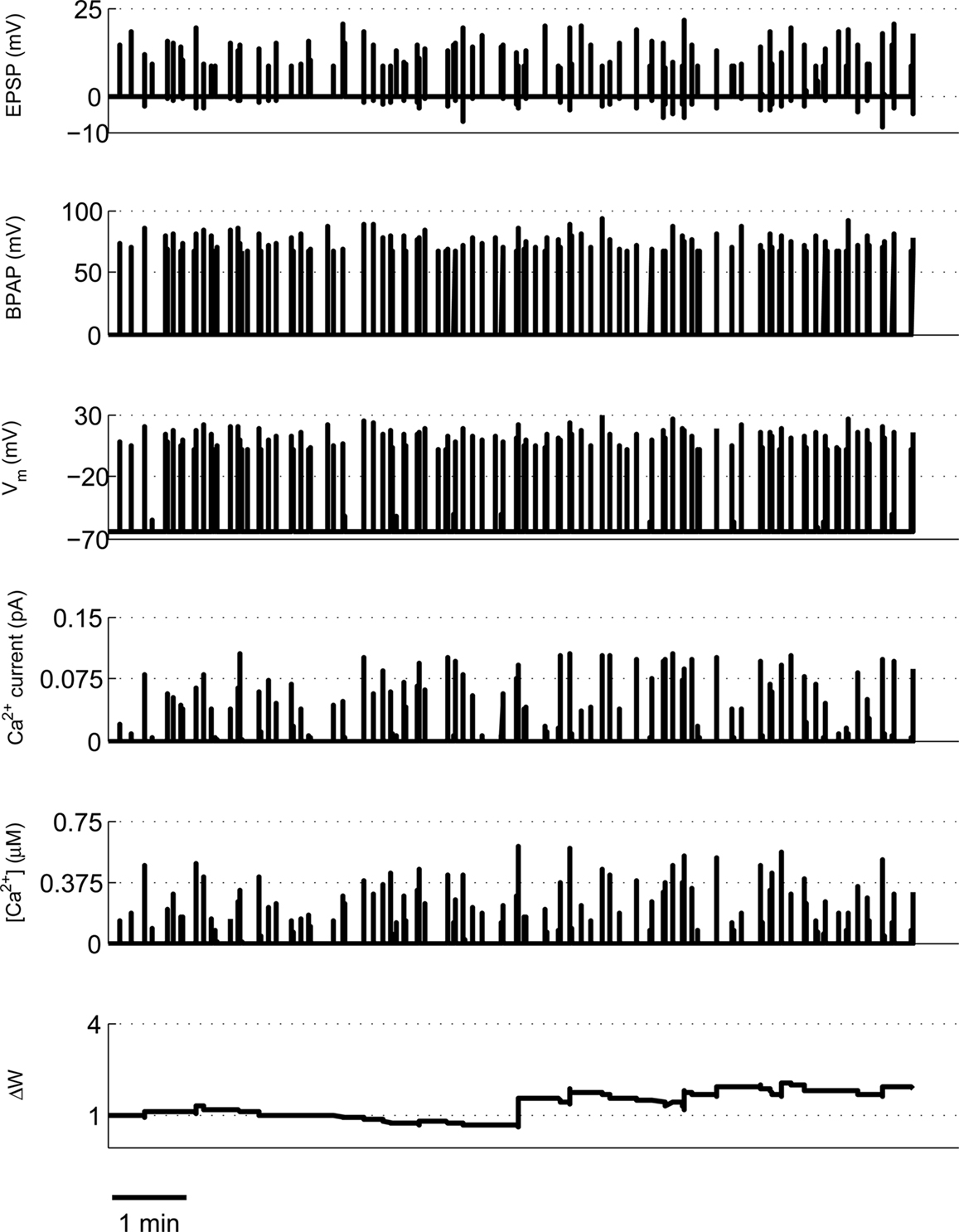
Figure 8. Example of predicted synaptic weight change during overlapping place cell activity. The model calculates spine [Ca2+] during a ∼16-min period of activity from two place cells (1A and 1B) with overlapping place fields. The synaptic weight change is then calculated from the peak spine [Ca2+] and shows a robust, rapidly developing potentiation.
We tested a set of four further pairs of place cells (2A and 2B, 2C and 2D, 3A and 3B, 4A and 4B) with overlapping place fields but with strikingly different spiking characteristics [for a full description of the place cell spike pattern characteristics and plasticity outcomes see Isaac et al. (2009)] and found in each case the model predicted robust LTP induction in agreement with the experimental data (Figures 9A–D). We also tested two further pairs of place cells with non-overlapping or adjacent place fields (1A and 1C, 2E and 2D) and found the model predicted only a small LTD for the non-overlapping pair and a small LTP for the adjacent pair (Figures 9E–F).
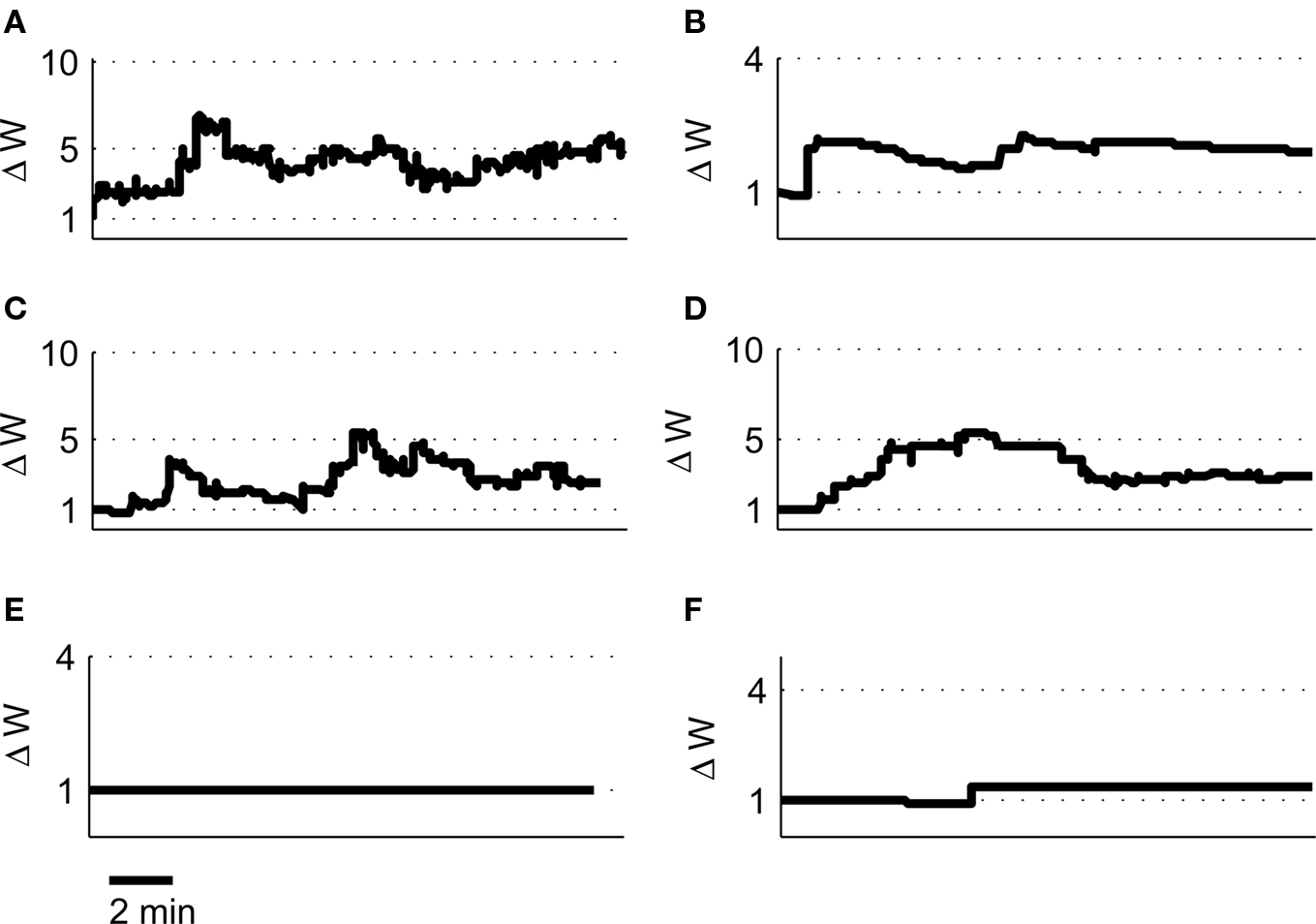
Figure 9. Predicted synaptic weight changes for overlapping and non-overlapping place cell activity. Calculated synaptic weight changes for four pairs of overlapping place cells 2A, 2B (A), 2C, 2D (B), 3A, 3B (C), and 4A, 4B (D) as well as one pair of non-overlapping place cells 1A, 1C (E) and one pair of adjacent place cells 2E, 2D (F).
Our original experimental data also tested a pair of place cells that had an asymmetric cross-correlation such that cell 1A preferentially fired just before cell 1B. Because classical STDP rules state that the temporal order of pre- and post-synaptic spikes controls the direction of synaptic plasticity (Bi and Poo, 1998; Song et al., 2000), the existence of this asymmetry suggested that when cell 1A was pre-synaptic and cell 1B post-synaptic then LTP would be induced but if the cells were reversed then LTD would be induced. However, when we reversed the place cell firing patterns such that cell 1B was pre-synaptic and cell 1A post-synaptic the model predicted LTP (Figure 10A) that corroborates the experimental results and closely reproduces the experimentally determined timecourse of LTP development (Isaac et al., 2009). We also manipulated the spike patterns in cell 1B to remove all spikes that occurred less than 100 ms after a spike in cell 1A leaving only spikes that occurred before any spike in cell 1A. Classical STDP rules would again predict that if cell 1A was pre-synaptic and the modified cell 1B was post-synaptic then LTD would be induced but the model predicted only marginal LTD (Figure 10B) in line with the experimental data (Isaac et al., 2009).
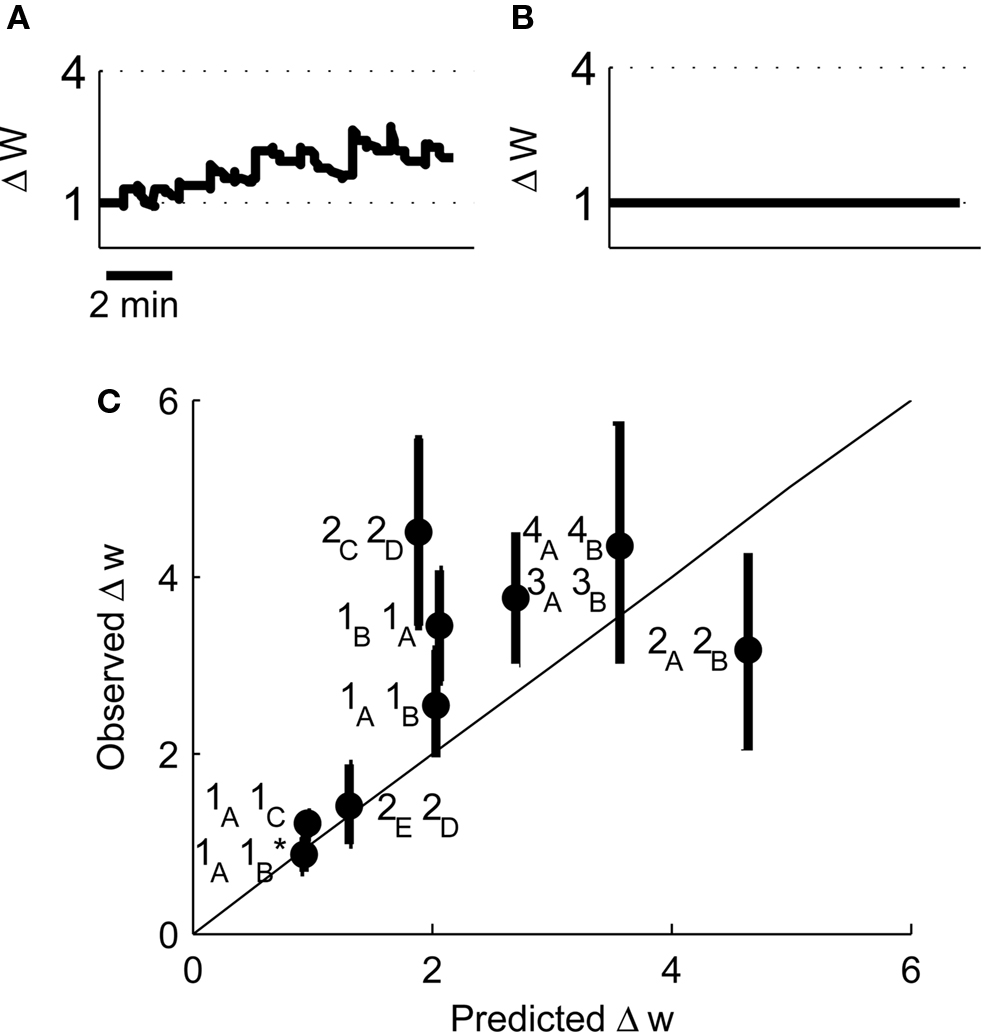
Figure 10. Predicted synaptic weight changes for place cell activity with specific spike patterns. Calculated synaptic weight changes for a pair of overlapping place cells with an asymmetric cross-correlation 1B, 1A (A) and a pair of place cells where all spike intervals with positive Δt less than 100 ms have been removed 1A, 1B (B). (C) A comparison between the induced plasticity predicted by the model and the observed plasticity from experimental data (Isaac et al., 2009).
Finally we have compared the experimentally determined plasticity outcome from nine pairs of place cells with the outcome predicted by our model. We find that the correlation between the predicted and observed values is significant (Figure 10C, r2 = 0.58, P < 0.05 by linear regression) and therefore conclude that the model successfully predicts the induction of synaptic plasticity by irregular activity patterns.
Discussion
The model described in this study incorporates two important components of Ca2+ dynamics in dendritic spines that are necessary for the induction of synaptic plasticity. Firstly, our model is capable of analyzing Ca2+ influx and concentration continuously and therefore it can determine the plasticity outcome of multiple synaptic events that occur in vivo in an irregular pattern. Secondly, [Ca2+] is modeled at the synapse in dendritic spines rather than at the soma. This is important since the critical Ca2+ signal for the induction of synaptic plasticity occurs at the spine. It also changes the relative importance of EPSP vs BPAP depolarization which has major implications for the predicted induction of STDP. This approach is validated by comparison of the predicted vs observed Ca2+ transients in response to either a single EPSP or coupled with a BPAP (Figure 2) (Bloodgood and Sabatini, 2007).
The absolute values for [Ca2+] within the dendrite required for the induction of synaptic plasticity have been estimated as 150–500 nM for LTD and >500 nM for LTP (Cormier et al., 2001). However, other researchers have estimated [Ca2+] within a spine in response to a single EPSP at 700 nM and a much higher 12 μM during pairing of post-synaptic depolarization with synaptic stimulation (Sabatini et al., 2002). This discrepancy could be explained in a number of ways. The [Ca2+] in a dendritic spine in response to synaptic stimulation could be considerably higher than in the dendritic shaft because of the diffusion barrier created by the spine neck. In addition, accurate absolute values for [Ca2+] measured by fluorescent Ca2+ indicators are difficult to achieve and therefore most studies are restricted to ratiometric measurements of transient [Ca2+] increases. For the purposes of synaptic plasticity this is sufficient since the increase in [Ca2+] triggers induction. Here, we have calculated the [Ca2+] based on a number of assumptions for channel conductance and Ca2+ diffusion. More importantly, we have modeled the relative [Ca2+] increases caused by various induction protocols and used these to define the graph in Figure 7 that predicts the plasticity outcome.
Inhibitory synaptic transmission has a major role regulating the induction of synaptic plasticity in the hippocampus. The transient depression of inhibition induced by activation of pre-synaptic cannabinoid or GABAB receptors facilitates the induction of LTP (Davies et al., 1991; Chevaleyre and Castillo, 2004). This modulation of synaptic plasticity is not included in our current model but incorporation of the hyperpolarizing effects of GABAergic transmission would be an important future improvement and might, for example, contribute to the frequency dependence of STDP induction.
NMDARs are not the only sources of Ca2+ within dendritic spines but are certainly the most important for the induction of synaptic plasticity. A role has also been demonstrated for Ca2+ stores present in the endoplasmic reticulum in dendrites and spines (linked to Ca2+ influx through NMDARs or mGluRs) and also voltage-dependent calcium channels present on the membrane of dendritic spines that generate local dendritic Ca2+ spikes (Golding et al., 2002; Remy and Spruston, 2007) and can contribute to some forms of LTD (Nevian and Sakmann, 2006). The contribution of non-NMDAR-mediated Ca2+ increases to synaptic plasticity induction is specifically omitted from our model but would be a useful future addition. There are also potential alternative mechanisms for the induction of synaptic plasticity that do not involve Ca2+ such as mGluRs (Moult et al., 2006) or muscarinic acetylcholine receptors (Dickinson et al., 2009) that are also specifically omitted from our model. Future experimental data may, however, require their addition.
There is a wealth of data on the spiking requirements for plasticity at various synapses in the cortex (Dan and Poo, 2006). However, these requirements have been shown to be somewhat different to those found in the hippocampus perhaps due to variations in dendritic architecture and NMDAR subunit expression and therefore we have restricted our model specifically to the Schaffer collateral synapse in the hippocampus. Even within the hippocampus there is some controversy surrounding the precise spiking requirements for STDP (Buchanan and Mellor, 2010) for example whether single pairs of spikes at low frequency can induce LTP (Bi and Poo, 1998; Debanne et al., 1998; Nishiyama et al., 2000; Wittenberg and Wang, 2006; Buchanan and Mellor, 2007; Campanac and Debanne, 2008; Kwag and Paulsen, 2009). These discrepancies can potentially be explained by variations in experimental conditions [For example, size of EPSPs, age of animals, frequency of stimulus presentation, presence of inhibitory inputs, etc. discussed in Buchanan and Mellor (2010)]. To reduce these discrepancies our model is based on data from acute hippocampal slices but future modifications could enable it to accurately replicate data from all systems including cortical synapses if one assumes that the general mechanism for the induction of synaptic plasticity is similar for all synapses that have NMDAR-dependent synaptic plasticity.
Our experimental data has revealed a critical role for muscarinic acetylcholine receptors in facilitating LTP induced by place cell firing patterns (Isaac et al., 2009). In the absence of muscarinic receptor activation no plasticity is induced but in the presence of a muscarinic agonist we obtain the results described above. This suggests that muscarinic receptor activation is permissive for the induction of synaptic plasticity under conditions where single synapses are activated and EPSP amplitude is small. A similar role has also been suggested for other G-protein coupled receptors such as mGluRs (Bashir et al., 1993) and β-adrenoreceptors (Seol et al., 2007). The observation that muscarinic receptor activation is not required when multiple synapses are activated and EPSP amplitude is large also demonstrates the critical role that multiple synaptic activation plays in the induction of synaptic plasticity. The model described in this study does not currently include a role for G-protein-mediated modulation of synaptic plasticity and this is an important consideration for future modifications and improvements. For example, it would be potentially possible to incorporate a negative feedback on Ca2+ influx under normal conditions that is inhibited by activation of G-protein coupled receptors or overridden by larger EPSPs.
Technical considerations make the visualization or recording of single synapses during behavior extremely difficult. This makes determination of the events that induce synaptic plasticity in the hippocampus almost impossible. These limitations could be circumvented by using the model described in this study to predict the plasticity outcome at a single synapse for any pattern of pre- and post-synaptic activity. Potentially, this will enable the determination of when synaptic plasticity is induced during behavior by examining the spike patterns of pairs of cells recorded during a memory task. This represents an exciting future application for this model.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Jack R. Mellor is supported by the Wellcome Trust and by the European Union ENI-NET. The Bristol Centre for Complexity Sciences is funded by the EPSRC, UK (EP/E501214/1) which supports OJLR and AG.
References
Bashir, Z. I., Bortolotto, Z. A., Davies, C. H., Berretta, N., Irving, A. J., Seal, A. J., Henley, J. M., Jane, D. E., Watkins, J. C., and Collingridge, G. L. (1993). Induction of LTP in the hippocampus needs synaptic activation of glutamate metabotropic receptors. Nature 363, 347–350.
Bear, M. F., Cooper, L. N., and Ebner, F. F. (1987). A physiological-basis for a theory of synapse modification. Science 237, 42–48.
Bi, G. Q., and Poo, M. M. (1998). Synaptic modifications in cultured hippocampal neurons: Dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 18, 10464–10472.
Bloodgood, B. L., and Sabatini, B. L. (2007). Nonlinear regulation of unitary synaptic signals by CaV(2.3) voltage-sensitive calcium channels located in dendritic spines. Neuron 53, 249–260.
Buchanan, K. A., and Mellor, J. R. (2007). The development of synaptic plasticity induction rules and the requirement for postsynaptic spikes in rat hippocampal CA1 pyramidal neurones. J. Physiol. 585, 429–445.
Buchanan, K. A., and Mellor, J. R. (2010). The activity requirements for spike timing-dependent plasticity in the hippocampus. Front. Synaptic Neurosci. 2, 1–5.
Campanac, E., and Debanne, D. (2008). Spike timing-dependent plasticity: a learning rule for dendritic integration in rat CA1 pyramidal neurons. J. Physiol. 586, 779–793.
Canepari, M., Djurisic, M., and Zecevic, D. (2007). Dendritic signals from rat hippocampal CA1 pyramidal neurons during coincident pre- and post-synaptic activity: a combined voltage- and calcium-imaging study. J. Physiol. 580, 463–484.
Castellani, G. C., Bazzani, A., and Cooper, L. N. (2009). Toward a microscopic model of bidirectional synaptic plasticity. Proc. Natl. Acad. Sci. U.S.A. 106, 14091–14095.
Chevaleyre, V., and Castillo, P. E. (2004). Endocannabinoid-mediated metaplasticity in the hippocampus. Neuron 43, 871–881.
Cho, K., Aggleton, J. P., Brown, M. W., and Bashir, Z. I. (2001). An experimental test of the role of postsynaptic calcium levels in determining synaptic strength using perirhinal cortex of rat. J. Physiol. 532, 459–466.
Cormier, R. J., Greenwood, A. C., and Connor, J. A. (2001). Bidirectional synaptic plasticity correlated with the magnitude of dendritic calcium transients above a threshold. J. Neurophysiol. 85, 399–406.
Dan, Y., and Poo, M. M. (2006). Spike timing-dependent plasticity: From synapse to perception. Physiol. Rev. 86, 1033–1048.
Davies, C. H., Starkey, S. J., Pozza, M. F., and Collingridge, G. L. (1991). GABA autoreceptors regulate the induction of LTP. Nature 349, 609–611.
Daw, M. I., Chittajallu, R., Bortolotto, Z. A., Dev, K. K., Duprat, F., Henley, J. M., Collingridge, G. L., and Isaac, J. T. R. (2000). PDZ proteins interacting with C-terminal GluR2/3 are involved in a PKC-dependent regulation of AMPA receptors at hippocampal synapses. Neuron 28, 873–886.
Debanne, D., Gahwiler, B. H., and Thompson, S. M. (1998). Long-term synaptic plasticity between pairs of individual CA3 pyramidal cells in rat hippocampal slice cultures. J. Physiol. 507, 237–247.
Dickinson, B. A., Jo, J., Seok, H., Son, G. H., Whitcomb, D. J., Davies, C. H., Sheng, M., Collingridge, G. L., and Cho, K. (2009). A novel mechanism of hippocampal LTD involving muscarinic receptor-triggered interactions between AMPARs, GRIP and liprin-alpha. Mol. Brain 2, 18.
Fernandez de Sevilla, D., Fuenzalida, M., Porto Pazos, A. B., and Buno, W. (2007). Selective shunting of the NMDA EPSP component by the slow afterhyperpolarization in rat CA1 pyramidal neurons. J. Neurophysiol. 97, 3242–3255.
Franks, K. M., Bartol, T. M. Jr., and Sejnowski, T. J. (2002). A Monte Carlo model reveals independent signaling at central glutamatergic synapses. Biophys. J. 83, 2333–2348.
Frick, A., Magee, J., and Johnston, D. (2004). LTP is accompanied by an enhanced local excitability of pyramidal neuron dendrites. Nat. Neurosci. 7, 126–135.
Froemke, R. C., Tsay, I. A., Raad, M., Long, J. D., and Dan, Y. (2006). Contribution of individual spikes in burst-induced long-term synaptic modification. J. Neurophysiol. 95, 1620–1629.
Gall, D., Prestori, F., Sola, E., D’Errico, A., Roussel, C., Forti, L., Rossi, P., and D’Angelo, E. (2005). Intracellular calcium regulation by burst discharge determines bidirectional long-term synaptic plasticity at the cerebellum input stage. J. Neurosci. 25, 4813–4822.
Golding, N. L., Staff, N. P., and Spruston, N. (2002). Dendritic spikes as a mechanism for cooperative long-term potentiation. Nature 418, 326–331.
Graupner, M., and Brunel, N. (2007). STDP in a bistable synapse model based on CaMKII and associated signaling pathways. PLoS Comput. Biol. 3, 2299–2323.
Grunditz, A., Holbro, N., Tian, L., Zuo, Y., and Oertner, T. G. (2008). Spine neck plasticity controls postsynaptic calcium signals through electrical compartmentalization. J. Neurosci. 28, 13457–13466.
Hansel, C., Artola, A., and Singer, W. (1996). Different threshold levels of postsynaptic [Ca2+]i have to be reached to induce LTP and LTD in neocortical pyramidal cells. J. Physiol. Paris 90, 317–319.
Hansel, C., Artola, A., and Singer, W. (1997). Relation between dendritic Ca2+ levels and the polarity of synaptic long-term modifications in rat visual cortex neurons. Eur. J. Neurosci. 9, 2309–2322.
Helias, M., Rotter, S., Gewaltig, M. O., and Diesmann, M. (2008). Structural plasticity controlled by calcium based correlation detection. Front. Comput. Neurosci. 2, 1–21.
Isaac, J. T., Buchanan, K. A., Muller, R. U., and Mellor, J. R. (2009). Hippocampal place cell firing patterns can induce long-term synaptic plasticity in vitro. J. Neurosci. 29, 6840–6850.
Isaac, J. T., Hjelmstad, G. O., Nicoll, R. A., and Malenka, R. C. (1996). Long-term potentiation at single fiber inputs to hippocampal CA1 pyramidal cells. Proc. Natl. Acad. Sci. U.S.A. 93, 8710–8715.
Isaac, J. T., Nicoll, R. A., and Malenka, R. C. (1995). Evidence for silent synapses: implications for the expression of LTP. Neuron 15, 427–434.
Ismailov, I., Kalikulov, D., Inoue, T., and Friedlander, M. J. (2004). The kinetic profile of intracellular calcium predicts long-term potentiation and long-term depression. J. Neurosci. 24, 9847–9861.
Jahr, C. E., and Stevens, C. F. (1990). A quantitative description of NMDA receptor-channel kinetic behavior. J. Neurosci. 10, 1830–1837.
Keller, D. X., Franks, K. M., Bartol, T. M. Jr., and Sejnowski, T. J. (2008). Calmodulin activation by calcium transients in the postsynaptic density of dendritic spines. PLoS One 3, e2045.
Kwag, J., and Paulsen, O. (2009). The timing of external input controls the sign of plasticity at local synapses. Nat. Neurosci. 12, 1219–1221.
Larson, J., Wong, D., and Lynch, G. (1986). Patterned stimulation at the theta-frequency is optimal for the induction of hippocampal long-term potentiation. Brain Res. 368, 347–350.
Lisman, J. (1989). A mechanism for the Hebb and the anti-Hebb processes underlying learning and memory. Proc. Natl. Acad. Sci. U.S.A. 86, 9574–9578.
Miller, P., Zhabotinsky, A. M., Lisman, J. E., and Wang, X. J. (2005). The stability of a stochastic CaMKII switch: dependence on the number of enzyme molecules and protein turnover. PLoS Biol. 3, e107. doi:10.1371/journal.pbio.0030107.
Moult, P. R., Gladding, C. M., Sanderson, T. M., Fitzjohn, S. M., Bashir, Z. I., Molnar, E., and Collingridge, G. L. (2006). Tyrosine phosphatases regulate AMPA receptor trafficking during metabotropic glutamate receptor-mediated long-term depression. J. Neurosci. 26, 2544–2554.
Nevian, T., and Sakmann, B. (2006). Spine Ca2+ signaling in spike-timing-dependent plasticity. J. Neurosci. 26, 11001–11013.
Nishiyama, M., Hong, K., Mikoshiba, K., Poo, M., and Kato, K. (2000). Calcium stores regulate the polarity and input specificity of synaptic modification. Nature 408, 584–588.
Palmer, L. M., and Stuart, G. J. (2009). Membrane potential changes in dendritic spines during action potentials and synaptic input. J. Neurosci. 29, 6897–6903.
Pike, F. G., Meredith, R. M., Olding, A. W. A., and Paulsen, O. (1999). Postsynaptic bursting is essential for ‘Hebbian’ induction of associative long-term potentiation at excitatory synapses in rat hippocampus. J. Physiol. 518, 571–576.
Remy, S., and Spruston, N. (2007). Dendritic spikes induce single-burst long-term potentiation. Proc. Natl. Acad. Sci. U.S.A. 104, 17192–17197.
Rubin, J. E., Gerkin, R. C., Bi, G. Q., and Chow, C. C. (2005). Calcium time course as a signal for spike-timing-dependent plasticity. J. Neurophysiol. 93, 2600–2613.
Sabatini, B. L., Oertner, T. G., and Svoboda, K. (2002). The life cycle of Ca2+ ions in dendritic spines. Neuron 33, 439–452.
Seol, G. H., Ziburkus, J., Huang, S., Song, L., Kim, I. T., Takamiya, K., Huganir, R. L., Lee, H. K., and Kirkwood, A. (2007). Neuromodulators control the polarity of spike-timing-dependent synaptic plasticity. Neuron 55, 919–929.
Shouval, H. Z., Bear, M. F., and Cooper, L. N. (2002). A unified model of NMDA receptor-dependent bidirectional synaptic plasticity. Proc. Natl. Acad. Sci. U.S.A. 99, 10831–10836.
Sjostrom, P. J., and Nelson, S. B. (2002). Spike timing, calcium signals and synaptic plasticity. Curr. Opin. Neurobiol. 12, 305–314.
Sjostrom, P. J., Turrigiano, G. G., and Nelson, S. B. (2001). Rate, timing, and cooperativity jointly determine cortical synaptic plasticity. Neuron 32, 1149–1164.
Sobczyk, A., and Svoboda, K. (2007). Activity-dependent plasticity of the NMDA-receptor fractional Ca2+ current. Neuron 53, 17–24.
Song, S., Miller, K. D., and Abbott, L. F. (2000). Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nat. Neurosci. 3, 919–926.
Urakubo, H., Honda, M., Froemke, R. C., and Kuroda, S. (2008). Requirement of an allosteric kinetics of NMDA receptors for spike timing-dependent plasticity. J. Neurosci. 28, 3310–3323.
Keywords: synaptic plasticity, hippocampus, dendritic spines, NMDA receptor, spike timing-dependent plasticity
Citation: Rackham OJL, Tsaneva-Atanasova K, Ganesh A and Mellor JR (2010) A Ca2+-based computational model for NMDA receptor-dependent synaptic plasticity at individual post-synaptic spines in the hippocampus. Front. Syn. Neurosci. 2:31. doi: 10.3389/fnsyn.2010.00031
Received: 21 January 2010;
Paper pending published: 22 February 2010;
Accepted: 27 June 2010;
Published online: 21 July 2010
Edited by:
Per Jesper Sjöström, University College London, UKReviewed by:
Harel Z. Shouval, University of Texas Medical School at Houston, USAThomas G. Oertner, Friedrich Miescher Institute for Biomedical Research, Switzerland
Copyright: © 2010 Rackham, Tsaneva-Atanasova, Ganesh and Mellor. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Jack R. Mellor, Department of Anatomy, Medical Research Council Centre for Synaptic Plasticity, University of Bristol, University Walk, Bristol, UK. e-mail: jack.mellor@bristol.ac.uk