Fragmentation: loss of global coherence or breakdown of modularity in functional brain architecture?

Introduction

Connectivity is key to understanding activity in neural systems (Sporns et al., 2000). Network connectivity in science and in engineering fields as diverse as mechanics, communication technology, public health, geography and town planning, is studied mathematically using the concepts of graph theory (Bollobas, 1998). Recently, graph theory is being applied to brain connectivity (Sporns and Zwi, 2004; Bullmore and Sporns, 2009) and its pathologies in Alzheimer's disease (Stam, 2004; Stam et al., 2007), brain tumors (Bartolomei et al., 2006), epilepsy (Ponten et al., 2007) and, in particular, schizophrenia (Bleuler, 1911/1950; Friston and Frith, 1995; Andreasen, 1999; Micheloyannis et al., 2006; Rubinov et al., 2009a).

Applying graph-theoretic concepts to the brain sheds new light on the basic principles of integration and segregation underlying adaptive cognitive processes, and on their disruption in maladaptive states. Schizophrenia has been understood as a cognitive disorder (Bleuler, 1911/1950) based on the breakdown of large-scale cortico-cerebellar-thalamic-cortical (Andreasen, 1999) or prefronto-temporal circuits (Friston and Frith, 1995; Goldman-Rakic and Selemon, 1997), or more generally the inability to integrate neural processes in different brain areas, a syndrome termed dysconnectivity (Stephan et al., 2006, 2009). The density of dendritic spines is reduced in the brains of subjects with schizophrenia. This condition may pare down, in particular, the input to pyramidal cells of the dorsolateral prefrontal and temporal cortex (Garey et al., 1998; Glantz and Lewis, 2000). These cells are glutamatergic and receive projections from the thalamus and widespread cortical areas, and hence are likely to be involved in higher-level cognition. Reduced connectivity may thus lead to fragmentation, a loss of coherence in cognitive activity.

The relevant graph-theoretical notion is the loss of network connectivity. Graph theory enables us to model the loss of connectivity in simulated neuronal networks and predict the time course of fragmentation. On the face of it, a crucial factor appears to be percolation. Percolation plays an important role in the evolution, growth, and maintenance of a large variety of natural, technological, and social systems (Ben Avraham and Havlin, 2000). It refers to the probability of existence of a path between every pair of nodes in a graph, or equivalently, the graph being “connected” (Bollobas, 1998; Kesten, 2006). Whilst many previous studies have examined cortical network connectivity in schizophrenia and other disorders, none to our knowledge have employed the concept of percolation, an issue that we presently redress.

The percolation function is the cumulative density function (CDF) of percolation as a function of connectivity. It is possible, in principle, to measure the percolation function in living neural tissue, by using progressive lesioning, for instance through the administration of inhibitory neurotransmitters (Breskin et al., 2006)—clearly something not feasible in humans. Observations on human brain functional connectivity may be compared to the theoretical percolation function for random networks (Erdös and Rényi, 1959). The percolation function Cp(n) of a random graph of n vertices and E edges is given by Cp(n) = e^{−e−k₁ (E−k₂)} (Erdös and Rényi, 1959), in which k₁ =2/n and k₂ = Arand(n) = ½ × n × ln(n) representing the anchor point of the random graph. Arand(n) is where the sigmoidal curve Cp(n) shows the greatest inflection. This critical point indicates the percolation threshold: if the number of connections in the graph is gradually reduced, a sudden breakdown of percolation occurs, and the network decomposes into several disconnected fragments.

The presence of a critical threshold motivates us to revisit the notion of cortical dysconnectivity as a sudden breakdown of percolation. There are, however, reasons to assume that the percolation threshold is neither the first, nor the most predominant, critical transition in the development of schizophrenia: brains are not random networks. In both the structural (Sporns and Zwi, 2004) and functional (Salvador et al., 2005; Achard et al., 2006; Bassett et al., 2006) domains, the hallmarks of brain organization include local clustering as expressed in high values for the Clustering Coefficient (CC), high global connectedness as specified by a short Characteristic Path Length (CPL) (Watts and Strogatz, 1998), and modularity (Murre and Sturdy, 1995)—a combination characteristic of modular small-world networks (He et al., 2009). Graph-theoretical studies (Murre and Sturdy, 1995; Watts and Strogatz, 1998) showed that small-world and modular networks can secure global connectivity with a small number of connections. For brains configured as modular small-worlds, a few connections will suffice to ensure percolation. Most likely, therefore, percolation is not the crucial bottleneck for brain pathologies such as schizophrenia.

We will propose as an alternative theoretical possibility that, instead, brain pathologies are associated with a breakdown in the local organization. In schizophrenia patients, functional connectivity in scalp EEG channels appears to reflect a loss of clustering after correcting for differences in the density of functional connections (Micheloyannis et al., 2006; Rubinov et al., 2009a). The question, therefore, arises, whether fragmentation can be understood as a critical breakdown in the ability of the brain to establish and maintain a modular small-world functional architecture. Here we show by numerical simulations that in neural activity networks, with loss of connectivity a self-organizing small-world neural network cannot sustain its local clustering, well before global connectivity breaks down.

Methods

The iterated logistic map f(x)= 1 − ax² is unimodal on [−1;1] → [−1;1] and capable of both periodic and chaotic behavior depending on its control parameter a. In this study, we construct networks of coupled logistic maps, all with parameter a = 1.7 such that the dynamics of a single unit are chaotic under iteration of a randomly chosen initial activation value. A unit xⁱ is coupled with coupling strength ε = 0.4 to any number M_i of other units in the network such that its activation value xⁱ_{n + 1} at iteration n + 1 depends on the activation value of itself and all adjacent units at iteration n:

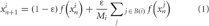
In this equation, B(i) is the set of units adjacent to unit i, M_i is the number of units adjacent to unit i. The coupling strength ε is divided by M_i, and has a compensation term (1 − ε) to make sure that logistic map of an individual unit retains its mapping [−1:1] → [−1:1], and thus functions properly for any numbers of adjacent units.

A network of this type can be used to study the buildup and breakdown of modularity resulting from Hebbian adaptive structural self-organization. It implements a simple rewiring rule based on synchronization of chaotic activity and rewires at most one connection per iteration, carefully keeping the network's total number of connections constant throughout the process. A single iteration of the network consists of four steps, to be repeated several times after an initial random inception:

1. Initialize the network. Randomly establish e connections between v units to create a (v, e) random network, and initialize every unit with a random activation value [−1:1]. Though values of v and e are chosen such that a network has a high probability of being connected, this is not required.
2. Update units. Synchronously update every unit's activation value from its own and all its adjacent units' activation values according to Equation (1).
3. Select pivot and candidate. Randomly select one unit from the network (the pivot). From all other units, select the one whose activation value is closest to the pivot's. This unit is the candidate.
4. Rewire if possible. Establish a connection between the pivot and the candidate if there is none. Then, from the units already adjacent to the pivot, select the one whose activation value is farthest from the pivot's, and cut its connection to keep the number of connections constant. If there is already a connection between the pivot and the candidate, or if the pivot has zero connections, nothing happens and this step is skipped.
5. Iteration completed. Go back to step 1.

Networks implementing these iterative steps exhibit development from an initial random configuration to modular small-world configurations (Gong and van Leeuwen, 2003; van den Berg and van Leeuwen, 2004; Rubinov et al., 2009b) But as it turns out, both the consistent build-up of connective modularity on one hand, or the loss of structural coherence due to functional fragmentation on the other, are a result of changing dynamic activity depending critically on the number of connections in the network. The influence of these numbers shows a close relationship to the percolation function of random graphs.

Results

Evolving Networks

A common principle for neural network evolution is preferential attachment (Barabási and Albert, 1999). This mechanism leads to networks that are scale-free, but not modular small-worlds. Only by combining preferential attachment with adaptive, Hebbian rewiring, does a network emerge that is scale-free and also has modular small-world network structure (Gong and van Leeuwen, 2003). An adaptive rewiring scenario for evolving networks allows networks with initially random or regular structures to develop into modular small-world structures (Gong and van Leeuwen, 2004; Rubinov et al., 2009b). The scenario requires network units (edges) that produce ongoing, non-random, non-periodic oscillatory activity. These could, for instance, be represented by spiking model neurons (Kwok et al., 2007) or by nonlinear maps as an extremely simplified model of neural mass activity (Breakspear et al., 2003a,b). With these simple units as edges, the vertices of the network represents the couplings of a coupled nonlinear map (Kaneko, 1989). Adaptive rewiring operates on this activity according to the general Hebbian principle of “what fires together wires together” (Paulsen and Sejnowski, 2000). At successive points during the systems ongoing spontaneous activity, connections are added between pairs of synchronously active but hitherto unconnected units, while connections between desynchronized units are removed (see Methods). Over time the network gradually assumes a modular, small-world structure (Figure 1).

FIGURE 1

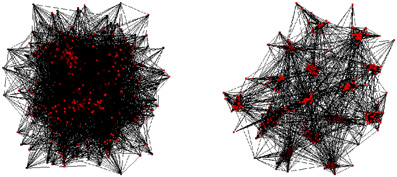
Figure 1. Adaptive rewiring leads from an initial random network (left), to modular small-world structure (right) in small iterative steps. Coupled chaotic oscillators intermittently synchronize and desynchronize their activity spontaneously in patterns of great variability. After some time a momentarily synchronized pair of units that are not connected receive a connection, which is removed from a pair that are connected but not synchronized. As this process continues, a modular, small-world structure emerges from an initially random configuration. To obtain a more detailed view of this phase transition, we use the adaptive rewiring scenario with coupled nonlinear maps (Kaneko, 1989) with initially randomly structured graphs, for a range of different numbers of vertices v: v = 300, 400, 500,…,1000 vertices and numbers of edges E that differ by small steps of 20. For each combination of v, E, across four million iterations we measured the CC and the CPL every one thousand iterations, resulting in a 4000 point record for each of five runs. The maximum, minimum, and mean values of the last 2000 points in each run were averaged over the five runs as illustrated in Figure 3.

Meanwhile a mixture of regular and irregular behavior is established in the network activity that is itself optimal for sustaining the small-world structure. Crucially, whilst low dimensional, ordered, and synchronized activity dominates within modular communities, high dimensional unsynchronized activity in connector hubs ensures that the system does not fragment (Rubinov et al., 2009b). The resulting systems can thus be thought of as “attractors” in the space of possible systems (Gong and van Leeuwen, 2004), which offers a potential explanation for their ubiquity in biological neural networks at different scales, including the entire brain (Barabási and Albert, 1999).

In this scenario, connectivity constitutes a critical limit for the evolution to small-world structure (Figure 2). When the number of edges is large enough, adaptive rewiring guarantees a robust evolution from random to small-world connectivity. Below this limit, this evolution is frustrated, and fails to reach a stable asymptotic state. With reduced connectivity levels, we first encounter critical fluctuation: intermittently during some episodes, clusterings are formed intermittently, which are annihilated in other episodes. This may reflect the intermittent occurrence of certain symptoms (e.g., delusions) as the brain disease first becomes manifest. For still lower connectivity levels, adaptive rewiring becomes completely ineffective; this may reflect the advanced state of the disease.

FIGURE 2

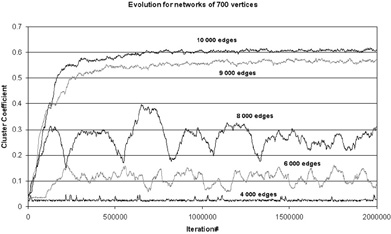
Figure 2. Self-organization from random to small-world critically in a network of 700 vertices. The self-organization occurs through adaptive rewiring. Whether a small-world emerges depends on the number of edges.

Percolation and Self-Organization in Small-Worlds

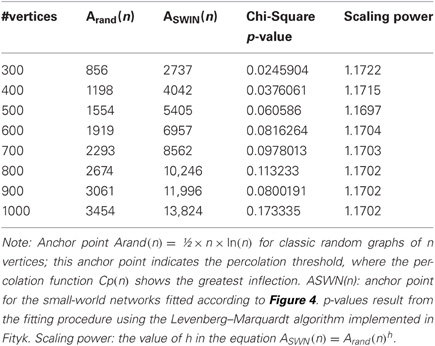
We compared the critical limit on the evolution to small-world structures to percolation thresholds of random networks with the same numbers of edges and vertices. Figure 4 shows that the observed minimum CC can be modeled as a linear function of Cp(n), with k₃ for offset and k₄ for amplitude: CCpred = k₃ + k₄Cp(n). Parameter k₃ was in the range [0.107:0.196], parameter k₄ in [0.392:0.459] and parameter k₁ in [0.001:0.006]. The behavior of these parameters across network sizes was not monotonic (Figure 4). Parameter k₂ however, the horizontal position of the anchor point, showed a universal scaling law to the anchor point in the percolation function of random graphs, namely (Table 1): A_SWN(n) = A_rand(n)^1.17.

TABLE 1

Table 1. Anchor points for random graphs and small-world networks.

Discussion

We propose that important insights into cortical activity and architecture can be obtained by modeling the activity-dependent rewiring of neural connections during development (Gong and van Leeuwen, 2003; Rubinov et al., 2009b). In our model, network connections evolve in accordance with the principle that the structure rewires in adaptation to spontaneous, on-going activity. Network structure thus evolves toward a modular small-world. This evolution, however, is only guaranteed if there are sufficiently many connections available. If connectivity is reduced below this number, the structure shifts toward randomness; in particular, local clustering is reduced.

Andreasen (1999) and Friston and Frith (1995) considered schizophrenia as fragmentation, understood as the breakdown of integration between widely distributed brain areas (Stephan et al., 2006, 2009). This breakdown can be associated with the loss of connectivity (Zalesky et al., 2011), in particular of input to Layer 3 pyramidal cells, an effect which is well-documented (e.g., Garey et al., 1998; Glantz and Lewis, 2000). Zalesky et al. (2011) observed widespread impairment in structural connectivity in schizophrenic patients, involving medial frontal, parietal/occipital and left frontal cortex. It should be observed that the loss of connectivity that may lead to the onset of schizophrenia can be relatively subtle. Across the population, inputs to layer 3 pyramidal cells are substantially reduced during late adolescence, the typical period for the onset of schizophrenia (Bourgeois et al., 1994). Given that brain connectivity is costly, it may well be that in normals, its density hovers just above the critical level (the anchor point in Figure 4), but in early schizophrenia it may fall just below this point.

The graph-theoretical concept of percolation tells us that a small decline in connectivity can lead to a sudden breakdown of global network coherence. Based on our results, however, we argue that fragmentation in brain pathologies such as schizophrenia may be considered theoretically as a breakdown in the local connectivity structure, prior to the loss of global coherence. The number minimally needed to secure local modularity, and hence to prevent it from shifting toward randomness in structure, is systematically related to, and greater than, that needed to secure global connectivity, even if the system has fallen into entirely random connectivity. This result is of potential importance for understanding the pathophysiological processes that give rise to this disorder.

The loss of local clustering in our model is in accordance with observations in schizophrenic patients by Micheloyannis et al. (2006) and Rubinov et al. (2009a). In Micheloyannis et al. (2006), the clinical group also showed longer path lengths than the controls, whereas in Rubinov et al. (2009a), the opposite was observed. We would have predicted path length to remain comparatively stable. Differences in methods limit the value of a direct comparison between these data. Nevertheless, we might attribute the discrepancy to the fact that in both studies comparisons were made, for statistical reasons, between networks that were thresholded to have identical connectivity. Whereas the above-mentioned effects of clustering remain relatively unaffected by threshold setting, the differences in path length rapidly disappear for lower thresholds (Figure 1 in Micheloyannis et al., 2006). Rubinov et al. (2009a) observed larger, but looser clusters in their networks. Similarly, Breakspear et al. (2003b) reported that although there were no significant increases in the occurrence of nonlinear interdependence between pairs of electrodes in schizophrenia, there was an increase in the co-occurrence in multiple (widespread) instances of nonlinear interdependence. This means that a relatively large number of global connections will have survived thresholding in Rubinov's study, leading to their observation of path length shortening.

It cannot be concluded from Rubinov's study, therefore, that global connectivity is stronger in schizophrenics than in normals; it could, however, be concluded that the global connectivity becomes stronger in schizophrenia relatively to their local connectivity. Such a conclusion would entirely be in accordance with the modularity breakdown observed in our model. Along the lines set out here, a shift in the balance from local to global connectivity is perfectly consistent with an overall loss of connectivity in early schizophrenia. Lee et al. (2003) introduced the notion of “overbinding”—the formation of excessive connections that are effectively random—and, as such, do not enable distinguishing external from internal sources, thus providing conditions favorable for phenomena such as hallucination.

A possible objection to our findings is the specific choice of our rewiring algorithm. Note, however, that in the present paper we sought to establish the principled possibility using the simplest possible model, rather than to establish the empirical validity through the most realistic model possible. Note that, as a consequence, the model contains only generic dynamical and adaptive principles. We have discussed elsewhere the robustness of this model (Gong and van Leeuwen, 2003, 2004; van den Berg and van Leeuwen, 2004; Kwok et al., 2007; Rubinov et al., 2009b).

An important limitation is that the model inevitably makes over-simplifying assumptions. In particular, it ignores the spatial embedding of the system. Inter-modular connections are physically of longer range than intra-modular ones and, therefore, have a higher metabolic cost and a greater vulnerability. They also originate from different cortical layers and involve different cell types. Preliminary analysis of models with more realistic constraints does not appear, however, to affect our conclusions. Clearly, a more differentiated model is needed to address empirical datasets such as (Rubinov et al., 2009a), an important goal of future work. However, it should also be noted that uncovering universal principles—such as those reported here—has the advantage of being “detail invariant”—that is, robust across a range of potential constraints, whereas findings arising in detailed models may not be robust to changes in those details.

We observed universal scaling behavior in adaptive self-organization of clustered small-world networks: the connectivity needed for these network properties to emerge under Hebbian rewiring scales with a universal power α = 1.17 to the percolation function in random networks. Note, first, that α> 1 might have been expected, given that the requirement to observe clustering and small-world structure are constraints additional to percolation. What is surprising is that these requirements are met with alpha very close to unity; near-linear scaling implies that these additional constraints can be realized with great efficiency.

In terms of Kolmogorov-complexity, small-worlds are compressible, whereas almost every possible network of n nodes and E edges (or equivalently a bit string of length L = ½n(n − 1) with E ones and L-E zeros) will be incompressible (Li and Vitányi, 1993). In this perspective, the ubiquity of small-world structure in real-world networks is quite astonishing: within human brains (Sporns and Zwi, 2004; Stam, 2004; Eguíluz et al., 2005; Salvador et al., 2005; Achard et al., 2006; Bartolomei et al., 2006; Micheloyannis et al., 2006; Ponten et al., 2007; Stam et al., 2007; Rubinov et al., 2009a; Bassett et al., 2010), as well as between them: networks of scientific co-authorship (Newman, 2001), collaborating movie actors (Watts and Strogatz, 1998; Amaral et al., 2000), social networks in general (Wasserman and Faust, 1994). Here we showed how such a network could arise with minimal connectivity close to random network percolation

What is the reason for the universality of the scaling exponent? We may wonder whether the same exponent found in other domains, could help us understand the principle. A study of class graphs in open-source, object-oriented software systems ranging from simple paint programs, peer-to-peer downloaders, racing games, database management software to a complete operating system, showed that the number of links between classes scales to the number of classes with an exact power α= 1.17. The authors found that class graphs are small-world networks at the critical threshold for the breakdown of modularity, which happens when developments to the system are widely dispersed and affect many unrelated classes in apparently distant modules (Valverde and Solé, 2007). The similarity of this finding to ours supports the view that the scaling exponent reflects a general feature in the emergence and breakdown of modular network structure.

The study of self-organizing modular small-world networks casts a new perspective on psychiatric illnesses characterized by disorganized cognition, such as schizophrenia, of which the expression has been attributed to fragmentation—a “subtle but pernicious disconnection” (Friston, 1996, p. 644). Rather than a breakdown in global connectivity, we propose that fragmentation is to be understood as a failure to organize the functional connectivity of the brain into a modular small-world structure. This is in accordance with the observed “random shift” in schizophrenic (Micheloyannis et al., 2006; Rubinov et al., 2009a) and Alzheimer patients (de Haan et al., 2009).

There are reasons why such a shift toward randomness is undesirable. Random networks are considered extremely uneconomical; in terms of cable length, an optimal configuration combines local modules with a limited number of large-scale connections (Murre and Sturdy, 1995). Even though our model does not consider distance, in terms of network topology it is still the case that information travels efficiently both within locally connected circuits of modular small-world graphs and between their circuits, which makes these networks efficient for transport or communication (Latora and Marchiori, 2001; Bassett et al., 2010).

The scaling observations tell us that fragmentation is a result of a breakdown in local, rather than global structure. With progressive loss of connectivity, the breakdown of modularity occurs before the breakdown of percolation. Ultimately, it may not matter which connections are lost first, the result may be a cascade of changes that lead to the network falling apart. For diagnosis, however, a proper understanding of the early stages of the disease is crucial; loss of modularity might offer a new perspective on the origins of the disease.

Data

One simulation consists of one network of v units and e connections, which is randomly initialized and then iterated exactly 4,000,000 times, simultaneously rearranging its connections and activity patterns, according to the adaptive rewiring scenario. The smallest simulation we adopt has v = 300 units and e = 2400 connections. During iteration, its CPL and its CC are taken every 1000th iteration (1000, 2000,…, 40,00,000) resulting in a 4000 point record, with a value for CC and a value for CPL at each point. Although the speed of convergence depends on the size of a network, 4, 000, 000 iterations prove to be enough to clearly discern asymptotic behavior for all simulations used in this investigation (Figure 3).

FIGURE 3

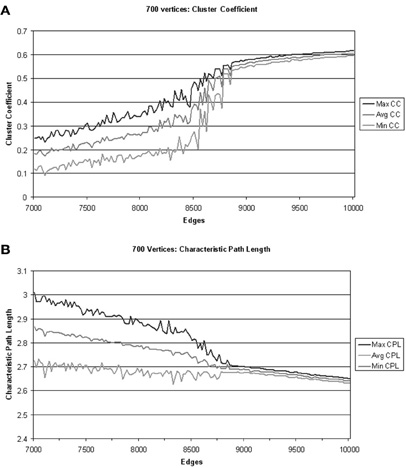
Figure 3. Evolution under adaptive rewiring of maximum, minimum, and average cluster coefficient and characteristic path length. (A) The values of minimum, maximum and average CC for networks of 700 vertices and edges ranging from [7000, 7020, 7040,…,10,000] after extensive adaptive rewiring. Note that beyond 9000 edges, CC-values tighten to a narrow range, indicating strong and consistent clustering behavior. (B) The values of minimum, maximum, and average CPL for networks of 700 vertices and edges ranging from [7000, 7020, 7040,…,10,000] after extensive adaptive rewiring. Beyond 9000 edges, CPL-values also tighten to a narrow range of low values. Thus, for 700 vertices, at least 9000 edges are needed for adaptive rewiring to converge to small-world structure.

From the 4000 point record, the maximum, minimum, and average values for both CPL and CC are calculated from the last 2000 points. For statistical robustness, we do any single simulation five times, and average the five values over this simulation-quintuple, resulting in a maximum, minimum, and average CC and CPL for the (v = 300, e = 2400) network.

We then start a new quintuple of simulations, increasing the number of connections e by 20, generating five networks with v = 300 units and e = 2420 connections, and calculate the maximum, minimum, and average CC and CPL values from these five new simulations. We keep starting new quintuples, repeatedly increasing e by 20, until e = 3300 and the batch of 300-quintuples is complete. From the entire batch, The six CC and CPL values of every (v, e) are taken to graph the asymptotic clustering and path-length behavior of networks of 300 units as it depends on the numbers of connections (Figure 4).

FIGURE 4

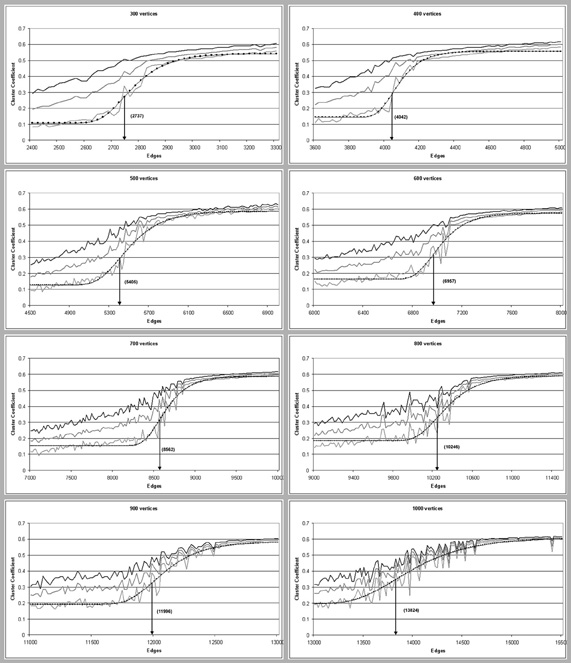
Figure 4. Universal scaling in the clustering threshold for self-organized small-world networks. Gray lines represent minimal, maximal and average observed values for clustering coefficient, the dotted line is the predicted clustering coefficient, CCpred, a linear function of the percolation function Cp(n) of a random graph of n vertices: CCpred = k₃ + k₄ × Cp(n) fitted with parameters k₃ and k₄ to the minimum observed clustering; the arrow indicates its anchor point ASWN(n) with the corresponding number of edges in parentheses.

This process is then repeated for a batch of quintuples of networks with 400 units and numbers of connections 3600, 3620,…, 5000 (see Figure 4, top-right box). We continue doing this for batches of networks with 500, 600, 700, 800, 900, and 1000 units, with connections increasing by 20, showing asymptotic clustering and path-length behavior depending on connectivity for networks of different sizes (Figure 4). Note that although for 300 units, connections ranged from e = 2400 to e = 3300, these numbers are different for larger networks.

For each of the eight batches, a phase transition was witnessed for both the CC and the CPL. To pin down the exact location of the steepest inclination in the phase transition of the CC (its center, or “anchor point”), the percolation function for classic random graphs was function-matched to the Minimum CC of every batch. The minimum cluster coefficient was chosen over the average and the maximum cluster coefficient because it has the steepest inclination, which facilitates the fitting best.

The entire process of fitting was done in Fityk under Linux using Levenberg–Macquardt an iterative curve-fitting algorithm which operates by minimizing the summed squares of the residuals, in this case the difference between minimal CC-values of n-edge simulation quintuples on the one hand, and the (Erdös and Rényi, 1959) percolation function's value for n edges on the other. Both graphs are depicted in overlay in Figure 4.

The Levenberg–Macquardt algorithm is sensitive to local minima which makes it inefficient when using completely random initial values. Initial parameters were hand-guessed separately for each of the eight subgraphs in Figure 4, after which the algorithm was ran until convergence beyond the program's six-digit resolution, a procedure that was repeated three times with small differences in the hand-guessed initial parameters. The final values did not differ within the program's six-digit resolution over the three repetitions, and convergence was very fast (typically well before 100 iterations).

The fits show significant deviations from the data curve, due to intrinsic fluctuations in the data. Nevertheless the fits adequately track the data curve. We, therefore, considered reliable the estimates of the scaling power and other model parameters. Even more reliable estimates could, in principle, be obtained by scaling up the network size to 2000, 5000, and 10,000 vertices, resources permitting, as computation time and data grow nonlinearly with network size.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Achard, S., Salvador, R., Whitcher, B., Suckling, J., and Bullmore, E. (2006). A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. J. Neurosci. 26, 63–72.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Amaral, L. A. N., Scala, A., Barthélémy, H., Stanley, H., and Newman, M. E. J. (2000). Classes of small-world networks. Proc. Natl. Acad. Sci. U.S.A. 97, 11149–11152.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Andreasen, N. C. (1999). A unitary model of schizophrenia. Bleuler's “Fragmented Phrene” as schizencephaly. Arch. Gen. Psychiatry 56, 781–787.

Pubmed Abstract | Pubmed Full Text

Barabási, A-L., and Albert, R. (1999). Emergence of scaling in random networks. Science 286, 509–512.

Pubmed Abstract | Pubmed Full Text

Bartolomei, F., Bosma, I., Klein, M., Baayen, J. C., Reijneveld, J. C., Postma, T. J., Heimans, J. J., van Dijke, B. W., de Munck, J. C., de Jongh, A., Cover, K. S., and Stam, C. J. (2006). Disturbed functional connectivity in brain tumour patients: evaluation by graph analysis of synchronization matrices. Clin. Neurophysiol. 117, 2039–2049.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bassett, D. S., Greenfield, D. L., Meyer-Lindenberg, A., Weinberger, D. R., Moore, S. W., and Bullmore, E. (2010). Efficient physical embedding of topologically complex information processing networks in brains and computer circuits. PLoS Comput. Biol. 6:e1000748. doi: 10.1371/journal.pcbi.1000748

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bassett, D. S., Meyer-Lindenberg, A., Achard, S., Duke, T., and Bullmore, E. (2006). Adaptive reconfiguration of fractal small-world human brain functional networks. Proc. Natl. Acad. Sci. U.S.A. 103, 19518–19523.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ben Avraham, D., and Havlin, S. (2000). Diffusion and Reactions in Fractals and Disordered Systems. Cambridge, UK: Cambridge University Press.

Bleuler, E. (1911/1950). Dementia Praecox or the Group of Schizophrenias. New York, NY: International Universities Press.

Bollobas, B. (1998). Modern Graph Theory. Berlin: Springer Verlag.

Bourgeois, J-P., Goldman-Rakic, P. S., and Rakic, P. (1994). Synaptogenesis in the prefrontal cortex of rhesus monkeys. Cereb. Cortex 4, 78–96.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Breakspear, M., Terry, J. R., and Friston, K. J. (2003a). Modulation of excitatory synaptic coupling facilitates synchronization and complex dynamics in a biophysical model of neuronal dynamics. Network 14, 703–732.

Pubmed Abstract | Pubmed Full Text

Breakspear, M., Terry, J., Friston, K. J., Williams, L., Brown, K., Brennan, J., and Gordon, E. (2003b). A disturbance of nonlinear interdependence in scalp EEG of subjects with first episode schizophrenia. Neuroimage 20, 466–478.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Breskin, I., Soriano, J., Moses, E., and Tlusty, T. (2006). Percolation in living neural networks. Phys. Rev. Lett. 97, 188102.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bullmore, E., and Sporns, O. (2009). Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 10, 186–198.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

de Haan, W., Pijnenburg, Y. A. L., Strijers, R. L. M., van der Made, Y., van der Flier, W. M., Scheltens, P., and Stam, C. J. (2009). Functional neural network analysis in frontotemporal dementia and Alzheimer's disease using EEG and graph theory. BMC Neurosci. 10, 101.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Eguíluz, V. M., Chialvo, D. R., Cecchi, G. A., Baliki, M., and Apkarian, A. V. (2005). Scale-free brain functional networks. Phys. Rev. Lett. 94, 018102.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Erdös, P., and Rényi, A. (1959). On random graphs. Publ. Math. (Debrecen) 6, 290–297.

Friston, K. J. (1996). Theoretical neurobiology and schizophrenia. Br. Med. Bull. 2, 644–655.

Pubmed Abstract | Pubmed Full Text

Friston, K. J., and Frith, C. D. (1995). Schizophrenia: a disconnection syndrome? Clin. Neurosci. 3, 88–97.

Pubmed Abstract | Pubmed Full Text

Garey, L. J., Ong, W. Y., Patel, T. S., Kanani, M., Davis, A., Mortimer, A. M., Barnes, T. R. E., and Hirsch, S. R. (1998). Reduced dendritic spine density on cerebral cortical pyramidal neurons in schizophrenia. J. Neurol. Neurosurg. Psychiatry 65, 446–453.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Glantz, L. A., and Lewis, D. A. (2000). Decreased dendritic spine density on prefrontal cortical pyramidal neurons in schizophrenia. Arch. Gen. Psychiatry 57, 65–73.

Pubmed Abstract | Pubmed Full Text

Goldman-Rakic, P. S., and Selemon, L. D. (1997). Functional and anatomical aspects of prefrontal pathology in schizophrenia. Schizophr. Bull. 23, 437–458.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gong, P., and van Leeuwen, C. (2003). Emergence of scale-free network with chaotic units. Physica A 321, 679–688.

Gong, P., and van Leeuwen, C. (2004). Evolution to a small-world network with chaotic units. Europhys. Lett. 67, 328–333.

He, Y., Wang, J., Wang, L., Chen, Z. J., Yan, C., Yang, H., Tang, H., Zhu, C., Gong, Q., Zang, Y., and Evan, A. C. (2009). Uncovering intrinsic modular organization of spontaneous brain activity in humans. PLoS One 4:e5226. doi: 10.1371/journal.pone.0005226

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kaneko, K. (1989). Chaotic but regular posi-nega switch among coded attractors by cluster-size variation. Phys. Rev. Lett. 63, 219–223.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kesten, H. (2006). What is percolation? Not. Am. Math. Soc. 53, 572–573.

Kwok, H. F., Jurica, P., Raffone, A., and van Leeuwen, C. (2007). Robust emergence of small-world structure in networks of spiking neurons. Cogn. Neurodyn. 1, 39–51.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Latora, V., and Marchiori, M. (2001). Efficient behavior of small-world networks. Phys. Rev. Lett. 87, 198701.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lee, K. H., Williams, L. M., Breakspear, M., and Gordon, E. (2003). Synchronous gamma activity: a review and contribution to an integrative neuroscience model of schizophrenia. Brain Res. Brain Res. Rev. 41, 57–78.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Li, M., and Vitányi, P. (1993). In an Introduction to Kolmogorov Complexity and Its Applications. New York, NY: Springer Verlag.

Micheloyannis, S., Pachou, E., Stam, C. J., Breakspear, M., Bitsios, P., Vourkas, M., Erimaki, S., and Zervakis, M. (2006). Small-world networks and disturbed functional connectivity in schizophrenia. Schizophr. Res. 87, 60–66.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Murre, J. M. J., and Sturdy, D. P. F. (1995). The connectivity of the brain: multi-level quantitative analysis. Biol. Cybern. 73, 529–545.

Pubmed Abstract | Pubmed Full Text

Newman, M. E. J. (2001). The structure of scientific collaboration networks. Proc. Natl. Acad. Sci. U.S.A. 98, 404–409.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Paulsen, O., and Sejnowski, T. J. (2000). Natural patterns of activity and long-term synaptic plasticity. Curr. Opin. Neurobiol. 10, 172–180.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ponten, S. C., Bartolomei, F., and Stam, C. J. (2007). Small-world networks and epilepsy: graph theoretical analysis of intracerebrally recorded mesial temporal lobe seizures. Clin. Neurophysiol. 118, 918–927.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rubinov, M., Knock, S. A., Stam, C. J., Micheloyannis, S., Harris, A. W. F., Williams, L. M., and Breakspear, M. (2009a). Small-world properties of nonlinear brain activity in schizophrenia. Hum. Brain Mapp. 30, 403–416.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rubinov, M., Sporns, O., van Leeuwen, C., and Breakspear, M. (2009b). Symbiotic relationship between brain dynamics and architectures. BMC Neurosci. 10, 55.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Salvador, R., Suckling, J., Coleman, M. R., Pickard, J. D., Menon, D., and Bullmore, E. (2005). Neurophysiological architecture of functional magnetic resonance images of human brain. Cereb. Cortex 15, 1322–1331.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sporns, O., Tononi, G., and Edelman, G. M. (2000). Theoretical neuroanatomy: relating anatomical and functional connectivity in graphs and cortical connection matrices. Cereb. Cortex 10, 127–141.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sporns, O., and Zwi, J. (2004). The small world of the cerebral cortex. Neuroinformatics 2, 145–162.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stam, C. J. (2004). Functional connectivity patterns of human magnetoencephalographic recordings: a “small-world” network? Neurosci. Lett. 355, 25–28.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stam, C. J., Jones, B. F., Nolte, G., Breakspear, M., and Scheltens, P. (2007). Small-world networks and functional connectivity in Alzheimer's disease. Cereb. Cortex 17, 92–99.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stephan, K. E., Baldeweg, T., and Friston, K. J. (2006). Synaptic plasticitiy and disconnection in schizophrenia. Biol. Psychiatry 59, 929–939.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stephan, K. E., Friston, K. J., and Frith, C. D. (2009). Dysconnection in schizophrenia: from abnormal synaptic plasticity to failures of self-monitoring. Schizophr. Bull. 35, 509–527.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Valverde, S., and Solé, R. V. (2007). Hierarchical small-worlds in software architecture. DCDIS Ser B Appl. Algor. 14, 1–11.

van den Berg, D., and van Leeuwen, C. (2004). Adaptive rewiring in chaotic networks renders small-world connectivity with consistent clusters. Europhys. Lett. 65, 459–464.

Watts, D. J., and Strogatz, S. H. (1998). Collective dynamics of “small world” networks. Nature 393, 440–442.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wasserman, S., and Faust, K. (1994). Social Network Analysis: Methods and Applications. Cambridge, UK: Cambridge University Press.

Zalesky, A., Fornito, A., Seal, M. L., Cocchi, L., Westin, C-F., and Bullmore, E. T. (2011). Disrupted axonal fiber connectivity in schizophrenia. Biol. Psychiatry 69, 80–89.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text