Mechanics of sister chromatids studied with a polymer model
- 1Institute for Theoretical Physics, Heidelberg University, Heidelberg, Germany
- 2German Cancer Research Center (DKFZ), Heidelberg, Germany
Sister chromatid cohesion denotes the phenomenon that sister chromatids are initially attached to each other in mitosis to guarantee the error-free distribution into the daughter cells. Cohesion is mediated by binding proteins and only resolved after mitotic chromosome condensation is completed. However, the amount of attachment points required to maintain sister chromatid cohesion while still allowing proper chromosome condensation is not known yet. Additionally the impact of cohesion on the mechanical properties of chromosomes also poses an interesting problem. In this work we study the conformational and mechanical properties of sister chromatids by means of computer simulations. We model both protein-mediated cohesion between sister chromatids and chromosome condensation with dynamic binding mechanism. We show in a phase diagram that only specific link concentrations lead to connected and fully condensed chromatids that do not intermingle with each other nor separate due to entropic forces. Furthermore we show that dynamic bonding between chromatids decrease the Young's modulus compared to non-bonded chromatids.
1. Introduction
In the interphase, eukaryote chromosomes are replicated and two identical copies of each chromosome, called sister chromatids, are present in the nucleus. In mitosis, chromosomes undergo a condensation into very compact, rod-like objects that have a high stiffness. Chromosome condensation is necessary for the error-free separation of different chromosomes since their territories are overlapping in interphase (1–3). To further ensure that sister chromatids are properly distributed to the two daughter cells, they are connected to each other, a phenomenon called sister chromatid cohesion. Cohesion is resolved in anaphase, after chromosome condensation is completed and all chromatid pairs are aligned at the equator of the mitotic spindle (4).
Without factors that facilitate cohesion, sister chromatids would quickly segregate due to physical properties. In particular, excluded volume interactions and entropic conditions that favor separated sister fibers would be sufficient to drive this segregation (5, 6). On the other hand, the mitotic condensation process involves the formation of cross-links within the chromatin fibers (7) leading to the presence of a large number of loops. This can even further facilitate the segregation process due to the entropic repulsive forces between loops within sister chromatids (8). Therefore attachment points between the two sister fibers are necessary. However, the abundance and position of attachments could have a profound influence on the conformational properties on sister chromatids and their condensation process. The main question that we target in this work is therefore: How does the combination of attachments between two sister chromatids and intra-chromatid cross-links determine the conformational properties of the sister chromatid system? We also address how the mechanical properties of a system of two connected chromatids is changed compared to single chromatids or non-bonded chromatids.
Cohesin is believed to be the main factor for the tethering of sister chromatids (9). This protein complex is composed of Smc1 and Smc3 subunits of the SMC family and Scc1 and Scc3 (10). It is believed to form ring-like structures when associated with chromosomes (11). Different models exist to explain the exact mechanism by which the cohesin complex attaches sister strands to each other. A common interpretation is that cohesion forms a ring around both strands (12). Another suggestion is that two cohesin rings each surround one strand of the chromatid pair and cohesion is established by binding of the two rings to each other (13). A recent study has shown that cohesin could also passively facilitate chromatid cohesion by maintaining intertwining between sister chromatids in addition to its active tethering mechanisms (14).
Experimental studies showed that the location of cohesin binding sites along chromosomes are not fixed. Although cohesin is enriched at the centromere region, sister chromatid cohesion is spread also along chromosome arms (15, 16). In particular, cohesin is mobile in the chromosomal domain and along the chromatin fiber, which in turn means that sites of cohesion are flexible and possibly transcription-dependent in interphase (17, 18). Dynamics of cohesin on the chromatin fiber could be possible through sliding of the cohesin ring along the fiber (12) or binding and unbinding of rings in the handcuff model (13). Interestingly, cohesion is established or reinforced genome-wide following DNA damage, thereby indicating that bonding between sister chromatids can be dynamically restructured (19–21).
While sister chromatid cohesion is important for the correct distribution of chromatids to the daughter cells, condensation of chromosomes in mitosis plays a key role for their error-free separation (1). The condensin complex and Topoisomerase II have been identified as key proteins facilitating proper condensation of chromosomes. Micromechanical experiments using micro pipettes were conducted to assess the internal organization of mitotic chromosomes. Direct measurements of the flexibility of single chromatids extracted from Xenopus laevis eggs showed a worm-like behavior of the chromatids (22). Pulling experiments revealed a high extensibility of chromatids and chromosomes extracted from cells including human chromosomes (22–26). However, chromosomes extracted from cells possess a much higher bending rigidity than egg extract chromatids, which could be due to different internal structures (27). Additionally, the influence of cohesion between sister chromatids on the mechanical properties of chromosomes is also not well understood.
In this work we introduce a polymer model for mitotic chromosomes that includes mechanisms for the condensation of each chromatid as well as cohesion between sister chromatids. We model the cohesion between sister chromatids by dynamic binding and unbinding between the two sister fibers. The condensation of each of the chromatids is realized by dynamic intra-chromatid looping, which accounts for the presence of binding proteins such as condesins. We use computer simulations to sample possible conformations for different model parameters. Our results show that inter-sister bonds and intra-fiber cross-links can act together to realize condensation and cohesion at the same time. However, we also show that the inter-sister and the intra-fiber bonds compete with each other due to entropic constraints. We only observe condensed and aligned sister chromatids for a small and sensitive range of model parameters.
In pulling simulations we further study the mechanical properties of sister chromatid systems at different levels of cohesion and compare the results with simulations of single chromatids. We show that binding between sister fibers lead to an increase of the elasticity of the chromosome and facilitates unfolding upon stretching forces. In contrast to our model, simple polymer models are not able to explain the experimental observation of force plateaus following linear regions.
2. Materials and Methods
2.1. Model for Mitotic Chromosomes
The sister chromatids are modeled as polymer chains consisting of typically N = 200 or N = 400 monomers each. Such coarse-graining approaches have proven useful, since it is not necessary to know the exact configuration on a detailed level when simulating the structure of a complete chromatid. The coarse-graining allows us to neglect interactions on smaller scales such as electrostatic interactions or van-der-Waals forces and is also necessary for computational feasibility. The chromosomes were simulated as polymers on a lattice based on the Bond Fluctuation Model (BFM), a lattice model incorporating self-avoidance (28, 29). The BFM has recently been extended to the Dynamic Loop Model, which has been successfully applied to inter- and metaphase chromosomes (30, 31).
In the BFM, monomers occupy a cube of 8 lattice sites and are connected to other monomers via bonds of fluctuating length (but otherwise static) allowing a maximal bond length of l.u. (lattice units) (28). With the Dynamic Loop Model, an additional binding mechanism has been introduced: monomers may temporarily establish a bond to other monomers nearby. In each Monte-Carlo step, all monomers are tried to move in a random direction. The move is accepted if the new site is unoccupied and the new bond vectors are allowed. If the monomer is now close enough to another monomer, a temporary bond is established with probability pbond. The lifetime of the bond is drawn from a Poisson distribution, with the simulation parameter τbond as its mean value. The bond dissolves again when its assigned lifetime expires. Each of these additional bonds between non-adjacent monomers forms a new loop of the chromatin fiber. The size of the loop is then determined by the separation of the two monomers along the fiber. The dynamic looping of the chromatin fiber results in a mean number of loops nloop and a mean loop concentration . It models how binding proteins such as the condensin complex can temporally bind chromatin segments to each other.
For the folding model of mitotic chromosomes we introduce a limitation to the size of the loops called cutoff length C. This means that monomers can only form a loop bond if their separation along the fiber is smaller than C. This cutoff length is firstly based on the observation that mitotic chromosomes form rod-like objects instead of spherically shaped clumps, which they do without limitation of the cutoff length. In this work we have used C = 25 for all simulations. The entropic forces that are exerted by the loops determine the mechanical properties of the model chromatid. Details of the model for single chromatids can be found in an earlier work (31).
For the sister chromatid systems we allowed not only the monomers of one strand to bond to each other and thus form loops within the chromatin fiber, but also for monomers belonging to different strands to bond to each other forming interlinks. The mechanism for these interlink bonds are essentially the same as for the loop bonds within one strand. If two monomers from both strands come into physical proximity of each other in the Monte Carlo process, they can form an additional bond with probability plink. A lifetime which is drawn from a Poisson distribution with mean τlink is assigned to this bond. Model sister chromatids can bind to each other through this dynamic link formation which results in a mean number of interlinks nlink and a mean link concentration . Just like the looping mechanism within one strand models condensin binding, this linking mechanism models how the cohesin complex binds sister chromatids to each other.
2.2. Pulling Simulations
For the pulling simulation, a force is introduced by a pulling potential Upull = −F · |rN − r1|. Here, r1 denotes the position of the first monomer of the chain and rN the position of the last monomer. The force F is a simulation parameter in units of kB T/l.u.. The Boltzmann factor with ΔUpull = Upull(current step) − Upull(proposed step) replaces the probability to move for the start and end monomer. In the pulling simulations, the ends of the two sister chromatids are concatenated permanently to each other in order to obtain a well defined pulling direction.
To avoid abrupt high pulling forces and too fast pulling of the fiber, we increase the pulling force gradually by small steps starting with a small value. After applying a new force, chains are first equilibrated and conformations then sampled from the equilibrium distribution. After typically sampling a few thousand conformations we then increase the pulling force by a small step again. Thus, in every point in the stress-strain diagram the chains are in equilibrium which means that our pulling simulation is a reversible and adiabatic process.
2.3. Autocorrelation Time
In one Monte-Carlo step as described above, the conformation changes only locally. Since we want to calculate ensemble mean values and corresponding fluctuations, independent samples have to be analyzed. We use the autocorrelation time C(t) to determine when two subsequent conformations in the Monte Carlo simulations are independent. The auto correlation function for an observable A(t) is defined as
and is usually normalized to . It measures whether samples are correlated (ρ(t) = 1) or uncorrelated (ρ(t) = 0). The auto correlation function goes to zero exponentially with time (i.e., Monte-Carlo steps). We use Sokal's automatic windowing algorithm to compute the integrated autocorrelation time τint (32). Conformations separated by 5 τint time-steps are treated as independent samples. As observable A we used the radius of gyration.
2.4. Radial Distribution Function
The radial distribution function (RDF) is a measure for the probability to find a pair of monomers at a separation r. It is defined as
where rij = ri − rj denotes the separation of monomers i and j. The sum is taken over all relevant monomers and the average is taken over the whole sample of conformations that we obtained with the MC simulations. Assuming an isotropic system the relevant measure becomes only dependent on the distance r but not the direction. In this work we calculate the RDF by taking all the distances between pairs of monomers and create a normalized histogram with them. Thus we obtain the probability distribution function to find two monomers at the distance of r from each other. We distinguish between the RDF calculated for monomers on the same chain giving information on the size of an individual chain, and the cross RDF for monomer pairs each belonging to a sister chain, which yields information on the distances between the two chains. With the cross RDF it is possible to distinguish between chromatids that are intermingled and those that are aligned but separated. Intermingled chains have a well localized RDF, whereas the RDF for separated chains is smeared out to larger distances.
2.5. Chromatin Density Distribution
The chromatin density distribution denotes the distribution of the average density of chain monomers that can be found in the vicinity of a single monomer. We calculate this property by counting the number of chain monomers in a sphere with radius rS around each monomer in the simulation and then averaging over all monomers in the system. We perform this calculation for all conformations that we sampled with the MC simulations yielding a probability distribution function for the average density. In the BFM, the bond length between monomers can have a distance of up to . Therefore we choose a larger radius for the calculation of the monomer density and set a value of rS = 6.
Furthermore, we distinguish between the average density of monomers that belong to the same chain as the monomer and the average density of monomers that belong to the sister chain. Both distributions are compared to each other to determine if sister chromatids are intermingled or separated. In the case of intermingled sister chromatids, both distributions are the same, since around all monomers, the average density of monomers belonging to the same chain is the same as the average density of monomers belonging to the sister chain. On the other hand, sister chromatids that are not intermingled and thus distinguishable from each other have different distributions. In this case, the average density of other monomers that belong to the same chain in the surrounding of a specific monomer is much higher than the average density of other monomers that belong to the sister chain because the distance to the sister chain is much larger.
3. Results
3.1. Model
The folding behavior of the chromatin fiber cannot be feasibly modeled on an atomistic scale. Instead, we pursue a coarse grained approach for the description of chromosomes in metaphase. The chromatin fiber is represented by a polymer chain with N monomers. Each monomer can be seen as an effective substitute for a statistical segment which has on average the same behavior on a more detailed scale. However, the small-scale details do not contribute to the large-scale folding properties and thus can be neglected (33).
In mitosis, chromosomes undergo a condensation into very compact, rigid and rod-like objects. This condensation is believed to be facilitated by different proteins, in particular the condensin complex (34). On the other hand, condensin was observed to be highly mobile within chromosomes in different stages of mitosis (35). To account for this phenomenon, we introduce a dynamic and probabilistic cross-linking mechanism of the chromatin fiber for single chromatids in mitosis. In our model, two non-adjacent monomers belonging to the same fiber can form an additional bond between each other when they come into close proximity by diffusion. The probability of the bond formation is given by a model parameter ploop. A lifetime τ drawn from a Poisson distribution with mean τloop is assigned to each bond. The formation of a bond means at the same time that a loop of chromatin fiber is established. In order to account for the observation that for example the ends of a chromatid can never be bound to each other we exclude arbitrarily large loops by introducing a size restriction C. This dynamic looping mechanism results in the condensation of chromatid into a rod-like object when the model parameters are chosen such that the average concentration of loops kp, loop, which denotes the average number of loops nloop over the number of monomers N is high. The motivation in the model for the incorporation of the size restriction for intra-fiber loops is based on the observation that long-range interactions of the chromatin fiber do not exist in mitosis. A possible reason for this lack of long-range interactions in mitosis could be that chromosomes fold up locally first when entering mitosis, for example through a length-wise condensation of the fiber (36), forming local, compact blobs. Such blobs would give rise to a chromatin-solvent interface which was not present before (as the blobs are much more compact than the loose interphase chromatin). A surface like this could prevent the formation of cross-links between chromatin segments that are in different blobs, effectively inhibiting long range contacts. Moreover, the chromatin fiber is not homogeneous along the genome but rather has variations in many different quantities such as gene density, different types of histone modifications or DNA methylation. These chemical variations along the chromatin fiber could also make it possible for binding proteins to distinguish between segments that are far away along the genome and segments which are close. This could provide a possible biological mechanism for the establishment of a cutoff length for the loop size in the chromatin fiber. Details and results for single chromatids can be found in a previous work (31).
In this work, each of the sister chromatids is modeled by such a dynamically looping fiber. Additionally we include the effects of sister chromatid cohesion by introducing a similar dynamic binding activity between the two sister fibers. Two segments, each belonging to one of the sister chromatids can form a bond upon collision with each other by diffusion. The rate of such associations is controlled by the probability plink while the dissociation rate is controlled by the lifetime of the cohesion bond that is drawn from a Poisson distribution with mean value τlink. This dynamic association and dissociation results in a mean concentration of sister bonds kp, link that is dependent on plink and τlink. Figure 1 shows a schematic description of the model highlighting the cross-linking and interlinking mechanism.
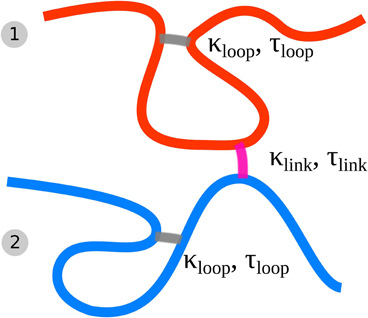
Figure 1. Schematic of the Dynamic Loop Model for mitotic sister chromatids. Each chain represents a coarse grained sister chromatid (fiber 1 and 2). The folding of each single chromatid is modeled by internal cross-linking of each of the chromatids forming chromatin loops (gray cross-links). Furthermore the model sister chromatids can be tethered to each other by inter-chromatid cross-links (purple cross-links). We model both kind of cross-links with a dynamic mechanism.
3.2. High Number of Attachment Points Prohibits Condensation of Chromatids
We sampled conformations for different parameter settings of ploop, τloop, plink, τlink resulting in different loop and link concentrations kp, loop and kp, link. Figure 2A shows a conformation with a large number of interlinks between the model sister chromatids. Such a high interlink concentration results in sister fibers that are highly intermingled and the overall shape of the indistinguishable mixture of the two fibers is rather spherical. Clearly, such kind of conformations do not resemble eukaryote chromosomes in mitosis after prophase. In Figure 2B we show the bonds between sister chromatids. If two segments from different sister fibers are bound to each other we visualize this by a red connection. The high number of interlinks prevents the sister chromatids from condensation and adoption of a rod-like shaped structure. Since such high interlink concentrations will inevitably result in such kind of intermingled fibers, we conclude that the number of tethering points between sister chromatids must be limited.
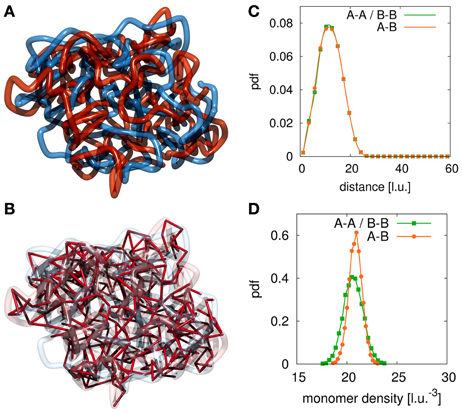
Figure 2. Example conformation for completely intermingled sister chromatids. The red and blue strands each represent one sister chromatid and the red links visualize the interlinks between the two fibers. (A) For large numbers of interlinks the two sister chromatids are strongly intermingled due to the many tethering points. Such conformations resemble the situation after chromosome replication but before mitotic condensation has taken place. (B) In this image we highlight the interlinks between the two sister chromatids. We observe that the large number of interlinks leads to an strong intermingling of the two chromatids. Since links between the sister fibers are randomly established upon collision of fiber segments they can be found anywhere along the fibers. (C) In this panel we show the radial distribution function between segments of the two sister chromatids. In the case of completely intermingled chromatids, the correlation between polymers belonging to the same chromatin fiber (A-A, B-B) and the correlation between monomers from the two different chains (A-B) are exactly the same. (D) This panel shows the density distribution of other monomers surrounding each monomer. In the intermingled state, the distribution of monomers of the sister chromatid in the vicinity of a monomer is the same as the distribution of monomers of the own fiber around this monomer. It shows that the environment of each single monomer does not indicate its membership to either one of the chains.
To assess the degree of intermingling between the two sister strands we calculate the radial distribution function for monomers belonging to each of the fibers and a cross-pair radial distribution function between monomer belonging to different sisters. Figure 2C shows these radial distribution functions for the completely intermingled state. All three distributions are identical, which means that the average positioning between monomers of different chains is the same as between monomers of the same chain. Additionally, we calculate the chromatin density distribution around each segment of the fibers. The results are shown in Figure 2D. The green curve shows the density distribution around a statistical segment that is produced by its own fiber. The orange curve shows the density distribution that is produced by the sister fiber. In the intermingled state, the same distribution can be found in the environment of all segments. Therefore, the two chains cannot be distinguished from each other in this intermingled state.
We performed simulations for settings with low linking probabilities and thus low ratios between association and dissociation rate for sister fibers. The results show that below a critical value for this rate, the entropic repulsion between the two condensed sister chromatids cannot be compensated by the dynamic linking mechanism. The sister chromatids become untethered and eventually drift away from each other as completely disconnected individual chains. This is verified by the radial distribution functions. In the case of disconnected sister chromatids, the distribution for monomer pairs belonging to the same fiber is the same in both sister chromatids. The cross-sister radial distribution function however shows that distances between the sisters is highly variable and unlimited.
Only in a small window for the association and dissociation rates for interlinks can the model chromatids been observed in a condensed state where they have the shape of mitotic chromosomes while still being tethered to each other and not intermingled or completely separated. Figures 3A,B shows an example conformation for chromosomes in this state. This situation highly resembles the state of mitotic chromosomes after condensation and segregation in prophase until metaphase. Here, the average number of interlinks is very small compared to the number of loops within each of the models sister chromatids. This allows each single chromatid to be in the condensed rod-like state. The two sisters are then held together by only a few links along the contour of the rod-like chromatids without forcing an intermingling of the fibers. The fact that sister chromatids are not intermingled is verified by the radial distribution function (Figure 3C) and the chromatin density distribution (Figure 3D). The radial distribution function between monomers from the same chain has its maximum at a much smaller distance than the radial distribution function between monomer pairs from sister fibers thus indicating that sister fiber monomers have on average a much larger distance to each other than monomers from the same chain. Furthermore, the average density of other monomers from the same chain around any monomer is much higher than the average density of monomers from the sister fiber.
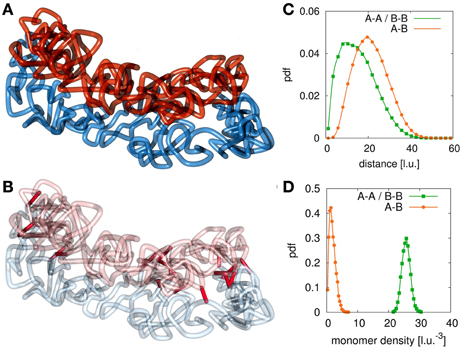
Figure 3. Example conformation for different configurations. (A) At certain values of the interlink concentration, sister chromatids segregate due to entropic repulsion but are still concatenated by a few interlinks. These configurations resemble the situation found in sister chromatid systems in metaphase. When the interlink concentration is further decreased, the two chromatin fibers separate completely from each other. (B) This figure highlights the present interlinks between the sister fibers. Interlinks are found along the contour of both model chromatids. (C) The radial distribution function between monomers of different fibers is shifted to larger values compared to the function between monomers of the same fiber. (D) The concentration of monomers of the own fiber is much higher than the concentration of monomers of the sister fiber around one monomer.
In Figure 4 we show a phase diagram for the different states of sister chromatids in this model. The diagram contains all the tested simulation setups with respect to mean interlink concentration between sister chromatids and mean loop concentration within each sister chromatid. For small interlink association to dissociation rates, sister chromatids separate since the entropic repulsive forces are stronger than the effective attractive forces by the dynamic interlinks. These setups result in separated sisters where the interlink concentration is zero. Large interlink concentrations result in intermingled sisters that do not have the characteristic rod-like shape. Only in a limited range of interlink concentrations, sister chromatids are both clearly distinguishable from each other and still connected.
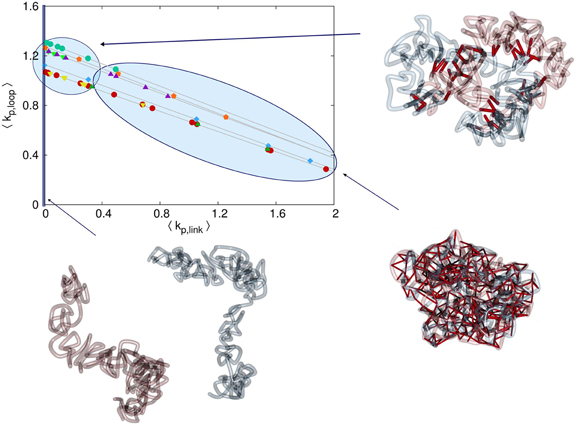
Figure 4. Phase diagram for the different possible configurations. The mean concentration of interlinks between the sister fibers is denoted by 〈kp, link〉 and the average concentration of intrafiber cross-links is denoted by 〈kp, loop〉. The different symbols in the diagram denote the different series of simulation runs. Note that the link concentrations are governed by the linking probabilities ploop, plink and the mean lifetime of links τloop, τlink. If the probability plink that one segment of the first sister chromatid forms a link with a segment of the second sister chromatid is very small, then the rate of interlink formation is not high enough to keep the two chromatids together. Entropic forces will then drive them away from each other and consequently the interlink concentration is kp, link = 0. For very high plink or long lifetimes τlink the interlink concentration becomes so high that the two sister fibers are completely intermingled. Only in a sensitive intermediate region of interlink concentrations do the sisters segregate properly but are hold together by some interlinks preventing them to drift away from each other.
3.3. Exclusive Permanent Linkage at the Centromere does not Guarantee Alignment of Sister Chromatids
In this model, we do not restrict the sites of binding between model chromatids. However, this means that the resulting sister chromatids are not necessarily aligned in parallel. Instead, conformations where one end of one chromatid is connected to the center part of the other chromatid are also possible. Also, some kind of torsion where sisters are wrapped around each other can also be observed in some conformations. These kind of conformations naturally form due to the entropic freedom of the chains.
A well established view in sister chromatid cohesion is that the sister chromatids are permanently linked to each other at the centromere region. In particular the concentration of cohesin has been found to be enhanced at the centromeres. To assess how such a permanent linkage can affect the conformational dynamics of model chromatids we perform calculations at which both sister strands are bonded to each other at the middle forming a star-like polymer. In the polymer models permanent links of monomers represent an infinitely high binding potential. Such a potential is assumed for example between genomically adjacent beats of the chain. In this work we assume that cohesin concentration is considerably higher at the centromere than at chromosome arms resulting in strong cohesion in this region. Therefore a permanent link between the two center monomers of each model sister chromatid efficiently accounts for this enhanced bonds at the centromere. Intra-fiber cross-linking for chromatid condensation is included as in all other simulations, too. We test the alignment of sister chromatids for different interlink concentrations ranging from kp, link = 0 to kp, link = 0.4.
Our simulation results show that permanent linkage at the centromere without any other regions of cohesion, holds the chromatids together but does not maintain parallel alignment of the model chromatids. Due to the entropic repulsion between the looping fibers, sisters take up configurations rather resembling crosses. On the other hand we observe that chromatids permanently linked to the each other in the middle are much more likely to align in parallel for small link concentrations. An example conformation is shown in Figure 5.
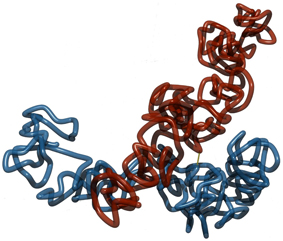
Figure 5. Two sister chromatids with a permanent link at the middle and no links otherwise. The single link at the middle holds model sister chromatids together. However, without further links at the arms, the entropic repulsive forces between the folded fibers makes it unfavorable for them to align in parallel to each other. Instead, a more cross-like conformation is preferred.
3.4. Elastic Behavior of Tethered Chromatids
Micromechanical experiments on extracted chromosomes in mitosis intend to study the elasticity of mitotic chromosomes and thereby draw conclusions on the internal folding behavior of the chromosomes. Such studies have let to the suggestion of a network model for the chromatin fiber in mitosis and to our model of a dynamically folding chromatin fiber (7). Micromechanical experiments are performed in vitro on chromosomes that can be isolated from cells or from egg extracts (27). Especially for cell extracted chromosomes it can be expected that chromosomes consist of two tethered sister chromatids which often cannot be distinguished from each other (27). Egg extracts on the other hand consist of single chromatids (37).
In this work we assess the mechanical properties of tethered sister chromosomes by measuring the elongation of model chromosomes under an external force. Model sister fibers are permanently linked to each other at the ends. This is done to ensure that the chromatids have the same end-to-end distances. Also it prevents them from drifting apart from each other even in the case that the tethering probability is set to zero. The pulling force is included by a potential Upull = F · |rN − r1| where r1 denotes the position of the first and rN the position of the last monomer in each fiber. Forces F are gradually increased and conformations are sampled at each value of the force. The mean end-to-end distances of the two fibers are then calculated from the sampled conformations. Upon induction of the stress, model chromosomes begin to restructure their internal organization, with regard to both, the cross-links and interlinks until they reach a new equilibrium situation.
Figures 6, 7 show example conformations of chromosomes under tension. In Figure 6 the situation of non-tethered sister chromatids is displayed. It can be observed that both chromatids try to avoid contact with each other due to the entropic repulsive forces. In Figure 7 stretched sister chromatids that are tethered to each other can be seen. The cohesin-mediated bonds cause the fibers to be close to each other and to align. In both cases it can be observed that for intermediate forces, only an elongation of the model chromatids can be observed while for larger forces the average number of intra-fiber cross-links is reduced and sister chromatids become inhomogeneous.
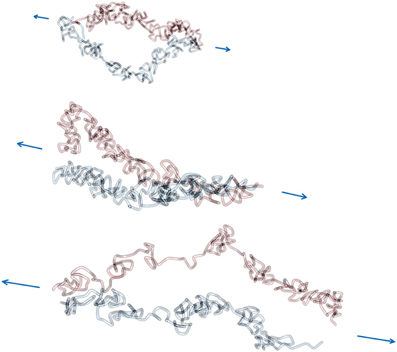
Figure 6. Force extension of non-interlinked model sister chromatids. Model chromatids are permanently linked together at the ends of the chromosome. The linking probability for interlinks is set to 0, which means that there are no interlinks between model sister chromatids. Therefore, segments of both fibers are not in close proximity along the contour and also not necessarily aligned even at higher pulling forces. The force was applied via a pulling potential Upull that is proportional to the end-to-end distance of each model sister chromatid and the given applied force F. In this figure three example conformations at forces 0.6, 1.2 and 1.8 kbT/l.u. are shown. The figure shows how the pulling force first cause a elongation of the model chromatids and eventually lead to a dissolution of the rod-like shaped structure of each of the two sister chromatids at large pulling forces. Note that in the visualization the chain ends where the chromatids were linked to each other are not shown.
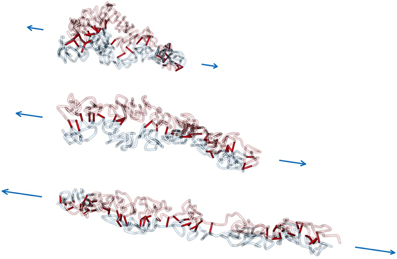
Figure 7. Force extension of interlinked model sister chromatids. In this scenario, a non-zero linking probability plink and mean link lifetime τlink is assumed. Consequently, the sister chromatids are aligned to each other during the whole pulling process. For large pulling forces the model chromatids disintegrate, but are still attached to each other.
The behavior of sister chromatids under tension is shown in Figure 8. As in the case of single chromatids, the stress-strain curve shows the characteristic behavior that was also observed in micromechanical experiments (27). For small forces, a linear dependency between force and relative elongation can be observed for the chromosomes. In this linear region, the average concentration of intra-fiber cross-links for both sister chromatids stays nearly unchanged. This means that for moderate forces, the chromatids are elongated but do not essentially change their average internal folding behavior. The elongation is also in part due to the straightening of chromosomes as well as the slight increase in average bond lengths between statistical segments.
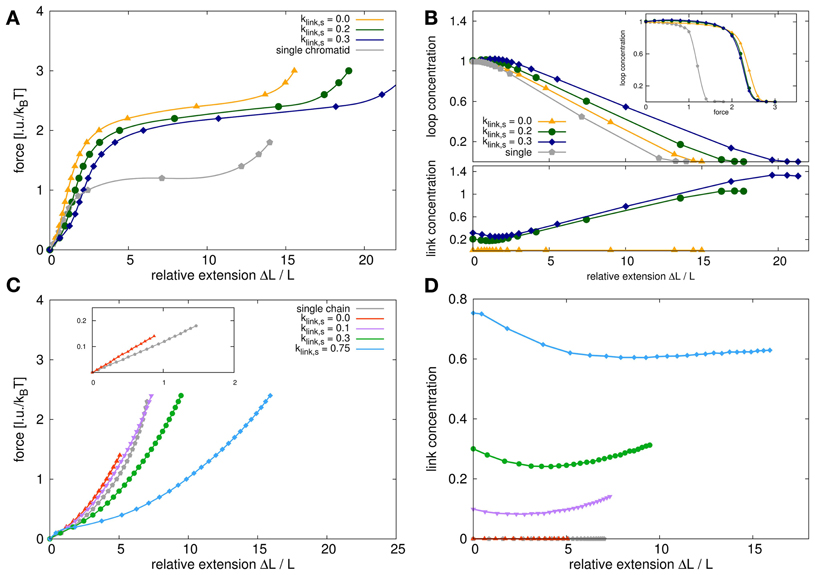
Figure 8. Force extension behavior for model sister chromatids and self-avoiding walks. (A) The panel shows the stress-strain curves for model chromatid systems with different link concentrations compared to the single model chromatid. The stress-strain curves all show a characteristic behavior with a linear elongation region for small extension followed by a force plateau for larger extensions. The slope of the curves in the linear region is proportional to Young's modulus which is a measure of elasticity. The Young's modulus for a system of two sister chromatids which are attached at the ends but nowhere else is higher than the Young's modulus of a single model chromatid. The Young's modulus decreases again, if the dynamic bonding mechanism between sisters is switched on and the link concentrations is increased. The plateau region for sister chromatids is significantly higher than for a single chromatid but again decreases with increased link concentrations. (B) This figure shows the loop and link concentrations in the systems upon stress. The upper panel shows the loop concentrations within the chromatids in dependency of the relative extension. For a single chromatid and untethered sister chromatids, the loop concentration remains fairly constant in the region of small extensions and decrease for larger extensions. For tethered sister chromatids, the loop concentration in fact first increases slightly upon stress and then also decreases with larger extensions. The inset shows the loop concentrations in dependency of the applied pulling force. Here we show that for small forces the loop concentrations for single chromatids and untethered sister chromatids at small forces are exactly the same and only differ slightly in the force plateau region. However, the relative extensions at the same forces are quite different for single chromatids and sister chromatid systems. (C) For comparison we also analyzed the force extension behavior of self-avoiding walks (SAWs) and systems of two tethered SAWs. The stress-strain curves have a different characteristics and especially do not show a long force plateau. In the initial linear region the entropic spring constant in the double chain system is higher than for the single chain but does not reach its doubled value due to excluded volume interactions between the chains. (D) The link concentration in dependency of the relative extension decreases first for small extensions and increases again for larger extensions. It has therefore the same tendency as for model chromatids but is not as pronounced due to the lack of internal loops that can be unfolded.
Comparing the stress-strain curves between single chromatids and non-tethered sister chromatids shows that the slope in the linear region is different in both situations. In the linear elongation region, each of the model sister chromatids is an entropic spring with a certain spring constant. Two identical, parallel springs would then show the behavior of a spring with a doubled spring constant. This is not the case in our simulations. The elasticity for the double-chromatid system is increased by only approx. 50% because we incorporate steric repulsion between the statistical segments of our model chromatids. This steric repulsion plays a role since it decreases the number of accessible conformations for two polymers that are very close to each other. Thus, it effectively changes the elasticity of the sister chromatid system.
When the sister fibers are tethered to each other by the dynamic linking mechanism, the slope in the initial linear region further decreases. This means that the Young's modulus for tethered fibers is smaller than that of untethered sister chromatids. In Figure 9 a close up of the linear region of the stress-strain curve is shown. We fitted the curves to determine Young's modulus Y which is given by
where denotes the stress and denotes the strain. We observed that the presence of tethering between the sisters decrease the overall slope of this region. However, our results also show that this part of the stress-strain curve does in fact deviate from a linear relationship between force and extension. The cohesion between sister chromatids thus have a profound influence on the mechanical properties of chromosomes. Especially the level of cohesion between sister chromatids strongly influences the elasticity. We find that the Young's modulus decreases with increasing inter-sister link concentrations.
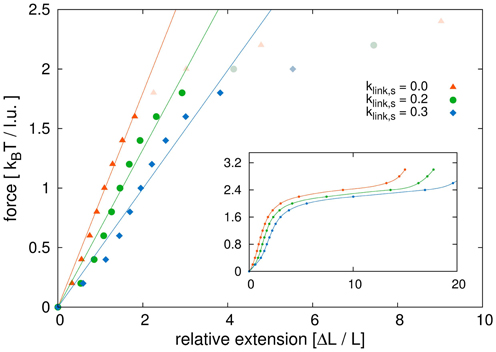
Figure 9. Initial region of stress-strain curve. Shown is a close-up view of the linear region of the stress-strain curves. We compare model sister chromatids with different link concentrations. We fitted the initial parts of the curves before the plateau area with linear functions. The dark points are those used for the fits, while the points in light color belong to the force extension curves but were not considered for the linear fits. The results show that non-tethered model chromatids have the highest Young's modulus and the modulus decreases with increasing link concentrations. The values for the Young's modulus are: Y1 = 0.90 kBT/l.u. for klink, s = 0.0, Y2 = 0.66 kBT/l.u. for klink, s = 0.2 and Y3 = 0.50 kBT/l.u. for klink, s = 0.3.
For large forces, the chromatids are not able to maintain the loop structure along their whole contour and the chromosomes become inhomogeneous as no intra-chain cross-links can form anymore in certain areas. Due to the high strain, each of the sister chromatids disintegrates as its internal loops dissolve. Thus, the chromatids can be extended without significantly increasing the pulling force resulting in a force plateau. The level of this force plateau is much lower in the case of the single model chromatid compared to sister chromatid systems. It is plausible that less force is needed to disintegrate a single chromatid than to disintegrate a system of two chromatids. More interesting is the observation that the force plateau decreases with increasing link concentrations. This means that sister chromatids that are connected to each other are also more easily disintegrated than unconnected sisters.
Figure 8B shows the corresponding link and loop concentrations as a function of the relative extension. In the linear force elongation region at small elongations, the loop concentration of single chromatids and unconnected sisters do not change. The loop concentration in connected chromatids even slightly increases. In the force plateau region, the loop concentration decreases rapidly as chromatids are pulled apart and the internal loop structure cannot be maintained along the complete chromosome anymore.
An interesting observation is that the concentration of interlinks strongly increases upon pulling chromosomes into the plateau region. This can be explained by the fact that the strain facilitates the alignment of sister chromatids. In turn, aligned sister chromatids are easier to be bonded to each other by links that are created upon collision of chromosomal parts. In a configuration where the mean concentration of interlinks is high before the pulling starts, the increase of the mean concentration of interlinks is also high. For kp, link, s = 0.3 (blue curve in Figure 8) the final concentration is kp, link, f ≈ 1.4 while for initial concentration of kp, link, s = 0.2 the final concentration is kp, link, f ≈ 1.0. This shows that bonding between aligned sister chromatids could be strengthened upon physical stress.
For comparison we perform simulations for a simpler polymer model, the self-avoiding walk (SAW). The force extension behavior for a single SAW and for double polymer systems with tethered SAWs is shown in Figure 8C. Simple polymers have obviously completely different force extension behaviors. In fact, for a Gaussian chain, which does not have excluded volume, the stress-strain curve is given by a Langevin function and the spring constant in the linear region is inverse proportional to the chain length. The inset in the panel shows the linear regions of the stress-strain curve for a single SAW and two SAWs that are only tethered to each other at the chain ends. We also performed simulations where SAWs could dynamically bind to each other. The corresponding stress-strain curves are also shown in Figure 8C. As in the case of our model chromatids, bonding also increases the elasticity for SAW systems. For high link concentrations, the two SAWs are also intermingled and the force extension changes its characteristics. Instead of a Langevin function-like behavior, we then first observe a initial sharper increase followed by a plateau area which then goes over to a Langevin-like tail for large elongations. Figure 8D shows the interlink concentrations depending on the relative elongation. It shows how upon small forces, the link concentration is reduced first because small forces de-mingle the SAWs. For large forces however, polymers are again brought to an elongated and aligned state where they can form links more easily and thus the link concentration increases again.
4. Discussion
In this work we analysed how sister chromatid conformation in mitosis is governed by the interplay between condensation and cohesion. In our model, each individual chromatin fiber can dynamically form size-restricted loops which can result in its coiling into rod-like objects. Additionally, sister fibers can dynamically establish interlinks between each other leading to a mean number of bonds. We explored the parameter space for the looping probability ploop and linking probability plink. For each parameter setting we sample equilibrium conformations with Monte Carlo simulations. Depending on the looping and linking parameters our model yields different loop and link concentrations for the model fibers. We thus show that the combination of these two mechanism can result in vastly different conformational states of sister chromatids.
We were able to characterize the resulting conformations of the sister chromatid system by three main types. Firstly, there is a minimum threshold for the ratio of association rate and dissociation rate for links if sisters are to stay bonded. Below this threshold, the entropic repulsive forces between sister chromatids exceeds the effective binding force by the dynamic linking. Sister chromatids would then drift away from each other. Furthermore, we found that in order to obtain a system of two clearly distinguishable chromatids there must be a cap in the mean concentration of links. For higher link concentrations, model sister chromatids are completely intermingled and not distinguishable from each other. From our results we can conclude that the mean number of links by which sister chromatids are bonded together has to lie within a sensitive region.
In this work, the mechanisms for looping of the chromatin fiber and for linking of sister chromatids are effective mechanisms that model the presence of binding proteins such as condensin and cohesin. However, we have to stress that the detailed binding mechanisms of these proteins are still under debate. Therefore we choose a probabilistic model for the effect of binding. Our model parameters ploop and plink effectively describe the binding affinity of fiber segments to each other. This affinity could be altered for example by different protein concentrations. In fact a recent model that explicitly includes diffusing proteins as binding partners for the chromatin fiber found that increased protein concentrations lead to higher number of binding points (38).
A number of studies have shown that genome-wide cohesion between sister chromatids can be established as a reaction to DNA damage by exogenous agents such as irradiation (19, 21). This damage-induced cohesion could facilitate the homologous recombination repair pathway by tightly holding the parts important for repair together. Here we show that an increase in the number of bonding regions between sister chromatids also results in their intermingling which makes it impossible for each chromatid to condense into a rod-like shaped object. However, it is evident that this condensation is crucial for chromosome segregation in mitosis since intermingled chromatids are hardly distinguishable. We therefore speculate that tight bonding of sisters upon formation of double-strand breaks (DSBs) prior to mitosis could also be a physical mechanism for cell cycle arrest since it inhibits the progression of chromosome condensation. This might also be a reason why one single DSB could trigger the establishment of cohesion in the whole genome.
Our simulations of the behavior of sister chromatid systems upon external stress show that it is qualitatively the same as for single chromatids. The stress-strain curve shows an initial linear region which is followed by a broad force plateau. In the linear region a spring-like behavior is observed and the force plateau is a decondensation region where the integrity of chromosomes is destroyed by external force. The emergence of force plateaus for large elongations has been observed in many experimental studies before (27). These experiments included single chromatids that were extracted from eggs (22) and chromosomes consisting of two chromatids extracted directly from cells (7, 25). In our present work we performed pulling simulations for single chromatids and also for bonded sister chromatid systems. We then compared the behavior of the two systems in order to obtain a better understanding of how experimental results for these could differ from each other.
Our results show that the required force to reach the plateau region is much higher for bonded sister chromatids than for single chromatids. However, when comparing bonded sister chromatids to non-bonded ones, we observe a decrease of the force plateau. Since the force plateau indicates the region where chromatids are disintegrated by the pulling force, this means that bonded sister chromatids are more easily unfolded by pulling forces. The level of the plateaus decreases with increasing number of bonds between sisters. An explanation for this could be that by being coupled to each other, pulling forces that act on one chromatid are also able to act on the other one. By this dragging effect, a force that is able to elongate one chromatid and thus prevents the formation of loops in this chromatid, could then prohibit the formation of loops in the sister chromatid, too. This mechanism could also be responsible for the decreased slope of the stress-strain curve in the region before the force plateau. Another factor could be that model sister chromatids are aligned in the pulling process. This alignment further facilitates the formation of bonds between them which in turn decreases the possibility of loop formation. Thus we can conclude that the amount of inter-sister cohesion can play a role for the mechanical properties of the chromosome. The differences of the mechanical properties of chromosomes in experimental studies could then be due to different amounts of cohesion between the sisters (25, 27).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We would like to thank Hansjörg Jerabek for fruitful discussions. Computer simulations were performed on bwGRiD (http://www.bw-grid.de), member of the German D-Grid initiative, funded by the Ministry for Education and Research (Bundesministerium für Bildung und Forschung) and the Ministry for Science, Research and Arts Baden-Wuerttemberg (Ministerium für Wissenschaft, Forschung und Kunst Baden-Württemberg).
Funding
Yang Zhang and Sebastian Isbaner gratefully appreciate funding by the German National Academic Foundation (Studienstiftung des Deutschen Volkes) and support by the Heidelberg Graduate School for Mathematical and Computational Physics in the Sciences (HGS MathComp).
References
1. Belmont AS. Mitotic chromosome structure and condensation. Curr Opin Cell Biol. (2006) 18:632–8. doi: 10.1016/j.ceb.2006.09.007
2. Swedlow JR, Hirano T. The Making of the mitotic chromosome: modern insights into classical questions. Mol. Cell. (2003) 11:557–69. doi: 10.1016/S1097-2765(03)00103-5
3. Cremer T, Cremer C. Chromosome territories, nuclear architecture gene regulation in mammalian cells. Nat Rev. Genet. (2001) 2:292–301. doi: 10.1038/35066075
4. Alberts B, Johnson A, Lewis J, Raff M, Roberts K, Walter P. Molecular biology of the cell/[Hauptbd.]. 4th Edn New York, NY: Garland (2002).
5. Jun S, Mulder B. Entropy-driven spatial organization of highly confined polymers: lessons for the bacterial chromosome. Proc Natl Acad Sci USA. (2006) 103:12388–93. doi: 10.1073/pnas.0605305103
6. Dockhorn R, Sommer J. A model for segregation of chromatin after replication: segregation of identical flexible chains in solution. Biophys J. (2011) 100:2539–47. doi: 10.1016/j.bpj.2011.03.053
7. Poirier MG, Marko JF. Mitotic chromosomes are chromatin networks without a mechanically contiguous protein scaffold. Proc Natl Acad Sci USA. (2002) 99:15393–97. doi: 10.1073/pnas.232442599
8. Bohn M, Heermann DW. Topological interactions between ring polymers: Implications for chromatin loops. J Chem Phys. (2010) 132:044904. doi: 10.1063/1.3302812
9. Michaelis C, Ciosk R, Nasmyth K. Cohesins: chromosomal proteins that prevent premature separation of sister chromatids. Cell (1997) 91:35–45. doi: 10.1016/S0092-8674(01)80007-6
10. Watanabe Y. Sister chromatid cohesion along arms at centromeres. Trends Genet. (2005) 21:405–12. doi: 10.1016/j.tig.2005.05.009
11. Gruber S, Haering CH, Nasmyth K. Chromosomal Cohesin forms a ring. Cell (2003) 112:765–77. doi: 10.1016/S0092-8674(03)00162-4
12. Haering CH, Farcas A, Arumugam P, Metson J, Nasmyth K. The cohesin ring concatenates sister DNA molecules. Nature (2008) 454:297–301. doi: 10.1038/nature07098
13. Zhang N, Kuznetsov SG, Sharan SK, Li K, Rao PH, Pati D. A handcuff model for the cohesin complex. J Cell Biol. (2008) 183:1019–31. doi: 10.1083/jcb.200801157
14. Farcas A, Uluocak P, Helmhart W, Nasmyth K. Cohesin's concatenation of sister DNAs maintains their intertwining. Mol Cell (2011) 44:97–107.
15. Tanaka T, Cosma MP, Wirth K, Nasmyth K. Identification of cohesin association sites at centromeres along chromosome arms. Cell (1999) 98:847–58. doi: 10.1016/S0092-8674(00)81518-4
16. Haering CH, Nasmyth K. Building and breaking bridges between sister chromatids. BioEssays (2003) 25:1178–91. doi: 10.1002/bies.10361
17. Lengronne A, Katou Y, Mori S, Yokobayashi S, Kelly GP, Itoh T, et al. Cohesin relocation from sites of chromosomal loading to places of convergent transcription. Nature (2004) 430:573–8. doi: 10.1038/nature02742
18. Glynn EF, Megee PC, Yu HG, Mistrot C, Unal E, Koshland DE, et al. Genome-wide mapping of the cohesin complex in the yeast Saccharomyces cerevisiae. PLoS Biol. (2004) 2:E259. doi: 10.1371/journal.pbio.0020259
19. Unal E, Heidinger-Pauli JM, Koshland D. DNA double-strand breaks trigger genome-wide sister-chromatid cohesion through Eco1 (Ctf7). Science (2007) 317:245–8. doi: 10.1126/science.1140637
20. Kim B, Li Y, Zhang J, Xi Y, Li Y, Yang T, et al. Genome-wide reinforcement of cohesin binding at pre-existing cohesin sites in response to ionizing radiation in human cells. J Biol Chem. (2010) 285:22784–92. doi: 10.1074/jbc.M110.134577
21. Ström L, Karlsson C, Lindroos HB, Wedahl S, Katou Y, Shirahige K, et al. Postreplicative formation of cohesion is required for repair induced by a single DNA break. Science (2007) 317:242–5. doi: 10.1126/science.1140649
22. Houchmandzadeh B, Dimitrov S. Elasticity measurements show the existence of thin rigid cores inside mitotic chromosomes. J Cell Biol. (1999) 145:215–23. doi: 10.1083/jcb.145.2.215
23. Poirier M, Eroglu S, Chatenay D, Marko JF. Reversible and irreversible unfolding of mitotic newt chromosomes by applied force. Mol. Biol. Cell. (2000) 11:269–76. doi: 10.1091/mbc.11.1.269
24. Poirier MG, Nemani A, Gupta P, Eroglu S, Marko JF. Probing chromosome structure with dynamic force relaxation. Phys Rev Lett. (2001) 86:360–363. doi: 10.1103/PhysRevLett.86.360
25. Almagro S, Riveline D, Hirano T, Houchmandzadeh B, Dimitrov S. The mitotic chromosome is an assembly of rigid elastic axes organized by structural maintenance of chromosomes (SMC) proteins and surrounded by a soft chromatin envelope. J Biol Chem. (2004) 279:5118–26. doi: 10.1074/jbc.M307221200
26. Sun M, Kawamura R, Marko JF. Micromechanics of human mitotic chromosomes. Phys Biol. (2011) 8:015003. doi: 10.1088/1478-3975/8/1/015003
27. Marko JF. Micromechanical studies of mitotic chromosomes. Chromosome Res. (2008) 16:469–97. doi: 10.1007/s10577-008-1233-7
28. Carmesin I, Kremer K. The bond fluctuation method: a new effective algorithm for the dynamics of polymers in all spatial dimensions. Macromolecules (1988) 21:2819–23. doi: 10.1021/ma00187a030
29. Deutsch HP, Binder K. Interdiffusion self-diffusion in polymer mixtures: A Monte Carlo study. J Chem Phys. (1991) 94:2294–304. doi: 10.1063/1.459901
30. Bohn M, Heermann DW. Diffusion-driven looping provides a consistent framework for chromatin organization. PLoS ONE (2010) 5:e12218. doi: 10.1371/journal.pone.0012218
31. Zhang Y, Heermann DW. Loops determine the mechanical properties of mitotic chromosomes. PLoS ONE (2011) 6:e29225. doi: 10.1371/journal.pone.0029225
32. Madras N, Sokal AD. The Pivot Algorithm: a highly efficient Monte Carlo method for the self-avoiding walk. J Stat Phys. (1988) 50:109–186. doi: 10.1007/BF01022990
33. Tark-Dame M, van Driel R, Heermann DW. Chromatin folding–from biology to polymer models and back. J Cell Sci. (2011) 124(Pt 6):839–45. doi: 10.1242/jcs.077628
34. Woodcock CL, Ghosh RP. Chromatin higher-order structure and dynamics. Cold Spring Harb Perspect Biol. (2010) 2:a000596. doi: 10.1101/cshperspect.a000596
35. Oliveira RA, Heidmann S, Sunkel CE. Condensin I binds chromatin early in prophase and displays a highly dynamic association with Drosophila mitotic chromosomes. Chromosoma (2007) 116:259–74. doi: 10.1007/s00412-007-0097-5
36. Marko JF. Linking topology of tethered polymer rings with applications to chromosome segratation and estimation of the knotting length. Phys Rev E. (2009) 79:051905. doi: 10.1103/PhysRevE.79.051905
37. Houchmandzadeh B, Marko JF, Chatenay D, Libchaber A. Elasticity and structure of eukaryote chromosomes studied by micromanipulation and micropipette aspiration. J Cell Biol. (1997) 139:1–12. doi: 10.1083/jcb.139.1.1
Keywords: chromosomes, cohesion, sister chromatids, polymer model, mechanical properties
Citation: Zhang Y, Isbaner S and Heermann DW (2013) Mechanics of sister chromatids studied with a polymer model. Front. Physics 1:16. doi: 10.3389/fphy.2013.00016
Received: 12 July 2013; Paper pending published: 14 August 2013;
Accepted: 16 September 2013; Published online: 09 October 2013.
Edited by:
Mario Nicodemi, Università degli Studi di Napoli Federico II, ItalyCopyright © 2013 Zhang, Isbaner and Heermann. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dieter W. Heermann, Institute for Theoretical Physics, Heidelberg University, Philosophenweg 19, D-69120 Heidelberg, Germany e-mail: heermann@tphys.uni-heidelberg.de
 Yang Zhang
Yang Zhang Sebastian Isbaner
Sebastian Isbaner Dieter W. Heermann
Dieter W. Heermann