Dendritic design as an archetype for growth patterns in nature: fractal and constructal views

Introduction

In a wide variety of situations the formation of patterns results from a growth process. Dendritic flow systems exist everywhere and at every scale ranging from the tiniest vessel network, in plants and mammals, through the scales of the rivers basins and deltas. Dendritic geometry characterizes the formation of our lungs and vascular system [1] but also the growth of bacterial colonies and stony corals [2, 3] in low nutrient environments. It characterizes growth shapes in natural systems but also generates configurations in a variety of physical processes [4]. Much effort has been devoted to understand the generation of configuration for fundamental reasons but also because of its impact in the industry. The impact maybe negative (e.g., dendritic growth in electrodeposition affects the quality of a metal plate or viscous fingering limits oil recovery in porous media) or positive (e.g., dendritic growth is used to improve catalytic effects because builds up structures with a large interface).

Among non-equilibrium systems, understanding natural systems is perhaps one of the most fascinating and challenging. In the case of human body, it is organized into several specific systems, each with its own function. Their structure has been the subject of much interest since a long time ago. Galen, for example, who lived in the second century A.D. and spent part of his lifetime in observation of the human body and its functioning, described the arteries as “trunks divided into many branches and twigs” that nourished the body [5].

An examination of the literature reveals that the most common form of branching in vascular system is bifurcation [6, 7]. While there are heterogeneities in morphological (diameters and lengths) and hemodynamic (pressure, flow, etc.) parameters, studies of blood vessels pointed out a relationship that links the radius of a parent vessel (immediately upstream from a vessel bifurcation) to the radii of the daughter (immediately downstream after a vessel bifurcation). The reduction of vessel size by a constant factor (2^−1/3) is of functional significance [8, 9], and is usually termed as Murray or Hess–Murray law. Despite proposed based on a theoretical grounds, Hess's and Murray's works went almost unnoticed for nearly five decades [10].

The idea behind Hess–Murray law is that the change in diameter, at each node of bifurcation, is justified based on minimum principles such as the power [9], resistance [11], volume [12], drag [13], etc., Later, [14] purposed an exponent of 0.43 (~2^−3/7) to all bifurcated vessels whose internal flows obey turbulent conditions. Branching angles are also obtain based on the minimization of the total volume of fluid by Murray [9].

Not only human vascular system comes in an astounding number of vessels, forming a network that resembles a tree-like shape. In fact, Hess–Murray law is supported by a number of empirical studies in the vascular systems of birds and mammals [15, 16], mammalian respiratory tree [17, 18], and plants [10, 19]. Lung design, for instances, resembles an inverted tree composed by a branching structure of 23 generations [17]. It seems that represents the most efficient structural transition linking atmosphere to cells [20].

Dendritic flow structures are not exclusive of living organisms. They are of common appearance in natural flow systems such as river basins and deltas. Their physical structure and evolution has been a subject of major interest [21, 22]. Empirical evidences led geomorphologists to propose a number of scaling laws that indicate that some properties of river basins are invariant. The first quantitative treatment of river network structure was presented by Horton [23]. To provide a means of comparing stream lengths, drainage areas, etc., indices of significance were attributed to streams. Horton's laws [21] state that stream number, average stream length, and average drainage area decrease geometrically with stream order defined by the Strahler ordering scheme of classifying stream segments [24]. Hack's law is a power law relationship between the length of the main stream of a river basin and the basin's area [25].

A configuration having an irregular or fragmented shape at different scales can be described by fractals. Basic characteristics of fractal geometry are self-similarity and fractional (fractal) dimension. In many cases is well suited to the description of systems that exhibit scaling behavior. Careful analysis of the vascular system [26–28], lungs [29, 30], and river basins [21, 31] reveal fractal scaling.

Physics includes principles that are laws of nature. Laws and calculus are sufficient to explain and quantify the natural phenomena. The constructal law is about the generation of flow configuration [6, 32]. The domain of this law is when a purpose exists and the system has the freedom to morph in the search of the best flow configuration. The emergence of dendritic flow networks understood in the light of constructal has been noticed by authors [6, 18, 33].

This brief overview is designed to introduce some of the advances that have occurred in our understanding of dendritic design of natural flow networks. This design is approached based on fractal and constructal perspectives. The paper is organized around two simple questions: why so many dendrite flow structures emerging in nature? apart from the shape, is there anything else in common between them?

Fractal-Like Features of Natural Dendritic Flow Networks

There is a general recognition that many characteristics of living systems can be expressed as scaling laws (typically of power law form) which indicate an invariance under appropriate changes of scale. Some of them can be related to fractal dimensions [26]. The significance of a fractal geometry as a design principle is defined by Mandelbrot [26] as the outcome of growth mechanisms grounded in self-similar, and recursive development from bud to tree. In flow systems, the fractal view is focused on their complexity and the characterization of that complexity through (fractal) measures and the dynamics of such measures.

Fractal concepts have been associated to a broad class of anatomic structures. A branching pattern that repeats itself over multiple length scales characterizes the respiratory and vascular networks. In these networks the daughter vessels sizes are recursively defined by those of the parent vessel. Mandelbrot [26] was the first to suggest that the respiratory tree is fractal, and subsequently quantitative characterization of other fractal anatomies (e.g., vascular networks, neural networks, urinary tract, brain folds, etc.) is studied by different authors [27, 28].

In dendritic flow structures, when vessels bifurcate their diameters should change by a certain factor, and the ratio of successive vessel diameters (symmetric daughters to parent) is 2^−1/3 referred to as Hess–Murray's law (d₁/d₀ = 2^−1/3). Within the framework of fractal geometry, the daughter diameter reduction factor depends on the fractal dimension D of the dendritic tree (i.e., d₁/d₀ = 2^−1/D). Thus, for a flow network described by the Hess–Murray law D is equal to 3 which means a volume-filling dendritic structure [26]. Vascular [34–36] and bronchial [1, 37, 38] trees have been found to have fractal-like features and a fractal dimension close to 3. Some organs, like the lungs, are constructed by fashioning together several fractal entities, namely the respiratory (bronchoalveolar), arterial and venous trees [1, 18]. The surface fractal dimension of the mammalian lung is about 2.5 with that of the bronchial tree of about 3 [1, 18]. The pulmonary vascular system has dimension fractal of about 3, and the fractal dimensions of diameter-element are 2.71 and 2.64 for pulmonary arteries and pulmonary veins, respectively, while the equivalent values for length-element are 1.97 and 2.86, respectively, [1, 35].

The existence of a fractal topology in flow systems is also viewed as imposing constrains on many processes that occur on it. In the respiratory tree, airflow synchrony [39], elastodynamic response [40], and signal propagation [41] are example of these processes. It seems that if the network has fractal properties, then the flows that are carried should be fractally distributed [42] and the output of dynamical physiologic networks should be also fractal [43]. Therefore, the output of trees such as the respiratory or vascular networks are fractal and multifractal statistical time series [44].

River basins consist of a main flow stream escorted by a hierarchy of side streams of decreasing lengths (i.e., dendritic network). Horton [23] was perhaps the first author to recognize the self-similar nature of river networks and many of their empirical measures can also be expressed as scaling laws. These laws reveal an invariance under changes of scale and can be linked to fractal dimensions [21, 26, 45]. Mandelbrot [26] suggested that the branching channel of river network is area-filling and takes on the dimension of a plane (i.e., 2). Several studies have shown that the branching channel of river network possess characteristics of fractals with a fractal dimension ranging from 1.6 to 1.95 [21, 46, 45].

The existence of a fractal configuration is very often associated to maximization of efficiency and more tolerance to variability. In this view, it provides an advantage in offering persistent functional role. Has this configuration greater efficiency?

The Constructal-Law Origin of the Natural Dendritic Flow Networks

The constructal law is about the generation of configuration (design, shape) in natural flow systems [6, 7, 38]: the necessity of design to occur, and the time direction of the phenomenon. It states that “For a finite-size flow system to persist in time (to live) it must evolve such that it provides greater and greater access to the currents that flow through it” [6, 32]. The constructal law asserts that for any flow system there is a property “configuration” and relates the generation of configuration to its greater access to flow or minimum travel time. This is possible because systems have the freedom to morph (i.e., freedom to change their configuration in time) to achieve their purpose of higher global performance under constraints.

Laws of Branched Vessel Networks to Fluid Flow

Dichotomy (pairing or bifurcation) is an optimized result in tree-flow structures provided by the constructal law [6, 7]. A central feature of branched vessels is that when a parent vessel branches into symmetric daughter vessels their diameters change by a constant factor (Hess–Murray law). This law was justified and extended based on the constructal design [6, 7].

Consider an incompressible flow through a parent vessel of diameter d₀ and length l₀ which bifurcates into two symmetric vessels of diameters d₁ and lengths l₁. According to the constructal design, flow structures spring out of objectives and constraints. The constraints are the total space occupied by the planar structure and the total volume occupied by the vessels that are constants. The purpose is the maximum flow access (or minimum global flow resistance) encountered by the fluid stream. For both laminar and turbulent flows the following expression is obtained [47]

$\begin{array}{cc}\frac{d_1}{d_0}=2^{-n_d}& (1)\end{array}$

where d₀ is the parent vessel diameter, and d₁ is the diameter of daughter vessels. The exponent n_d depends on the flow regime: for laminar flow n_d is 1/3 (which agrees with the Hess–Murray law) but for turbulent flow n_d is 3/7 (which agrees with the Uylings' modification). It is also found that the lengths l are described by an equation similar to Equation (1) (i.e., l₁/l₀ = 2^−nl) and the power exponent n_l is found to be 1/3 and 1/7, respectively, for laminar and turbulent flows. These are new results provided by the constructal design, and also indicate that the geometry similarity d/l is preserved in going from each parent vessel to daughter vessels for all bifurcated vessels whose fluid stream is under laminar flow conditions. In turbulent flow conditions, the geometry similarity that is preserved is d^1/3/l. In this study, branching angles in the bifurcation are also derived based on the constructal law [47].

Natural branched networks, such as the coronary vasculature [48] and the respiratory tree [37], are characterized by asymmetric sizes at bifurcations, which may be an important determinant of flow distribution. According to Horsfield et al. [49], the respiratory tree can be modeled by using explicit rules that specify asymmetric morphological attributes in a deterministic way. This model is based on counting bifurcations inwards from the periphery. Other approaches, focused on change in size of consecutive vessels generation, are provided by Reis [50], Serrenho and Miguel [51], Miguel [52]. Based on the constructal law, a comprehensive generalized scaling equations are presented for the vessels diameters and lengths of non-symmetric flow structures [51]

$\begin{array}{cc}{d}_0^{n_D}=\frac{1}{2}\text{}\left[\left(1+\frac{d_2^{n_D}}{d_1^{n_D}}\right)d_1^{n_D}+\left(1+\frac{d_2^{-n_D}}{d_1^{-n_D}}\right)d_2^{n_D}\right]& (2)\end{array}$

$\begin{array}{cc}{l}_0^{n_L}=\frac{1}{2}\text{}\left[\left(1+\frac{l_2^{n_L}}{l_1^{n_L}}\right)l_1^{n_L}+\left(1+\frac{l_2^{-n_L}}{l_1^{-n_L}}\right)l_2^{n_L}\right]& (3)\end{array}$

Here n_D = 1/n_d and n_L = 1/n_l. For laminar flow n_D = n_L = 3 but for turbulent flow n_D = 7/3 and n_L = 7. Murray's law and Uylings' modification are obtained from Equation (2) by formally setting the d₁ = d₂ (symmetric vessels).

Constructal Branching Levels of the Respiratory Tree

The purpose of the lungs is the supply of oxygen to the blood and the drainage of carbon dioxide from it. Basically, there are two main flow mechanisms to accomplish this purpose: streams/convection (low-resistivity flow) and diffusion (high-resistivity flow). In the lungs, air moves from trachea through successive bifurcations of the respiratory tree into ducts of decreasing diameter up to reach the alveoli. Therefore, lungs stem from the need to connect a source (or sink) with several points (volume). Constructal design begins with the objective and constraints. The purpose is to provide minimum resistance (maximum access) to flow, and the constraint is the thorax volume. Reis et al. [20] showed that within this perspective the architecture that emerges is a tree branched dichotomously over 23 generations. They showed that this tree geometry constitutes the best oxygen access to the tissues but also the best for carbon dioxide removal [i.e., the minimum of Equation (9) is attained at 23.4 and 23.2 for O₂ and CO₂, respectively, but as the number of bifurcations must be an integer, it must be 23]. This number of bifurcation levels matches the 23 levels that the literature indicates for the lungs [17].

Reis et al. [20] also predicted the dimension of the alveolar sac, the total alveolar surface area, the total alveolar volume, and the total length of the airways. Besides, they reported that there is a constant characteristic length (i.e., the ratio of the square of the airway diameter to its length is a constant) that characterizes all individuals of the same species, which is linked to the characteristics of the space allocated to the respiratory process. It determines univocally the branching level of the respiratory tree.

In the lung, air moves through a multiscale branching network. According to the continuity equation, the reduction of vessel sizes by a constant factor (Hess–Murray law) leads to a relationship between velocities in parent and daughters vessels that can be expressed by v₁ = 2^−1/3v₀ (symmetric daughter vessels), where v₀ is the velocity in the parent vessel diameter, and v₁ is the velocity in the daughter vessels. In the Weibel's generation scheme [17] vessels are classified according to their proximity to the trachea (i.e., trachea is level 0). Therefore, the size of this vessel is related with the size of vessels at level i by d_i/d₀ = 2^−i·n_d, and then the relationship between the velocity in the first vessel and the velocity in the vessels at level i is

$\begin{array}{cc}{v}_0=2^{i·n_d}{v}_i& (4)\end{array}$

where v₀ is the velocity in first vessel (trachea).

To perform its function safely and efficiently, lungs should provide a velocity near the acinar level not larger than the diffusion velocity. The Peclet number is a measure between convection and diffusion. For Pe ~ 1 both processes are about equally important but if Pe < 0.3 convection is so slow that dispersive effects are dominated by molecular diffusion [4]. Therefore,

$\begin{array}{cc}P{e}_i=\frac{v_i{d}_i}{D_{df}}=2^{-2i{n}_d}\frac{v_0{d}_0}{D_{df}}<0.3& (5)\end{array}$

where Pe_i is the Peclet number at branching generation i and D_df is the diffusion coefficient for oxygen or carbon dioxide in air (i.e., 22.1 × 10⁻⁶ m²/s and 17.6 × 10⁻⁶ m²/s, respectively, at temperature of 36°C).

The trachea has a diameter of about 25 mm, and at rest airflow through it experiences a velocity of about 80 cm/s [17, 20]. So, the Peclet number for the respiratory tree at branching generation 23 is 0.02 and 0.03 for O₂ and CO₂, respectively, which is much less than the criterion of Pe₂₃ < 0.3. This criterion is satisfied for tracheal air velocities up to around 8 m/s. Therefore, lung design not only maximize the airflow access under the constraints posed to the flow but, after the 23 generations of branches, it also promotes an efficient slowing of air velocity permitting the gas exchange between the air within the alveoli and the pulmonary capillaries.

In summary, minimum resistance (maximum access) provided by a tree with 23 levels of bifurcation and Pe₂₃ < 0.3 enables the respiratory tree (dendritic network) acting as basic supportive flow paths along which flows need to survive are propagated.

Lung as a Natural Porous Media: Resistance and Homothety Ratio

Tree pattern of tubes may be viewed as a porous material [18] and the fluid flow may be approached based on hydrodynamics and on the geometric description of the network. Miguel [53] derived analytical expressions for steady and transient flows, both for laminar and turbulent conditions.

Fluid flow through porous materials is generally well characterized by the Darcy's law. Darcy's law, just as the Hagen–Poiseuille equation, assumes a linear relation between the pressure drop and the fluid flow velocity with the proportional coefficient depending on the fluid viscosity (fluid property) and intrinsic permeability of media (transport property for flow). It is valid at small values of the Reynolds and for dendritic flow systems can be written as [53]

$\begin{array}{cc}{\left(\frac{\Delta p}{\rho \nu Q}\right)}_1=\frac{32{\text{l}}_0}{{\alpha }_{sf}{d}_{\text{o}}^4}\frac{1-2^{1-3n_d}}{1-{(1-2^{1-3n_d})}^{i+1}}& (6)\end{array}$

Therefore, the intrinsic dimensionless permeability, K*, is given by

$\begin{array}{cc}{K}^{\ast }=\frac{1}{32}\frac{\left[1-{\left(2^{1-3n_d}\right)}^{i+1}\right]}{1-2^{1-3n_d}}& (7)\end{array}$

and the total dimensionless volume of the network, V*, is

$\begin{array}{cc}{V}^{\ast }=\frac{\pi }{4}\frac{\left[1-{\left(2^{1-3n_d}\right)}^{i+1}\right]}{1-2^{1-3n_d}}& (8)\end{array}$

where K* is the intrinsic dimensionless permeability (=K/d₀₂), V* is the total dimensionless volume of the network (= V/l₀d₀₂), ν is the kinematic fluid viscosity, p is the pressure, Q is the airflow, ρ is the air density and α_sf is a shape factor.

Lungs can be viewed as a network with vessels flow resistances (bronchial tree) and diffusive resistances (acinar level). This means that at the higher scale the flow is characterized by viscous forces while at the small scale, diffusional transfer of gases dominates. According to [20], the global dimensionless resistance is given by

$\begin{array}{cc}{R}^{\ast }=\frac{256{\text{l}}_0^2{D}_{df}{\varphi }_g\nu }{\pi d_0^4{R}_{g}T\left({\varphi }_{g0}-{\varphi }_g\right)}(i+1)+\frac{0.13}{\pi }{2}^{-2n_{d}i}& (9)\end{array}$

where R* is the global dimensionless resistance (and 1/R* is the global dimensionless permeation), i is the number of bifurcations of the tree, T is the temperature, D_df is the diffusivity of gas (O₂ or CO₂) in the air, R_g is the gas (O₂ or CO₂) constant, and ϕ_g and ϕ_g0 are the concentration of gas (O₂ or CO₂) at the acinar level, respectively, and can be obtained from Reis et al. [20]. The first term on the right-hand side of Equation (9) represents the global resistance associated to higher scale (tree network) and the second term is the global diffusive resistance of acinar and sub-acinar scales.

Important design features can be understood in the light of Equations (6–9). As mentioned before, the geometric ratio that optimizes the diameters between parent and daughters vessels (i.e., the homothety ratio) is 2^−1/3 or ~0.79 (Hess–Murray law). What is the meaning of this result from the perspective of these equations?

For the 23 generations of branches, Figure 1 shows K*, V* and 1/R* vs. the 2^−nd. According to this figure, 1/R* is almost constant up to 2^−nd = 0.79 but after it rapidly decreases. On the other hand, K* and V* increase with 2^−nd especially for 2^−nd > 0.79. A homothety ratio of 0.79 means that the best design solution is between the (almost) maximum global permeation and a good V* and K*. Therefore, global permeation (1/R*) is dominant in this trade-off because is essential to survival.

FIGURE 1

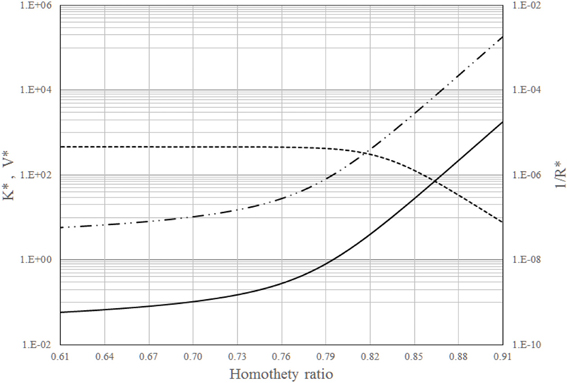
Figure 1. Dimensionless intrinsic permeability (^_______), volume (^__..__..__), and global permeation (^{__ __ __}) vs. the homothety ratio (i.e., reduction factor between parent and daughters vessels): 23 generations of branches in the dendritic network.

Mauroy et al. [54] suggest that the average homothety ratio for small lung vessels (around the generation 16) is about 0.85. Figure 2 shows K*, V* and 1/R* vs. 2^−nd for the 16th to the 23rd generations of the tree network. According to this figure, an increase of homothety ratio from 0.79 to 0.85 yields a reduction of about 30% in permeation and an increase of about 250% in volume and in intrinsic permeability. This means that a small decrease in permeation is offset by a huge increase in intrinsic permeability (to gas flow). This result agrees with the explanation presented by Mauroy et al. [54] that state that this zone of the respiratory tree is built with a certain safety factor to mitigate asthma or other episodes characterized by progressive narrowing of small airways.

FIGURE 2

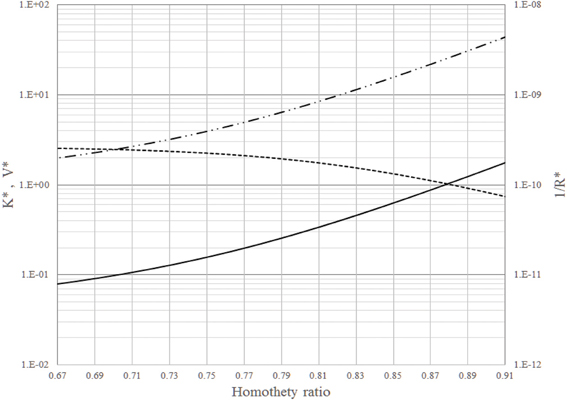
Figure 2. Dimensionless intrinsic permeability (^_______), volume (^__..__..__), and global permeation (^{__ __ __}) vs. the homothety ratio (i.e., reduction factor between parent and daughters vessels): from the 16th to the 23rd generations of branches in the dendritic network.

Lung design seems to have incorporated another safety feature. During sedentary and light activity less than 50% of the alveolar surface is involved in gas exchange between the alveolar air and pulmonary blood, while during heavy breathing the percentage reaches 80% [55]. This means that most of time operates below its full capacity (i.e., full capacity occurs only for extreme conditions), and therefore, has a considerable degree of redundancy that can be used when is necessary.

Finally, another interesting result is the finding that the total pressure difference (or drop) at each branching level of the tree is the same. Consider dichotomic branches whose length and diameter between parent and daughter vessels change by a constant factor (i.e., d₁/d₀ = l₁/l₀ = 2^−1/3). As the total flow at each branching level is a constant (i.e., Q₀ = Σ_jQ_1j = Σ_jQ_2j = ….), then the gas transport efficiency for each one of the 23 generations of branches, that carry air since the trachea, is equivalent, because the total pressure difference at each branching level is the same.

Scaling Laws of River Basins and the Constructal Law

Like the respiratory tree, river basins also display the same dendritic flow design. At the smallest scale (soil), Darcy flow prevails but at higher scale, channeling is developed where the smaller tributaries move more and more water flow into the bigger channels.

River basins also generate their area-to-point flow configuration in accordance with the constructal law. The river channels evolve such that, for a certain water flow input, the ensuing flow structure has less flow resistance to the drainage basin. Consider an elemental area filled with a stream. Minimizing the flow resistance with respect to a shape parameter of the stream is equivalent to minimize the peak pressure, and the configuration that provides easier flow access is obtained [6, 56]. Next, a larger area (first construct) filled entirely with elemental streams is considered, and the geometry of this first construct is optimized by repeating the procedure used in the optimization of the elemental stream. Higher order constructs are also optimized using a similar procedure until the specified area is completely covered. Therefore, the configuration that emerges is a fluid tree in which optimization has been performed at every scale [6, 56]. The dendrite network for river basins is the optimal result for point to area flow access.

The scaling laws of river basins are counterparts of the allometric laws of biology. The design features of the constructal dendritic network provides a theoretical basis for Horton's and Hack's laws, but also a more accurate exponent for Melton's law, i.e., 2.45 instead of 2 [6, 56]. Geophysical scaling laws are not unique with regard to be based on dendritic networks. Based on the idea of two constructal trees for maximum fluid-flow access and minimum heat loss, [57] showed that the Kleiber's law (i.e., the 3/4-power metabolic scaling) is predictable from pure theory.

Final Remarks

Configuration is ubiquitous in nature and a key subject in science. In this review, dendritic flow configurations in Nature are treated under to different views: as fractal objects and as problem of access to flow (i.e., line/area/volume to point or point to line/area/volume) under the constructal law.

Fractals were introduced by Benoit Mandelbrot in the 1970s. The fractal view is focused on the complexity of systems and the characterization of that complexity through (fractal) measures and the dynamics of such measures. Fractal objects are statistically self-similar and the value measured for a property depends on the scale or resolution at which it is measured (scaling). The self-similarity and scaling can be quantitatively measured by the fractal dimension. The existence of a fractal topology suggests a maximization of the efficiency of transport, more tolerant to variability and more adaptive to changes (internal or external). The respiratory tract studied in this paper is a good example of this. Why do fractal topologies occur? What they tell us about nature? The answer is provided by the constructal paradigm of Adrian Bejan, which had its start in 1996. It clearly links configuration and dynamics. For systems that are not purposeless (i.e., the ultimate target is to persist) and are free to morph, configuration is the constructal path to carry currents (mass, fluid, heat, information, etc.) more and more easily over time. Configuration features can be anticipated based on the line/area/volume-to-point flow access optimization. Therefore, although the differences both fractal and constructal views changed our view of the Nature, and laid important foundations for measuring and understanding the complexity of design.

Benefits associated to dendritic flow networks explain why Nature seems to prefer these configurations. These benefits are common to biological and geophysical systems and are covered by the same law. In both cases, dendritic flow configuration acts as basic supportive path along which flows need to “persist” are propagated, and underlies allometric laws. In this sense, dendritic design links and unites biological and geophysical flow systems.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Maina JN. Functional Morphology of the Vertebrate Respiratory Systems. New York, NY: Taylor and Francis (2002).

2. Ben Jacob E. Bacterial self-organization: co-enhancement of complexification and adaptability in a dynamic environment. Philos Trans R Soc Lond A (2003) 361:1283–312. doi: 10.1098/rsta.2003.1199

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

3. Miguel AF. Constructal pattern formation in stony corals, bacterial colonies and plant roots under different hydrodynamics conditions. J Theor Biol (2006) 242:954–61 doi: 10.1016/j.jtbi.2006.05.010

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

4. Bejan A, Dincer I, Lorente S, Miguel AF, Reis AH. Porous and Complex Flow Structures in Modern Technologies. New York, NY: Springer (2004). doi: 10.1007/978-1-4757-4221-3

CrossRef Full Text

5. Galen. Galen on Nerves, Veins and Arteries: A Critical Edition and Translation from the Arabic, with Notes, Glossary and an Introductory Essay. Michigan, IN: Xerox University Microfilms (1975).

6. Bejan A. Shape and Structure from Engineering to Nature. Cambridge: Cambridge University Press (2000).

7. Bejan A, Lorente S. Design with Constructal Theory. New Jersey, NJ: Wiley (2008). doi: 10.1002/9780470432709

CrossRef Full Text

8. Hess WR. Das prinzip des kleinsten kraftverbrauchs im dienste hämodynamischer forschung. Arch Anat Physiol. (1914) 2:1–62. doi: 10.1007/BF01680715

CrossRef Full Text

9. Murray CD. The physiological principle of minimum work. Proc Natl Acad Sci USA. (1926) 12:207–14. doi: 10.1073/pnas.12.3.207

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

10. Rosen, R. Optimality Principles in Biology. New York, NY: Plenum Press (1967). doi: 10.1007/978-1-4899-6419-9

CrossRef Full Text

11. Rashevsky N. The principle of adequate design. In: Rosen R, editor. Foundations of Mathematical Biology. New York, NY: Academic Press(1973). p. 143–75. doi: 10.1016/B978-0-12-597203-1.50010-5

CrossRef Full Text

12. Horsfield K, Cumming G. Angles of branching and diameters of branches in the human bronchial tree. Bull Math Biophys. (1967) 29:245–59. doi: 10.1007/BF02476898

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

13. Zamir M. The role of shear forces in arterial branching. J Gen Physiol. (1975) 67:213–22. doi: 10.1085/jgp.67.2.213

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

14. Uylings HBM. Optimization of diameters and bifurcation angles in lung and vascular tree structures. Bull Math Biol. (1977) 39:509–20. doi: 10.1007/BF02461198

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

15. Sherman TF. On connecting large vessels to small. J Gen Physiol. (1981) 78:431–53. doi: 10.1085/jgp.78.4.431

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

16. LaBarbera M. The design of fluid transport systems: a comparative perspective. In: Bevan JA, Kaley G, Rubanyi GM, editors. Flow Dependent Regulation of Vascular Function. New York, NY: Oxford Press. (1995). p. 3–27. doi: 10.1007/978-1-4614-7527-9_1

CrossRef Full Text

17. Weibel ER. Morphometrics of the lung. In: Fenn WO, Rahn H, editors. The Handbook of Physiology. American Physiological Society. Washington, DC: American Physiological Society (1964). p. 285–307.

18. Miguel AF. Lungs as a natural porous media: architecture, airflow characteristics and transport of suspended particles. In: Delgado JMPQ, editor. Heat and Mass Transfer in Porous Media. New York, NY: Springer (2012). p. 115–137. doi: 10.1007/978-3-642-21966-5_5

CrossRef Full Text

19. McCulloh KA, Sperry JS, Adler FR. Water transport in plants obeys Murray's law. Nature (2003) 421:939–42. doi: 10.1038/nature01444

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

20. Reis AH, Miguel AF, Aydin M. Constructal theory of flow architecture of the lungs. Med Phys. (2004) 31:1135–140. doi: 10.1118/1.1705443

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

21. Rodríguez-Iturbe I, Rinaldo A. Fractal River Basins. New York, NY: Cambridge University Press (1997).

22. Mantilla R, Gupta VK, Troutma BM. Extending generalized Horton laws to test embedding algorithms for topologic river networks. Geomorphology (2012) 151–152:13–26. doi: 10.1016/j.geomorph.2012.01.002

CrossRef Full Text

23. Horton RE. Erosional development of streams and their drainage basins; hydrophysical approach to quantitative morphology. Bull Geol Soc Am. (1945) 56:275–70. doi: 10.1130/0016-7606(1945)56[275:EDOSAT]2.0.CO;2

CrossRef Full Text

24. Strahler AN. Quantitative analysis of watershed geomorphology. EOS Trans AGU. (1957) 38:913–20. doi: 10.1029/TR038i006p00913

CrossRef Full Text

25. Hack JT. Studies of longitudinal stream profiles in Virginia and Maryland. US Geol Surv Prof Pap. (1957) 294-B:45–97.

26. Mandelbrot BB. The Fractal Geometry of Nature. New York, NY: W. H. Freeman (1982).

27. Zamir M. On fractal properties of arterial trees. J Theor Biol. (1999) 197:517–26. doi: 10.1006/jtbi.1998.0892

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

28. Bui AV, Manasseh R, Liffman K, Šutalo ID. Development of optimized vascular fractal tree models using level set distance function. Med Eng Phys. (2010) 32:790–94. doi: 10.1016/j.medengphy.2010.04.014

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

29. Nelson TR, Manchester DK. Modeling of lung morphogenesis using fractal geometries. IEEE Trans Med Imaging (1988) 7:321–27. doi: 10.1109/42.14515

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

30. Kitaoka H, Itoh H. Spatial distribution of the peripheral airways: application of fractal geometry. Forma (1991) 6:181–91.

31. Campos D, Fort J, Méndez V. Transport on fractal river networks: application to migration fronts. Theor Popul Biol. (2006) 69:88–93. doi: 10.1016/j.tpb.2005.09.001

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

32. Bejan A. Street network theory of organization in nature. J Adv Transport. (1996) 30:85–107. doi: 10.1002/atr.5670300207

CrossRef Full Text

33. Bejan A, Zane JP. Design in Nature: How the Constructal Law Governs Evolution in Biology, Physics, Technology, and Social Organization. New York, NY: Doubleday (2012).

34. Jiang ZL, Kassab GS, Fung YC. Diameter-defined Strahler system and connectivity matrix of the pulmonary arterial tree. J Appl Physiol. (1994) 76:882–92.

Pubmed Abstract | Pubmed Full Text

35. Huang W, Yen RT, McLaurine M, Bledsoe G. Morphometry of the human pulmonary vasculature. J Appl Physiol. (1996) 81:2123–133.

Pubmed Abstract | Pubmed Full Text

36. Huo Y, Kassab GS. Intraspecific scaling laws of vascular trees. J R Soc Interface (2012) 9:190–200. doi: 10.1098/rsif.2011.0270

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

37. Weibel ER, Gomez DM. Architecture of the human lung. Science (1962) 137:577–85. doi: 10.1126/science.137.3530.577

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

38. Miguel AF. Quantitative unifying theory of natural design of flow systems: emergence and evolution. In: Rocha L, Lorente S, Bejan A, editors. Constructal Law and the Unifying Principle of Design. New York, NY: Springer (2013). p. 21–38. doi: 10.1007/978-1-4614-5049-8_2

CrossRef Full Text

39. Altemeier WA, McKinney S, Glenny RW. Fractal nature of regional ventilation distribution. J Appl Physiol. (2000) 88:1551–7.

Pubmed Abstract | Pubmed Full Text

40. Bates JHT, Maksym GM, Navajas D, Suki B. Lung tissue rheology and 1/f noise. Ann Biomed Eng. (1994) 22:674–81. doi: 10.1007/BF02368292

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

41. Suki B. Fluctuations and power laws in pulmonary physiology. Am J Respir Crit Care Med. (2002) 166:133–7. doi: 10.1164/rccm.200202-152PP

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

42. Glenny RW, Robertson HT, Yamashiro S, Bassingthwaighte JB. Applications of fractal analysis to physiology. J Appl Physiol. (1991) 70:2351–67.

Pubmed Abstract | Pubmed Full Text

43. Bassingthwaighte JB, Liebovitch LS, West BJ. Fractal Physiology. New York, NY: Oxford University Press (1994). doi: 10.1007/978-1-4614-7572-9

CrossRef Full Text

44. West BJ. Fractal physiology and the fractional calculus: a perspective. Front Physiol. (2010) 1:12. doi: 10.3389/fphys.2010.00012

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

45. Turcotte D. Fractals and Chaos in Geology and Geophysics. Cambridge: Cambridge University Press (1997). doi: 10.1017/CBO9781139174695

CrossRef Full Text

46. Claps P, Oliveto G. Reexamining the determination of the fractal dimension of river networks. Water Resour Res. (1996) 32:3123–35. doi: 10.1029/96WR01942

CrossRef Full Text

47. Bejan A, Rocha LAO, Lorente S. Thermodynamic optimization of geometry: T- and Y-shaped constructs of fluids streams. Int J Therm Sci. (2000) 39:949–60. doi: 10.1016/S1290-0729(00)01176-5

CrossRef Full Text

48. Kalsho G, Kassab GS. Bifurcation asymmetry of the porcine coronary vasculature and its implications on coronary flow heterogeneity. Am J Physiol. (2004) 287:H2493–H2500.

Pubmed Abstract | Pubmed Full Text

49. Horsfield K, Dart G, Olson DE., Filley GF, Cumming G. Models of the human bronchial tree. J Appl Physiol. (1971) 31:207–17.

Pubmed Abstract | Pubmed Full Text

50. Reis AH. Laws of non-symmetric optimal flow structures, from the macro to the micro scale. In: Vafai K, editors. 4th International Conference on Porous Media and Its Applications in Science, Engineering, and Industry. New York, NY: Institute of Physics (2012). p. 89–94.

51. Serrenho A, Miguel AF. Accessing the influence of Hess-Murray law on suspension flow through ramified structures. Defect Diffus Forum (2013) 334:322–28. doi: 10.4028/www.scientific.net/DDF.334-335.322

CrossRef Full Text

52. Miguel AF. The emergence of design in pedestrian dynamics: locomotion, self-organization, walking paths and constructal law. Phys Life Rev. (2013) 10:168–90. doi: 10.1016/j.plrev.2013.03.007

CrossRef Full Text

53. Miguel AF. Dendritic structures for fluid flow: laminar, turbulent and constructal design. J Fluid Struct. (2010) 26:330–35. doi: 10.1016/j.jfluidstructs.2009.11.004

CrossRef Full Text

54. Mauroy B, Filoche M, Weibel ER, Sapoval B. An optimal bronchial tree may be dangerous. Nature (2004) 427:633–36. doi: 10.1038/nature02287

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

55. Hou C, Huxley VH, Gheorghiu S, Pfeifer P. Oxygen diffusion through the fractal landscape of the lung. In: Losa GA, Merlini D, Nonnenmacher TF, Weibel ER, editors. Fractals in Biology and Medicine, Vol IV. Basel: Birkhäuser Publishing (2005). p. 17–30. doi: 10.1007/3-7643-7412-8_2

CrossRef Full Text

56. Reis AH. Constructal view of scaling laws of river basins. Geomorphology (2006) 78: 201–6. doi: 10.1016/j.geomorph.2006.01.015

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

57. Bejan A. The tree of convective heat streams: its thermal insulation function and the predicted 3/4-power relation between body heat loss and body size. Int J Heat Mass Transf. (2001) 44:699–704. doi: 10.1016/S0017-9310(00)00138-1

CrossRef Full Text