Light-Effect Transistor (LET) with Multiple Independent Gating Controls for Optical Logic Gates and Optical Amplification
- 1Nanoscale Science Program, University of North Carolina at Charlotte, Charlotte, NC, USA
- 2Department of Electrical and Computer Engineering, University of North Carolina at Charlotte, Charlotte, NC, USA
- 3Center for Optoelectronics and Optical Communications, University of North Carolina at Charlotte, Charlotte, NC, USA
- 4Advanced Materials Research Institute, University of New Orleans, New Orleans, LA, USA
Modern electronics are developing electronic-optical integrated circuits, while their electronic backbone, e.g., field-effect transistors (FETs), remains the same. However, further FET down scaling is facing physical and technical challenges. A light-effect transistor (LET) offers electronic-optical hybridization at the component level, which can continue Moore's law to the quantum region without requiring a FET's fabrication complexity, e.g., physical gate and doping, by employing optical gating and photoconductivity. Multiple independent gates are therefore readily realized to achieve unique functionalities without increasing chip space. Here we report LET device characteristics and novel digital and analog applications, such as optical logic gates and optical amplification. Prototype CdSe-nanowire-based LETs show output and transfer characteristics resembling advanced FETs, e.g., on/off ratios up to ~1.0 × 106 with a source-drain voltage of ~1.43 V, gate-power of ~260 nW, and a subthreshold swing of ~0.3 nW/decade (excluding losses). Our work offers new electronic-optical integration strategies and electronic and optical computing approaches.
Introduction
As basic electronics building blocks, a field-effect transistor's (FET's) primary switching function is widely used in both logic and memory chips. A typical FET is a three-terminal device consisting of source (S), drain (D), and gate (G) contacts—where the S-D conductivity is modulated to realize on and off states by applying a voltage or an applied electric field through G [1]. Although FETs have evolved structurally from early planar to their current 3D geometries in parallel with the continual shrinkage of its lateral size, the basic operating principle remains the same. This has led to ever greater fabrication complexity, and ultimately to challenges in gate fabrication and doping control [2–6]. Various new technologies, such as FinFETs [4, 7], and tunnel-FETs [8], have been developed in recent years to enable the continuation of Moore's law [9], but further development with current technologies are uncertain [10]. Other options are being explored as alternatives, which include semiconductor nanowire (SNW) based FETs [11–13], FETs comprised of 2D materials [14, 15], and FETs with sophisticated gate structures [16], such as multiple independent gates [5, 6] or a gate with embedded ferroelectric material [17]. There is, however, no clear pathway for overcoming a FET's intrinsic physical limitations [18–20] dictated by its operation mechanism, such as random dopant fluctuations [3] and gate fabrication complexities [21], and no viable rival technology currently exists. We offer a competitive alternative with additional unique functionalities. The light-effect transistor (LET) is a two-terminal device composed of a metal-semiconductor-metal (M-S-M) structure, where each M-S junction serves as either the S or D contact, and the two contacts are separated by a semiconductor nanostructure-based channel. Figure 1 contrasts SNW-based LET and FET structures to reveal the apparent structural simplicity offered by a LET—no physical gate is required. A LET's operation mechanism is distinctly different from a FET in two regards: (i) the S-D conductivity is solely modulated by light or an optical frequency electromagnetic field, which contrasts a FET's electrostatic control through an applied DC voltage, and (ii) current carriers are generated through optical absorption rather than by thermal activation of dopants. In other words, a LET employs optical gating based upon the well-known photoconductive mechanism [22] that has typically been of interest in photo-detection. Inherent advantages stem from a LET's simplistic architecture, which include (i) eliminating gate fabrication complexity, and (ii) avoiding difficulties with doping control. These attributes remove the two primary challenges or intrinsic limitations for down scaling conventional FETs to the quantum regime [23], and they offer the potential for reduced fabrication costs. While a LET's most basic application emulates a FET when it operates under one-beam illumination (as in a photo-detector), it offers functions not readily achievable by either a FET [24] or a photo-detector [25, 26], when it operates differently than a typical photo-detector (e.g., when responding to multiple independent light beams).
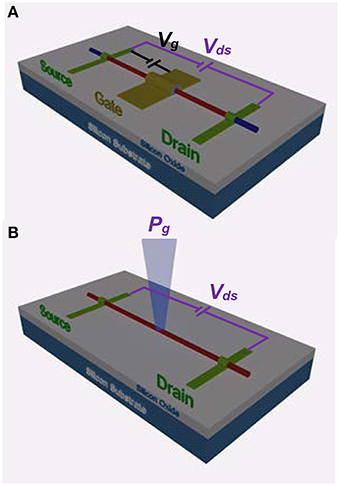
Figure 1. Schematic comparison between a semiconductor-nanowire-based (SNW-based) field-effect transistor (FET) and a light-effect transistor (LET). (A) A FET is a three terminal device where the source-drain, S-D, current, is driven by an S-D voltage, and may be modulated through a gate (G) voltage applied through its G contact. (B) A LET is a two terminal device where the S-D current is modulated with one or multiple independently controlled light beams fused together through an optical combiner. Color codes are SNWs in red, S and D contacts in green, G contact in yellow, and the gate dielectric (under the G contact) is in bluish-gray. The blue-colored SNW tips past the S and D contacts indicate different FET doping types along the conducting SNW channel. It is assumed that these devices are resting upon an insulating substrate.
Light-induced electrical conductivity changes are a well-known phenomenon typically used for photo-detection. In fact, SNW devices structurally similar to our LET have been investigated as photo-detectors [25, 26]. At first glance, it may appear that a LET simply employs a photo-detector's switching function to emulate a FET. In reality, most photo-detectors lack desirable FET-like characteristics and are therefore unsuitable for LET use. It is therefore important to understand the differences between a photo-detector, LET, and FET to appreciate the LET's novelty. Photo-detection typically relies upon a p-n junction-based device, because it usually offers superior performance over a simpler M-S-M device based on the photoconductive mechanism. This arises from the M-S-M structure typically requiring a larger bias to drive carriers through the S region [1, 22]. Note that a p-n junction based photo-detector has a distinctly different I-V characteristic under illumination than a photoconductive-based one, and only the latter can offer a light I-V resembling that of a FET with gate voltage on. The photoconductive mode's disadvantage is eased through reduced device dimensions, as demonstrated by SNW-based photo-detectors [25, 26], and the LET application in this work. Its structural simplicity should provide further advantages at the genuine nanoscale. We note that photo-detector structures that are difficult to dope may also employ a M-S-M structure [1, 22]. Therefore, a LET does not employ a new device structure or mechanism. Its novelty stems from its stringent electrical and optical characteristics that can (i) replicate the basic switching function of the modern FET with competitive (and potentially improved) characteristics, and (ii) enable new functionalities not available in modern FETs nor offered by conventional photo-detectors. While under single-beam illumination, a LET yields a high on/off ratio under optical gating, which resembles a FET under gate-voltage control or a photo-detector with high photoconductive gain. Despite this similarity, a LET should be characterized with a pertinent FET parameter known as “subthreshold swing,” which measures how much gate action is required to turn the device on, and is normally not of interest in photo-detection applications. Under simultaneous multi-beam illumination, which is usually irrelevant for photo-detection, the multiple independent gating capability enables a LET to demonstrate previously unreported functions, such as optical logic (AND and OR) gates and optical amplification as an analog application. In contrast, multiple independent gating has been a very challenging task for FETs [6]. These unique functionalities are of great interest for optical computing and novel optical detectors. To summarize, LET novelty, in comparison to photo-detectors, is two-fold. First, LETs are characterized electrically in a very different manner than photo-detectors, as photo-detectors are not typically explored for the electronic functions found in a FET. Second, LETs utilize their multi-beam response while a photo-detector does not. In comparison to FETs, a LET's gating mechanism is distinctly different from a FET's, which easily enables a LET's multi-gate capability, and allows a LET to offer functions beyond those in a typical FET. Furthermore, a LET's frequency response or switching speed is limited by the carrier transit time through its conducting channel. While this effect is shared with a FET, a FET's response is limited by its gate capacitance.
In this work, we employ readily available CdSe SNWs [27, 28] to demonstrate the LET concept and functions. We first characterize the material and devices, and then explore single-beam optical gating effects with different wavelengths and laser powers (Pg(λg)), manifested in both output characteristic (Ids − Vds) and transfer characteristic (Ids − Pg). Finally, we operate the LET by applying multiple independent beams to demonstrate novel device functions, which are not achievable in conventional FETs, such as, optical logic gates and optical amplification.
Materials and Methods
Nanowire Synthesis and Device Fabrication
CdSe nanowires were grown in a vertical array through gold-catalyzed chemical vapor deposition, as described elsewhere, [27] and were then dispersed in alcohol and drop cast onto a Si/SiO2 chip, which consists of Si substrate coated with a 300-nm thick SiO2 layer. After CdSe nanowires were dispersed onto a chip, a thin poly-methyl methacrylate (PMMA) layer was spin coated onto the chip, followed by electron-beam lithography to open channels at a nanowire's ends. Exposed PMMA was removed by developing the chip. Afterwards, the chip was transferred to a thermal evaporator (Cressington-308R) for indium metallization (30 nm), followed by lift-off in acetone to obtain a finished device. The other indium wire end was bonded to a large gold pad used for placement of a gold-coated electrical probe. The samples were air stabilized for at least a week prior to testing.
LET Characterization
Optical gating through Pg(λg) has two basic control parameters: wavelength, λg, and power level, Pg, under one-beam CW operation, but it can be readily extended to other operation modes. For instance, multiple independent beams and pulsed illumination may be represented as Pg(λg1, λg2,…,λgN) and Pg(t, λg1, λg2,…,λgN), respectively. We fully characterize LET output and transfer characteristics under one-beam CW operation with two illumination conditions: (i) illuminating the center of the SNW with a focused CW laser (“focused illumination”) with an optical diffraction-limited spot size at wavelengths of 633, 532, 442, or 325 nm; and (ii) illuminating the LET uniformly with “white light” from a halogen lamp (“uniform illumination”).
The novel LET concept requires performance metrics for evaluation and comparison against FETs; thus, FET figures of merit are adapted, such as the two important input-output relationships: (i) “output characteristics” or Ids vs. Vds under a constant illumination condition Pg(λg), which is equivalent to the FET's output characteristic under a constant gate voltage Vg; and (ii) “transfer characteristics” or Ids vs. Pg(λg) under a constant Vds, which is equivalent to a FET's Ids vs. Vg under a constant Vds. A FET's gate voltage, Vg, is replaced by a LET's gate power Pg(λg), which not only serves the same function of modulating S-D conductivity but also offers an avenue to achieve novel functions beyond those in a FET. Characteristic (i) is shared by both LET and photo-detection applications, while characteristic (ii) is required for LETs and FETs as a measure of turn-on energy, and in particular, for LETs to realize novel functions.
Optical and Electrical Measurements
Ids vs. Vds measurements were collected with a Keithley® 2401 low voltage sourcemeter® that was remotely operated with LabTracer v2.9 software via a GPIB connection. For currents below ~1 nA, a Stanford Research System SR570 current pre-amplifier was used in conjunction with the Keithley®. Illumination sources consisted of halogen light, 532, 441.6, and 325 nm lasers ported through a Horiba LabRAM HR800 confocal Raman system with an internal 632.8 nm laser. Due to limited probe spacing for electrical measurements, all illumination sources were focused through a 50x long working distance (LWD) objective lens (N.A. = 0.50), except 325 nm, which went through a 10x MPLAN objective lens (N.A. = 0.25). Laser powers were limited to absolute powers of ~3 μW, as measured on the sample side of the microscope lens, to avoid potential laser-induced material modifications. Laser powers were altered through a combination of a standard neutral density filter in the Raman system and an adjustable neutral density filter in the laser path. Laser powers were measured with a Thor Labs PM100D power meter, and six and ten averaged measurements were used for D1 and D2, respectively, to calculate average powers. The total power of the halogen light was estimated to be 69.1 μW.
Estimated Actual Power Absorbed
The laser spot size is estimated by the optical diffraction limit formula 1.22λ/N.A., where N.A. is the numerical aperture of the microscope lens. The fraction of the laser power actually absorbed is estimated by taking the ratio of the nanowire diameter to the laser spot size. The estimated ratios for the 632.8, 532, 441.6, and 325 nm lasers are 5.18, 6.16, 7.43, and 10.1% for a nanowire with an 80 nm diameter (device D1). For halogen illumination, the fraction of actual absorbed light is estimated using the ratio of the nanowire's cross section to the total illumination area. For the 50x LWD (10x MPLAN) objective lens, the illumination area is ~279 (~1450) μm2. The ratio for the 80 nm wide/10 μm long nanowire (D1) is ~3.2 10−6, and the power estimation for light actually absorbed is ~0.22 μW (which is comparable to that for the focused laser beam). All the illumination powers mentioned in the manuscript were applied powers, unless an actually absorbed power was explicitly stated.
Results
Nanowire and Device Characterization
Figure 2 provides material and device characteristics. Figure 2A displays an SEM image of a 10-μm-long CdSe SNW (device 1 or D1) with indium (In) contacts forming M-S junctions at each end. The uniform single-crystalline CdSe SNW was grown in wurtzite phase along the [0001] axis with a diameter of ~80 nm, as revealed by the low magnification transmission electron microscopy (TEM) image in Figure 2B, with the selected area diffraction pattern (SADP) as inset, and Figure 2C's high-resolution TEM (HRTEM) image showing a 0.69 nm inter-planar spacing. The gold catalyst at the SNW end (Figure 2B) suggests the vapor-liquid-solid growth mechanism [29]. The CdSe-SNW's laser-power-dependent photoluminescence (PL), Figure 2D, shows a strong emission peak at 1.78 eV that matches CdSe's bandgap energy [30]. The inset overlays a PL map upon an optical image to demonstrate relatively homogenous SNW emission, and by extension, homogenous material quality across the SNW channel. In Figure 2E, the output characteristic, S-D current Ids vs. S-D voltage Vds, is demonstrated for the device with and without light illumination using a halogen light, where illumination optically modulates or “gates” the electrical conductivity between dark (“off”) and illuminated (“on”) states. The Ids vs. Vds curves for these two states clearly resembles those of a FET's off and on states [1], respectively, especially when Vds < ~7 V.
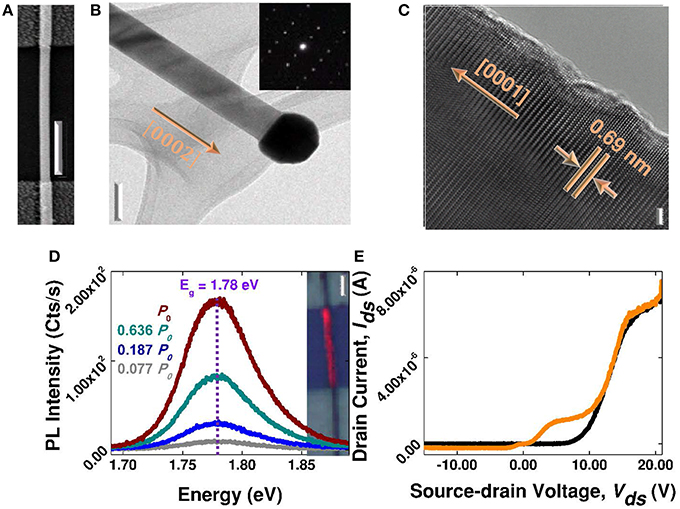
Figure 2. LET characterization. (A) SEM image of a typical In-CdSe-In device (2 μm scale bar). (B) TEM (100 nm scale bar) with SAED inset, and (C) HRTEM image (2 nm scale bar) of a representative CdSe nanowire. The TEM results indicate single crystalline CdSe with well-ordered lattice plane spacing of 0.69 nm along the [0001] growth direction. (D) PL spectra obtained under 442 nm excitation at different powers (P0 = 1.5 μW). Inset contains PL map overlaid upon an optical image of D1 (4 μm scale bar). (E) Source-drain current, Ids, as a function of source-drain voltage, Vds, under dark (black line), and halogen light illumination (orange line) conditions.
Output and Transfer Characteristic
Results for two devices, device 1 (D1) and device 2 (D2) with lengths of ~10 and ~5.5 μm and similar diameters (~80 nm), are presented to illustrate general LET properties, and to demonstrate the potential for characteristic tuning and optimization. The two devices were fabricated in essentially the same way.
Device dark currents reveal negligible reverse bias current and rectification (diode-like behavior) under forward bias, e.g., Figure 2E. LET operation occurs under forward bias for both devices. Rectification is indicative of asymmetric In/CdSe contacts for both devices, where one M-S junction is close to ohmic and the other forms a Schottky contact [31]; large asymmetric contacts are desired as they drastically reduce the dark current or off state and thereby improve the on/off ratio. The Schottky barrier largely determines the turn-on voltage, VD, on, which is ~8 V for D1 and >21 V for D2. For instance, D2 shows nearly resistive behavior up to Vds = 21 V with Ids reaching only ~15 pA, compared to D1's range from ~1 nA to ~4 μA over 1–21 V. The vast difference between the two devices might stem from a thin SeOx layer (x = 2–3) [32] at the In/CdSe junction, although the details require further study. These results hint that dark or off state parameters can be controlled through M-S contact engineering.
Representative LET output characteristics are shown in Figures 3A–D for D1 and in Figures 3E,F for D2, respectively, to exemplify how LET performance depends on the gate power/wavelength, illumination condition, and device variation. D1 exhibits two well-separated plateaus, respectively, starting at Vds ~ 4–5 and ~14–18 V depending on the gate wavelength and power. For example, the second plateau's onset is at ~14–15 V for 633 nm illumination but shifts to ~16–18 V under 442 nm excitation. Two tunable plateaus can potentially offer two distinct, customizable on states. For D2, the first and second plateau are comparatively not well separated, and both 532 nm and halogen illumination have their first plateau at ~2 V with respective power-dependent, second plateaus at ~6–7.5 V (532 nm) and ~5–5.75 V (halogen). Each plateau appears at respectively lower Vds values than in D1, and because of the extremely low dark current, the long second plateau extends to the highest Vds measured. For D1, the maximum on/off ratios typically occur at Vds < 5 V, and vary from 102 to 104 depending on the gate power and wavelength. For instance, Figure 3B contains on/off ratios of ~5 × 104 and ~2 × 104 at Vds = 1.43 and 4.95 V, respectively, when Pg(532 nm) ≈ 2 μW. The on/off ratios for D2 in Figure 3E are ~1.0 × 106 and ~1.1 × 106 at Vds = 1.43 and 4.95 V when Pg(532 nm) ≈ 2.6 μW. When Pg(halogen) ≈ 69 μW in Figure 3F, the on/off ratios are ~6 × 105 and ~1 × 106 at Vds = 1.43 and 4.95 V, respectively.
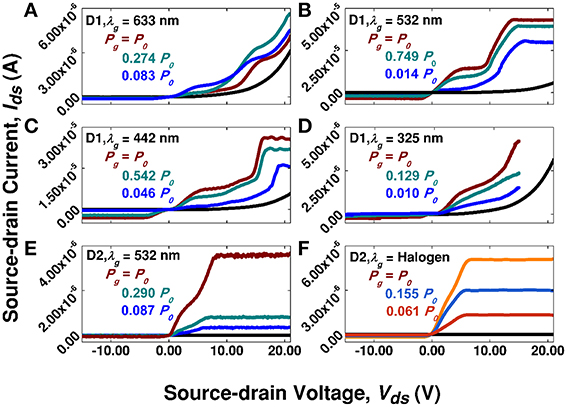
Figure 3. LET output characteristics: Source-drain current, Ids, as a function of the applied source-drain voltage, Vds with varying gate power, Pg, and wavelength, λg, for two devices (D1 and D2). (A–D) are for D1 under 633, 532, 442, and 325 nm illumination with P0 values of 1.40, 2.07, 2.38, and 2.25 μW, respectively, while (E,F) are for D2 under 532 nm and halogen excitation with respective P0 values of 1.38 and 69.1 μW. The dark current is represented as black lines.
Differences between D1 and D2 indicate that a LET's characteristics may be tuned and optimized through material and device engineering. A large M-SNW contact barrier is generally desirable for producing small off state currents over the operation range, and can be optimized to maximize the on/off ratio. Note that current levels for different “gate” wavelengths in Figures 3A–D showed considerable variations, which is fundamentally due to wavelength-dependent light-matter interaction effects, e.g., absorption and carrier dynamics, and illumination conditions, e.g., power density and beam size. This feature offers the unique LET advantage of flexibility in achieving gate functions compared to FETs.
The transfer characteristics allow extraction of several performance metrics. A FET's threshold gate voltage, VT, and subthreshold swing, S, are respectively defined as the onset of a linear region in the Ids − Vg curve (i.e., voltage-controlled resistor behavior), and as the inverse linear slope on a semi-log Ids − Vg plot [4]. Their physical interpretations, respectively, are the gate voltage required for device operation and the gate voltage increment to induce an order of magnitude current change below VT. A small S-value implies a small energy or power consumption to turn on or operate a FET. Figure 4 contains D1's and D2's transfer characteristics, which in general, resemble a FET's transfer characteristics, e.g., increasing Ids as the gate power Pg increases under constant Vds, except a LET replaces Vg with Pg. A LET's threshold gate power, PT, then, corresponds to the onset of a linear Ids − Pg region for a given λg, and SLET is its subthreshold swing. Significantly, FETs usually do not operate in the “subthreshold swing” region, while a LET can employ this range to realize optical logic gates and for an interesting optical amplification effect. Taking D2's Ids vs. Pg curves, Figure 4E, with λg = 532 nm as examples, typical PT and SLET values at Vds = 1.43 (4.98) V are, respectively, ~30. (~30.) nW, and ~2.8 (~2.5) nW/decade. For reference, advanced FETs have respective VT and S parameters of 100–200 mV, and ~70–90 mV/decade [33]. At Vds = 1.43 V, Pg = 0.11 μW yields Ids ≈ 0.35 μA, and a LET dynamic power consumption of ~0.5 μW, which is comparable to advanced FETs [34]. A LET's off-state energy consumption can be very low. For instance, the dark current is ~1 pA at Vds = 1.43 V with a corresponding off power consumption of ~1.5 pW, which is lower than a FET of similar length [34]. Switching energy, or the amount of energy needed to go from off to on states, is a frequently quoted metric. Our current measurement system prevented a direct measurement of the switching time, although it may be reasoned that LETs can have lower switching energies than modern FETs. Note that a LET may be viewed as a FET without the gate, which means that a LET's switching time is limited by the carrier transit time rather than a FET's capacitive delay. Most direct band gap semiconductors possess room temperature carrier lifetimes on the order of 100 ps without an applied bias, where applying a bias, especially for a short conducting channel length, reduces the transit time by more quickly wiping out free carriers. Simple estimates based on D2's performance support lower switching energies in LETs. For example, even an assumed 100 ps delay time would yield a switching energy of 0.05 fJ/switch (0.5 μW × 100 ps) associated with the S-D current, and 0.01 fJ/switch (0.1 μW × 100 ps) from the optical gating action, which yields a total switching energy less than typical FET values of 0.1–1.0 fJ/switch [35]. The switching energy could be further reduced by reducing the channel length and optimizing the contacts.
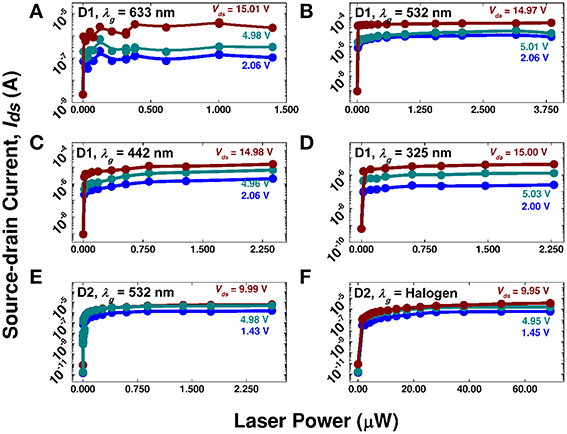
Figure 4. LET transfer characteristics: Source-drain current, Ids, as a function of laser power under different source-drain voltages, Vds. (A–D) are for device D1, while (E,F) are for device D2 using the same conditions as in Figure 3.
Application Demonstrations
LET transfer characteristics are used to illustrate the underlying principles for a few important applications. D2's 532 nm illumination characteristics, Figure 4E, are re-plotted on a double log scale in Figure 5A, with only Vds = 1.43 and 4.98 V shown for clarity, to more clearly portray the three major operating regions: super-linear (dark gray region), linear (medium gray), and sublinear/saturation (light gray). Different regions can offer different unique applications, as the examples highlighted below.
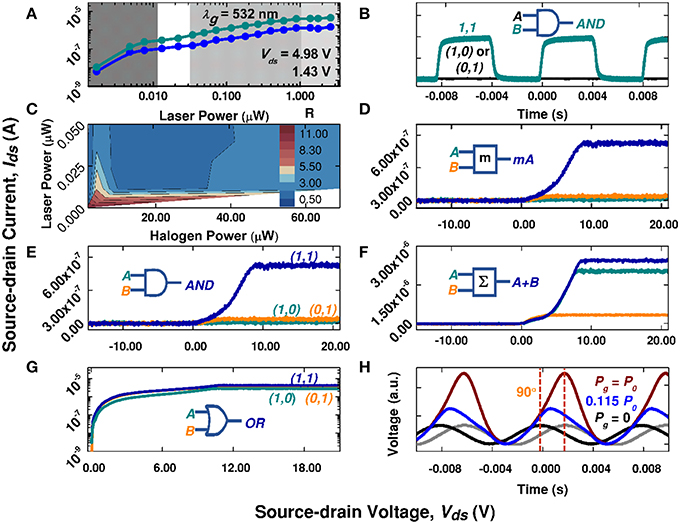
Figure 5. Selected LET functionality demonstrations using D2. The axes are source-drain current, Ids, vs. source-drain voltage, Vds, except where noted otherwise. (A) Log-log plot of Ids vs. Pg curves under 532 nm excitation with Vds values of 1.43 and 4.98 V, where the three shaded areas are visual guides for distinguishing the super-linear (dark gray), linear (medium gray), and saturation (light gray) regions used to demonstrate LET behaviors and applications in (B–H). (B) Optically modulated AND logic gate where A = Vds (5.00 V) and B = modulated Pg(532 nm) (up to 2.60 μW in amplitude). Dark line, Vds = 5 V and Pg = 0; green line, Vds = 5 V and Pg is modulated. (C) Various operation regions, according to ratio R (see text for definition), achievable with two-beam illumination under a fixed Vds of 5.0 V. (D) A typical R >> 1 operation point, with Pg1(532 nm) = 2 nW and Pg2(halogen) = 1.57 μW, used as a demonstration of optical amplification; and (E) contains the same data as (D) but used as a demonstration of an optical AND gate instead. (F) A typical R ≈ 1 operation point, with Pg1(532 nm) = 0.63 μW and Pg2(halogen) = 0.7 μW, used as a demonstration of a summation operation. (G) A typical R ≈ ½operation point, with Pg1(532 nm) = 0.63 μW and Pg2(halogen) = 69.1 μW, used as an optical OR logic gate. (H) LET operation under electrical modulation of Vds(t), while varying Pg (P0 = 2.60 μW). The outputs Ids(t) were measured through a sampling resistor. The input is shown in gray (normalized to the black Pg = 0 output curve).
AND Logic Gate and Voltage Amplifier
Figure 5B demonstrates single beam illumination as a hybrid AND logic gate, which replicates the most basic FET logic function [1, 36], using electrical input A = Vds and optical input B = Pg with output denoted as AxB. This is achieved when Vds = 5V and Pg is modulated between 0 and 2.60 μW. One-beam operation could also act as a current source or voltage amplifier when operating in the output characteristic's saturation region, or even when utilizing a LET's two distinct on states (e.g., the first and second plateaus in Figure 3B) to realize two-level logic gate and voltage amplifier functions. Furthermore, two LET devices may be combined in parallel or series to respectively create universal NOR and NAND logic gates, as shown in Figure A1 in Supplementary Material with their corresponding truth tables.
Multi-Independent-Gate Capability
An important LET advantage is multi-independent-gate operation, where optical gates do not increase device dimensions. As an example, two-beam operation is demonstrated with independently controlled uniform illumination with halogen light and focused illumination from a 532 nm laser, denoted as Pg1 and Pg2, respectively. Illumination by either individual light beam produces its corresponding transfer characteristics, e.g., Ids vs. Pg in Figure 4, while two-beam illumination results in a 3D Ids vs. (Pg1,Pg2) plot (Figure A2-A in Supplementary Material). However, the two-beam response fundamentally reflects the linearity of the single-gate response shown in Figure 5A. To more clearly show this effect, a current enhancement factor R is introduced by converting Ids(Pg1,Pg2) to R(Pg1,Pg2), where R = Ids(Pg1,Pg2)/[Ids(Pg1) + Ids(Pg2)]. Figure A1-A's in Supplementary Material data were converted with this definition and the corresponding R-values are displayed in Figure 5C's contour plot. Using the LET response characteristics in Figures 5A,C, we demonstrate a few distinctly different LET functions that are not readily achievable using a FET, and can be realized with a single LET device. Figures 5D–G demonstrate dual-gate applications in three important R(Pg1,Pg2) regions illustrated in Figure 5C. Additionally, the nonlinear response under 633 nm is also extended to two beam illumination with the addition of halogen light (Figure A3 in Supplementary Material).
Optical amplification
This occurs in Figure 5A's super-linear or subthreshold swing region and yields a region where R >> 1, for instance, R ≈ 9–11 in Figure 5C. Figure 5D yields single beam induced currents of Ids, 532nm ≈ 11 nA (dark cyan line) and Ids, halogen ≈ 37 nA (orange line), while simultaneous illumination produced ~11 times their sum with a Ids, 2beam ≈ 525 nA (royal blue line). If the laser beam is viewed as a weak optical signal to be measured, and the halogen light (~1.6 μW) as a gate signal, an amplification factor of m ≈ 48 is obtained. Optically-induced amplification of a LET's electronic signal replicates three-terminal phototransistor function, e.g., a bipolar transistor with a semi-transparent electrode [37], where a small base-emitter bias leads to photo-current amplification. This feature may find broad application in weak optical signal detection.
Optical AND logic gate
Results shown in Figure 5D can also be used for important optical logic operations, such as that in Figure 5E. Two individually applied optical gates, with inputs of A and B, respectively, produce two low current or off states represented as (1,0) or (0,1) in addition to the (0,0) off state (not shown for clarity). Only under simultaneous illumination does output C produce the on or (1,1) state. LET-enabled optical logic operations could lead to new optical or quantum computing approaches [38].
Optical summation
Sum operations can be realized in Figure 5C's linear response region, e.g., R = 1, as illustrated in Figure 5F. In this figure, Pg1, 532nm and Pg1, halogen generate two independent signals of 2.00 and 0.32 μA, while simultaneous illumination produces a current of 2.43 μA or approximately their numerical sum. This region is convenient for producing multiple states, such as for memory devices.
Optical OR logic gate
Current saturation is achieved when R = ½, and can function as an optical OR logic gate, Figure 5G. When A = Pg1(532 nm) = 0.63 μW and B = Pg2(halogen) = 69.1 μW, individual illumination as (1,0) and (0,1) states or dual illumination as the (1,1) state all produce comparable Ids values; all three on states contrast the off state with pA-level Ids denoted as (0,0) (not shown for clarity). A single LET could perform more complex logic functions concurrently by combining Vds control with dual optical gate ability, such as a three-terminal AND gate with output AxBxC, or with simultaneous AND and OR gates with Ax(B+C) output. Truth tables for these logic operations and their proposed symbols are provided in the Appendix (Figure A4 in Supplementary Material). Significantly, a single LET can realize complex logic functions that typically require multiple FETs, but could require fewer devices to perform identical or enhanced functionality. Thus, LETs offer an additional pathway for achieving high device densities on a single chip.
Differentiator and Optically Gated Phase Tuner
Complementary to the above mentioned functions, LETs can also be used as a differentiator under zero or low Pg, and as a phase tuner as Pg is increased. Figure 5H shows the Ids(t) vs. Vds(t) curves for different Pg values, where Vds(t) is a sine wave modulation with an amplitude of 5.0 V and a DC offset to remove the negative portion. The Ids(t) curve exhibits a 90° phase delay with respect to Vds(t) when Pg = 0, which indicates that the device functions as a differentiator by converting a sine wave into a cosine wave; increasing Pg results in a tunable phase shift that gradually approaches zero, e.g., at Pg = 2.6 μW. This effect can be understood as changing the LET's impedance by varying the gate power.
Discussion
LET Operation Mechanism
The Ids − Vds curves in Figure 3 may be understood qualitatively with the photo-conductivity model proposed by Mott and Gurney [22]. The first plateau could be associated with the “primary photoconductivity” which produces current as a result of photo-generated electrons and holes flowing through the nanowire under applied bias. A steady state condition is formed when just enough external carriers entering the nanowire through the electrodes replenish those leaving the device. Under single point illumination, the collection efficiency, Ψ, can be approximately described by:
where w is the carrier's mean free path (which is proportional to the applied field), L is the nanowire's length, and x0 is the illumination site measured from the anode (cathode) when the carriers are electrons (holes). This theory suggests a continuous photocurrent increase from Vds = 0 until saturation at a sufficiently large Vds to produce w >> L and Ψ → 0.5 (see Figure A5 in Supplementary Material for simulated Ψ vs. Vds curves). Under uniform illumination, the collection efficiency is then:
If all photons are absorbed, the sum of the collection efficiencies of both electrons and holes will yield a quantum efficiency, ηQE, defined as Iph/(eNph), where Iph is the photo-induced current, and Nph is the number of absorbed photons. When current saturation occurs, ηQE = 100%. For instance, absorbing 2 μW of 620 nm light with ηQE = 100% yields a 1 μA current. As Vds approaches VD, on, a major Schottky barrier reduction [31, 39] allows excess carriers to enter the nanowire through the electrodes, which then produce a drastic Ids increase that allows ηQE >> 1. The detailed operation mechanism is likely much more complex than that described by the simple photoconductive mode, and deserves further investigation.
Significantly, the collection efficiency is expected to improve drastically at low Vds with nanometer-length devices (Figure A5 in Supplementary Material), which should further reduce the static power consumption and provide lower Vds than those demonstrated here. The maximum applied laser power is about 3 μW and corresponds to a power density of ~0.60 W/mm2, which is less than that delivered by an efficient light-emitting diode [40]. The gate power actually used is only about 10% of the applied power because the laser spot size is considerably larger than the nanowire diameter (see Section Materials and Methods for energy loss estimates). Reducing the beam size closer to the SNW's diameter could reduce Pg by at least a factor of 10 [41], and as is well established in FET devices, reducing the channel length can further reduce the required Vds (Figure A5 in Supplementary Material). Enhanced efficiency and reduced energy consumption could significantly reduce thermal issues plaguing nanoscale FET-containing electronics devices. We note that FETs posses a thermal dynamic limit of S ≥ (kT/q) ln(10) = 60 mV/decade at 300 K, whereas for LETs, SLET is extrinsic in nature through its dependence of w on the carrier density, which in turn depends on the defect density. Thus, SLET can be significantly improved by shortening the conduction channel, perfecting the material quality, and by choosing materials with strong absorption.
Pathways to Further Miniaturization and Integration
LETs are also capable of quantum scale operation. A LET's structural simplicity removes potential obstacles that FETs face for further down scaling. A LET shares the same limit of a FET, that is, the nanostructure dimensions practically achievable, e.g., 1–7 nm for Si nanowires [42], but LETs do not require complex and sophisticated fabrication steps for physical gates and doping. In general, ballistic transport theory suggests that commercially viable currents could be achieved in quantum structures [43]. Quantum conductance, which limits 1-D ballistic transport, is given by G = nG0, where G0 = 2e2/h is the minimum conductance and n are integers representing quantized energy levels. This equation [44] yields a maximum quantum impedance for the conducting channel of Z0 = 1/G0 = 12.9 kΩ. The on-state energy consumption could be as low as ~13 nW/LET when Ids = 1 μA, and the required minimal Vds would only be 13 mV (not including the voltage drop over the S/M junctions). Given the highly localized nature of the 1-D energy density of states, LET conductivity is expected to be quantized, and thus, tunable using different photon energies.
Industry may employ at least two basic illumination modes in an integrated LET circuit depending on the application: (i) uniform, broad-area illumination over a high-density LET array with SNWs, or (ii) separated light beams directed to individual or small groups of LETs through, for instance, sharp fiber tips or nanoscale emitters embedded on the same chip. For either mode, multiple light sources of the same or different wavelength(s) and/or intensities can be combined into one beam but controlled independently.
Conclusion
In this work, we presented the LET concept as a drastically different approach for FET-based IC technologies by using an all optical, rather than a physical gate mechanism. A LET explores the well-known photoconductivity attribute of a semiconductor that is naturally and commonly used for photo-detection. Here, we demonstrate digital and analog applications typically only achievable with transistors, as well as, functions that FETs cannot achieve. Most significantly, the LET gate function can provide much greater flexibility than a FET, including tunable gate properties and multiple independent gates. Notably, a LET can continue Moore's law without the FET complications and limitations associated with gate fabrication and doping control through: (i) a simple device architecture to potentially reduce fabrication costs; (ii) feasible down scaling to the quantum level; (iii) efficient, multi-functional ability in a single device; and (iv) operation at low energy consumption, which negate thermal issues plaguing nanoscale electronics devices. The general LET operation principle is independent of a particular material system, thus, when applied to silicon, the existing silicon-based microelectronic and photonic technologies can be readily adopted by LET technology. The LET concept can also be extended to develop other light-effect devices.
Author Contributions
YZ and WZ guided work at UNCC and UNO respectively. JM and YZ conducted the optical and electrical measurements and analyzed the data, SR grew the CdSe nanowires and fabricated the devices, and KW collected the TEM data and created the 3D schematics in Figure 1. YZ and JM wrote the manuscript. All authors have reviewed, edited, and commented on this manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was partially supported with funds from YZ's Bissell Distinguished Professorship at UNC-Charlotte. We extend deep appreciation and thanks to Dr. Quiyi Ye and Dr. Kwok Ng for valuable discussions and comments. JM thanks John “Jack” Krause for useful electronics-related discussions. SR thanks Shuke Yan for assistance in device fabrication.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/article/10.3389/fphy.2016.00008
References
2. Fried DM, Duster JS, Kornegay, KT. High-performance p-type independent-gate FinFETs. IEEE Electron Device Lett. (2004) 25:199–201. doi: 10.1109/LED.2004.825160
3. Shinada T, Okamoto S, Kobayashi T, Ohdomari I. Enhancing semiconductor device performance using ordered dopant arrays. Nature (2005) 437:1128–31. doi: 10.1038/nature04086
4. Ferain I, Colinge CA, Colinge JP. Multigate transistors as the future of classical metal-oxide-semiconductor field-effect transistors. Nature (2011) 479:310–6. doi: 10.1038/nature10676
5. De Marchi M, Sacchetto D, Frache S, Zhang J, Gaillardon PE, Leblebici Y, et al. Polarity control in double-gate, gate-all-around vertically stacked silicon nanowire FETs. In: 2012 IEEE International Electron Devices Meeting (IEDM) (2012) (San Francisco, CA).
6. Ernst T. Controlling the polarity of silicon nanowire transistors. Science (2013) 340:1414–5. doi: 10.1126/science.1238630
7. Huang XJ, Lee WC, Kuo C, Hisamoto D, Chang LL, Kedzierski J, et al. Sub-50 nm p-channel FinFET. IEEE Trans Electron Devices (2001) 48:880–6. doi: 10.1109/16.918235
8. Ionescu AM, Riel H. Tunnel field-effect transistors as energy-efficient electronic switches. Nature (2011) 479:329–37. doi: 10.1038/nature10679
10. ITRS. 2012 Updates to the International Technology Roadmap for Semiconductors (2012). Gaithersburg, MD.
11. Cui Y, Zhong ZH, Wang DL, Wang WU, Lieber CM. High performance silicon nanowire field effect transistors. Nano Lett. (2003) 3:149–52. doi: 10.1021/nl025875l
12. Thelander C, Agarwal P, Brongersma S, Eymery J, Feiner LF, Forchel A, et al. Nanowire-based one-dimensional electronics. Mater Today (2006) 9:28–35. doi: 10.1016/S1369-7021(06)71651-0
13. Appenzeller J, Knoch J, Bjork MI, Riel H, Schmid H, Riess W. Toward nanowire electronics. IEEE Trans. Electron Devices (2008) 55, 2827–45. doi: 10.1109/TED.2008.2008011
14. Ko H, Takei K, Kapadia R, Chuang S, Fang H, Leu PW, et al. Ultrathin compound semiconductor on insulator layers for high-performance nanoscale transistors. Nature (2010) 468:286–9. doi: 10.1038/nature09541
15. Zhou C, Wang X, Raju S, Lin Z, Villaroman D, Huang B, et al. Low voltage and high ON/OFF ratio field-effect transistors based on CVD MoS2 and ultra high-k gate dielectric PZT. Nanoscale (2015) 7:8695–700. doi: 10.1039/C5NR01072A
16. Theis TN, Solomon PM. It's time to reinvent the transistor! Science (2010) 327:1600–1. doi: 10.1126/science.1187597
17. Salahuddin S Datta, S. Use of negative capacitance to provide voltage amplification for low power nanoscale devices. Nano Lett. (2008) 8: 405–10. doi: 10.1021/nl071804g
18. Frank DJ, Dennard RH, Nowak E, Solomon PM, Taur Y, Wong HSP. Device scaling limits of Si MOSFETs and their application dependencies. Proc IEEE (2001) 89:259–88. doi: 10.1109/5.915374
19. Bernstein K, Frank DJ, Gattiker AE, Haensch W, Ji BL, Nassif SR, et al. High-performance CMOS variability in the 65-nm regime and beyond. IBM J Res Dev. (2006) 50:433–49. doi: 10.1147/rd.504.0433
20. Haensch W, Nowak EJ, Dennard RH, Solomon PM, Bryant A, Dokumaci OH, et al. Silicon CMOS devices beyond scaling. IBM J Res Dev. (2006) 50:339–61. doi: 10.1147/rd.504.0339
21. Ng HT, Han J, Yamada T, Nguyen P, Chen YP, Meyyappan M. Single crystal nanowire vertical surround-gate field-effect transistor. Nano Lett. (2004) 4:1247–52. doi: 10.1021/nl049461z
22. Mott NF, Gurney RW. Electronic Processes in Ionic Crystals. London: Oxford University Press (1940).
23. Ferry DK. Materials science - nanowires in nanoelectronics. Science (2008) 319:579–80. doi: 10.1126/science.1154446
24. Wong HSP. Beyond the conventional transistor. IBM J Res Dev. (2002) 46:133–68. doi: 10.1147/rd.462.0133
25. Kind H, Yan HQ, Messer B, Law M, Yang PD. Nanowire ultraviolet photodetectors and optical switches. Adv Mater. (2002) 14:158–60. doi: 10.1002/1521-4095(20020116)14:2<158::AID-ADMA158>3.0.CO;2-W
26. Soci C, Zhang A, Xiang B, Dayeh SA, Aplin DPR, Park J, et al. ZnO nanowire UV photodetectors with high internal gain. Nano Lett. (2007) 7:1003–9. doi: 10.1021/nl070111x
27. Wang K, Rai SC, Marmon J, Chen J, Yao K, Wozny S, et al. Nearly lattice matched all wurtzite CdSe/ZnTe type II core-shell nanowires with epitaxial interfaces for photovoltaics. Nanoscale (2014) 6:3679–85. doi: 10.1039/c3nr06137j
28. Rai SC, Wang K, Chen JJ, Marmon JK, Bhatt M, Wozny S, et al. Enhanced broad band photodetection through piezo-phototronic effect in CdSe/ZnTe core/shell nanowire array. Adv Electron Mater. (2015) 1:1400050. doi: 10.1002/aelm.201500118
29. Wagner RS, Ellis WC. The vapor-liquid-solid mechanism of crystal growth. Appl Phys Lett. (1964) 4:89–90. doi: 10.1063/1.1753975
31. Shockley W, Pearson GL. Modulation of conductance of thin films of semi-conductors by surface charges. Phys Rev. (1948) 74:232–3. doi: 10.1103/PhysRev.74.232
32. Masson DP, Lockwood DJ, Graham MJ. Thermal oxide on CdSe. J Appl Phys. (1997) 82:1632–9. doi: 10.1063/1.366263
33. Kyung CMEM. Nano Devices and Circuit Techniques for Low-Energy Applications and Energy Harvesting. New York, NY: Springer (2015).
34. Nowak EJ. Maintaining the benefits of CMOS scaling when scaling bogs down. IBM J Res Dev. (2002) 46:169–80. doi: 10.1147/rd.462.0169
36. Huang Y, Duan XF, Cui Y, Lauhon LJ, Kim KH, Lieber CM. (2001). Logic gates and computation from assembled nanowire building blocks. Science (2013) 294:1313–7. doi: 10.1126/science.1066192
37. Shive JN. The properties of germanium phototransistors. J Opt Soc Am. (1953) 43:239–44. doi: 10.1364/JOSA.43.000239
38. Tucker RS. The role of optics in computing. Nat Photon (2010) 4:405. doi: 10.1038/nphoton.2010.162
39. Tung RT. The physics and chemistry of the Schottky barrier height. Appl Phys Rev. (2014) 1:011304. doi: 10.1063/1.4858400
40. Zhao YJ, Tanaka S, Pan CC, Fujito K, Feezell D, Speck JS, et al. (2011). High-power blue-violet semipolar (2021) InGaN/GaN light-emitting diodes with low efficiency droop at 200 A/cm2. Appl Phys Express 4:082104. doi: 10.1143/APEX.4.082104
41. Schuck PJ, Weber-Bargioni A, Ashby PD, Ogletree DF, Schwartzberg A, Cabrini S. Life beyond diffraction: opening new routes to materials characterization with next-generation optical near-field approaches. Adv Funct Mater. (2013) 23:2539–53. doi: 10.1002/adfm.201203432
42. Weber B, Mahapatra S, Ryu H, Lee S, Fuhrer A, Reusch TCG, et al. Ohm's law survives to the atomic scale. Science (2012) 335:64–7. doi: 10.1126/science.1214319
43. Kurniawan O, Ng MF, Koh WS, Leong ZY, Li E. Simplified model for ballistic current-voltage characteristic in cylindrical nanowires. Microelectron J. (2010) 41:155–61. doi: 10.1016/j.mejo.2010.01.013
Keywords: light-effect transistor, Field-effect transistor, Moore's law, II-VI semiconductor, CdSe nanowire, optical logic gate, optical amplification, metal-semiconductor-metals
Citation: Marmon JK, Rai SC, Wang K, Zhou W and Zhang Y (2016) Light-Effect Transistor (LET) with Multiple Independent Gating Controls for Optical Logic Gates and Optical Amplification. Front. Phys. 4:8. doi: 10.3389/fphy.2016.00008
Received: 23 January 2016; Accepted: 03 March 2016;
Published: 21 March 2016.
Edited by:
Qiyin Fang, McMaster University, CanadaReviewed by:
Munir El-Desouki, King Abdulaziz City for Science and Technology, Saudi ArabiaDarek Palubiak, EnviroSen Inc., Canada
Copyright © 2016 Marmon, Rai, Wang, Zhou and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yong Zhang, yong.zhang@uncc.edu;
Weilie Zhou, wzhou@uno.edu
 Jason K. Marmon1,2,3
Jason K. Marmon1,2,3  Kai Wang
Kai Wang Yong Zhang
Yong Zhang