- Department of Bioengineering, Rice University, Houston, TX, USA
We review methods of understanding cellular interactions through computation in order to guide the synthetic design of mammalian cells for translational applications, such as regenerative medicine and cancer therapies. In doing so, we argue that the challenges of engineering mammalian cells provide a prime opportunity to leverage advances in computational systems biology. We support this claim systematically, by addressing each of the principal challenges to existing synthetic bioengineering approaches—stochasticity, complexity, and scale—with specific methods and paradigms in systems biology. Moreover, we characterize a key set of diverse computational techniques, including agent-based modeling, Bayesian network analysis, graph theory, and Gillespie simulations, with specific utility toward synthetic biology. Lastly, we examine the mammalian applications of synthetic biology for medicine and health, and how computational systems biology can aid in the continued development of these applications.
Introduction and Overview
Over the past three decades, rapid advances in computational power, subcellular data resolution, and the sophistication of bioengineering design has led to cellular machinery being increasingly controlled for practical application (Buetow, 2005; Cheng, 2007; Vendruscolo and Dobson, 2011). The advent of this field of “synthetic biology” has been touted as a reservoir of novel solutions for many of society's most pressing problems, including challenges in computing, health, and regenerative medicine (Gersbach et al., 2007; Lu et al., 2009; Ruder et al., 2011). For instance, the creation of the first-ever genetic toggle switch and the repressilator by synthetic biologists at the turn of the century allowed for an unprecedented degree of cellular control—and, in the case of the former, a digital state that could lay the groundwork for organic computing (Elowitz and Leibler, 2000; Gardner et al., 2000). In subsequent years, biologists constructed oscillators (capable of biological timekeeping), pulse generators (for transcellular signal transmission), and even signaling filters (for cellular signal processing) through carefully mapped gene circuits (Basu et al., 2004, 2005; Stricker et al., 2008; Khalil and Collins, 2010).
However, while each of these individual discoveries led to numerous applications of genetic engineering in biomedicine, we still lack tools with the robustness required for transformative applications. For instance, true “plug-and-play” cellular machines remain a work in progress, in part due to the heterogeneity and adaptability of biological networks (Kobayashi et al., 2004; Arkin, 2008). The routine engineering of mammalian cells, too, is still a distant possibility (Khalil and Collins, 2010). Because synthetic biology has largely been applied to microbes due to mammalian cell complexity, its impact on medicine has been limited.
Achieving these benchmarks is admittedly easier said than done. Whereas the promises and potential of the synthetic biology field lie in characterizing the cellular alphabet, the puzzle of words and sentences that define cell signaling and behavior currently present a higher order of complexity (Endy, 2005). Moreover, the field of synthetic biology is still in its infancy, compared to the equivalent of “the Wright brothers … putting pieces of wood and paper together” (Kwok, 2010). Some leading researchers have even suggested that “the complexity of synthetic biological systems over the past decade has reached a plateau” (Purnick and Weiss, 2009).
One way biologists have started to reinvigorate the field is through advances in combinatorial logic-based circuits (Lu et al., 2009; Wang et al., 2011; Michelotti et al., 2012; Wang and Buck, 2012). These formalisms possess the distinct advantages of providing a standardized framework that is adaptable across levels of abstraction as well as dynamical properties that can be estimated and combined by straightforward mathematical operations. Showing early progress, combinatorial logic-based circuits have been designed into sophisticated information processing tools in clonal mammalian cells like HeLa and MCF-7 (Xie et al., 2011; Nevozhay et al., 2013). However, noise, heterogeneity, complexity of structure, and time-dependent rewiring across biological scales limit the degree of control enabled by these experimental methods (Purnick and Weiss, 2009; Kwok, 2010). We propose that these challenges can be tackled by capitalizing on advances in computational systems biology that are uniquely valuable for synthetic cell design. We argue that a new perspective on the role of systems modeling in synthetic biology can promote the development of new therapies for human health by enabling the complex design capability required for mammalian cell engineering.
Computational Techniques and Advances: Systems Biology Applications
Computational methods are widely employed within synthetic biology as design tools, providing simulations of bioengineered systems in advance of their cellular assembly (Chandran et al., 2009; Ellis et al., 2009; Purnick and Weiss, 2009; Smolke and Silver, 2011) (Figure 1). Historically, these coupled computational-experimental approaches have contributed to many of the “milestone” discoveries in the field over the past two decades (Table 1). However, modeling used in synthetic biology until now has been generally limited to biocircuits and control systems, in part because the field emerged from genetic engineering where circuit representations are common (Mukherji and van Oudenaarden, 2009). The consequence of this limited paradigm is that significant advances in human health from this field remain out of reach, as gene circuit models prove to be increasingly insufficient for characterizing mammalian cell behavior (Purnick and Weiss, 2009).
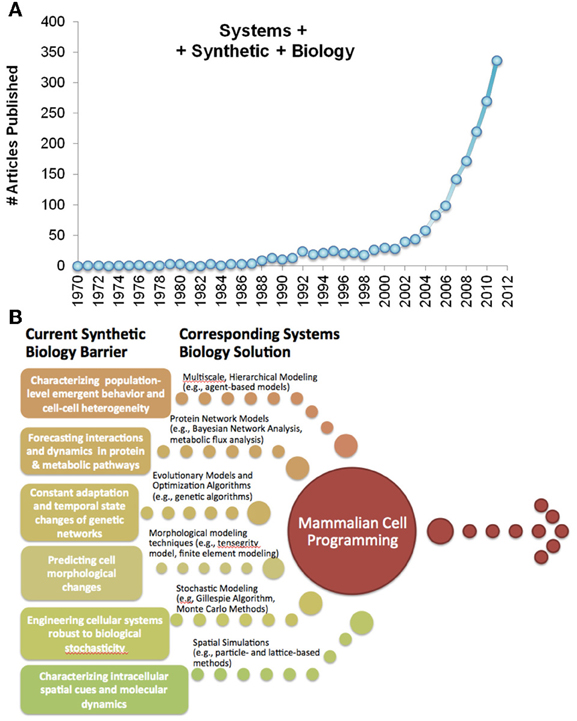
Figure 1. (A) PUBMED references to Systems and Synthetic biology over the last four decades. (B) Recent advances in systems biology can be applied toward surmounting specific limitations to existing synthetic biology, paving the way to mammalian cell engineering.
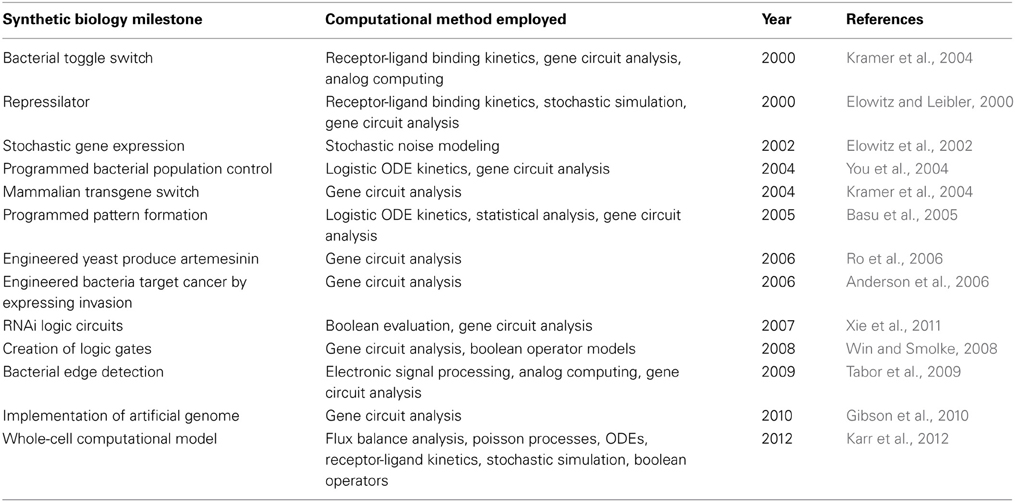
Table 1. Synthetic biology milestones employing computational methods, as well as those that were built conceptually from computational paradigms.
In the aggregate, this “insufficiency” stems from a set of core properties of biological systems that current synthetic approaches do not fully capture: (1) scale, with the need to elicit controlled behavior across cell, tissue, and organ levels (Miller et al., 2012); (2) simultaneity, as defined by the highly networked nature of cell signaling (Jeong et al., 2000, 2001; Marcotte, 2001); (3) state adaptation dynamics, or the non-linear temporal fluctuations of such networks (Slusarczyk et al., 2012); (4) shape, due to the relevance of cell morphology in defining environmental interactions (Ben-Ze'ev et al., 1988; Singhvi et al., 1994); (5) stochasticity, with noise and randomness being significant determinants of cellular behavior (Thattai and van Oudenaarden, 2001; Pedraza and van Oudenaarden, 2005; Chopra and Kamma, 2006; Purnick and Weiss, 2009); and (6) spatial dependencies, both intracellular and extracellular in nature (Andrianantoandro et al., 2006). With the present focus on microbial engineering, many of these characteristics can be safely neglected; at mammalian levels of complexity, they render the behavior of synthetic systems difficult to predict a priori.
Although these challenges are manifold, they are not insurmountable. The answers may lie in systems biology. This computational discipline seeks to shift the basic molecular biology paradigm from isolation to coordination: from characterizing individual components of cell behavior to analyzing how these components function in tandem (Kitano, 2002a,b). Accordingly, systems bioengineers bring a diverse array of computational modeling techniques—drawing on mathematics, computer science, and engineering—to bear on questions of both mechanism and design at the cell and tissue levels (Kitano, 2001; Alon, 2007). In doing so, the field provides computational tools to characterize behavioral patterns at the cellular level that will be the building blocks of more sophisticated synthetic design. Systems biology approaches are particularly powerful in characterizing cell–cell interactions across scales, such as in capillary patterning and organ development, where the gene circuits approach in synthetic biology has proven limited in capturing adaptation, cellular heterogeneity and spatial hierarchy (Yingling et al., 2005; Qutub et al., 2009; Long et al., 2013). As such, many of the challenges to applying synthetic biology toward controlling mammalian tissue can be addressed in part by methods and techniques that are well-developed in systems bioengineering. Here, we discuss each of these roadblocks categorically, with the associated tools to address them.
Scale: Hierarchical, Agent-Based Modeling, and Rule-Based Formalisms
Characterizing population-level emergent behavior and cell–cell heterogeneity has long been recognized as a principal goal and challenge in synthetic biology (Canton et al., 2008; Neumann and Neumann-Staubitz, 2010; Young and Alper, 2010). Traditional synthetic designs have assumed identical expression patterns across a cell population, as the standard biocircuit framework does not permit the simulation of cell behavioral variability (Elowitz et al., 2002; Ozbudak et al., 2002; Blake et al., 2003; You et al., 2004). Moreover, the limited capacity for gene circuit models to characterize emergent behavior—defined formally as patterns that emerge from a myriad of relatively simple interactions—inhibits scale-dependent design (Benner and Sismour, 2005). As a mammalian example, if intricate cerebral function results from the coordinated function of millions of individual neurons, any synthetic design applied to the brain must first require accurate simulations of how neural cell-level changes manifest on the cerebral tissue-level. Deriving such scale-driven causal links from observed principles is non-trivial at best.
One systems biology method to address the research challenge of emergence in biology is agent-based modeling. The approach has a simple premise: such systems exhibit emergent behavior that arises from the interactions between individual actors (or agents) and, consequently, would be impossible to know a priori (Chandran et al., 2009). An agent is defined here as a discrete entity that has behavior, can adapt, carries “genetic codes,” holds variables and data, is governed by individual rules, and is spatially defined. Fundamentally, this class of modeling method diverges from biocircuit models, which typically characterize fluctuations in state variables governed by differential relationships. Supplanting the latter's top-down, intracellular perspective with the former's bottom-up, multi-scale viewpoint permits the simulation of heterogeneity while eliminating the need to derive inter-scale relationships beforehand (Chandran et al., 2009).
Notably, agent-based modeling encompasses a broad range of variations in implementation, rather than any specific algorithm or rule-set. Existing libraries, such as MASON, Repast, and Swarm, allow for the construction of multi-scale agent-based models atop adaptable frameworks, facilitating their use by synthetic biologists with limited prior exposure to the technique. This methodology has been employed toward modeling brain capillary regeneration (Long et al., 2013), immunological and inflammatory responses (Bailey et al., 2007; Chandran et al., 2009; Pothen et al., 2013), and cancer progression (Wang et al., 2009; Basanta et al., 2012; Wodarz et al., 2012; Walker and Southgate, 2013), among other topics. Within synthetic biology specifically, agent-based models have also simulated tissue development, tissue formation, and microbial chemotaxis (Endler et al., 2009).
Similarly rule-based formalisms are also being applied to coarse-grain patterns in chemical-kinetic models (Feret et al., 2009; Yang et al., 2010), providing scalable tools to describe complex interactions in cellular systems that begin at the molecular level.
Simultaneity: Graph Theory and Network Analysis
Forecasting interactions and dynamics in protein and metabolic pathways is crucial for fine-tuned control of mammalian synthetic bioengineering. Whereas traditional kinetic- and gene circuit-based methods use simplified pathways to represent these signaling dynamics, in many cases the relationships between molecules are highly non-linear (Marcotte, 2001) and multiplex, i.e., multiple inputs combine to a single output. Signals that propagate from A->B->C at regular intervals are rare; more common are those for which such variations as A->C<->B and B->A->C->A dictate the targeted result, with time- and state-dependent transitions (Kestler and Kühl, 2008). Common, too, are linkages between parallel molecular pathways that each simultaneously affect the output of the other (Jeong et al., 2000, 2001). These oscillations render more complex cell pathways intractable for traditional biocircuit methods, which are generally based on small set of ordinary differential equations (ODEs) (Kestler and Kühl, 2008).
Several types of network models allow for better predictive simulation of these multiplex interactions. Graph methods, for example, are a class of models that represent pathway components as networked nodes, and graph-based approaches have been used to model cellular machinery including genes, proteins and other subcellular compartments (Ma'ayan et al., 2005; Pe'er, 2005). The interactions between components are drawn as edge connections between the relevant nodes (Ma'ayan et al., 2005). Graph-based models vary in implementation to capture different kinds of molecular relationships (e.g., Boolean gene expression, stochastic transitions between molecular states), but are all particularly adept at identifying complex network modules, or certain structural features that “dominate” the behavior of the larger network. In mammalian cells, as an example, researchers have had early success in characterizing the dynamics of key feedforward modules and motifs, helping to enable the circuit design of adaptive gene expression (Bleris et al., 2011).
One common type of acyclic graph method, known as Bayesian Network Analysis, is a form of directed statistical modeling designed to capture conditional dependencies between probabilistic events (Pe'er, 2005). In a Bayesian network model, probabilities define the relationship between the current node and its predecessor or parent in a graph (Alterovitz et al., 2007). Markov models are another network-based technique that can provide a framework to describe molecular or cellular states and the weighted probability of transitioning between them. The power of these methods lies in their ability to facilitate the reverse engineering of multiplex networks based on molecular expression, molecular activity and/or cell behavior data, serving as a precursor to synthetic modifications of existing molecular pathways (Barnes et al., 2011). However, for gene or protein pathways with more complex topology—such as those examples offered above—cyclic graph models might be necessary, for which a variety of analytical tools and approaches are described by computational biologists in the literature (particularly from research on neural networks) (Bianchini et al., 2006; Scarselli et al., 2009; Bowsher, 2010; Bonnet et al., 2013).
State Adaptation Dynamics: Evolutionary Models, Optimization Algorithms
In parallel with the above techniques, another suite of computational methods permits not only the analysis of cellular pathways, but also directly facilitates their synthetic design. Known as evolutionary algorithms, these methods can predict state changes in the behavior of signaling pathways over time, through adaptation or random mutation, by modeling this rewiring directly (Hallinan et al., 2010; Chen et al., 2011; Mobashir et al., 2012). In the same vein, these methods allow for the de novo construction and optimization of genetic networks by way of simulation (Bloom and Arnold, 2009), “evolving” a set of viable pathway designs that meet the specified constraints (Hallinan et al., 2010). Though these algorithms vary in construction, a subset of methods known as genetic algorithms—in which populations of potential networks “compete” against each other—are of particular utility to synthetic biologists due to their ease-of-implementation (Mitchell, 1998). Many alternative optimization techniques exist, e.g., simulated annealing, hill climbing, and gradient descent, which can be applied to optimize synthetic network architectures and the design of synthetic constructs (Zomaya and Kazman, 2010). In addition to these, combinatorial “tuning” strategies have been successfully applied toward model-guided, programmable control of gene expression in mammalian cells via RNAi (Beisel et al., 2008). A unique advantage of evolutionary and optimization algorithms is their ability to (A) be applied broadly to many forms of models, including ODEs and rule-based simulations and (B) generate a diverse array of functional network topologies.
Shape: Morphological Modeling and Computational Cell Phenotyping
Thus, far, synthetic biology research has largely omitted studies on cell shape. The few exceptions in the literature focus on morphological properties as reporters for specific signaling cascades or to control specific spatial features (Yeh et al., 2007; Tanaka and Yi, 2009). For instance, one recent work described controlled shape changes of synthetic yeast cells (Tanaka and Yi, 2009). Rather than modeling how a gene circuit would induce specific cell morphology a priori, the study's authors varied α-factor pathway inputs to observe shape changes until the desired shape was achieved—in this case, one that upregulated the formation of mating projections (Tanaka and Yi, 2009). Another study scored filopodial and lamellipodial phenotypes as indicators for successful synthetic rewiring of Rho GTPase signaling (Yeh et al., 2007).
Despite the few studies in this area, cell morphology is often a characteristic of central importance to synthetic biology experiments. For instance, synthetic systems seeking to modulate cell–cell interactions must necessarily account for morphological and spatial-dependent interactions between cells (Ben-Ze'ev et al., 1988; Singhvi et al., 1994). These membrane adjacency and receptor localization are drivers of pathways like Delta-Notch signaling, in which a signaling cascade is triggered by the binding of two transmembrane proteins on adjacent cells (Appel et al., 2001). Moreover, cell behavior—and at a higher scale, tissue functionality—is often predicated on geometry (Haeuptle et al., 1983). For example, optimizing a synthetic cell for metabolic filtration necessitates that its membrane surface area be maximized for nutrient exchange, such as through inward folds (Gahan, 2005). Doing so requires leveraging computational modeling to predict three-dimensional shape response to changes in genetic circuit design.
Examples of methods for geometrical-rendered modeling of cells include tensegrity models, Voronoi-based simulations, and molecular dynamics models. The concept of “tensegrity” stems from geodesic design, in which an object's shape is maintained through the joint effect of structural members in continuous tension and those in discontinuous compression (Huang et al., 2006). Though abstract in concept, computational models of tensegrity have been demonstrated to approximate cell shape and mechanics, providing a representation for simulating cell morphology in vitro (Huang et al., 2006). Tensegrity principles have been used to represent cytoskeletal elements, allowing for changes in these proteins induced by regulatory networks (e.g., focal adhesion kinases) to be assessed for their effects on cell shape (Kardas et al., 2013). An alternative geometrical model is the Voronoi diagram, a mathematical concept of dividing space into distinct regions based on proximity to initial seed points. Voronoi diagrams provide a useful means of constraining complex cell shapes into adjacent spatial tessellations, a technique particularly useful to study patterning at the cell population- or tissue-level (Schaller and Meyer-Hermann, 2005; Luengo-Oroz et al., 2008). Lastly, molecular dynamics simulations of cell shape represent cells as collections of individual molecules in Newtonian motion, either abstractly (as particles) or concretely (as cytoskeletal elements), to model an agglomerated cellular structure at high resolution—albeit at greater computational cost (Rapaport, 2004; Pfaendtner et al., 2010).
Linking geometric-based models to gene network simulations offers the opportunity to guide synthetic biocircuit design in silico such that specific cell morphologies can be engineered. Previously, this method has led to a complete representation of osteocyte cytoskeleton dynamics (Kardas et al., 2013). In conjunction, computational cell phenotyping enables changes in morphology to be quantitatively measured and tracked, such that the desired design can be achieved. Phenotyping techniques couple high-fidelity cell imaging with processing metrics to parse shape information (Chung et al., 2008; Sozzani and Benfey, 2011; Ryan et al., 2013). These shape metrics can facilitate the computer-aided design of synthetic networks.
Stochasticity: Gillespie Algorithm and Monte Carlo Methods
Perhaps the most significant research challenge in synthetic bioengineering is enabling the design of cellular systems that are robust to biological stochasticity (Chopra and Kamma, 2006; Purnick and Weiss, 2009). Existing gene circuit models are largely deterministic, behaving in highly reproducible ways. These models, as alluded to previously, present regulatory networks as homogeneous concentrations of molecules modulated by parameterized rate constants through coupled differential equations.
Yet there exists increasing evidence that biological networks and intracellular behavior are innately stochastic (Thattai and van Oudenaarden, 2001). Whereas noise effects are often assumed to be negligible at the population level, noise can play a significant role at the single-cell level, e.g., where a small number of molecular interactions may trigger a cascade of downstream protein signaling (Thattai and van Oudenaarden, 2001; Pedraza and van Oudenaarden, 2005). Furthermore, research indicates the phenomenon of noise propagation, in which cell-level stochasticity can accrue at the population-level to create emergent behavior that deviates substantially from the desired target, a phenomena recently documented in E. Coli, leading to a loss of synchrony between cells (Hooshangi et al., 2005; Hornung and Barkai, 2008). Such studies suggest that complex synthetic systems cannot be engineered without first accounting for stochasticity in the circuit design.
Fortunately, there exist a wide variety of computational techniques to capture and predict this biological stochasticity at the systems level. One specific approach, known as the Gillespie Algorithm, rejects the deterministic ODE approach of modeling chemical-kinetics in favor of stochastic representations of molecular interactions (Gillespie, 2007). This algorithm explicitly simulates each “reaction” (or interaction event) along a network, with the probability of a successful “reaction” dependent on both the rate properties and a random walk (Gillespie, 2007). For synthetic biology applications, these reactions can be defined as discrete regulatory steps along a specific gene circuit, allowing the effects of noise along the circuit to be well-characterized.
The Gillespie algorithm belongs to a larger class of stochastic modeling techniques known as Monte Carlo methods, which can be adapted to suit the needs of a specific biocircuit design (Athale, 2001). Monte Carlo methods, while varied in implementation, share the property of employing random simulations over many iterations to quantify properties of biological systems.
Spatial Dependencies: Particle- and Lattice-Based Methods
Traditional synthetic biology designs are based on assumptions of biochemically homogenous cell interiors, but for gene circuit designs of higher complexity, this set of assumptions is unlikely to hold (Agapakis et al., 2012). Often, the spatial information associated with a protein or pathway inside the cell can influence the end-behavior of a molecular network (Agapakis et al., 2012). In addition to variations in metabolic conditions (e.g., pH levels), spatial cues can also present as receptor- or organelle- localization, intracellular polarity, and even topological sequestration (Harold, 1991; Roze et al., 2011; Lee et al., 2012). Characterizing intracellular spatial dependences and molecular dynamics becomes particularly important in mammalian cells, for which fine spatial organization of regulatory pathways is commonplace.
To this end, particle- and lattice-based computational techniques can be employed to model spatial systems within a synthetic cell (Spicher et al., 2011; Klann and Koeppl, 2012). Rather than simulate bulk flow, particle-based models track molecules separately and in discrete quantities (Takahashi et al., 2005), as alluded to above in the description of molecular dynamic models (see the Shape section). In systems biology, such methods have already been applied toward characterizing single-cell gradient sensing in the presence of multiple competitive ligands (Liou and Chen, 2012). Particle models could be similarly applicable to synthetic biology in engineering mammalian cells to function as fine-tuned hypoxic or nitric oxide sensors, in an effort to minimize effects of ischemic stroke—to name just one instance.
The complexity of particle models is mitigated by the availability of open source simulators, including E-Cell and ChemCell (Klann and Koeppl, 2012). Many of these implementations also allow particle simulations to be combined with models of other classes. As an example, a spatial derivative of the Gillespie algorithm can integrate stochastic modeling with space-dependent computation (Takahashi et al., 2005).
Spatial modeling can also be performed using PDE models; examples include gene circuits defining chemical diffusion-mediated interactions between localized cell populations (Song et al., 2009). In other applications to synthetic biology, these spatial techniques have been combined with mechanistic models, such as kinetic RNA folding simulations, to provide fine-tuned control of gene expression along a specific component of a regulatory pathway (Carothers et al., 2011). PDE formalisms offer relative simplicity of construction compared to other spatiotemporal methods, with the caveat of not being well-suited to highly heterogeneous spatial environments.
Applications for Mammalian Cells and Human Health
Until now, the overwhelming focus of research and progress in synthetic biology has been on prokaryotic cells: mostly bacteria (commonly E. Coli) and assorted microbes. This is a natural consequence of the knowledge gap described previously; prokaryotic cells are orders of magnitude simpler than eukaryotic ones—not to mention easier to manipulate. They could be said to represent the “crawling” stage of synthetic biology. However, if the ultimate goal of the discipline is to uncover novel therapeutic targets and treatments in biomedicine, such strict characterization of non-mammalian systems will restrain our ability to advance human health. In the end, we must learn to walk.
To do so means confronting the complexity that the in vivo mammalian system brings. Methods already employed in systems biology to characterize this complexity can open up the boundaries of modern medicine. As an example, it is not difficult to imagine a future where computational models enable the design of synthetic neural progenitor cells programmed to promote recovery post-ischemic stroke. To foster an era of personalized medicine, this potential could revolutionize the manner in which we approach tissue engineering: cells grown en masse, and then programmed to meet the specific needs of the patient. Moreover, such customizable cells would permit targeted regeneration to a degree that simple stem cell treatments cannot achieve. Such innovations, while distant, are attainable, but they necessitate the coupling of systems approaches with synthetic biology.
Concluding Comments
Bringing the sister disciplines of synthetic and systems biology closer together could recast the gene circuit paradigm, and enhance our ability to engineer and program cells for applications across energy, computing and biomedicine. Leveraging a computational toolkit refined by systems biologists for the last half-century offers a unique catalyst that to help pave the future of synthetic biology.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Agapakis, C. M., Boyle, P. M., and Silver, P. A. (2012). Natural strategies for the spatial optimization of metabolism in synthetic biology. Nat. Chem. Biol. 8, 527–535. doi: 10.1038/nchembio.975
Alon, U. (2007). An Introduction to Systems Biology: Design Principles of Biological Circuits. Chapman and Hall/CRC Press.
Alterovitz, G., Liu, J., Afkhami, E., and Ramoni, M. F. (2007). Bayesian methods for proteomics. Proteomics 7, 2843–2855. doi: 10.1002/pmic.200700422
An, G., Mi, Q., Dutta−Moscato, J., and Vodovotz, Y. (2009). Agent−based models in translational systems biology. Wiley Interdiscip. Rev. Syst. Biol. Med. 1, 159–171. doi: 10.1002/wsbm.45
Anderson, J. C., Clarke, E. J., Arkin, A. P., and Voigt, C. A. (2006). Environmentally controlled invasion of cancer cells by engineered bacteria. J. Mol. Biol. 355, 619–627. doi: 10.1016/j.jmb.2005.10.076
Andrianantoandro, E., Basu, S., Karig, D. K., and Weiss, R. (2006). Synthetic biology: new engineering rules for an emerging discipline. Mol. Syst. Biol. 2, 10–13. doi: 10.1038/msb4100073
Appel, B., Givan, L. A., and Eisen, J. (2001). Delta-Notch signaling and lateral inhibition in zebrafish spinal cord development. BMC Dev. Biol. 1:13. doi: 10.1186/1471-213X-1-13
Arkin, A. (2008). Setting the standard in synthetic biology. Nat. Biotechnol. 26, 771–773. doi: 10.1038/nbt0708-771
Athale, C. (2001). Monte Carlo cell simulations. Genome Biol. 3:reports2001. doi: 10.1186/gb-2001-3-1-reports2001
Bailey, A. M., Thorne, B. C., and Peirce, S. M. (2007). Multi-cell agent-based simulation of the microvasculature to study the dynamics of circulating inflammatory cell trafficking. Ann. Biomed. Eng. 35, 916–936. doi: 10.1007/s10439-007-9266-1
Barnes, C. P., Silk, D., Sheng, X., and Stumpf, M. P. H. (2011). Bayesian design of synthetic biological systems. Proc. Natl. Acad. Sci. U.S.A. 108, 8645–8650. doi: 10.1073/pnas.1017972108
Basanta, D., Gatenby, R. A., and Anderson, A. R. A. (2012). Exploiting evolution to treat drug resistance: combination therapy and the double bind. Mol. Pharm. 9, 914–921. doi: 10.1021/mp200458e
Basu, S., Gerchman, Y., Collins, C. H., Arnold, F. H., and Weiss, R. (2005). A synthetic multicellular system for programmed pattern formation. Nature 434, 1130–1134. doi: 10.1038/nature03461
Basu, S., Mehreja, R., Thiberge, S., Chen, M.-T., and Weiss, R. (2004). Spatiotemporal control of gene expression with pulse-generating networks. Proc. Natl. Acad. Sci. U.S.A. 101, 6355–6360. doi: 10.1073/pnas.0307571101
Beisel, C. L., Bayer, T. S., Hoff, K. G., and Smolke, C. D. (2008). Model-guided design of ligand-regulated RNAi for programmable control of gene expression. Mol. Syst. Biol. 4, 1–13. doi: 10.1038/msb.2008.62
Benner, S. A., and Sismour, A. M. (2005). Synthetic biology. Nat. Rev. Genet. 6, 533–543. doi: 10.1038/nrg1637
Ben-Ze'ev, A., Robinson, G. S., Bucher, N. L., and Farmer, S. R. (1988). Cell–cell and cell-matrix interactions differentially regulate the expression of hepatic and cytoskeletal genes in primary cultures of rat hepatocytes. Proc. Natl. Acad. Sci. U.S.A. 85, 2161–2165. doi: 10.1073/pnas.85.7.2161
Bianchini, M., Gori, M., Sarti, L., and Scarselli, F. (2006). Recursive processing of cyclic graphs. IEEE Trans. Neural Netw. 17, 10–18. doi: 10.1109/TNN.2005.860873
Blake, W. J., KAErn, M., Cantor, C. R., and Collins, J. J. (2003). Noise in eukaryotic gene expression. Nature 422, 633–637. doi: 10.1038/nature01546
Bleris, L., Xie, Z., Glass, D., Adadey, A., Sontag, E., and Benenson, Y. (2011). Synthetic incoherent feedforward circuits show adaptation to the amount of their genetic template. Mol. Syst. Biol. 7, 1–12. doi: 10.1038/msb.2011.49
Bloom, J. D., and Arnold, F. H. (2009). In the light of directed evolution: pathways of adaptive protein evolution. Proc. Natl. Acad. Sci. U.S.A. 106, 9995–10000. doi: 10.1073/pnas.0901522106
Bonnet, E., Calzone, L., Rovera, D., Stoll, G., Barillot, E., and Zinovyev, A. (2013). BiNoM 2.0, a Cytoscape plugin for accessing and analyzing pathways using standard systems biology formats. BMC Syst. Biol. 7:18. doi: 10.1186/1752-0509-7-18
Bowsher, C. G. (2010). Stochastic kinetic models: dynamic independence, modularity and graphs. Ann. Stat. 38, 2242–2281. doi: 10.1214/09-AOS779
Buetow, K. H. (2005). Cyberinfrastructure: empowering a “third way” in biomedical research. Science 308, 821–824. doi: 10.1126/science.1112120
Canton, B., Labno, A., and Endy, D. (2008). Refinement and standardization of synthetic biological parts and devices. Nat. Biotechnol. 26, 787–793. doi: 10.1038/nbt1413
Carothers, J. M., Goler, J. A., Juminaga, D., and Keasling, J. D. (2011). Model-driven engineering of RNA devices to quantitatively program gene expression. Science 334, 1716–1719. doi: 10.1126/science.1212209
Chandran, D., Copeland, W. B., Sleight, S. C., and Sauro, H. M. (2009). Mathematical modeling and synthetic biology. Drug Discov. Today Dis. Models 5, 299–309. doi: 10.1016/j.ddmod.2009.07.002
Chen, B.-S., Hsu, C.-Y., and Liou, J.-J. (2011). Robust design of biological circuits: evolutionary systems biology approach. J. Biomed. Biotechnol. 2011:304236. doi: 10.1155/2011/304236
Cheng, T. (2007). Moore's law meets the life sciences. IEEE Des. Test Comput. 24, 4. doi: 10.1109/MDT.2007.23
Chopra, P., and Kamma, A. (2006). Engineering life through synthetic biology. In Silico Biol. 6, 401–410.
Chung, K., Crane, M. M., and Lu, H. (2008). Automated on-chip rapid microscopy, phenotyping and sorting of C. elegans. Nat. Methods 5, 637–643. doi: 10.1038/nmeth.1227
Ellis, T., Wang, X., and Collins, J. J. (2009). Diversity-based, model-guided construction of synthetic gene networks with predicted functions. Nat. Biotechnol. 27, 465–471. doi: 10.1038/nbt.1536
Elowitz, M. B., and Leibler, S. (2000). A synthetic oscillatory network of transcriptional regulators. Nature 403, 335–338. doi: 10.1038/35002125
Elowitz, M. B., Levine, A. J., Siggia, E. D., and Swain, P. S. (2002). Stochastic gene expression in a single cell. Science 297, 1183–1186. doi: 10.1126/science.1070919
Endler, L., Rodriguez, N., Juty, N., Chelliah, V., Laibe, C., and Li, C. (2009). Designing and encoding models for synthetic biology. J. R. Soc. Interface 6, S405–S417. doi: 10.1098/rsif.2009.0035.focus
Feret, J., Danos, V., Krivine, J., Harmer, R., and Fontana, W. (2009). Internal coarse-graining of molecular systems. Proc. Natl. Acad. Sci. U.S.A. 106, 6453–6458. doi: 10.1073/pnas.0809908106
Gahan, P. B. (2005). Life: the science of biology (7th edn) W. K. Purves, D. Sadava, G. H. Orians and H. C. Heller, W. H. Freeman and Co, 1121 pp., ISBN 0-7167-9856-5 (2004). Cell Biochem. Funct. 23, 221. doi: 10.1002/cbf.1179
Gardner, T. S., Cantor, C. R., and Collins, J. J. (2000). Construction of a genetic toggle switch in Escherichia coli. Nature 403, 339–342. doi: 10.1038/35002131
Gersbach, C. A., Phillips, J. E., and García, A. J. (2007). Genetic engineering for skeletal regenerative medicine. Annu. Rev. Biomed. Eng. 9, 87–119. doi: 10.1146/annurev.bioeng.9.060906.151949
Gibson, D. G., Glass, J. I., Lartigue, C., Noskov, V. N., Chuang, R.-Y., and Algire, M. A. (2010). Creation of a bacterial cell controlled by a chemically synthesized genome. Science 329, 52–56. doi: 10.1126/science.1190719
Gillespie, D. T. (2007). Stochastic simulation of chemical kinetics. Annu. Rev. Phys. Chem. 58, 35–55. doi: 10.1146/annurev.physchem.58.032806.104637
Haeuptle, M. T., Suard, Y. L., Bogenmann, E., Reggio, H., Racine, L., and Kraehenbuhl, J. P. (1983). Effect of cell shape change on the function and differentiation of rabbit mammary cells in culture. J. Cell Biol. 96, 1425–1434. doi: 10.1083/jcb.96.5.1425
Hallinan, J. S., Misirli, G., and Wipat, A. (2010). Evolutionary computation for the design of a stochastic switch for synthetic genetic circuits. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2010, 768–774. doi: 10.1109/IEMBS.2010.5626353
Harold, F. M. (1991). Biochemical topology: from vectorial metabolism to morphogenesis. Biosci. Rep. 11, 347–382. discussion: 382–385. doi: 10.1007/BF01130213
Hooshangi, S., Thiberge, S., and Weiss, R. (2005). Ultrasensitivity and noise propagation in a synthetic transcriptional cascade. Proc. Natl. Acad. Sci. U.S.A. 102, 3581–3586. doi: 10.1073/pnas.0408507102
Hornung, G., and Barkai, N. (2008). Noise propagation and signaling sensitivity in biological networks: a role for positive feedback. PLoS Comput. Biol. 4:e8. doi: 10.1371/journal.pcbi.0040008
Huang, S., Sultan, C., and Ingber, D. (2006). “Tensegrity, dynamic networks, and complex systems biology: emergence in structural and information networks within living cells,” in Complex Systems Science in Biomedicine, eds T. S. Deisboeck and J. Y. Kresh (Springer), 283–310. doi: 10.1007/978-0-387-33532-2_11
Jeong, H., Mason, S. P., Barabási, A.-L., and Oltvai, Z. N. (2001). Lethality and centrality in protein networks. Nature 411, 41–42. doi: 10.1038/35075138
Jeong, H., Tombor, B., Albert, R., Oltvai, Z. N., and Barabási, A.-L. (2000). The large-scale organization of metabolic networks. Nature 407, 651–654. doi: 10.1038/35036627
Kardas, D., Nackenhorst, U., and Balzani, D. (2013). Computational model for the cell-mechanical response of the osteocyte cytoskeleton based on self-stabilizing tensegrity structures. Biomech. Model. Mechanobiol. 12, 167–183. doi: 10.1007/s10237-012-0390-y
Karr, J. R., Sanghvi, J. C., Macklin, D. N., Gutschow, M. V., Jacobs, J. M., and Bolival, B. (2012). A whole-cell computational model predicts phenotype from genotype. Cell 150, 389–401. doi: 10.1016/j.cell.2012.05.044
Kestler, H. A., and Kühl, M. (2008). From individual Wnt pathways towards a Wnt signalling network. Philos. Trans. R. Soc. B Biol. Sci. 363, 1333–1347. doi: 10.1098/rstb.2007.2251
Khalil, A. S., and Collins, J. J. (2010). Synthetic biology: applications come of age. Nat. Rev. Genet. 11, 367–379. doi: 10.1038/nrg2775
Kitano, H. (2002a). Systems biology: a brief overview. Science 295, 1662–1664. doi: 10.1126/science.1069492
Klann, M., and Koeppl, H. (2012). Spatial simulations in systems biology: from molecules to cells. Int. J. Mol. Sci. 13, 7798–7827. doi: 10.3390/ijms13067798
Kobayashi, H., and Kærn, M. Araki, M., Chung, K., Gardner, T. S., Cantor, C. R. (2004). Programmable cells: interfacing natural and engineered gene networks. Proc. Natl. Acad. Sci. U.S.A. 101, 8414–8419. doi: 10.1073/pnas.0402940101
Kramer, B. P., Viretta, A. U., Daoud-El Baba, M., Aubel, D., Weber, W., and Fussenegger, M. (2004). An engineered epigenetic transgene switch in mammalian cells. Nat. Biotechnol. 22, 867–870. doi: 10.1038/nbt980
Lee, H., DeLoache, W. C., and Dueber, J. E. (2012). Spatial organization of enzymes for metabolic engineering. Metab. Eng. 14, 242–251. doi: 10.1016/j.ymben.2011.09.003
Liou, S.-H., and Chen, C.-C. (2012). Cellular ability to sense spatial gradients in the presence of multiple competitive ligands. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 85:11904. doi: 10.1103/PhysRevE.85.011904
Long, B. L., Rekhi, R., Abrego, A., Jung, J., and Qutub, A. A. (2013). Cells as state machines: cell behavior patterns arise during capillary formation as a function of BDNF and VEGF. J. Theor. Biol. 326, 43–57. doi: 10.1016/j.jtbi.2012.11.030
Lu, T. K., Khalil, A. S., and Collins, J. J. (2009). Next-generation synthetic gene networks. Nat. Biotechnol. 27, 1139–1150. doi: 10.1038/nbt.1591
Luengo-Oroz, M. A., Duloquin, L., Castro, C., Savy, T., Faure, E., and Lombardot, B. (2008). “Can voronoi diagram model cell geometries in early sea-urchin embryogenesis?,” in Biomedical Imaging: From Nano to Macro, 2008. ISBI 2008. 5th IEEE International Symposium on, (Paris), 504–507.
Ma'ayan, A., Blitzer, R. D., and Iyengar, R. (2005). Toward predictive models of mammalian cells. Annu. Rev. Biophys. Biomol. Struct. 34, 319–349. doi: 10.1146/annurev.biophys.34.040204.144415
Michelotti, N., Johnson-Buck, A., Manzo, A. J., and Walter, N. G. (2012). Beyond DNA origami: a look on the bright future of nucleic acid nanotechnology. Wiley Interdiscip. Rev. Nanomed. Nanobiotechnol. 4, 139. doi: 10.1002/wnan.170
Miller, M., Hafner, M., Sontag, E., Davidsohn, N., Subramanian, S., and Purnick, P. E. M. (2012). Modular design of artificial tissue homeostasis: robust control through synthetic cellular heterogeneity. PLoS Comput. Biol. 8:e1002579. doi: 10.1371/journal.pcbi.1002579
Mobashir, M., Schraven, B., and Beyer, T. (2012). Simulated evolution of signal transduction networks. PLoS ONE 7:e50905. doi: 10.1371/journal.pone.0050905
Mukherji, S., and van Oudenaarden, A. (2009). Synthetic biology: understanding biological design from synthetic circuits. Nat. Rev. Genet. 10, 859–871. doi: 10.1038/nrg2697
Neumann, H., and Neumann-Staubitz, P. (2010). Synthetic biology approaches in drug discovery and pharmaceutical biotechnology. Appl. Microbiol. Biotechnol. 87, 75–86. doi: 10.1007/s00253-010-2578-3
Nevozhay, D., Zal, T., and Balázsi, G. (2013). Transferring a synthetic gene circuit from yeast to mammalian cells. Nat. Commun. 4, 1451. doi: 10.1038/ncomms2471
Ozbudak, E. M., Thattai, M., Kurtser, I., Grossman, A. D., and van Oudenaarden, A. (2002). Regulation of noise in the expression of a single gene. Nat. Genet. 31, 69–73. doi: 10.1038/ng869
Pedraza, J. M., and van Oudenaarden, A. (2005). Noise propagation in gene networks. Science 307, 1965. doi: 10.1126/science.1109090
Pe'er, D. (2005). Bayesian network analysis of signaling networks: a primer. Sci. STKE 2005:pl4. doi: 10.1126/stke.2812005pl4
Pfaendtner, J., De La Cruz, E. M., and Voth, G. A. (2010). Actin filament remodeling by actin depolymerization factor/cofilin. Proc. Natl. Acad. Sci. U.S.A. 107, 7299–7304. doi: 10.1073/pnas.0911675107
Pothen, J. J., Poynter, M. E., and Bates, J. H. T. (2013). The inflammatory twitch as a general strategy for controlling the host response. J. Immunol. 190, 3510–3516. doi: 10.4049/jimmunol.1202595
Purnick, P. E. M., and Weiss, R. (2009). The second wave of synthetic biology: from modules to systems. Nat. Rev. Mol. Cell Biol. 10, 410–422. doi: 10.1038/nrm2698
Qutub, A. A., Mac Gabhann, F., Karagiannis, E. D., Vempati, P., and Popel, A. S. (2009). Multiscale models of angiogenesis: integration of molecular mechanisms with cell- and organ-level models. IEEE Eng. Med. Biol. Mag. 28, 14–31. doi: 10.1109/MEMB.2009.931791
Rapaport, D. C. (ed.). (2004). The Art of Molecular Dynamics Simulation. ISBN:0521825687. Cambridge, UK: Cambridge University Press, 564. doi: 10.1017/CBO9780511816581
Ro, D.-K., Paradise, E. M., Ouellet, M., Fisher, K. J., Newman, K. L., and Ndungu, J. M. (2006). Production of the antimalarial drug precursor artemisinic acid in engineered yeast. Nature 440, 940–943. doi: 10.1038/nature04640
Roze, L. V., Chanda, A., and Linz, J. E. (2011). Compartmentalization and molecular traffic in secondary metabolism: a new understanding of established cellular processes. Fungal Genet. Biol. 48, 35–48. doi: 10.1016/j.fgb.2010.05.006
Ruder, W. C., Lu, T., and Collins, J. J. (2011). Synthetic biology moving into the clinic. Science 333, 1248–1252. doi: 10.1126/science.1206843
Ryan, D. R., Hu, J., Long, B. L., and Qutub, A. A. (2013). “Predicting Endothelial Cell Phenotypes in Angiogenesis,” in ASME 2nd Global Congress on NanoEngineering for Medicine and Biology, (Boston, MA).
Scarselli, F., Gori, M., Tsoi, A. C., Hagenbuchner, M., and Monfardini, G. (2009). Computational capabilities of graph neural networks. IEEE Trans. Neural Netw. 20, 81–102. doi: 10.1109/TNN.2008.2005141
Schaller, G., and Meyer-Hermann, M. (2005). Multicellular tumor spheroid in an off-lattice Voronoi-Delaunay cell model. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 71:51910. doi: 10.1103/PhysRevE.71.051910
Singhvi, R., Stephanopoulos, G., and Wang, D. I. C. (1994). Effects of substratum morphology on cell physiology. Biotechnol. Bioeng. 43, 764–771. doi: 10.1002/bit.260430811
Slusarczyk, A. L., Lin, A., and Weiss, R. (2012). Foundations for the design and implementation of synthetic genetic circuits. Nat. Rev. Genet. 13, 406–420. doi: 10.1038/nrg3227
Smolke, C. D., and Silver, P. A. (2011). Informing biological design by integration of systems and synthetic biology. Cell 144, 855–859. doi: 10.1016/j.cell.2011.02.020
Song, H., Payne, S., Gray, M., and You, L. (2009). Spatiotemporal modulation of biodiversity in a synthetic chemical-mediated ecosystem. Nat. Chem. Biol. 5, 929–935. doi: 10.1038/nchembio.244
Sozzani, R., and Benfey, P. N. (2011). High-throughput phenotyping of multicellular organisms: finding the link between genotype and phenotype. Genome Biol. 12, 219. doi: 10.1186/gb-2011-12-3-219
Spicher, A., Michel, O., and Giavitto, J.-L. (2011). “Interaction-based simulations for integrative spatial systems biology,” in Understanding the Dynamics of Biological System, eds W. Dubitzky, J. Southgate, and H. Fuß (New York, NY: Springer), 195–231. doi: 10.1007/978-1-4419-7964-3_10
Stricker, J., Cookson, S., Bennett, M. R., Mather, W. H., Tsimring, L. S., and Hasty, J. (2008). A fast, robust and tunable synthetic gene oscillator. Nature 456, 516–519. doi: 10.1038/nature07389
Tabor, J. J., Salis, H., Simpson, Z. B., Chevalier, A. A., Levskaya, A., and Marcotte, E. M. (2009). A synthetic genetic edge detection program. Cell 137, 1272. doi: 10.1016/j.cell.2009.04.048
Takahashi, K., Arjunan, S. N. V., and Tomita, M. (2005). Space in systems biology of signaling pathways–towards intracellular molecular crowding in silico. FEBS Lett. 579, 1783–1788. doi: 10.1016/j.febslet.2005.01.072
Tanaka, H., and Yi, T.-M. (2009). Synthetic morphology using alternative inputs. PLoS ONE 4:e6946. doi: 10.1371/journal.pone.0006946
Thattai, M., and van Oudenaarden, A. (2001). Intrinsic noise in gene regulatory networks. Proc. Natl. Acad. Sci. U.S.A. 98, 8614–8619. doi: 10.1073/pnas.151588598
Vendruscolo, M., and Dobson, C. M. (2011). Protein dynamics: Moore's law in molecular biology. Curr. Biol. 21, R68–R70. doi: 10.1016/j.cub.2010.11.062
Walker, D. C., and Southgate, J. (2013). The modulatory effect of cell–cell contact on the tumourigenic potential of pre-malignant epithelial cells: a computational exploration. J. R. Soc. Interface 10, 1–12. doi: 10.1098/rsif.2012.0703
Wang, B., and Buck, M. (2012). Customizing cell signaling using engineered genetic logic circuits. Trends Microbiol. 20, 376–384. doi: 10.1016/j.tim.2012.05.001
Wang, B., Kitney, R. I., Joly, N., and Buck, M. (2011). Engineering modular and orthogonal genetic logic gates for robust digital-like synthetic biology. Nat. Commun. 2, 508. doi: 10.1038/ncomms1516
Wang, Z., Birch, C. M., Sagotsky, J., and Deisboeck, T. S. (2009). Cross-scale, cross-pathway evaluation using an agent-based non-small cell lung cancer model. Bioinformatics 25, 2389–2396. doi: 10.1093/bioinformatics/btp416
Win, M. N., and Smolke, C. D. (2008). Higher-order cellular information processing with synthetic RNA devices. Science 322, 456–460. doi: 10.1126/science.1160311
Wodarz, D., Hofacre, A., Lau, J. W., Sun, Z., Fan, H., and Komarova, N. L. (2012). Complex spatial dynamics of oncolytic viruses in vitro: mathematical and experimental approaches. PLoS Comput. Biol. 8:e1002547. doi: 10.1371/journal.pcbi.1002547
Xie, Z., Wroblewska, L., Prochazka, L., Weiss, R., and Benenson, Y. (2011). Multi-input RNAi-based logic circuit for identification of specific cancer cells. Science 333, 1307. doi: 10.1126/science.1205527
Yang, J., Meng, X., and Hlavacek, W. S. (2010). Rule-based modelling and simulation of biochemical systems with molecular finite automata. IET Syst. Biol. 4, 453–466. doi: 10.1049/iet-syb.2010.0015
Yeh, B. J., Rutigliano, R. J., Deb, A., Bar-Sagi, D., and Lim, W. A. (2007). Rewiring cellular morphology pathways with synthetic guanine nucleotide exchange factors. Nature 447, 596–600. doi: 10.1038/nature05851
Yingling, M., O'Neill, T., Skalak, T. C., and Peirce-Cottler, S. (2005). A cellular automata model of circulating cell adhesion and transmigration in the microvaculature. IEEE Syst. Inform. Eng. Des. Symp. 1, 356–361. doi: 10.1109/SIEDS.2005.193280
You, L., Cox, R. S., Weiss, R., and Arnold, F. H. (2004). Programmed population control by cell–cell communication and regulated killing. Nature 428, 868–871. doi: 10.1038/nature02491
Keywords: systems biology, synthetic biology, mammalian cell, computational biology, regenerative medicine, gene circuits, signaling network, multiscale modeling
Citation: Rekhi R and Qutub AA (2013) Systems approaches for synthetic biology: a pathway toward mammalian design. Front. Physiol. 4:285. doi:10.3389/fphys.2013.00285
Received: 25 April 2013; Accepted: 19 September 2013;
Published online: 09 October 2013.
Edited by:
John J. Rice, Functional Genomics and Systems Biology, USAReviewed by:
John J. Rice, Functional Genomics and Systems Biology, USALingchong You, Duke University, USA
Copyright © 2013 Rekhi and Qutub. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Amina A. Qutub, Department of Bioengineering, Rice University, MS-142, 6100 Main Street, Houston TX 77005-1892, USA e-mail: aminaq@rice.edu
 Rahul Rekhi
Rahul Rekhi Amina A. Qutub
Amina A. Qutub