- Department of Plant Sciences, University of California Davis, Davis, CA, USA
Models of myriad forms are rapidly becoming central to biology. These range from statistical models that are fundamental to the interpretation of experimental results to ordinary differential equation models that attempt to describe the results in a mechanistic format. Models will be more and more essential to biologists but this growing importance requires all model users to become more sophisticated about what is in a model and how that limits the usability of the model. This review attempts to relay the potential pitfalls that can lie within a model.
Introduction
Biology has long aspired to be an absolute hard science where observations can be both described and predicted with mathematical precision using algorithms or models. With the rapidly increasing power and decreasing cost of computational capacity, this drive toward models and their use is rapidly being pushed into nearly every part of biology with significant benefit to our understanding of the underlying biology (Yuh et al., 1998; Locke et al., 2005; Jonsson et al., 2006; Millar et al., 2006). Thus, modeling is an important aspect of biology that will only become more critical to the successful progress of biological sciences. However, as with every new method that requires a significant increase in specialized knowledge, complications with the use, and application of models can potentially hinder or mislead biological understanding. Largely these problems arise because every model is a reductionist description or analysis of empirical data, which requires assumptions to be made at the beginning of the modeling process. If the general user or reader does not fully know these assumptions and what they mean in a biological context, it is possible for inaccurate models to permeate and bias entire research fields. This review is meant to look at the specific applications of models in the typical biologist’s research program and how some of the underlying assumptions may be influencing the obtained results or even preventing results from coming to light. A broader knowledge of these potential impacts is necessary to enable models both computational and statistical to obtain their proper place in the biologist’s experimental toolkit.
Model Assumptions and Inferential Influence
A nearly universal type of model that research labs use on a daily basis that is not often recognized are statistical models. When using these statistical models, especially for the analysis of genomic data such as transcriptomic or metabolomic, the majority of biological users largely use preformed computational package that contain built in statistical models to test their data (Basten et al., 1999; Gentleman et al., 2004). In this process, the typical biological user does not manipulate the structure of the model, which in this case is the specific terms and relationships among terms within the algorithm and often does not even investigate the specific settings or explore underlying assumptions. However, these statistical settings have a dramatic ability to alter the result that is generated by the computational package, which may be inaccurate if the statistical setting does not reflect the biological expectation. I will go through several examples of how common statistical model assumptions can influence the inference that the outcome may provide.
Independence and Multiple Corrections
A key procedure in all genomics analysis is to conduct a statistically appropriate adjustment of the P value to account for the fact that most genomics tests have a high number of repeated tests (Benjamini and Hochberg, 1995; Doerge and Churchill, 1996; Doerge, 2002; Storey, 2002). The goal of this approach is to account for the fact that if a researcher conducts 10,000 tests, for instance 10,000 transcripts between two conditions, they will expect 500 of these to be significant by random chance using a significance level (α) of 0.05. However, this test presumes that the 10,000 tests are independent. In contrast, the biology of gene expression regulatory networks suggests that they are typically hierarchical. As such, 10,000 transcripts are in all likelihood not independent tests and we currently do not know how many independent events these transcripts actually represent. In this setting, conducting a false discovery rate (FDR) at an a priori defined value of 0.05 may in fact be so overly conservative that all true positive results may be removed of their significance. For instance, in an analysis of expression changes in response to the introduction of a biosynthetic enzyme, AOP2, the only components identified were other genes within the biosynthetic pathway (Wentzell et al., 2007). However, an ensuing deeper analysis of the same array data showed that just below the significance threshold was a signature indicating that this gene also altered the circadian clocks oscillation (Kerwin et al., 2011). This threshold effect hiding is also apparent with this gene where an expression QTL analysis using a conservative significance threshold did not identify this locus as having global impacts whereas the more specific and thus more liberal analysis showed that this AOP2 QTL did impact the majority of oscillatory genes (West et al., 2007; Kerwin et al., 2011). As such, FDRs should be considered as tools within data analysis that are necessary but should not be forced into a fixed value. Instead, the researcher should query the data at multiple levels to ascertain the most appropriate FDR given their ability to biologically validate the results.
Random Error
Another key assumption of nearly all genomics papers utilizing statistics is contained in the following statement “The model tested is yi = μ + Pi + εi, the error, εi, is assumed to be normally distributed with mean 0 and variance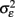 
” (Kliebenstein et al., 2006). In this statement the variance due to stochastic error within the system is assumed to be random with a normal distribution. However, it is rapidly being found in prokaryotes that εi is not purely random and is in fact controlled by genetic variation that is likely to be present within a genomic experiment (Veening et al., 2008). Additionally, results are starting to show that εi is also genetically controlled within eukaryotes (Jarosz and Lindquist, 2010; Jimenez-Gomez et al., 2011; Makumburage and Stapleton, 2011). Thus, it is likely that the assumption of stochastic noise being a random error with a particular variance is not an appropriate model in genomic experiments and that the researcher should investigate the ability to utilize a random error model in each and every instance. Future work will be required to develop new approaches that can simultaneously account for genetic control over both the average and variance of a phenotype.
Normalization and Biology
When scientists generate large genomics datasets there is often a desire to standardize this data using proper statistical theory prior to any data analysis or modeling approach. These include normalization of the data to force it into a normal distribution and the elimination of >3σ outliers. Typically this normalization takes the form of a log 2 transformation but there are other approaches, all with similar intentions to force biological data into a proper statistical framework of the generalized linear model (GLM). However, the pushing of biological data into a statistical framework, while statistically proper, may not be fundamentally proper biology. As mentioned above, the routine transformation of transcript data into log 2 values is a simple example of this type of assumption concerning biological relationships (Doerge, 2002). If a researcher normalizes data such as that for glucosinolate concentration, metabolite concentration or disease resistance within Arabidopsis by log 2 to increase its normality, then this will eliminate the ability to observe biologically validated epistatic interactions (Wentzell et al., 2007; Rowe and Kliebenstein, 2008; Rowe et al., 2008). This is a result of the fact that epistatic interactions inherently cause deviations from normality. While log 2 or other methods nicely transform data into a normal distribution for statistical purposes, the transformation also imparts an implication that the organism measures its transcripts on a log basis rather than an absolute basis because we are now testing for significance on the log basis. This may or may not accurately reflect the relationship of expression kinetics as chemistry has nicely shown that enzymatic reactions adhere to absolute concentrations of protein, substrate, and product according to Michaelis–Menten relationships. It is possible that the log 2 transformations of expression data may not be reflective of biological relationships.
All of these observations lead to a significant issue with most normalization approaches because they are conducted blindly prior to conducting any investigation of the data (Doerge, 2002; Fiehn et al., 2005). This could have serious consequences on the results obtained. For instance, if there is some form of genetic interaction in a large genomic dataset that generates a synthetic phenotype not previously seen it is likely to result in genotypes that appear to be >3σ outliers for a range of phenotypes (Bomblies et al., 2007; Rowe and Kliebenstein, 2008; Rowe et al., 2008; Bikard et al., 2009). If these values are removed before actual data analysis, then these unique and novel interactions would be deleted. As such, it is critical to query the data prior to imposing a specific model of how the data should be distributed to ensure that the observed biology agrees with the statistical model that is being imposed. More frequent use of non-parametric or distribution free models may be a solution, but these models also incorporate biological assumptions based upon the statistical model assumptions. Alternatively new statistical models may need to be developed with biological systems explicitly in mind.
Random Stochastic Models and When is Biology Real
Occasionally genomics data is tested with random models to see if an observation can be explained by random chance. However, there is the possibility that biology and random models can lead to the same observation and that in these cases it becomes difficult to state with precision what is occurring based on the modeling. An example of this is the analysis of quantitative genetic variation of various genomics traits, such as metabolomics and transcriptomics, across defined genotype populations. In these experiments, researchers measure thousands to tens of thousands of traits across tens or hundreds of genotypes. The biological data lead to a view that there are regions of the genome that control a majority of observed phenotypes (transcripts, metabolites, etc.), QTL hotspots (Brem et al., 2002; Schadt et al., 2003; Monks et al., 2004; Brem and Kruglyak, 2005; Keurentjes et al., 2006; West et al., 2007; Rowe et al., 2008).
In contrast to the biology, a complication of these massive genomics datasets is that there is dramatically more traits measured (i.e., individual transcripts or metabolites) than there are independent genotypes causing an imbalanced matrix. This generates a situation where there is inherently a covariance matrix between transcripts or metabolites due to the limited genotype sampling. This matrix imbalance is properly of statistical concern and several modeling efforts have shown that if you recreate a random covariance matrix with properties similar to that found in biological data that you can create similar patterns of hotspots as seen in biological data (Breitling et al., 2008; Kang et al., 2008). This has led to a number of literature conversations suggesting that because a random model with purely statistical abstractions can recreate biology that the researcher must presume that the biology is be caused by random chance and thereby hotspots do not really exist (Breitling et al., 2008; Kang et al., 2008; Kliebenstein, 2009; Montgomery and Dermitzakis, 2009; Verdugo et al., 2010).
The common view when biology and random models yield the same observation is that the scientist is supposed to assume that the observation is due to stochastic random noise within the data and not from biological causality. However in the case of QTL hotspots, numerous hotspots have been cloned in Arabidopsis and yeast and the underlying causal genes validated as causing the significant genome wide events. They include genes that encode for enzymes, transcription factors, and almost any gene that a molecular biologist could logically predict to alter the expression of networks or pathways of genes (Brem et al., 2005; Keurentjes et al., 2007; Wentzell et al., 2007; Jiménez-Gómez et al., 2011; Kerwin et al., 2011). The biological validation of causality showed that the mathematical random model which could recreate biology was not true and did not provide biologically relevant insight.
The above observations show that it may not be a universally applicable approach to presume that when a random stochastic null model recreates biological observations that the biology is inherently random or stochastic. In both of the above examples, proper statistically theory led to models that could explain (hotspots and epistasis) by random fluctuations in mathematical equations yet in both instances, the biology could be linked to specific causal genes showing that they were not random events. This potential for null models to be dramatically overly cautious in attempting to describe what is or is not real suggests that the broader research community needs to re-evaluate other similar instances where random models caused people to stop studying interesting biology.
Competing Models and Biological Testing
Occasionally research fields will delve so deep into modeling that it is possible to lose a connection with the actual biology. This is most easily visible in fields where there are two competing models that can both give decent approximations of the biological phenomena being investigated. A prime example of this is the field of quantitative genetics and population biology where there is a long term debate about genetic variation and if it is predominantly additive or epistatic (Turelli, 1988; Falconer and Mackay, 1996; Mackay, 2001; Carlborg and Haley, 2004; Carlborg et al., 2006; Gjuvsland et al., 2007; Hill et al., 2008). Both sides of the argument can identify models and corroborating data that prove one side and counter the other side’s modeling approaches. This then has left the field largely in a state of stasis with little movement toward an answer. Because this has largely become a debate of models, there has been an apparent loss of recognition that the only way to test which of two nearly equivalent models is correct is via a biological analysis. Identifying this biological test of the models would require a coordinated analysis by both sides of the argument to test the two models, additive and epistatic, over a broad range of diverse biological assumptions to identify when the two models would in fact give different answers when given the same sets of input. This would then identify the precise biological experiment or experiments required to settle the argument of models. As more biological research fields begin to move into modeling it is important to ensure that all models are validated using an independent biological experiment. However, it is critical that this experiment is not simply designed to validate an aspect of the model being described, more importantly this experiment should be explicitly designed to test where two models disagree. Only in this instance is it possible to state that a model and its assumptions and conclusions can be truly tested and validated. Without these explicit tests between models rather than validation of single models, biological fields can become balkanized and inert while arguing between models.
Model Constraints and Predicting the Unpredictable
A final complication of model reliance may come from the shear fact that models are by definition a reductionist description of what we currently know. These models while being limited to the experimental tests that we have currently conducted do have the ability to begin to expand into previously unidentified mechanisms and occasionally untested conditions and thereby illuminate biology that had not previously been observed (Jönsson et al., 2005; Locke et al., 2005; Jonsson et al., 2006; Millar et al., 2006; Saithong et al., 2010a,b). However, these new model-based predictions are inherently within the parameter space of all previously conducted experiments and it is not clear if they are truly unique observations or simply ones that the biologists had not yet formalized in a manuscript. While these new observations and predictions are useful and important, it is the unpredicted and as of yet completely unknown biology that is truly the most important to access in the future. Because models are based on human understanding of a scientific field, our base assumptions inherently shape the models that are developed and could thereby constrain our ability to find new biology that does not agree with these assumptions, such as the central dogma prior to the discovery of regulatory RNA. Thus, while it is important to work toward a model-based predictive nature of biology, it is critical to have an equal if not larger efforts directed to identifying new biology that was never previously considered either due to flawed assumptions or never looking (Fan et al., 2011; Kerwin et al., 2011).
Conclusion
The development and application of models are a fundamental component of systems and computational biology that necessary to enable a deeper understanding of ever growing datasets. With this potential great benefit, there is also a risk that an overly strong, focused, and specific push to modeling runs the risk of encapsulating biological nature at its current state without fully enabling the incorporation of new and unexpected knowledge. To prevent this possibility, it is critical that the users of models and the readers of their papers develop a more sophisticated understanding of how models and their built in assumptions can influence a research result or field. Further, I would argue that it is these assumptions that are as important to test as the actual model outcome because both are inherently making statements about the biology, which is the ultimate goal. It is only with this detailed and universal understanding of the assumptions within models that we will begin to truly display potential and power of models in increased understanding and rate of discovery in biological systems.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This effort was funded by the NSF DBI grant 0820580 and NSF IOS grant 1021861 to Daniel J. Kliebenstein.
References
Basten, C. J., Weir, B. S., and Zeng, Z.-B. (1999). QTL Cartographer, Version 1.13. Raleigh, NC: Department of Statistics, North Carolina State University.
Benjamini, Y., and Hochberg, Y. (1995). Controlling the false discovery rate – a practical and powerful approach to multiple testing. J. R. Stat. Soc. Series B Stat. Methodol. 57, 289–300.
Bikard, D., Patel, D., Le Mette, C., Giorgi, V., Camilleri, C., Bennett, M. J., and Loudet, O. (2009). Divergent evolution of duplicate genes leads to genetic incompatibilities within A. thaliana. Science 323, 623–626.
Bomblies, K., Lempe, J., Epple, P., Warthmann, N., Lanz, C., Dangl, J. L., and Weigel, D. (2007). Autoimmune response as a mechanism for a Dobzhansky-Muller-type incompatibility syndrome in plants. PLoS Biol. 5, e236. doi:10.1371/journal.pbio.0050236
Breitling, R., Li, Y., Tesson, B. M., Fu, J., Wu, C., Wiltshire, T., Gerrits, A., Bystrykh, L. V., de Haan, G., Su, A. I., and Jansen, R. C. (2008). Genetical genomics: spotlight on QTL hotspots. PLoS Genet. 4, e1000232. doi:10.1371/journal.pgen.1000232
Brem, R. B., and Kruglyak, L. (2005). The landscape of genetic complexity across 5,700 gene expression traits in yeast. Proc. Natl. Acad. Sci. U.S.A. 102, 1572–1577.
Brem, R. B., Storey, J. D., Whittle, J., and Kruglyak, L. (2005). Genetic interactions between polymorphisms that affect gene expression in yeast. Nature 436, 701–703.
Brem, R. B., Yvert, G., Clinton, R., and Kruglyak, L. (2002). Genetic dissection of transcriptional regulation in budding yeast. Science 296, 752–755.
Carlborg, O., and Haley, C. S. (2004). Epistasis: too often neglected in complex trait studies? Nat. Rev. Genet. 5, 618–625.
Carlborg, O., Jacobsson, L., Ahgren, P., Siegel, P., and Andersson, L. (2006). Epistasis and the release of genetic variation during long-term selection. Nat. Genet. 38, 418–420.
Doerge, R. W. (2002). Mapping and analysis of quantitative trait loci in experimental populations. Nat. Rev. Genet. 3, 43–52.
Doerge, R. W., and Churchill, G. A. (1996). Permutation tests for multiple loci affecting a quantitative character. Genetics 142, 285–294.
Falconer, D. S., and Mackay, T. F. C. (1996). Introduction to Quantitative Genetics. Harlow: Longman.
Fan, J., Crooks, C., Creissen, G., Hill, L., Fairhurst, S., Doerner, P., and Lamb, C. (2011). Pseudomonas sax genes overcome aliphatic isothiocyanate-mediated non-host resistance in Arabidopsis. Science 331, 1185–1188.
Fiehn, O., Wohlgemuth, G., and Scholz, M. (2005). “Setup and annotation of metabolomic experiments by integrating biological and mass spectrometric metadata,” in Data Integration in the Life Sciences Proceedings, Vol. 3615 (Berlin: Springer Verlag), 224–239.
Gentleman, R. C., Carey, V. J., Bates, D. M., Bolstad, B., Dettling, M., Dudoit, S., Ellis, B., Gautier, L., Ge, Y. C., Gentry, J., Hornik, K., Hothorn, T., Huber, W., Iacus, S., Irizarry, R., Leisch, F., Li, C., Maechler, M., Rossini, A. J., Sawitzki, G., Smith, C., Smyth, G., Tierney, L., Yang, J. Y. H., and Zhang, J. H. (2004). Bioconductor: open software development for computational biology and bioinformatics. Genome Biol. 5, R80.
Gjuvsland, A. B., Hayes, B. J., Omholt, S. W., and Carlborg, O. (2007). Statistical epistasis is a generic feature of gene regulatory networks. Genetics 175, 411–420.
Hill, W. G., Goddard, M. E., and Visscher, P. M. (2008). Data and theory point to mainly additive genetic variance for complex traits. PLoS Genet. 4, e1000008. doi:10.1371/journal.pgen.1000008
Jarosz, D. F., and Lindquist, S. (2010). Hsp90 and environmental stress transform the adaptive value of natural genetic variation. Science 330, 1820–1824.
Jimenez-Gomez, J. M., Corwin, J. A., Joseph, B., Maloof, J. N., and Kliebenstein, D. J. (2011). Genomic analysis of QTLs and genes altering natural variation in stochastic noise. PLoS Genet. 7, e1002295. doi:10.1371/journal.pgen.1002295
Jiménez-Gómez, J. M., Wallace, A. D., and Maloof, J. N. (2011). Network analysis identifies ELF3 as a QTL for the shade avoidance response in Arabidopsis. PLoS Genet. 6, e1001100. doi:10.1371/journal.pgen.1001100
Jönsson, H., Heisler, M., Reddy, G., Agrawal, V., Gor, V., Shapiro, B., Mjolsness, E., and Meyerowitz, E. (2005). Modeling the organization of the Wuschel domain in the shoot apical meristem. Bioinformatics 21, i232–i240.
Jonsson, H., Heisler, M. G., Shapiro, B. E., Meyerowitz, E. M., and Mjolsness, E. (2006). An auxin-driven polarized transport model for phyllotaxis. Proc. Natl. Acad. Sci. U.S.A. 103, 1633–1638.
Kang, H. M., Ye, C., and Eskin, E. (2008). Accurate discovery of expression quantitative trait loci under confounding from spurious and genuine regulatory hotspots. Genetics 180, 1909–1925.
Kerwin, R. E., Jiménez-Gómez, J. M., Fulop, D., Harmer, S. L., Maloof, J. N., and Kliebenstein, D. J. (2011). Network quantitative trait loci mapping of circadian clock outputs identifies metabolic pathway-to-clock linkages in Arabidopsis. Plant Cell 23, 471–485.
Keurentjes, J. J. B., Fu, J. Y., de Vos, C. H. R., Lommen, A., Hall, R. D., Bino, R. J., van der Plas, L. H. W., Jansen, R. C., Vreugdenhil, D., and Koornneef, M. (2006). The genetics of plant metabolism. Nat. Genet. 38, 842–849.
Keurentjes, J. J. B., Fu, J. Y., Terpstra, I. R., Garcia, J. M., van den Ackerveken, G., Snoek, L. B., Peeters, A. J. M., Vreugdenhil, D., Koornneef, M., and Jansen, R. C. (2007). Regulatory network construction in Arabidopsis by using genome-wide gene expression quantitative trait loci. Proc. Natl. Acad. Sci. U.S.A. 104, 1708–1713.
Kliebenstein, D. (2009). Quantitative genomics: analyzing intraspecific variation using global gene expression polymorphisms or eQTLs. Annu. Rev. Plant Biol. 60, 93–114.
Kliebenstein, D. J., West, M. A., van Leeuwen, H., Loudet, O., Doerge, R. W., and St Clair, D. A. (2006). Identification of QTLs controlling gene expression networks defined a priori. BMC Bioinformatics 7, 308. doi:10.1186/1471-2105-7-308
Locke, J. C. W., Millar, A. J., and Turner, M. S. (2005). Modelling genetic networks with noisy and varied experimental data: the circadian clock in Arabidopsis thaliana. J. Theor. Biol. 234, 383–393.
Mackay, T. F. C. (2001). The genetic architecture of quantitative traits. Annu. Rev. Genet. 35, 303–339.
Makumburage, G., and Stapleton, A. (2011). Phenotype uniformity in combined-stress environments has a different genetic architecture than in single-stress treatments. Front. Plant Sci. 2:12. doi:10.3389/fpls.2011.00012
Millar, A., Brown, P., Saithong, T., Salazar, D., Locke, J., Carre, I., and Rand, D. (2006). Mechanistic modelling of flowering regulators based on molecular data. Comp. Biochem. Physiol. Part A Mol. Integr. Physiol. 143, S164–S164.
Monks, S. A., Leonardson, A., Zhu, H., Cundiff, P., Pietrusiak, P., Edwards, S., Phillips, J. W., Sachs, A., and Schadt, E. E. (2004). Genetic inheritance of gene expression in human cell lines. Am. J. Hum. Genet. 75, 1094–1105.
Montgomery, S. B., and Dermitzakis, E. T. (2009). The resolution of the genetics of gene expression. Hum. Mol. Genet. 18, R211–R215.
Rowe, H. C., Hansen, B. G., Halkier, B. A., and Kliebenstein, D. J. (2008). Biochemical networks and epistasis shape the Arabidopsis thaliana metabolome. Plant Cell 20, 1199–1216.
Rowe, H. C., and Kliebenstein, D. J. (2008). Complex genetics control natural variation in Arabidopsis thaliana resistance to Botrytis cinerea. Genetics 180, 2237–2250.
Saithong, T., Painter, K. J., and Millar, A. J. (2010a). Consistent robustness analysis (CRA) identifies biologically relevant properties of regulatory network models. PLoS ONE 5, e15589. doi:10.1371/journal.pone.0015589
Saithong, T., Painter, K. J., and Millar, A. J. (2010b). The contributions of interlocking loops and extensive nonlinearity to the properties of circadian clock models. PLoS ONE 5, e13867. doi:10.1371/journal.pone.0013867
Schadt, E. E., Monks, S. A., Drake, T. A., Lusis, A. J., Che, N., Colinayo, V., Ruff, T. G., Milligan, S. B., Lamb, J. R., Cavet, G., Linsley, P. S., Mao, M., Stoughton, R. B., and Friend, S. H. (2003). Genetics of gene expression surveyed in maize, mouse and man. Nature 422, 297–302.
Storey, J. D. (2002). A direct approach to false discovery rates. J. R. Stat. Soc. Series B Stat. Methodol. 64, 479–498.
Turelli, M. (1988). Phenotypic evolution, constant covariances, and the maintenance of additive variance. Evolution 42, 1342–1347.
Veening, J. W., Smits, W. K., and Kuipers, O. P. (2008). Bistability, epigenetics, and bet-hedging in bacteria. Annu. Rev. Microbiol. 62, 193–210.
Verdugo, R. A., Farber, C. R., Warden, C. H., and Medrano, J. F. (2010). Serious limitations of the QTL/Microarray approach for QTL gene discovery. BMC Biol. 8, 96. doi:10.1186/1741-7007-8-96
Wentzell, A. M., Rowe, H. C., Hansen, B. G., Ticconi, C., Halkier, B. A., and Kliebenstein, D. J. (2007). Linking metabolic QTLs with network and cis-eQTLs controlling biosynthetic pathways. PLoS Genet. 3, e162. doi:10.1371/journal.pgen.0030162
West, M. A. L., Kim, K., Kliebenstein, D. J., van Leeuwen, H., Michelmore, R. W., Doerge, R. W., and St Clair, D. A. (2007). Global eQTL mapping reveals the complex genetic architecture of transcript level variation in Arabidopsis. Genetics 175, 1441–1450.
Keywords: model, quantitative genetics, statistical model, mechanistic model, gene expression, epistasis, additivity
Citation: Kliebenstein DJ (2012) Model misinterpretation within biology: phenotypes, statistics, networks, and inference. Front. Plant Sci. 3:13. doi: 10.3389/fpls.2012.00013
Received: 28 November 2011;
Paper pending published: 20 December 2011;
Accepted: 14 January 2012;
Published online: 31 January 2012.
Edited by:
Mark Lange, Washington State University, USAReviewed by:
Janusz Marek Bujnicki, International Institute of Molecular and Cell Biology in Warsaw, PolandJavier Botto, Agronomia Universidad de Buenos Aires, Argentina
Copyright: © 2012 Kliebenstein. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Daniel J. Kliebenstein, Department of Plant Sciences, University of California Davis, One Shields Avenue, Davis, CA 95616, USA. e-mail: kliebenstein@ucdavis.edu