- 1Department of Biomedical Engineering, Eindhoven University of Technology, Eindhoven, Netherlands
- 2Yale-NUS College, Singapore, Singapore
- 3Institute for Complex Molecular Systems, Eindhoven University of Technology, Eindhoven, Netherlands
The biomass composition represented in constraint-based metabolic models is a key component for predicting cellular metabolism using flux balance analysis (FBA). Despite major advances in analytical technologies, it is often challenging to obtain a detailed composition of all major biomass components experimentally. Studies examining the influence of the biomass composition on the predictions of metabolic models have so far mostly been done on models of microorganisms. Little is known about the impact of varying biomass composition on flux prediction in FBA models of plants, whose metabolism is very versatile and complex because of the presence of multiple subcellular compartments. Also, the published metabolic models of plants differ in size and complexity. In this study, we examined the sensitivity of the predicted fluxes of plant metabolic models to biomass composition and model structure. These questions were addressed by evaluating the sensitivity of predictions of growth rates and central carbon metabolic fluxes to varying biomass compositions in three different genome-/large-scale metabolic models of Arabidopsis thaliana. Our results showed that fluxes through the central carbon metabolism were robust to changes in biomass composition. Nevertheless, comparisons between the predictions from three models using identical modeling constraints and objective function showed that model predictions were sensitive to the structure of the models, highlighting large discrepancies between the published models.
Introduction
Flux balance analysis (FBA), a constraint-based modeling approach, is widely used in predicting metabolic fluxes based on stoichiometric metabolic models, in particular, large-scale or genome-scale metabolic models (GSMs; Orth et al., 2010). Stoichiometric metabolic models are typically underdetermined because the number of reactions in the model is usually larger than the number of metabolites (Bonarius et al., 1997; Kauffman et al., 2003). Therefore, in most cases, constraint-based analysis yields multiple feasible flux solutions. To narrow down the space of feasible solutions, additional constraints can be imposed by specifying the range of fluxes through any particular reaction. In addition to the application of constraints, an objective function is usually defined for identifying biologically relevant flux solutions. The most commonly used objective function for FBA is the biomass objective function (BOF), which is to maximize the efficiency of biomass production, i.e., growth rate (Feist and Palsson, 2010). Biomass production is mathematically represented by a so called “biomass reaction” which, in essence, is a collection of all individual biomass constituents together with their fractional contributions to the overall cellular biomass, and energetic requirements for the biomass generation.
Knowledge of the biomass composition is crucial for predicting flux distribution in metabolic models using FBA because the intracellular fluxes are dependent on the fluxes contributing to biomass synthesis (Pramanik and Keasling, 1997; Schwender and Hay, 2012). Therefore, an important consideration during the development of GSMs is to define the biomass composition, ideally for the condition under study. Experimental evidence indicates that the biomass composition varies between species, cell types and physiological conditions (Novak and Loubiere, 2000; Hay and Schwender, 2011). However, due to a lack of organism-specific and/or condition-specific experimental information, the biomass compositions used in plant GSMs are often collected from diverse types of measurements, experiments, research groups, and even different cell types and plant species (Collakova et al., 2012).
Some computational methods have been developed to estimate the fractional contribution of a precursor to the biomass reaction in microorganisms, e.g., calculating the coefficients of deoxy-nucleotide triphosphates (dNTPs) and nucleotide triphosphates (NTPs) according to the fraction of DNA and RNA (Thiele and Palsson, 2010). Nevertheless, these approaches can only be used for amino acids, NTPs (ATP, GTP, CTP, UTP), and dNTPs (dATP, dGTP, dCTP, dTTP). Given the existence of multiple organelles in plants, one needs to be cautious when applying these approaches to plant models.
With the increasing use of network reconstructions and constraint-based approaches, a need has arisen to clearly define and demonstrate the relevance of the modeling parameters, such as biomass composition, for predicting metabolic fluxes. Work examining the influence of the biomass composition on the predicted fluxes has mostly been done on models of microorganisms, in particular Escherichia coli (Pramanik and Keasling, 1997; Feist et al., 2007). Most recently, a sensitivity analysis of a yeast model suggested that model predictions are sensitive to variations in biomass composition (Dikicioglu et al., 2015). These observations naturally lead to questions about the sensitivity of flux predictions in plant metabolic networks to biomass composition and the robustness of plant metabolic models. Thus far, there are very limited studies exploring the effects of changes in biomass composition on the flux distributions in plants. Plant metabolic networks are significantly more complex than those of microorganisms due to the presence of multiple compartments and parallel metabolic pathways. A study on a model of oilseed rape suggested that flux predictions are sensitive to the contents of oil and protein, which are the major storage components in oil seed (Schwender and Hay, 2012). However, in a study of Arabidopsis heterotrophic cell culture, central carbon metabolism has been observed to be robust to different conditions despite the significant differences in the resulting biomass compositions (Williams et al., 2010). Given that plants are adapted to grow in diverse environmental conditions, plant metabolism is expected to be flexible in face of perturbations. Thus, it deserves theoretical exploration on basis of constraint-based metabolic models to assess the influence of changing biomass composition on predicted fluxes.
Arabidopsis, a model organism for plant biology, has been studied extensively with systems-biology approaches. In this study, we started by reviewing the published Arabidopsis metabolic models followed by an investigation of the impact of changing the biomass composition on the flux predictions in large- or genome-scale plant metabolic models, in particular, the fluxes through central metabolic pathways [i.e., glycolysis, pentose phosphate pathway (PPP), TCA cycle, and mitochondrial electron transport chain (ETC)]. This is because these existing large-scale metabolic networks of plants provided mostly qualitative predictions of intracellular fluxes for primarily central carbon metabolism. Furthermore, previous work has shown that fluxes of central carbon metabolism dominate the FBA results, with little to no flux through the secondary metabolic pathways (Collakova et al., 2012). Here, we focused on study on three published models of Arabidopsis, which have different biomass compositions and network structures. We systematically evaluated the influence of biomass composition on the outcome of FBA simulations in three ways: (1) using different biomass compositions with the same model; (2) using the same biomass composition with different models; (3) varying individual components of the biomass composition and maintenance cost. Our analyses indicate that (i) the central metabolic fluxes are relatively stable in face of varying biomass composition, regardless of model structure; and (ii) the model structure is the main factor in determining the variation in computational results generated by using FBA.
Methods
Stoichiometric Models
In this study, we compared and investigated three published stoichiometric models of Arabidopsis, denoted as Poolman (Poolman et al., 2009), AraGEM (de Oliveira Dal'Molin et al., 2010a), and AraCore (Arnold and Nikoloski, 2014). The Systems Biology Markup Language (SBML) format for the Poolman and AraCore model were available from supplementary files of the corresponding paper. The direction of the phenylpyruvate carboxylase reaction in the Poolman model has been corrected as reported in their subsequent publication (Williams et al., 2010). For the AraGEM model, an updated version was obtained from http://web.aibn.uq.edu.au/cssb/resources/Genomes.html. In this study, we simulated the cellular metabolism of Arabidopsis cells growing on glucose as carbon and energy sources under aerobic heterotrophic conditions.
Although all major biomass components (i.e., cell wall, protein, lipid, carbohydrate, DNA, and RNA) were taken into account in the three models via representative metabolites or corresponding precursors, the biomass components included in these three models are not exactly the same. For example, xylose and γ-aminobutyric acid (GABA) were not considered in Poolman model, but were included in AraGEM and AraCore models. Similarly, soluble metabolites were only considered in AraCore model, but not in Poolman and AraGEM models. To keep the list of biomass components as consistent as possible between the three models, we added some additional biomass transporters to the models if required. It is noted that not all newly added biomass components can be produced by all models, e.g., maltose, xylose, and GABA cannot be produced in Poolman model, coniferyl-alcohol, coumaryl-alchol, sinapyl-alcohol, and xylose cannot be produced by AraCore model as these metabolites are not present in AraCore. Therefore, in this study, we only added new biomass components that can be produced by all the three Arabidopsis models. In total, we added nine new biomass transporters to Poolman model and seven for AraGEM (Supplementary Data 1).
Biomass Equations
The biomass compositions used in this study were extracted from previous studies, hereafter referred to as PoolmanBOF, AraGEMBOF, and AraCoreBOF, corresponding to the biomass composition used in Poolman, AraGEM and AraCore model, respectively (Supplementary Data 2). Since three condition-specific biomass compositions (reflecting carbon-limiting, nitrogen-limiting, and optimal growth conditions) have been employed in the AraCore model, here we chose the carbon-limiting biomass reaction to represent AraCoreBOF. The original biomass composition of each model, together with the calculation of weight percentage of biomass components (Figure 1) is provided in Supplementary Data 2.
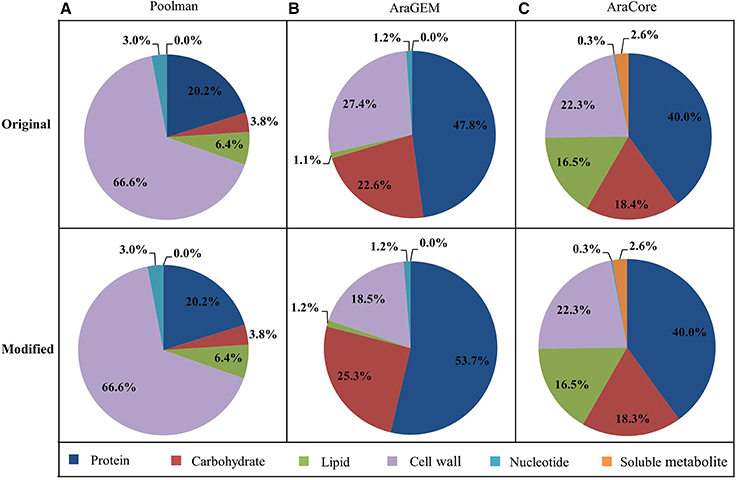
Figure 1. Weight percentage of the biomass components. The original and modified (used for simulations) weight percentage for each class of metabolites contributing to biomass synthesis is displayed. The composition is displayed for Poolman model (A), AraGEM model (B), and AraCore model (C). The calculations for each class of metabolites are shown in Supplementary Data 2.
Due to the different units originally used in the three studies (mmol/g/L in Poolman and mmol/g DW in AraGEM and AraCore), the biomass compositions were normalized to enable a fair comparison. These calculations were performed by weight, defining 1 unit of flux through the biomass equation equals to 1 g of biomass. The details of these calculations are provided in Supplementary Data 2. Finally, we used the normalized biomass equations to perform our model simulations.
Model Simulations
FBA was used to determine the flux solutions at steady-state condition. All simulations were performed using FBA in geometric mode (Smallbone and Simeonidis, 2009) as implemented in the COBRA toolbox (Becker et al., 2007) executed in MATLAB (The MathWorks, version R2012a). Geometric FBA enables a unique optimal solution that is central to the range of possible flux distributions. The Gurobi Optimizer (http://www.gurobi.com, version 5.0.2) solver in combination with the COBRA toolbox were used to solve the linear programming problems. In our study, the biomass equation was maximized to obtain the optimal solution of the metabolic model as described elsewhere (Orth et al., 2010). Formally, the FBA problem can be stated as follows:
where vgrowth is the flux that the biomass reaction carries, representing growth rate, c is the vector of biomass coefficients, whose component ci indicates the ratio of v metabolite Xi required for the formation of a unit of biomass, S is the stoichiometric matrix, is a vector of all reaction fluxes in the system, also referred to as the flux distribution, vmin and vmax represent lower and upper bounds for the flux of each reaction, respectively. GAM refers to growth associated maintenance.
To simulate the cellular behavior of Arabidopsis cells, we constrained the glucose uptake rates at 10 flux units, which was the only source of carbon and energy. AraCore represents a photoautotrophic cell, which does not have organic sources for heterotrophic scenarios, but it can also be utilized to simulate heterotrophic conditions by adapting the energy source (Arnold and Nikoloski, 2014). Consequently, we added an additional glucose exchange reaction “Im_Glc” to AraCore model. Ammonia (NH3) and hydrogen sulfide (H2S) were constrained to be utilized as the sole N and S sources, respectively, because AraGEM and AraCore can only grow with H2S and NH3 as the S and N sources, respectively. Since SO is the sole S source in the Poolman model, it does not have an H2S transporter. We therefore added an H2S transporter to Poolman model, namely “H2S_tx”, enabling H2S as sole sulfur source in all models. Pi is the sole P source input in all three models. Additionally, non-growth associated maintenance (NGAM) was included in all simulations with a value of 2.02, which is a normalized flux unit referring to the value reported in Poolman model (Supplementary Data 2). Similarly, GAM was fixed at 53.26 flux units in this study, which was scaled based on the value reported in AraGEM model. Imported or exported metabolites are always freely exchangeable across the system boundary to provide the necessary nutrients and remove secreted substances.
The biomass equation (i.e., BOF) is generated by defining all of the biomass constituents, in which all the precursor metabolites are assembled in one single reaction with corresponding coefficients (Feist and Palsson, 2010; Thiele and Palsson, 2010). For a fair comparison, we only considered the biomass components which can be produced by all three models in the three biomass equations (Supplementary Data 2). This results in new biomass compositions for AraGEM and AraCore models because some biomass metabolites such as xylose and maltose that cannot be produced by all three models are not taken into account in our biomass reaction. The modified weight percentages of biomass compositions that are included in our biomass reactions differs slightly from the original ones for the three models (Figure 1).
To investigate the influence of biomass composition on the predicted fluxes, we performed three scenarios in each model with the biomass equations of PoolmanBOF, AraGEMBOF, and AraCoreBOF, respectively. We replaced the coefficient of each biomass component in the biomass equation with the corresponding values in the other two models. In total, nine scenarios were simulated in the study, namely “Poolman-PoolmanBOF,” “Poolman-AraGEMBOF,” “Poolman-AraCoreBOF,” “AraGEM-PoolmanBOF,” “AraGEM-AraGEMBOF,” “AraGEM-AraCoreBOF,” “AraCore-PoolmanBOF,” “AraCore-AraGEMBOF,” and “AraCore-AraCoreBOF.” To assess the differences between predicted fluxes obtained from different scenarios, we define the biomass composition given in each model as the “reference” scenario. Thus, “Poolman-PoolmanBOF,” “AraGEM-AraGEMBOF,” and “AraCore-AraCoreBOF” are the “reference” scenarios in Poolman, AraGEM, and AraCore model, respectively.
To confirm the confidence of the predictions, flux variability analysis (FVA) was conducted for the nine model-biomass combinations, which determines the range of possible solutions for each reaction while giving rise to the same optimal value for the objective function (Mahadevan and Schilling, 2003).
Results
Comparisons between Plant Flux-Balanced Models
Origins and Uses of Biomass Compositions in Plant Flux-Balanced Models
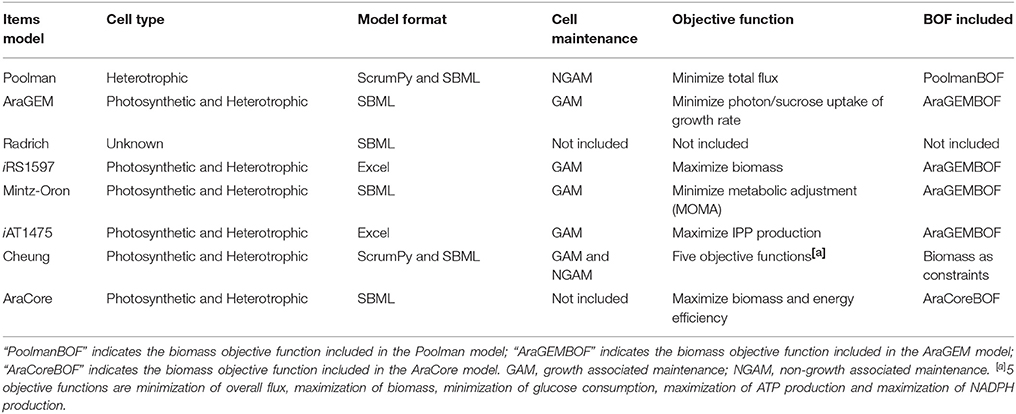
To understand how the biomass composition data is obtained in published metabolic models, we surveyed the source of data used in formulating biomass equations in the existing large-scale metabolic models of plants (Table 1). From the survey, it was verified that only 5 out of 21 models had their biomass compositions measured by the research group that constructed the model, whereas, the remaining 16 studies either do not include any biomass information or adopted from other research groups, some of which were from other organisms. Furthermore, within the surveyed plant metabolic networks, 6 of 21 (29%) used biomass data as the objective function, 11 of 21 (52%) used biomass data as constraints, whereas the rest did not perform any FBA simulations.
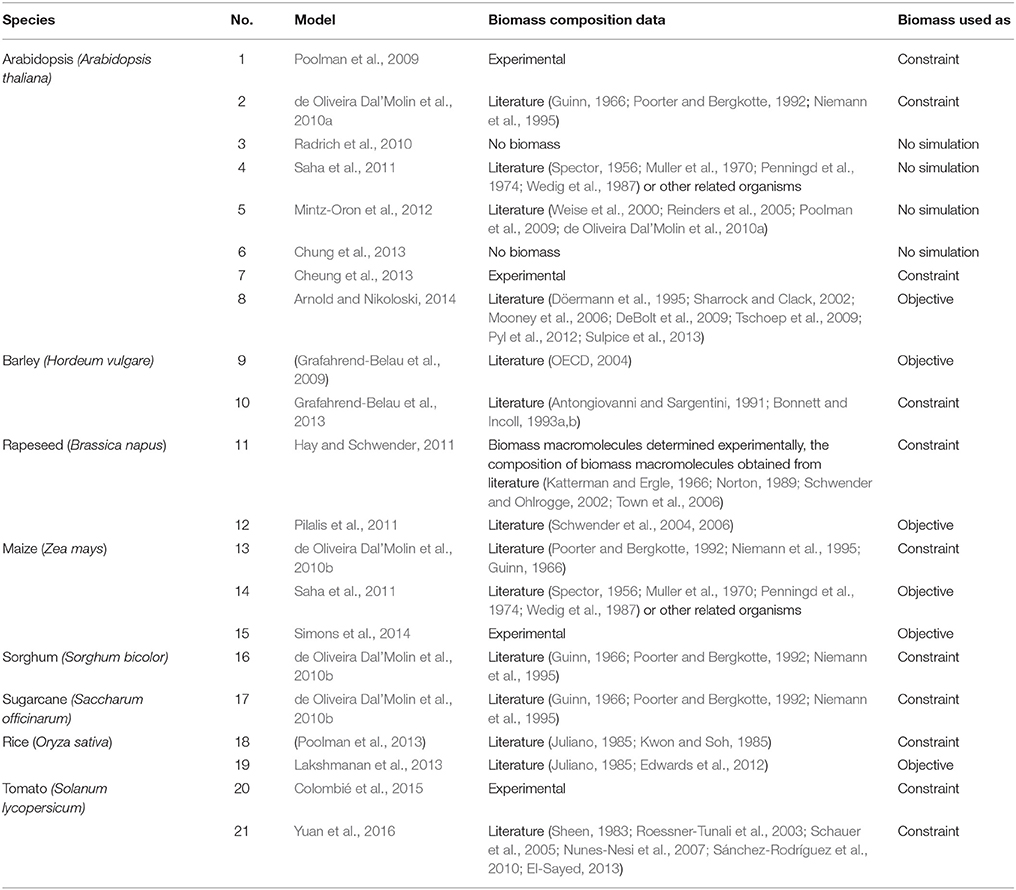
Table 1. Summary of the origin of biomass data in the existing large-scale metabolic models of plants.
General Properties of Published Arabidopsis Flux-Balanced Models
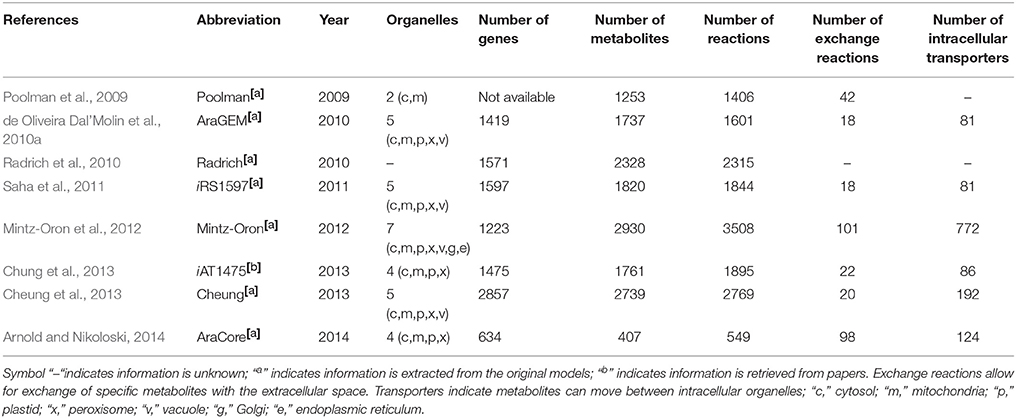
To investigate the variability of the biomass compositions and structure of the models for the same species, we chose Arabidopsis since eight metabolic models were published since 2009. The general statistics of the available Arabidopsis models to date is summarized in Table 2. In general, we observed an increase in the number of genes, metabolites, reactions, and transporters included in Arabidopsis metabolic models over time, but this increase was not uniform. For example, the number of metabolites and reactions in the model of Mintz-Oron et al. (2012) is much larger than that of AraGEM (de Oliveira Dal'Molin et al., 2010a), but the latter has more genes than the former. Toward the compartmentalization, the organelles included in each model are relatively invariant over time. The various Arabidopsis genome-scale models were reviewed more extensively elsewhere (Collakova et al., 2012; de Oliveira Dal'Molin and Nielsen, 2013; Baghalian et al., 2014; Arnold et al., 2015).
Besides the general statistics, these models differ in several aspects, for instance, the inclusion of cellular maintenance costs (Table 3). The models are quite different regarding cell maintenance, because its experimental quantification is a major challenge (Sweetlove et al., 2013).
Three Arabidopsis Models have Different Biomass Compositions
Poolman, AraGEM, and AraCore models each use a different biomass composition to simulate cell growth. Although the relative amounts of each biomass component for all three models were derived from experimental data, they relied entirely on different sources. Poolman model used measurements from their own group for modeling a heterotrophic cell culture, while, AraGEM and AraCore used data for various tissues for Arabidopsis or related species. As a further comparison, we analyzed the macromolecular compositions for each model (Supplementary Data 2), finding the three models differ significantly in the composition of biomass macromolecules (Figure 1). In Poolman model, cell wall comprised more than half of cell biomass. In contrast, cells contain higher amounts of protein in AraGEM and AraCore model. Experimental evidence indicates that the distributions of biomass components are very tissue-specific (Ohlrogge and Browse, 1995; Mueller et al., 2003). One would expect that the biomass compositions of AraGEM and AraCore to be similar as both models represent photosynthetic leaf cells. While there are some similarities in terms of the proportions of cell wall, carbohydrate, and protein, there are also major differences. For example, the proportion of lipid in AraCore biomass is much larger than in AraGEM biomass (18.4 vs. 1.1%). This could be explained by the fact that biomass data in AraGEM model is collected from different organisms.
Differences in Central Carbon Metabolism between the Three Arabidopsis Models
Going beyond merely comparing general network characteristics, we compared the models at the individual reaction level, concentrating on the compartmentation and reversibility of reactions in central carbon metabolism, which is an essential biological process to sustain growth and biomass synthesis (Supplementary Figure 1). We focused on three Arabidopsis models, Poolman, AraGEM, and AraCore models, which have distinct model structures and biomass compositions. Generally, the three models covered all the listed central metabolic reactions (Supplementary Table 1). Compared with the other two models, AraGEM did not include PPi-dependent phosphofructokinase (EC 2.7.1.90), NADP-dependent non-phosphorylating glyceraldehyde-3-phosphate dehydrogenase (EC 1.2.1.9) or NAD-dependent 6-phosphogluconate dehydrogenase (EC 1.1.1.343). Moreover, AraGEM uses two lumped reactions to represent the electron transport chain (ETC) reactions, which are referred to as alternative oxidase pathway (AOX) and cytochrome C oxidase pathway (COX). In contrast, Poolman and AraCore models incorporate separate reactions to describe the ETC. Beyond these differences, the localization and directionality of central metabolic reactions in the three models are not always consistent. For example, the reaction catalyzed by phosphoenolpyruvate carboxylase (EC 4.1.1.31) in Poolman model operates in the opposite direction compared to other two models, which was corrected in a subsequent publication (Williams et al., 2010). For AraCore, some reactions known to be reversible, such as aconitase (EC 4.2.1.3) and fumarase (EC 4.2.1.2), are set as irreversible. Poolman model is not fully compartmentalized, so most of the reactions involved in central carbon metabolic pathways are assigned to the cytosol.
The Impact of Biomass Composition and Model Structure on Central Metabolic Fluxes
Central Carbon Metabolism is Robust to Changes in Biomass Composition
To test the sensitivity of FBA solutions to the biomass composition, nine scenarios described in the Methods Section were simulated with three flux-balanced metabolic models of Arabidopsis, Poolman, AraGEM, and AraCore models, in combination with their respective biomass compositions. The maximization of growth rate is used as the objective function subjecting to mass-balance constraints, and setting the glucose uptake rates as 10 flux units (“Methods”). In particular, we analyzed how central metabolic reactions listed in Supplementary Table 1 respond to a change in biomass composition. The results are illustrated in Figure 2 in which the differences in color intensity between columns (compare horizontally) reflects the differences in flux values of each reaction calculated by the three biomass compositions. It can be seen that for the majority of the reactions, in particular the glycolytic reactions, the flux patterns were very similar. This indicates a high stability of the central carbon metabolism in Arabidopsis with respect to biomass composition, regardless of model structures.
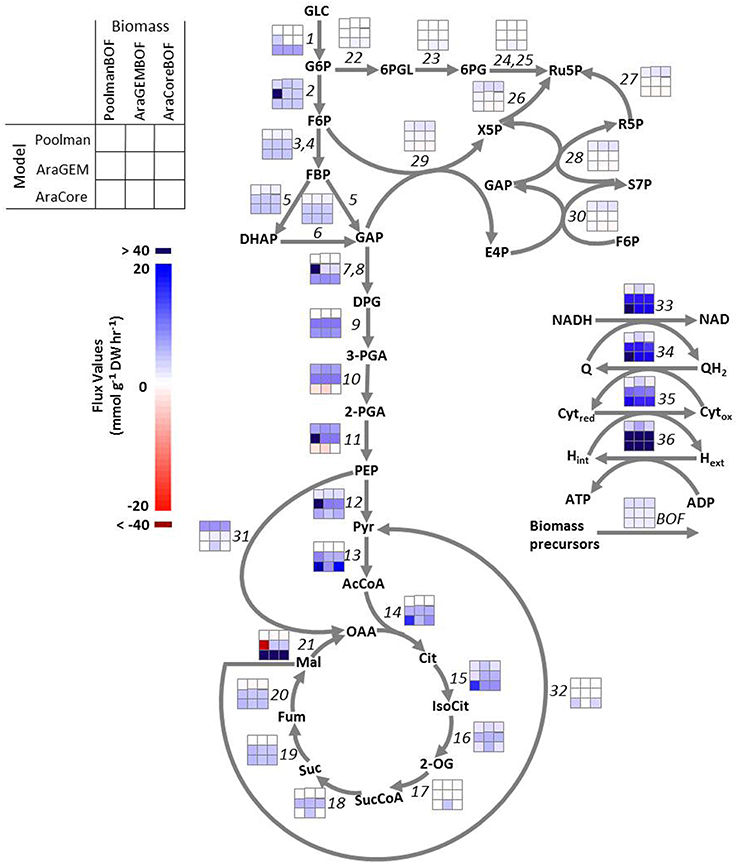
Figure 2. Flux maps of central carbon metabolism predicted from three Arabidopsis models: Poolman model, AraGEM model, and AraCore model. Fluxes were predicted using three different biomass compositions in each model: PoolmanBOF, the biomass composition included in Poolman model; AraGEMBOF, biomass composition included in AraGEM model; AraCoreBOF, biomass composition included in AraCore model. Each reaction is numbered, referencing Table S1, and the color intensity of each box corresponds to the flux value (mmol g−1 DW h−1) for the respective labeled reaction in each scenario. The results calculated by different biomass compositions with the same model can be interpreted by comparing between columns (compare horizontally). The results calculated by the same biomass composition with different models can be interpreted by comparing between rows (compare vertically). DW, Dry cell weight. Metabolite abbreviations are as follows: GLC, glucose; 2-OG, 2-oxoglutarate; 3-PGA, 3-phosphoglycerate; 2-PG, 2-phosphoglycolate; G6P, glucose-6-phosphate; F6P, fructose-6-phosphate; 6PGL, 6-phosphogluconolactone; 6PG, 6-phosphogluconate; Ru5P, ribulose-5-phosphate; R5P, ribose-5-phosphate; X5P, xylulose-5-phosphate; S7P, sedoheptulose-7-phosphate; E4P, erythrose-4-phosphate; FBP, fructose-1,6-biphosphate; DHAP, dihydroxyacetone phosphate; DPG, glycerate-1,3-bisphosphate; PEP, phosphoenol pyruvate; OAA, oxalacetic acid; GAP, glyceraldehyde-3-phosphate; 2-PGA, 2-phosphoglycerate; Pyr, pyruvate; Cit, citrate; IsoCit, threo-isocitrate; Suc, succinate; SucCoA, succinyl-CoA; Fum, fumarate; Mal, malate; QH2, ubiquinone; Q, ubiquinol; Cytred, cytochrome reduced; Cytox, cytochrome oxidized; Fdred, ferredoxin reduced; Fdox, ferredoxin oxidized.
Some reactions showed larger flexibility in our predictions. The flux distribution predicted by AraCore model with AraGEMBOF resulted in flux through 2-oxoglutarate dehydrogenase reaction (reaction 17), a reaction belonging to the TCA cycle, whereas this reaction did not carry flux with PoolmanBOF and AraCoreBOF. The flux distributions through the TCA cycle reflect the function of the metabolic network, and its operation largely depends on the cell type and the considered physiological context (Sweetlove et al., 2010). In addition, 2-oxoglutarate (2-OG) is an essential intermediate for the biosynthesis of amino acids such as glutamine and glutamate (Supplementary Figure 1). Given that AraGEMBOF contains a much higher amount of glutamine and glutamate (Supplementary Data 2), it is not surprising that 2-oxoglutarate dehydrogenase reaction carried non-zero flux implemented with AraGEMBOF in AraCore model. For AraGEM model, the biomass composition greatly affected the fluxes through glyceraldehyde-3-phosphate dehydrogenase (EC 1.2.1.9/1.2.1.12; reaction 7 and 8), phosphoglycerate kinase (EC 2.7.2.3; reaction 9), phosphoglycerate hydratase (EC 4.2.1.11; reaction 11), pyruvate kinase (EC 2.7.1.40; reaction 12) and malate dehydrogenase (EC 1.1.1.37; reaction 21). For example, the use of PoolmanBOF on the AraGEM model gave rise to higher fluxes through malate dehydrogenase compared to using AraGEMBOF, which is due to a reaction cycle that malate dehydrogenase involves in with PoolmanBOF. Commonly, the great changes occurred at the branch points of glycolysis and the TCA cycle, where there were drains for the synthesis of cellular constituents. Under heterotrophic conditions, it is generally thought that the oxidative PPP (OPPP) predominately provides reducing power for the production of biomass, in particular for fatty acid synthesis. As a result, we would expect the OPPP reactions to be active in our simulations. However, OPPP reactions carried no flux in any of the predicted solutions of Poolman and AraGEM model. Interestingly, for AraCore model, using AraGEMBOF resulted in small flux through OPPP reactions such as glucose 6-phosphate (EC 1.1.1.49; reaction 22), 6-phosphogluconolactonase (EC 3.1.1.31; reaction 23) and 6-phosphogluconate dehydrogenase (EC 1.1.1.44/1.1.1.343; reaction 24, 25). Previously, Williams et al. (2010) showed that the OPPP was poorly predicted by Poolman model, which was suggested to be caused by the error in assigning the reversibility of the NADP+-dependent glyceraldehyde-3-phosphate dehydrogenase (EC 1.2.1.13; Cheung et al., 2013).
Model Structure has a Large Impact on Model Predictions
Furthermore, we assessed the effects of model structures on the flux predictions by comparing the model predictions from the same biomass equation with different models (Figure 2, comparisons between rows; compare vertically). It is apparent that the vast majority of central metabolic reactions carried different fluxes from each other, despite the application of identical biomass composition and boundary constraints. For example, the hexokinase reaction (reaction 1), which converts glucose to glucose-6-phosphate for entry into glycolysis, carried significantly different fluxes in three Arabidopsis models, irrespective of the biomass equation used. Based on 10 flux units of glucose, the Poolman model produces 2.84 units of biomass by using the biomass equation of Poolman model (i.e., PoolmanBOF), while the models of AraGEM and AraCore synthesize 1.53 and 1.42 biomass units respectively. Similarly, Poolman model yields the highest biomass by using AraGEMBOF and AraCoreBOF (2.40 and 2.12 flux units, respectively), while, AraGEM generates the lowest biomass (1.29 and 1.13 flux units, respectively; Figure 2). This indicates that the Poolman model predicts more efficient conversion of glucose into biomass compared to the other two models. Overall, model structure has a large impact on the model prediction made with FBA, which highlights the importance of the quality of metabolic models on the variation of model predictions.
To quantify the variation of fluxes in face of changing biomass composition and model structure, we calculated the standard deviation, a robust measure for the dispersion within a set of data, for each reaction fluxes that were predicted from nine model-biomass equation combinations. We then compared the median of the standard deviation (Supplementary Data 3). The medians of the standard deviations of reaction fluxes for the cases with the same biomass composition but different models (4.59, 3.35, and 3.22 for PoolmanBOF, AraGEMBOF, and AraCoreBOF combinations, respectively) were systematically higher than that of simulations with the same metabolic network (0.29, 0.53, and 1.98 for Poolman, AraGEM, and AraCore combinations). This indicates that the predicted fluxes were considerably more dispersed when using different models, despite of the same biomass equation, revealing that model structure has a larger impact on the FBA predictions.
For further confirmation, FVA was performed to examine the flux capacity for each reaction under the 9 model-biomass combinations (Supplemental Data 4). FVA analysis showed that 10 of 33 considered reactions (pyruvate dehydrogenase, reaction 13; citrate synthase, reaction 14; succinate thiokinase, reaction 18; complex II, reaction 19; glucose 6-phosphate dehydrogenase, reaction 22; 6-phosphogluconolactonase, reaction 23; ribulose-phosphate 3-epimerase, reaction 26; ribulose 5-phosphate epimerase, reaction 27; transketolase 1, reaction 28; and transketolase 2, reaction 29) have non-overlapping flux variability ranges in the compared scenarios and agreed with the FBA analysis. However, the rest have a large range of possible flux values in, at least one of considered scenarios, resulting in overlapping flux variability ranges in the compared scenarios, which are not comparable.
Robustness of Growth Rate Predictions with Respect to Changes in Individual Biomass Component and Maintenance Cost
From Figure 2, we observed that growth rate is not sensitive to the biomass composition. Considering the BOF is the employed objective in this study, which is the most commonly used objective for FBA (Feist and Palsson, 2010), we further analyzed the impact of changing the fractional contribution of each single biomass component on the growth rates with the “reference” scenarios—Poolman-PoolmanBOF, AraGEM-AraGEMBOF, and AraCore-AraCoreBOF three scenarios. The coefficient of each compound in the biomass equation was independently varied 30% up or down (this value referred to Pinchuk et al., 2010) in each “reference” scenario, while the composition of the rest of the biomass components was kept unchanged. The resulting model predictions of the growth rates were compared with that of “reference” biomass equation. Overall, our analyses showed that the predicted growth rates were not sensitive to changes in the ratios of biomass components. For instance, growth rates in AraGEM and AraCore models were altered by, at most, 4 and 6%, respectively (Supplementary Tables 3, 4). The only exception is in the Poolman model where a 30% decrease or increase of the composition of cell wall led to 19.9% and 14.3% variation in growth rate, respectively (Supplementary Table 2). This discrepancy is not unexpected as cell wall is the largest part (66.6%) of the overall biomass composition in the Poolman model (Figure 1).
Our analysis preferentially revealed that growth rate has a larger change at higher coefficient in terms of C atom. Given that glucose, which is the carbon and energy source, was used as the limiting nutrient in the analyses in this study, we would expect growth rate correlates to the fractional coefficient of C atom. To quantify this effect, we calculated the Pearson correlation coefficient (PCC), a measure of the linear dependence between two variables, for all predicted growth rates simulated by decreasing and increasing of each single biomass component by 30% (Supplementary Figure 2). We also calculated the correlation coefficients between changes in growth rate and the coefficient in terms of weight (Supplementary Figure 3). We found that the correlations among the coefficient in terms of weight were systematically similar to the observed correlations among the coefficient in terms of C atoms (Supplementary Figure 2), indicating that when the fractional contribution of C atoms were altered, the growth rates were increased or decreased in a synchronized fashion.
In addition to the structure of the metabolic network and biomass composition, the in silico growth rate can also be influenced by the maintenance cost, i.e., GAM and NGAM. Therefore, we evaluated the influence of maintenance on the predicted growth rates with three “reference” scenarios characterized by constraints on: (i) no maintenance, (ii) sole GAM, (iii) sole NGAM, and (iv) GAM and NGAM. We then compared the growth rates of scenario (i), (ii), and (iii) with that of scenario (iv), separately. The analyses showed that the influence of maintenance parameters varies with the used model. The exclusion of GAM and/or NGAM changes the growth rate by, at most, 29.6 and 1.3% in AraGEM model and AraCore model, respectively (Supplementary Table 5). Given that AraGEM and AraCore models describe the ETC reactions quite differently (Section Differences in Central Carbon Metabolism between the Three Arabidopsis Models), it is unsurprising to observe large discrepancies between the influence of maintenance cost on growth rate predictions for these two models. It is worth mentioning that the growth rate predicted from the Poolman model did not change with the maintenance, which is biologically implausible. This is because there exist futile cycles in Poolman model (Arnold et al., 2015).
Discussion
In this study, we investigated the effect of biomass composition and model structure on steady-state flux predictions in the metabolic models of Arabidopsis. Different combinations (three models and three biomass equations) were tested to cover multiple possibilities for biomass composition. Our results demonstrated that flux predictions of the central metabolic network are fairly insensitive to changes in biomass composition, regardless of the employed metabolic networks (Figure 2). Biomass demands are a principal drive of the flux distributions in metabolic models, therefore one would expect the flux distributions to be sensitive to changes in the biomass composition. However, several experimental studies provided evidence that central carbon metabolism is rather stable when the substrate source remains unchanged (Rontein et al., 2002; Spielbauer et al., 2006; Junker et al., 2007; Williams et al., 2008, 2010). In a study of heterotrophic Arabidopsis cell culture, fluxes through the central metabolic network measured by metabolic flux analysis (MFA) were observed to be unchanged under different physiological conditions, despite under which the biomass composition altered (Williams et al., 2008). Consistently, Spielbauer et al. (2006) found that flux distributions of central carbon metabolism were stable in maize endosperm. Nonetheless, under conditions with different substrates provided, the flux distribution in the central carbon metabolism altered significantly (Junker et al., 2007). The noticeable stability of central carbon metabolism has been extensively demonstrated in many microorganism studies (Pramanik and Keasling, 1997, 1998; Feist et al., 2007).
Our results also showed that 30% variations in individual biomass precursor had a minor effect on the growth rates with Arabidopsis models (Supplementary Tables 2–4). This observation is in agreement with the previously reported findings (Pramanik and Keasling, 1998; Puchalka et al., 2008). Puchalka et al. (2008) reported that varying a single biomass component by 20% up or down has a negligible effect (< 1%) on the growth rate. Due to the large number of macromolecules such as protein and carbohydrate in the cell, it is not surprising that single biomass component, which makes up the macromolecules did not significantly affect the growth rate. However, in other studies, it was found that varying the macromolecular composition had considerable effect on the flux simulations (Feist et al., 2007; Nookaew et al., 2008). Similarly, our analyses showed that the effect of maintenance cost on growth rate was limited (Supplementary Table 5), which contradicts previous results of E. coli model that maintenance cost had larger impact on growth rate prediction (Feist et al., 2007). However, it is important to point out that the growth yield altered merely by 5% when increasing or decreasing GAM twofold in the study of Puchalka et al. (2008), whereas, the effect of NGAM depends on the rate of carbon source supply. The discrepancies of the effect of maintenance cost on growth rate predictions of models of different organisms is likely to due to the difference in lifestyle and metabolic behavior of the different organisms.
Sensitivity analyses of biomass composition performed on different models often yields conflicting results. According to the sensitivity analysis on the E. coli model of Feist et al. (2007), small changes in biomass composition did not significantly affect growth rates, while, cellular maintenance cost can considerably influence growth rate prediction. However, the study of the E. coli model of Varma and Palsson (1994) noted that predictions of constraint-based model are not very sensitive to maintenance, including GAM and NGAM. Recently, Dikicioglu et al. (2015) found that the predicted fluxes of the metabolic models of yeast were sensitive to biomass composition. These are likely caused by inherent differences in the respective metabolic networks. To verify this, we examined the differences of FBA solutions between different models by constraining the same biomass outputs and cellular maintenance costs, and our results indicated that model structure has a larger impact on the flux predictions than the biomass composition (Figure 2). Moreover, our analyses of the impact of maintenance on the predicted growth rates showed large differences between the three examined models that represent the ETC reaction differently (Supplementary Table 5). These observations indicate the structure of metabolic models is a major determinant of the variation in model predications.
Although, our analysis indicated the robustness of the growth rate and central metabolic fluxes in response to changes in biomass composition and maintenance cost, it does not suggest that it is sufficient to generalize biomass composition from any cell type within a plant or from other closely related organisms. This is because the biomass composition for different tissues and organisms may include metabolites specific to them, which need specific determination. Notably, variables other than model structure, such as the P/O ratio have considerable impacts on flux distributions according to previous reports (Feist et al., 2007).
Conclusions
In this study, we reviewed the characteristics of published Arabidopsis metabolic models, concentrated on three particular models with distinct model structures and different compositions of biomass components. We examined the sensitivity of predicted fluxes to biomass composition, which is particularly relevant to plant metabolic models for which the biomass data is often collected from various sources. Our analysis showed that central metabolic fluxes as well as growth rates were insensitive to the variations in biomass composition, but were significantly affected by model structure. This work represents a thorough set of analyses performed in plants by means of constraint-based modeling, thereby providing relevant information about how critical FBA solutions can be affected by biomass composition, and more importantly by the structure of the models. Despite differences in several aspects such as model structure and number of metabolites and reactions included, each of the evaluated models has its own merits. Comparative analysis of the models paves the way for exploring the existence of principles that are relevant for the regulation and robustness of plant central carbon metabolism.
Author Contributions
HY, CC, PH, and NV conceived and designed the work. HY carried out all simulations and drafted the manuscript. CC, PH, and NV revised the manuscript. All authors read and approved the final version of the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like to thank China Scholarship Council (CSC) for awarding a scholarship to HY. We also thank Dr. Mark G. Poolman for kindly providing the biomass composition data used in their Arabidopsis model, and Dr. Dong-Yup Lee for proving the working space for HY when preparing for the manuscript.
Supplementary Material
The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fpls.2016.00537
References
Antongiovanni, M., and Sargentini, C. (1991). Variability in chemical composition of straws. Opt. Méditerranéen. Série-Sémin. 16, 49–53.
Arnold, A., and Nikoloski, Z. (2014). Bottom-up metabolic reconstruction of Arabidopsis and its application to determining the metabolic costs of enzyme production. Plant Physiol. 165, 1380–1391. doi: 10.1104/pp.114.235358
Arnold, A., Sajitz-Hermstein, M., and Nikoloski, Z. (2015). Effects of varying nitrogen sources on amino acid synthesis costs in Arabidopsis thaliana under different light and carbon source conditions. PLoS ONE 10:e0116536. doi: 10.1371/journal.pone.0116536
Baghalian, K., Hajirezaei, M. R., and Schreiber, F. (2014). Plant metabolic modeling: achieving new insight into metabolism and metabolic engineering. Plant Cell 26, 3847–3866. doi: 10.1105/tpc.114.130328
Becker, S. A., Feist, A. M., Mo, M. L., Hannum, G., Palsson, B. Ø., and Herrgard, M. J. (2007). Quantitative prediction of cellular metabolism with constraint-based models: the COBRA Toolbox. Nat. Protoc. 2, 727–738. doi: 10.1038/nprot.2007.99
Bonarius, H. P. J., Schmid, G., and Tramper, J. (1997). Flux analysis of underdetermined metabolic networks: the quest for the miss in constraints. Trends Biotechnol. 15, 308–314. doi: 10.1016/S0167-7799(97)01067-6
Bonnett, G. D., and Incoll, L. D. (1993a). Effects on the stem of winter barley of manipulating the source and sink during grain-filling. 1. Changes in accumulation and loss of mass from internodes. J. Exp. Bot. 44, 75–82. doi: 10.1093/jxb/44.1.75
Bonnett, G. D., and Incoll, L. D. (1993b). Effects on the stem of winter barley of manipulating the source and sink during grain-filling. 2. Changes in the composition of water-soluble carbohydrates of internodes. J. Exp. Bot. 44, 83–91. doi: 10.1093/jxb/44.1.83
Cheung, C. Y. M., Williams, T. C. R., Poolman, M. G., Fell, D. A., Ratcliffe, R. G., and Sweetlove, L. J. (2013). A method for accounting for maintenance costs in flux balance analysis improves the prediction of plant cell metabolic phenotypes under stress conditions. Plant J. 75, 1050–1061. doi: 10.1111/tpj.12252
Chung, B. K. S., Lakshmanna, M., Klement, M., Mohanty, B., and Lee, D. Y. (2013). Genome-scale in silico modeling and analysis for designing synthetic terpenoid-producing microbial cell factories. Chem. Eng. Sci. 103, 100–108. doi: 10.1016/j.ces.2012.09.006
Collakova, E., Yen, J. Y., and Senger, R. S. (2012). Are we ready for genome-scale modeling in plants? Plant Sci. 191–192, 53–70. doi: 10.1016/j.plantsci.2012.04.010
Colombié, S., Nazaret, C., Bénard, C., Biais, B., Mengin, V., Solé, M., et al. (2015). Modelling central metabolic fluxes by constraint-based optimization reveals metabolic reprogramming of developing Solanum lycopersicum (tomato) fruit. Plant J. 81, 24–39. doi: 10.1111/tpj.12685
DeBolt, S., Scheible, W. R., Schrick, K., Auer, M., Beisson, F., Bischoff, V., et al. (2009). Mutations in UDP-glucose:sterol glucosyltransferase in Arabidopsis cause transparent test a phenotype and suberization defect in seeds. Plant Physiol. 151, 78–87. doi: 10.1104/pp.109.140582
de Oliveira Dal'Molin, C. G., and Nielsen, L. K. (2013). Plant genome-scale metabolic reconstruction and modeling. Curr. Opin. Biotechnol. 24, 271–277. doi: 10.1016/j.copbio.2012.08.007
de Oliveira Dal'Molin, C. G., Quek, L.-E., Palfreyman, R. W., Brumbley, S. M., and Nielsen, L. K. (2010b). C4GEM, a genome-scale metabolic model to study C4 plant metabolism. Plant Physiol. 154, 1871–1885. doi: 10.1104/pp.110.166488
de Oliveira Dal'Molin, C. G., Quek, L. E., Palfreyman, R. W., Brumbley, S. M., and Nielsen, L. K. (2010a). AraGEM, a genome-scale reconstruction of the primary metabolic network in Arabidopsis. Plant Physiol. 152, 579–589. doi: 10.1104/pp.109.148817
Dikicioglu, D., Kirdar, B., and Oliver, S. G. (2015). Biomass composition: the “elephant in the room” of metabolic modelling. Metabolomics 11, 1690–1701. doi: 10.1007/s11306-015-0819-2
Döermann, P., Hoffmann-Benning, S., Balbo, I., and Benning, C. (1995). Isolation and characterization of an Arabidopsis mutant deficient in the thylakoid lipid digalactosyl diacylglycerol. Plant Cell 7, 1801–1810. doi: 10.1105/tpc.7.11.1801
Edwards, J. M., Roberts, T. H., and Atwell, B. J. (2012). Quantifying ATP turnover anoxic coleoptiles of rice (Oryza sativa) demonstrates preferential allocation of energy to protein synthesis. J. Exp. Bot. 63, 4389–4402. doi: 10.1093/jxb/ers114
El-Sayed, H. E. A. (2013). Exogenous application of ascorbic acid for improve germination, growth, water relations, organic and inorganic components in tomato (Lycopersicon esculentum Mill.) plant under salt-stress. NY Sci. J. 6, 123–139.
Feist, A. M., Henry, C. S., Reed, J. L., Krummenacker, M., Joyce, A. R., Karp, P. D., et al. (2007). A genome-scale metabolic reconstruction for Escherichia coli K-12 MG 1655 that accounts for 1260 ORFs and thermodynamic information. Mol. Sys. Biol. 3:121. doi: 10.1038/msb4100155
Feist, A. M., and Palsson, B. O. (2010). The biomass objective function. Curr. Opin. Microbiol. 13, 344–349. doi: 10.1016/j.mib.2010.03.003
Grafahrend-Belau, E., Junker, A., Eschenröder, A., Muller, J., Schreiber, F., and Junker, B. H. (2013). Multiscale metbolic modeling: dynamic flux balance analysis on a whole-plant scale. Plant Physiol. 163, 637–647. doi: 10.1104/pp.113.224006
Grafahrend-Belau, E., Schreiber, F., Koschutzke, D., and Junker, B. H. (2009). Flux balance analysis of barley: a computational approach to study systematic properties of central metabolism. Plant Physiol. 149, 585–598. doi: 10.1104/pp.108.129635
Guinn, G. (1966). Extraction of nucleic acids from lyophilized plant material. Plant Physiol. 41, 689–695. doi: 10.1104/pp.41.4.689
Hay, J., and Schwender, J. (2011). Metabolic network reconstruction and flux variability analysis of storage synthesis in developing oilseed rape (Brassica napus L.) embryos. Plant J. 67, 526–541. doi: 10.1111/j.1365-313X.2011.04613.x
Juliano, B. O. (1985). “Rice hull and rice straw,” in Rice: Chemistry and Technology, ed B. O. Juliano (St. Paul, MN: The American Association of Cereal Chemists Incorporated), 699.
Junker, B. H., Lonien, J., Heady, L. E., Rogers, A., and Schwender, J. (2007). Parallel determination of enzyme activities and in vivo fluxes in Brassica napus embryos grown on organic or inorganic nitrogen source. Phytochemistry 68, 2232–2242. doi: 10.1016/j.phytochem.2007.03.032
Katterman, F. R., and Ergle, D. R. (1966). RNA composition in cotton. Plant Physiol. 41, 553–556. doi: 10.1104/pp.41.3.553
Kauffman, K. J., Prakash, P., and Edwards, J. S. (2003). Advances in flux balance analysis. Curr. Opin. Biotechnol. 14, 491–496. doi: 10.1016/j.copbio.2003.08.001
Kwon, Y. W., and Soh, C. H. (1985). Characteristics of nuclear DNA in rice roots of Japonica and Indica × Japonica varieties. Agric. Res. Seoul Natl. Univ. 10, 63–68.
Lakshmanan, M., Zhang, Z., Mohanty, B., Kwon, J. Y., Choi, H. Y., Nam, H. J., et al. (2013). Elucidating rice cell metabolism under flooding and drought stresses using flux-based modeling and analysis. Plant Physiol. 162, 2140–2150. doi: 10.1104/pp.113.220178
Mahadevan, R., and Schilling, C. H. (2003). The effects of alternate optimal solutions in constraint-based genome-scale metabolic models. Metab. Eng. 5, 264–276. doi: 10.1016/j.ymben.2003.09.002
Mintz-Oron, S., Meir, S., Malitsky, S., Ruppin, E., Aharoni, A., and Shlomi, T. (2012). Reconstruction of Arabidopsis metabolic network models accounting for subcellular compartmentalization and tissue-specificity. Proc. Natl. Acad. Sci. U.S.A. 109, 339–344. doi: 10.1073/pnas.1100358109
Mooney, B. P., Miernyk, J. A., Michael Greenlief, C., and Thelen, J. J. (2006). Using quantitative proteomics of Arabidopsis roots and leaves to predict metabolic activity. Physiol. Plant. 128, 237–250. doi: 10.1111/j.1399-3054.2006.00746.x
Mueller, L. A., Zhang, P., and Rhee, S. Y. (2003). AraCyc: a biochemical pathway database for Arabidopsis. Plant Physiol. 132, 453–460. doi: 10.1104/pp.102.017236
Muller, F., Dijkhuis, D. J., and Heida, Y. S. (1970). On the relationship between chemical composition and digestibility in vivo of roughages. Agric. Res. Rep. 736, 1–27.
Niemann, G. J., Pureveen, J. B. M., Eijkel, G. B., Poorter, H., and Boon, J. J. (1995). Differential chemical allocation and plant adaptation: a Py-MS study of 24 species differing in relative growth rate. Plant Soil 175, 275–289. doi: 10.1007/BF00011364
Nookaew, I., Jewett, M. C., Meechai, A., Thammarongtham, C., Laoteng, K., Cheevadhanarak, S., et al. (2008). The genome-scale metabolic model ilN800 of Saccharomyces cerevisiae and its validation: a scaffold to query lipid metabolism. BMC Syst. Biol. 2:71. doi: 10.1186/1752-0509-2-71
Norton, G. (1989). “Nature and biosynthesis of storage proteins,” in Oil Crops of the World, ed G. Röbbelen, R. K. Downey, and A. Ashri (New York, NY: McGraw-Hill), 165–191.
Novak, L., and Loubiere, P. (2000). The metabolic network of Lactococcus lactis: distribution of 14C– labeled substrates between catabolic and anabolic pathways. J. Bacteriol. 182, 1136–1143. doi: 10.1128/JB.182.4.1136-1143.2000
Nunes-Nesi, A., Carrari, F., Gibon, Y., Sulpice, R., Lytovchenko, A., Fisahn, J., et al. (2007). Deficiency of mitochondrial fumarase activity in tomato plants impairs photosynthesis via an effect on stomatal function. Plant J. 50, 1093–1106. doi: 10.1111/j.1365-313X.2007.03115.x
OECD (2004). “Consensus document on compositional considerations for new variety of barley (Hordeum vulgare): key food and feed nutrients and anti-nutrients,” in Series on the Safety of Novel Foods and Feeds, ed OECD (Paris: OECD Environmental Health and Safety Publications), 1–42.
Ohlrogge, J., and Browse, J. (1995). Lipid biosynthesis. Plant Cell 7, 957–970. doi: 10.1105/tpc.7.7.957
Orth, J. D., Thiele, I., and Palsson, B. Ø. (2010). What is flux balance analysis? Nat. Biotechnol. 28, 245–248. doi: 10.1038/nbt.1614
Penningd, F. W., Brunstin, A. H., and Vanlaar, H. H. (1974). Products, requirements and efficiency of biosynthesis - quantitative approach. J. Theor. Biol. 45, 339–377. doi: 10.1016/0022-5193(74)90119-2
Pilalis, E., Chatziioannou, A., Thomasset, B., and Kolisis, F. (2011) An in silico compartmentalized metabolic model of Brassica napus enables the systemic study of regulatory aspects of plant central metabolism. Biotechnol. Bioeng. 108, 1673–1682. doi: 10.1002/bit.23107
Pinchuk, G. E., Hill, E. A., Geydebrekht, O. V., Ingeniis, J. D., Zhang, X., Osterman, A., et al. (2010). Constraint-based model of Shewanella oneidensis MR-1 metabolism: a tool for data analysis and hypothesis generation. PLoS Comput. Biol. 6:e1000822. doi: 10.1371/journal.pcbi.1000822
Poolman, M. G., Kundu, S., Shaw, R., and Fell, D. A. (2013). Responses to light intensity in a genome scale model of rice metabolism. Plant Physiol. 162, 1060–1072. doi: 10.1104/pp.113.216762
Poolman, M. G., Miguet, L., Sweetlove, L. J., and Fell, D. A. (2009). A genome-scale metabolic model of Arabidopsis and some of its properties. Plant Physiol. 151, 1570–1581. doi: 10.1104/pp.109.141267
Poorter, H., and Bergkotte, M. (1992). Chemical composition of 24 wild species differing in relative growth rate. Plant Cell Environ. 15, 221–229. doi: 10.1111/j.1365-3040.1992.tb01476.x
Pramanik, J., and Keasling, J. D. (1997). Stoichiometric model of Escherichia coli metabolism: incorporation of growth-rate dependent biomass composition and mechanistic energy requirements. Biotechnol. Bioeng. 56, 398–421.
Pramanik, J., and Keasling, J. D. (1998). Effects of Escherichia coli biomass composition on central metabolic fluxes predicted by a stoichiometric model. Biotechnol. Bioeng. 60, 230–238.
Puchalka, J., Oberhardt, M. A., Godinho, M., Bielecka, A., Regenhardt, D., Timmis, K. N., et al. (2008). Genome-scale reconstruction and analysis of the Pseudomonas putida KT2440 metabolic network facilitates applications in biotechnology. PLoS Comput. Biol. 4:e1000210. doi: 10.1371/journal.pcbi.1000210
Pyl, E. T., Piques, M., Ivakov, A., Schulze, W., Ishihara, H., Stitt, M., et al. (2012). Metabolism and growth in Arabidopsis depend on the daytime temperature but are temperature-compensated against cool nights. Plant Cell 24, 2443–2469. doi: 10.1105/tpc.112.097188
Radrich, K., Tsuruoka, Y., Dobson, P., Gevorgyan, A., Swainston, N., Baart, G., et al. (2010). Integration of metabolic databases for the reconstruction of genome-scale metabolic networks. BMC Sys. Bio. 4:114. doi: 10.1186/1752-0509-4-114
Reinders, A., Panshyshyn, J. A., and Ward, J. M. (2005). Analysis of transport activity of Arabidopsis sugar alcohol permease homolog AtPLT5. J. Biol. Chem. 280, 1594–1602. doi: 10.1074/jbc.M410831200
Roessner-Tunali, U., Hegemann, B., Lytovchenko, A., Carrari, F., Bruedigam, C., Granot, D., et al. (2003). Metabolic profiling of transgenic tomato plants overexpressing hexokinase reveals that the influence of hexose phosphorylation diminishes during fruit development. Plant Physiol. 133, 84–99. doi: 10.1104/pp.103.023572
Rontein, D., Dieuaide-Noubhani, M., Dufourc, E. J., Raymond, P., and Rolin, D. (2002). The metabolic architecture of plant cells. iStability of central metabolism and flexibility of anabolic pathways during the growth cycle of tomato cells. J. Biol. Chem. 277, 43948–43960. doi: 10.1074/jbc.M206366200
Saha, R., Suthers, P. F., and Maranas, C. D. (2011). Zea mays iRS1563: a comprehensive genome-scale metabolic reconstruction of maize metabolism. PLoS ONE 6:e21784. doi: 10.1371/journal.pone.0021784
Sánchez-Rodríguez, E., Rubio-Wilhelmi, M., Cervilla, L. M., Blasco, B., Rios, J. J., Rosales, M. A., et al. (2010). Genotypic differences in some physiological parameters symptomatic for oxidative stress under moderate drought in tomato plants. Plant Sci. 178, 30–40. doi: 10.1016/j.plantsci.2009.10.001
Schauer, N., Zamir, D., and Fernie, A. R. (2005). Metabolic profiling of leaves and fruit of wild species tomato: a survey of the Solanum lycopersicum complex. J. Exp. Bot. 56, 297–307. doi: 10.1093/jxb/eri057
Schwender, J., Goffman, F., Ohlrogge, J. B., and Shachar-Hill, Y. (2004). Rubisco without the Calvin cycle improves the carbon efficiency of developing green seeds. Nature 432, 779–782. doi: 10.1038/nature03145
Schwender, J., and Hay, J. O. (2012). Predictive modeling of biomass component tradeoffs in Brassica napus developing oilseeds based on in silico manipulation of storage metabolism. Plant Physiol. 160, 1218–1236. doi: 10.1104/pp.112.203927
Schwender, J., and Ohlrogge, J. B. (2002). Probing in vivo metabolism by stable isotope labeling of storage lipids and proteins in developing Brassica napus embryos. Plant Physiol. 130, 347–361. doi: 10.1104/pp.004275
Schwender, J., Shachar-Hill, Y., and Ohlrogge, J. B. (2006). Mitochondrial metabolism in developing embryos of Brassica napus. J. Biol. Chem. 281, 34040–34047. doi: 10.1074/jbc.M606266200
Sharrock, R. A., and Clack, T. (2002). Patterns of expression and normalized levels of the five Arabidopsis phytochromes. Plant Physiol. 130, 442–456. doi: 10.1104/pp.005389
Sheen, S. J. (1983). Biomass and chemical composition of tobacco plants under high density growth. Beitr. Tabakforsch. Int. 12, 35–42.
Simons, M., Saha, R., Amiour, N., Kumar, A., Guillard, L., Clément, G., et al. (2014). Assessing the metabolic impact of nitrogen availability using a compartmentalized maize leaf genome-scale model. Plant Physiol. 166, 1659–1674. doi: 10.1104/pp.114.245787
Smallbone, K., and Simeonidis, E. (2009). Flux balance analysis: a genometric perspective. J. Theor. Biol. 258, 311–315. doi: 10.1016/j.jtbi.2009.01.027
Spielbauer, G., Margl, L., Hannah, L. C., Römisch, W., Ettenhuber, C., Bacher, A., et al. (2006). Robustness of central carbohydrate metabolism in developing maize kernels. Phytochemistry 67, 1460–1475. doi: 10.1016/j.phytochem.2006.05.035
Sulpice, R., Nikoloski, Z., Tschoep, H., Antonio, C., Kleessen, S., Larhlimi, A., et al. (2013). Impact of the carbon and nitrogen supply on relationships and connectivity between metabolism and biomass in a broad panel of Arabidopsis accessions. Plant Physiol. 162, 347–363. doi: 10.1104/pp.112.210104
Sweetlove, L. J., Beard, K. F., Nunes-Nesi, A., Fernie, A. R., and Ratcliffe, R. G. (2010). Not just a circle: flux modes in the plant TCA cycle. Trends Plant Sci. 15, 462–470. doi: 10.1016/j.tplants.2010.05.006
Sweetlove, L. J., Williams, T. C. R., Cheung, C. Y. M., and Ratcliffe, R. G. (2013). Modelling metabolic CO2 evolution – a fresh perspective on respiration. Plant Cell Environ. 36, 1631–1640. doi: 10.1111/pce.12105
Thiele, I., and Palsson, B. Ø. (2010). A protocol for generating a high-quality genome-scale metabolic reconstruction. Nat. Protoc. 5, 93–121. doi: 10.1038/nprot.2009.203
Town, C. D., Cheung, F., Maiti, R., Crabtree, J., Haas, B. J., Wortman, J. R., et al. (2006). Comparative genomics of Brassica oleracea and Arabidopsis thaliana reveal gene loss, fragmentation, and dispersal after polyploidy. Plant Cell 18, 1348–1359. doi: 10.1105/tpc.106.041665
Tschoep, H., Gibon, Y., Carillo, P., Armengaud, P., Szecowka, M., Nunes-Nesi, A., et al. (2009). Adjustment of growth and central metabolism to a mild but sustained nitrogen-limitation in Arabidopsis. Plant Cell Environ. 32, 300–318. doi: 10.1111/j.1365-3040.2008.01921.x
Varma, A., and Palsson, B. O. (1994). Parametric sensitivity of stoichiometric flux balance models applied to wild-type Escherichia coli metabolism. Biotechnol. Bioeng. 45, 69–79. doi: 10.1002/bit.260450110
Wedig, C. L., Jaster, E. H., and Moore, K. J. (1987). Hemicellulose monosaccharide composition and in vitro disappearance of orchard grass and alfalfa hay. J. Agr. Food Chem. 35, 214–218. doi: 10.1021/jf00074a012
Weise, A., Barker, L., Kühn, C., Lalonde, S., Buschmann, W. B. F., and Ward, J. M. (2000). A new subfamily of sucrose transporters, SUT4, with low affinity/high capacity localized in enucleate sieve elements of plants. Plant Cell 12, 1345–1355. doi: 10.1105/tpc.12.8.1345
Williams, T. C. R., Miguet, L., Masakapalli, S. K., Kruger, N. J., Sweetlove, L. J., and Ratcliffe, R. G. (2008). Metabolic network fluxes in heterotrophic Arabidopsis cells: stability of the flux distribution under different oxygenation conditions. Plant Physiol. 148, 704–718. doi: 10.1104/pp.108.125195
Williams, T. C. R., Poolman, M. G., Howden, A. J. M., Schwarzlander, M., Fell, D. A., Ratcliffe, R. G., et al. (2010). A genome-scale metabolic model accurately predicts fluxes in central carbon metabolism under stress conditions. Plant Physiol. 150, 311–323. doi: 10.1104/pp.110.158535
Keywords: biomass composition, model structure, sensitivity, flux balance analysis, central carbon metabolism, Arabidopsis, large-scale metabolic model
Citation: Yuan H, Cheung CYM, Hilbers PAJ and van Riel NAW (2016) Flux Balance Analysis of Plant Metabolism: The Effect of Biomass Composition and Model Structure on Model Predictions. Front. Plant Sci. 7:537. doi: 10.3389/fpls.2016.00537
Received: 27 January 2016; Accepted: 05 April 2016;
Published: 26 April 2016.
Edited by:
Zoran Nikoloski, Max-Planck Institute of Molecular Plant Physiology, GermanyReviewed by:
Samuel Seaver, Argonne National Laboratory, USABiswapriya Biswavas Misra, University of Florida, USA
Copyright © 2016 Yuan, Cheung, Hilbers and van Riel. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: C. Y. Maurice Cheung, maurice.cheung@yale-nus.edu.sg;
Natal A. W. van Riel, N.A.W.v.Riel@tue.nl
 Huili Yuan
Huili Yuan C. Y. Maurice Cheung
C. Y. Maurice Cheung Peter A. J. Hilbers
Peter A. J. Hilbers Natal A. W. van Riel
Natal A. W. van Riel