Probabilistic Model of Onset Detection Explains Paradoxes in Human Time Perception

A very basic computational model is proposed to explain two puzzling findings in the time perception literature. First, spontaneous motor actions are preceded by up to 1–2 s of preparatory activity (Kornhuber and Deecke, 1965). Yet, subjects are only consciously aware of about a quarter of a second of motor preparation (Libet et al., 1983). Why are they not aware of the early part of preparation? Second, psychophysical findings (Spence et al., 2001) support the principle of attention prior entry (Titchener, 1908), which states that attended stimuli are perceived faster than unattended stimuli. However, electrophysiological studies reported no or little corresponding temporal difference between the neural signals for attended and unattended stimuli (McDonald et al., 2005; Vibell et al., 2007). We suggest that the key to understanding these puzzling findings is to think of onset detection in probabilistic terms. The two apparently paradoxical phenomena are naturally predicted by our signal detection theoretic model.

Introduction

How does the brain process temporal information? How do we determine the onsets of stimuli? Despite the impressive volume and quality of recent work in this area (Leon and Shadlen, 2003; Coull et al., 2004; Eagleman et al., 2005; Battelli et al., 2008; Brass and Haggard, 2008), the exact mechanism of time perception is not completely known yet. Here we focus specifically on two well-known puzzling findings in onset perception, and describe a simplistic model that explains the apparent contradictions.

It has been shown (Kornhuber and Deecke, 1965; Deecke and Kornhuber, 1978) that self-paced motor actions are preceded by a gradually increasing neural signal known as the readiness potential (RP), recordable from the scalp using EEG. The RP is particularly salient around the vertex. Single-cell recordings in monkeys in the underlying region, the supplementary motor area (SMA), have confirmed there are neurons that start firing at up to 2.6 s prior to motor execution (Romo and Schultz, 1987). However, Libet et al. (1983) has famously used a cross-modal timing method to measure the earliest time at which subjects detect any sense of motor preparation (the “urge” or intention of wanting to make the action), and it was found that subjects reported that they had the intention to move only about 250 ms prior to motor execution. One question that has exercised the imagination of researchers for decades is: why don’t we become aware of the motor preparation earlier, perhaps as early as the onset of the RP? We call this the Kornhuber–Deecke–Libet paradox, due to their pioneering but apparently contradictory findings.

The second finding: Titchener’s law of attentional prior entry (Titchener, 1908) states that attended stimuli are perceived quicker (i.e., having earlier onset) when compared to unattended stimuli. Numerous papers have provided psychophysical evidence for this claim using the temporal-order-judgment (TOJ) task (Stelmach and Herdman, 1991; Jaskowski, 1993; Shore et al., 2001; Spence et al., 2001; McDonald et al., 2005). In this task, two stimuli are presented simultaneously and attention is directed to one of them either endogenously or exogenously. Subjects typically report that the attended stimulus appeared first providing empirical support for attentional prior entry. Consequently, numerous researchers have suggested that attention accelerates the rate of information processing (Stelmach and Herdman, 1991; Jaskowski, 1993; Carrasco and McElree, 2001; Shore et al., 2001; Spence et al., 2001; Schneider and Bavelier, 2003). However, an electrophysiological study reported no corresponding temporal difference between the neural signals for attended and unattended stimuli (McDonald et al., 2005). The authors argued that attentional prior entry was a result of the in increase in signal strength caused by attention (Störmer et al., 2009) and not of differential speed of neural processing. Another study (Vibell et al., 2007) reported a 4–10 ms difference between the ERPs that are associated with stimuli that are judged to be 38 ms apart – a physiological finding that is too small to either match or explain the size of the behavioral effect.

Here we propose a simple model that can naturally explain the apparent contradiction in these findings. The key idea is that time perception, just as in perception in general, is constrained by noise and uncertainty. Many previous modeling studies have employed these concepts (for a review see Chater et al., 2007), and the current work is by no means presented as a replacement or competitor to these influential models. The focus is on presenting what can be considered as a simplest case of how these concepts can be applied, in order to specifically explain the two puzzling findings described above.

For instance, one may think that the preparatory activity preceding self-paced action starts at an exact time point prior to motor execution, as indicated by the RP measure. However, the RP is the result of averaging over many trials. To determine the onset of preparatory activity in every trial, the brain does not have the luxury of averaging to reduce noise. Of course, in the RP there is also noise from the EEG measurement. But even for actual neuronal activity, there is trial-by-trial fluctuation, which is not necessarily meaningful with respect to neural processing. Given such presence of noise, perception essentially depends on a decision process (Green and Swets, 1966); the brain has to decide what the true signal is even though it is corrupted by noise. According to Bayesian decision theory (Kersten et al., 2004) or signal detection theory (Green and Swets, 1966), the statistically optimal observer sets a criterion (or threshold) to decide whether the evidence represents signal or noise. We apply this concept to develop a model that can determine the onset of a stimulus.

Materials and Methods

Probabilistic Onset Detection

We modeled onset perception as an uninterrupted process of signal detection. In a task where a signal is to occur within a certain epoch and the subject is to determine its onset, one natural way the brain could solve this problem is to perform signal detection at every time point. The reported onset T would be at the point where the signal is first detected within the trial epoch. Note that even though we are treating time as a discrete variable, the same simulations can be done when time is treated as a continuous variable. However, it has previously been suggested that certain aspects of perception may be based on discrete sampling at about 12.5 Hz (VanRullen et al., 2007), and this is followed for the additional benefit of ease of computation.

At every time point, the chance of detection depends on the signal and noise distributions. We call the whole duration of a trial “trial epoch,” while the period in which the signal is present “signal interval.” In all our simulations we assume that the signal has a positive value during the signal interval and a value of 0 in the rest of the trial epoch. Further, we call the value of the signal that is not corrupted by noise simply “true signal” and the value of the signal corrupted by noise “internal evidence.” Note that the problem that the brain deals with, and that we are modeling here, is how to use the internal evidence in order to guess the onset of the true signal.

We used a signal detection theoretic framework (Green and Swets, 1966), according to which the brain sets a criterion for detection, and gives a positive response when the internal evidence crosses the criterion. Due to the presence of noise, the estimated onset T is a random variable with a certain distribution P(T). We ran the signal detection model on multiple trials in order to empirically obtain the distribution P(T).

In each trial, the signal had a random onset and was detected at a particular time bin. If the signal was not detected by the end of the trial epoch, the system was forced to guess the onset randomly using a uniform distribution over the duration of the whole trial epoch. There were two alternatives to this method that we considered. First, trials in which the signal was not detected could simply be discarded. However, such an approach does not punish misses and resulted in extremely high optimal criteria, which missed the signal on a very large percentage of the trials. Second, for trials in which the signal was not detected, the system could have chosen the last time bin as the correct answer. This option seemed further removed from what the brain might do in a similar situation. Thus, we decided to choose the onset from a uniform distribution as the best way of approximating how the brain may deal with this problem.

Modeling the Kornhuber–Deecke–Libet Paradox

We presented the same true signal multiple times, each time with an onset chosen uniformly at random. We modeled the noise at each time bin to come from a Gaussian distribution with a mean of 0 and SD of 1. The units here are arbitrary and all other variables are expressed in terms of the SD of the noise distribution. For each series of simulations we used a different criterion. In each trial, we recorded the detection time relative to the onset of the true signal in that trial (that is, we subtracted the onset from the detection time). In this way, we approximated the probability distribution of the relative detection time. We then computed the mean square error (MSE) for the resulting distribution. The mean squared error is simply E[(T−t_0)^2] where t_0 is the true onset and E[] denotes expected value. Mathematically, the MSE equals the variance of the estimated onset plus the squared error of the estimation (also called bias):

E[(T−t_0)^2] = Var(T) + (E[T]−t_0)^2 = variance + bias^2

We defined the optimal criterion as the one that minimizes the MSE. We chose to use the mean squared error as it is one of the most widely used measures in statistics to quantify the amount of deviation from a value. It may appear as if the choice of MSE is central to our model but we believe that this is not the case. Initial models using the absolute deviation from the true onset (defined as E[|T−t_0|]) provided similar results.

The true signal was either a step or a slowly rising function designed to approximate the RP. The step function started at 0, then rose sharply to a particular value, and finally went back to 0 again until the rest of the trial epoch. The slowly rising function started at 0, then rose slowly to a particular value (we used a log-sinusoidal function to approximate the RP), and finally went back to 0 again until the rest of the trial epoch.

Modeling Attentional Prior Entry

We calculate the respective optimal distributions of two signals – an attended signal and an unattended signal – with identical shapes and noise levels. Compared to the unattended signal, the attended signal was modeled with greater signal strength. In accordance with the method for finding the optimal distribution, the onsets of the two stimuli were still random in each trial, but this time the attended stimulus preceded the unattended stimulus by a fixed time gap, which we called the onset advantage. Using the two distributions, P(T_a) and P(T_u), we then calculated P(T_a<T_u), the probability that the attended stimulus is perceived first. We varied the onset advantage from negative values (unattended signal first) to positive values (attended signal first) in order to estimate the location of the point of subjective simultaneity.

Results

Probabilistic Onset Detection

We varied the stimulus interval, the trial epoch, signal-to-noise ratio, and criterion used. For each set of values for the above variables we obtained a distribution of onset estimations P(T) by running 10,000 trials. We were interested in finding the criterion level that would minimize the MSE.

Figure 1 shows the simulated distribution P(T) under different criterion levels, for the same signal (stimulus interval = 2 s) and a constant Gaussian noise level (signal-to-noise ratio, S/N = 2.5). One could see that at low criterion levels, P(T) is skewed to the left. This is because at such liberal criterion, the system produces early false positives even in the absence of a true signal. At a higher criterion level, P(T) is skewed to the right, because at a conservative criterion, the system may miss the early part of the signal and only detect it at a later stage.

FIGURE 1

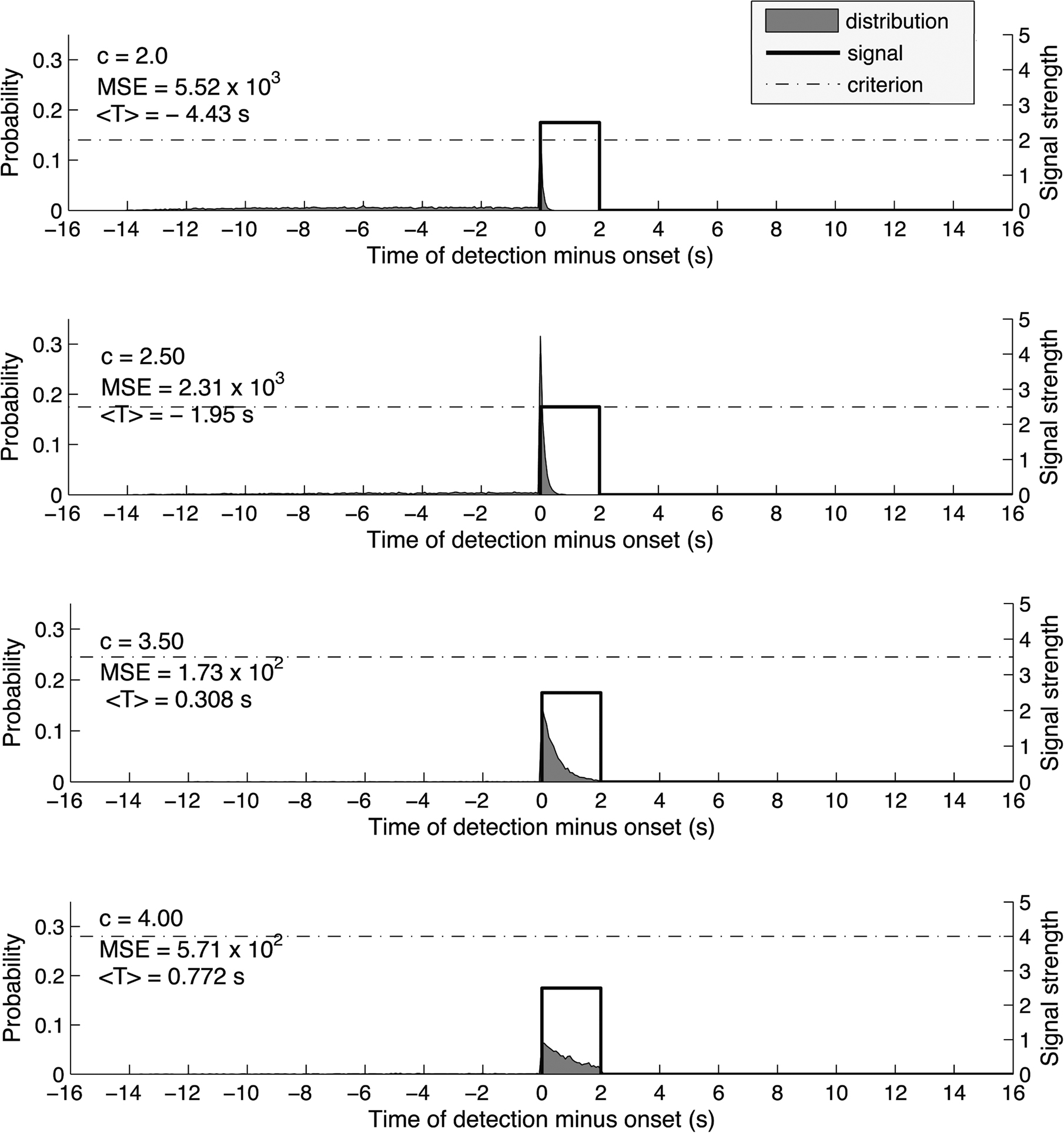
Figure 1. We set the duration of the trial epoch to 16 s and broke the time interval into 200 time bins, in accordance with a signal sampling rate of 12. 5 Hz. The signal was a step function and had duration of 2 s, constant signal strength of 2.5 times the SD of the noise which was modeled to have a Gaussian distribution with a mean of 0 and SD of 1. We computed the distribution of detection times for each of 21 values of the criterion, from c = 0 to c = 5 (only 4 of them are shown in this figure). Detection times vary from 14 s prior to the onset of the signal to 16 s after the onset because the onset could have had its onset anytime between the beginning and 14th second of the 16-s trial epoch. To compute each distribution, we simulated a signal detection task 10,000 times. As the criterion for detection increased, so did the mean estimated onset<T>. The mean square error (MSE) first decreased and then increased again, reaching its minimum for c = 3.5. Thus, the optimal detection strategy is achieved for c = 3.5 and produces an average estimate of the onset 308 ms later than the true onset of the signal.

The crucial question is what would be the optimal criterion and the corresponding P(T). For the system to perform satisfactorily in this task, it must take into account two factors: bias and consistency. We would like the system to give an average response that is close to the actual onset. Also, we would like it to give responses that are not extremely varied across trials. These two factors are jointly captured by the statistical construct of mean squared error (MSE) (Degroot, 1980), which characterizes how well a system behaves with respect to both bias and consistency. Our simulations showed that at an optimal criterion (Figure 1, 3rd panel), P(T) should be mildly skewed to the right under the present noise level. This means that an optimal system cannot afford to use a criterion that is low enough to guarantee that the first bit of the signal will always be detected; at such low criterion it would produce too many early false positives to upset the overall performance (Figure 1, 1st and 2nd panel). Similarly, an optimal system cannot afford to place the criterion too high since the signal would be missed too often and this would result in more uncertainty in the onset detection (Figure 1, 4th panel). Rather, it would use a criterion that is higher than the average signal strength. The signal would still be detected because the presence of noise is sufficient to push the signal over the criterion such that the system is actually most likely to report the true signal onset as T. Also, the signal lasts for more than one sampling point, such that even if the signal is not detected immediately at the first point, it is likely to be detected shortly afterward.

We achieved similar qualitative results by varying the length of the trial epoch and the stimulus interval, as well as the signal-to-noise ration, thus confirming that our results are not dependent on the particular values of these variables.

The Kornhuber–Deecke–Libet Paradox

We then simulated how an optimal system would determine the onset of a slowly ramping-up signal, in order to shed light on the mechanism underlying introspective reports of the onset of motor preparation (see Introduction).

Figure 2 shows the simulated distribution P(T) under different criterion levels, for a signal that has a shape similar to the RP (duration = 2 s, S/N at the peak of the signal = 5). The choice of signal-to-noise ratio was motivated by previous electrophysiological studies. For example, Kargo and Nitz (2004) recorded from cells in the monkey motor cortex and reported the ratio of mean spiking rate to the SD of the spiking rate to be between 2 and 6 and to increase with training. These values are in agreement with similar measurements from the monkey pre-motor and motor cortex (Crammond and Kalaska 2000; Lecas et al. 1986; Churchland et al., 2006).

FIGURE 2

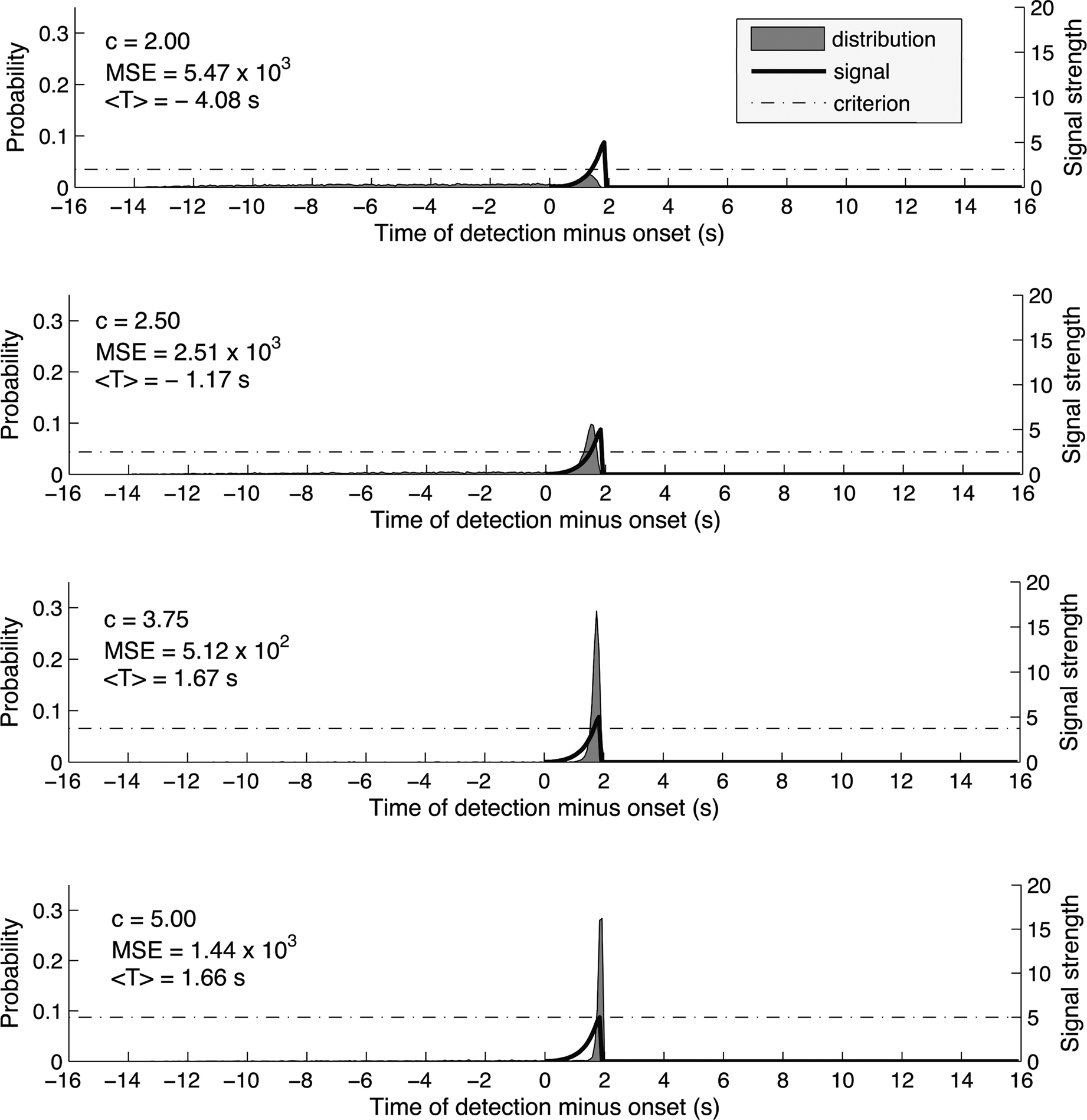
Figure 2. As in Figure 1 we used a trial epoch duration of 16 s and 200 time bins. The signal was a log-sinusoidal function that approximates the shape of the readiness potential. Specifically the signal strength at time bin n is s(n) = (s_peak/2)*{1−sin[log(−(n−a)/T)]}, where s_peak is the peak signal strength (we used 5 times the SD of the noise distribution), a = signal onset + signal duration and T = signal duration/exp(pi/2). We computed the distributions for 23 values of the criterion, from c = 0 to c = 5.5 by simulating 10,000 signal detection tasks. Again, as the criterion for detection increased, so did the mean estimated onset<T>. The mean square error (MSE) first decreased and then increased again, reaching its minimum for c = 3.75. Thus, the optimal detection strategy is achieved for c = 3.75 and produces an average estimate of the onset 1.67 s later than the true onset of the signal.

One could see that at the optimal criterion, the expected time of reported onset, i.e., expected T, is much later than the onset of the signal where it begins to ramp up. The reason for this late T is the ramping-up shape of the signal. In order to detect the earliest onset, the system would need to set a criterion almost as low as baseline. But at that criterion, given the presence of noise, the system’s performance would be upset by a high amount of early false positives. In order to reduce variability, the optimal system would set a higher criterion, inducing a bias toward late detection in order to maintain a reasonable level of consistency.

Attentional Prior Entry

Psychophysical findings (Stelmach and Herdman, 1991; Jaskowski, 1993; Shore et al., 2001; Spence et al., 2001; Schneider and Bavelier, 2003) support the principle of attention prior entry (Titchener, 1908), which states that attended stimuli are perceived faster than unattended stimuli. However, an electrophysiological study reported no corresponding temporal difference between the neural signals for attended and unattended stimuli (McDonald et al., 2005). In that study, attentional prior entry was associated with changes in the strength, not the timing, of neural responses to visual targets. We investigated whether our model can account for these surprising results.

We assume that attention boosts the signal-to-noise ratio of a true signal, either by increasing the signal magnitude, reducing the noise level, or both. Figure 3 (left panels) shows the P(T) associated with two similar signals with different signal-to-noise ratio, assuming that the system behaves optimally in both situations. One can see that for the stronger signal (lower left panel), P(T) is less skewed to the right, as compared to the weaker signal (upper left panel). This is because if the signal is strong, it is more likely to be detected immediately after the true onset. The fact that the stronger signal is associated with a P(T) that is less skewed to right means that the expected value of T, or the statistical average T, for the stronger signal is going to be earlier than the expected value of T for the weaker signal, even if the actual signal onsets are the same for both, and importantly, even if the most likely reported T (i.e., the peaks of the distributions) are the same for both. Because psychophysical experiments supporting the law of prior entry typically use a temporal-order-judgment (TOJ) procedure in which subjects determine which of two stimuli come first over many trials, the results correspond to the statistical average or expected value of T. This value would be earlier when the signal-to-noise ratio is high.

FIGURE 3

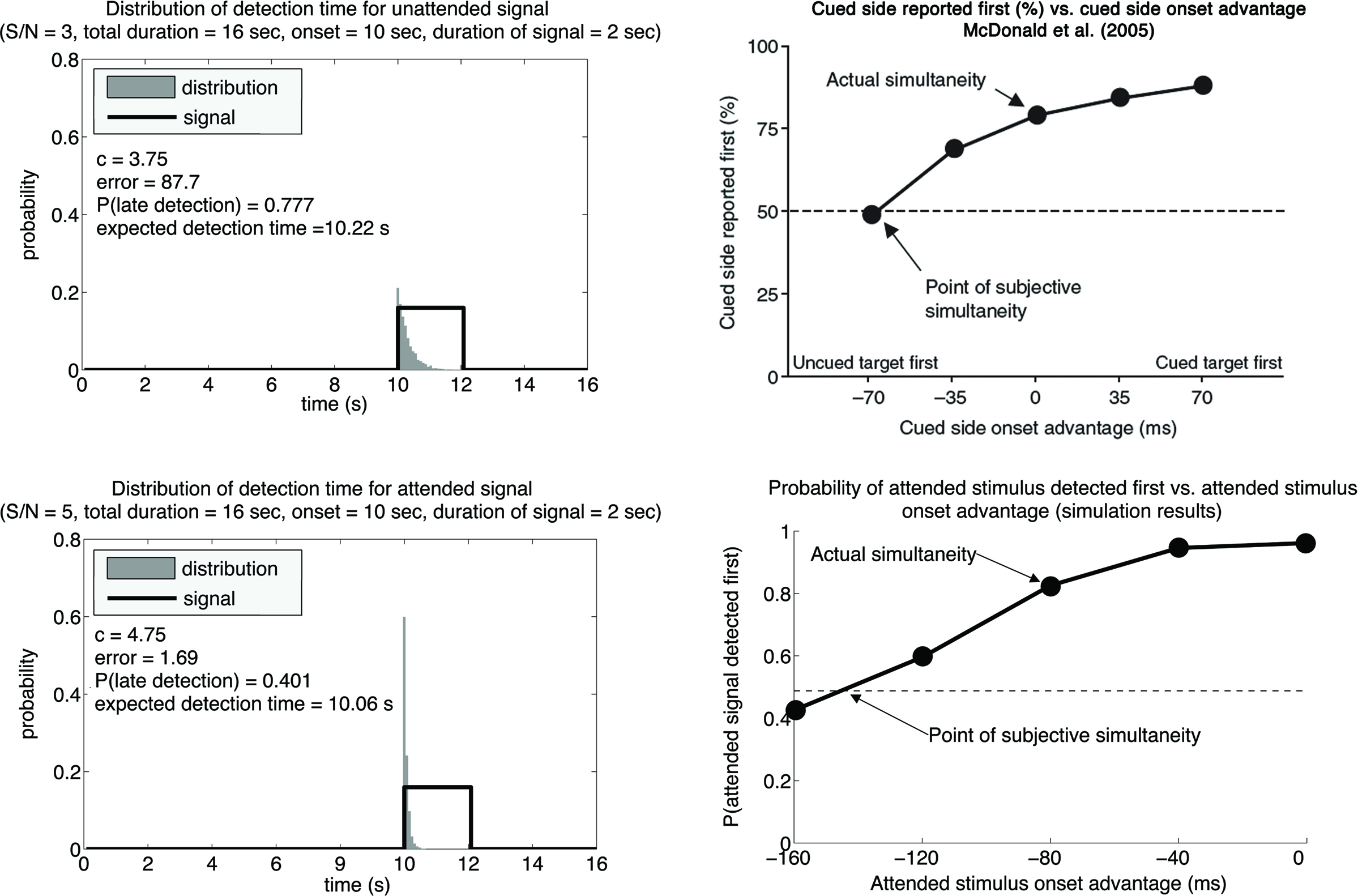
Figure 3. Left panels: We set the duration of the trial epoch to 16 s and the signal onset to the 10th second of the trial epoch. The signal was a step function with signal-to-noise ration of either 3 (upper panel) or 5 (lower panel) simulating an unattended and an attended condition. In the former case the optimal criterion was c = 3.75 resulting in 220 ms delay for the onset estimate; in the latter case the optimal criterion was c = 4.75 resulting in 60 ms delay for the onset estimate. This shows that lower signal-to-noise ratios result in later optimal estimates of the signal onset. Right panels: Data obtained by varying the cued onset advantage. Upper panel shows the data obtained by McDonald et al. (2005). Lower panel shows data simulated by our signal detection model. For each value of the onset advantage we first computed the optimal criterion for the attended and unattended signals (signal-to-noise ratios of 5 and 3, respectively) and then compared the average onset detection in each case. Each estimation was done on the basis of 10,000 trials. We qualitatively approximated the experimental data by McDonald et al.

To make this point more clear, we have extended our model to stimulate a TOJ experiment. Figure 3 (upper right panel) shows the actual data supporting prior entry adapted from McDonald et al. (2005). Figure 3 (lower right panel) shows the simulated data from our model. It can be seen that if attention changes the signal-to-noise ratio for a stimulus, our model predicts results that are qualitatively similar to the actual data.

Discussion

Summary of Results

Our model provides an explanation to the apparent contradiction in the Kornhuber–Deecke–Libet paradox. The RP is averaged over many trials. Although it may reflect the shape of the underlying signal, the brain does not have the luxury of averaging when it has to make a decision in real time after each motor action. The early part of the RP might be on average higher than baseline, but in fact the signal-to-noise ratio is weak, as compared to the later part of the preparatory activity. To detect the earliest part, the system would have to use a very low criterion and may therefore suffer from low consistency because of the false alarms generated. To detect the onset of the RP, the brain must set a certain criterion by taking into account the trade-off between bias and consistency. Our analysis suggests that the optimal trade-off would mean that a reasonably consistent system would give a sufficiently large late bias. This may explain why we are only aware of the later part of the preparatory activity. The findings by Libet et al. (1983) and Kornhuber and Deecke (1965) may therefore be consistent with the possibility that the brain is behaving close to optimality, given the presence of noise.

Second, our model also helps to explain the discrepancy of results regarding attentional prior entry. Previous work has failed to find shifts of ERP onsets that reflect the behavioral effect that attention seems to speed up perception. McDonald et al. (2005) specifically suggested that the behavioral effect of attention prior entry may be associated with down-stream decisional mechanisms. Our model captures what such mechanism may be. Specifically, one could judge a sensory stimulus to arise earlier than another one even when the sensory signals underlying both of them have the same onset. An increase in signal-to-noise ratio, which is likely to be induced by attention, would be sufficient to increase the likelihood for a stimulus to be judged as arising early. This is especially salient when we average the results of temporal judgments over many trials. A reasonably sensitive system should detect the onset of a stimulus relatively accurately on most trials. However, there might be a small portion of trials in which the onset was detected late, because the early part of the signal was missed due to chance fluctuation. When we look at averaged results over many trials, these “late” detection trials would play a role. We assume that attention boosts signal-to-noise ratio, and thereby reduces these “late” detection trials, which means the attended stimuli would be judged as arising earlier on average.

Limitations of the Model

Is the model we proposed here realistic? Admittedly, it is unlikely that the brain treats each data point independently and performs signal detection on each of them. This is an abstraction that allows ease of computation and illustration. However, we have also tried augmenting the model such that it accumulates evidence over time (Ratcliff and McKoon, 2008), or performs temporal smoothing of the data before the onset is determined retrospectively (Rao et al., 2001). A third model incorporates Poisson-like neural noise with positive baseline neuronal activity (Ma et al., 2006). All of these models produced similar results thus providing evidence that our conclusion do not depend on the specific parameters of our model (see Supplementary Materials for details). The reason for that is that the key characteristic of the model (the necessity of a high criterion in order to minimize the total amount of error) is present in all of the above versions. So long as there is uncertainty and onset is defined as the first instance where the signal passes a criterion, all of our arguments hold and the results are to be expected.

In our model, we assume that the brain tries to minimize error in its onset judgments, even for endogenously generated signal (i.e., the motor preparation activity, or “intention”). Is this a reasonable assumption? How can the brain compute the MSE for such judgments given that the true onset of the motor preparation activity is not known? We acknowledge it is unclear how the brain can achieve this exact computation. It is likely that the brain does not directly compute MSE in such situations, but rather uses some heuristics developed from other situations where the true onset of the event can be verified. However, it is important to note that our argument does not depend on the brain actually computing the exact value of the MSE. Our argument, as in many other modeling studies (e.g., “Bayesian” models, Ma et al., 2006), is that our results would be obtained if the brain was engineered to try to achieve some kind of optimality. Whereas we do not know for sure whether the brain is exactly engineered to perform this way, such assumptions form a reasonable basis for building a model, which can then allow us to compare the results of the model to actual data. In our case, by assuming some kind of error minimization, we found that we can explain the two paradoxes quite well.

The idea that a high criterion would predict late onset detection is not new. In fact, Libet et al. (1983) suggested that if a subject used a high threshold (or criterion), this will predict a late onset detection of the RP, thus explaining why the felt intention was late in their results. However, Libet et al. suggested that the system would still need to decide when to start applying such a threshold, or in the case of a random-walk-like model (see Figure S2 in Supplementary Material), when to start accumulating evidence. They further suggested that such evidence accumulation mechanisms “would have to be initiated at the onset of averaged RP, preceding the achievement of threshold for the decision” (Libet et al., 1983, p. 637). This means that the system or the observer would still need to be aware of the approximate onset of the RP for such mechanisms to work. We do not agree. In our model, the observer has no knowledge of the onset of the signal. Instead, a criterion is applied throughout and the system constantly accumulates evidence. The reason why constant accumulation is needed is precisely because the system could not know when is the true onset of the RP; if this were known, there would be no need for using a threshold in the first place. Our model demonstrates that even if the averaged onsets of the RP is not known, the system or the observer can still try to achieve the most optimal detection time given that the signal is embedded in noise.

The parameters chosen for the model may seem ad hoc. But our modest goal here is mainly to demonstrate as an example case of how this could work conceptually. We have not been able to provide analytic solutions to some most of the optimization problems yet. We hope future work can address these issues.

A related criticism could be that the model does not specify the neuronal mechanism underlying onset detection. Currently the exact neuronal mechanism is unknown, and we hesitate to speculate about such details. The model we propose is on a more abstract, general cognitive level. A useful analogy is that signal detection theory has been useful for perception research even though a neuronal mechanism for detection criterion has not been specified. In fact, recent work in neurophysiology tends to adopt diffusion-style models (Gold and Shadlen, 2007) which, unlike signal detection theory, take into account the dynamics of the decision process. However, this should not mean that the basic concept of signal detection theory is irrelevant. Our model can be similarly considered as a conceptual device that allows us to resolve certain controversies and paradoxes in time perception. The key ingredient behind this conceptual device is the idea that the brain needs to deal with noise and uncertainty, regardless of the exact mechanism.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Stanislav Nikolov, Department of Mathematics, Massachusetts Institute of Technology; Dobromir A. Rahnev and Hakwan C.Lau, Department of Psychology, Columbia University. We thank Will Penny, Matt Davidson and Brian Maniscalco for helpful input. Hakwan C. Lau is supported by an internal grant from Columbia University.

Supplementary Material

The Supplementary Material for this article can be found online at http://www.frontiersin.org/psychology/consciousness research/paper/10.3389/fpsyg.2010.00037/

References

Battelli, L., Walsh, V., Pascual-Leone, A., and Cavanagh, P. (2008). The “when” parietal pathway explored by lesion studies. Curr. Opin. Neurobiol. 18, 120–126.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brass, M., and Haggard, P. (2008). The what, when, whether model of intentional action. Neuroscientist 14, 319–325.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Carrasco, M., and McElree, B. (2001). Covert attention accelerates the reate of visual information processing. Proc. Natl. Acad. Sci. U.S.A. 98, 5363–5367.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chater, N., Tenenbaum, J., and Yuille, A. (2007). Probabilistic models of cognition: conceptual foundations. Trends Cogn. Sci. 10, 287–291.

CrossRef Full Text

Churchland, M. M., Santhanam, G., and Shenoy, K. V. (2006). Preparatory activity in premotor and motor cortex reflects the speed of the upcoming reach. J. Neurophysiol. 96, 3130–3146.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Coull, J. T., Vidal, F., Nazarian, B., and Macar, F. (2004). Functional anatomy of the attentional modulation of time estimation. Science 303, 1506–1508.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Crammond, D. J., and Kalaska, J. F. (2000). Prior information in motor and premotor cortex: activity during the delay period and effect on pre-movement activity. J. Neurophysiol. 84, 986–1005.

Pubmed Abstract | Pubmed Full Text

Deecke, L., and Kornhuber, H. H. (1978). An electrical sign of participation of the mesial “supplementary” motor cortex in human voluntary finger movement. Brain Res. 159, 473–476.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Degroot, M. (1980). Probability and Statistics, 2nd edn. MA: Addison–Wesley.

Eagleman, D. M., Tse, P. U., Buonomano, D., Janssen, P., Nobre, A. C., and Holcombe, A. O. (2005). Time and the brain: how subjective time relates to neural time. J. Neurosci. 25, 10369–10371.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gold, J. I., and Shadlen, M. N. (2007). The neural basis of decision making. Annu. Rev. Neurosci. 30, 535–574.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Green, D., and Swets, J. (1966). Signal Detection Theory and Psychophysics. New York: John Wiley and Sons, Inc.

Jaskowski, P. (1993). Selective attention and temporal-order judgment. Perception 22, 681–689.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kargo, W. J., and Nitz, D. A. (2004). Improvements in the signal-to-noise ratio of motor cortex cells distinguish early versus late phases of motor skill learning. J. Neurosci. 25, 5560–5569.

CrossRef Full Text

Kersten, D., Mamassian, P., and Yuille, A. (2004). Object perception as Bayesian inference. Annu. Rev. Psychol. 55, 271–304.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kornhuber, H., and Deecke, L. (1965). Hirnpotentialänderungen bei Willkürbewegungen und passiven Bewegungen des Menschen: Bereitschaftspotential und reafferente Potentiale. Pflugers Arch. Gesamte Physiol. Menschen Tiere 284, 1–17.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lecas, J. C., Requin, J., Anger, C., and Vitton, N. (1986). Changes in neuronal activity of the monkey precentral cortex during preparation for movement.J. Neurophysiol. 56, 1680–1702.

Pubmed Abstract | Pubmed Full Text

Leon, M. I., and Shadlen, M. N. (2003). Representation of time by neurons in the posterior parietal cortex of the macaque. Neuron 38, 317–327.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Libet, B., Gleason, C. A., Wright, E. W., and Pearl, D. K. (1983). Time of conscious intention to act in relation to onset of cerebral activity (readiness-potential). The unconscious initiation of a freely voluntary act. Brain, 106, 623–642.

CrossRef Full Text

Ma, W. J., Beck, J. M., Latham, P. E., and Pouget, A. (2006). Bayesian inference with probabalistic population codes. Nat. Neurosci. 9, 1432–1438.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

McDonald, J. J., Teder-Salejarvi, W. A., Di Russo, F., and Hillyard, S. A. (2005). Neural basis of auditory-induced shifts in visual time-order perception. Nat. Neurosci. 8, 1197–1202.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rao, R. P., Eagleman, D. M., and Sejnowski, T. J. (2001). Optimal smoothing in visual motion perception. Neural Comput. 13, 1243–1253.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ratcliff, R., and McKoon, G. (2008). The diffusion decision model: theory and data for two-choice decision tasks. Neural Comput. 20, 873–922.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Romo, R., and Schultz, W. (1987). Neuronal activity preceding self- initiated or externally timed arm movements in area 6 of monkey cortex. Exp. Brain Res. 67, 656–662.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schneider, K. A., and Bavelier, D. (2003). Components of visual prior entry. Cogn. Psychol. 47, 333–366.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shore, D. I., Spence, C., and Klein, R. M. (2001). Visual prior entry. Psychol. Sci. 12, 205–212.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Spence, C., Shore, D. I., and Klein, R. M. (2001). Multisensory prior entry. J. Exp. Psychol. Gen. 130, 799–832.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stelmach, L. B., and Herdman, C. M. (1991). Directed attention and perception of temporal order. J. Exp. Psychol. Hum. Percept. Perform. 17, 539–550.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Störmer, V. S., McDonald, J. J., and Hillyard, S. A. (2009). Cross-modal cueing of attention alters appearance and early cortical processing of visual stimuli. Proc. Natl. Acad. Sci. U.S.A. 106, 22456–22461.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Titchener, E. N. (1908). Lectures on the Elementary Psychology of Feeling and Attention. New York: Macmillan.

VanRullen, R., Carlson, T., and Cavanagh, P. (2007). The blinking spotlight of attention. Proc. Natl. Acad. Sci. U.S.A. 104, 19204–19209.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Vibell, J., Klinge, C., Zampini, M., Spence, C., and Nobre, A. C. (2007). Temporal order is coded temporally in the brain: early event-related potential latency shifts underlying prior entry in a cross-modal temporal order judgment task. J. Cogn. Neurosci. 19, 109–120.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text