- Department of Psychology, Vanderbilt University, Nashville, TN, USA
We investigated how mere exposure to complex objects with correlated or uncorrelated object features affects later category learning of new objects not seen during exposure. Correlations among pre-exposed object dimensions influenced later category learning. Unlike other published studies, the collection of pre-exposed objects provided no information regarding the categories to be learned, ruling out unsupervised or incidental category learning during pre-exposure. Instead, results are interpreted with respect to statistical learning mechanisms, providing one of the first demonstrations of how statistical learning can influence visual object learning.
Introduction
Humans can acquire knowledge about the structure of their environment by mere exposure through statistical learning (Saffran et al., 1996). This mechanism is thought to divide a nearly infinite number of element combinations into a small number of “chunks” (Orban et al., 2008). Consistent with statistical leaning, growing evidence from artificial scene and artificial grammar learning suggests that information about the visual and auditory environment can be learned without feedback through this kind of chunking mechanism (Knowlton and Squire, 1996; Saffran et al., 1999; Fiser and Aslin, 2001; Lany and Gomez, 2008).
While there is evidence that statistical learning occurs, evidence that it facilitates later learning is incomplete. Some role for statistical learning has been demonstrated in the speech domain (Graf Estes et al., 2007). Here, we investigated whether statistical learning of correlations between different dimensions1 of visual objects facilitates later learning to categorize those objects with feedback.
Conceivably, exposure could produce familiarity with object features, increasing their perceptual differentiation (e.g., Gibson and Gibson, 1955; Goldstone and Steyvers, 2001). Alternatively, correlations between dimensions of objects could be learned, creating meaningful “chunks” of visual features. For example, Fiser and Aslin (2001) showed that participants formed such chunks after unsupervised exposure to artificial “scenes” in which several complex shapes were arranged on a grid. Participants were able to learn “combos” of shapes whose relative positions in the grid were correlated during pre-exposure. They used the term statistical learning to describe this phenomenon and this is the terminology we continue to use here. A Bayesian model of statistical learning that aims to explain this chunk formation has been proposed by Orban et al. (2008).
Critically, we are not asking whether people incidentally learn object categories from exposure: Prior work suggests they can (Knowlton and Squire, 1993; Clapper and Bower, 1994; Ashby et al., 1999; Palmeri and Flanery, 2002; Wills et al., 2004). For example, in some of this previous work, participants are first exposed to objects that belong to one or more structured categories. After exposure, they are asked to perform tasks like deciding which objects in a test set belong to the exposed category or not, or they are asked to discriminate objects in terms of whether they belong in the same category or not based on the prior exposure. The interest of most of these studies lies in showing that categories are formed during pre-exposure. Through some mechanism, participants discover that a group of exemplars is similar to each other and dissimilar to another group of exemplars. Clapper and Bower (1994), for instance, examined how the order of presentation during pre-exposure is critical for eliciting this realization, whereby a new category is spontaneously formed when a group of similar exemplars is followed by a dissimilar oddball. Family resemblance and other graded category structures are well suited to these types of designs because they allow categorization of new exemplars based on similarity to exemplars of the pre-exposed category or categories.
In contrast to the formation of categories at pre-exposure, our concern here is the formation of perceptual chunks that can subsequently be used for various purposes, including category learning. Prioritized knowledge of such perceptual chunks could facilitate or hinder the solution of whatever problem the observer is faced with later. To investigate this issue, we needed to depart from family resemblance structures, both at pre-exposure and transfer. Indeed, the collections of pre-exposed objects in our experiment have no category structure relevant to what is learned later. Instead, we manipulated the correlational structure of the pre-exposed objects such that pairs of dimensions had values that were correlated with each other but not with other correlated dimension pairs.
Statistical learning could allow subjects to learn which object dimensions “go together” and which do not. During category learning, participants might then preferentially make use of conjunctions of dimensions that went together during pre-exposure. In order to test this hypothesis, we needed a category structure in which some combinations of dimensions had to be attended while others had to be ignored. Furthermore we wanted a structure that was complex enough so that participants would be discouraged from strategies like forming simple single-dimension rules and remembering exceptions (Nosofsky et al., 1994). An “exclusive or” rule applying to some feature combinations but not others fitted these requirements and allowed us to test the hypothesis of chunk formation at pre-exposure. Pre-exposure would facilitate category learning if the categorization rule required attention to previously correlated dimensions and would be detrimental if the categorization rule required attention to previously uncorrelated dimensions.
In this experiment, we manipulated the correlational structure of the objects at pre-exposure. Participants in all conditions then learned to categorize a set of new objects with feedback; specifically, there were two equal-size categories that could be distinguished based on an “exclusive or” rule applied to some combinations of two object dimensions (diagnostic combinations), but not other dimensions (non-diagnostic combinations). Critically, the statistical structure of the categorized objects was the same in all conditions for all participants. All that differed was the kind of pre-exposure they received.
Materials and Methods
Participants
A total of 137 Vanderbilt undergraduates and members of the general community participated; nine were dropped due to technical errors, leaving 128 participants, 79 female, with an average age of 20.4 and 14.0 years of education.
Stimuli
Pre-exposure objects
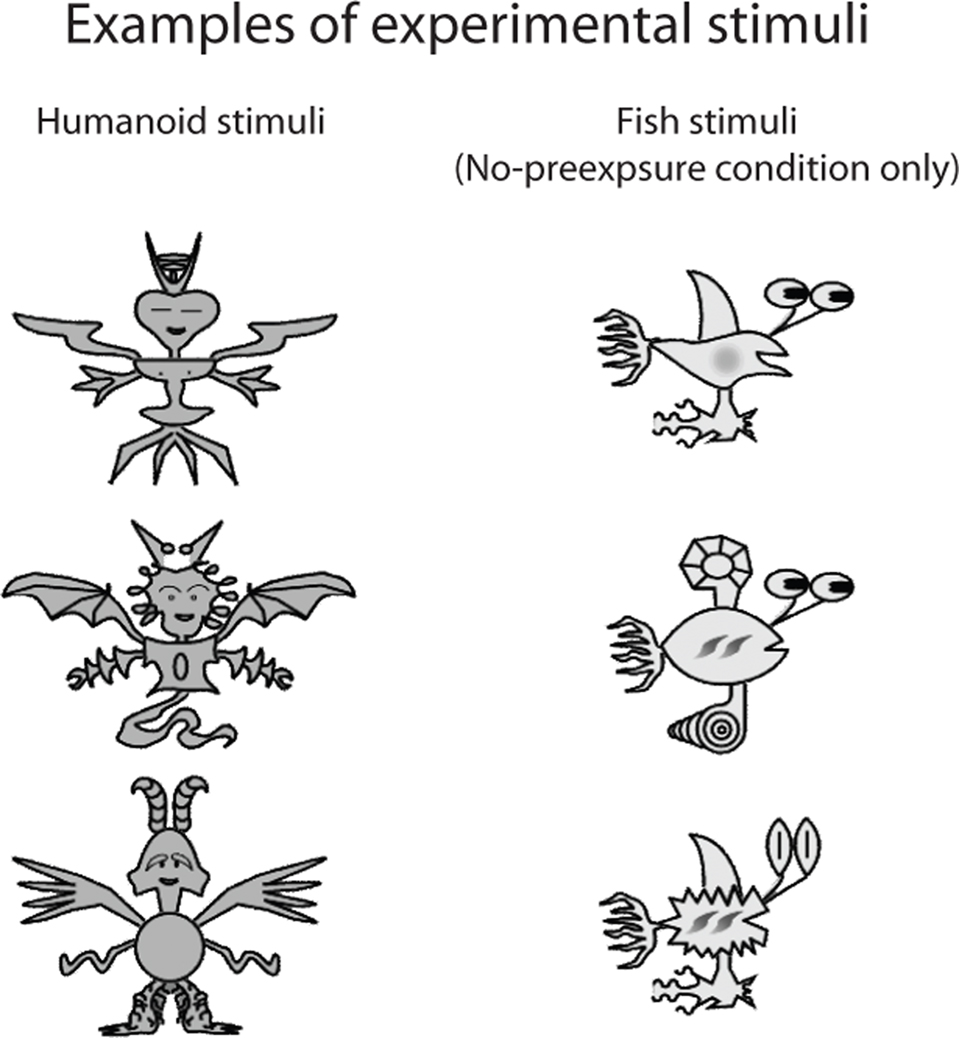
Novel objects were artificial humanoids (Figure 1), spanning ≈5.5° of visual angle. There were six dimensions (antenna, head, wings, body, arms, and legs) with five possible feature values for each one (antenna and legs had only four values as these dimensions were not manipulated experimentally, see below).
Participants were randomly assigned to one of four groups. Three groups were pre-exposed to humanoids, while the fourth group was a no-pre-exposure control. The three pre-exposure object sets varied in the kinds of correlations they contained across dimensions, but were perfectly matched in the frequency with which individual features occurred (abstract dimensional and feature structures for the pre-exposure conditions are included in the appendices). Of the six dimensions, four (head, wings, body, and arms) were manipulated experimentally and two (antennae and legs) were used as individuating features (specifically, antennae and legs were uncorrelated with each other and with any of the other four dimensions and had identical statistical properties in all conditions).
In the Correlated (Diagnostic) condition, the values of head and body were perfectly correlated and the values of wings and arms were perfectly correlated; this Correlated condition is deemed “Diagnostic” because during later category learning, the conjoint values of either the head and body or of the wings and arms were sufficient for perfect categorization. In the Correlated (Non-Diagnostic) condition, the values of head and wings were perfectly correlated and the values of body and arms were perfectly correlated; this Correlated condition is deemed “Non-Diagnostic” because the conjoint values of either the head and wings or the body and arms were insufficient for perfect categorization. In fact, this is an understatement: using the conjunctions of head and wings or body and arms in a categorization strategy would result in chance performance during category learning. There was a total of 32 objects in each Correlated stimulus set. These objects were randomly sampled during pre-exposure phase. All five values of each dimension were used in constructing the correlated pre-exposure stimulus sets.
In the Uncorrelated condition the pre-exposed objects had randomly assigned feature values along each of the four experimentally manipulated dimensions; all five values of each dimension were sampled.
Finally, the No-Pre-Exposure group saw no humanoid stimuli during pre-exposure; instead, they were exposed to a set of cartoon fish that had been used in other experiments.
Category learning objects
All four groups were trained to categorize the same 16 humanoids. Head, wings, body, and arms each varied across two equally frequent values, while antennae and legs varied across four values. While all five dimension values occurred during pre-exposure, none of the training exemplars had been experienced during pre-exposure. The humanoid objects could be categorized with perfect accuracy using either of two possible two-dimensional “exclusive or” rules requiring attention to two dimensions, for instance head and body. An object might always be in category A if it had either a furry head and square body or a bald head and a round body but never in category A if it had a furry head and a round body or a bald head and a square body. A rule with the same abstract structure could also be applied to the wing and arm dimensions. Critically, successful combinations used to categorize stimuli were head and body or wings and arms; these were the dimensions correlated in the Correlated (Diagnostic) condition of pre-exposure. Two combinations that could not be used to categorize the stimuli were head and wings or body and arms; these were the dimensions correlated in the Correlated (non-Diagnostic) conditions of pre-exposure.
Procedure
During pre-exposure, participants viewed a sequence of 480 pre-exposure humanoids. The Correlated (Non-Diagnostic) and Correlated (Diagnostic) groups each saw 15 random sequences of the 32 pre-exposure humanoids constructed for their respective conditions (480 trials). The Uncorrelated group saw a random set of 480 humanoids. The No-Pre-Exposure group saw a set if imaginary fish randomly selected over the 480 trials.
During pre-exposure, we asked participants to press the space bar whenever a stimulus was displayed off-center (12.5% of trials). Before pre-exposure, participants viewed a series of examples of fish stimuli (the same stimuli viewed in the No-Pre-Exposure condition) that were either on-center or off-center, labeled so that participants could understand how far off-center the stimuli had to be. Pre-exposure stimulus duration and ISI were 700 ms.
Following pre-exposure, participants in all four conditions were trained to categorize with feedback the same set of 16 stimuli, presented randomly over 35 blocks (560 trials). Each stimulus was presented for 1 s. “Mog” or “Nib” feedback, shown for 1 s, followed 300 ms after the response or 300 ms after the disappearance of the object.
Results
We analyzed accuracy and reaction time during category learning as a function of learning epoch (seven training epochs). Not surprisingly, accuracy increased and reaction time decreased over the course of learning [accuracy: F(6,744) = 68.71, MSe = 2.2, p < 0.0001; RT: F(6,744) = 23.1, MSe = 1.4, p < 0.0001]. However, given the difficulty of the exclusive or rule, accuracy in the last two learning epochs was bimodally distributed, with some participants near ceiling while others remained near chance; this occurred in all four conditions. Therefore, we divided our participants into high performing and low-performing groups based on a median split of accuracy during the last two epochs of category learning (epochs 6 and 7). Accuracy and mean correct response time in epochs 1–5 were then subjected to a between-subjects ANOVA with factors of Pre-exposure condition and Performance Group. This ensured that the data analyzed in the ANOVA differed from the data used to select groups, while limiting potential ceiling effects. Accuracy in high performers during epochs 1–5 was indeed superior to accuracy in lower performers [F(1,120) = 132.0, p < 0.0001].
Figure 2 shows that, in the High Performers Group only, accuracy was higher for the Uncorrelated and Correlated (Diagnostic) pre-exposure conditions than the Correlated (non-Diagnostic) and No-Pre-exposure conditions [main effect: F(3,120) = 5.06, MSe = 0.010, p < 0.005; Pre-exposure × Performance Group interaction: F(3,120) = 3.52, MSe = 0.010, p < 0.05]. Planned comparisons confirmed that, among High Performers, those in the Correlated (Diagnostic) and Uncorrelated conditions had higher accuracy than those in the Correlated (non-Diagnostic) and No-pre-exposure conditions [ts(30) > 2.2, p’s < 0.05]. Participants in the Uncorrelated and Correlated (Diagnostic) did not differ from each other, nor did those in the No-Pre-Exposure and Correlated (non-Diagnostic) conditions [ts(30) < 1]. In contrast, there were no effects of Pre-exposure among the Low Performers groups (Fs < 1).
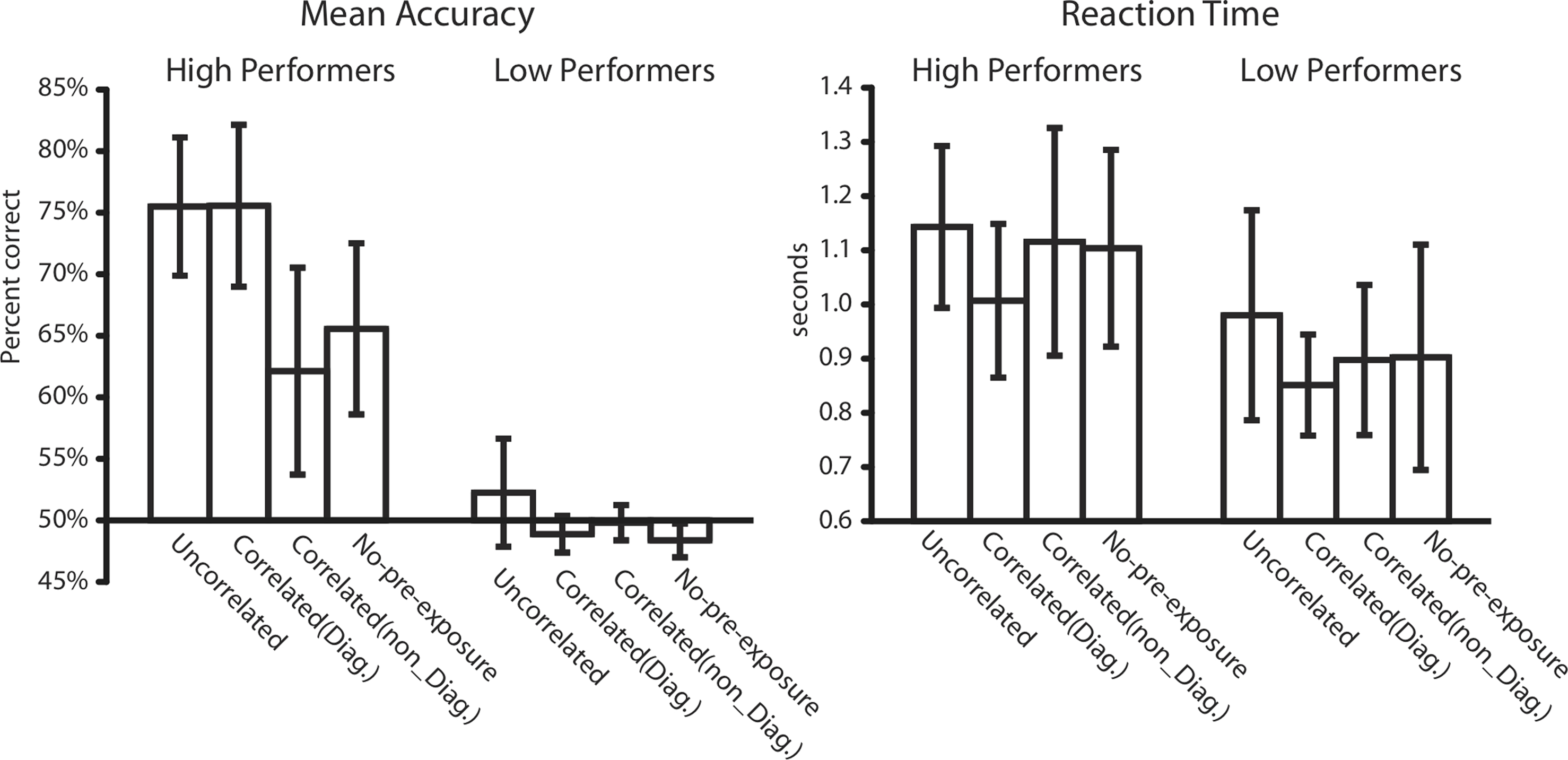
Figure 2. Mean accuracy and reaction time for Experiment 2, plotted separately for high and low performers. Error Bars are between-subjects 95% confidence intervals.
While correct response time was longer for high than low performers [F(1,120) = 10.8, MSe = 0.101, p < 0.005], response time differed little across pre-exposure conditions and Pre-exposure did not interact with Performance Group (Fs < 1).
Discussion
Our results suggest an effect of statistical learning during pre-exposure on later category learning. We hypothesize that if two dimensions have correlated values during pre-exposure, they might form a perceptual “chunk” that can be attended during category learning. This in turn could lead participants to test hypotheses about jointly attended features, speeding learning in the Correlated (Diagnostic) condition and slowing learning in the Correlated (Non-Diagnostic) condition. Based solely on the superior accuracy in the Correlated (Diagnostic) condition relative to the Correlated (non-Diagnostic) condition, statistical learning might have facilitated category learning, impaired category learning, or both. However, comparison to the Uncorrelated and No-Pre-Exposure conditions allows a more nuanced interpretation, whereby statistical learning may actually impair category learning by directing attention to counter-productive feature combinations.
First, superior performance of the Uncorrelated group over the No-Pre-Exposure group suggests an effect of feature familiarity. Because participants in the Uncorrelated group were pre-exposed to exemplars with randomly combined features, improvement cannot be accounted for by learning to jointly attend to dimensions with correlated values. Two possible reasons for this effect fall under the rubric of feature familiarity: One possibility is that Uncorrelated pre-exposure increased perceptual fluency with the stimulus features (e.g., Conroy et al., 2005), providing an advantage in encoding and remembering the dimension values. A second possibility is that this group acquired knowledge about the dimensional structure of the stimuli, and was thereby better able to test hypotheses or allocate attention more efficiently. For instance, they could have learned that all objects have the same number of parts in the same configuration, that hands do not constitute dimensions that are separate from arms, etc. Thus, participants in the Uncorrelated group might have had a head start relative to the No-pre-exposure group in knowing what the stimulus dimensions were and could thus test relevant hypotheses more quickly.
But feature familiarity cannot be the whole story. If it was, then performance in the Correlated (non-Diagnostic) pre-exposure condition should have been the same as the Uncorrelated condition, but it was not. Instead, it appears that statistical learning in the Correlated (non-Diagnostic) condition impaired category learning. Accuracy in the Correlated (non-Diagnostic) condition was no better than the No-Pre-Exposure condition, suggesting that the benefit of familiarity was counter-acted by some other variable – presumably statistical learning.
In our case, statistical learning seemed to impose a cost on later category learning, but it did not seem to provide a clear benefit. Performance in the Correlated (Diagnostic) condition was no better than the Uncorrelated baseline. This finding in itself highlights the importance of using both no-exposure controls and uncorrelated controls in future studies of possible transfer from statistical learning onto later explicit learning. Nevertheless, such a null result is not straightforward to explain. A lack of power or some complicated interaction of feature correlation and of a priori salience of particular dimensions could potentially explain this finding. Another possibility, however, is that something about the Uncorrelated condition was highly effective in boosting performance, such that it was more than a mere feature familiarity baseline. One possible explanation comes from theories of latent inhibition, which posit that correlated features are actually less salient than uncorrelated features (McLaren et al., 1989; McLaren and Mackintosh, 2000). Greater release from latent inhibition in the Uncorrelated relative to the Correlated conditions might have caused an extra boost in performance in the Uncorrelated condition; this possibility demands future research.
In closing, we investigated the effect of pre-exposure on subsequent category learning, when the pre-exposure phase contained no information about the categories to be later learned. We focused on three possible effects of pre-exposure: perceptual fluency with features, acquisition of dimensional structure, and formation of perceptual “chunks” as potential influences. Our results demonstrate that pre-exposure to objects can facilitate or impair category learning. The inferior performance of the Correlated (non-Diagnostic) group relative to the Correlated (Diagnostic) and Uncorrelated groups demonstrates that participants encoded relationships between object features during pre-exposure. Category learning can lead to the creation of new object features from combinations of subfeatures (Schyns and Rodet, 1997; Goldstone, 2000). Mere exposure can facilitate the recognition of repeated spatial configurations of novel shapes embedded in “artificial scenes” (Fiser and Aslin, 2001). Like in Fiser and Aslin, in this study, perceptual chunks were formed during pre-exposure, not during category learning. Also like Fiser and Aslin, in our study, the correlated features were clearly distinct, somewhat spatially separated parts and their combination did not form gestalt wholes, unlike the features used in the studies by Goldstone (2000) and Schyns and Rodet (1997). So it may be more prudent to interpret our findings in terms of joint attention to learned conjunctions rather than in terms of the formation of novel single features through “unitization.”
Pre-exposure facilitated category learning in both the Uncorrelated and Correlated (Diagnostic) conditions. The advantage of the Uncorrelated condition over the No-Pre-Exposure condition demonstrates that pre-exposure to the stimulus features themselves improved category learning, possibly through familiarization with the basic constraints of the stimulus set and learning the dimensional structure of the stimuli. More puzzling is the failure of the Correlated (Diagnostic) condition to cause better categorization performance than the Uncorrelated condition. This might have been caused by lack of salience of the particular correlated feature conjunctions in the Correlated (Diagnostic) condition or by greater latent inhibition in the Correlated than the Uncorrelated conditions.
Clearly, there remains much to learn about the specific mechanisms, perhaps many in kind, that allow unsupervised learning during exposure to objects to influence later supervised category learning. Therein lie interesting theoretical challenges and promising avenues in the design of more effective training programs for category learning.
Appendix
The tables below show the detailed abstract structure of the stimuli used in the experiment.
In each of the tables, columns represent a different stimulus dimension and rows represent different stimuli. Each number corresponds to a feature value for a given stimulus dimension – for instance, “1” in the arms column might refer to hairy arms and “2” might refer to tentacle arms. As appropriate, in some tables, the final column shows the category of the stimulus when the stimuli in the table are used within the category learning phase of that experiment.
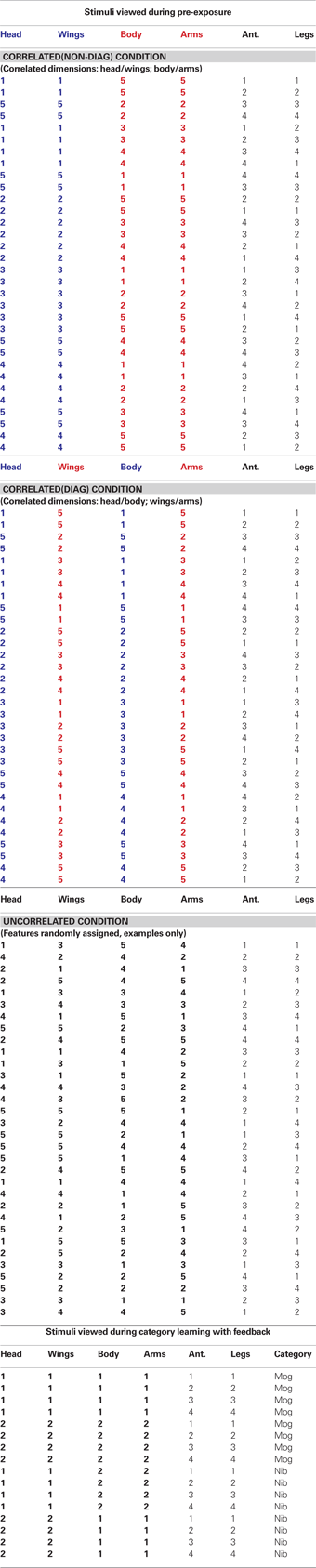
Note that the particular features that corresponded to particular numbers in the table were rotated across participants to ensure that results were not restricted to particular combinations of features. A total of four feature-to-number mappings were yoked across conditions so that participants in all conditions were exposed to the same feature-to-number mappings.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by the Temporal Dynamics of Learning Center (SBE-0542013), an NSF Science of Learning Center, and a grant from the James S. McDonnell Foundation. We thank Jenna Lea Green and Elise Masur for their assistance testing participants in the experiments.
Footnote
- ^Here, dimension refers to a component of an object that can vary systematically (e.g., the shape of the body), whereas feature refers to a particular value along a dimension (e.g., a square body).
References
Ashby, F. G., Queller, S., and Berretty, P. M. (1999). On the dominance of unidimensional rules in unsupervised categorization. Percept. Psychophys. 61, 1178–1199.
Clapper, J. P., and Bower, G. H. (1994). Category invention in unsupervised learning. J. Exp. Psychol. Learn. Mem. Cogn. 20, 443–460.
Conroy, M. A., Hopkins, R. O., and Squire, L. R. (2005). On the contribution of perceptual fluency and priming to recognition memory. Cogn. Affect. Behav. Neurosci. 5, 14–20.
Fiser, J., and Aslin, R. N. (2001). Unsupervised statistical learning of higher-order spatial structures from visual scenes. Psychol. Sci. 12, 499–504.
Gibson, J. J., and Gibson, E. J. (1955). Perceptual learning: differentiation or enrichment? Psychol. Rev. 62, 32–41.
Goldstone, R. L. (2000). Unitization during category learning. J. Exp. Psychol. Hum. Percept. Perform. 26, 86–112.
Goldstone, R. L., and Steyvers, M. (2001). The sensitization and differentiation of dimensions during category learning. J. Exp. Psychol. Gen. 130, 116–139.
Graf Estes, K., Evans, J. L., Alibali, M. W., and Saffran, J. R. (2007). Can infants map meaning to newly segmented words? Statistical segmentation and word learning. Psychol. Sci. 18, 254–260.
Knowlton, B. J., and Squire, L. R. (1993). The learning of categories: parallel brain systems for item memory and category knowledge. Science 262, 1747–1749.
Knowlton, B. J., and Squire, L. R. (1996). Artificial grammar learning depends on implicit acquisition of both abstract and exemplar-specific information. J. Exp. Psychol. Learn. Mem. Cogn. 22, 169–181.
Lany, J., and Gomez, R. L. (2008). Twelve-month-old infants benefit from prior experience in statistical learning. Psychol. Sci. 19, 1247–1252.
McLaren, I. P., Kaye, H., and Mackintosh, N. J. (1989). “An associative theory of the representation of stimuli: applications to perceptual learning and latent inhibition,” in Parallel Distributed Processing: Implications for Psychology and Neurobiology, ed. R. G. M. Morris (Oxford: Oxford University Press). 103–130.
McLaren, I. P., and Mackintosh, N. J. (2000). An elemental model of associative learning: I. Latent inhibition and perceptual learning. Anim. Learn. Behav. 28, 211–246.
Nosofsky, R. M., Palmeri, T. J., and McKinley, S. C. (1994). Rule-plus-exception model of classification learning. Psychol. Rev. 101, 53–79.
Orban, G., Fiser, J., Aslin, R. N., and Lengyel, M. (2008). Bayesian learning of visual chunks by human observers. Proc. Natl. Acad. Sci. U.S.A. 105, 2745–2750.
Palmeri, T. J., and Flanery, M. A. (2002). “Memory systems and perceptual categorization,” in The Psychology of Learning and Motivation, Vol. 41, ed. B. H. Ross (New York , NY: Academic Press). 141–189.
Saffran, J. R., Aslin, R. N., and Newport, E. L. (1996). Statistical learning by 8-month-old infants. Science 274, 1926–1928.
Saffran, J. R., Johnson, E. K., Aslin, R. N., and Newport, E. L. (1999). Statistical learning of tone sequences by human infants and adults. Cognition 70, 27–52.
Schyns, P. G., and Rodet, L. (1997). Categorization creates functional features. J. Exp. Psychol. Learn. Mem. Cogn. 23, 681–696.
Keywords: category learning, mere exposure, unsupervised learning, statistical learning, rule learning, cognition, classification learning, visual categorization
Citation: Folstein JR, Gauthier I and Palmeri TJ (2010) Mere exposure alters category learning of novel objects. Front. Psychology 1:40. doi: 10.3389/fpsyg.2010.00040
Received: 22 May 2010;
Paper pending published: 08 June 2010;
Accepted: 14 July 2010;
Published online: 10 August 2010
Edited by:
Emmanuel Pothos, Swansea University, UKReviewed by:
Fraser Milton, University of Exeter, UKWolf van Paemel, University of Leuven, Belgium
Copyright: © 2010 Folstein, Gauthier and Palmeri. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Jonathan R. Folstein, Department of Psychology, Vanderbilt University, PMB 407817, 2301 Vanderbilt Place, Nashville, TN 37240-7817, USA. e-mail: jonathan.r.folstein@gmail.com