- 1 Department of Methods and Statistics, Utrecht University, Utrecht, Netherlands
- 2 Department of Philosophy, Groningen University, Groningen, Netherlands
This mini-review illustrates that testing the traditional null hypothesis is not always the appropriate strategy. Half in jest, we discuss Aristotle’s scientific investigations into the shape of the earth in the context of evaluating the traditional null hypothesis. We conclude that Aristotle was actually interested in evaluating informative hypotheses. In contemporary science the situation is not much different. That is, many researchers have no particular interest in the traditional null hypothesis. More can be learned from data by evaluating specific expectations, or so-called informative hypotheses, than by testing the traditional null hypothesis. These informative hypotheses will be introduced while providing an overview of the literature on evaluating informative hypothesis.
Introduction
The present mini-review argues that testing the traditional null hypothesis is not always the appropriate strategy. That is, many researchers have no particular interest in the hypothesis “nothing is going on” (Cohen, 1990). So why test a hypothesis one is not really interested in? The APA stresses in its publication manual that null hypothesis testing should be a starting point for statistical analyses: “Reporting elements such as effect sizes and confidence intervals are needed to convey the most complete meaning of the results” (American Psychological Association, 2001, p. 33; see also Fidler, 2002). In the current paper we go beyond this first step of reporting effect sizes and confidence intervals, arguing that specific expectations should be evaluated directly. As Osborne (2010) stated: “The world doesn’t need another journal promulgating 20th century thinking, genuflecting at the altar of p < 0.05. I challenge us to challenge tradition” (p. 3). This is exactly what we set out to do in the current paper. Statistical tools for the evaluation of informative hypotheses are becoming available and are more often used in applications. We provide an overview of the current state of affairs for the evaluation of informative hypotheses. But first we argue, half in jest, what is “wrong” with the traditional null hypothesis and introduce the informative hypothesis.
One important prior note has to be made. Researchers like Wagenmakers et al. (2008) criticize T-tests for rendering no legitimate results and argue that p-values are prone to misinterpretation. Others, such as Coulson et al. (2010), or Fidler and Thompson (2001), explicitly argue against solely reporting p-values and argue for using confidence intervals. Along similar lines, using focused contrasts which could be used to evaluate expectations directly is proposed by Rosenthal et al. (2000). However, in the current paper we will focus on developments in statistics that move beyond using confidence intervals, effect sizes, and planned contrasts.
What is “Wrong” with the Traditional Null Hypothesis?
Cohen (1994) aptly summarized the criticism of traditional null hypothesis testing in the title of his paper “The earth is round (p < 0.05).” Let us elaborate on his criticism using an example inspired by this title originally meant to instruct and entertain.
The question of the shape of the earth was a recurring issue in scientific debate during the era of Aristotle (384–322 BC; see Rusell, 1997). By that time, the Greek idea that the earth was round dominated scientific thinking. The only serious opponents were the atomists Leucippus and Democritus, who still believed that the earth was a flat disk floating in the ocean, as certain ancient Mesopotamian philosophers had maintained. Now let us embark on some historical science fiction to tell the story of how Aristotle in his scientific investigations might have used different ways of evaluating hypotheses1.
We propose that in order to falsify the old Mesopotamian hypothesis, Aristotle might have used an approach based on testing the traditional null hypothesis:
H0: The shape of the earth is a flat disk,
H1: The shape of the earth is not a flat disk.
Clearly, these hypotheses are no statistical hypotheses and no actual statistical inference could have been carried out; these hypotheses are purely designed to serve as an example.
So, in the set up of our reverse science fiction, Aristotle would have gathered data about the shape of the earth and found evidence against the null hypothesis, for example: stars that were seen in Egypt were not seen in countries north of Egypt, while stars that never were beyond the range of observation in northern Europe were seen to rise and set in Egypt. Such observations could not be taken as evidence of a flat earth. H0 would have been rejected, leading Aristotle to conclude that the earth cannot be represented by a flat disk.
In actual fact, Aristotle agreed with Pythagoras (582 to ca. 507 BC), who believed that all astronomical objects have a spherical shape, including the earth. So, once again embarking on an episode of imaginary history, Aristotle might also have tested:
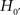 : The shape of the earth is a sphere,
: The shape of the earth is a sphere,
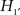 : The shape of the earth is not a sphere.
: The shape of the earth is not a sphere.
Now, imagine that Aristotle continued his search for data and that he gathered data yielding evidence against (!) the null hypothesis2: while standing on a mountain top, he noticed that the Earth’s surface has many irregularities and concluded that if enough irregularities could be observed, this might provide just enough evidence to reject the null hypothesis. And so it might have happened that Aristotle once again rejected the null hypothesis, concluding that the earth is not a sphere [Cohen: “The earth is round (p < 0.05)”].
What can be learned from this conclusion? Not much! Both hypothesis tests reject the traditional null hypotheses H0 and 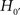 . As a next step, following the Neyman–Pearson procedure of hypothesis testing, we could tentatively adopt the alternative hypotheses H1 and
. As a next step, following the Neyman–Pearson procedure of hypothesis testing, we could tentatively adopt the alternative hypotheses H1 and 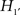 . This procedure tells us that the earth is neither a flat disk nor a sphere and consequently we remain ignorant of the earth’s actual shape. This ignorance is a result of the “catch-all” alternative hypothesis as proposed by Neyman and Pearson (1967). Unfortunately, the catch-all includes all shapes that are non-flat and non-spherical, for example pear-shaped3.
. This procedure tells us that the earth is neither a flat disk nor a sphere and consequently we remain ignorant of the earth’s actual shape. This ignorance is a result of the “catch-all” alternative hypothesis as proposed by Neyman and Pearson (1967). Unfortunately, the catch-all includes all shapes that are non-flat and non-spherical, for example pear-shaped3.
Rather than using the hypothesis tests given above, we might argue that Aristotle was actually interested in evaluating:
HA: The shape of the earth is a flat disk,
versus
HB: The shape of the earth is a sphere.
In such a direct comparison the conclusion will be more informative.
What does this Historical Example Teach Us?
Evaluating specific expectations directly produces more useful results than sequentially testing traditional null hypotheses against catch-all rivals. We argue that researchers are often interested in the evaluation of informative hypotheses and already know that the traditional null hypothesis is an unrealistic hypothesis. This presupposes that prior knowledge often is available; if this is not the case, testing the traditional null hypothesis is appropriate. In most applied articles, however, prior knowledge is indeed available in the form of specific expectations about the ordering of statistical parameters.
Let us illustrate this using an example of Van de Schoot et al. (2010). The authors investigated the association between popularity and antisocial behavior in a large sample of young adolescents from preparatory vocational schools (VMBO) in the Netherlands. In this setting, young adolescents are at increased risk of becoming (more) antisocial. Five so-called sociometric status groups were defined in terms of a combination of social preference and social impact: a popular, rejected, neglected, controversial, and an average group of adolescents. Each sociometric status group was characterized by distinct behavioral patterns which influenced the quality of social relations. For example, peer rejection was found to be related to antisocial behavior, whereas popular adolescents tended to be considered as well-known, attractive, athletic, and socially competent, although this group could also be antisocial, as was shown by Van de Schoot et al. (2010).
Suppose we want to compare these five sociometric status groups on the number of committed offenses reported to the police last year (minor theft, violence, and so on) and let the groups be denoted by μ1 for the mean on the number of committed offenses for the popular group, μ2 for the rejected group, μ3 for the neglected group, μ4 for the controversial group and μ5 for the average group. Different types of hypotheses can be formulated that are used in the procedures and are described in the remainder of this paper.
First, informative hypotheses can be formulated denoted by 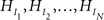 for a set of N hypotheses. These hypotheses contain information about the ordering of the parameters in a model, in our example the five means. Such expectations about the ordering of parameters can stem from previous studies, a literature review or even academic debate. Consider an imaginary hypothesis with inequalities between the five mean scores,
for a set of N hypotheses. These hypotheses contain information about the ordering of the parameters in a model, in our example the five means. Such expectations about the ordering of parameters can stem from previous studies, a literature review or even academic debate. Consider an imaginary hypothesis with inequalities between the five mean scores, 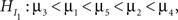 where the neglected group is expected to commit fewer offenses compared to the popular group, who in turn are expected to commit fewer offenses compared to the average group, and so on. If no information is available about the ordering, this is denoted by a comma. Another expectation could be the hypothesis
where the neglected group is expected to commit fewer offenses compared to the popular group, who in turn are expected to commit fewer offenses compared to the average group, and so on. If no information is available about the ordering, this is denoted by a comma. Another expectation could be the hypothesis 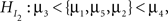 where the neglected group is expected to commit fewer offenses compared to the popular, average, and rejected groups. There is no expected ordering between these three groups, but all three are expected to commit fewer offenses than the controversial group. The research question would be which of the two informative hypotheses receives most support from the data.
where the neglected group is expected to commit fewer offenses compared to the popular, average, and rejected groups. There is no expected ordering between these three groups, but all three are expected to commit fewer offenses than the controversial group. The research question would be which of the two informative hypotheses receives most support from the data.
Second, there is the traditional null hypothesis (denoted by H0), which states that nothing is going on and all groups have the same score, H0: μ1 = μ2 = μ3 = μ4 = μ5. Third, if no constraints are imposed on any of the means and any ordering is equally likely, the hypothesis is called a “catch-all” alternative hypothesis, or an unconstrained hypothesis (denoted by HU): HU: μ1, μ2, μ3, μ4, μ5. In the next section we present an overview of possible alternatives for traditional null hypothesis testing to evaluate one or more informative hypotheses.
Evaluating Informative Hypotheses
Different procedures are described in a range of sources that allow for the evaluation of informative hypotheses. We present an overview of technical papers, software, and applications for two types of approaches: (1) hypothesis testing approaches and (2) model selection approaches. Note that we limit ourselves to a discussion of papers where software is available for applied researchers.
Hypothesis Testing Approach
Some approaches reported in the literature render a p-value for the comparison of HI with H0 or with HU. First, an adaptation of the traditional F-test for analysis of variance (ANOVA) was proposed by Silvapulle et al. (2002, see also Silvapulle and Sen, 2004), called the F-bar test. It is a confirmatory method to test one single informative hypothesis in two steps, for example:
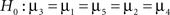
versus
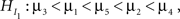
and
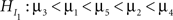
versus
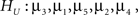
where in the second hypothesis test 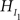 serves as the null hypothesis. Software for the F-bar test is described in Kuiper et al. (2010), but applications have not yet, to our knowledge, been reported in the literature. Application of the F-bar test is easy using the software4 and the results are comparable with a classical F-test. The disadvantage is that only one single informative hypothesis at a time can be evaluated and this only for univariate ANOVA.
serves as the null hypothesis. Software for the F-bar test is described in Kuiper et al. (2010), but applications have not yet, to our knowledge, been reported in the literature. Application of the F-bar test is easy using the software4 and the results are comparable with a classical F-test. The disadvantage is that only one single informative hypothesis at a time can be evaluated and this only for univariate ANOVA.
Testing informative hypotheses for structural equation models (SEM) is described in Stoel et al. (2006), where constraints are imposed on variance terms to obtain only positive values (see also Gonzalez and Griffin, 2001). A likelihood ratio test is used and the software is available in the statistical package R (R Development Core Team, 2005)5.
The procedure described in Van de Schoot et al. (2010) also makes use of a likelihood ratio test, but goes one step further than Stoel et al. (2006). A parametric bootstrap procedure is used in combination with inequality constraints imposed on regression coefficients. The methodology consists of several steps to be performed with the aid of commonly used software, Mplus (Muthén and Muthén, 2007)6. Van de Schoot and Strohmeier (in press) introduce the methodology to non-statisticians and show that using this method results in a power gain. That is, fewer participants are needed to obtain a significant effect compared to a default chi-square test.
Model Selection Approach
A second way of evaluating an informative hypothesis is to use a model selection approach. This is not a test of the model in the sense of hypothesis testing, rather it is an evaluation between statistical models using a trade-off between model fit and model complexity. Several competing statistical models may be ranked according to their value on the model selection tool used and the one with the best trade-off is the winner of the model selection competition.
There is a variety of model selection procedures commonly used in practical applications, most notably Akaike’s information criterion (AIC; Akaike, 1973), the Bayesian information criterion (BIC; Schwarz, 1978), and the deviance information criterion (DIC; Spiegelhalter et al., 2002). Problems with these standard model selection tools in the context of evaluating informative hypotheses arise because the tools are not equipped to deal with inequality constraints (Mulder et al., 2009a; Van de Schoot et al., under review-b). Although the model selection tools differ in their expression, the result always consists of two parts: the likelihood of the best fitting hypothesis within the model is a measure of model fit; and an expression containing the number of (effective) parameters of the model is a measure of complexity. The greater the number of dimensions, the greater the compensation for model complexity becomes. So, adding a parameter should be accompanied by an increase in model fit to accommodate for the increase in complexity. The problem is that the expression of complexity is based on the number of parameters in the model and cannot take inequality constraints into account. That is, 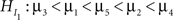 and
and 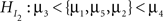 would receive the same measure for complexity, which is unwanted, because
would receive the same measure for complexity, which is unwanted, because 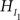 is more parsimonious than
is more parsimonious than 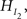 due to more restriction imposed on the five means.
due to more restriction imposed on the five means.
Alternative model selection tools have been proposed in the literature. First, an alternative model selection procedure is the paired-comparison information criterion (PCIC) proposed by Dayton (1998, 2003), with an application in Taylor et al. (2007). The PCIC is an exploratory approach which computes a default model selection tool for all logically possible subsets of group orderings. Only the source code for the programming language GAUSS was available for the PCIC (Dayton, 2001), but Kuiper and Hoijtink (2010) made the PCIC available in a user friendly interface7. The disadvantage of the PCIC is that it is an exploratory approach.
Second, the literature also contains one modification of the AIC that can be used in the context of inequality constrained ANOVA models. It is called the order-restricted information criterion (ORIC; Anraku, 1999; Kuiper et al., in press) with an application in Hothorn et al. (2009). It can be used for the evaluation of models differing in the order restrictions among a set of means. Inequality constraints are taken into account in the estimation of the likelihood and in the penalty term of the ORIC. Software for ORIC is described in Kuiper et al. (2010). The ORIC is as yet only available for ANOVA models, but a generalization is under construction.
Alternatives for the BIC and the DIC are under construction: see Romeijn et al. (under review) and Van de Schoot et al. (under review-a), respectively.
Finally, one other method of model selection, which is receiving more and more attention in the literature, involves the evaluation of informative hypothesis using Bayes factors. In this method each (informative) hypothesis of interest is provided with a “degree of support” which tells us exactly how much support there is for each of the hypotheses under investigation. This process involves collecting evidence that is meant to provide support for or against a given hypothesis; as evidence accumulates, the degree of support for a hypothesis increases or decreases.
The methodology of evaluating a set of inequality constrained hypotheses has proven to be a flexible tool that can deal with many types of constraints. We refer to the book of Hoijtink et al. (2008b), and the papers of Van de Schoot et al. (in press) and Van de Schoot et al. (2011) as a first step for interested readers. For a philosophical background, see Romeijn and Van de Schoot (2008) and for more information on hypothesis elicitation, see Van Wesel et al. (under review). Various papers describe comparisons between traditional null hypothesis testing and Bayesian evaluation of informative hypotheses; see Kuiper and Hoijtink (2010), Hoijtink et al. (2008b), Hoijtink and Klugkist (2007), and Van de Schoot et al. (2011).
Software is available for8:
– AN(C)OVA models (Klugkist et al., 2005; Kuiper and Hoijtink, 2010; Van Wesel et al., 2010) with an application in Van Well et al. (2009);
– Multivariate linear models including time-varying and time-invariant covariates (Mulder et al., 2009a,b) with an application in Kammers et al. (2009);
– Latent class analyses (Hoijtink, 2001; Laudy et al., 2005a) with applications in Laudy et al. (2005b) and Van de Schoot and Wong (in press);
– Order-restricted contingency tables (Laudy and Hoijtink, 2007; see also Klugkist et al., 2010) with applications in Meeus et al. (2010) and Meeus et al. (in press).
Conclusion
Statistics have come a long way since the early beginnings of testing the traditional null hypothesis of “nothing is going on.” Developments in statistics, in particular specific developments in the evaluation of informative hypothesis, allow researchers to directly evaluate their expectations specified with inequality constraints. This mini-review illustrates that testing the traditional null hypothesis is not always an appropriate strategy. We argued that more can be learned from data by evaluating informative hypotheses, than by testing the traditional null hypothesis. These informative hypotheses were introduced by means of an example. Finally, we presented the current state of affairs in the area of evaluating informative hypotheses.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgment
Supported by a grant from the Netherlands organization for scientific research: NWO-VICI-453-05-002.
Footnotes
- ^The historical figure Aristotle never denied that the earth was round; in fact, from the third century BC onward, no educated person in the history of Western civilization believed that the earth was flat. Indeed, Erasthenes (276–195 BC) gave a reasonable approximation of the earth’s circumference and provided strong support for the hypothesis that the earth is round.
- ^At the time, no one was able to see the earth as a whole and know it to be a sphere by direct observation. But it was possible to derive some conclusions from the hypothesis that the earth is a sphere and use these to test the null hypothesis. For example, one could predict that if someone sailed west for a sufficient amount of time, this person would return to the original starting point (Magellan did this). Or one could predict that if the earth was a sphere, ships at sea would first show their sails above the horizon, and then later, as they sailed closer, their hulls (Galileo observed this). These precise predictions, if exactly confirmed, would establish a provisional objective reality for the idea that the earth is a sphere.
- ^Admittedly, not all methodologists would agree on this point. In response to Aristotle’s imagined disappointment, Popper would have argued that this insight is all that Aristotelian science, or any science for that matter, can hope for. When it comes to general hypotheses, or hypotheses that are beyond the reach of direct verification, we can only be sure of their falsification. Direct positive evidence for hypotheses about the shape of the earth cannot be obtained, so there would be no reason for Aristotle to be disappointed. Popper would have argued that as there is no way to prove that the earth is spherical from direct verification, we can only hypothesize that it has the shape of a sphere. Since Aristotle found evidence demonstrating that the earth is not spherical, this hypothesis is rejected. In fact, according to Popperian reasoning, Aristotle should rejoice in the fact that at least he now knows the earth is not a sphere!
- ^The software can be downloaded at http://vkc.library.uu.nl/vkc/ms/research/ProjectsWiki/Informative%20hypotheses.aspx
- ^The corresponding scripts can be downloaded from the Web site of Psychological Methods.
- ^The software can be downloaded at staff.fss.uu.nl/agjvandeschoot
- ^The software can be downloaded at http://vkc.library.uu.nl/vkc/ms/research/ProjectsWiki/Informative%20hypotheses.aspx
- ^The software can be downloaded at http://vkc.library.uu.nl/vkc/ms/research/ProjectsWiki/Informative%20hypotheses.aspx
References
Akaike, H. (1973). “Information theory as an extension of the maximum likelihood principle,” in Second International Symposium on Information Theory, eds B. N. Petrov and F. Csaki (Budapest: Akademiai Kiado), 267–281.
American Psychological Association. (2001). Publication Manual of the American Psychological Association, 5th Edn. Washington, DC: Author.
Anraku, K. (1999). An information criterion for parameters under a simple order restriction. J. R. Stat. Soc. Series B 86, 141–152.
Coulson, M., Healey, M., Fidler, F., and Cumming, G. (2010). Confidence intervals permit, but do not guarantee, better inference than statistical significance testing. Front. Quant. Psychol. Meas. 1:26. doi: 10.3389/fpsyg.2010.00026
Gonzalez, R., and Griffin, D. (2001). Testing parameters in structural equation modelling: every “one” matters. Psychol. Methods 6, 258–269.
Fidler, F. (2002). The fifth edition of the APA publication manual: why its statistics recommendations are so controversial. Educ. Psychol. Meas. 62, 749–770.
Fidler, F., and Thompson, B. (2001). Computing correct confidence intervals for ANOVA fixed-and random-effects effect sizes. Educ. Psychol. Meas. 61, 575–604.
Hoijtink, H. (2001). Confirmatory latent class analysis: model selection using Bayes factors and (pseudo) likelihood ratio statistics. Multivariate Behav. Res. 36, 563–588.
Hoijtink, H., Huntjes, R., Reijntjes, A., Kuiper, R., and Boelen, P. (2008a). “An evaluation of Bayesian inequality constrained analysis of variance,” in Bayesian Evaluation of Informative Hypothesis, Chapter 5, eds H. Hoijtink, I. Klugkist, and P. A. Boelen (New York: Springer), 27–52.
Hoijtink, H., Klugkist, I., and Boelen, P. A. (2008b). Bayesian Evaluation of Informative Hypotheses. New York: Springer.
Hoijtink, H., and Klugkist, I. (2007). Comparison of hypothesis testing and Bayesian model selection. Qual. Quant. 41, 73–91.
Hothorn, L., Vaeth, M., and Hothorn, T. (2009). Trend tests for the evaluation of exposure-response relationships in epidemiological exposure studies. Epidemiol. Perspect. Innov. doi:10.1186/1742–5573–6–1 [Epub ahead of print].
Kammers, M., Mulder, J., De Vignemont, F., and Dijkerman, H. (2009). The weight of representing the body: addressing the potentially indefinite number of body representations in healthy individuals. Exp. Brain Res. 204, 333–342.
Klugkist, I., Laudy, O., and Hoijtink, H. (2005). Inequality constrained analysis of variance: a Bayesian approach. Psychol. Methods 10, 477–493.
Klugkist, I., Laudy, O., and Hoijtink, H. (2010). Bayesian evaluation of inequality and equality constrained hypotheses for contingency tables. Psychol. Methods 15, 281–299.
Kuiper, R. M., and Hoijtink, H. (2010). Comparisons of means using exploratory and confirmatory approaches. Psychol. Methods 15, 69–86.
Kuiper, R. M., Hoijtink, H. and Silvapulle, M. J. (in press). An Akaike-type information criterion for model selection under inequality constraints. Biometrika.
Kuiper, R. M., Klugkist, I., and Hoijtink, H. (2010). A fortran 90 program for confirmatory analysis of variance. J. Stat. Softw. 34, 1–31.
Laudy, O., Boom, J., and Hoijtink, H. (2005a). “Bayesian computational methods for inequality constrained latent class analysis,” in New Development in Categorical Data Analysis for the Social and Behavioral Sciences, eds A. V. der Ark and M. A. C. K. Sijtsma (London: Erlbaum), 63–82.
Laudy, O., Zoccolillo, M., Baillargeon, R., Boom, J., Tremblay, R., and Hoijtink, H. (2005b). Applications of confirmatory latent class analysis in developmental psychology. Eur. J. Dev. Psychol. 2, 1–15.
Laudy, O., and Hoijtink, H. (2007). Bayesian methods for the analysis of inequality constrained contingency tables. Stat. Methods Med. Res. 16, 123–138.
Meeus, W., Van de Schoot, R., Keijsers, L., Schwartz, S. J., and Branje, S. (2010). On the progression and stability of adolescent identity formation. A five-wave longitudinal study in early-to-middle and middle-to-late adolescence. Child Dev. 81, 1565–1581.
Meeus, W., Van de Schoot, R., Klimstra, T., and Branje, S. (in press). Change and stability of personality types in adolescence: A five-wave longitudinal study in early-to-middle and middle-to-late adolescence. Dev. Psychol.
Mulder, J., Hoijtink, H., and Klugkist, I. (2009a). Equality and inequality constrained multivariate linear models: objective model selection using constrained posterior priors. J. Stat. Plan. Inference 140, 887–906.
Mulder, J., Klugkist, I., Van de Schoot, R., Meeus, W., Selfhout, M., and Hoijtink, H. (2009b). Bayesian model selection of informative hypotheses for repeated measurements. J. Math. Psychol. 53, 530–546.
Muthén, L. K., and Muthén, B. O. (2007). Mplus: Statistical Analysis with Latent Variables: User’s Guide. Los Angeles, CA: Muthén & Muthén.
Neyman, J., and Pearson, E. (1967). Joint Statistical Papers. Cambridge: Cambridge University Press.
Osborne, J. W. (2010). Challenges for quantitative psychology and measurement in the 21st century. Front. Psychol. 1:1. doi: 10.3389/fpsyg.2010.00001
R Development Core Team. (2005). R: A Language and Environment for Statistical Computing [Computer software]. Vienna: R Foundation for Statistical Computing.
Romeijn, J. W., and Van de Schoot, R. (2008). “A philosopher’s view on Bayesian evaluation of informative hypotheses,” in Bayesian Evaluation of Informative Hypotheses, eds H. Hoijtink, I. Klugkist, and P. Boelen (New York: Springer), 329–358.
Rosenthal, R., Rosnow, R. L., and Rubin, D. B. (2000). Contrasts and Effect Sizes in Behavioral Research: A Correlational Approach. Cambridge: Cambridge University Press.
Rusell, J. B. (1997). Inventing the Flat Earth: Columbus and Modern Historians. Burnham: Greenwood Press.
Silvapulle, M. J., and Sen, P. K. (2004). Constrained Statistical Inference: Order, Inequality, and Shape Constraints. London: John Wiley Sons.
Silvapulle, M. J., Silvapulle, P., and Basawa, I. V. (2002). Tests against inequality constraints in semiparametric models. J. Stat. Plan. Inference 107, 307–320.
Spiegelhalter, D. J., Best, N. G., Carlin, B. P., and Van Der Linde, A. (2002). Bayesian measures of model complexity and fit. J. R. Stat. Soc. Series B 64, 583–639.
Stoel, R. D., Galindo-Garre, F., Dolan, C., and Van den Wittenboer, G. (2006). On the likelihood ratio test in structural equation modeling when parameters are subject to boundary constraints. Psychol. Methods 4, 439–455.
Taylor, S., Zvolensky, M. J., Cox, B. J., Deacon, B., Heimberg, R. G., Ledley, D. R., Abramowitz, J. S., Holaway, R. M., Sandin, B., Stewart, S. H., Coles, M., Eng, W., Daly, E. S., Arrindell, W. A., Bouvard, M., and Cardenas, S. J. (2007). Robust dimensions of anxiety sensitivity: development and initial validation of the anxiety sensitivity index-3. Psychol. Assess. 19, 176–188.
Van de Schoot, R., Hoijtink, H., and Deković, M. (2010). Testing inequality constrained hypotheses in SEM models. Struct. Equ. Modeling 17, 443–463.
Van de Schoot, R., Hoijtink, H., Mulder, J., Van Aken, M. A. G., Orobio de Castro, B., Meeus, W., and Romeijn, J.-W. (2011). Evaluating expectations about negative emotional states of aggressive boys using Bayesian model selection. Dev. Psychol. 47, 203–212.
Van de Schoot, R., Mulder, J., Hoijtink, H., van Aken, M. A. G., Dubas, J. S., de Castro, B. O., Meeus, W., and Romeijn, J.-W. (in press). Psychological functioning, personality and support from family: an introduction Bayesian model selection. Eur. J. Dev. Psychol.
Van de Schoot, R., and Strohmeier, D. (in press). Testing informative hypotheses in SEM Increases Power: An illustration contrasting classical hypothesis testing with a parametric bootstrap approach. Int. J. Behav. Dev.
Van de Schoot, R., and Wong, T. (in press). Do antisocial young adults have a high or a low level of self-concept? Self Identity. doi:10.1080/15298868.2010.517713 [Epub ahead of print].
Van Well, S., Kolk, A. M., and Klugkist, I. (2009). The relationship between sex, gender role identification, and the gender relevance of a stressor on physiological and subjective stress responses: sex and gender (mis)match effects. Int. J. Psychophysiol. 32, 427–449.
Keywords: null hypothesis testing, Bayesian analysis, informative hypothesis, inequality constraints
Citation: Van de Schoot R, Hoijtink H and Jan-Willem R (2011) Moving beyond traditional null hypothesis testing: evaluating expectations directly. Front. Psychology 2:24. doi: 10.3389/fpsyg.2011.00024
Received: 16 September 2010;
Accepted: 07 February 2011;
Published online: 22 February 2011.
Edited by:
Heather M. Buzick, Educational Testing Service, USAReviewed by:
Andrew Jones, American Board of Surgery, USAFiona Fidler, LaTrobe University, Australia
Copyright: © 2011 Van de Schoot, Hoijtink and Jan-Willem. This is an open-access article subject to an exclusive license agreement between the authors and Frontiers Media SA, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Rens Van de Schoot, Department of Methodology and Statistics, Utrecht University, P.O. Box 80.140, 3508 TC Utrecht, Netherlands. e-mail: a.g.j.vandeschoot@uu.nl
