How is information integrated across the attributes of an option when making risky choices? In most descriptive models of decision under risk, information about risk, and reward is combined multiplicatively (e.g., expected value; expected utility theory, Bernouli, 1738/1954; subjective expected utility theory, Savage, 1954; Edwards, 1955; prospect theory, Kahneman and Tversky, 1979; rank-dependent utility, Quiggin, 1993; decision field theory, Busemeyer and Townsend, 1993; transfer of attention exchange model, Birnbaum, 2008). That is, (some transform of) probability is multiplied by (some transform of) reward to give a value for a risky prospect, and the prospect with the maximum value is then chosen.
Here I argue that information integration in risky decision-making may be additive. Integration is additive in other domains and, if cognitive processes are shared, integration may be additive in risky choice too. Further, although valuations of risky prospects show multiplicative integration of risk and reward, integration is additive for judgments of attractiveness and, if risky decisions are based on attractiveness rather than valuation, integration in risky choice may be additive. Finally, I show that, for simple risky choices, an additive model can mimic a multiplicative model, and vice versa. Implications for the assessment of the stability of risky preference are profound – stable parameters in the multiplicative model will correspond with different stable parameters in the additive model and, further, the mode of integration itself may vary from time to time or context to context.
Judgments of Non-Risky Prospects
In a wide variety of decisions that do not involve risk, the additive model describes people’s valuation of options better than the multiplicative model. For example, people average across descriptive adjectives when judging the likeability of a person (Anderson, 1981). In consumers’ decision-making, information is averaged over attributes (Troutman and Shanteau, 1976). Prior expectancies are averaged with perceptual experiences in judging the quality of a wide variety of products (Dougherty and Shanteau, 1999). Preferences for sandwich and drink lunches involve an additive combination of information (Shanteau and Anderson, 1969). When pretending to be Father Christmas, children combine deservingness and achievement information additively to decide what present a child should receive (Anderson and Butzin, 1978). To the extent that common cognitive processes operate in all decisions, the additive model may also be operating in decisions involving risk.
Judgments of Risky Prospects
Buying prices, selling prices, bids, and certainty equivalents are often used to value risky options. For example, Tversky (1967a,b) had inmates give the minimum price for which they would sell an opportunity to play a simple gambles of the form “p chance of x otherwise nothing.” Tversky found that there was a p by x interaction when predicting price but not logarithm of price and thus Tverksy rejected the additive model and concluded that his data were well described by a subjective expected utility model with a power law utility function and a subjective probability function. This finding has been replicated with more complicated gambles of the form “p chance of gaining x and q chance of loosing y” (Anderson and Shanteau, 1970), when risks and rewards were presented as verbal phrases (e.g., “a somewhat likely chance to win a watch”) rather than as numbers (Shanteau, 1974), and for strength-of-preference judgments for pairs of gambles (Mellers et al., 1992a). In contrast, ratings of favorableness, attractiveness, and the likelihood of playing are better described by an additive model (Sjöberg, 1968; Levin et al., 1985; Mellers et al., 1992b; Mellers and Chang, 1994). Multiplicative integration for valuations and additive integration for attractiveness has been found within the same experiment (e.g., Mellers et al., 1992a; Mullet, 1992).
It is not obvious to me whether choices will be more closely linked to valuation or attractiveness judgments. To the best of my knowledge, no one has explicitly compared additive models with multiplicative models using choice data. It may be that an additive model proves successful.
The Importance of a Complete Choice Model
The information integration process cannot be considered in isolation from other cognitive steps. For example, because the logarithmic transform turns summing into multiplying [log(a) + log(b) = log(ab)] and an exponential transform turns multiplying into adding [exp(a) exp(b) = exp(a + b)], one must model the possible transformation of choice attributes into their subjective value, the integration of these values, and the translation of integrated values into a choice. In some circumstances multiplicative and averaging processes are equivalent. For example, Massaro and Friedman (1990) show that when information is combined additively in a perceptron (Rosenblatt, 1958) as a linear sum of input activations and a subsequent sigmoid transform is applied, this model is equivalent, for the case of two responses, to the (multiplicative) fuzzy logic model (Oden and Massaro, 1978).
Mathematical Specification of the Model
In the following modeling I show that a multiplicative and additive model can mimic one another. The valence V(pi, xi) of a simple risky outcome Gi of the form “pi chance of xi otherwise nothing” is given by
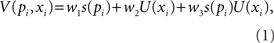
where s(.) is the subjective probability function and U(.) is the utility function and the subscript i indexes different gambles. Without loss of generality, I constrain the ws to be in the range 0–1 and w1 + w2 + w3 = 1. The restricted model with w1 + w2 = 1/2 and w3 = 0 is the additive model. The restricted model with w1 = w2 = 0 and w3 = 1 is the multiplicative model.
To provide a complete model of choice, I use Luce’s choice rule to give the probability of choosing gamble Gi from a set of N gambles.
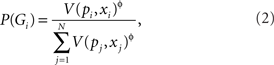
ɸ is a free parameter which produces chance responding when ɸ = 0 and increasingly deterministic as ɸ increases. Utility is assumed to be a power function of money:

where γ is a free parameter greater than zero. When 0 < γ < 1, the utility function is concave. Subjective probability is assumed to follow the form suggested by Wu and Gonzalez (1996):
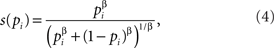
where β is a free parameter greater than zero. When 0 < β < 1, the subjective probability function has an inverse-S-shape.
Model Mimicry
To illustrate how additive and multiplicative models can mimic one another, I generated data from a base model with γ = 1/2, β = 2/3, ɸ = 1, and w1 = w2 = w3 = 1/3. The exact parameter values are not crucial to the argument. These values are loosely based on the well established findings of a concave utility function, an inverse-S-shaped probability weighting function, and probability matching. These particular w parameters give the subjective value of a gamble as the sum of the subjective probability, subjective utility, and their product.
The choice set used is the set of all possible choices of the form “p1 chance of x1 otherwise nothing” or “p2 chance of x2 otherwise nothing” that can be constructed using probabilities .1, 0.3, 0.5, 0.7, and 0.9 and amounts 20, 40, 60, 80, and 100. (In modeling, amounts were scaled for convenience by dividing by 100 so that amounts lay on the same interval, roughly, as probabilities.) Raw data take the form of the probability of choosing Gamble 1 according to the base model.
Figure 1 shows how the fit of the model to these data varies with the parameter choice. Fit is calculated as the likelihood that the model could generate the data. Obviously the base model which generated the data fits best. But other models fit well too. The panels in Figure 1 shows the likelihood surfaces as model parameters deviate away from the best fit. High points on the surface represent good model fits. Figure 1A show how such simple choices do not constrain the forms of the utility and weighting functions very well. The broad flat maximum on the likelihood surface shows that, although γ = 1/2 and β = 2/3 provides the best fit, these parameters can vary considerably with only a minimal effect on the model fit (see Zeisberger et al., in press). This is not of central concern here, but is quite often overlooked in modeling decision-making under risk. Figure 1B show how the model fit is affected by switching the mode of information integration. As w3 = 1 − w1 − w2 (without loss of generality), the points in the horizontal plane represent all possible mixtures of information integration. At the leftmost corner of the plot where w1 = w2 = 0 and w3 = 1 (i.e., a purely multiplicative model) the fit is somewhat compromised. The other two corners of the surface represent a model where only probability is weighted or where only amount is weighted, and are also similarly badly fitting. But for a ridge in the middle of the surface (the area colored red), quite large variation in the information integration has a small effect. Figure 1C shows the most important result. Here, the error surface is plotted as a function of ɸ, the determinism parameter in the Luce choice rule, and w3 [I constrained w1 = w2 = (1 − w3)/2 here]. There is a ridge of roughly equal likelihood which passes through the base model at ɸ = 1, w3 = 1/3 where the log likelihood of the data given the model is −200.972. At one end, where w3 = 0 and the model is completely additive, the log likelihood is −201.060. At the other end, where w3 = 1 and the model is completely multiplicative, the log likelihood is −201.308. This means that, whatever mode of integration one chooses for the model, it can be completely compensated for by varying the degree of determinism in the choice rule. The more additive the model, the higher the value of ɸ needed to compensate. This result holds for a purely additive base model and a purely multiplicative base model. In short, with choices between these simple gambles, one cannot discriminate between additive and multiplicative models of decision under risk.
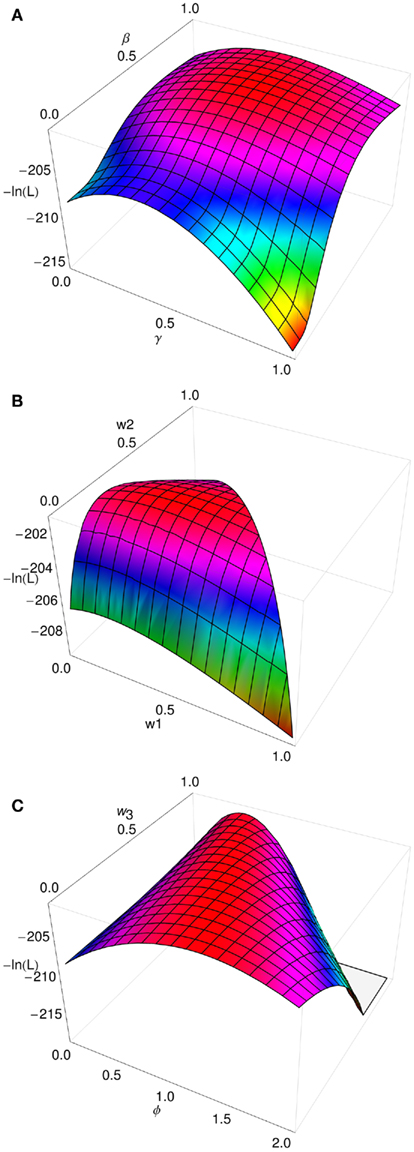
Figure 1. The (log) likelihood of the data given the model, ln (L). (A) A wide range of utility and weighting function parameters provide good fits. (B) A wide range of integration modes provide a good fit. (C) Any integration mode can be fitted by adjusting response determinism. Non-graphed parameters match those of the base model.
Discussion
This special issue is about the stability, or otherwise, of risky preferences across time or context. To assess the stability of preferences, one can identify and fit a model of risky choice to data from two or more times or contexts and then compare parameters across times or contexts (see Zeisberger et al., 2011, for a review). Here, I have suggested that information integration in risky choice may be additive rather than multiplicative. I have shown that, for two-branch choices with one non-zero branch, additive and multiplicative models can mimic one another. There are two implications of these findings for the stability of risky preferences. First, even if some parameter value are stable over time, this does not mean that correct model has been identified. Because an additive model can mimic a multiplicative model, stable parameters from the multiplicative model map on to stable-but different-parameters in the additive model: the data do not discriminate between models, and the parameter values from a particular model cannot be directly interpreted outside of the model. Second, even if there is stability in the utility and weighting functions (but see Stewart, 2009, for demonstrations of malleability), there may be variation in information integration over time or context. For example, Ordóñez and Benson (1997) find people switch integration rules under time pressure, and Mellers et al. (1992b) find that the mode of integration depends on the range of probabilities used in the question set.
In closing, I note that the ability of additive and multiplicative models to mimic one another offers an explanation for the success of the decision by sampling model I have proposed elsewhere (Stewart et al., 2006) in accounting for risky choice. In the model, attributes are selected and compared to other attributes in memory. Favorable comparisons are counted in an accumulator, and the prospect whose accumulator gets to threshold first is selected. Because, for each prospect, favorable comparisons are counted in a single accumulator, information about how well an amount compares to other amounts memory is effectively combined additively with information about how well a probability compares to other probabilities in memory. For example, the subjective value of a simple gamble like a “30% chance of winning $100” is effectively the proportion of probabilities in memory less than 30% (because the target 30% will compare favorably to these) plus the proportion of amounts in memory less than $100 (because the target $100 will compare favorably to these). Despite the decision by sampling model combining risk and reward information additively, it is able to fit, for example, the classic paradoxes in Kahneman and Tverksy (1979) prospect theory paper (see Stewart and Simpson, 2008; Stewart, 2009) because it can vary in the degree of determinism in responding by altering the threshold to which accumulators race. In short, psychologically plausible process models of risky decision-making need not have an explicit multiplicative integration of information to provide a good descriptive account.
References
Anderson, N. H., and Butzin, C. A. (1978). Integration-theory applied to children’s judgments of equity. Dev. Psychol. 14, 593–606.
Anderson, N. H., and Shanteau, J. C. (1970). Information integration in risky decision making. J. Exp. Psychol. 84, 441–451.
Bernouli, D. (1738/1954). Expositions of a new theory of the measurement of risk. Econometrica 22, 23–36.
Busemeyer, J. R., and Townsend, J. T. (1993). Decision field theory: a dynamic-cognitive approach to decision making in an uncertain environment. Psychol. Rev. 100 432–459.
Dougherty, M. P. R., and Shanteau, J. (1999). Averaging expectancies and perceptual experiences in the assessment of quality. Acta Psychol. (Amst) 101, 49–67.
Kahneman, D., and Tversky, A. (1979). Prospect theory: an analysis of decision under risk. Econometrica 47, 263–291.
Levin, I. R., Johnson, R. D., Russo, C. P., and Delden, P. J. (1985). Framing effects in judgment tasks with varying amounts of information. Organ. Behav. Hum. Decis. Process. 36, 362–377.
Massaro, D. W., and Friedman, D. (1990). Models of integration given multiple sources of information. Psychol. Rev. 97, 225–252.
Mellers, B. A., and Chang, S. (1994). Representations of risk judgments. Organ. Behav. Hum. Decis. Process. 57, 167–184.
Mellers, B. A., Chang, S. J., Birnbaum, M. H., and Ordóñez, L. D. (1992a). Preferences, prices, and ratings is risky decision-making. J. Exp. Psychol. Hum. Percept. Perform. 18, 347–361.
Mellers, B. A., Ordóñez, L. D., and Birnbaum, M. H. (1992b). A change-of-process theory for contextual effects and preference reversals in risky decision making. Organ. Behav. Hum. Decis. Process. 52, 331–369.
Mullet, E. (1992). The probability (utility rule in attractiveness judgments of positive gambles. Organ. Behav. Hum. Decis. Process. 52 246–255.
Oden, G. C., and Massaro, D. W. (1978). Integration of featural information in speech perception. Psychol. Rev. 85, 172–191.
Ordóñez, L. D., and Benson, L. (1997). Decisions under time pressure: how time constraint affects risky decision making. Organ. Behav. Hum. Decis. Process. 71, 121–140.
Quiggin, J. (1993). Generalized Expected Utility Theory: The Rank-Dependent Model. Norwell, MA: Kluwer Academic Publishers.
Rosenblatt, F. (1958). The perceptron: a probabilistic model for information storage and organization in the brain. Psychol. Rev. 65, 386–408.
Shanteau, J. C., and Anderson, N. H. (1969). Test of a conflict model for preference judgment. J. Math. Psychol. 6, 312–325.
Sjöberg, L. (1968). Studies of the rated favorableness of offers to gamble. Scand. J. Psychol. 9, 257–273.
Stewart, N. (2009). Decision by sampling: the role of the decision environment in risky choice. Q. J. Exp. Psychol. 62, 1041–1062.
Stewart, N., and Simpson, K. (2008). “A decision-by-sampling account of decision under risk,” in The Probabilistic Mind: Prospects for Bayesian Cognitive Science, eds L. N. Chater and M. Oaksford (Oxford, England: Oxford University Press), 261–276.
Troutman, C. M., and Shanteau, J. (1976). Do consumers evaluate products by adding or averaging attribute information? J. Consum. Res. 3, 101–106.
Tversky, A. (1967a). Utility theory and additivity analysis of risky choices. J. Exp. Psychol. 75, 27–36.
Wu, G., and Gonzalez, R. (1996). Curvature of the probability weighting function. Manage. Sci. 42, 1676–1690.
Citation: Stewart N (2011) Information integration in risky choice: identification and stability. Front. Psychology 2:301. doi: 10.3389/fpsyg.2011.00301
Received: 12 July 2011;
Accepted: 11 October 2011;
Published online: 15 November 2011.
Copyright: © 2011 Stewart. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: neil.stewart@warwick.ac.uk
