- 1 Department of Psychology, University of Kansas, Lawrence, KS, USA
- 2 Computer Engineering Department, Istanbul Kultur University, Istanbul, Turkey
- 3 Department of Biostatistics, University of Kansas Medical Center, Kansas City, KS, USA
Network science describes how entities in complex systems interact, and argues that the structure of the network influences processing. Clustering coefficient, C – one measure of network structure – refers to the extent to which neighbors of a node are also neighbors of each other. Previous simulations suggest that networks with low C dissipate information (or disease) to a large portion of the network, whereas in networks with high C information (or disease) tends to be constrained to a smaller portion of the network (Newman, 2003). In the present simulation we examined how C influenced the spread of activation to a specific node, simulating retrieval of a specific lexical item in a phonological network. The results of the network simulation showed that words with lower C had higher activation values (indicating faster or more accurate retrieval from the lexicon) than words with higher C. These results suggest that a simple mechanism for lexical retrieval can account for the observations made in Chan and Vitevitch (2009), and have implications for diffusion dynamics in other fields.
Introduction
Collections of interconnected units, or networks, have long been used in various domains in Cognitive Science (e.g., artificial neural networks, Rosenblatt, 1958; McClelland et al., 1986; networks of semantic memory, Quillian, 1967; Collins and Loftus, 1975; linguistic nections, Lamb, 1970). Recent developments in other fields including mathematics, physics, and computer science have sparked interest in a new type of network analysis known as network science (Watts, 2004; see also Jasny et al., 2009). In the network science approach, nodes represent entities, and links represent simple relationships between entities in a complex system. A fundamental assumption of network science is that the large-scale structure of the system has consequences for the dynamics of that system (Watts and Strogatz, 1998).
To give a concrete example, consider a social system comprised of people who are friends with each other. In a network science analysis of this system, nodes would represent individual people, and links would represent friendships between particular people (alternatively, links could be defined by financial exchanges between people, sexual relationships, etc.). How widely and quickly disease (e.g., Balcan et al., 2009) or innovations (Valente, 1995) spread through that social network depends on who is connected to whom. Another example of how network structure influences network dynamics can be seen in studies of the efficiency of search algorithms in various types of networks (e.g., Kleinberg, 2000).
Network science is often used to model complex social, biological, and technological systems (for reviews see Albert and Barabási, 2002; Boccaletti et al., 2006; Newman, 2010). However, this approach has also been used to model complex cognitive systems (for an application to neural systems see Sporns et al., 2004), and has provided novel insights into several domains of cognition including semantic memory (Steyvers and Tenenbaum, 2005; for a review see Borge-Holthoefer and Arenas, 2010a), language development (Hills et al., 2009a,b), and lexical retrieval (Vitevitch, 2008). Previous psychological research in each of these cognitive domains has identified and thoroughly examined a myriad of characteristics about individual words – such as the frequency, length, and concreteness of a word – that influence processing. What is relatively less studied and understood in the psychological perspective is – for lack of a better term – the collective behavior of words. That is, how does a group of words facilitate or interfere with the processing of a given word. (For psycholinguistic work that begins to examine this issue at the phonological level see Luce and Pisoni, 1998 and at the semantic level see Nelson et al., 1993.) Network science offers researchers a novel set of tools to explore such interactions among entities in large systems, and motivated the present work.
Using the network science approach, Vitevitch (2008) constructed a network from approximately 20,000 English words in which nodes in the network represented phonological word-forms, and (unweighted, undirected) links between nodes indicated phonological similarity between words. Two words were phonologically similar if a single phoneme could be substituted, added, or deleted from one word to form the other word. This psychologically valid metric (see Experiment 2 of Luce and Large, 2001) is widely used in psycholinguistic research to assess similarity between two words (e.g., Luce and Pisoni, 1998; see also Greenberg and Jenkins, 1967), and is more generally referred to as Levenshtein distance. Analysis of the phonological network in English revealed several structural features that were also found in phonological networks of Spanish, Mandarin, Hawaiian, and Basque (Arbesman et al., 2010; see Arbesman et al., 2010 for additional discussion of how phonological networks differ from other systems). Given the presence of these structural features in the phonological networks of several languages, Chan and Vitevitch(2009, 2010) wondered how certain network structures might influence language processing.
Of the variety of measurements that are often used to describe the structure of a network, two are most relevant to the present investigation: degree and clustering coefficient. Degree refers to the number of connections that a node has. In the context of the phonological network of Vitevitch (2008), degree corresponds to the number of word-forms that sound similar to a given word (based on the one-phoneme metric described above). In the psycholinguistic literature, this measure is referred to as phonological neighborhood density (Luce and Pisoni, 1998), but we will use the term degree to maintain consistency with the network perspective that motivated the present study. (This does not mean we are reinventing, or redefining the term “neighborhood density” in any way; we simply wish to use the term degree to maintain consistency with the network science literature that motivated the present study.) Much psycholinguistic research has demonstrated that degree influences a variety of language-related processes including spoken word production (e.g., Vitevitch, 2002b; Vitevitch and Stamer, 2006, 2009), spoken word recognition (e.g., Luce and Pisoni, 1998; Vitevitch, 2002a), word learning (e.g., Storkel et al., 2006), reading (Yates et al., 2004), and serial recall (e.g., Roodenrys et al., 2002). In Figure 1, degree corresponds to the lines that connect the words badge and log to their respective neighbors (note that both words have 13 neighbors).
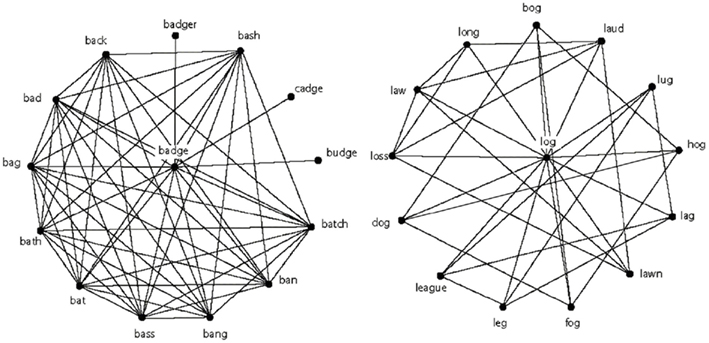
Figure 1. The word badge has high C and the word log has low C, but both words have the same number of neighbors (a.k.a. degree). In these networks, connections are placed between words that are phonologically similar using the one-phoneme metric described in the text. For the sake of visual clarity, connections from the neighbors to other words in the lexical network are not shown.
In contrast to degree, the clustering coefficient, C (Watts and Strogatz, 1998), measures the extent to which neighbors of a given node are also neighbors of each other. This characteristic is represented in Figure 1 by the lines that connect a neighbor of badge and log to another neighbor of badge and log. C ranges from 0 (none of the immediate neighbors of a node are connected to each other) to 1 (all of the immediate neighbors of a node are fully interconnected). In the present study, C (i.e., the local clustering coefficient for an undirected graph) was computed for each word as in [Eq.1]:

ejk refers to the presence of a connection (or edge) between two neighbors (j and k) of node i, |…| is used to indicate cardinality, or the number of elements in the set (not absolute value), and ki refers to the degree (i.e., neighborhood density) of node i. Thus, the (local) clustering coefficient is the number of connections that actually exist among the neighbors of a given node divided by the number of connections that could possibly exist among the neighbors of a given node.
Just as degree has demonstrable influences on various language-related processes, C has been shown to influence the processes of spoken word recognition and production (Chan and Vitevitch, 2009, 2010). In all current models of spoken word recognition, auditory input partially activates a number of words in long-term memory that resemble the input (McClelland and Elman, 1986; Norris, 1994; Luce and Pisoni, 1998). From those similar sounding candidates, one word is recognized as the word that was heard, and its meaning is retrieved from long-term memory resulting in comprehension. Chan and Vitevitch (2009) found in two word recognition tasks – perceptual identification, where listeners indicate the word that they heard in the presence of white noise, and lexical decision, where listeners indicate whether the stimulus was a real word in English or a made-up word, like “foosh” – that words with high C (badge in Figure 1) were responded to more slowly and less accurately than words with low C (log in Figure 1), even though the words were equivalent on a number of other characteristics (e.g., degree, frequency of occurrence, etc.).
To account for these observations, Chan and Vitevitch (2009) offered a verbal description of the spoken word recognition process inspired by the network science approach. Note that current models of spoken word recognition view the mental lexicon as a collection of arbitrarily ordered phonological representations, and the process of lexical retrieval as a special instance of pattern matching. Lexical retrieval occurs in these models because a given word-form best matches the acoustic–phonetic input (or other sources of evidence). Chan and Vitevitch (2009) instead suggested that the mental lexicon could be viewed as a (small-world) network, and lexical retrieval could be viewed as a search through that network, much like the PageRank algorithm (Page et al., 1998) searches through the structured network of information that is the World-Wide Web. Interestingly, Griffiths et al. (2007) demonstrated that the PageRank algorithm could be used in a semantic network constructed from word association data to predict performance of participants who were shown a letter of the alphabet and asked to name the first word beginning with that letter that came to mind.
In the present report we used a network simulation to examine the verbal description that Chan and Vitevitch (2009) gave for the process of spoken word recognition. In the description of their findings, Chan and Vitevitch (2009) started with the network structure for the phonological lexicon observed by Vitevitch (2008). Overlaying that structure was the additional assumption that “activation” would “spread” from an initially activated node to the nodes that it was connected to, and then on to the nodes that they in turn were connected to (which included the node from which activation was initially received). Although other models of cognitive processing often include additional parameters such as inhibition, decay of activation, threshold levels, etc., no such assumptions were made in the description offered by Chan and Vitevitch (2009).
In the case of a word with low C in the mental lexicon (log in Figure 1), Chan and Vitevitch (2009) suggested that the small number of interconnections among the neighbors would result in some of the activation from the neighbors spreading back to the target word, and the remaining activation dispersing to the rest of the network (i.e., words related to the neighbors of log, but not shown in Figure 1). The strongly activated target word, log, would “stand out” from the less activated neighbors (and less activated neighbors of neighbors), resulting in rapid and accurate retrieval from the lexicon of target words with low C.
In the case of a word with high C in the mental lexicon (badge in Figure 1), where the neighbors are highly interconnected with each other, most of the activation will remain amongst the interconnected neighbors rather than spread back to the target word or to the rest of the network as happens for words with low C. With a highly activated target word as well as highly activated neighbors, discrimination of the target word becomes more difficult, resulting in slower and less accurate retrieval of target words with high C from the lexicon. Note that for words with high C, activation will spread to the target word and to the rest of the lexicon, but to a lesser extent than for words with low C. Furthermore, given the different way in which activation disperses in the two types of networks, the amount of activation that a word with high C ends up with is likely to be less than the amount of activation that a word with low C ends up with. This additional difference in the amount of activation for words with high versus low C might also contribute to the processing differences observed in Chan and Vitevitch (2009).
To more precisely examine the description of spoken word recognition offered by Chan and Vitevitch (2009), we simulated the spread of activation across small networks that had the same degree (i.e., phonological neighborhood density), but varied in C. (See Lewandowsky (1993) for the benefits of computationally examining even simple verbal descriptions.) The concept of spreading activation is commonly used to model the search process in various domains of cognition. More broadly speaking, the concept of spreading activation resembles diffusion dynamics in network science; that is, how a disease or a fad spreads across a system. Previous network simulations of diffusion dynamics by Newman (2003; see also Naug, 2008) demonstrated that information (or disease) will spread widely across a network with low clustering coefficient, but in a network with high clustering coefficient information/disease will be constrained to a more restricted region of the network. (For examples of studies exploring diffusion dynamics in cognitively relevant domains see Borge-Holthoefer and Arenas, 2010b, and Borge-Holthoefer et al., 2011.)
Although the account offered by Chan and Vitevitch (2009) is consistent with the results of the simulation by Newman (2003), it is important to note that Newman (2003) assessed how widely “activation” would be dispersed in the network (or how many nodes would be “infected”), not how the dispersion of activation affected a specific item. In the present simulation we directly examined how the spreading of activation in networks that varied in clustering coefficient influenced the final activation value of a specific node, simulating the retrieval of that item from the mental lexicon.
Materials and Methods
Although there is much value in using mathematically abstract networks to examine network dynamics (as in Newman, 2003), we instead selected nodes from the phonological network analyzed in Vitevitch (2008) in order to more directly and more realistically examine how lexical structure might influence lexical processing. Each node in this network represented a phonological word-form (not a semantic concept), and (unweighted, bidirectional) links connected nodes that were phonologically related to each other (based on the substitution, addition, or deletion of one phoneme in a word, a Levenstein distance of 1; Luce and Pisoni, 1998). The full network analyzed in Vitevitch (2008) contained 19,340 nodes, had a mean degree (<k>) equal to 9.105, an average path length (ℓ) equal to 6.05, an average clustering coefficient of 0.126, a network density of 0.001, a degree distribution that deviated from a power-law, and exhibited assortative mixing by degree.
Recall that the nodes in the network examined in Vitevitch (2008) corresponded to phonological word-forms. Degree refers to the number of connections per node. In the context of the phonological network examined in Vitevitch (2008) degree referred to the number of “phonological neighbors” that a word had. The average path length referred to the number of connections that had to be traversed to connect any two nodes in the (largest component of the) network. For example, to get from the word cat to the word dog, one can traverse the links between the nodes corresponding to the words bat, bag, and bog.
The clustering coefficient, C, characterizes the extent to which neighbors of a node are also neighbors of each other. A clustering coefficient of 0 indicates that none of the neighbors of a node are neighbors of each other, whereas a value of 1 indicates that all of the neighbors of a node are neighbors of each other (Watts and Strogatz, 1998). It is important to note that degree and clustering coefficient are independent measures. As reported in Chan and Vitevitch (2010), the correlation between degree, k, and C for the 6,281 words with two or more neighbors (the minimum number of neighbors required to compute C) from the network examined in Vitevitch (2008) is r = 0.005, p = 0.68. That is, a word with many neighbors, k, could have high or low C. Similarly, a word with few neighbors, k, could have high or low C. Furthermore, we did a correlation analysis between C and k for the items used in the present simulation and found that r (22) = −0.24 (p = 0.25), indicating that there is no correlation between C and k for the items used in the present simulation.
Conceptually similar to the clustering coefficient is the measurement known as network density, which measures the number of connections that exist in an entire network in relation to the maximal number of connections that could exist in that network. A network density value near 0 indicates that there are actually few connections in the network compared to the number of connections that could exist in the network. A network density value near 1 indicates that the number of connections in the network is approaching the maximal number of connections that could exist in the network. (The term “network density” is from the field of network science, and should not be confused with the term “phonological neighborhood density” from the field of psycholinguistics.)
The degree distribution refers to the proportion of nodes that have a given number of links. Networks with degree distributions that follow a power-law are called scale-free networks, and have attracted attention because of certain structural and dynamic properties (Albert and Barabási, 2002). See Vitevitch (2008) and Arbesman et al. (2010) for a discussion of why the degree distribution of phonological networks is likely to deviate from a power-law.
Assortative mixing by degree refers to the way in which nodes connect to each other; specifically a highly connected node tends to connect to other nodes that are also highly connected (Newman, 2002). In other words, there is a positive correlation between the degree of a node and the degree of its neighbors. See Arbesman et al. (2010) for a discussion of the processing implications of this network characteristic.
In the present simulation, we wished to examine the influence of C on processing in nodes with a wide range of degree. Twelve pairs of nodes ranging in degree from 3 to 40 were selected from the lexical network in Vitevitch (2008). Even though the nodes in each pair had the same degree, one node in each pair had low C, and the other node in the pair had high C. The nodes in each pair were chosen such that C for each node 0 < C < 1, and the difference in clustering coefficient between the nodes was maximal (with the node having the minimal value of C being classified as having low C, and the node having the maximal value of C being classified as having high C). For nodes with low degree, the difference in clustering coefficient tended to be in the range of 0.2–0.3. However, for nodes with higher degree, there were fewer nodes to select from and the difference in clustering coefficient was less; these items were, nevertheless, included in the simulation. Overall the difference in C between the low C nodes (mean = 0.21; SD = 0.06) and the high C nodes (mean = 0.46; SD = 0.12) was statistically significant [t(22) = 6.38, p < 0.0001].
In addition to extracting the 24 target nodes from the larger network analyzed in Vitevitch (2008), we also extracted the neighbors of each target, as well as the neighbors of the neighbors (i.e., the two-hop neighborhood) from the larger network to create 24 “mini” networks. The two-hop neighborhood allowed us to simulate the spread of activation to (admittedly a smaller-scale version of) the rest of the network. Figure 2 shows an illustration of the one-hop and the two-hop neighborhood of a node.
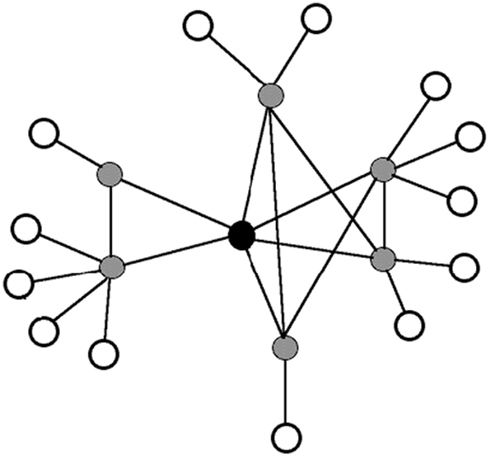
Figure 2. An illustration of a one-hop and two-hop neighborhood. The target node is shown in black, the neighbors of the target node are shown in gray (i.e., one-hop neighbors of the target node), and the neighbors of the neighbors are shown in white (i.e., two-hop neighbors of the target node). For visual clarity, only a few connections among nodes are drawn.
For the 24 mini-networks – each consisting of a target word, its neighbors, and the neighbors of the neighbors – we computed network density to verify that the High and Low C networks were comparable in number of nodes and number of connections in the networks. There was no statistically significant difference in network density for the words with low C (mean = 0.075 neighbors; SD = 0.06) and the words with high C [mean = 0.084 neighbors; SD = 0.06; t(22) = 0.35, p = 0.72]. Values of degree, clustering coefficient, and network density for the selected nodes can be found in Table A1 in the Appendix.
Note that the present simulation uses an abstraction of or simply the structural relationships among nodes found in the phonological network examined in Vitevitch (2008). The identity of the nodes (i.e., the word corresponding to that node), as well as other variables that are typically examined in psycholinguistic experiments – word frequency, word length, concreteness, etc. – are not directly represented in the structure of the network. Using this abstract network structure essentially results in those characteristics being held constant or controlled between the nodes with low and high C, therefore these variables will not affect the outcome of the present simulations. The use of an abstract network also facilitates generalizing the present results to other domains that examine diffusion dynamics.
The term “spreading activation” has been used to mean many different things in many different and diverse models of cognitive processing (cf., Collins and Loftus, 1975; Anderson, 1983; MacKay, 1987). In the present simulation, activation is defined as a limited cognitive resource, which spreads unimpeded between connected nodes, and does not decay over time. Furthermore, in the present simulation the length of a link between two nodes does not correspond to any psychological construct, such as relatedness. The links between nodes in the present simulation indicate that two nodes simply are phonologically related (based on the one phoneme metric), not that some word pairs are more related than others. Because the length of the links is meaningless (and the links are not weighted, which is an alternative way of representing varying amounts of “relatedness”) activation in the present simulation does not diminish as it spreads between two connected nodes.
We recognize that the assumptions we employ regarding activation and its spread in the current simulation are simple and may differ from other cognitive models that employ “spreading activation.” We favor this simpler approach for a couple of reasons. First, these simple assumptions facilitate our ability to generalize more broadly the present results to other domains that examine diffusion dynamics. Second, we see no reason to include additional assumptions simply because other models include those assumptions. In the present simulation we invoke the principle of parsimony, so that we may examine how many psychological phenomena can be accounted for with as simple a model as possible.
In the present simulation, the target node received an initial burst of activation of 100 arbitrary units. A portion of the initial activation was retained by the target word. We varied this proportion in increments of 0.10, ranging from 0.10 to 0.90 to explore the possibility that different outcomes might emerge at different amounts of retained activation. The amount of activation that was not retained in the target node was equally divided (i.e., spread) amongst the one-hop neighbors of the target word. Similar to the target node, each one-hop neighbor retained a portion of the activation it received from the target node. The portion of activation that was not retained in a one-hop neighbor node was spread equally to the nodes to which it was connected (including the target, other one-hop neighbors, and the two-hop neighbors). Activation that reached the two-hop neighbors (i.e., the white nodes in Figure 2) was sent back to the one-hop neighbors (i.e., the gray nodes in Figure 2) and to other two-hop neighbors to which that node was connected (N.B., these connections were omitted from Figure 2 for the sake of visual clarity), resulting in activation spreading back and forth between the target, the one-hop neighbors, and the two-hop neighbors over 10 discrete time steps.
Retrieval of the target items occurred after activation spread from node to node for 10 discrete time steps. At this point the activation values of the target words were compared. We recognize that current models of word recognition and memory might implement the retrieval process differently than the simplified criterion employed in the present simulation, but it is important to keep in mind that the different mechanisms commonly employed in those models (e.g., an activation threshold that must be crossed, different resting levels of activation, etc.) produce isomorphic results. The present simulation is not intended to discriminate among models of word recognition or memory, or among the different mechanisms employed in such models. Rather, we simply wished to computationally examine the retrieval mechanism described by Chan and Vitevitch (2009).
The activation value in the target node can be mapped to the dependent variables examined in Chan and Vitevitch (2009) – response latency and accuracy – in the following ways: (1) activation values are inversely related to response latency, such that higher activation values indicate that lexical retrieval occurred rapidly, and lower activation values indicate that lexical retrieval required more time to be completed, and (2) activation values are directly related to accuracy, such that higher activation values indicate more accurate retrieval from the lexicon, and lower activation values indicate less accurate retrieval from the lexicon. The assumptions we make regarding the mapping of the activation values in the target nodes to the dependent variables of response latency and accuracy enable us to qualitatively compare the results of our simulations to the results of the two psycholinguistic experiments reported by Chan and Vitevitch (2009).
It is also important to note that it is only the activation value of the target nodes – not the activation value of neighboring nodes, or a comparison between the activation value of the target and its neighboring nodes – that is relevant for comparison to the experiments reported in Chan and Vitevitch (2009). Although the mechanism described in Chan and Vitevitch (2009) referenced the activation of a target word to the activation of its neighbors, all that was assessed in the two experiments reported in Chan and Vitevitch (2009) was – via the dependent variables of response latency and accuracy – the “activation” of the target words.
Furthermore, in the present network simulation, target nodes receive activation from the initial burst of activation to the target node and, in subsequent time steps, from their neighboring nodes. In contrast, non-target nodes (i.e., one-hop and two-hop neighbors) receive activation only in subsequent time steps from their connections to the target and to other nodes. The difference in the timing and source of activation that target and non-target nodes receive makes it impossible for a non-target node to have a higher activation value than a target node. This leads to the idealized situation in which the model always correctly retrieves the target word, which contrasts with the perceptual errors that are observed in natural human performance (i.e., slips of the ear; Vitevitch, 2002a) and that occur in laboratory based tasks. Although “perfect” performance in a model may lack ecological validity, it is not uncommon for models of cognitive processing to perform in this way (e.g., Levelt et al., 1999). Such performance does not diminish the novel insights into a cognitive process that these models may provide.
To describe the simulation algorithmically, at time step 1 the target node, n, was given an activation of 100 units. A proportion of that activation stayed in the target node, according to Eq.2, and the remaining amount of activation was spread equally to all the neighbors of node n, according to Eq.3.

where reservoir (t, n) is the activation retained at node n at time step t, r is the proportion of the activation (ranging from 0.1 to 0.9 in increments of 0.1) retained at node n, inflow (t, n) is the amount of activation that node n received at time-step t, outflow (t, n) is the amount of activation that spreads to each of the neighbors of node n at time t, and degree (n) is the number of neighbors of node n. The total amount of activation at a given node was computed by adding reservoir (t, n) to reservoir (t−1, n). At the end of 10 time steps the total amount of activation in the target nodes with low and high C was examined.
If the spreading activation mechanism implemented in the networks varying in C adequately captures the lexical retrieval process described by Chan and Vitevitch (2009), then – based on the mapping assumptions described above – target nodes with low C will have higher activation values than target nodes with high C after 10 time steps. If the predicted results are indeed observed, this will demonstrate that the simple description offered by Chan and Vitevitch (2009) is minimally sufficient to account for the results obtained in two psycholinguistic experiments. In addition, obtaining the predicted results will further demonstrate that the large-scale structure of the lexicon influences processing – a point that has been overlooked in current models of spoken word recognition.
More broadly, the results of the present simulation have implications for network science as well. Recall that previous simulations (e.g., Newman, 2003) looked at the extent to which information or diseases dispersed across networks varying in C. The present simulation instead examined how the spread of activation in such networks might influence a specific node. Therefore the results of the present simulation offer a different perspective and new insight into studies of dispersion dynamics in complex systems.
Results
Linear multiple regression was used to examine the influence that network structure – as measured by the clustering coefficient (using the continuous values of C listed in Table A1 in the Appendix) – as well as degree, proportion of activation retained, and network density had on the final activation value in the target nodes after 10 time steps had elapsed in the simulation. The final activation value in the 24 target nodes was examined across 9 different levels of retained activation (24 networks * 9 levels of retained activation = 216 simulations).
The results of the analysis indicated that all four of the independent variables contributed significantly, though not equally, to final activation value [R2 = 0.999, F(4, 211) = 43108.25, p < 0.0001]. In the following descriptions of the analysis we report the beta coefficients (β; also known as standardized coefficients) for each variable. The magnitude of β allows one to compare the relative contribution of each independent variable in the prediction of the dependent variable. The sign (±) associated with the β coefficient indicates the direction of the relationship between the independent and dependent variables. We also report for each β coefficient the results of a t-test, which indicates that the independent variable made a statistically significant contribution to the prediction of the dependent variable (even though the value of β might be numerically small).
Not surprisingly, target nodes that retained a larger proportion of incoming activation had higher activation values at the end of 10 time steps than target nodes that retained a smaller proportion of incoming activation [β = +0.999, t(211) = 414.96, p < 0.0001]. The proportion of activation retained in a node was manipulated to verify that any influence of C that we might observe in the present simulation was not due to a unique setting of a particular parameter (see Pitt et al., 2006).
More germane to the question of how clustering coefficient influences the retrieval of a specific node, target nodes with lower C had higher activation values than target nodes with higher C after 10 time steps [β = −0.026, t(211) = −10.12, p < 0.0001]. As per the mapping assumptions between activation values and response latency and accuracy, the results suggest that target words with lower C are retrieved more quickly and more accurately than target words with higher C.
Activation values as a function of degree and C when the proportion of activation retained at a node (r in Eqs 2 and 3) equaled 0.3 and 0.7 are shown in Figure 3. These values of r were selected for illustrative purposes only; we wished to avoid extreme values of r (e.g., 0.1 and 0.9) as well as the middle value of r (0.5). In none of the simulations was there ever a case in which a target node with higher clustering coefficient had more activation than the target node with the same degree but lower clustering coefficient. The influence of C on activation values in Figure 3 is seen by the consistently higher activation values for target nodes with lower C (the diamonds) compared to the activation values for target nodes with higher C (the squares).
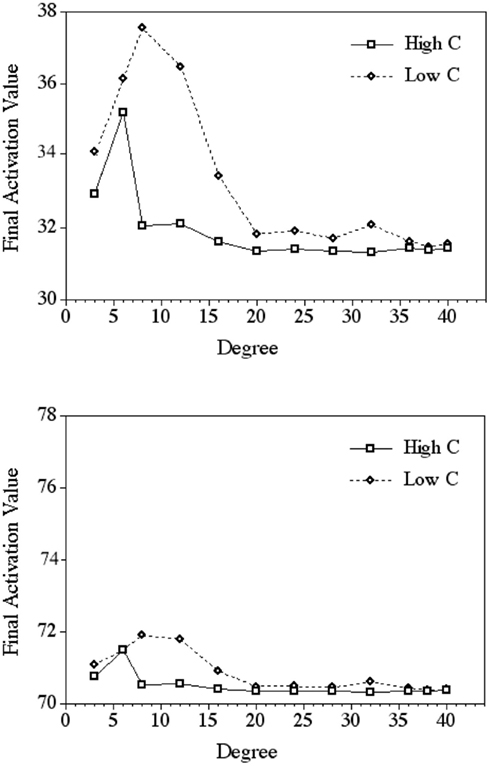
Figure 3. Final activation values in the target nodes after 10 time steps as a function of C and degree. The top panel shows the results of the simulation when (the proportion of activation retained at a node) r = 0.3, and the bottom panel shows the results when r = 0.7. These results are illustrative of other values of r. For instances in which the markers appear on top of one another the difference in activation value between high and low C was observed in the tenth, or hundredth position.
Interestingly, degree also influenced the final activation values in the target nodes. Target nodes with lower degree (i.e., few phonological neighbors) had a higher activation value at the end of 10 time steps than target nodes with higher degree [i.e., many phonological neighbors; β = −0.025, t(211) = −5.91, p < 0.0001]. As per the mapping assumptions between activation values and response latency and accuracy, the results suggest that target words with few phonological neighbors are retrieved more quickly and accurately than target words with many phonological neighbors. The influence of degree on activation values can be seen in Figure 3 by the relatively higher activation values for target nodes with lower degree compared to the activation values for target nodes with higher degree for both high and low C nodes; degree is plotted on the x-axis.
This finding replicates numerous studies examining the influence of degree (known in the psycholinguistic literature as phonological neighborhood density) in spoken word recognition (e.g., Luce and Pisoni, 1998). We included in the present simulation nodes with a wide range of degree simply to be able to generalize more broadly our findings of the influence of the clustering coefficient on processing. We did not design the present simulation to nor set out to replicate the previously observed results regarding the influence of degree on spoken word recognition. Observing the influence of degree on activation levels in the present simulation was, therefore, unexpected.
Although network density in the high and low C networks was not statistically different, network density did have a small, but statistically significant, influence on the final activation values in the target nodes. Recall that the network science term network density measures the number of connections that exist in an entire network in relation to the maximal number of connections that could exist in that network (with a range from 0 to 1), and should not be confused with the psycholinguistic term phonological neighborhood density (which corresponds to the term degree in the present context). Target nodes with higher network density had higher activation values at the end of 10 time steps than target nodes with lower network density [β = +0.012, t(211) = 2.79, p < 0.01]. As per the mapping assumptions between activation values and response latency and accuracy, this result suggests that target words embedded in denser networks will be retrieved more quickly and accurately than target words embedded in sparser networks. The influence of network density on diffusion dynamics has been examined in other domains studied with network science (e.g., Buskens and Yamaguchi, 1999). However, the influence of network density observed in the present simulation is (to the best of our knowledge) a novel finding in the domain of psycholinguistics. Future psycholinguistic experiments could examine how network density influences spoken word recognition (see also Geer and Luce, 2011).
Discussion
In the present simulation we created 24 mini-networks (extracted from the larger network of phonological word-forms examined in Vitevitch, 2008) that varied in degree and clustering coefficient (as well as the proportion of activation retained in a node) to examine the influence of network structure on the cognitive process of spoken word recognition. A simple form of spreading activation was used to model the search and retrieval process during spoken word recognition. This simplified form of spreading activation can be viewed as a special instance of diffusion dynamics (e.g., the spread of disease through a social network), a topic commonly examined in network science (e.g., Newman, 2003; Naug, 2008; Borge-Holthoefer and Arenas, 2010b; Borge-Holthoefer et al., 2011). Four factors were shown to influence the final activation value of the target nodes: (1) the proportion of activation retained in each node, (2) degree, (3) clustering coefficient, and (4) network density.
Not unexpectedly the results of our simulations showed that the proportion of activation retained in each node influenced the final activation value of the target nodes. Nodes that retained more activation had higher activation values at the end of 10 time steps than nodes that retained less activation. The proportion of activation retained in each node was manipulated in order to explore the possibility that different outcomes might emerge at different amounts of retained activation. However, qualitatively similar outcomes were observed across the different proportions of retained activation.
Somewhat unexpectedly – because we did not set out to directly replicate this effect – we observed an influence of degree on the final activation values. Degree was manipulated in the present simulation in order to generalize the results across a wide range of values for degree. We observed, however, that target nodes with higher degree had less activation than target nodes with lower degree. This result suggests that words with higher degree are retrieved more slowly and less accurately than words with lower degree, which replicates many psycholinguistic experiments examining the influence of phonological neighborhood density during spoken word recognition (e.g., Luce and Pisoni, 1998; Vitevitch, 2003).
Although the effect of degree observed in the present simulation replicated the results commonly found in studies of spoken word recognition, different influences of neighborhood density (degree) have been observed in other language-related processes. In the case of speech production, words with many neighbors are produced more quickly and accurately than words with few neighbors (e.g., Vitevitch, 2002b; Vitevitch and Sommers, 2003; cf., Vitevitch and Stamer, 2006, 2009). It is important to note, however, that different mechanisms are believed to underlie the effects of neighborhood density observed in other language-related processes [see Vitevitch and Storkel (submitted) for a description of the mechanism used in word learning]. Vitevitch (2002b) and others suggested that during speech production the effects of neighborhood density emerge from the interaction of word-forms via representations of phonological segments. In those accounts of speech production, word-forms do not interact directly with each other in the lexicon (as they do in the present simulation and in current models of spoken word recognition). Words that sound similar to the target word become activated only by activation spreading through shared phonological segments (or semantic information). Indeed, Gordon and Dell (2001) showed how a two-step interactive-activation model consisting of separate layers for semantic features, words, and phonological segments with excitatory and bidirectional connections between layers (but no connections between nodes within a layer) could produce the effects of neighborhood density typically observed in speech production.
The present simulation differs from the connectionist network used by Gordon and Dell (2001) in a couple ways. First, there are no connections among words in the Gordon and Dell (2001) model; the present simulation does contain connections among words. Second, the Gordon and Dell (2001) model contained representations of individual phonological segments, words, and semantic information; the present simulation contained only phonological word-forms. We appreciate the value of representing other types of information in a model (e.g., phonological segments, or semantic information), but a complex network that includes two types of nodes with links connecting one type to another is beyond the scope of the present investigation. Such networks – known as bipartite networks – are very complicated mathematical entities, and still pose significant challenges to network scientists.
Admittedly, the complexity of bipartite networks might be viewed by some as a limitation of the network science approach in the study of cognition. We believe, however, that the network science approach has other advantages for the study of cognition that outweigh such shortcomings. For example, the network science approach provided the tools that enabled Chan and Vitevitch (2009) to examine the influence of a new, previously unexplored characteristic of words on spoken word recognition, namely clustering coefficient, C. Interestingly, the results of the present simulation showed that target nodes with lower C had higher activation levels after 10 time steps than target nodes with higher C. This result suggests that words with lower clustering coefficients are retrieved more quickly and accurately than words with higher clustering coefficients, replicating the results of psycholinguistic experiments reported by Chan and Vitevitch (2009).
This result also suggests that a simple diffusion mechanism – commonly examined in many other domains explored by network science – could be used to account for the cognitive process of spoken word recognition (see Borge-Holthoefer and Arenas, 2010b; Borge-Holthoefer et al., 2011 for a similar account in other cognitive domains). Furthermore, the present simulation contributes more broadly to network science by demonstrating that diffusion dynamics can affect processing of an individual node. Studies of diffusion dynamics typically examine how many nodes in a system are affected during diffusion (e.g., Newman, 2003; Naug, 2008).
Finally, the results of the present simulation showed that target nodes embedded in denser networks had higher activation values after 10 time steps than target nodes embedded in sparser networks. Although previous psycholinguistic research has shown that immediate neighbors of a word influence processing (e.g., Luce and Pisoni, 1998), the present result suggests that more distant neighbors, and the connectivity among those distant neighbors might also influence spoken word recognition. To the best of our knowledge the influence of network density on language processing has not been reported previously in the psycholinguistic literature, thus indicating a new direction for future psycholinguistic research.
We acknowledge that the present simulation is a simplified version of the structure and processes we envision occurring in the larger phonological network. However, it is important to keep in mind that “[m]odels are not intended to capture fully the processes they attempt to elucidate. Rather, they are explorations of ideas about the nature of cognitive processes. In these explorations, simplification is essential – through simplification, the implications of the central ideas become more transparent” (McClelland, 2009, p. 11). We believe the present simulation has greatly elucidated the manner in which network structure might influence lexical retrieval during spoken word recognition.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was supported in part by grants from the National Institutes of Health to the University of Kansas through the Schiefelbusch Institute for Life Span Studies (National Institute on Deafness and Other Communication Disorders (NIDCD) R01 DC 006472), the Mental Retardation and Developmental Disabilities Research Center (National Institute of Child Health and Human Development P30 HD002528), and the Center for Biobehavioral Neurosciences in Communication Disorders (NIDCD P30 DC005803).
References
Albert, R., and Barabási, A. L. (2002). Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47–97.
Anderson, J. R. (1983). A spreading activation theory of memory. J. Verbal Learn. Verbal Behav. 22, 261–295.
Arbesman, S., Strogatz, S. H., and Vitevitch, M. S. (2010). The structure of phonological networks across multiple languages. Int. J. Bifurcat. Chaos 20, 679–685.
Balcan, D., Colizza, V., Goncalves, B., Hu, H., Ramasco, J. J., and Vespignani, A. (2009). Multiscale mobility networks and the spatial spreading of infectious diseases. Proc. Natl. Acad. Sci. U.S.A. 106, 21484–21489.
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., and Hwang, D. (2006). Complex networks: structure and dynamics. Phys. Rep. 424, 175–308.
Borge-Holthoefer, J., and Arenas, A. (2010a). Semantic networks: structure and dynamics. Entropy 12, 1264–1302.
Borge-Holthoefer, J., and Arenas, A. (2010b). Categorizing words through semantic memory navigation. Eur. Phys. J. B 74, 265–270.
Borge-Holthoefer, J., Moreno, Y., and Arenas, A. (2011). Modeling abnormal priming in Alzheimer’s patients with a free association network. PLoS ONE 6, e22651. doi:10.1371/journal.pone.0022651
Buskens, V., and Yamaguchi, K. (1999). A new model for information diffusion in heterogeneous social networks. Sociol. Methodol. 29, 281–325.
Chan, K. Y., and Vitevitch, M. S. (2009). The influence of the phonological neighborhood clustering-coefficient on spoken word recognition. J. Exp. Psychol. Hum. Percept. Perform. 35, 1934–1949.
Chan, K. Y., and Vitevitch, M. S. (2010). Network structure influences speech production. Cogn. Sci. 34, 685–697.
Collins, A. M., and Loftus, E. F. (1975). A spreading-activation theory of semantic processing. Psychol. Rev. 82, 407–428.
Geer, M., and Luce, P. A. (2011). Neighbors of neighbors in spoken word recognition: the enemy of my enemy is my friend. Presentation at the 52nd Annual Meeting of the Psychonomic Society, Seattle, WA.
Gordon, J. K., and Dell, G. S. (2001). Phonological neighborhood effects: evidence from aphasia and connectionist models. Brain Lang. 79, 21–23.
Greenberg, J. H., and Jenkins, J. J. (1967). “Studies in the psychological correlates of the sound system of American English,” in Readings in the Psychology of Language, eds L. A. Jakobovits and M. S. Miron (Englewood Cliffs, NJ: Prentice-Hall), xi, 636, 186–200.
Griffiths, T., Steyvers, M., and Firl, A. (2007). Google and the mind: predicting fluency with PageRank. Psychol. Sci. 18, 1069–1076.
Hills, T. T., Maouene, M., Maouene, J., Sheya, A., and Smith, L. (2009a). Longitudinal analysis of early semantic networks: preferential attachment or preferential acquisition? Psychol. Sci. 20, 729–739.
Hills, T. T., Maouene, M., Maouene, J., Sheya, A., and Smith, L. (2009b). Categorical structure among shared features in networks of early-learned nouns. Cognition 112, 381–396.
Jasny, B. R., Zahn, L. M., and Marshall, E. (2009). Connections: introduction to special issue. Science 325, 405.
Lamb, S. (1970). “Linguistic and cognitive networks,” in Cognition: A Multiple View, ed. P. Garvin (New York: Spartan Books), 195–222.
Levelt, W. J. M., Roelofs, A., and Meyer, A. S. (1999). A theory of lexical access in speech production. Behav. Brain Sci. 22, 1–75.
Luce, P. A., and Large, N. (2001). Phonotactics, neighborhood density, and entropy in spoken word recognition. Lang. Cogn. Process. 16, 565–581.
Luce, P. A., and Pisoni, D. B. (1998). Recognizing spoken words: the neighborhood activation model. Ear Hear. 19, 1–36.
MacKay, D. G. (1987). “The asymmetrical relationship between speech perception and production,” in Perspectives on Perception and Action, eds H. Heuer and A. F. Sanders (Hillsdale, NJ: Erlbaum), 301–333.
McClelland, J. L., and Elman, J. L. (1986). The TRACE model of speech perception. Cogn. Psychol. 18, 1–86.
McClelland, J. L., Rumelhart, D. E., and Hinton, G. E. (1986). “The appeal of parallel distributed processing,” in Parallel Distributed Processing, Vol. 1, eds D. E. Rumelhart, J. L. McClelland, and the PDP Research Group (Cambridge, MA: MIT Press), 3–44.
Naug, D. (2008). Structure of the social network and its influence on transmission dynamics in a honeybee colony. Behav. Ecol. Sociobiol. (Print) 62, 1719–1725.
Nelson, D. L., Bennett, D. J., Gee, N. R., Schreiber, T. A., and McKinney, V. (1993). Implicit memory: effects of network size and interconnectivity on cued recall. J. Exp. Psychol. Learn. Mem. Cogn. 19, 747–764.
Norris, D. (1994). Shortlist: a connectionist model of continuous speech recognition. Cognition 52, 189–234.
Page, L., Brin, S., Motwani, R., and Winograd, T. (1998). The PageRank Citation Ranking: Bringing Order to the Web (Tech. Rep.). Stanford, CA: Stanford Digital Library Technologies Project.
Pitt, M. A., Kim, W., Navarro, D. J., and Myung, J. I. (2006). Global model analysis by parameter space partitioning. Psychol. Rev. 113, 57–83.
Quillian, M. R. (1967). Word concepts: a theory and simulation of some basic semantic capabilities. Behav. Sci. 12, 410–430.
Roodenrys, S., Hulme, C., Lethbridge, A., Hinton, M., and Nimmo, L. M. (2002). Word-frequency and phonological-neighborhood effects on verbal short-term memory. J. Exp. Psychol. Learn. Mem. Cogn. 28, 1019–1034.
Rosenblatt, F. (1958). The perceptron: a probabilistic model for information storage and organization in the brain. Psychol. Rev. 65, 386–408.
Sporns, O., Chialvo, D., Kaiser, M., and Hilgetag, C. C. (2004). Organization, development and function of complex brain networks. Trends Cogn. Sci. (Regul. Ed.) 8, 418–425.
Steyvers, M., and Tenenbaum, J. B. (2005). The large-scale structure of semantic networks: statistical analyses and a model of semantic growth. Cogn. Sci. 29, 41–78.
Storkel, H. L., Armbruster, J., and Hogan, T. P. (2006). Differentiating phonotactic probability and neighborhood density in adult word learning. J. Speech Lang. Hear. Res. 49, 1175–1192.
Valente, T. W. (1995). Network Models of the Diffusion of Innovations. Cresskill, NJ: Hampton Press.
Vitevitch, M. S. (2002a). Naturalistic and experimental analyses of word frequency and neighborhood density effects in slips of the ear. Lang. Speech 45, 407–434.
Vitevitch, M. S. (2002b). The influence of phonological similarity neighborhoods on speech production. J. Exp. Psychol. Learn. Mem. Cogn. 28, 735–747.
Vitevitch, M. S. (2003). The influence of sublexical and lexical representations on the processing of spoken words in English. Clin. Linguist. Phonetics 17, 487–499.
Vitevitch, M. S. (2008). What can graph theory tell us about word learning and lexical retrieval? J. Speech Lang. Hear. Res. 51, 408–422.
Vitevitch, M. S., and Sommers, M. S. (2003). The facilitative influence of phonological similarity and neighborhood frequency in speech production in younger and older adults. Mem. Cognit. 31, 491–504.
Vitevitch, M. S., and Stamer, M. K. (2006). The curious case of competition in Spanish speech production. Lang. Cogn. Process. 21, 760–770.
Vitevitch, M. S., and Stamer, M. K. (2009). The Influence of Neighborhood Density (and Neighborhood Frequency) in Spanish Speech Production: A Follow-Up Report. Spoken Language Laboratory Technical Report, 1, 1-6. University of Kansas, KU ScholarWorks. Available at: http://hdl.handle.net/1808/5500
Watts, D. J., and Strogatz, S. H. (1998). Collective dynamics of ‘small-world’ networks. Nature 393, 440–442.
Yates, M., Locker, L., and Simpson, G. B. (2004). The influence of phonological neighborhood on visual word perception. Psychon. Bull. Rev. 11, 452–457.
Appendix
Keywords: network science, simulation, clustering coefficient, mental lexicon, word recognition
Citation: Vitevitch MS, Ercal G and Adagarla B (2011) Simulating retrieval from a highly clustered network: implications for spoken word recognition. Front. Psychology 2:369. doi: 10.3389/fpsyg.2011.00369
Received: 23 August 2011;
Paper pending published: 20 September 2011;
Accepted: 24 November 2011;
Published online: 14 December 2011.
Edited by:
Thomas Hills, University of Basel, SwitzerlandReviewed by:
Thomas Hills, University of Basel, SwitzerlandJavier Borge-Holthoefer, University of Zaragoza, Spain
Jean K. Gordon, University of Iowa, USA
Copyright: © 2011 Vitevitch, Ercal and Adagarla. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Michael S. Vitevitch, Spoken Language Laboratory, Department of Psychology, University of Kansas, 1415 Jayhawk Blvd., Lawrence, KS 66045, USA. e-mail: mvitevit@ku.edu

