- 1 Laboratory of Psychophysics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
- 2 Laboratoire Psychologie de la Perception, Université Paris Descartes, Paris, France
- 3 Centre National de la Recherche Scientifique, UMR 8158, Paris, France
- 4 Center for Neuro-Engineering and Cognitive Science, University of Houston, Houston, TX, USA
- 5 Department of Electrical and Computer Engineering, University of Houston, Houston, TX, USA
To investigate the integration of features, we have developed a paradigm in which an element is rendered invisible by visual masking. Still, the features of the element are visible as part of other display elements presented at different locations and times (sequential metacontrast). In this sense, we can “transport” features non-retinotopically across space and time. The features of the invisible element integrate with features of other elements if and only if the elements belong to the same spatio-temporal group. The mechanisms of this kind of feature integration seem to be quite different from classical mechanisms proposed for feature binding. We propose that feature processing, binding, and integration occur concurrently during processes that group elements into wholes.
Research Questions
Does binding operate on pre-processed features or are feature processing and binding concurrent operations? What is the relationship between features and their carriers? What happens to features whose carriers become invisible? How do the inhibitory processes that operate on carriers affect feature processing and binding? Why and when features are segregated or integrated? Does attention play a role in these processes?
Introduction
To make sense of the world surrounding us, the brain has to extract and interpret information from the vast amount of photons impinging on our photoreceptors. The interpretation of information requires the establishment of spatio-temporal relations between different elements. How these processes of information extraction and interpretation lead to perception, learning, development, and knowledge have been fundamental problems in philosophy, psychology, neuroscience, and artificial intelligence. For example, empiricism and behaviorism are based on the principle of association. Elements that co-occur repetitively or persistently in spatial and/or temporal proximity become associated, i.e., relations are established among them so as to bind them into more complex entities. The Hebbian postulate offers a possible mechanism whereby such associations can be implemented in neural systems (Hebb, 1949). In contrast to these hierarchical approaches that build more complex entities from combinations of simpler entities, Gestalt psychologists suggested that stimuli become organized into wholes, or Gestalts, that cannot be reduced to associative combinations of their parts. Both associationist and Gestaltist views are still prevalent today as one considers the binding problem at its various levels, from perception to knowledge.
In visual perception, most approaches to the binding problem are guided by the parallel and hierarchical organization of the early visual system. Information is carried by parallel pathways from the retina to higher levels of cortex, for example, by retino-cortical magnocellular and parvocellular pathways, and cortico-cortical dorsal and ventral pathways. Neurons in different visual areas generate distinctive responses to different stimulus attributes. For example, neurons in area MT are sensitive to motion whereas neurons in the blob regions of V1 are particularly sensitive to color. There appears to be a hierarchy within pathways; for example, complex shape selectivity appears to result from a hierarchy in the ventral pathway, starting with orientation selectivity, leading to curvature selectivity, and finally to complex shape selectivity (Connor et al., 2007). This hierarchy has been suggested to be accompanied by a shift in reference frames, from retinotopic reference frames in early areas to object-centered reference frames in higher areas (Connor et al., 2007). If different attributes of a stimulus are processed in different parts of the brain according to different reference frames, how are they associated with each other to underlie the unified percepts that we experience?
The hierarchy in the visual system is often interpreted to support the associationist view. It is assumed that the early visual system computes a set of stimulus attributes (e.g., oriented boundary segments, color, texture) and the binding consists of selectively associating different attributes with each other by, for example, hierarchical convergence (e.g., Riesenhuber and Poggio, 1999b), neural synchrony (Singer, 1999), or by an attentional scanning mechanism (Treisman and Gelade, 1980; Treisman, 1998).
In analyzing the binding problem in its broader context, one has to recognize that there are several stimulus attributes that need to be bound together, thereby leading to a variety of binding problems. Treisman (1996) pointed out the existence of at least seven types of binding, including “property binding” (e.g., how color and shape of the same object are bound together), “part binding” (how different parts of an object, such as boundary segments, are segregated from the background and bound together), “location binding” (how shape and location information, believed to be represented in ventral and dorsal pathways, respectively, are bound together) and “temporal binding” (how binding operates across time when an object moves). It is highly likely that these different types of binding operations are not independent from each other but work in an interactive way. Furthermore, while most theoretical approaches assume as a starting point simple “features,” such as oriented line segments and color patches, it is highly likely that the computation of even these basic features is not independent from their binding operations. To appreciate this last point, one needs to first recognize that the computation of features is not instantaneous, but takes time. Second, under normal viewing conditions, our eyes undergo complex movements. Many objects in the environment are also in motion and thereby cause dynamic occlusions. As a result, the representation of the stimulus in retinotopic areas is highly dynamic, transient, and intermingled. Under these conditions, one cannot assume that features are already computed and ready for binding operations; instead, one needs to address the problem of how to simultaneously compute and bind features through interactive processes. Consider for example a moving object. Due to occlusions, the features of the moving object will overlap with those of the background or with those of other occluding objects. The receptive fields of neurons in retinotopic areas will receive a succession of brief and transient excitations from a variety of features, some belonging to the same object, some belonging to different objects. To compute features, the visual system should be able to decide whether to segregate information (when it belongs to different objects) or integrate information (when it belongs to the same object). The object file theory (Kahneman et al., 1992) assumes that an object file is opened and indexed by location and features are inserted to this file over time to allow processing. However, this poses a “chicken-and-egg” problem: In order to decide distinct objects, one needs to have access to their features; but unambiguous processing of features, in turn, needs the opening of distinct object files. This vicious circle suggests, again, that the processing of features need to co-occur with their binding.
In this paper, we summarize our recent findings from studies where we examined the spatio-temporal dynamics of feature processing and integration. In order to assess the temporal interval during which the stimulus is processed, we used brief presentations of features (a vernier offset presented for 20 ms).
The Sequential Metacontrast Paradigm
We presented a vernier stimulus that comprises a vertical line with a small gap in the middle. The vernier was presented for 20 ms, followed by blank screen (inter-stimulus interval, ISI) for 30 ms, and then a pair of lines neighboring the vernier. The central vernier stimulus is rendered invisible because the flanking lines exert a metacontrast effect (Figure 1A; Stigler, 1910; Alpern, 1953; Bachmann, 1994; Breitmeyer and Ögmen, 2006).
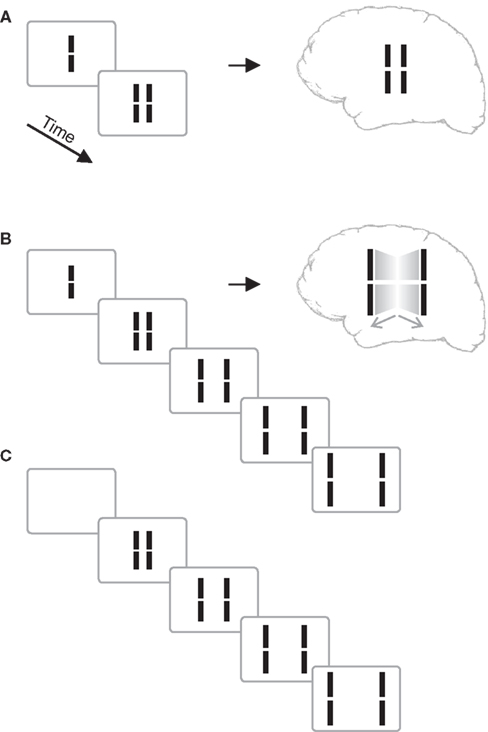
Figure 1. (A) Classical metacontrast. A central vernier (i.e., a vertical line with a small gap in the middle) is followed by two, non-overlapping verniers. The central vernier is rendered largely invisible if the flanks appear 50 ms later. (B) Sequential metacontrast. The central vernier is followed by four successive pairs of flanking verniers. A percept of two motion streams to the left and right is elicited with the central line being invisible. (C) Sequence as in (B) without the central vernier. Copyright © 2006 ARVO. Reproduced from Otto et al. (2006).
In an extension of the metacontrast masking paradigm called sequential metacontrast (Piéron, 1935; Otto et al., 2006), the central vernier was followed not just by one pair of flanking lines but by three further ISI-line pairs creating the percept of two streams of lines expanding from the center (Figure 1). To verify the very strong masking effect in sequential metacontrast, we presented the above sequence with (Figure 1B) and without (Figure 1C) the central vernier in a two-interval forced-choice paradigm and asked observers to indicate which interval contained the central vernier stimulus. Performance was close to chance level (Otto et al., 2006).
In the next step, we added a small offset to the vernier, i.e., the lower part of the vernier was offset either to the left or right relative to the upper part (Figure 2A). The first question is what happens to this feature (the vernier offset)? Will it disappear from consciousness altogether along with its carrier stimulus (the central vernier)? Here we define the carrier as the stimulus that contains the feature. Thus, our experiments will determine whether the visibility of the feature can be dissociated from the visibility of its carrier.
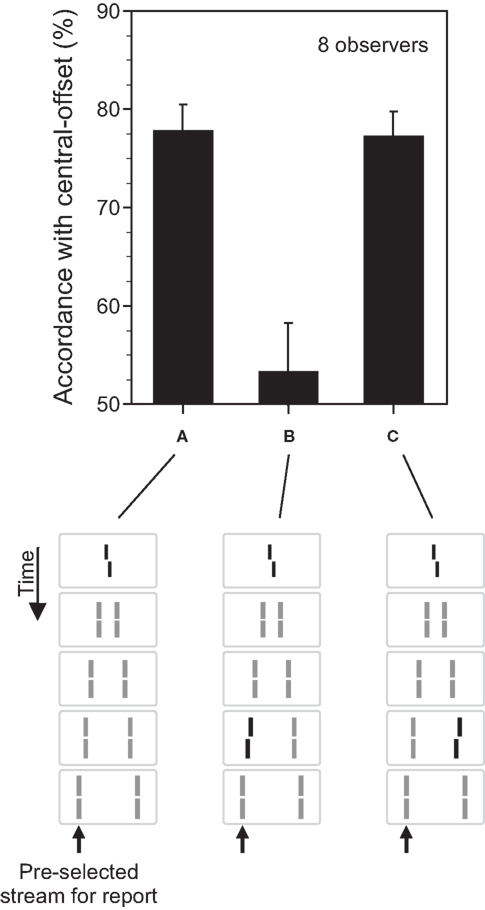
Figure 2. The fate of invisible features. (A) The central line was randomly offset to the left or right (central-offset). As in Figure 1, it was followed by non-offset, flanking lines. Observers were asked to attend to the leftward motion stream (as indicated by the arrow) and to discriminate the offset direction perceived in this motion stream. Responses were assessed with respect to their accordance with the central-offset. Although the central line was rendered invisible by sequential metacontrast, observers could discriminate the offset very well. Phenomenologically, only one moving line with one vernier offset is perceived. (B) We added a second offset to the penultimate line in the attended motion stream. When the vernier and line offsets were in opposite directions, offsets canceled out each other indicating a combination of the two offsets. (C) Performance, compared to (A), is virtually not changed when the second offset is added to the penultimate line in the unattended motion (lines with offsets are highlighted in black for graphical sake; all lines had the same luminance in the experiments; Copyright © 2006 ARVO. Adapted from Otto et al. (2006).
To answer these questions, we first asked observers to attend to one of the motion streams and, in a forced-choice task, report the offset direction of the vernier perceived in that motion stream. We then computed the accordance of their responses with the offset direction of the invisible central vernier. The accordance, also called dominance, was significantly higher than chance performance (Figure 2A) indicating that, even though the retinotopic carrier of the vernier offset was invisible, the vernier offset was perceived as part of the motion stream.
In order to address whether the processing of the vernier offset continues during this binding, in addition to the central vernier, we introduced an additional vernier offset to one of the lines, e.g., the penultimate line in the attended motion stream (Figure 2B). If the processing of the vernier continues during the motion stream, it should integrate with other verniers inserted into the motion stream. If not, the two verniers would be perceived as two different features belonging to the same motion stream and, as such, they will not be integrated. Our results show that the processing of verniers within the motion stream continues so that, for example, when the two verniers have opposite offset directions, they cancel each other (Figure 2B). In order to assess whether the integration of information is specific to motion streams into which the verniers are bound, we presented the additional vernier offset at the penultimate line in the unattended motion stream (Figure 2C). Here, we found no integration (compare Figure 2A with Figure 2C). Hence, unconscious feature processing and integration is specific to motion streams. The processes uncovered by our stimuli reveal the properties of what Treisman (1996) defined as “location binding” and “temporal binding.” Our results show that feature processing continues during these binding operations. This results in feature integration which is mathematically equivalent to an integration (summation) process. The mathematical integration operation is linear and so is the feature integration we have observed with the vernier offsets. The percentage of dominance for the combined presentation of the vernier and the flank-offset is the sum of the dominance levels when the central and flank vernier are presented alone (Otto et al., 2009). Hence, when the flank-offset is in the same direction as the central vernier offset, performance improves. In general, all offsets within a motion trajectory are linearly summed (within about 500 ms).
For the stimulus shown in Figure 2, the central vernier is bound to both motion streams. We argue that the central vernier is attributed to both streams because motion grouping is ambiguous since the vernier is at the center of the expanding motion. To investigate the role of motion grouping on feature integration in sequential metacontrast, we performed an experiment with two parallel motion streams (Figure 3). To disambiguate motion grouping, we added a line next to the vernier on the right or left hand side. Now, the vernier in the first frame groups either with the left (Figure 3C) or the right (Figure 3D) stream according to motion correspondences between the first two frames. Integration of the central- and the flank-offset occurs only when the two offsets are in the same grouped motion stream.
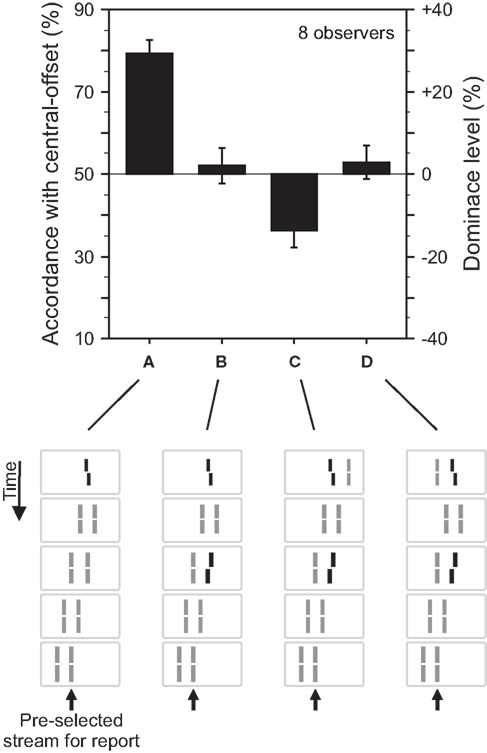
Figure 3. Grouping based feature integration. (A) The central line was followed by two streams of lines shifting in parallel. Observers were asked to attend to the right motion stream. The offset of the central vernier is discriminated well. (B) Performance is changed when an additional offset is added to the second line of the right motion stream. These results are analogous to the experiment shown in Figure 2. (C) The central line is flanked by an additional line on the right side. Performance is dominated by the additional offset (performance is below 50% because we determined responses in accordance with the central-offset and the second flank-offset was in the opposite direction. To ease intuition, this accordance level can be transformed into dominance level by subtracting 50%. As a result, the sign of the dominance level reflects dominance of the central- or flank-offset, respectively). We suggest that the additional line disambiguates the motion grouping, present in (A,B), by assigning the “central” line to the left, unattended motion stream. The flank-offset in the right, attended stream determines performance. (D) The additional line is presented to the left of the central line, which elicits the percept of two bending motion streams. Performance is virtually not changed compared to (B). We suggest that the additional line changes the motion percept (bend motion) but not the grouping of the “central” line to the right motion stream. Hence, central-offset and flank-offset are integrated. Copyright © 2006 ARVO. Adapted from Otto et al. (2006).
Although the above results clearly show the specificity of vernier processing according to motion streams, one cannot directly infer a perceptual integration. Observers may be perceiving two distinct verniers in the motion stream and, in the forced-choice task, may be combining their offsets cognitively in order to produce a binary response or respond randomly to either one. However, the invisibility of the vernier ensures that only one fused offset is available and the task is well defined. In addition, observers can hardly, if at all, determine whether the central line or the penultimate flanking line was offset (Otto et al., 2006. Phenomenologically, only one moving line with only one vernier offset is perceived (see for example the animations in Otto et al., 2006). Finally, we have quantified the level of integration between different verniers in a motion stream by measuring their individual and combined responses. Figure 4 provides an example where we varied the length of the motion sequence from 4 to 10 flanking lines.
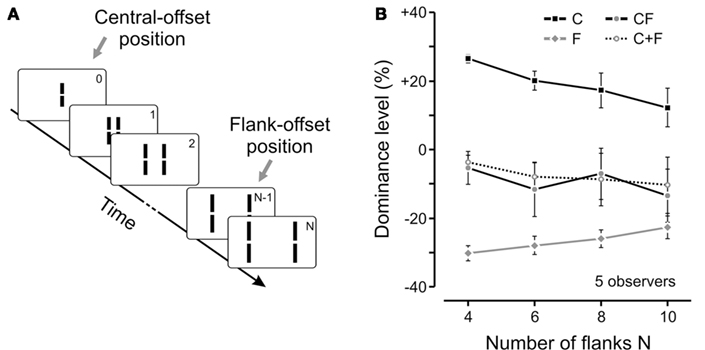
Figure 4. (A) We extended the experiment shown in Figure 1 by adding more and more flanking lines to the sequence (i.e., sequences with 4, 6, 8, or 10 pairs of flanking lines). The flank-offset was always presented in the penultimate frame (no offset is shown in the illustration). (B) We presented only the central-offset (C), only the flank-offset (F), or both offsets together in the attended stream (CF). In general, dominance decreased (as indicated by absolute values closer to 0) for longer lasting sequences, i.e., the more non-offset flanking lines were added. Interestingly, the integration of central- and flank-offset was virtually not changed as it was always well predicted by the linear sum of performance levels in conditions C and F (see C + F). Notably, in the longest sequence, the distance between the central- and the flank-offset (which was presented in frame 9) was 0.5° with an SOA of 370 ms. Hence, feature integration was not changed during a substantial spatio-temporal window. Copyright © 2009 by the American Psychological Association. Reproduced with permission. The official citation that should be used in referencing this material is Otto et al. (2009). The use of APA information does not imply endorsement by APA.
In these experiments, when present, the flanking vernier was always inserted to the penultimate line in the sequence and its offset direction was always the opposite of the central vernier. In order to measure quantitatively the integration between different verniers, we calculated the accordance of observers’ responses with respect to the central vernier and subtracted 50% (see also Figure 3). As a result, positive and negative values of the dominance level reflect the dominance of central or flank verniers, respectively. We measured the observers responses to the central (C, in Figure 4B) and flanking (F, in Figure 4B) verniers in isolation, as well as when they were presented together in the motion stream (CF, in Figure 4B). We have then calculated the algebraic sum of C and F conditions (C + F in Figure 4B) and compared it to the CF condition. As one can see from Figure 4B, a linear integration predicts the combined result very well. The experiments showed that this linear integration rule holds in a wide-range of conditions, where we varied the position, the distance, and the orientation of the vernier carrying the flank-offset as well as the magnitude of the offsets (Otto et al., 2009). We believe that this is strong support for automatic integration, since it is not likely that a cognitive strategy would produce such accurate quantitative integration across a broad range of stimulus conditions and configurations. Finally, a fourth line of evidence for automatic integration comes from the experiments discussed in the next section.
The Role of Attention
In all the experiments reported up to here, observers attended to one pre-determined motion stream and reported the vernier offset that they perceived within this motion stream. Thus, as the attended stream and the stream selected for perceptual report were always the same, the results cannot clarify whether attention plays a role in these binding and integration effects. In order to study the role of attention, we used a cueing paradigm. We modified the experiment shown in Figure 4 by keeping the length of the sequence to four flanking lines and by introducing an auditory cue (Figure 5).
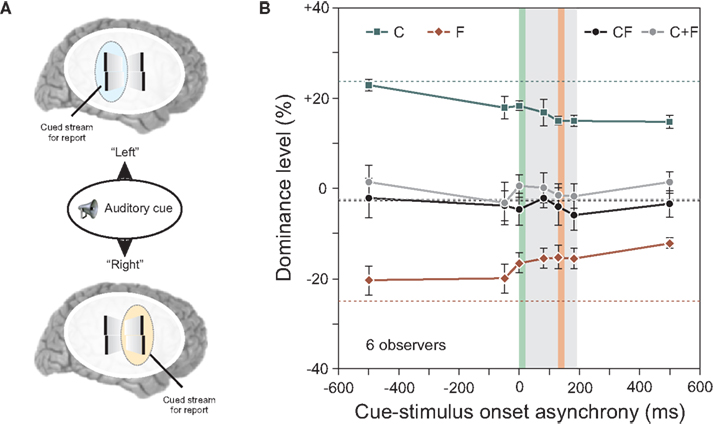
Figure 5. (A) An auditory cue indicated the motion stream, for which the offset should be reported. We varied the cue-stimulus onset asynchrony from −500 to 500 ms. (B) Performance in conditions C and F decreased the later the auditory cue was presented (i.e., the absolute value of the dominance level is reduced). Except for this general decay, integration of central- and flank-offset was virtually not changed as it was always well predicted by the linear sum of performance levels in conditions C and F (see C + F). Dotted lines indicate performance when observers attended to always the same stream without the use of an auditory cue. The grey area indicates the stimulus duration, the vertical green line the onset of the central line, the vertical red line the onset of the offset flank. Copyright © 2006 ARVO. Reproduced from Otto et al. (2010a).
The auditory cue indicated to the observer which stream, left or right, to attend for reporting the perceived vernier offset. The timing between the auditory cue and the visual stimulus ranged from −500 ms to +500 ms relative to the motion sequence onset.
The results for the conditions C and F in Figure 5 show a slight decay as a function of cue-stimulus onset asynchrony. This decay was also found for single, static stimuli (results not shown; see Otto et al., 2010a). Because the decay is independent of stimulus type or timing, we suggest that it is of central origin. Other than this decay, the cue had little effect on the results, and the algebraic summation rule did apply (Figure 5B). Hence, whether attention is distributed to both streams (when the cue was presented after the motion streams) or focused (when the cue was presented before the motion streams) has no effect on the processing and integration of features. These experiments showed that focused selective attention on one stream is not necessary for stream-specific integration.
Merging Motion Streams
The results so far showed that features remain segregated according to motion grouping relations and their processing and integration takes place within each motion stream. As we have mentioned at the beginning of the article, under normal viewing conditions, moving objects overlap and occlude each other. The visual system needs to decide whether to integrate or segregate overlapping features. To study this problem, we presented two sequential metacontrast sequences next to each other so that two of the four motion streams merged at a common point (Figures 6A–C).
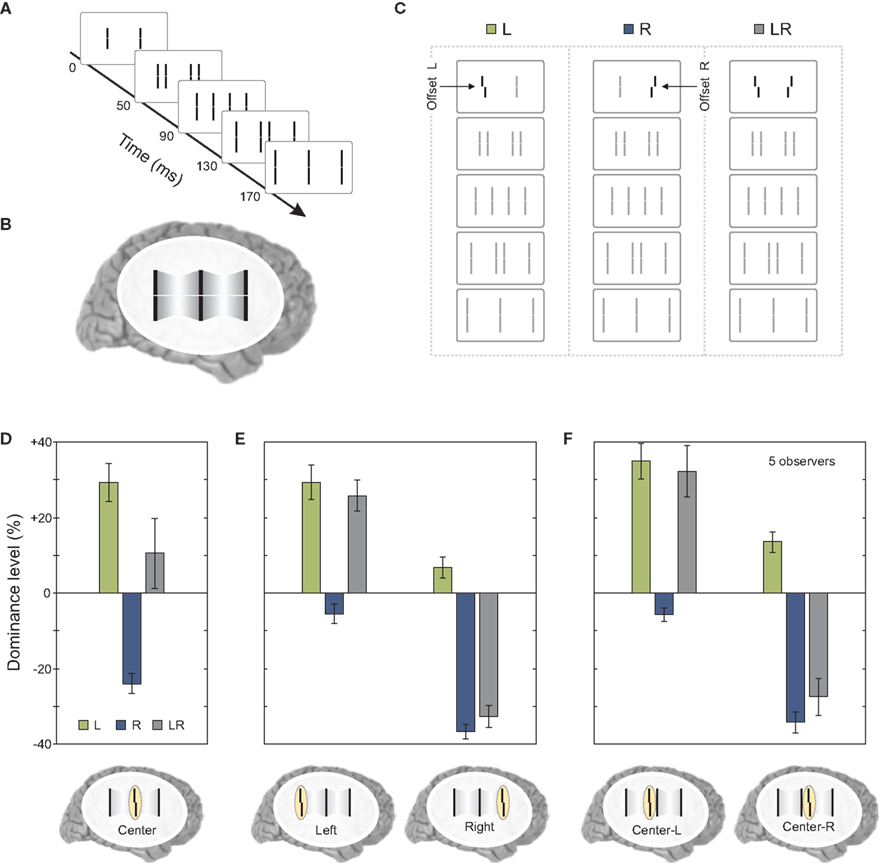
Figure 6. Merging motion streams. (A) We presented to sequential metacontrast sequences (see Figure 1) next to each other so that two motion streams terminated in a common line. (B) The percept of two merging motion streams is elicited. (C) In three conditions, the left, the right, or both lines in the first frame were offset. All flanking lines were non-offset. (D) Offsets from the left and right sequence were combined (i.e., the left and right offset cancel out each other in condition LR) when the merging motion streams were attended. (E) This effect is not found when the outer left or outer right motion stream was attended. (F) We did not present the last frame [see (A)]. Hence, the central motion streams did not merge in a common line. Offsets were not integrated similar to (E). Copyright © 2006 ARVO. Reproduced from Otto et al. (2010a).
When observers attended to the central line where the two streams merged, vernier information coming from the two streams was found to be integrated (Figure 6D). However, this integration did not occur when observers attended to the left or right terminal lines, which produced results replicating the finding that the vernier offset remains specific to its motion stream (Figure 6E). Moreover, the combination of vernier offsets as found in Figure 6D does require the merging of the two streams since, when the last frame was omitted and the observers attended the left or right element in the center, no integration was found (Figure 6F).
Next, we asked observers to report the central line but also selectively attend to one of the motion streams. In this case, there was no integration of verniers coming from different motion streams; the visual system was able to segregate feature information and avoid integration (Figure 7B). The results were similar to the case where the two streams did not merge (compare Figure 7B to Figure 6F). In order to determine whether this segregation was due to focused and maintained attention on a single stream, we repeated the same experiment with the exception that the task condition (attend center line with left or right stream) was signaled to the observer by an auditory cue delivered 320 ms after the motion streams merged (i.e., with a cue-stimulus onset asynchrony of 500 ms). The results were similar to the case where observers focused their attention on a single stream, i.e., features were segregated and the observers reported the feature associated with the cued stream (compare Figures 7B,C). Thus, in cases where different motion streams merge, the integration of feature information is not mandatory, but flexible. This flexible integration does not necessitate focused and maintained attention.
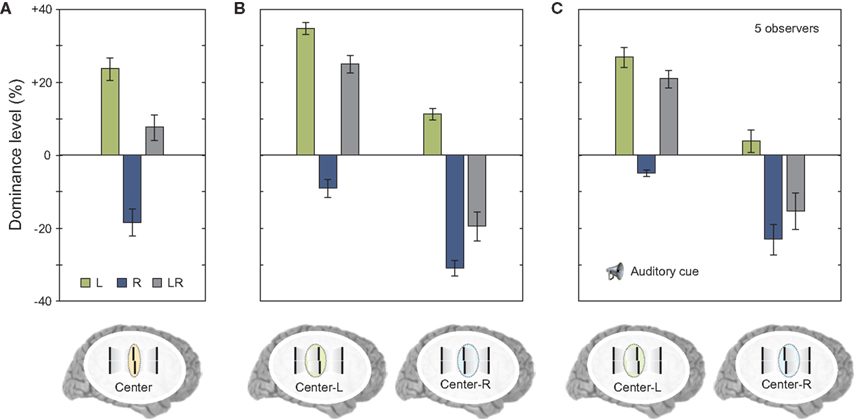
Figure 7. (A) We repeated the experiment shown in Figure 6D. Results were virtually identical. (B) Next we asked observers to attend selectively to the stream coming from the left or from the right to the center. Offsets were not combined similar to experiments shown in Figure 6F. (C) We repeated the experiment but presented a post-cue that indicated the stream for perceptual report only after the motion streams were presented (with a cue-stimulus onset asynchrony of 500 ms). There was a small general decay of performance (as in Figure 5). Critically, offsets were not integrated although the motion streams merged in the last frame. Copyright © 2006 ARVO. Reproduced from Otto et al. (2010a).
An Ecological Framework: The Problems of Motion Blur and Moving Ghosts
The studies outlined above were motivated by the observations that under normal viewing conditions, the visual system needs to compute features at the same time as it binds them. This is because the computation of a feature requires decisions regarding whether transient stimulations generated come from the same or different objects. Our results show that the carrier of a stimulus can be rendered invisible and the corresponding feature can be integrated with features presented at retinotopic locations different than the retinotopic location of its carrier. Why is the perception of the carrier inhibited and why is the feature integrated with other features in a non-retinotopic manner?
Under normal viewing conditions, a briefly presented stimulus can remain visible for more than 100 ms, a phenomenon known as visible persistence (Haber and Standing, 1970; Coltheart, 1980). This should imply that moving objects appear extensively blurred; however, in general we do not experience motion blur (e.g., Ramachandran et al., 1974; Burr, 1980; Hogben and Dilollo, 1985; Farrell et al., 1990; Castet, 1994; Bex et al., 1995; Chen et al., 1995; Westerink and Teunissen, 1995; Bedell and Lott, 1996; Burr and Morgan, 1997; Hammett, 1997). Another problem associated with object motion is the problem of “moving ghosts” (Ögmen, 2007). Since a moving object stimulates each retinotopically localized neuron only for a brief time period, no retinotopic neuron by itself will receive sufficient stimulation to extract features of the stimulus1. Thus, moving stimuli should appear as “ghosts,” i.e., blurred and quasi-uniform in character, devoid of specific featural qualities. This happens when stimuli move at excessively high speeds but not for ecologically observed speeds. We suggest that the visual system solves motion blur and moving ghosts problems by two complementary mechanisms. The carriers and features are first registered in retinotopic representations. The spatial extent of motion blur is curtailed by inhibitory mechanisms that make stimuli, as the central vernier in our displays, invisible on a retinotopic basis (Ögmen, 1993, 2007; Chen et al., 1995; Purushothaman et al., 1998). However, the features of the retinotopically inhibited stimuli are not destroyed; instead, based on prevailing motion grouping relations, they are attributed to motion streams where they are processed and bound (Otto et al., 2006, 2009; Ögmen et al., 2006; Ögmen, 2007; Breitmeyer et al., 2008). This non-retinotopic, motion grouping based feature processing provides the solution to the moving ghosts problem. While features of an object activate retinotopically organized cells momentarily, they remain relatively invariant along the motion path of the object. This allows sufficient time for non-retinotopic mechanisms to receive and process incoming stimuli as they become segregated according to prevailing motion grouping relations. Thus, we suggest that features that become dissociated from their carriers are mapped into non-retinotopic representations following spatio-temporal grouping relations.
When and why are features integrated? Most vision problems are ill-posed (Poggio et al., 1985). For example, the light that shines on a photoreceptor is always the product of the illuminance (e.g., sun light) and the reflectance (properties of the object): luminance = illuminance × reflectance. Hence, the luminance value is not sufficient to determine reflectance. Solving such ill-posed problems can take substantial amounts of time and needs to take contextual information into account, making a short-term retinotopic analysis impossible. Consider the following situation. A car drives through a street. Because of shadows and reflecting lights, the car elicits a series of very different luminance and chromacity signals on the retina. For example, the red of the car may be almost invisible when driving through a dark shadow but bright and well visible when in sun light. The brain usually discounts for the illuminance (color constancy). However, for the fast running car, processing time is too short when computed at each retinotopic location. Moreover, it is not necessary to compute the reflectance of the car at each location and instance given the knowledge that car colors do not change. Hence, averaging across the features along a motion trajectory may be a first step toward a good estimate of the car color. Vernier offset integration is just a toy version of such a scenario. For this and other reasons, we would like to argue that most visual processes occur in fact in non-retinotopic frames of reference – including feature processing, binding, and integration. Using a different approach than the sequential metacontrast paradigm, we have shown evidence for non-retinotopic processes of vernier offsets (as used here; Ögmen et al., 2006; Aydin et al., 2011b), motion, form, and attention in visual search (Boi et al., 2009, 2011). In addition, perceptual learning in the sequential metacontrast paradigm occurs within non-retinotopic rather than retinotopic coordinates (Otto et al., 2010b).
Where does feature integration occur? We used high density EEG and inverse solutions. We found that the insula showed enhanced activity when vernier offsets are integrated (Plomp et al., 2009). The insula is one of the areas involved in all sorts of integration processes and consciousness (e.g., Craig, 2009).
Implications for Models of Binding
In classical models of binding by synchrony, features are bound together when their neural representations fire simultaneously or with a common frequency and phase relation (e.g., Singer, 1999). For example, when a red square and a green disk are presented, neurons coding for red and squareness fire synchronously and similarly neurons coding for green and diskness. When the combination of colors and form changes, the synchronization changes accordingly. However, synchronization is not a mechanism per se for computing binding but may be a way of communicating information. Therefore, the crucial question that remains is how grouping, feature processing, integration, and binding take place in our stimuli. Synchronization may be an outcome of computational mechanisms underlying these processes; however, it does not provide, in itself, a causal explanation for the outcome. As a result, to test whether synchronization can explain our results necessitates models that would be able to carry out the aforementioned processes and produce synchronization as an emergent property.
Can our results be explained by the association principle and the related convergent coding models? Particularly, averaging of features is a classical property of many models of grandmother cell coding to avoid the curse of dimensionality (Riesenhuber and Poggio, 1999a). The sequential metacontrast paradigm is quite robust to substantial changes, i.e., changes in ISI, spacing between lines, number and orientation of lines, and contrast polarity (see Figure 4; Otto et al., 2009). On the other hand, small spatio-temporal details do matter when they change the grouping (Figure 3). Hence, it is hard to explain with most convergent coding schemes how for each conceivable motion stream, there are hard wired detectors binding offsets together. Moreover, sequential metacontrast is not limited to vernier offsets; hence, the number of possible motion groups and feature bindings is virtually unlimited (see also Footnote 1).
Often it is proposed that a master map of attention binds features of retinotopic, basic features maps together, particularly, to solve the property binding problem (Treisman, 1998). However, the role of attention in our dynamic stimuli appears to be different. Within a given stream, vernier offset integration occurs automatically without focused attention. When attention is focused on the stream, only the integrated sum of the vernier offsets, rather than individual offsets, can be read-out. On the other hand, attention can play a major role when it comes to combining different, independent motion trajectories into more complex motion structures (Figures 6 and 7).
As a path toward the solution, we propose the following non-retinotopic processing scheme shown in Figure 8 (Ögmen, 2007; Ögmen and Herzog, 2010).
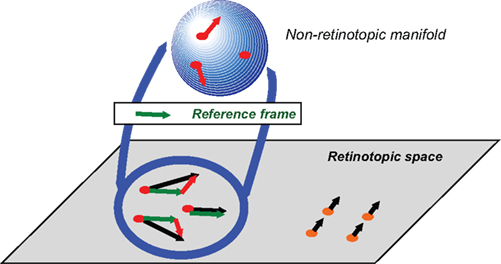
Figure 8. Schematic depiction of the proposed approach to conceptualize non-retinotopic representations wherein feature processing, binding, and integration take place. The two-dimensional plane at the bottom of the figure depicts the retinotopic space in early vision. In this example, a group of dots (shown in red) moves rightward and a second group of dots (shown in orange) moves upward. A fast motion segregation and grouping operation establishes two distinct local neighborhoods, which are mapped into two different non-retinotopic representations (for clarity, the figure shows only the non-retinotopic representation for rightward moving dots). A vector decomposition takes place (e.g., Johansson, 1973) and a common vector for the neighborhood (dashed green vector) serves as the reference frame for the neighborhood. The stimulus in the local neighborhood is mapped on a non-retinotopic manifold (for depiction purposes a sphere is used). This allows the processing and integration of features in a manner that remains invariant to their global motion. Features that are mapped to common manifolds become candidates for binding into groups (from Ögmen and Herzog, 2010).
The retinotopic space is depicted at the bottom of the Figure as a two-dimensional plane. A group of dots move rightward (highlighted in red) while another group of dots move upward (highlighted in orange). Based on differences in motion vectors, the two local neighborhoods are mapped into two different non-retinotopic representations; for clarity the figure shows only the non-retinotopic representation for the rightward moving dots. Each feature, visible or not, is attributed to a motion group. The invisibility of the carrier of the feature indicates the inhibition of its retinotopic activity. A common vector for each neighborhood is determined (dashed green vector) and serves as the reference frame for that neighborhood. All motion vectors are decomposed into a sum of the reference motion and a residual motion vector. The stimulus in the local neighborhood is mapped on a manifold (in Figure 8, for depiction purposes a sphere is used), i.e., a geometric structure that preserves local neighborhood relations. However, the surface can be stretched and deformed. The residual motion vectors, or relative motion components with respect to the reference frame, are then applied to the manifold so as to deform it to induce transformations that the shape undergoes during motion. Features that are mapped into this manifold within a pre-determined spatio-temporal window become integrated. Thus, according to this approach, feature processing and binding occurs largely in non-retinotopic representations that are built from ongoing motion grouping relations in the retinotopic space. Two different motion streams are mapped into two different manifolds and remain segregated in agreement with our results. When the streams merge, a common point in the retinotopic space signals occlusion. We suggest that observers can read-out information about different motion streams by accessing their distinct manifold representations and resolve the occlusion in a flexible way by attributing to the common point the feature information associated with the attended stream. This is illustrated in Figure 9.
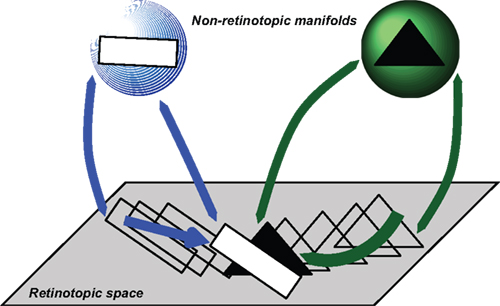
Figure 9. Depiction of how occluded objects are represented and processed. According to this approach, retinotopic areas serve as a relay where features are transferred to non-retinotopic areas according to spatio-temporal grouping relations. A second role of retinotopic areas is to resolve depth order and occlusion relations. While the entire shapes of objects can be accessed from their non-retinotopic representations, visibility of the parts is dictated by retinotopic activities. In this example, observers can recognize a complete triangle (amodal completion) but only those parts that are un-occluded in retinotopic representations become visible.
In this example, a square and a triangle move and according to motion grouping relations, a non-retinotopic representation is created for each motion stream. The retinotopic information is conveyed to the appropriate non-retinotopic representations where processing of features takes place. Thus, according to our theory, the first major role of retinotopic processes is to establish grouping relations and convey feature information to non-retinotopic areas according to these grouping relations. Grouping and attention are independent but interactive processes (Aydin et al., 2011a). A second role of retinotopic representations is to resolve depth order and occlusion relations and thereby determine those features that will gain visibility. Figure 9 shows a time instant when the rectangle and the triangle occlude each other. The reciprocal relationships between retinotopic and non-retinotopic activities reveal occlusion properties and establish visibility based on this information. In the example shown in Figure 9, the rectangle is in the foreground and becomes fully visible; only the un-occluded parts of the triangle become visible. However, since the triangle is stored and computed in non-retinotopic representations, the percept is not that of two disjoint segments, but instead a single triangle (amodal completion). Applying this concept to the merging streams, one can see that an observer can access the vernier information of the streams independently because they are stored in separate representations. The point where the streams merge constitutes an ambiguous occlusion point because, unlike the square-triangle example of Figure 9, the shape at the point where the two streams merge (line) can belong to either stream. Thus, based on attentional cueing, the offset of either stream can be attributed to the point of occlusion.
Conclusion
In summary, the sequential metacontrast paradigm is a versatile tool to investigate many aspects of vision including consciousness, spatio-temporal grouping, attention, and feature integration. We have shown how features of invisible elements can still become visible at other elements and even integrated with other features. Feature integration occurs only when elements belong to one spatio-temporal group. Our findings show how the human brain integrates even very briefly presented information at a very subtle spatial scale.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported in part by award number R01 EY018165 from NIH and the Swiss National Science (SNF) Foundation project “The Dynamics of Feature Integration.”
Footnote
- ^One may argue that neurons can collect information through their spatio-temporally oriented receptive fields (Burr, 1980; Burr et al., 1986; Pooresmaeili et al., 2012). While this may work for stimuli undergoing simple motion, for natural stimuli it would necessitate a staggering number of pre-wired receptive fields for every imaginable motion trajectory starting from every possible point.
References
Aydin, M., Herzog, M. H., and Ögmen, H. (2011a). Attention modulates spatio-temporal grouping. Vision Res. 51, 435–446.
Aydin, M., Herzog, M. H., and Ögmen, H. (2011b). Barrier effects in non-retinotopic feature attribution. Vision Res. 51, 1861–1871.
Bachmann, T. (1994). Psychophysiology of Visual Masking: The Fine Structure of Conscious Experience. Commack, NY: Nova Science.
Bedell, H. E., and Lott, L. A. (1996). Suppression of motion-produced smear during smooth pursuit eye movements. Curr. Biol. 6, 1032–1034.
Bex, P. J., Edgar, G. K., and Smith, A. T. (1995). Sharpening of drifting, blurred images. Vision Res. 35, 2539–2546.
Boi, M., Ögmen, H., Krummenacher, J., Otto, T. U., and Herzog, M. H. (2009). A litmus test for human retino- vs. non-retinotopic processing. J. Vis. 9, 5, 1–11.
Boi, M., Vergeer, M., Ögmen, H., and Herzog, M. H. (2011). Nonretinotopic exogenous attention. Curr. Biol. 21, 1732–1737.
Breitmeyer, B. G., Herzog, M. H., and Ögmen, H. (2008). Motion, not masking, provides the medium for feature attribution. Psychol. Sci. 19, 823–829.
Breitmeyer, B. G., and Ögmen, H. (2006). Visual Masking: Time Slices through Conscious and Unconscious Vision. Oxford: Oxford University Press.
Burr, D. C., and Morgan, M. J. (1997). Motion deblurring in human vision. Proc. Biol. Sci. 264, 431–436.
Burr, D. C., Ross, J., and Morrone, M. C. (1986). Seeing Objects in Motion. Proc. R. Soc. Lond. B Biol. Sci. 227, 249–265.
Castet, E. (1994). Effect of the ISI on the visible persistence of a stimulus in apparent motion. Vision Res. 34, 2103–2114.
Chen, S., Bedell, H. E., and Ögmen, H. (1995). A target in real motion appears blurred in the absence of other proximal moving targets. Vision Res. 35, 2315–2328.
Connor, C. E., Brincat, S. L., and Pasupathy, A. (2007). Transformation of shape information in the ventral pathway. Curr. Opin. Neurobiol. 17, 140–147.
Craig, A. D. (2009). How do you feel – now? The anterior insula and human awareness. Nat. Rev. Neurosci. 10, 59–70.
Farrell, J. E., Pavel, M., and Sperling, G. (1990). The visible persistence of stimuli in stroboscopic motion. Vision Res. 30, 921–936.
Haber, R. N., and Standing, L. G. (1970). Direct estimates of apparent duration of a flash. Can. J. Psychol. 24, 216.
Hammett, S. T. (1997). Motion blur and motion sharpening in the human visual system. Vision Res. 37, 2505–2510.
Hogben, J. H., and Dilollo, V. (1985). Suppression of visible persistence in apparent motion. Percept. Psychophys. 38, 450–460.
Johansson, G. (1973). Visual-perception of biological motion and a model for its analysis. Percept. Psychophys. 14, 201–211.
Kahneman, D., Treisman, A., and Gibbs, B. J. (1992). The reviewing of object files: object-specific integration of information. Cogn. Psychol. 24, 175–219.
Otto, T. U., Ögmen, H., and Herzog, M. H. (2006). The flight path of the phoenix-the visible trace of invisible elements in human vision. J. Vis. 6, 1079–1086.
Otto, T. U., Ögmen, H., and Herzog, M. H. (2009). Feature integration across space, time, and orientation. J. Exp. Psychol. Hum. Percept. Perform. 35, 1670–1686.
Otto, T. U., Ögmen, H., and Herzog, M. H. (2010a). Attention and non-retinotopic feature integration. J. Vis. 10, 1–13.
Otto, T. U., Ögmen, H., and Herzog, M. H. (2010b). Perceptual learning in a nonretinotopic frame of reference. Psychol. Sci. 21, 1058–1063.
Ögmen, H. (2007). A theory of moving form perception: synergy between masking, perceptual grouping, and motion computation in retinotopic and non-retinotopic representations. Adv. Cogn. Psychol. 3, 67–84.
Ögmen, H., and Herzog, M. H. (2010). The geometry of visual perception: retinotopic and nonretinotopic representations in the human visual system. Proc. IEEE Inst. Electr. Electron. Eng. 98, 479–492.
Ögmen, H., Otto, T. U., and Herzog, M. H. (2006). Perceptual grouping induces non-retinotopic feature attribution in human vision. Vision Res. 46, 3234–3242.
Plomp, G., Mercier, M. R., Otto, T. U., Blanke, O., and Herzog, M. H. (2009). Non-retinotopic feature integration decreases response-locked brain activity as revealed by electrical neuroimaging. Neuroimage 48, 405–414.
Poggio, T., Torre, V., and Koch, C. (1985). Computational vision and regularization theory. Nature 317, 314–319.
Pooresmaeili, A., Cicchini, G. M., Morrone, M. C., and Burr, D. (2012). “Non-retinotopic processing” in Ternus motion displays modeled by spatiotemporal filters. J. Vis. 12(1):10, 1–15.
Purushothaman, G., Ögmen, H., Chen, S., and Bedell, H. E. (1998). Motion deblurring in a neural network model of retino-cortical dynamics. Vision Res. 38, 1827–1842.
Ramachandran, V. S., Rao, V. M., and Vidyasagar, T. R. (1974). Sharpness constancy during movement perception – short note. Perception 3, 97–98.
Riesenhuber, M., and Poggio, T. (1999a). Are cortical models really bound by the “binding problem?” Neuron 24, 87–93.
Riesenhuber, M., and Poggio, T. (1999b). Hierarchical models of object recognition in cortex. Nat. Neurosci. 2, 1019–1025.
Singer, W. (1999). Neuronal synchrony: a versatile code for the definition of relations? Neuron 24, 49–65.
Stigler, R. (1910). Chronophotische Studien über den Umgebungskontrast. Pflügers Arch. Gesamte Physiol. Menschen Tiere 134, 365–435.
Treisman, A. (1998). Feature binding, attention and object perception. Philos. Trans. R. Soc. Lond. B Biol. Sci. 353, 1295–1306.
Treisman, A. M., and Gelade, G. (1980). A feature-integration theory of attention. Cogn. Psychol. 12, 97–136.
Keywords: feature binding, feature processing, feature integration, sequential metacontrast paradigm, feature inheritance
Citation: Herzog MH, Otto TU and Ögmen H (2012) The fate of visible features of invisible elements. Front. Psychology 3:119. doi: 10.3389/fpsyg.2012.00119
Received: 15 January 2012; Accepted: 01 April 2012;
Published online: 27 April 2012.
Edited by:
Snehlata Jaswal, Indian Institute of Technology Ropar, IndiaCopyright: © 2012 Herzog, Otto and Ögmen. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Michael H. Herzog, Laboratory of Psychophysics, Ecole Polytechnique Fédérale de Lausanne, EPFL SV BMI LPSY, Station 19, 1015 Lausanne, Switzerland. e-mail: michael.herzog@epfl.ch
