Finding Your Way from the Bed to the Kitchen: Reenacting and Recombining Sensorimotor Episodes Learned from Human Demonstration

1. Introduction

Cognitive science has traditionally equated cognition with the processing of symbolic internal representations of an external world [e.g., Pylyshyn (1984), Fodor and Pylyshyn (1988), Newell (1990), and Anderson (1996)]. While clearly humans experience some kind of “inner world,” i.e., the ability to imagine their environment and their own interactions with it embodied/situated theories of cognition [e.g., Varela et al. (1991), Clancey (1997), Clark (1997), and Lakoff and Johnson (1999)] have questioned the traditional view of symbolic mental representations. In artificial intelligence research, in particular, some have argued for the need of “symbol grounding” (Harnad, 1990), i.e., the grounding of amodal symbolic representations in non-symbolic iconic and categorical representations that allow to connect senses to symbols, while others have argued that the “physical grounding” of “embodied” and “situated” robots simply makes representation unnecessary [e.g., Brooks (1991)]. In this context, alternative accounts of cognition as based on different types of mental simulation or emulation have gained substantial interest [e.g., Barsalou (1999), Hesslow (2002), Grush (2004), Gallese (2005), and Svensson (2013)]. According to these theories, the “inner world” and the human capacity for imagination are based on internally simulated action and perception, i.e., the brain’s ability to (re- or pre-) activate itself as if it was in actual sensorimotor interaction with the external world.

While there have been many advances in providing robots with some kind of inner world, the inner worlds of robots have traditionally been based on predefined ontologies and still lack in complexity and flexibility compared to the inner worlds of humans. In this paper, we describe a learning mechanism that enables a simulated robot to mentally imagine moving around in an apartment environment. The robot does not only repeat previously experienced routes but also shows a kind of organic compositionality (Tani et al., 2008), allowing it to reenact – and recombine – parts of previous sensory–motor interactions in novel ways. The basic mechanism underlying this is grounded in simulation theories, in particular, the type of mechanisms suggested by Hesslow (2002) and consists of learning associations between sensor and motor events.

In the present work, we combine previous efforts on internal simulation (Stening et al., 2005; Ziemke et al., 2005; Svensson, 2013) with those on Learning from Demonstration (LFD) (Billing, 2012) into a model that can learn from human demonstrations and reenact the demonstrated behavior both overtly and covertly. We here evaluate several aspects of such covert action: (1) can the robot produce internal simulations similar to a previously executed overt behavior; (2) to what extent can the system produce internal simulations of new behavior, that is, reenact and recombine previously experienced episodes into a novel path through the environment; and (3) how can such internal simulations in a robot be compared with simulation theories of human cognition?

The rest of this paper is organized as follows. Simulation theories of cognition are introduced in Section 2, and a problem statement of recombining previous experiences into novel simulations is presented in Section 3. The modeling technique, based on Predictive Sequence Learning (PSL), is presented in Section 4, followed by a description of the experimental setup in Section 5. Our hypotheses are made explicit in Section 6. Results are presented in Section 7, and the paper is concluded with a discussion in Section 8.

2. Simulation Theories

In simple terms, simulation theories explain cognition as simulated actions and perceptions. The term simulation, as used in this paper, is more specifically related to the following two notions:

• Reactivation: Simulation is the reactivation of various brain areas, especially areas along the sensory and motor hierarchies, and

• Prediction: The covert or simulated actions can directly evoke sensory activity that corresponds to the activity of the sensory organs that has previously occurred following action execution in that context.

Ideas relating to reactivation and prediction are not new but have received renewed attention in the last couple of decades [e.g., Damasio (1994), Barsalou (1999), Möller (1999), Hesslow (2002), Gallese (2003), and Grush (2004)]. The idea of reactivation can be found dating (at least) as far back as the British empiricists and associationists (Hesslow, 2002).

Alexander Bain suggested that thinking is essentially a covert or weak form of behavior that does not activate the body and is therefore invisible to an external observer […]. Thinking, he suggested, is restrained speaking or acting (Hesslow, 2002, p. 242).

The idea of restrained actions was also popular among some of the behaviorists, perhaps most prominently Watson, who viewed cognition or thinking as motor habits in the larynx (Watson, 1913, p. 84), cited in Hickok (2009). While the idea of reactivation in these early theories was rather underspecified and susceptible to criticism (for example, the finding that paralysis induced to the muscles by curare did not have any observable effects on thinking) (Smith et al., 1947; Hesslow, 2002), modern theories of simulation and reactivation [e.g., Barsalou (1999), Hesslow (2002), and Grush (2004)] further specify the nature of the reactivations (i.e., simulated actions and perceptions) based on both behavioral studies using elaborate experimental setups and a large body of neuroscientific evidence, e.g., Jeannerod (2001). We do not elaborate on the empirical evidence cited in support for simulation theories in this paper, but reviews can be found in Colder (2011), Hesslow (2012), and Svensson (2013).

Given that simulation theories have been put forward to explain many different cognitive phenomena and span a wide range of disciplines, such as linguistics [e.g., Zwaan (2003)], neuroscience (Colder, 2011), and psychology [e.g., Barsalou (1999)], they are not entirely coherent in their particular details of implementation and hypotheses about the underlying mechanisms. They also differ with regard to their view of knowledge and the relation between the cognitive agent and its environment (Svensson, 2007, 2013). However, to some extent, they share a commitment to the reactivation hypothesis and/or the prediction hypothesis. The following subsections provide a summary of three of the perhaps most commonly cited simulation theories: Hesslow’s simulation hypothesis (Hesslow, 2002), Grush’s emulation theory of representation (Grush, 2004), and Barsalou’s notions of perceptual symbol systems and situated conceptualizations (Barsalou, 1999, 2005).

2.1. Simulation Hypothesis

Hesslow (2002, 2012) argued that his simulation hypothesis rests on three basic assumptions:

• Simulation of actions: We can activate motor structures of the brain in a way that resembles activity during normal action but does not cause any overt movement.

• Simulation of perception: Imagining perceiving something is essentially the same as actually perceiving it, only the perceptual activity is generated by the brain itself rather than by external stimuli.

• Anticipation: There exist associative mechanisms that enable both behavioral and perceptual activity to elicit perceptual activity in the sensory areas of the brain (Hesslow, 2002, p. 242). Most importantly, a simulated action can elicit perceptual activity that resembles the activity that would have occurred if the action had actually been performed.

A central claim of the simulation hypothesis is that it is not necessary to posit some part of the brain or some autonomous agent self-performing the simulation, but the anticipation mechanism will ensure that most actions are accompanied by probable perceptual consequences (Hesslow, 2002). That means there is no need to posit an independent agent (i.e., homunculus) that evaluates the simulation; rather, the (simulated) sensory events will elicit previously learned affective consequences that guide future behavior by rewarding or punishing simulated actions. The mechanisms that ensure that the simulations are established are likely to be realized by neural mechanisms located in many different areas of the brain, rather than there being a single neural mechanism for anticipation (Svensson et al., 2009b; Svensson, 2013).

2.2. Emulation Theory of Representation

Grush (2004) proposed a general theory of representation based on the control-theoretic concept of emulation or forward modeling. The concept of a forward model is well known in motor control and has, in that context, also been linked to seemingly more mental abilities such as forming mental images of actions [e.g., Wolpert et al. (1995)].

Generally, a forward model (ϕ) takes the current state (x_t) of the system and a control signal (u_t), and estimates the consequences of that control signal in terms of a new state of the system $\left({\widehat{x}}_{t+1}\right)$, at some future time t + 1:

${\widehat{x}}_{t+1}=\mathrm{\varphi }\left(x_t,u_t\right)$ (1)

The forward model acts in combination with the controller, or inverse model π:

${\widehat{u}}_t=\mathrm{\pi }\left(x_t\right)$ (2)

An illustration of an agent implementing forward and inverse models along the principles put forward by Hesslow (2002) and Grush (2004) is presented in Figure 1. We should, however, note that the forward and inverse models are here depicted as associations between perceptions and actions, not functions of the system’s state as defined in equations (1) and (2). Grush (2004) uses a Kalman filter to compute the system state based on perceptual information. However, Hesslow (2002) takes an associationist’s perspective and argues for an implicit state representation.

FIGURE 1

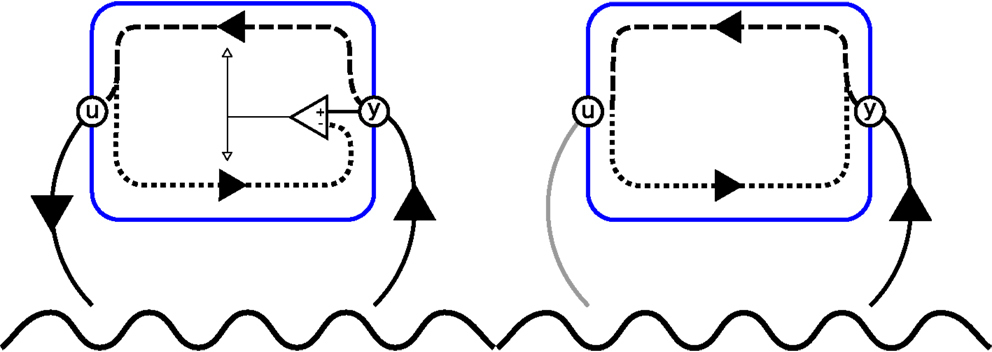
Figure 1. Left, an agent, encapsulated by a blue line, that perceives (y) and acts (u) upon its environment, depicted as a sine wave. The dashed line depicts the inverse model ϕ, and the dotted line represents the forward model ω. The prediction error given by the comparator is used to update both models (white arrow). Right, the same agent conducting internal simulation. Here, output of the forward model is not (only) used for learning but fed back into the inverse model in order to compute the next action. As a result, the iterative process can continue without overt interactions with the world.

While, as already noted above, forward and inverse models of the motor system have been linked to mental imagery, the general idea of simulation theories is that simulations are not restricted to only the immediate control of the body. As can be seen in, e.g., Barsalou (1999)’s theory of perceptual symbol systems and situated conceptualizations, simulations can also include more distal and distant aspects of embodied interaction (Svensson et al., 2009b).

2.3. Perceptual Symbol Systems

Barsalou (1999, 2005) proposed a theory of perceptual symbol systems, consisting of three parts: (1) perceptual symbols, i.e., the reenactment of modality-specific states; (2) simulators and associated simulations; and (3) situated conceptualizations. For readability, we only focus on the latter (Barsalou, 1999) for a description of parts 1 and 2. According to Barsalou (2005), our ability to categorize and conceptualize the world depends on a particular type of simulation, which he terms situated conceptualizations, in which the conceptualizer is placed directly in the respective situations, creating the experience of being there … (Barsalou, 2005, p. 627). Barsalou illustrated this as follows:

Consider a situated conceptualization for interacting with a purring house cat. This conceptualization is likely to simulate how the cat might appear perceptually. When cats are purring, their bodies take particular shapes, they execute certain actions, and they make distinctive sounds. All these perceptual aspects can be represented as modal simulations in the situated conceptualization. Rather than amodal redescriptions representing these perceptions, simulations represent them in the relevant modality-specific systems (Barsalou, 2005, p. 626–627).

In such a situation, simulated perceptions and actions/emulations are connected into simulated chains of embodied interactions that involve bodily aspects as well as physical and social aspects of the environment and enable our conceptual understanding of the situation.

3. Problem Statement

One of the key premises of simulation theories is that the capacity to reenact previous experiences covertly allows the agent to get away from the here and now and generate the experience of a novel sequence of events. This allows the agent to “try out” different scenarios without the effort and possible dangers of actually executing them.

As an example, close your eyes and imagine yourself in your home. You wake up, get out of the bed, go through the bedroom door, continuing the shortest way out of the building – it is quite easy to imagine, even if you have never taken exactly this path before. You combine previous experiences from your home into something new.

An abstraction of the scenario described above is given in Figure 2. With the knowledge of getting from A to B and from C to D, the internal simulation exploits that intersection to postulate a possible way of getting from A to D or C to B. An agent standing at A can of course follow the known path from A toward B and look for opportunities to reach D, but with many behaviors to choose from the goal quickly becomes unreachable. Internal simulations drastically reduce the effort of trying out different combinations of known behaviors in the real world.

FIGURE 2

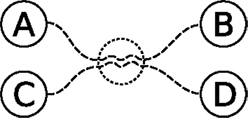
Figure 2. Abstract depiction of two paths, from A to B and from C to D. The two paths, depicted as dashed lines, share some experiences, indicated with a dotted circle, allowing the agent to combine previously experienced episodes into new behavior, e.g., going from A to D. See text for details.

Despite the fact that simulation theories constitute common sources of inspiration for roboticists, the basic scenario described above has to our knowledge never been computationally analyzed using internal simulation. Over the last two decades, computational models, such as HAMMER (Demiris and Hayes, 2002; Demiris and Khadhouri, 2006; Demiris et al., 2014), MOSAIC (Wolpert and Kawato, 1998; Haruno et al., 2003), MTRNN (Yamashita and Tani, 2008), and MSTNN (Jung et al., 2015), have received significant attention. These models all rely on prediction and to some extent a pairing of forward and inverse models, and some have been used for internal simulation. But none have, to our knowledge, been used for generating novel, goal-directed behavior using internal simulation.

Tani (1996) presents an early approach to model-based learning using a recurrent neural network that generates an internal simulation of future sensory input. Another example of goal-directed planning using internal simulations was presented by Baldassarre (2003). While both these models produce simulations of goal-directed behavior, they do not learn from human demonstrations.

Pezzulo et al. (2013) argued that there is a need for grounded theories, including simulation theories, to develop better process models of “how grounded phenomena originate during development and learning and how they are expressed in online processing” and that an important challenge is explaining “how abstract concepts and symbolic capabilities can be constructed from grounded categorical representations, situated simulations, and embodied processes.” The grounded cognition approach and Barsalou’s situated conceptualization (Barsalou, 1999, 2005; Barsalou et al., 2003) suggest that abstract thinking and other cognitive phenomena are based on and consist of processing involving bodily (e.g., proprioceptive, interoceptive, and emotional) states as well as the physical and social environment. Therefore, computational models of simulation theories need to better reflect the bodies and environments that humans inhabit to develop richer concepts that can be used to think about the world and oneself.

Here, we directly address the latter part of this question by evaluating to what extent the robot model, based on the principles of simulation theories, can internalize the environment and generate new behavior in the form of internal simulations. Specifically, we are interested in to what degree the robot model can produce goal-directed covert action and to what degree the internal simulation replicates the sensory–motor interactions of the overt behavior.

3.1. Computational Models of Internal Simulation

A possible approach of implementing simulations as proposed by Hesslow (2002) in computational agents can be found already in the work of Rumelhart et al. (1986) on artificial neural networks. They suggested that it is possible to “run a mental simulation” by having one network that produces actions based on sensory input and another that predicts how those actions change the world. By replacing the actual inputs with the predicted inputs, the networks would be able to simulate future events (Rumelhart et al., 1986, p. 41–42). The assumption is that if the predicted sensory input is similar enough to the actual sensory input, the agent can be made to operate covertly where the predicted sensory input is used instead of the actual sensory input. Two early implementations of simulation-like mechanisms of this kind were the “Connectionist Navigational Map (CNM)” of Chrisley (1990) and the simulated robot (arm) “Murphy” by Mel (1991). The theoretical motivation behind the connectionist navigational map was the transition from non-conceptual to conceptual knowledge [see, e.g., Barsalou (1999)], and later models have focused on, for example, allocentric spatial knowledge (Hiraki et al., 1998), learning the spatial layout of a maze-like environment [e.g., Jirenhed et al. (2001) and Hoffmann and Möller (2004)], obstacle avoidance (Gross et al., 1999), and robot dreams (Svensson et al., 2013).

These experiments have shown that the computational agents can learn to produce internal simulations that guide behavior in the absence of sensory input. However, it is not a trivial task to construct such simulations. For example, one can easily imagine that if predictions start to diverge from the actual sensory states, simulations will drift and become increasingly imprecise. Jirenhed et al. (2001) found that some behaviors caused states in which predictions could not be learnt which hindered successful internal simulations to develop, and Hoffmann and Möller (2004) identified an accumulation of error as the chains of predictions increase in length, which could restrict the ability to create longer sequences of simulations. On the other hand, in Baldassarre (2003)’s model, noisy predictions did not accumulate for each time step. Others have suggested that the states in internal simulations should not be judged by their correspondence to real sensory input, rather the important aspect is that the internal simulations constructed by the robot support successful behavior (Gigliotta et al., 2010). For example, Ziemke et al. (2005) demonstrated a simple internal simulation in a Khepera robot [K-Team (2007)], using a feed forward neural network. The network generated both actions and expected percepts, allowing the robot to reenact earlier sensory–motor experiences and move blindfolded through its environment. Despite the fact that the actions produced during internal simulation produced roughly the same coherent behavior, the internally generated sensor percepts used for blind navigation were actually quite different from the previously experienced real sensory inputs.

The current models of mechanisms based on simulation theories have shown the viability of creating internal models out of simple sensory–motor associations, but the environments have often been of very low complexity. For example, the environments consist of very simple mazes without obstacles/objects [e.g., Jirenhed et al. (2001) and Ziemke et al. (2005)] or with only a few simple block shaped obstacles/objects [e.g., Tani (1996) and Gross et al. (1999)].

Two computational models that have been used in more complex settings are HAMMER (Demiris and Simmons, 2006; Demiris et al., 2014) and the recurrent neural network models by Tani and colleagues (Tani et al., 2008; Yamashita and Tani, 2008; Jung et al., 2015).

Already in an early presentation of the model (Demiris and Hayes, 2002), HAMMER was used for internal simulation in the context of imitation learning. Framed as active imitation, Demiris and Hayes (2002) present a system producing a set of parallel internal simulations. The output of each simulation, generated by paired forward and inverse models, is compared with the demonstrator’s observed state, and the error is used to assign a confidence level to each simulation. Since each pair of forward and inverse models is trained to implement a specific behavior, the method can be used for imitation. Together with the MOSAIC model (Haruno et al., 2003), HAMMER constituted significant inspiration for our own previous work on behavior recognition (Billing et al., 2010). For further positioning of the HAMMER architecture in relation to other cognitive architectures, please refer to Vernon (2014).

Another topic of interest has been the formation of concepts and abstractions of the sensorimotor flow in internal simulations. For example, Stening et al. (2005) developed a two-level architecture in which the higher level was able to form internal simulations of the “rough” structure of the environment, based on simple categories, such as “corner” or “corridor,” developed through unsupervised learning at the lower level. Another example is Tani et al. (2008), who investigated the development of flexible behavior primitives achieving a kind of “organic compositionality” in a humanoid robot, and the robot was also able to reactivate the primitives internally in a mental simulation. These types of behavior primitives could be seen as potential buildings blocks of the situated conceptualizations suggested by Barsalou (2005).

4. Predictive Sequence Learning

As discussed in Section 3, we are interested in investigating how prior experiences can be combined into new, goal-directed behavior during both overt and covert actions. The proposed system is based on our earlier work on Learning from Demonstration (LFD) (Billing and Hellström, 2010) and the PSL algorithm [e.g., Billing et al. (2011a,b, 2015)]. PSL resembles many of the principles put forward in Sections 2–3 and implements forward and inverse models as a joint sensory–motor mapping:

${\widehat{e}}_{t+1}=f\left({\mathrm{\eta }}_t\right)$ (3)

where e_t = (u_t−1, y_t) represents a sensory–motor event at time t, comprising perceptions y_t and actions $u_{t-1}·{\widehat{e}}_{t+1}$ is the predicted event estimate. A sequence of events constitutes the sensory–motor event history η:

${\mathrm{\eta }}_t=\left(e_1,e_2,\dots ,e_t\right)$ (4)

PSL constitutes a minimalist approach to prediction and control, compared to, e.g., HAMMER (Demiris and Hayes, 2002; Demiris and Khadhouri, 2006) and CTRNN (Yamashita and Tani, 2008), as discussed in Section 2. Both HAMMER and CTRNN have been evaluated in LFD settings and could be expected to produce more accurate prediction and control, especially with high-dimensional and noisy data. However, for the present evaluation, PSL was chosen since it, in contrast to the HAMMER architecture, represents a fully defined algorithm, leaving less room for platform specific interpretations. It also takes an associationist approach to learning, implementing a direct perception – action mapping closely resembling Hesslow’s simulation hypothesis (Hesslow, 2012) as depicted in Figure 1 [compared with the use of a state estimate, equations (1) and (2)]. In this respect, PSL is model free (Billing et al., 2011a) and, in the form used here, comprises only two parameters: membership function size (τ) and the precision constant $\widehat{\alpha }$. Both parameters are described in detail below.

With a closer connection to biology, CTRNN represents a theoretically interesting alternative but requires much larger training times and could therefore pose practical problems for conducting the kind of evaluations presented here.

In the language of control theory, we would define a transfer function describing the relation between the system’s inputs and outputs. An estimator, such as maximum likelihood, would then be used to estimate the parameters for the model. For an introduction to this perspective in robotics, see, e.g., Siegwart and Nourbakhsh (2004). Here, we take a different approach and formulate f [equation (3)] as a set of fuzzy rules, referred to as hypotheses (h), describing temporal dependencies between a sensory–motor event e_t+1 and a sequence of past events (e_t−|h|+1, e_t−|h|+2, …, e_t), defined up until current time t:

$h:\left({\Upsilon }_{\mathrm{\tau }+1}\text{\hspace{0.17em}is\hspace{0.17em}}{E}_1^h\wedge {\Upsilon }_{\mathrm{\tau }+2}\text{\hspace{0.17em}is\hspace{0.17em}}{E}_2^h\wedge \dots \wedge {\Upsilon }_t\text{\hspace{0.17em}is\hspace{0.17em}}{E}_{\left|h\right|}^h\right)\stackrel{C}{\Rightarrow }{\Upsilon }_{t+1}\text{\hspace{0.17em}is\hspace{0.17em}}{Ē}^h.$ (5)

where ϒ_i is the event variable, and E^h(e) is a fuzzy membership function returning a membership value for a specific e_t. The right-hand side ${Ē}^h$ is a membership function comprising expected events at time t + 1. |h| denotes the length of h, i.e., the number of left-hand-side conditions of the rule. τ equals t − |h|. C represents the confidence of h within a specific context, described in the following section. Both E and Ē are implemented as standard cone membership functions with base width ε [e.g., Klir and Yuan (1995)].

A set of hypotheses is used to compute f [equation (3)], producing a prediction ${\widehat{e}}_{t+1}$ given a sequence of past sensory–motor events η. The process of matching hypotheses to data is described in Section 1, and the use of PSL as forward and inverse models during overt and covert actions is described in Section 3.

As hypotheses represent weighted associations between a sequence of sensory–motor events, PSL can be viewed as a variable-order Markov model. Generated hypotheses are initially associating a single e_t with ${\widehat{e}}_{t+1}$, implementing a first-order association. In cases where e_t does not show Markov property, an additional hypothesis is generated: $\left(e_{t-1},e_t\right)\Rightarrow {\widehat{e}}_{t+1}$, implementing a second-order association. Seen as a directed graph between sensory–motor events, PSL implements several aspects of a joint procedural–episodic memory (Vernon et al., 2015). For a detailed description of the learning process of PSL, please refer to Billing et al. (2015).

PSL is not expected to produce a better estimate in terms of prediction error than what can be gained using control theory approaches, but allows estimated mapping functions, defined as sets of hypotheses, to be recombined in order to produce novel behavior. This property is not as easily achieved using a control-theoretic approach.

4.1. Matching Hypotheses

Given a sequence of sensory–motor events, η = (e₁, e₂, …, e_t), a match α_t(h) is given by

${\mathrm{\alpha }}_t\left(h\right)=\underset{i=0}{\stackrel{\left|h\right|-1}{\wedge }}{E}_i^h\left(e_{t-i}\right)$ (6)

where ∧ is implemented as a min-function.

Hypotheses are grouped into fuzzy sets C whose membership value C(h) describes the confidence of h at time t:

$C\left(h\right)=\frac{{\displaystyle \sum _{k=t_h}^t}{\mathrm{\alpha }}_k\left(h\right){Ē}^h\left(e_{k+1}\right)}{{\displaystyle \sum _{k=t_h}^t}{\mathrm{\alpha }}_k\left(h\right)}$ (7)

where t_h is the creation time of h. Each set C represents a context and can be used to implement a specific behavior or part of a behavior. The responsibility signal λ_t(C) is used to control which contexts are active at a specific time. The combined confidence value ${\tilde{C}}_t\left(h\right)$, for hypothesis h, is a weighted average over all C:

${\tilde{C}}_t\left(h\right)=\frac{{\displaystyle \sum _C}C\left(h\right){\mathrm{\lambda }}_t\left(C\right)}{{\displaystyle \sum _C}{\mathrm{\lambda }}_t\left(C\right)}$ (8)

where ${\tilde{C}}_t$ is a single fuzzy set representing the combination of all active contexts at time t. Hypotheses contribute to a prediction in proportion to their membership in $\tilde{C}$, their length, and match α_t(h). The aggregated prediction $\widehat{E}\left(e_{t+1}\right)$ is computed using the Larsen method [e.g., Fullér (2000)]:

$\widehat{E}\left(e_{t+1}\right)=\underset{h}{\vee }{Ē}_h\left(e_{t+1}\right)\tilde{C}\left(h\right)\left|h\right|{\mathrm{\alpha }}_t{\left(h\right)}^2$ (9)

During learning, new hypotheses are created when $\widehat{E}\left(e_{t+1}\right)<\widehat{\mathrm{\alpha }}$, that is, when the observed sensory–motor event e_t+1 in the training data does not match the prediction. The precision constant $\widehat{\mathrm{\alpha }}\in \left[0,1\right]$ is, in fuzzy-logic terms, an α-cut, i.e., $\widehat{\alpha }$ specifies a threshold for prediction precision, where a high value results in highly precise predictions and a large number of hypotheses, while a small $\widehat{\alpha }$ renders less hypotheses, and less precise predictions [see Billing et al. (2011b) for details].

While the PSL algorithm used here is identical to earlier work, a different defuzzification method is used. Billing et al. (2015) employed a center of max defuzzification method, while we here use a probabilistic approach. $\widehat{E}$ is treated as a probability distribution and converted to crisp values by randomly selecting a predicted sensory–motor event $\widehat{e}\in \widehat{E}$ in proportion to their membership in $\widehat{E}$.

The PSL mapping function [equation (3)] can now be redefined as context-dependent forward and inverse models:

${ŷ}_{t+1}=\mathrm{\varphi }\left({\mathrm{\eta }}_t,{\mathrm{\lambda }}_t\right)$ (10)

${\widehat{u}}_t=\mathrm{\pi }\left({\mathrm{\eta }}_t,{\mathrm{\lambda }}_t\right)$ (11)

4.2. Illustrative Example

Figure 3 presents an example of PSL applied to a simplified robot scenario. Consider a robot placed in an environment depicted as a gray area in the figure. A demonstration (η), comprising 8 sensory motor events, shows how to get from its current location to the goal (G). Using η as training data, PSL generates a knowledge base comprising 9 hypotheses, under context C.

FIGURE 3

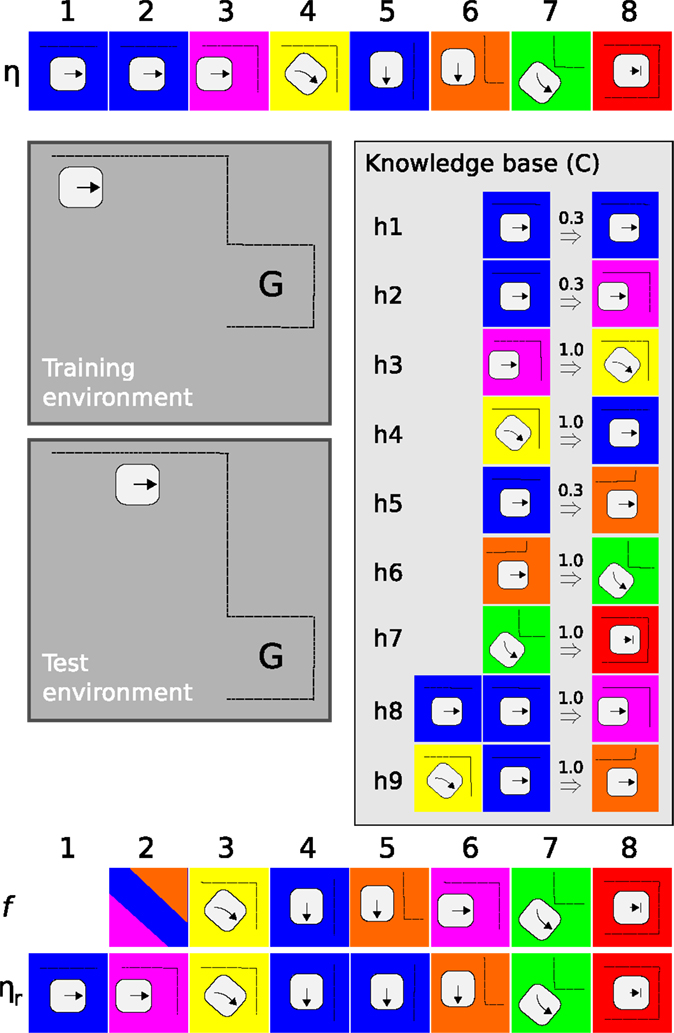
Figure 3. An illustrative example of PSL. A robot, illustrated as a square with rounded corners, and an arrow indicating its direction are placed in a simple environment with dotted lines representing obstacles. G marks the goal location. Colored squares represent unique sensory–motor events. See text for details.

When placed in the test environment, PSL is used as a controller to generate a sequence of actions from start to goal. Note that the starting location is not identical and that the test environment is slightly different from the one used for training. The output produced by PSL is presented in Figure 3 as f, aligned with the event sequence η_r observed while executing selected actions. At time step 1, PSL bases its prediction on a single (blue) sensory–motor event which, according to the knowledge base, can have three possible outcomes (h1, h2, and h5). PSL selects among these in proportion to the confidence levels, represented by the number above hypotheses’ arrows in the figure. The action associated with the selected sensory–motor event is executed and the robot approaches the corner at time step 2. Predictions are again based on η_r, h3 is selected, and a right turn is issued.

While continuing this thought example, PSL will produce correct predictions at t = 3 and 4, incorrect prediction at t = 5 and 6, and finally catching up with correct predictions at t = 7 and 8. Errors are only perceptual and appropriate actions are executed also in these cases, allowing the robot to stay on path also when there are differences between predicted and observed sensory–motor events.

In a realistic scenario, there will never be an exact match between hypotheses in the knowledge base and observed perceptions and actions. Matching perceived data to sensory–motor events is controlled by the membership function [equation (5)]. A wide membership, with a large τ, allows many hypotheses to be selected, increasing the robot’s ability to act also in relatively novel situations. However, a value of τ that is too large reduces precision as a larger number of hypotheses match observed data, increasing the risk that inappropriate actions are selected even in well-known environments. A balance between the two allows certain variability in the environment, while still producing stable behavior. This balance can hence be seen as a type of exploration – exploitation trade-off present in many machine learning approaches.

4.3. Overt and Covert Actions

Hypotheses generated by PSL are used in two modes: (1) as a robot controller (overt action) and (2) for internal simulation (covert action). In Mode 1, the forward model is ignored, and π_psl [equation (11)] is directly used as a controller for the robot. All sensory–motor events e_t comprises perceptions y_t from the robot’s sensors and actions u_t = π_psl(η_t, λ_t). This process resembles Figure 1 (left) with the distinction that learning is only active when the robot is teleoperated by a human teacher.

Mode 2 resembles the right part of Figure 1. π_psl is here paired with ϕ_psl (Eq. 10) to create a reentrant system. Here, only e₁ = (∅, y₁) is taken from the robot’s sensors. All events ${\widehat{e}}_{t>1}$ are generated by

${\widehat{e}}_{t+1}=\left({\mathrm{\pi }}_{\mathit{psl}}\left({\mathrm{\eta }}_t,{\mathrm{\lambda }}_t\right),{\mathrm{\varphi }}_{\mathit{psl}}\left({\mathrm{\eta }}_t,{\mathrm{\lambda }}_t\right)\right)$ (12)

${\mathrm{\eta }}_t=\left(e_1,{\widehat{e}}_2,\dots ,{\widehat{e}}_t\right)$ (13)

As a result, the internal simulation is only based on e₁, the demonstrations used to train PSL, and the responsibility signal λ_t. While λ is in general time varying and can be computed dynamically, using a method for behavior recognition (Billing et al., 2011b, 2015), it was here used as a constant goal signal.

For analytic purposes, we also need to define the prediction error δ_t(C):

${\mathrm{\delta }}_t\left(C\right)=1-\widehat{E}\left(C,e_t\right)$ (14)

representing the error for context C at time t. $\widehat{E}\left(C,e_t\right)$ denotes the context specific aggregate [equation (9)]. As mentioned above, e_t>1 is not available during covert action. In this case, we consider $e_t\approx {\widehat{e}}_t$, allowing computations of prediction errors also during internal simulation.

Based on our measure of prediction error, the confidence γ_t(C) in context C at time t is given by

${\mathrm{\gamma }}_t\left(C\right)=\frac{{\mathrm{\gamma }}_{t-1}\left(C\right)\text{exp}\left(\frac{{\left(E\left(C,e_t\right)-1\right)}^2}{2{\mathrm{\lambda }}^2}\right)}{{\displaystyle \sum _{i=1}^N}\left[{\mathrm{\gamma }}_{t-1}\left(C_i\right)\text{exp}\left(\frac{{\left(E\left(C_i,e_t\right)-1\right)}^2}{2{\mathrm{\lambda }}^2}\right)\right]}$ (15)

This definition of confidence has its roots in the MOSAIC architecture (Haruno et al., 2003) and has previously been used to compute the responsibility signal λ_t = γ_t online (Billing et al., 2015).

5. Experimental Setup

To evaluate to what degree the model is able to produce goal-directed behavior during both overt and covert actions, nine test cases were evaluated. A simulated Kompaï robot (Robosoft, 2011) placed in an apartment environment (Figure 4) was selected as a test platform. Microsoft Robotics Developer Studio (MRDS) was used for robot simulations. The apartment environment is a standard example environment, freely available from Microsoft (2015). PSL¹ and related software was implemented using Java™. Motivation and hypotheses follow in Section 6.

FIGURE 4

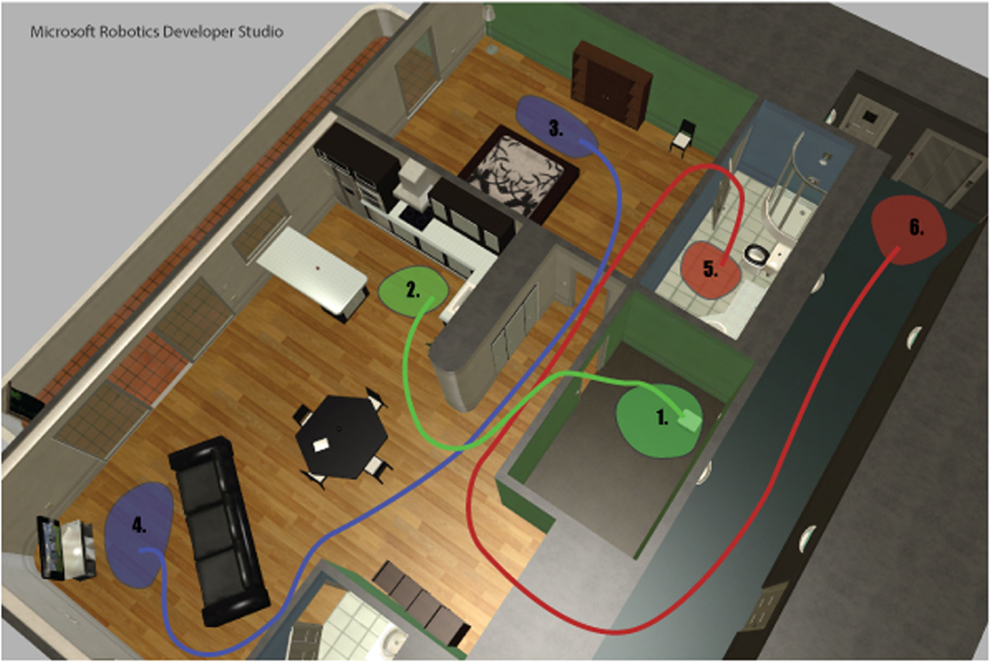
Figure 4. Simulated apartment environment. Green, blue, and red lines indicate approximate paths from start (1, 3, and 5) to goal (2, 4, and 6) locations, for the three demonstrated behaviors, ToKitchen, ToTV, and GoOut. See text for details.

The Kompaï robot was equipped with a 270° laser scanner and controlled by setting linear and angular speeds converted to motor torques by the low-level controller. The 271 laser scans were converted into a 20-dimensional vector where each element represents the mean distance within a 13.5° segment of the laser data. In total, each sensory–motor event e comprised 20 sensor dimensions from the laser data and two motor dimensions (linear and angular speeds). All data were sampled over 20 Hz, and as a result, each sensory–motor event had a temporal extension of 50 ms.

A similar setup was used in previous evaluations of PSL (Billing et al., 2011b, 2015). While the setup is still far from humanoid sensor and motor complexity, the Kompaï robot is designed to act in human environments and does represent a significant increase in environmental and perceptual complexity compared to previous work using simulated Khepera robots (Jirenhed et al., 2001; Stening et al., 2005; Ziemke et al., 2005; Svensson et al., 2009a).

Three behaviors with different start and goal locations were demonstrated by remote controlling the robot using a joy pad:

• ToKitchen: From the storage room (Area 1) to the kitchen (Area 2);

• ToTV : From the bed (Area 3) to the TV (Area 4);

• GoOut: From the bathroom (Area 5) to the elevator (Area 6).

Each behavior was demonstrated four times, producing a total of 12 demonstrations. During demonstration, sensor readings and executed motor commands were recorded. Laser scans were given a maximum distance of 16 m and the membership function base (ε) was set to 1.6 m. $\widehat{\mathrm{\alpha }}=0.9$ for all conditions. Parameter selection was based on previous work (Billing et al., 2015), where a similar setup was used. Preliminary demonstrations were recorded to select suitable start and stop locations and to verify the technical implementation. These demonstrations were thereafter discarded. A set of 12 demonstrations was then recorded for the final training set. These demonstrations were verified by training PSL on all demonstrations from a single behavior and letting PSL act as a controller for the robot, reproducing the demonstrated behavior. All demonstrations passed verification; hence, no recordings were discarded.

For the following test cases, all 12 demonstrations were used as training data for PSL. During training, each behavior was given a unique context [equation (7)], allowing a top-down responsibility signal [equation (8)] to bias selection of hypotheses when PSL was used as a controller. As a result, the selection of specific context can be said to indicate a goal in the form of the target location of the corresponding behavior. PSL was trained on all 12 demonstrations for eight epochs each. One epoch is here defined as a single presentation of all 12 demonstrations² in random order.

In each test phase, the robot was placed on one of the three starting locations (Areas 1, 3, and 5, Figure 4) and executed with a top-down responsibility signal [λ(C)] selecting one of the three goal locations presented during the demonstration phase. For selected context, λ(C) = 1.0. The responsibility signal for other contexts was set to λ(C) = 0.1, allowing hypotheses from these contexts to influence prediction, but down-prioritized in competition with hypotheses trained under the selected context. See Section 4 for a detailed mathematical formulation.

All combinations of the three starting positions and three goals (contexts) were tested, constituting a total of nine conditions: storage to kitchen (ToKitchen), bed to kitchen, bathroom to kitchen, storage to TV, bed to TV (ToTV), bathroom to TV, storage to elevator, bed to elevator, and bathroom to elevator (GoOut). Note that ToKitchen, ToTV, and GoOut were the behaviors used in the demonstration and training phase. Each condition was executed 20 times using overt action and another 20 times using covert action (internal simulation), producing a total of 360 trials³. See Section 4.3 for a detailed description of the two modes of execution.

6. Hypotheses

Following the basic premise presented in Section 3, successful internal simulation should be able to produce realistic sensory–motor interactions of a novel path through the environment.

H1: the simulated robotic system should be able to reenact all nine conditions presented in Section 5, producing an internal simulation connecting the sensory–motor state perceived at the starting point, with the sensory–motor state corresponding to the goal.

In humans and animals, internal simulations happen at different temporal scales (Svensson et al., 2009b; Svensson, 2013), comprising automatic unconscious mental simulations involved in, for example, perception that occur at a very rapid time scale and often involve detailed sensor and motor states [e.g., Gross et al. (1999), Möller (1999), and Svensson et al. (2009b)]. Deliberate mental simulations, e.g., mental imagery, occur at time scales corresponding to the overt behavior (Guillot and Collet, 2005). For example, Anquetil and Jeannerod (2007) studied humans performing mental simulations of grasping actions in both first and third person perspectives. The time to complete simulated actions was found to be closely similar in the two conditions. The approach used here runs internal simulations solely on a sensory–motor level, with exactly the same speed (20 Hz) as the overt behavior.

H2: internal simulations are therefore expected to display a similar temporal extension as the corresponding overt behavior.

7. Results

Figure 5A presents sensor perceptions (laser scans) generated during overt action, plotted in relation to the executed path from the bed (Area 5, Figure 4) to the kitchen (Area 2). While both bed and kitchen were present as start and goal locations in the training data, the path from bed to kitchen was not demonstrated. The robot model combines previously experienced episodes from several different demonstrations into a novel path, corresponding to the schematic illustration from A to D presented in Figure 2.

FIGURE 5

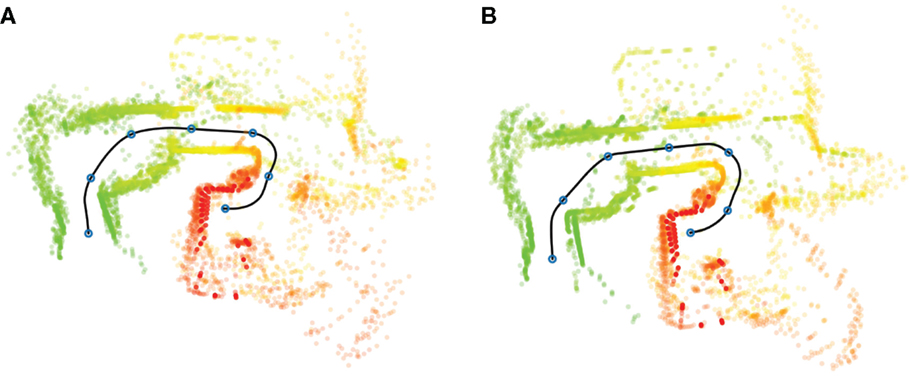
Figure 5. Illustration of sensory–motor interactions along a path from bed (Area 5, Figure 4) to the kitchen (Area 2), using overt (A) and covert (B) action. An approximate path is generated from executed actions and illustrated as a black line. Colored points represent laser scans in relation to the executed path, from start (green) to goal (red). This path was not presented during training and corresponds to the A to D path in Figure 2, i.e., a novel path generated through the recombination of previously experienced episodes. Blue circles along the path mark 2.5-s intervals.

The path from bed to kitchen was also executed covertly (Figure 5B). In this case, actions were not sent to the robot controller and the path (black line) was reconstructed from the sequence of covert actions. Presented sensor percepts are not taken from the robot’s sensors, but instead generated by the internal (PSL) model.

As an illustration of how information from the different demonstrations were used during internal simulation, prediction errors, and confidence levels for each context (behavior) is presented in Figure 6. As visible in the figure, the ToTV context is initially generating relatively small prediction errors, leading to high confidence levels for this context (c.f. Section 3). After about 10 s, ToTV is starting to produce larger errors, leading to a switch in confidence to the ToKitchen context. This switch is the result of a strong responsibility signal [λ_t(C)] for the ToKitchen context and also associated with the robot turning toward the kitchen (c.f. Figure 5).

FIGURE 6

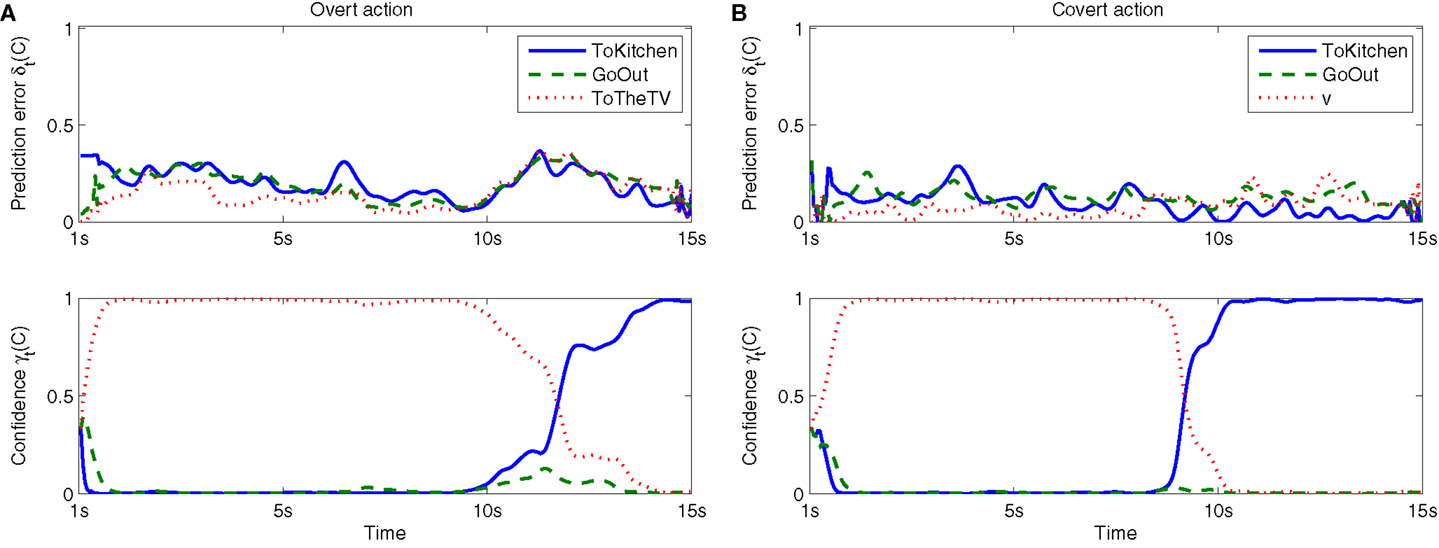
Figure 6. Prediction errors and confidence levels for overt (A) and covert (B) runs from bed to kitchen, as depicted in Figure 5. Values are given for each context (c.f. Section 5). See Section 3 for definitions.

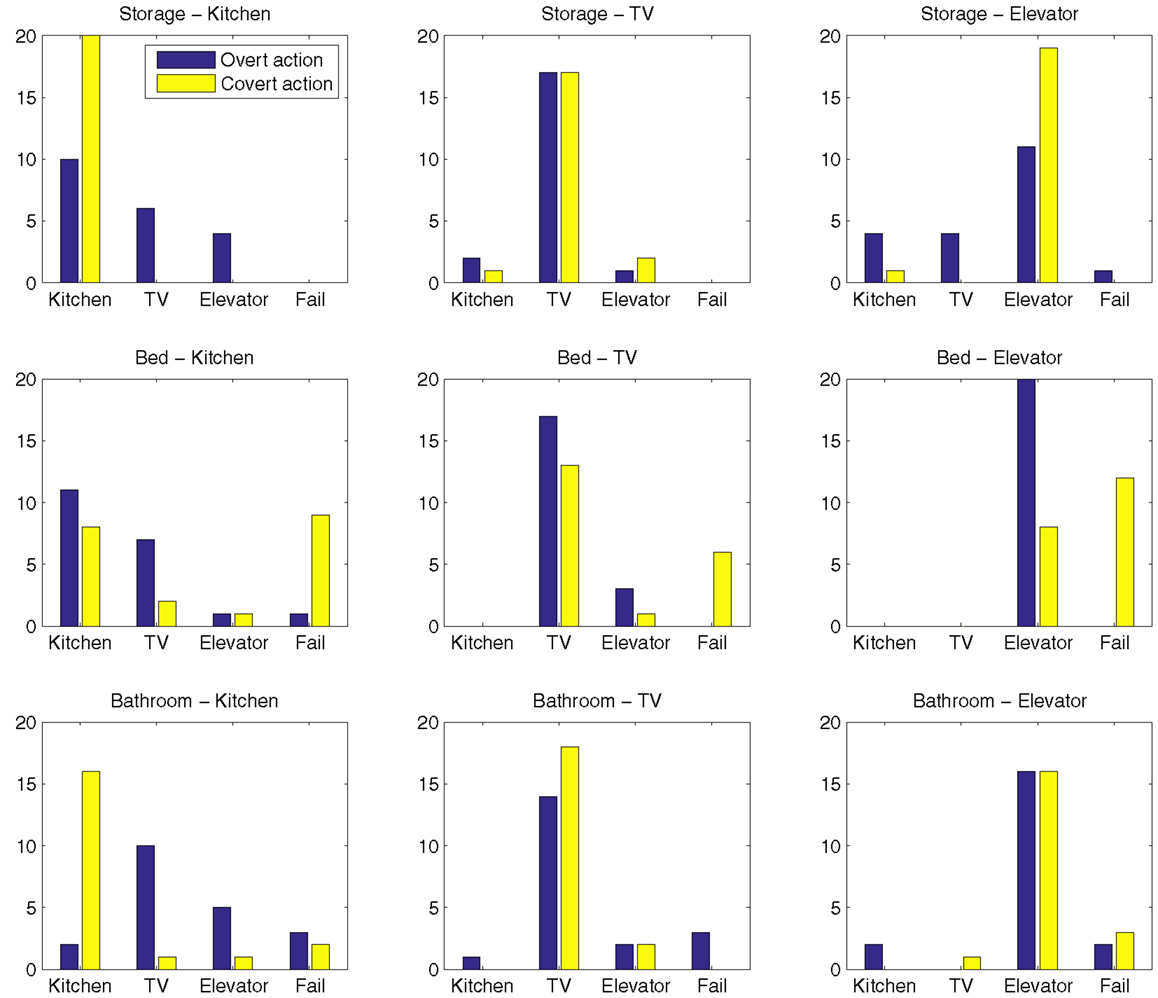
Both examples presented in Figure 5 are successful in the sense that the correct goal, indicated by the top-down signal λ, was reached. Over all nine conditions executed with overt action, the correct goal was reached in 65% of all runs. In 29% of the runs, one of the remaining two goals was reached, leaving 6% of the runs failed, in the sense that no goal was reached.

In runs with covert action, the robot did not move. In order to determine how the internal simulation terminated, the sensory–motor patterns of all 180 covert runs were plotted (as in Figure 5B) and the goal was visually identified. Over all nine conditions, the correct goal was reached in 75% of all runs, a different goal was reached in 7% of the runs and 18% of the runs were classified as failed.

Goal reaching frequencies for each condition, including both overt and covert runs, are presented in Figure 7. Examples of failed internal simulations and internal simulations reaching the wrong goal are given in Figure 8.

FIGURE 7

Figure 7. Goal reaching frequencies for each condition.

FIGURE 8

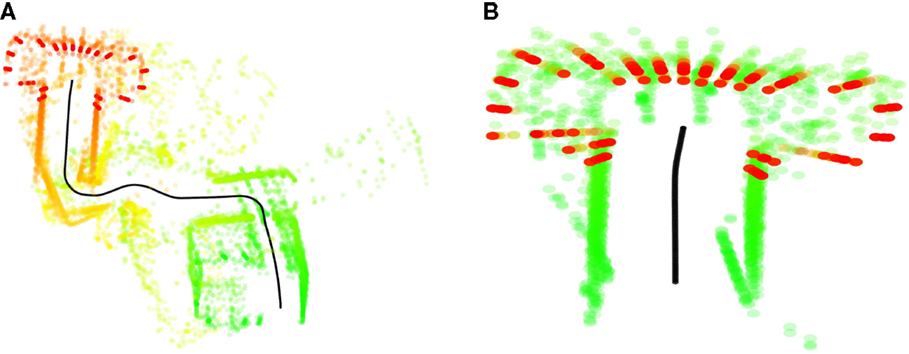
Figure 8. (A) Internal simulation from the storage room (Area 1, Figure 4), here depicted in green, to the TV (Area 4), depicted in red. The simulation diverges from the path indicated by the active context (ToTV) and terminates in a sensory–motor pattern more similar to the elevator (Area 6). (B) Unsuccessful internal simulation from bed (Area 5, Figure 4) to the kitchen (Area 2). The simulation appears to mistake the bed for the entrance corridor and terminates quickly in front of the elevator.

7.1. Simulation Time

In order to test hypothesis 2 (Section 6), simulation time is compared to the time of the overt behavior, presented in Figure 9. Some conditions, Bed to Kitchen and Bathroom to TV, display similar temporal distributions. However, seen over all conditions, the correlation between overt and covert execution times is weak, with internal simulations producing both longer (Storage to TV) and shorter (bottom three conditions, Figure 9) execution times. A two-tailed t-test over all runs reveals a significant difference between overt and covert execution times (p < 0.005).

FIGURE 9

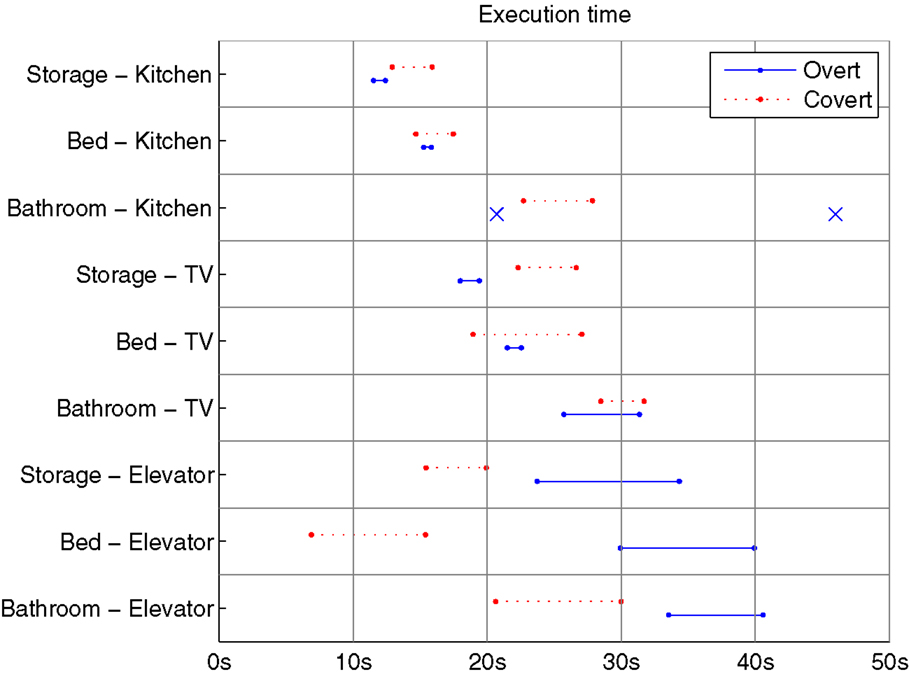
Figure 9. Execution time, i.e., time to reach the goal, from all successful runs in each condition. Solid and dashed lines represent the 95% confidence interval of the means of overt and covert runs, respectively. Conditions with few successful runs are displayed as × marking execution times for individual runs, rather than a distribution.

The strongest difference between overt and covert execution times is found in conditions Storage to TV and Bed–Elevator, with the former showing longer covert execution times, and the latter shorter times for covert runs. A deeper analysis of these conditions is presented below.

Typical runs from Storage to TV are displayed in Figure 10. The internal simulation (b) is semantically correct; it replicates all important aspects of the overt execution (a), but misrepresents the first part of the path, through the storage room depicted in green. The total execution time of the simulated path is in this case almost twice as long as its overt counterpart, 30 versus 18 s. The time of exit from the storage room is 17.5 s in the covert condition and 4.0 s in the overt case, implying that the vast majority of the temporal difference between the two conditions appears in the storage room.

FIGURE 10

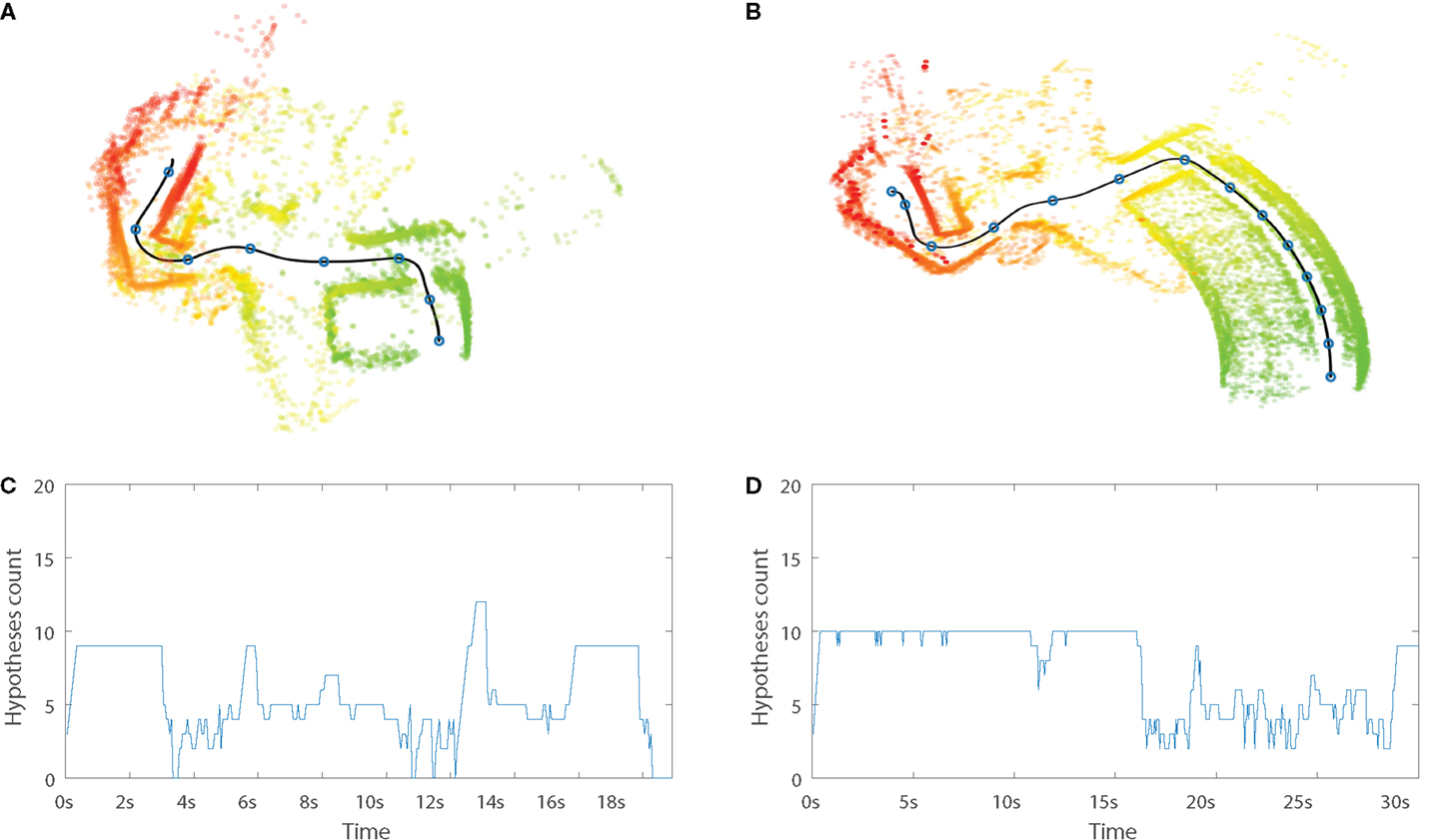
Figure 10. Typical runs from condition Storage to TV. Upper plots present laser scans in relation to the executed path, generated during overt (A) and covert (B) runs from storage room (green) to TV (red). Blue circles along the path, represented by the black line, mark 2.5-s intervals. Lower plots present number of matching hypotheses over time, for overt (C) and covert (D) runs. See text for details.

This distortion of the internal simulation could not be explained by a difference in prediction error. A two tailed t-test showed no significant difference between prediction errors for overt and covert conditions over the relevant periods, 0 < t < 4 s and 0 < t < 7.5 s, respectively (p = 0.24). The observed distortion may instead be explained by a closer analysis of the PSL model. Figures 10C,D depicts number of matching hypotheses over time. The number of matching hypotheses is here defined as number of h for which α_t(h) > 0 [c.f. Equation (6)]. A large number of matching hypotheses indicate larger uncertainty in the model. Both overt and covert runs display an initial period where a relatively large number of hypotheses match present sensory–motor events. Both these periods roughly correspond to the time it took to exit the storage room, 4 and 17.5 s, respectively.

In overt mode, large model uncertainty is not a problem as long as suitable actions are selected. Events are driven forward through interaction with the environment. However, in covert mode, the PSL model must also produce suitable perceptions in order to drive the internal simulation. A larger number of matching hypotheses is likely to produce oscillating perceptions, leading to simulation distortion. This explanation is further supported by significantly larger prediction errors being generated in the storage room, compared to the rest of the executed path. This difference was observed during covert simulation (p < 0.005), but not for the overt condition (p = 0.14).

A similar analysis of Bed–Elevator (Figure 11) reveals the opposite effect. In this case, the covert execution reproduces both start and goal correctly but misses parts of the path in between. Specifically, the corridor leading up to the elevator, visible in the overt run (a) is missing in the internal simulation (b). While the first 15 s of the covert run appears similar to its overt counterpart, the total time is much shorter, 18 s compared to 29 s. Hence, the shorter simulation time is due to a lost segment of the simulation rather than a general increase in execution speed over the whole simulation. At t = 15 s, the robot is approaching a door leading to the corridor, followed by a left turn toward the elevator. An enlargement of this sequence of events, from t = 14 s to t = 20 s, is presented in Figure 11C. The door shows up in the figure as a narrow passage just before the left turn. It is likely that sensory interactions, when exiting the door and facing the corridor wall, are similar to perceptions when approaching the elevator. This hypothesis is confirmed by comparing sensor events from the covert condition to a subset of events from the overt case, when approaching the elevator (24 < t < 26 s). A period between 16.25 and 17 s from the covert case shows very similar sensor interactions to the selected period from the covert condition. This pinpoints the time where events from the door passage are confused with events form the elevator, and a segment for the original path disappears. Figure 11D presents a magnification of the covert condition, with laser scans prior to 16.5 s are colored in green and scans after 16.5 s are red. Green scans belong to the door passage, while red scans represent the elevator.

FIGURE 11

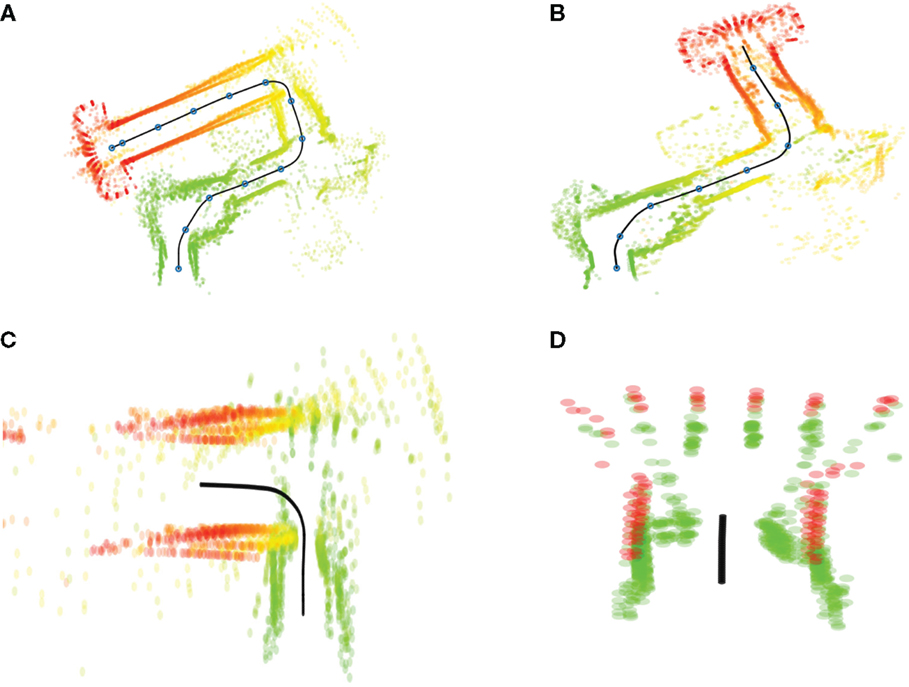
Figure 11. Typical runs from condition Bed–Elevator. (A) Laser scans in relation to the path, executed overtly from bed (green) to the elevator (red). Blue circles along the path, represented by the black line, mark 2.5-s intervals. (B) Corresponding laser scans generated in covert mode. (C) Magnification of selected period (14–20 s) from the overt condition. (D) Corresponding (15–17 s) magnification from covert condition. See text for details.

8. Discussion

We present a robot model that can execute both overt and covert actions based on human demonstrations. The presented system, implemented on a simulated Kompaï robot (Robosoft, 2011), can learn from several demonstrations and execute a novel path through an apartment environment toward a goal. We also demonstrate that the system is able to generate internal simulations of sensory–motor experiences from executing a specific goal-directed behavior.

The model presents an associationist’s approach to control an internal simulation, representing knowledge as coordination between perceptions and actions. Hence, despite the fact that the model is evaluated as a method for path following and generation, the system state is only represented implicitly, and very little application specific information is introduced. Models using simulated experience [c.f. Sutton and Barto (1998)] to improve valuations of explicitly represented system states exist in the form of reinforcement learning Dyna-based algorithms [e.g., Santos et al. (2012) and Lowe and Ziemke (2013)]. However, these algorithms are limited to updating (either randomly or heuristically) already experienced states and do not simulate novel paths. We use a morphologically simple robot, allowing us to study the principles of simulation in human-like environments without introducing the complexity of a humanoid robot. The selected platform [Microsoft (2015)] is freely available, facilitating replication of, and comparisons with, the present study.

The results provide support for Hypothesis 1 (Section 6). The system can generate the sensory–motor experiences of executing a novel path through the environment, without actually executing these actions. The robot model is able to pursue goals during both overt and covert behaviors. While the proportion of runs leading to a goal was slightly lower in the covert condition (82%), compared to 94% during overt action, the robot’s ability to pursue the correct goal is significantly better during covert action.

One possible interpretation of this result is that internal simulation could potentially be beneficial as a training exercise since difficult skills are “easier” to execute covertly, increasing the likelihood of successful reenaction. Motor imagery and other forms of imagery have been used to increase the performance of athletes and for rehabilitation (Guillot and Collet, 2005; Munzert et al., 2009). Of particular interest to our experiment is the work of Vieilledent et al. (2003), who investigated the influence of mental imagery on path navigation. In their study, subjects were to navigate blindfolded three different 12.5-m long hexagonal shapes, indicated by wooden beams laid out on the floor. They found that a learning period, including either mental imagery, mental imagery, and simultaneous walking or walking with sensory feedback from a wooden beam, resulted in increased performance compared to a resting condition or walking without mental imagery.

In a similar study, Commins et al. (2013) did not find any increase in performance of mental imagery, but they did find that errors increased with distance in both the actual walking condition and imagery condition. Thus, more studies are needed to investigate the actual benefit of mental imagery in navigation. While it is possible that there are several factors that contribute to the differences in performance, our finding that goal pursuit is easier to execute covertly might be a clue to why mental training is advantageous in some cases.

With regard to the differences observed between the overt and covert runs, it should be noted that humans do not necessarily perform perfectly when acting based on internal simulations. Vieilledent et al. (2003) and Commins et al. (2013) showed that blind navigation resulted in similar trajectories and relatively accurate behaviors in terms of both deviation from target and temporal extension, but Vieilledent et al. (2003) found that in the blindfolded condition, the path was not as straight and turns where not as sharp leading to a more circular shape and also some distortions of the overall shape. From a simulation theory perspective, it would be suggested that even the blindfolded walking is based on chained simulations of covert actions and perceptions, but in this case guided by the additional proprioceptive feedback.

In light of these results, we should not expect the robot model to reproduce a perfect trajectory toward the target during covert action. This appears to be the case. We hypothesized (H2, Section 6) that successful internal simulations should have the same temporal extension as their overt counterpart. This hypothesis was not confirmed. The model generated internal simulations that were both longer and shorter than the overt counterparts, producing significantly different temporal distributions compared to overt results. Two cases were analyzed in detail: (1) indicating prolongation due to sensory–motor event oscillation caused by high model uncertainty (Figure 10) and (2) abbreviation caused by strong event similarities along the simulated path (Figure 11).

These results indicate that multiple types of distortions could affect internal simulations. If similar effects are present also during human mental imagery, we should be able to find longer simulation times in situations that are difficult for participants to reenact covertly. It is also possible that participants demonstrate shorter execution times during mental imagery in cases where it is easy for participants to mistake one location for another, causing parts of the path to be left out from the internal simulation. Both these, and other, effects may appear simultaneously, and it may therefore be difficult to analyze mental imagery solely based on its total execution time.

Author Contributions

The main content of the paper was written by EB and HS, with input from TZ and RL. Software implementations and experiments were executed by EB, including creations of figures. TZ and RL contributed with valuable background knowledge, edits, and shorter sections of text.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^The Java™ implementation of Predictive Sequence Learning and related libraries are freely available as a software repository at https://bitbucket.org/interactionlab/psl, licensed under GNU GPL3.
2. ^Repeated presentation of the same training data allows PSL to form stable statistical dependencies between sensory–motor events and to extend the temporal window, i.e., creating longer hypotheses, when needed. This repeated presentation of sensor data may not be completely realistic from a biological point of view but can be seen as a standard method similar to the many epochs used when training, e.g., artificial neural networks.
3. ^Log files from human demonstrations and all 360 simulated trails are available for download at https://bitbucket.org/interactionlab/psl/branch/reenact

References

Anderson, J. R. (1996). ACT: a simple theory of complex cognition. Am. Psychol. 51, 355. doi: 10.1037/0003-066X.51.4.355

CrossRef Full Text | Google Scholar

Anquetil, T., and Jeannerod, M. (2007). Simulated actions in the first and in the third person perspectives share common representations. Brain Res. 1130, 125–129. doi:10.1016/j.brainres.2006.10.091

PubMed Abstract | CrossRef Full Text | Google Scholar

Baldassarre, G. (2003). “Forward and bidirectional planning based on reinforcement learning and neural networks in a simulated robot,” in Anticipatory Behavior in Adaptive Learning Systems: Foundations, Theories, and Systems, Vol. 2684, eds M. V. Butz, O. Sigaud, and P. Grard (Berlin; Heidelberg: Springer Verlag), 179–200.

Google Scholar

Barsalou, L. W. (1999). Perceptual symbol systems. Behav. Brain Sci. 22, 577–660. doi:10.1017/S0140525X99532147

CrossRef Full Text | Google Scholar

Barsalou, L. W. (2005). “Situated conceptualization,” in Handbook of Categorization in Cognitive Science, eds H. Cohen and C. Lefebvre (Amsterdam: Elsevier Science Ltd.), 619–650.

Google Scholar

Barsalou, L. W., Simmons, K. W., Barbey, A. K., and Wilson, C. D. (2003). Grounding conceptual knowledge in modality-specific systems. Trends Cogn. Sci. 7, 84–91. doi:10.1016/S1364-6613(02)00029-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Billing, E. A. (2012). Cognition Rehearsed – Recognition and Reproduction of Demonstrated Behavior. Ph.D. thesis, Umeå University, Department of Computing Science, Umeå.

Google Scholar

Billing, E. A., and Hellström, T. (2010). A formalism for learning from demonstration. Paladyn J. Behav. Robot. 1, 1–13. doi:10.2478/s13230-010-0001-5

CrossRef Full Text | Google Scholar

Billing, E. A., Hellström, T., and Janlert, L. E. (2010). “Behavior recognition for learning from demonstration,” in Proceedings of IEEE International Conference on Robotics and Automation (Anchorage, AK: IEEE), 866–872.

Google Scholar

Billing, E. A., Hellström, T., and Janlert, L. E. (2011a). “Predictive learning from demonstration,” in Agents and Artificial Intelligence: Second International Conference, ICAART 2010, Valencia, Spain, January 22–24, 2010. Revised Selected Papers, eds J. Filipe, A. Fred, and B. Sharp (Berlin: Springer Verlag), 186–200.

Google Scholar

Billing, E. A., Hellström, T., and Janlert, L. E. (2011b). “Robot learning from demonstration using predictive sequence learning,” in Robotic Systems – Applications, Control and Programming, ed. A. Dutta (Rijeka: InTech), 235–250.

Google Scholar

Billing, E. A., Hellström, T., and Janlert, L. E. (2015). Simultaneous recognition and reproduction of demonstrated behavior. Biol. Inspired Cogn. Archit. 12, 43–53. doi:10.1016/j.bica.2015.03.002

CrossRef Full Text | Google Scholar

Brooks, R. A. (1991). Intelligence without representation. Artif. Intell. 47, 139–159. doi:10.1016/0004-3702(91)90053-M

CrossRef Full Text | Google Scholar

Chrisley, R. (1990). “Cognitive map construction and use: a parallel distributed processing approach,” in Connectionist Models: Proceedings of the 1990 Summer School (San Mateo, CA: Morgan Kaufman), 287–302.

Google Scholar

Clancey, W. J. (1997). Situated Cognition: On Human Knowledge and Computer Representations. Cambridge: Cambridge University Press.

Google Scholar

Clark, A. (1997). Being There: Putting Brain, Body, and World Together Again. Cambridge, MA: MIT Press.

Google Scholar

Colder, B. (2011). Emulation as an integrating principle for cognition. Front. Hum. Neurosci. 5:54. doi:10.3389/fnhum.2011.00054

PubMed Abstract | CrossRef Full Text | Google Scholar

Commins, S., McCormack, K., Callinan, E., Fitzgerald, H., Molloy, E., and Young, K. (2013). Manipulation of visual information does not change the accuracy of distance estimation during a blindfolded walking task. Hum. Mov. Sci. 32, 794–807. doi:10.1016/j.humov.2013.04.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Damasio, A. R. (1994). Descartes’ Error: Emotion, Reason, and the Human Brain. New York: GP Putnam’s Sons.

Google Scholar

Demiris, J., and Hayes, G. R. (2002). “Imitation as a dual-route process featuring predictive and learning components: a biologically plausible computational model,” in Imitation in Animals and Artifacts, eds K. Dautenhahn and C. L. Nehaniv (Cambridge, MA: MIT Press), 327–361.

Google Scholar

Demiris, Y., Aziz-Zadeh, L., and Bonaiuto, J. (2014). Information processing in the mirror neuron system in primates and machines. Neuroinformatics 12, 63–91. doi:10.1007/s12021-013-9200-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Demiris, Y., and Khadhouri, B. (2006). Hierarchical attentive multiple models for execution and recognition of actions. Rob. Auton. Syst. 54, 361–369. doi:10.1016/j.robot.2006.02.003

CrossRef Full Text | Google Scholar

Demiris, Y., and Simmons, G. (2006). Perceiving the unusual: temporal properties of hierarchical motor representations for action perception. Neural Netw. 19, 272–284. doi:10.1016/j.neunet.2006.02.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Fodor, J. A., and Pylyshyn, Z. W. (1988). Connectionism and cognitive architecture: a critical analysis. Cognition 28, 3–71. doi:10.1016/0010-0277(88)90031-5

CrossRef Full Text | Google Scholar

Fullér, R. (2000). Introduction to Neuro-Fuzzy Systems. Heidelberg: Physica-Verlag.

Google Scholar

Gallese, V. (2003). The manifold nature of interpersonal relations: the quest for a common mechanism. Philos. Trans. R. Soc. Lond. B Biol. Sci. 358, 517–528. doi:10.1098/rstb.2002.1234

PubMed Abstract | CrossRef Full Text | Google Scholar

Gallese, V. (2005). Embodied simulation: from neurons to phenomenal experience. Phenomenol. Cogn. Sci. 4, 23–48. doi:10.1007/s11097-005-4737-z

CrossRef Full Text | Google Scholar

Gigliotta, O., Pezzulo, G., and Nolfi, S. (2010). “Emergence of an internal model in evolving robots subjected to sensory deprivation,” in From Animals to Animats 11, eds S. Doncieux, B. Girard, A. Guillot, J. Hallam, J.-A. Meyer, and J.-B. Mouret (Berlin; Heidelberg: Springer Verlag), 575–586.

Google Scholar

Gross, H. M., Heinze, A., Seiler, T., and Stephan, V. (1999). Generative character of perception: a neural architecture for sensorimotor anticipation. Neural Netw. 12, 1101–1129. doi:10.1016/S0893-6080(99)00047-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Grush, R. (2004). The emulation theory of representation: motor control, imagery, and perception. Behav. Brain Sci. 27, 377–396. doi:10.1017/S0140525X04000093

PubMed Abstract | CrossRef Full Text | Google Scholar

Guillot, A., and Collet, C. (2005). Duration of mentally simulated movement: a review. J. Mot. Behav. 37, 10–20. doi:10.3200/JMBR.37.1.10-20

PubMed Abstract | CrossRef Full Text | Google Scholar

Harnad, S. (1990). The symbol grounding problem. Physica D 42, 335–346. doi:10.1016/0167-2789(90)90087-6

CrossRef Full Text | Google Scholar

Haruno, M., Wolpert, D. M., and Kawato, M. (2003). “Hierarchical MOSAIC for movement generation,” in International Congress Series 1250 (Paris: Elsevier Science B.V.), 575–590.

Google Scholar

Hesslow, G. (2002). Conscious thought as simulation of behaviour and perception. Trends Cogn. Sci. 6, 242–247. doi:10.1016/S1364-6613(02)01913-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Hesslow, G. (2012). The current status of the simulation theory of cognition. Brain Res. 1428, 71–79. doi:10.1016/j.brainres.2011.06.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Hickok, G. (2009). Eight problems for the mirror neuron theory of action understanding in monkeys and humans. J. Cogn. Neurosci. 21, 1229–1243. doi:10.1162/jocn.2009.21189

PubMed Abstract | CrossRef Full Text | Google Scholar

Hiraki, K., Sashima, A., and Phillips, S. (1998). From egocentric to allocentric spatial behavior: a computational model of spatial development. Adapt.Behav. 6, 371–391. doi:10.1177/105971239800600302

CrossRef Full Text | Google Scholar

Hoffmann, H., and Möller, R. (2004). “Action selection and mental transformation based on a chain of forward models,” in From Animals to Animats 8, eds S. Schaal, A. Ijspeert, A. Billard, S. Vijayakumar, J. Hallam, and J.-A. Meyer (Cambridge, MA: MIT Press), 213–222.

Google Scholar

Jeannerod, M. (2001). Neural simulation of action: a unifying mechanism for motor cognition. Neuroimage 14, S103–S109. doi:10.1006/nimg.2001.0832

PubMed Abstract | CrossRef Full Text | Google Scholar

Jirenhed, D. A., Hesslow, G., and Ziemke, T. (2001). “Exploring internal simulation of perception in mobile robots,” in Proceedings of the Fourth European Workshop on Advanced Mobile Robotics, eds K. O. Arras, A. J. Baerveldt, C. Balkenius, W. Burgard, and R. Siegwart (Lund: Lund University Cognitive Studies), 107–113.

Google Scholar

Jung, M., Hwang, J., and Tani, J. (2015). Self-organization of spatio-temporal hierarchy via learning of dynamic visual image patterns on action sequences. PLoS ONE 10:e0131214. doi:10.1371/journal.pone.0131214

PubMed Abstract | CrossRef Full Text | Google Scholar

Klir, G. J., and Yuan, B. (1995). Fuzzy Sets and Fuzzy Logic: Theory and Applications. New Jersey: Prentice Hall.

Google Scholar

K-Team. (2007). Khepera Robot. Available at: www.k-team.com

Google Scholar

Lakoff, G., and Johnson, M. (1999). Philosophy in the Flesh: The Embodied Mind and its Challenge to Western Thought. New York: Basic Books.

Google Scholar

Lowe, R., and Ziemke, T. (2013). “Exploring the relationship of reward and punishment in reinforcement learning,” in IEEE Symposium on Adaptive Dynamic Programming And Reinforcement Learning (ADPRL) (Singapore: IEEE), 140–147.

Google Scholar

Mel, B. W. (1991). A connectionist model may shed light on neural mechanisms for visually guided reaching. J. Cogn. Neurosci. 3, 273–292. doi:10.1162/jocn.1991.3.3.273

PubMed Abstract | CrossRef Full Text | Google Scholar

Microsoft. (2015). Microsoft Robotic Developer Studio. Available at: http://www.microsoft.com/robotics/

Google Scholar

Möller, R. (1999). “Perception through anticipation. A behaviour-based approach to visual perception,” in Understanding Representation in the Cognitive Sciences, eds A. Riegler, M. Peschl, and A. von Stein (New York: Springer US), 169–176.

Google Scholar

Munzert, J., Lorey, B., and Zentgraf, K. (2009). Cognitive motor processes: the role of motor imagery in the study of motor representations. Brain Res. Rev. 60, 306–326. doi:10.1016/j.brainresrev.2008.12.024

PubMed Abstract | CrossRef Full Text | Google Scholar

Newell, A. (1990). Unified Theories of Cognition. Cambridge, MA: Harvard University Press.

Google Scholar

Pezzulo, G., Barsalou, L. W., Cangelosi, A., Fischer, M. H., McRae, K., and Spivey, M. (2013). Computational grounded cognition: a new alliance between grounded cognition and computational modeling. Front. Psychol. 3:612. doi:10.3389/fpsyg.2012.00612

PubMed Abstract | CrossRef Full Text | Google Scholar

Pylyshyn, Z. W. (1984). Computation and Cognition: Toward a Foundation for Cognitive Science. Cambridge, MA: The MIT Press.

Google Scholar

Robosoft. (2011). Kompai Robot. Available at: www.robosoft.com

Google Scholar

Rumelhart, D. E., Smolensky, P., McClelland, J. L., and Hinton, G. E. (1986). “Schemata and sequential thought processes in PDP models,” in Parallel Distributed Processing, eds J. L. McClelland, D. E. Rumelhart, and C. P. R. Group (Cambridge, MA: MIT Press), 7–57.

Google Scholar

Santos, M., Martín, H. J. A., López, V., and Botella, G. (2012). Dyna-H: a heuristic planning reinforcement learning algorithm applied to role-playing game strategy decision systems. Knowl. Based Syst. 32, 28–36. doi:10.1016/j.knosys.2011.09.008

CrossRef Full Text | Google Scholar

Siegwart, R., and Nourbakhsh, I. R. (2004). Introduction to Autonomous Mobile Robots. London: MIT Press.

Google Scholar

Smith, S. M., Brown, H. O., Toman, J. E. P., and Goodman, L. S. (1947). The lack of cerebral effects of d-tubocurarine. Anesthesiology 8, 1–14. doi:10.1097/00000542-194701000-00001

CrossRef Full Text | Google Scholar

Stening, J., Jacobsson, H., and Ziemke, T. (2005). “Imagination and abstraction of sensorimotor flow: towards a robot model,” in Proceedings of the Symposium on Next Generation Approaches to Machine Consciousness: Imagination, Development, Intersubjectivity and Embodiment (AISB’05) (Hatfield: The University of Hertfordshire), 50–58.

Google Scholar

Sutton, R. S., and Barto, A. G. (1998). Reinforcement Learning: An Introduction. Cambridge, MA: MIT Press.

Google Scholar

Svensson, H. (2007). Embodied Simulation as Off-line Representation. Licentiate thesis, Department of Computer and Information Science, Institute of Technology, Linköping University, Linköping.

Google Scholar

Svensson, H. (2013). Simulations. Ph.D. thesis, Department of Computer and Information Science, Institute of Technology, Linköping University, Linköping.

Google Scholar

Svensson, H., Morse, A., and Ziemke, T. (2009a). “Representation as internal simulation: a minimalistic robotic model,” in Proceedings of the Thirty-First Annual Conference of the Cognitive Science Society (Austin, TX: Cognitive Science Society, Inc.), 2890–2895.

Google Scholar

Svensson, H., Morse, A. F., and Ziemke, T. (2009b). “Neural pathways of embodied simulation,” in Anticipatory Behavior in Adaptive Learning Systems: From Psychological Theories to Artificial Cognitive Systems, Vol. 5499, eds G. Pezzulo, M. V. Butz, O. Sigaud, and G. Baldassarre (Berlin; Heidelberg: Springer), 95–114.

Google Scholar

Svensson, H., Thill, S., and Ziemke, T. (2013). Dreaming of electric sheep? Exploring the functions of dream-like mechanisms in the development of mental imagery simulations. Adapt. Behav. 21, 222–238. doi:10.1177/1059712313491295

CrossRef Full Text | Google Scholar

Tani, J. (1996). Model-based learning for mobile robot navigation from the dynamical systems perspective. IEEE Trans. Syst. Man Cybern. B Cybern. 26, 421–436. doi:10.1109/3477.499793

PubMed Abstract | CrossRef Full Text | Google Scholar

Tani, J., Nishimoto, R., and Paine, R. W. (2008). Achieving “organic compositionality” through self-organization: reviews on brain-inspired robotics experiments. Neural Netw. 21, 584–603. doi:10.1016/j.neunet.2008.03.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Varela, F., Thompson, E., and Rosch, E. (1991). The Embodied Mind: Cognitive Science and Human Experience. Cambridge: MIT Press.

Google Scholar

Vernon, D. (2014). Artificial Cognitive Systems: A Primer. London: The MIT Press.

Google Scholar

Vernon, D., Beetz, M., and Sandini, G. (2015). Prospection in cognition: the case for joint episodic-procedural memory in cognitive robotics. Front. Robot. AI 2:19. doi:10.3389/frobt.2015.00019

CrossRef Full Text | Google Scholar

Vieilledent, S., Kosslyn, S. M., Berthoz, A., and Giraudo, M. D. (2003). Does mental simulation of following a path improve navigation performance without vision? Cogn. Brain Res. 16, 238–249. doi:10.1016/S0926-6410(02)00279-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Watson, J. B. (1913). Psychology as the behaviorist views it. Psychol. Rev. 20, 158–177. doi:10.1037/h0074428

CrossRef Full Text | Google Scholar

Wolpert, D. M., Ghahramani, Z., and Jordan, M. I. (1995). An internal model for sensorimotor integration. Science 269, 1880–1882. doi:10.1126/science.7569931

PubMed Abstract | CrossRef Full Text | Google Scholar

Wolpert, D. M., and Kawato, M. (1998). Multiple paired forward and inverse models for motor control. Neural Netw. 11, 1317–1329. doi:10.1016/S0893-6080(98)00066-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Yamashita, Y., and Tani, J. (2008). Emergence of functional hierarchy in a multiple timescale neural network model: a humanoid robot experiment. PLoS Comput. Biol. 4:e1000220. doi:10.1371/journal.pcbi.1000220

PubMed Abstract | CrossRef Full Text | Google Scholar

Ziemke, T., Jirenhed, D.-A., and Hesslow, G. (2005). Internal simulation of perception: a minimal neuro-robotic model. Neurocomputing 68, 85–104. doi:10.1016/j.neucom.2004.12.005

CrossRef Full Text | Google Scholar

Zwaan, R. A. (2003). “The immersed experiencer: toward an embodied theory of language comprehension,” in Psychology of Learning and Motivation, Vol. 44 (San Diego, CA: Academic Press), 35–62.

Google Scholar