In search of the neural circuits of intrinsic motivation
- 1 Ecole Polytechnique Federale de Lausanne, EPFL-CRAFT, Lausanne, Switzerland
- 2 Sony Computer Science Laboratory Paris, Paris, France
Children seem to acquire new know-how in a continuous and open-ended manner. In this paper, we hypothesize that an intrinsic motivation to progress in learning is at the origins of the remarkable structure of children's developmental trajectories. In this view, children engage in exploratory and playful activities for their own sake, not as steps toward other extrinsic goals. The central hypothesis of this paper is that intrinsically motivating activities correspond to expected decrease in prediction error. This motivation system pushes the infant to avoid both predictable and unpredictable situations in order to focus on the ones that are expected to maximize progress in learning. Based on a computational model and a series of robotic experiments, we show how this principle can lead to organized sequences of behavior of increasing complexity characteristic of several behavioral and developmental patterns observed in humans. We then discuss the putative circuitry underlying such an intrinsic motivation system in the brain and formulate two novel hypotheses. The first one is that tonic dopamine acts as a learning progress signal. The second is that this progress signal is directly computed through a hierarchy of microcortical circuits that act both as prediction and metaprediction systems.
Introduction
Imagine an 8-month-old toddler playing with a plastic toy car. He grasps the toy, examines it from different angles, puts it on the floor again, pushes it from the side, makes it turn over, and sometimes by chance, manages to have it rolling. Then, he spends some time banging the toy on the floor to produce interesting sounds but after a moment he seems to lose interest in this noisy activity. As he looks around, he sees just a few steps away an old magazine unfortunately left on the floor. He walks to this novel exciting target, and methodologically starts to tear it into pieces.
Why did this child suddenly lose interest in his current activity to pick up another one? What is generating curiosity/interest/exploration in the first place? We will not have understood a crucial part of children's remarkable learning capabilities until we will be able to understand the neural processes that led to such kinds of organized behavior sequences. Indeed, two fundamental characteristics of children's development seem to be linked with the way they explore their environment.
First, children seem to acquire new know-how in a continuous and open-ended manner. Their capabilities for acting and perceiving continuously reach new level of sophistication as they engage in increasingly complex activities. In just a few months, children learn to control their body, discriminate between themselves and others, recognize sounds, smells, tactile and visual patterns and other multimodal situations, interact with people and objects, crawl, stand, walk, jump, hop, run, treat others as intentional beings, participate with them in joint attention processes, in non-verbal and verbal communication, exchange shared meanings and symbolic references, play games, engage in pretend play, and eventually integrate society as autonomous social beings. A significant amount of data describes how new skills seem to build one upon another, suggesting a continuum between sensory-motor development and higher cognitive functions (Gallese and Lakoff, 2005 ). But the driving forces that shape this process remain largely unknown.
Second, childrens’ developmental trajectories are remarkably structured (Thelen and Smith, 1994 ). Each new skill is acquired only when associated cognitive and morphological structures are ready. For example, children typically learn first to roll over, then to crawl, and sit, and only when these skills are operational, do they begin to learn how to stand. Likewise, sudden transitions occur from apparent insensitivity to input to stages of extraordinary sensitivity to new data. Some pieces of information are simply ignored until the child is ready for them. It is as if children were born equipped with natural means for measuring and handling complexity in order to learn in the most effective way.
Most existing views fail to account for the open-ended and self-organized nature of developmental processes. Development is either reduced to an innately defined maturational process controlled by some sort of internal clock, or, in contrast, pictured as a passive inductive process in which the child or the animal simply catches statistical regularities in the environment (see (Karmiloff-Smith, 1992 ; Thelen and Smith, 1994 ) for a critical review of current views of development). More generally, epigenetic developmental dynamics as a whole are rarely addressed as an issue as research tends to focus simply on the acquisition of particular isolated skills. We intend to explore an alternative view, namely that epigenetic development is an intrinsically motivated active process. This view hypotheses that at the origins of the remarkable structure of developmental sequences lies a basic internal impulse to search, investigate and make sense of the world and progress in learning. This driving force shapes exploration in specific ways permitting efficient learning. In this view, infants engage in exploratory activities for their own sake, not as steps toward other extrinsic goals. Of course, adults help by scaffolding their environment proposing learning opportunities, but this is just help: eventually, infants decide by themselves what they do, what they are interested in, and what their learning situations are. Far from a passive shaping, development has to be viewed as a fundamentally active and autonomous process.
Several researcher in psychology seem to suggest that such a kind of system exists in the human brain and that human behavior can be intrinsically motivated. However, they have postulated many different mechanisms at the origins of what we may call curiosity or other incentives for exploration. The central hypothesis of this paper is that intrinsically motivating activities corresponds to expected decrease in prediction error. We argue that children (and adults) act in order to maximize progress in prediction and that this incentive shape their exploratory strategy. After reviewing how concepts related to intrinsic motivation systems have been elaborated and discussed in psychology, neuroscience and machine learning, we present a computational model of circuits that can compute and optimize progress in prediction. Through a series of experiments with physical robots we show how these circuits can indeed lead to organized sequences of behavior of increasing complexity, characteristic of many behavioral and developmental patterns observed in humans and mammals. We then review different hypotheses about where the circuitry underlying such an intrinsic motivation system could be located in the brain. In particular, we discuss the putative role of tonic dopamine as a signal of progress and formulate hypotheses about neocortical columns acting both as prediction and metaprediction systems. Eventually, we present a novel research program to study intrinsically motivated learning, involving brain imagery experiments during exploratory behavior.
Intrinsic Motivation Systems: History of a Construct
This section presents an overview of the complex history of the concept of intrinsic motivation system. First, it reviews psychological models of intrinsic motivation. Second, it examines how neuroscience research, despite dominant views hostile to this kind of construct, has nevertheless examined closely mechanisms linked with novelty-seeking behavior. Third, it argues that some recent machine learning models are good candidates for bridging the gap between psychological and neuroscience models, offering a concrete instantiation of intrinsic motivation system in the form of progress-driven control architectures.
Psychology
In psychology, an activity is characterized as intrinsically motivated when there is no apparent reward except the activity itself (Ryan and Deci, 2000 ). People seek and engage in such activities for their own sake and not because they lead to extrinsic reward. In such cases, the person seems to derive enjoyment directly from the practice of the activity. Following this definition, most children playful or explorative activities can be characterized as being intrinsically motivated. Also, many kinds of adult behavior seem to belong to this category: free problem-solving (solving puzzles, cross-words), creative activities (painting, singing, writing during leisure time), gardening, hiking, etc. Such situations are characterized by a feeling of effortless control, concentration, enjoyment and a contraction of the sense of time (Csikszenthmihalyi, 1991 ).
A first bloom of investigations concerning intrinsic motivation happened in the 1950s. Researchers started by trying to give an account of exploratory activities on the basis of the theory of drives (Hull, 1943 ), which are non-nervous-system tissue deficits (like hunger or pain) that the organisms try to reduce. For example, (Montgomery, 1954 ) proposed a drive for exploration and (Harlow, 1950 ) a drive to manipulate. This drive naming approach had many short-comings which were criticized by White in 1959 (White, 1959 ): intrinsically motivated exploratory activities have a fundamentally different dynamics. Indeed, they are not homeostatic: the general tendency to explore is never satiated and is not a consummatory response to a stressful perturbation of the organism's body. Moreover, exploration does not seem to be related to any non-nervous-system tissue deficit.
Some researchers then proposed another conceptualization. Festinger's theory of cognitive dissonance (Festinger, 1957 ) asserted that organisms are motivated to reduce dissonance, that is the incompatibility between internal cognitive structures and the situations currently perceived. Fifteen years later a related view was articulated by Kagan stating that a primary motivation for humans is the reduction of uncertainty in the sense of the “incompatibility between (two or more) cognitive structures, between cognitive structure and experience, or between structures and behavior” (Kagan, 1972 ). However, these theories were criticized on the basis that much human behavior is also intended to increase uncertainty, and not only to reduce it. Human seem to look for some forms of optimality between completely uncertain and completely certain situations.
In 1965, Hunt developed the idea that children and adult look for optimal incongruity (Hunt, 1965 ) He regarded children as information-processing systems and stated that interesting stimuli were those where there was a discrepancy between the perceived and standard levels of the stimuli. For, Dember and Earl (1957) the incongruity or discrepancy in intrinsically-motivated behaviors was between a person's expectations and the properties of the stimulus. Berlyne (1960) developed similar notions as he observed that the most rewarding situations were those with an intermediate level of novelty, between already familiar and completely new situations. Whereas most of these researchers focused on the notion of optimal incongruity at the level of psychological processes, a parallel trend investigated the notion of optimal arousal at the physiological level (Hebb, 1955 ). As over-stimulation and under-stimulation situations induce fear (e.g., dark rooms, noisy rooms), people seem to be motivated to maintain an optimal level of arousal. A complete understanding of intrinsic motivation should certainly include both psychological and physiological levels.
Eventually, a last group of researchers preferred the concept of challenge to the notion of optimal incongruity. These researchers stated that what was driving human behavior was a motivation for effectance (White, 1959 ), personal causation (De Charms, 1968 ), competence, and self-determination (Deci and Ryan, 1985 ).
In the recent years, the concept of intrinsic motivation has been less present in mainstream psychology but flourished in social psychology and the study of practices in applied settings, in particular in professional and educational contexts. Based on studies suggesting that extrinsic rewards (money, high grades, prizes) actually destroy intrinsic motivation (an idea actually articulated by Bruner in the 1960s (Bruner, 1962 )), some employers and teachers have started to design effective incentive systems based on intrinsic motivation. However, this view is currently at the heart of many controversies (Cameron and Pierce, 2002 ).
In summary, most psychological approaches of intrinsic motivation postulate that “stimuli worth investigating” are characterized by a particular relationship (incompatibility, discrepancy, uncertainly, or in contrast, predictability) between an internal predictive model and the actual structure of the stimulus. This invites us to consider intrinsically motivating activities not only at the descriptive behavioral level (no apparent reward except the activity itself) but also primarily in respect to particular internal models built by an agent during its own personal history of interaction. To progress in the elucidation of this relationship and investigate among all the psychological models presented which are the ones really susceptible (1) to drive children's development and (2) to be supported by plausible neural circuits, we will now give an overview of the neuroscience and machine learning research regarding intrinsic motivation systems.
Neuroscience
In neuroscience, dominant views in behavioral neuropsychology have impeded for a long time discussions about putative intrinsic causes to behavior. Learning dynamics in brain systems are still commonly studied in the context of external reward seeking (food, sex, etc.) and very rarely as resulting from endogenous and spontaneous processes. Actually, the term “reward” has been misleading as it is used in a diffent manner in neuropsychology and in machine learning (Oudeyer and Kaplan, 2007 ; White, 1989 ; Wise, 1989 ). In behavioral neuropsychology, rewards are primarily thought as objects or events that increased the probability and intensity of behavioral actions leading to such objects: “rewards make you come back for more” (Thorndike, 1911 ). This means the function of rewards is based primarily on behavioral effects interpreted in a specific theoretical paradigm. As Schultz puts it “the exploration of neural reward mechanisms should not be based primarily on the physics and the chemistry of reward objects but on specific behavioral theories that define reward function” ((Schultz, 2006 ) p. 91)
In computational reinforcement learning, a reward is only a numerical quantity used to drive an action-selection algorithm so that the expected cumulated value of this quantity is maximal in the future. In such context, rewards can be thought primarily as internal measures rather than external objects (as clearly argued by Sutton and Barto (1998) ). This may explain why it is much easier from a machine learning perspective to considerer the intrinsic motivation construct as a natural extension of the reinforcement learning paradigm, whereas dominant behavioral theories and experimental methodology in neuroscience does not permit to consider such construct. This is certainly one reason why complex behaviors that do not involve any consummatory reward are rarely discussed.
In the absence of experimental studies concerning intrinsically motivated behaviors, we can consider what resembles the most: exploratory behaviors. The extended lateral hypothalamic corridor, running from the ventral tegmental area to the nucleus accumbens, has been recognized as a critical piece of a system responsible for exploration. Pankseep calls it the SEEKING system (Panksepp, 1998 ) (different terms are also used as for instance behavioral activation system (Gray, 1990 ) or behavioral facilitation system (Depue and Iacono, 1989 )). “This harmoniously operating neuroemotional system drives and energizes many mental complexities that humans experience as persistent feelings of interest, curiosity, sensation seeking and, in the presence of a sufficiently complex cortex, the search for higher meaning.” ((Panksepp, 1998 ) p.145). This system, a tiny part compared to the total brain mass, is where one of the major dopamine pathway initiates (for a discussion of anatomical issue one can refer, for instance, to (Rolls, 1999 ; Stellar, 1985 )).
The roles and functions of dopamine are known to be multiple and complex. Dopamine is thought to influence behavior and learning through two, somewhat decoupled, forms of signal: phasic (bursting and pausing) responses and tonic levels (Grace, 1991 ). A set of experimental evidence shows that dopamine activity can result from a large number of arousing events including novel stimuli and unexpected rewards (Hooks and Kalivas, 1994 ; Schultz, 1998 ; Fiorillo, 2004 ). On the other hand, dopamine activity is suppressed by events that are associated with reduced arousal or decreased anticipatory excitement, including the actual consumption of food reward and the omission of expected reward (Schultz, 1998 ). More generally, dopamine circuits appear to have a major effect on our feeling of engagement, excitement, creativity, our willingness to explore the world, and to make sense of contingencies (Panksepp, 1998 ). More precisely, growing evidence currently supports the view of dopamine as a crucial element of incentive salience (“wanting processes”) different from hedonic activation processes (“liking processes”) (Berridge, 2007 ). Injections of GABA in the ventral tegmental area and of a dopamine receptor agonistic in the nucleus accumbens cause rats to stop searching for a sucrose solution, but still drink the liquid when moved close to the bottle (Ikemoto and Panksepp, 1999 ). Parkinsonian patients who suffer from degeneration of dopaminergic neurons experience not only psychomotor problems (inability to start voluntary movement) but also more generally an absence of appetite to engage in exploratory behavior and a lack of interest for pursuing cognitive tasks (Bernheimer et al., 1973 ). When the dopamine system is artificially activated via electrical or chemical means, humans and animals engage in eager exploration of their environment and display signs of interest and curiosity (Panksepp, 1998 ). Likewise, the addictive effects of cocaine, amphetamine, opioids, ethanol, nicotine and canabinoid are directly related to the way they activate dopamine systems (Carboni et al., 1989 ; Pettit and Justice, 1989 ; Yoshimoto et al., 1991 ). Finally, too much dopamine activity are thought to be at the origins of uncontrolled speech and movement (Tourette's syndrome), obsessive-compulsive disorder, euphoria, overexcitement, mania and psychosis in the context of schizophrenic behavior (Bell, 1973 ; Grace, 1991 ; Weinberger, 1987 ; Weiner and Joel, 2002 ).
Things get even more complex and controversial when one tries to link these observation with precise computational models. Hypotheses concerning phasic dopamine's potential role in learning have flourished in the last ten years. Schultz and colleagues have conducted a series of recording of midbrain dopamine neurons firing patterns in awake monkeys under various behavioral conditions which suggested that dopamine neurons fire in response to unpredicted reward (see Schultz, 1998 for a review). Based on these observations, they develop the hypothesis that phasic dopamine responses drive learning by signalling an error that labels some events as “better than expected”. This type of signalling has been interpreted in the framework of computational reinforcement learning as analogous to the prediction error signal of the temporal difference (TD) learning algorithm (Sutton, 1988 ). In this scheme, a phasic dopamine signal interpreted as TD-error plays a double role (Baldassarre, 2002 ; Barto, 1995 ; Doya, 2002 ; Houk et al., 1995 ; Khamassi et al., 2005 ; Montague et al., 1996 ; Schultz et al., 1997 ; Suri and Schultz, 2001 ). First, this error is used as a classical training signal to improve future prediction. Second, it is used for finding the actions that maximize reward. This so-called actor-critic reinforcement learning architecture have been presented as a relevant model to account for both functional and anatomical subdivisions in the midbrain dopamine system. However, most of the simple mappings that were first suggested, in particular the association of the actor to matrisome and the critic to the striosome part of the striatum are now seriously argued to be inconsistent with known anatomy of these nuclei (Joel et al., 2002 ).
Computational models of phasic dopamine activity based on the error signal hypothesis have also raised controversy for other reasons. One of them, central to our discussion, is that several stimuli that are not associated with reward prediction are known to activate the dopamine system in various manner. This is in particular the case for novel, unexpected “never-rewarded” stimuli (Fiorillo, 2004 ; Hooks and Kalivas, 1994 ; Horvitz, 2000 , 2002 ; Ikemoto and Panksepp, 1999 ). The classic TD-error model does account for novelty responses. As a consequence, Kakade and Dayan suggested to extend the framework including for instance “novelty bonuses” (Kakade and Dayan, 2002 ) that distort the structure of the reward to include novelty effects (in a similar manner that “exploration bonuses” permit to ensure continued exploration in theoretical machine learning models (Dayan and Sejnowski, 1996 )). More recently, Smith et al. (2006) presented another TD-error model model in which phasic dopamine activation is modeled by the combination of “Surprise” and “Significance” measures. These attempts to reintegrate novelty and surprise components into a model elaborated in a framework based on extrinsic reward seeking may successfully account for a larger number of experimental observations. However, this is done in the expense of a complexification of a model that was not meant to deal with such type of behavior.
Some authors developed an alternative hypothesis to the reward prediction error interpretation, namely that dopamine promotes behavioral switching (Oades, 1985 ; Redgrave et al., 1999 ). In this interpretation, dopaminergic-neuron firing would be an essential component for directing attentional processes to unexpected, behaviorally important stimuli (related or unrelated to rewards). This hypothesis is supported by substantial evidence but stays at a very general explanation level. Actually, Kakade and Dayan (2002) argued that this interpretation is not incompatible with reward error-signaling hypothesis provided that the model is modified to account for novelty effect.
The incentive salience hypotheses, despite their psychological foundations, are not yet supported by many computational models. But they are some progress in this direction. In 2003, McClure et al. (2003) argued that incentive salience interpretation is not incompatible with the error signal hypothesis and presented a model where incentive salience is assimilated to expected future reward. Another recent interesting investigation can be found in (Niv et al., 2006 ) concerning an interpretation of tonic responses. In this model, tonic levels of dopamine is modeled as encoding “average rate of reward” and used to drive response vigor (slower or faster responding) into a reinforcement learning framework. With this dual model, the authors claim that their theory “dovetails neatly with both computational theories which suggest that the phasic activity of dopamine neurons reports appetitive prediction errors and psychological theories about dopamine's role in energizing responses” (Niv et al., 2006 ).
In summary, despite many controversies, converging evidence seems to suggest that (1) dopamine plays a crucial role in exploratory and investigation behavior, (2) the meso-accumbens dopamine system is an important brain component to rapidly orient attentional resources to novel events. Moreover, current hypotheses may favor a dual interpretation of dopamine's functions where phasic dopamine is linked with prediction error and tonic dopamine involved in processes of energizing responses.
Machine Learning
In reviewing the neuroscience literature, we have already discussed some examples of machine learning models that have lead to interesting new interpretations of neurophysiologic data. Unfortunately (but not unsurprisingly), more recent research in this field are not well known by psychologists and neuroscientists. During the last 10 years, the machine learning community has begun to investigate architectures that permit incremental and active learning (see for instance Thrun and Pratt (1998) as well as Belue et al. (1997) , Cohn et al. (1996) ). Interestingly, the mechanisms developed in these papers have strong similarities with mechanisms developed in the field of statistics, where it is called “optimal experiment design” (Fedorov, 1972 ). Active learners (or machines that perform optimal experiments) are machines that ask, search and select specific training examples in order to learn efficiently.
More specifically, a few researchers have started to address the problem of designing motivation systems to drive active learning. The idea is that a robot controlled by such systems would be able to autonomously explore its environment not to fulfill predefined tasks but driven by some form of intrinsic motivation that pushes it to search for situations where learning happens efficiently (Barto et al., 2004 ; Huang and Weng, 2002 , Kaplan and Oudeyer, 2004 ; Marshall et al., 2004 ; Oudeyer et al., 2007 ; Oudeyer and Kaplan, 2006 ; Schmidhuber, 1991 ; Steels, 2004 ). Technically, most of these control systems can be viewed as particular types of reinforcement learning architectures (Sutton and Barto, 1998 ), where “rewards” are not provided externally by the experimenter but self-generated by the machine itself. The term “intrinsically motivated reinforcement learning” has been used in this context (Barto et al., 2004 ).
Most of the research has largely ignored the history of the intrinsic motivation construct as it was elaborated in psychology during the last 50 years and sometimes reinvented concepts that existed several decades before (basically, different forms of optimal incongruity). Nevertheless, it could be argued that they introduced a novel type of understanding that could potentially permit to bridge the gap between the psychological conceptions of intrinsic motivation and the neuroscience observations. Let us examine how.
Most machine learning systems deal with the issue of building a predictive model of a given environment. They make errors and through some kind of feedback process manage to progress in their predictions. Prediction errors are also central to most of the models and concepts we have discussed in psychology and neuroscience. The concepts of novelty, surprise, uncertainty and incongruity correspond approximately to unexpected prediction, or in other words, significant errors in prediction. Symmetrically, the concepts of competence, effectance, self-determination, and personal causation characterize situations where prediction is accurate, which means there are small errors in prediction. In an implicit or explicit manner, error in prediction is, therefore, crucial to most of these models.
Moreover, in the neuroscience and psychological models we have discussed, the implicit idea is that the animal or person selects actions based on the prediction error. However, models differ in how this error is used. Some argue that the animal acts in order to maximize error in order to look for novel and surprising situations, others argue that it should minimize error looking for situations of mastery and a last group argue for balanced situations where incongruity is “optimal” and novelty at an “intermediate” level.
Researchers conducting experiments with artificial intrinsic motivation systems have been experiencing with this design issue. From a machine learning point of view, it is relatively easy to criticize the “maximize” and “minimize” incentives. The first one pushes the animal to focus exclusively on the most unpredictable noisy parts of its environment, where learning is basically impossible. The second leads to strategies where the organism is basically immobile, avoiding novel stimulus as much as possible, which seems also a bad strategy for learning in the long term. Eventually, maintaining error at intermediary values is a too imprecise notion to permit a coherent and scalable optimization strategy.
A more interesting hypothesis would be that, in certain cases, animals and humans act in order to optimize learning progress, that is to maximize error reduction. This would mean that they avoid both predictable and unpredictable situations in order to focus on the ones, that are expected to maximize the decrease in prediction error. In that sense, the kind of “optimal incongruity” discussed in most models can be traced back to a simple principle: the search for activities where error reduction is maximal. Moreover, this model permits to articulate a direct link between a putative prediction error signal and behavioral switching patterns. Figure 1 illustrates how a progress-driven control system operates on an idealized problem. Confronted with four sensorimotor contexts characterized by different learning profiles, the motivation for maximizing learning progress results in avoiding situations that are already predictable (context 4) or too dificult to predict (context 1), in order to focus first on the context with the fastest learning curve (context 3) and eventually, when the latter starts to reach a “plateau,” to switch the second most promising learning situation (context 2).
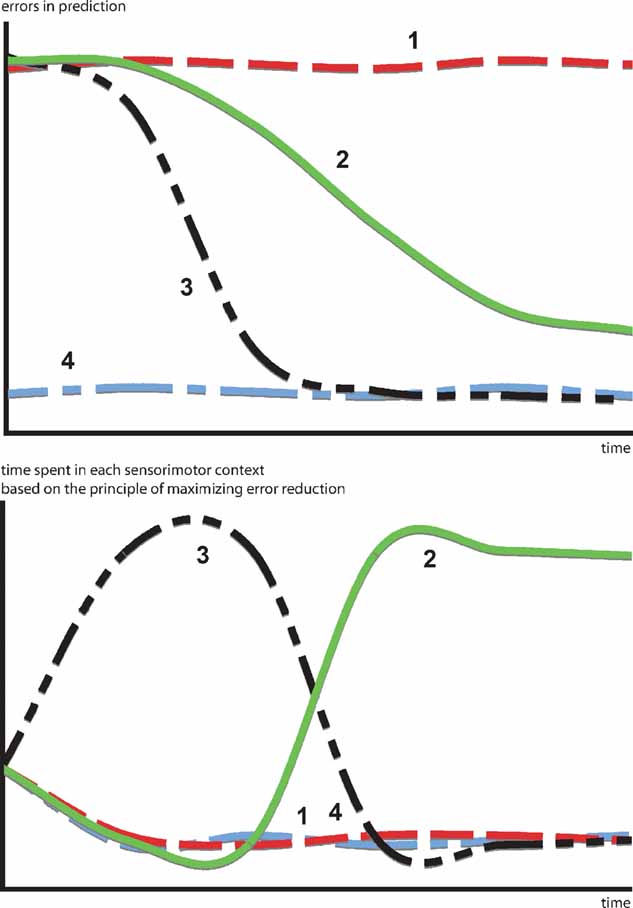
Figure 1. How a progress-driven control system operates on an idealized problem. Confronted with four sensorimotor contexts characterized by different learning profiles. The motivation for maximizing learning progress results in avoiding situations already predictable (context 4) or too difficult to predict (context 1), in order to focus first on the context with the fastest learning curve (context 3) and eventually, when the latter starts to reach a “plateau” to switch to the second most promising learning situation (context 2). This intrinsic motivation system allows the creation of an organized exploratory strategy necessary to engage in open-ended development.
We call “progress niches” situations of maximal progress. Progress niches are not intrinsic properties of the environment. They result from a relationship between a particular environment, a particular embodiment and a particular time in the developmental history of the animal. Once discovered, progress niches progressively disappear as they become more predictable.
Such type of progress-driven machine learning architectures are good candidates to shed new lights on neurophysiology of intrinsic motivation. Several researchers have described models for computing learning progress. One of the first theoretical machine learning architecture implementing the principle of maximizing error reduction was described by Schmidhuber (1991) , but no experiment in complex environments were conducted at that time. We have recently presented a critical discussion of the similarities and differences of these models (Oudeyer et al., 2007 ) and described a novel architecture capable to evaluate learning progress in complex noisy continuous environments such as the one encountered in robotic experiments. The next section presents this architecture.
Computing and Optimizing Progress in Prediction
We have designed an architecture that permits to compute and optimize progress in prediction. This architecture is described in full details in (Oudeyer et al., 2007 ). In this section, we will just give a general overview of its functioning and present some robotic experiments we have performed to test its behavior. Our intent is to show two things: first, that it is possible (though not trivial) to implement an intrinsic motivation system to progress in learning and second, that such a system permits not only to optimize learning but also to produce an organized exploration strategy and at a more general level to produce structured developmental patterns.
The Challenges of Learning Progress Measurement
Building an intrinsically motivated machine searching for learning progress implies complicated and deep issues. The idealized problem illustrated on Figure 1 allowed us to make more concrete the intuition that focusing on activities where prediction errors decrease most can generate organized developmental sequences. Nevertheless, the reality is in fact not as simple. Indeed, in this idealized problem, four different sensorimotor situations/activities were predefined. Thus it was assumed that when the idealized machine would produce an action and make a prediction about it, it would be automatically associated with one of the predefined kinds of activities. Learning progress would then be simply computed by, for example, comparing the difference between the mean of errors in prediction at time t and at time t - θ. In contrast, infants do not come to the world with an organized predefined set of possible kinds of activities. It would in fact be contradictory, since they are capable of open-ended development, and most of what they will learn is impossible to know in advance. It also occurs for a developmental robot, for which the world is initially a fuzzy blooming flow of unorganized sensorimotor values. In this case, how can we define learning progress? What meaning can we attribute to “maximizing the decrease of prediction errors?”
A first possibility would be just to compute learning progress at time t as the difference between the mean prediction errors at time t and at time t - θ. But implementing this on a robot quickly shows that it is in fact nonsense. For example, the behavior of a robot motivated to maximize such a progress would be typically an alternation between jumping randomly against walls and periods of complete immobility. Indeed, passing from the first behavior (highly unpredictable) to the second (highly predictable) corresponds to a large decrease in prediction errors, and so to a large internal reward. So, we see that there is a need to compute learning progress by comparing prediction errors in sensorimotor contexts that are similar, which leads us to a second possible approach.
In order to describe this second possibility, we need to introduce a few formal notations and precisions about the computational architecture that will embed intrinsic motivation. Let us denote a sensorimotor situation with the state vector x(t) (e.g., a given action performed in a given context), and its outcome with y(t) (e.g., the perceptual consequence of this action). Let us call M a prediction system trying to model this function, producing for any x(t) a prediction y′(t). Once the actual evolution y′(t) is known, the error ex(t) = | y(t) - y′(t) in prediction can be computed and used as a feedback to improve the performances of M. At this stage, no assumption is made regarding the kind of prediction system used in M. It could be for instance a linear predictor, a neural network or any other prediction method currently used in machine learning. Within this framework, it is possible to imagine a first manner to compute a meaningful measure of learning progress. Indeed, one could compute a measure of learning progress px(t) for every single sensorimotor situation x through the monitoring of its associated prediction errors in the past, for example with the formula:
where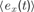 
is the mean of ex values in the last τ predictions. Thus, we here compare prediction errors in exactly the same situation X, and so we compare only identical sensorimotor contexts. The problem is that, whereas this is an imaginable solution in small symbolic sensorimotor spaces, this is inapplicable to the real world for two reasons. The first reason is that, because the world is very large, continuous and noisy, it never happens to an organism to experience twice exactly the same sensorimotor state. There are always slight differences. A possible solution to this limit would be to introduce a distance function d(xm, xn) and to define learning progress locally in a point x as the decrease in prediction errors concerning sensorimotor contexts that are close under this distance function:
where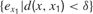 
denotes the mean of all 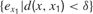values in the last τ predictions, and where δ is a small fixed threshold. Using this measure would typically allow the machine to manage to repeatedly try roughly the same action in roughly the same context and identify all the resulting prediction errors as characterizing the same sensorimotor situation (and thus overcoming the noise). Now, there is a second problem which this solution does not solve. Many learning machineries, and in particular the one used by infants, are fast and characterized by “one-shot learning.” In practice, this means that typically, an infant who observes the consequence of a given action in a given context will readily be able to predict very well what happens if exactly the same action happens in the same context again. Learning machines such as memory-based algorithms also show this feature. As a consequence, if learning progress is defined locally as explained above, a given sensorimotor situation will be typically interesting only for a very brief amount of time, and will hardly direct further exploration. For example, using this approach, a robot playing with a plastic toy might try to squash it on the ground to see the noise it produces, experiencing learning progress in the first few times it tries, but would quickly stop playing with it and typically would not try to squash it for example on the sofa or on a wall to hear the result. This is because its measure of potential learning progress is still too local.
Iterative Regional Measure of Learning Progress
Thus, we conclude that there really is a need to build broad categories of activities (e.g., squashing plastic toys on surfaces or shooting with the foot in small objects) as those pre-given in the initial idealized problem. The computation of learning progress will only become both meaningful and efficient if an automatic mechanism allows for the distinction of these categories of activities, typically corresponding to not-so-small regions in the sensorimotor space. We have presented a possible solution, based on the iterative splitting of the sensorimotor space into regions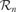 
. Initially, the sensorimotor space is considered as one big region, and progressively regions split into sub-regions containing more homogeneous kinds of actions and sensorimotor contexts (the mechanisms of splitting are detailed in [Oudeyer et al., 2007
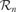]). In each region , the history of prediction errors {e} is memorized and used to compute a measure of learning progress that characterizes this region:
where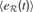 
is the mean of 
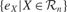values in the last τ predictions.
Given this iterative region-based operationalization of learning progress, there are two general ways of building a neural architecture that uses it to implement intrinsic motivation. A first kind of architecture, called monolithic, includes two loosely coupled main modules. The first module would be the neural circuitry implementing the prediction machine M presented earlier, and learning to predict the x → y mapping. The second module would be a neural circuitry meta M organizing the space into different regions 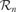and modelling the learning progress of M in each of these regions, based on the inputs (x(t), ex(t)) provided by M. This architecture makes no assumption at all on the mechanisms and representations used by the learning machine M. In particular, the splitting of the space into regions is not informed by the internal structure of M. This makes this version of the architecture general, but makes the scalability problematic in real-world structured inhomogeneous spaces where typically specific neural resources will be recruited/built for different kinds of activities.
This is why we have developed a second architecture, in which the machines M and metaM are tightly coupled. In this version, each region 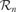is associated with a circuit 
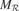, called an expert, as well as with a regional meta machine meta 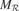. A given expert 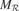is responsible for the prediction of y given x when x is a situation which is covered by 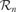Also, each expert 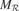is only trained on inputs (x, y) where x belongs to its associated region 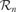. This leads to a structure in which a single expert circuit is assigned for each non-overlapping partition of the space. The meta-machine meta 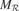associated to each expert circuit can then compute the local learning progress of this region of the sensorimotor space (See Figure 2
(b) for a symbolic illustration of this splitting/assignment process). The idea of using multiple experts has been already explored in several works including for instance (Doya et al., 2002
; Baldassarre, 2002
; Jordan and Jacobs, 1994
; Kawato, 1999
; Khamassi et al., 2005
; Tani and Nolfi, 1999
)
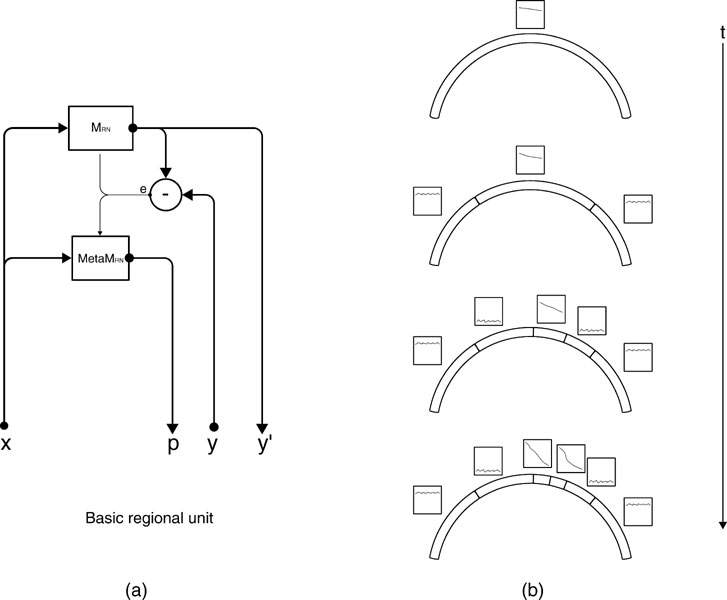
Figure 2. (a) An intrinsic motivation system is based on a population of regional units, each comprising an expert predictor 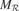that learns to anticipate the consequence y of a given sensorimotor context x belonging to its associated region of expertise 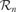, and a metapredictor meta 
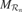modelling the learning progress of 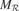in the close past. The learning progress defines the interestingness of situations belonging to a given context, and actions are chosen in order to reach maximally interesting situations. Once the actual consequence is known, 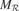and meta 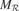get updated. meta 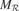re-evaluates the error curve linked with this context and computes an updated measure of the learning progress (local derivative of curve). (b) Illustration of the splitting/assignment process based on self-organized classification system capable of structuring an infinite continuous space of particular situations into higher-level categories (or kinds) of situations. An expert predictor/metapredictor circuit is assigned to each region.
Action Selection Circuit
The basic circuits we just described permit to compute an internal reward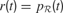 
, each time an action is performed in a given sensorimotor context, depending on how much learning progress has been achieved in a particular region 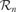. An intrinsic motivation to progress corresponds to the maximization of the amount of this internal reward. Mathematically, this can be formulated as the maximization of future expected rewards (i.e., maximization of the return), that is
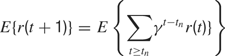
where γ(0 ≤ γ ≤ 1) is the discount factor, which assigns less weight on the reward expected in the far future. We can note that at this stage, it is theoretically easy to combine this intrinsic reward for learning progress with the sum of other extrinsic rewards re(t) coming from other sources, for instance in a linear manner with the formula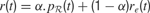 
(the parameter α measuring the relative weight between intrinsic and extrinsic rewards).
This formulation corresponds to a reinforcement learning problem (Sutton and Barto, 1998
) and thus the techniques developed in this field can be used to implement an action selection mechanism which will allow the system to maximize future expected rewards efficiently (e.g., Q-learning (Walkins and Dayan, 1992
), TD-learning (Sutton, 1988
), etc.). However, predicting prediction error reduction is, by definition, a highly non-stationary problem (progress niches appear and disappear in time). As a consequence, traditional “slow” reinforcement learning techniques are not well adapted in this context. In (Oudeyer et al., 2007
), we describe a very simple action-selection circuit that avoids problems related to delayed rewards and makes it possible to use a simple prediction system which can predict r(t + 1) and so evaluate E{r(t + 1)} Let us consider the problem of evaluating E{r(t + 1)} given a sensory context S(t) and a candidate action M(t), constituting a candidate sensorimotor context SM(t) = x(t) covered by region 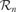. In our architecture, we approximate E{r(t + 1)} with the learning progress that was achieved in 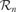with the acquisition of its recent exemplars, i.e. 
where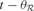 
is the time corresponding to the last time region and the associated expert circuit processed a new exemplar. The action–selection loop goes as follows:
in a given sensory S(t) context, the robot makes a list of the possible values of its motor channels M(t) which it can set; If this list is infinite, which is often the case since we work in continuous sensorimotor spaces, a sample of candidate values is generated;
each of these candidate motor vectors M(t) associated with the sensory context S(t) makes a candidate SM(t) vector for which the robot finds out the corresponding region
; then the formula we just described is used to evaluate the expected learning progress E{r(t + 1)} that might be the result of executing the candidate action M(t) in the current context;the action for which the system expects the maximal learning progress is chosen with a probability 1 - ε and executed, but sometimes a random action is selected (with a probability ε, typically 0.35 in the following experiments).
after the action has been executed and the consequences measured, the system is updated.
More sophisticated action-selection circuits could certainly be envisioned (see, for example, (Sutton and Barto, 1998 )). However, this one revealed to be surprisingly efficient in the real-world experiments we conducted.
Experiments
We have performed a series of robotic experiments using this architecture. In these experiments, the robot actively seeks out sensorimotor contexts in which it can experience learning progress given its morphological and cognitive constraints. Whereas a passive strategy would lead to very inefficient learning, an active strategy allows the learner to discover and exploit learning situations fitted to its biases. In one experiment, the four-legged robot is placed on a play mat (for more details, see (Oudeyer and Kaplan, 2006 ; Oudeyer et al., 2007 )). The robot can move its arms, its neck and mouth and can produce sounds. Various toys are placed near the robot, as well as a pre-programed “adult” robot which can respond vocally to the other robot in certain conditions. At the beginning of an experiment, the robot does not know anything about the structure of its continuous sensorimotor space (which actions cause which effects). Given the size of the space, exhaustive exploration would take a very long time and random exploration would be inefficient.
During each robotic experiment, which lasts approximately half a day, the flow of values of the sensorimotor channels are stored, as well as a number of features which help us to characterize the dynamics of the robot's development. The evolution of the relative frequency of the use of the different actuators is measured: the head pan/tilt, the arm, the mouth and the sound speakers (used for vocalizing), as well as the direction in which the robot is turning its head. Figure 3 shows data obtained during a typical run of the experiment.
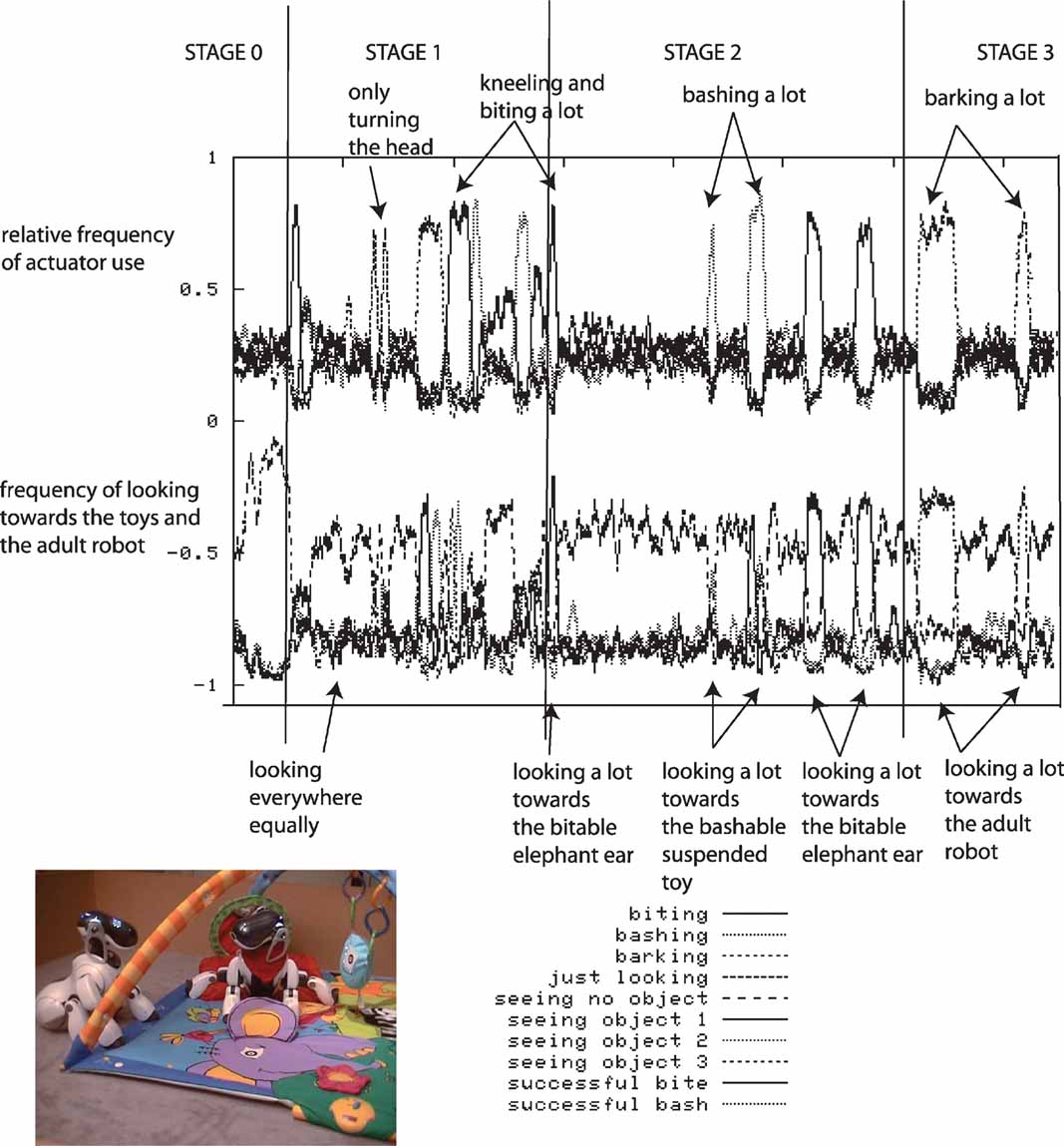
Figure 3. Typical experimental run. The robot, placed on a play mat, can move its arms, its neck and mouth and produce sounds. Various toys are placed near the robot, as well as a pre-programed “adult” robot which can respond vocally to the other robot in certain conditions. Results obtained after a typical run of the experiment are shown. Top curves: relative frequency of the use of the use of different actuators (head pan/tilt, arm, mouth, sound speaker). Bottom curves: frequency of looking toward each object and in particular toward pre-programed robot.
At the beginning of the experiment, the robot has a short initial phase of random exploration and body babbling. During this stage, the robot's behavior is equivalent to the one we would obtain using random action selection: we clearly observe that in the vast majority of cases, the robot does not even look at or act on objects; it essentially does not interact with the environment.
Then there is a phase during which the robot begins to focus successively on playing with individual actuators, but without knowing the appropriate affordances: first there is a period where it focuses on trying to bite in all directions (and stops bashing or producing sounds), then it focuses on just looking around, then it focuses on trying to bark/vocalize toward all directions (and stops biting and bashing), then on biting, and finally on bashing in all directions (and stops biting and vocalizing).
Then, the robot comes to a phase in which it discovers the precise affordances between certain action types and certain particular objects. It is at this point focusing either on trying to bite the bitable object (the elephant ear), or on trying to bash the bashable object (the suspended toy).
Eventually, it focuses on vocalizing towards the “adult” robot and listens to the vocal imitations that it triggers. This interest for vocal interactions was not pre-programed, and results from exactly the same mechanism which allowed the robot to discover the affordances between certain physical actions and certain objects.
The developmental trajectories produced by these experiments can be interpreted as assimilation and accommodation phases if we retain the Piagetian's terminology (Piaget, 1952 ). For instance, the robot “discovers” the biting and bashing schema by producing repeated sequences of these kinds of behavior, but initially these actions are not systematically oriented towards the bitable or the bashable object. This stage corresponds to “assimilation.” It is only later that “accommodation” occurs as biting and bashing starts to be associated with their respective appropriate context of use.
Our experiments show that functional organization can emerge even in the absence of explicit internal schema structures and that developmental patterns can spontaneously self-organize, driven by the intrinsic motivation system. We have discussed elsewhere how these type of patterns are relevant to interpret some results from the developmental psychology and language acquisition literature (Kaplan and Oudeyer, 2007a ,2007b ).
Speculations About the Neural Circuits of Intrinsic Motivation
The central hypothesis of this paper is that intrinsically motivating activities corresponds to expected prediction error decrease. Through a computer model and robotic experiments, we have shown how such situations could be recognized, memorized, and anticipated. We have also illustrated how such a progress-based reinforcement signal could permit to self-organize structured exploration patterns. This section will now investigate several speculative hypotheses about the neural circuits that could perform a similar function in the brain: how expected prediction error decrease could be signaled and measured.
Hypothesis 1: Tonic Dopamine as a Signal of Expected Prediction Error Decrease
We have already reviewed several elements of the current complex debate on the role and function of dopamine in action selection and learning. Based on our investigations with artificial intrinsic motivation systems, we would like to introduce yet another interpretation of the potential role of dopamine by formulating the hypothesis that tonic dopamine acts as a signal of “progress niches,” i.e. states where prediction error of some internal model is expected to decrease. As experimental researches in neuroscience have not really studied intrinsically motivated activities per se, it is not easy at this stage to assess whether this hypothesis is compatible or incompatible with the other interpretations of dopamine we have reviewed. Nevertheless, we can discuss how this interpretation fits with existing hypotheses and observations of the dopamine's functions.
We have previously discussed the interpretation of tonic dopamine as a ‘wanting’ motivational signal (incentive salience hypothesis). In the context of intrinsically motivated behavior, we believe this view is compatible with the hypothesis of dopamine as signal of “progress niches.” Dopamine acts as an invitation to investigate these “promising” states. This interpretation is also coherent with investigations that were conducted concerning human affective experience during stimulation of the dopamine circuits. When the lateral hypothalamus dopamine system is stimulated (part of the SEEKING system previously discussed), people report a feeling that “something very interesting and exciting is going on” (Panksepp (1998) , p. 149 based on experiments reported in Heath (1963) , Quaade et al. (1974) ). This corresponds to subjective affective states linked with intrinsically motivating activities (Csikszenthmihalyi, 1991 ).
In addition, Berridge articulates the proposition that “dopamine neurons code an informational consequence of learning signals, reflecting learning, and prediction that is generated elsewhere the brain but do not cause any new learning themselves” (Berridge (2007) , p. 405]). In this view, dopamine signals are a consequence and not a cause of learning phenomena happening elsewhere in the brain. This is consistent with the fact that dopamine neurons originating in the midbrain are recognized to have only sparse direct access to the signals information that needs to be integrated by an associative learning mechanism. All the signals that they receive are likely to be “highly processed already by forebrain structures before dopamine cells get much learning-relevant information” (Berridge (2007) , p. 406, see also Dommett et al. (2005) ).
In our model, this progress signal is used as a reinforcement to drive action-selection and behavioral switching. This aspect of our architecture could lead to a similar interpretation of the role of dopamine in several previous (and now often criticized) actor-critic models of action-selection occurring in the basal ganglia (Baldassarre, 2002 ; Barto, 1995 ; Doya, 2002 ; Houk et al., 1995 ; Khamassi et al., 2005 ; Montague et al., 1996 ; Schultz et al., 1997 ; Suri and Schultz, 2001 ). Let us recall that the dorsal striatum receives glutamate inputs from almost all regions of the cerebral cortex. Striatal neurons fire in relation to movement of a particular body part but also to preparation of movement, desired outcome of a movement, to visual and auditory stimuli and to visual saccades toward a particular direction. In most actor-critic computational models of the basal ganglia, dopamine responses originating the substantia nigra is interpreted as increasing the synaptic strength, between currently active striatal input and output elements (thus shaping the policy of the actor in an actor-critic interpretation). With this mechanism, if the striatal outputs corresponds to motor responses and that dopamine cells become active in the presence of an unexpected reward, the same pattern of inputs should elicit the same pattern of motor outputs in the future. One of the criticism to this interpretation is that “if DA neurons respond to surprise/arousing events, regardless of appetitive or aversive values, one would postulate that DA activation does not serve to increase the likelihood that a given behavioral response is repeated under similar input conditions” (Horvitz (2002) p. 70). Progress niches can be extrinsically rewarding (i.e., progress in playing poker sometimes result in gaining some money) or aversive (i.e., risk-taking behavior in extreme sports). Therefore, we believe our hypothesis is compatible with interpretations of the basal-ganglia based action-selection circuits that control the choice of actions during cortico-striato-thalamo-cortical loops.
However, the precise architecture of this reinforcement learning architecture remains at this stage very open. A seducing hypothesis would be that the much studied reinforcement learning architectures based on short prediction error phasic signals could be just reused with an internal self-generated reward, namely expected progress. This should lead to a complementary interpretation of the role of phasic and tonic dopamine in intrinsically motivated behavior in reinforcement. An alternative hypothesis is that tonic dopamine is directly used as a reinforcement signal. As previously discussed, Niv and colleagues assimilated the role of tonic dopamine to an average reward signal in a recent computational model (Niv et al., 2006 ), a view which seems to contradict the hypothesis articulated a few years ago that tonic dopamine signal reports a long-run average punishment rate (Daw et al., 2002 ). Our hypothesis is based on the difference of two long-run average prediction error rate (Equation 3). We will now discuss how and where this progress signal could me measured.
Hypothesis 2: Cortical Microcircuits as Both Prediction and Metaprediction Systems
Following our hypothesis that tonic dopamine acts as signal of prediction progress, we must now guess where learning progress could be computed. For this part, our hypothesis will be that cortical microcircuits ac as both prediction and metaprediction systems and therefore can directly compute regional learning progress, through an unsupervised regional assignment as this is done in our computational model.
However, before considering this hypothesis let us briefly explore some alternative ones. The simpler one would be that progress is evaluated in some way or another in the limbic system itself. If indeed, as many authors suggests, phasic responses of dopamine neurons report prediction error in certain contexts, their integration over time could be easily performed just through the slow accumulation of dopamine in certain part of neural circuitry (hypothesis discussed in (Niv et al., 2006 )). By comparing two running average of the phasic signals one could get an approximation of Equation 1. However, as we discussed in the previous section, to be appropriately measured, progress must be evaluated in regional manner, by local “expert” circuits. Although it is not impossible to imagine an architecture that would maintain such type of regional specialized circuitry in the basal ganglia (see for instance the multiple expert actor-critic architectures described by (Khamassi et al., 2005 )), we believe this is not the most likely hypothesis.
As we argued, scalability considerations in real-world structured inhomogeneous spaces favor architectures in which neural resources can be easily recruited or built for different kinds of initially unknown activities. This still leaves many possibilities. Kawato argues that, from a computational point of view, “it is conceivable that internal models are located in all brain regions having synaptic plasticity, provided that they receive and send out relevant information for their input and output” (Kawato, 1999 ). Doya (1999) suggested broad computational distinction between the cortex, the basal ganglia, and the cerebellum, each of those associated with a particular type of learning problems, unsupervised learning, reinforcement learning and supervised learning, respectively. Another potential candidate location, the hippocampus has often been described as a comparator of predicted and actual events (Gray, 1982 ) and fMRI studies revealed that its activity was correlated with the occurrence of unexpected events (Ploghaus et al., 2000 ). Among all these possibilities, we believe the most promising direction of exploration is the cortical one, essentially because the cortex offers the type of open-ended unsupervised“expert circuits” recruitment that we believe are crucial for the computation of learning progress.
A single neural microcircuit forms an immensely complicated network with multiple recurrent loops and highly heterogeneous components (Douglas and Martin, 1998 ; Mountcastle, 1978 ; Shepherd, 1988 ). Finding what type of computation could be performed with such a high dimensional dynamical system is a major challenge for computational neuroscience. To explore our hypothesis, we must investigate whether the computational power and evolutionary advantage of columns can be unveiled if these complex networks are considered not only as predictors but performing both prediction and metaprediction functions (by not only anticipating future sensorimotor events but also its own errors in prediction and learning progress).
In recent years, several computational models explored how cortical circuits could be used as prediction devices. Maas and Markram suggested to view a column as a liquid state machine (LSM) (Maas et al., 2002 ) (which is somewhat similar to Echo State Networks described by Jaeger (Jaeger, 2001 ; Jaeger and Haas, 2004 )). Like the Turing machine, the model of a LSM is based on a rigorous mathematical framework that guarantees, under idealized conditions, universal computing power for time series problems. More recently, Deneve et al. (2007) presented a model of a Kalman filter based on recurrent basis function networks, a kind of model that can be easily mapped onto cortical circuits. Kalman filters share some similarity with the kind of metaprediction machinery we have discussed in this article, as they also deal with modeling errors made by prediction of internal models. However, we must admit that there is not currently any definitive experimental evidence or computational model that supports precisely the idea that cortical circuit actually compute their own learning progress.
If indeed we could show that cortical microcircuits can signal this information to other parts of the brain, the mapping with our model would be easy. Lateral inhibition mechanisms, specialization dynamics and other self-organizing processes that are typical of cortical plasticity should permit without problems to perform the type of regionalization of the sensorimotor space that our architecture features. As previously argued, action-selection could then be realized by some form of subcortical actor-critic architecture, similar to the one involved in the optimization of extrinsic forms of rewards.
Finally, we believe our hypothesis is consistent from an evolutionary perspective, or at least that an “evolutionary story” can be articulated around it. The relatively “recent” invention of the cortical column circuits correlates roughly with the fact that only mammals seems to display intrinsically motivated behavior. Once discovered by evolution, cortical columns have multiplied themselves leading to the highly expanded human cortex (largest number of cortical neurons (1010) among all animals, closely followed by large cetaceans and elephants (Roth and Dicke, 2005 ), over 1000 fold expansion from mouse to man to provide 80% of the human brain). What can make them so advantageous from an evolutionary point of view? It is reasonable to suppose that intrinsic motivation systems appeared after (or on top of) an existing machinery dedicated to the optimization of extrinsic motivation. For an extrinsically motivated animal, value is linked with specific stimuli, particular visual patterns, movement, loud sounds, or any bodily sensations that signal that basic homeostatic physiological needs like food or physical integrity are (not) being fulfilled. These animals can develop behavioral strategies to experience the corresponding situations as often as possible. However, when an efficient strategy is found, nothing pushes them further toward new activities. Their development stops there.
The apparition of a basic cortical circuit that could not only acts as predictor but also as metapredictor capable of evaluating its own learning progress can be seen as a major evolutionary transition. The brain manages now to produce its own reward, a progress signal, internal to the central nervous system with no significant biological effects on non-nervous-system tissues. This is the basis of an adaptive internal value system for which sensorimotor experiences that produce positive value evolve with time. This is what drives the acquisition of novel skills, with increasing structure and complexity. This is a revolution, yet it is essentially based on the old brain circuitry that evolved for the optimization of specific extrinsic needs. If we follow our hypothesis, the unique human cortical expansion has to be understood as a coevolutionary dynamical process linking larger “space” for learning and more things to learn. In some way, it is human culture, as a huge reservoir of progress niches, that has put pressure in having more of these basic processing units.
Perspectives
We are aware that it is always hazardous to make too simple mappings between machine models and biological systems. However, since cybernetics pioneers (Rosenblueth et al., 1943 ), computational models clearly had a fundamental influence of our views of brain processes and we have already mentioned several very successful outcomes that resulted of wise comparison between an artificial model and neurophysiologic observations (Cordeschi, 2002 ). We believe that to successfully test hypotheses suggested by computational models, we need to engage in a truly interdisciplinary program. First, we must start to really study intrinsic motivation from an neuroscience point of view, which means getting data of what is going on in the brain during such type of exploratory behavior. In addition, we must find a way of comparing the experiments conducted with human subjects with the behavior of artificial models, which in such a context is not an easy problem.
For the adult and infant studies, experiments could consist in observing infant and adults’ behavior during their exploration of virtual environment, monitoring in real-time their neural dynamics using brain imagery techniques (for instance using a similar experimental set up than the one used in (Koepp et al., 1998 )). Conducting experiments in virtual world offers a number of interesting advantages compared to experiments in real physical environment. In virtual worlds, learning opportunities can be easily controlled and designed. One could for instance create a virtual environment designed so that the degree of learning opportunities becomes an experimental variable, permitting easy shifts from rich and stimulating environments to boring and predictive worlds. Moreover, virtual worlds can be made suffciently simple, abstract and novel in order to feature learning opportunities that do not depend too much on previously acquired skills. Embodiment plays a crucial role in shaping developmental trajectories and sequences of skills acquisition (see also Lakoff and Johnson (1998) in that respect). Paradoxically, this means that in order to identify novel exploration patterns and compare human trajectories with the ones of an artificial agent, we must create situations where the embodiment is radically different from natural human embodiment. In such a case, the human and the artificial agent would have to master an (equally) unknown body in an (equally) unknown world. To some extent this proposed approach is related to Galantucci's experiments on dynamics of convention formation in an novel, previously unknown medium (Galantucci, 2005 ). The expected outcome of this kind of experiment is to obtain a first characterization of the types of cortical neural assemblies involved in intrinsically motivated behavior, a kind of data which currently lacks to progress.
Research in psychology and neuroscience provides important elements supporting the existence of intrinsic motivation systems. Computational models permit to investigate possible circuits necessary for different elements of an intrinsic motivation system and to explore their structuring effect on behavioral and developmental patterns. It is likely that many diverse lines of experimental data can potentially be explained in common terms if we consider children as active seekers of progress niches, who learn how to focus on what is learnable in the situation they encounter and on what can be effciently grasped at a given stage of their cognitive and physiological development. But to progress in such an understanding, we need to define a novel research program combining infant studies, analysis of realistic computational model and experiments with robots and virtual agents. We believe that if such a research agenda can be conducted, we are about to reach a stage where it will be for the first time possible to study the cascading consequences in development that small changes in motivation systems can provoke.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential confiict of interest.
References
Baldassarre, G. (2002) A modular neural-network model of the basal ganglia's role in learning and selection motor behaviors. J. Cogn. Sys. Res. 3, 5-13.
Barto, A. (1995). Adaptive critics and the basal ganglia. In Models of information processing in the basal ganglia,, J. Houk, J. Davis, and D. Beiser, eds., Cambridge, MA, USA, MIT Press, PP. 215-232.
Barto, A., Singh, S., and Chentanez, N. (2004). Intrinsically motivated learning of hierarchical collections of skills. In Proceedings of the 3rd International Conference on Development and Learning (ICDL 2004), Salk Institute, San Diego.
Bell, D. (1973) The experimental reproduction of amphetamine psychosis. Arch. Gen. Psychiatry. 29, 35-40.
Belue, M., Bauer, K., and Ruck, D. (1997) Selecting optimal experiments for multiple output multi-layer perceptrons. Neural Comput. 9, 161-183.
Bernheimer, H., Birkmayer, W., Hornykiewicz, Jellinger, K., and Seitelberger, F. (1973) Brain dopamine and the syndromes of parkinson and huntington: Clinical, morphological and neurochemical correlations. J. Neurol. Sci. 20, 415-455.
Berridge, K. C. (2007) The debate over dopamine's role in reward: the case of incentive salience. Psychopharmacology 191, 391-431.
Cameron, J., and Pierce, W. (2002). Rewards and Intrinsic Motivation: Resolving the Contoversy (Bergin and Garvey Press).
Carboni, E., Imperato, A., Perezzani, L., and Di Chiara, G. (1989) Amphetamine, cocaine, phencyclidine and nomifensine increases extra-cellullar dopamine concentrations preferentially in the nucleus accumbens of freely moving rats. Neuroscience 28, 653-661.
Cohn, D., Ghahramani, Z., and Jordan, M. (1996) Active learning with statistical models. J. Artif. Intel. Res. 4, 129-145.
Cordeschi, R. (2002). The Discovery of the Artifical. Behavior, Mind and Machines, Before and Beyond Cybernetics (Kluwer academic publishers, Dordrecht).
Daw, N., Kakade, S., and Dayan, P. (2002) Opponent interactions between serotonin and dopamine. Neural Netw. 15, 603-616.
De Charms, R. (1968). Personal Causation: The Internal Affective Determinants of Behavior (New York, Academic Press).
Deci, E., and Ryan, R. (1985). Intrinsic Motivation and Self-Determination in Human Behavior. Plenum Press.
Dember, W. N., and Earl, R. W. (1957) Analysis of exploratory, manipulatory and curiosity behaviors. Psychol. Rev. 64, 91-96.
Deneve, S., Duhamel, J.-R., and Pouget, A. (2007) Optimal sensorimotor integration in recurrent cortical networks: A neural implementation of kalman filters. J. Neurosci. 27, 5744-5756.
Depue, R., and Iacono, W. (1989) Neurobehavioral aspects of affective disorders. Ann. Rev. Psychol. 40, 457-492.
Dommett, E., Coizet, V., Blatha, C., Martindale, J., Lefebre, V., Walton, N., Mayhew, J., Overton, P., and Redgrave, P. (2005). How visual stimuli activate dopaminergic neurons at short latency. Science, 307, 1476-1479.
Douglas, R., and Martin, K. (1998). Neocortex. In The Synaptic Organization of the Brain,, G.M. Shepherd ed., (Oxford University Press) PP. 459-509.
Doya, K. (1999) What are the computations of cerebellum, basal ganglia, and the cerebral cortex. Neural Netw. 12, 961-974.
Doya, K., Samejima, K., Katagiri, K., and Kawato, M. (2002) Multiple modelbased reinforcement learning. Neural Comput. 14, 1347-1369.
Galantucci, B. (2005) An experimental study of the emergence of human communication systems. Cogn. Sci. 29, 737-767.
Gallese, V., and Lakoff, G. (2005). The braińs concepts: role of sensorymotor conceptual knowledge. Cogn. Neuropsychol. 21.
Grace, A. A. (1991) Phasic versus tonic dopamine release and the modulation of dopamine system responsivity: a hypothesis for the etiology of schizophrenia. Neuroscience 41, 1-24.
Gray, J. (1982). The Neuropsychology of Anxiety: An Enquiry into the Functions of the Septo-Hippocampal System (Oxford, Clarendon Press).
Harlow, H. (1950) Learning and satiation of response in intrinsically motivated complex puzzle performances by monkeys. J. Comp. Physiolo. Psychology 43, 289-294.
Heath, R. G. (1963) Electrical self-stimulation of the brain in man. American J. Psychiatry 120, 571-577.
Hooks, M., and Kalivas, P. (1994) Involvement of dopamine and excitatory amino acid transmission in novelty-induced motor activity. J. Pharmacol Exp. Ther. 269, 976-988.
Horvitz, J.-C. (2000). Mesolimbocortical and nigrostriatal dopamine responses to salient non-reward events. Neuroscience 96, 651-656.
Horvitz, J.-C. (2002). Dopamine gating of glutamatergic sensorimotor and incentive motivational input signals to the striatum. Behav. Brain Res. 137, 65-74.
Houk, J., Adams, J., and Barto, A. (1995). A model of how the basal ganglia generate and use neural signals that predict reinforcement. In Models of Information Processing in the Basal Ganglia,, J. Houk, J. Davis and D. Beiser eds. (MIT press) PP. 249-270.
Huang, X., and Weng, J. (2002). Novelty and reinforcement learning in the value system of developmental robots. In Proceedings of the 2nd International Workshop on Epigenetic Robotics: Modeling Cognitive Development in Robotic Systems, C. Prince, Y. Demiris, Y. Marom, H. Kozima and C. Balkenius eds. Lund University Cognitive Studies 94, PP. 47-55.
Hull, C. L. (1943). Principles of Behavior: An Introduction to Behavior Theory (New-York: Appleton-Century-Croft).
Hunt, J. M. (1965) Intrinsic motivation and its role in psychological development. Nebraska Symposium on Motivation, 13, 189-282.
Ikemoto, S., and Panksepp, J. (1999) The role of nucleus accumbens dopamine in motivated behavior: a unifying interpretation with special reference to rewardseeking. Brain Res. Rev. 31, 6-41.
Jaeger, H. (2001). The echo state approach to analyzing and training recurrent neural networks. Technical Report, GMD Report 148, GMD - German National Research Institute for Computer Science.
Jaeger, H., and Haas, H. (2004) Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication. Science 304, 78-80.
Joel, D., Niv, Y., and Ruppin, E. (2002) Actor-critic models of the basal ganglia: New anatomical and computational perspectives. Neural Netw. 15, 535-547.
Jordan, M., and Jacobs, R. (1994) Hierarchical mixtures of experts and the em algorithm. Neural Comput. 6, 181-214.
Kaplan, F., and Oudeyer, P.-Y. (2004). Maximizing learning progress: an internal reward system for development. In Embodied Artificial Intelligence F. Iida, R. Pfeifer, L. Steels and Y. Kuniyoshi eds. LNCS 3139, (Springer-Verlag, London, UK) PP. 259-270.
Kaplan, F., and Oudeyer, P.-Y. (2007a) The progress-drive hypothesis: an interpretation of early imitation. In Models and Mechanisms of Imitation and Social Learning: Behavioural, Social and Communication Dimensions,, C. Nehaniv and K. Dautenhahn eds. (Cambridge University Press) PP. 361-377.
Kaplan, F., and Oudeyer, P.-Y. (2007b) Un robot motivé pour apprendre: le role des motivations intrinseques dans le developpement sensorimoteur. Enfance 59, 46-58.
Karmiloff-Smith, A. (1992). Beyond Modularity: A Developmental Perspective on Cognitive Science (MIT Press).
Kawato, M. (1999) Internal models for motor control and trajectory planning. Curr. Opin. Neurobiol. 9, 718-727.
Khamassi, M., Lachèze, L., Girard, B., Berthoz, A., and Guillot, A. (2005) Actor-critic models of reinforcement learning in the basal ganglia. Adapt. Behav. 13, 131-148.
Koepp, M., Gunn, R., Cunningham, V., Dagher, A., T., J., Brooks, D. J., Bench, C. J., and Grasby, P. M. (1998) Evidence for striatal dopamine release during a video game. Nature 393, 266-267.
Lakoff, G., and Johnson, M. (1998). Philosophy in the Flesh: the Embodied Mind and its Challenge to Western Thought (Basic Books).
Maas, W., Natschlager, T., and Markram, H. (2002) Real-time computing without stable states: a new framework for neural computation based on perturbations. Neural Comput. 14, 2531-2560.
Marshall, J., Blank, D., and Meeden, L. (2004). An emergent framework for self-motivation in developmental robotics. In Proceedings of the 3rd International Conference on Development and Learning (ICDL 2004), San Diego Salk Institute,.
McClure, S., Daw, N., and Montague, P. (2003). A computational substate for incentive salience. Trends Neurosci. 26.
Montague, P., Dayan, P., and Sejnowski, T. (1996) A framework for mesencephalic dopamine systems based on predictive hebbian learning. J. Neurosci. 16, 1936-1947.
Montgomery, K. (1954) The role of exploratory drive in learning. J. Comp. Physiol. Psychol. 47, 60-64.
Mountcastle, V. (1978). An organizing principle for cerebral function: The unit model and the distributed system. In The Mindful Brain., G. Edelman and V. Mountcastle eds. (MIT press).
Niv, Y., Daw, N., Joel, D., and Dayan, P. (2006). Tonic dopamine: opportunity costs and the control of response vigor. Psychopharmacology 507-520.
Oades, R. (1985) The role of noradrenaline in tuning and dopamine in switching between signals in the cns. Neurosci. Biobehav. Rev. 9, 261-282.
Oudeyer, P.-Y., and Kaplan, F. (2007). What is intrinsic motivation? a typology of computational approaches. Front. Neurorobot. 1.
Oudeyer, P.-Y., Kaplan, F., and Hafner, V. (2007) Intrinsic motivation systems for autonomous mental development. IEEE Trans. Evol. Comput. 11, 265-286.
Panksepp, J. (1998). Affective neuroscience: the Foundations of Human and Animal Emotions. (Oxford University Press).
Pettit, H., and Justice, J. Jr. (1989). Dopamine in the nucleus accumbens during cocaine self-administration as studied by in vivo microdialysis. Pharmacol. Biochem. Behav. 34, 899-904.
Ploghaus, A., Tracey, I., Clare, S., Gati, J., Rawlins, J., and Matthews, P. (2000) Learning about pain: the neural substrate of the prediction error of aversive events. Proc. Natl. Acad. Sci. 97, 9281-9286.
Quaade, F., Vaernet, K., and Larsson, S. (1974) Stereotaxic stimulation and electrocoagulation of the lateral hypothalamus in obese humans. Acta. Neurochir. 30, 111-117.
Redgrave, P., Prescott, T., and Gurney, K. (1999). Is the short latency dopamine response too short to signal reward error? Trends Neurosci. 22, 146-151.
Rosenblueth, A., Wiener, N., and Bigelow, J. (1943) Behavior, purpose and teleology. Philos. Sci. 10, 18-24.
Roth, G., and Dicke, U. (2005) Evolution of the brain and intelligence. Trends Cogn. Sci. 9, 250-257.
Ryan, R., and Deci, E. (2000) Intrinsic and extrinsic motivations: Classic definitions and new directions. Contemp. Educ. Psychol. 25, 54-67.
Schmidhuber, J. (1991). Curious model-building control systems. In Proceeding International Joint Conference on Neural Networks, Singapore. IEEE, Vol. 2, PP. 1458-1463.
Schultz, W. (2006) Behavioral theories and the neurophysiology of reward. Annu. Rev. Psychol. 57, 87-115.
Schultz, W., Dayan, P., and Montague, P. (1997) A neural substrate of prediction and reward. Science 275, 1593-1599.
Shepherd, G. M. (1988). A basic circuit for cortical organization. In Perspectives in Memory Research M. Gazzaniga ed. (MIT Press) PP. 93-134.
Smith, A., Li, M., Becker, S., and Kapur, S. (2006) Dopamine, prediction error and associative learning: a model-based account. Netw. Comput. Neural Sys. 17, 61-84.
Steels, L. (2004). The autotelic principle. In Embodied Artificial Intelligence, I. Fumiya, R. Pfeifer, L. Steels and K. Kunyoshi eds. Vol. 3139 of Lecture Notes in AI, (Berlin, Springer Verlag) PP. 231-242.
Suri, R., and Schultz, W. (2001) Temporal difference model reproduces anticipatory neural activity. Neural Comput. 13, 841-862.
Sutton, R., and Barto, A. (1998). Reinforcement Learning: An Introduction (Cambridge, MA, MIT Press).
Tani, J., and Nolfi, S. (1999) Learning to perceive the world as articulated: An approach for hierarchical learning in sensory-motor systems. Neural Netw. 12, 1131-1141.
Thelen, E., and Smith, L. B. (1994). A Dynamic Systems Approach to the Development of Cognition and Action (Boston, MA, USA, MIT Press).
Weinberger, D. R. (1987) Implications of normal brain development for the pathogenesis of schizophrenia. Arch. Gen. Psychiatry 44, 660-669.
Weiner, I., and Joel, D. (2002). Dopamine in schizophrenia: dysfunctional information processing in basal ganglia-thalamocortical split circuits. In Handbook of Experimental Pharmacology, vol 154/II, Dopamine in the CNS II,, G. Chiara ed. (Springer) PP. 417-472.
White, N. M. (1989). Reward or reinforcement: what's the difference? Neurosci.Biobehav. Rev. 13, 181-186.
Wise, R. (1989). The brain and reward. In The Neuropharmacological Basis of Reward,, J. Liebman and S. Cooper, eds. (Clarendon Press) PP. 377-424.
Keywords: intrinsic motivation, curiosity, exploration, dopamine, cortical microcircuits, meta-learning, development
Citation: Frederic Kaplan and Pierre-Yves Oudeyer (2007). In search of the neural circuits of intrinsic motivation. Front. Neurosci. 1:1. 225-236. doi: 10.3389/neuro.01/1.1.017.2007
Received: 15 August 2007;
Paper pending published: 01 September 2007;
Accepted: 01 September 2007;
Published online: 15 October 2007
Edited by:
Idan Segev, Hebrew University, IsraelReviewed by:
Peter Dayan, University College London, UKKenji Doya, Okinawa Institute of Science and Technology, Japan
Copyright: © 2007 Kaplan and Oudeyer. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Frederic Kaplan EPFL - CRAFT / CE 1 628 Station 1 CH - 1015 Lausanne, Switzerland. e-mail: frederic.kaplan@epfl.ch