Neuroanatomical correlates of developmental dyscalculia: combined evidence from morphometry and tractography
1
Department of Psychiatry and Behavioral Sciences, Stanford University, CA, USA
2
Department of Psychology, Stanford University, CA, USA
3
Program in Neuroscience, Stanford University, CA, USA
4
Symbolic Systems Program, Stanford University, CA, USA
Poor mathematical abilities adversely affect academic and career opportunities. The neuroanatomical basis of developmental dyscalculia (DD), a specific learning deficit with prevalence rates exceeding 5%, is poorly understood. We used structural MRI and diffusion tensor imaging (DTI) to examine macro- and micro-structural impairments in 7- to 9-year-old children with DD, compared to a group of typically developing (TD) children matched on age, gender, intelligence, reading abilities and working memory capacity. Voxel-based morphometry (VBM) revealed reduced grey matter (GM) bilaterally in superior parietal lobule, intra-parietal sulcus, fusiform gyrus, parahippocampal gyrus and right anterior temporal cortex in children with DD. VBM analysis also showed reduced white matter (WM) volume in right temporal-parietal cortex. DTI revealed reduced fractional anisotropy (FA) in this WM region, pointing to significant right hemisphere micro-structural impairments. Furthermore, FA in this region was correlated with numerical operations but not verbal mathematical reasoning or word reading. Atlas-based tract mapping identified the inferior longitudinal fasciculus, inferior fronto-occipital fasciculus and caudal forceps major as key pathways impaired in DD. DTI tractography suggests that long-range WM projection fibers linking the right fusiform gyrus with temporal-parietal WM are a specific source of vulnerability in DD. Network and classification analysis suggest that DD in children may be characterized by multiple dysfunctional circuits arising from a core WM deficit. Our findings link GM and WM abnormalities in children with DD and they point to macro- and micro-structural abnormalities in right hemisphere temporal-parietal WM, and pathways associated with it, as key neuroanatomical correlates of DD.
Mathematical skills are becoming increasingly critical for achieving academic and professional success. Dyscalculia is a developmental learning deficit estimated to have a prevalence of about 5–6% (Butterworth, 2005
; Cohen Kadosh and Walsh, 2007
; Rubinsten and Henik, 2009
). Developmental dyscalculia (DD) can be defined as “a disorder of numerical competence and arithmetic skill which is manifest in children of normal intelligence who do not have acquired neurological injuries” (Temple, 2002
). The prevalence of mathematical difficulties arising from non-specific attentional, working memory and reading disabilities has an even higher prevalence rate, estimated to range from 5% to 20% of young children depending on the precise criteria used (Berch and Mazzocco, 2007
). Although their prevalence rates are at least as high as dyslexia and reading disabilities, dyscalculia and related mathematical disabilities have received much less attention from developmental neuroscientists.
Normative functional neuroimaging studies have implicated the intra-parietal sulcus (IPS) within the posterior parietal cortex (PPC) as a region specifically involved in the representation and manipulation of numerical quantity (Dehaene et al., 2003
). With experience and learning, the IPS builds an increasingly amodal, language-independent semantic representation of numerical quantity (Bruandet et al., 2004
; Ansari, 2008
; Rosenberg-Lee et al., 2009
). In addition to the IPS, depending on the nature and complexity of specific tasks, mathematical information processing also critically involves activation and deactivation in a more distributed network of regions within the dorsal visual stream encompassing the superior parietal lobule (SPL), the angular and supramarginal gyri in the PPC and the ventral visual stream encompassing the lingual and fusiform gyri in the inferior temporal cortex (Menon et al., 2000
; Rickard et al., 2000
; Zago et al., 2001
; Delazer et al., 2003
; Grabner et al., 2008
; Wu et al., 2009
). Functional neuroimaging studies examining the neural basis of dyscalculia have yielded mixed results in these regions. Price et al. (2007)
reported hypoactivation of the IPS in dyscalculic children during number comparison tasks, while Simos et al. (2008)
demonstrated increased neurophysiological activity in inferior and superior parietal regions in the right hemisphere in children with mathematical difficulties compared to controls. One potential reason for these discrepancies is that the profile of functional deficits in mathematical task processing varies with the level of task difficulty and type of operation performed. Thus, for example, Kesler et al. (2006)
found that, compared with controls, children with Turner syndrome recruited additional neural resources in frontal and parietal regions during an easier, two-operand math task, whereas during a more difficult three-operand task, they showed significantly less activation in frontal, parietal and subcortical regions than controls. Moreover, mathematical abilities in children involve multiple cognitive processes, most notably visuo-spatial processing and working memory (Adams and Hitch, 1998
; Swanson and Beebe-Frankenberger, 2004
), and the relative contribution of these processes changes with instruction and development (Meyer et al., 2009
). Little is currently known about functional abnormalities underlying the neural basis of these component processes in children with DD. Recent conceptual models of dyscalculia raise the possibility that heterogeneous deficits in DD can arise from common abnormalities (Rubinsten and Henik, 2009
).
One approach to the systematic investigation of DD in children is to examine whether there are neuroanatomical and structural differences in the brains of these children when compared to well-matched TD controls. White matter (WM) and gray matter (GM) integrity are crucial for nearly all higher cognitive operations (Johansen-Berg and Behrens, 2006
). However, only one study to date has used voxel-based morphometry (VBM) to examine GM and WM integrity in DD. Rotzer et al. (2008)
reported decreased GM volume in the right IPS, anterior cingulate cortex, left inferior frontal gyrus, and bilateral middle frontal gyri in 9-year-old children, compared to IQ matched controls. They also reported WM volume reductions in the left frontal cortex and right parahippocampal gyrus in children with DD. It is, however, not clear whether the two groups were matched on reading and working memory abilities. Furthermore, morphometric studies leave unclear whether WM microstructural and tract deficits underlie DD. In TD children, van Eimeren et al. (2008)
reported that FA in the left superior corona radiata and the inferior longitudinal fasciculus were correlated with mathematical abilities in TD children. The precise anatomical location, however, remains unknown because the analysis was constrained to large WM regions. Nevertheless, it is noteworthy that the laterality and location of the deficits differs considerably from those reported by Rotzer et al. (2008)
. Related studies in children with neurodevelopmental and neurogenetic disorders have suggested that mathematical difficulties may be related to GM abnormalities in the IPS and surrounding WM within the PPC. Isaacs et al. (2001)
reported reduced left parietal GM in children with low birth weight. Molko et al. (2003)
observed abnormal sulcal depth in bilateral IPS in adults with Turner syndrome (Bruandet et al., 2004
). Barnea-Goraly et al. (2005)
found that fractional anisotropy (FA) of WM tracts in left parietal WM matter adjacent to the IPS was significantly correlated with arithmetic ability in 7- to 19-year-old children and adolescents with 22q11.2 deletion (velocardiofacial) syndrome. However, mathematical difficulties in these neurodevelopmental disorders are typically accompanied by profound visuo-spatial and reading disabilities, thereby limiting their generalizability to pure DD.
Over the past several years diffusion tensor imaging (DTI) and VBM measures have been used to identify consistent white matter integrity and gray matter density deficits in children with reading disability (Ben-Shachar et al., 2007
; Schlaggar and McCandliss, 2007
; Kronbichler et al., 2008
; Richards et al., 2008
; Steinbrink et al., 2008
). Parallel efforts in the domain of dyscalculia have been slow to develop, and the precise anatomical locations and identity of WM tracts that are impaired in children with DD is currently unknown.
The recruitment and assessment of a homogenous group of children with DD, as well as a well-matched TD control group, presents particular challenges. Except for the study by Rotzer et al. (2008)
, previous brain imaging studies of DD have been limited by relatively small sample sizes, wide age ranges, poor neuropsychological evaluation and assessments, and, most problematically, the presence of other comorbid cognitive disabilities. Here we report findings from a well-characterized cohort, comprising 23 children with DD and 24 TD children matched for IQ, age, gender, reading ability and working memory. We examined macro-structural and micro-structural integrity using measurements of GM and WM volume, and fractional anisotropy (FA) in DD. We also examined the relation between micro-structural deficits and key individual subscales of the Wechsler Individual Aptitude Test, 2nd edition (WIAT-II) (Wechsler, 2001
). We used DTI tractography in order to delineate abnormal WM pathways and to link WM and GM abnormalities. Finally, we conducted a novel classification analysis to examine whether network-level connectivity differs between children with DD and TD children. Based on prior neuroimaging studies in children and adults, we hypothesized that children with DD would should deficits in dorsal PPC and inferior temporal cortex GM and WM.
Participants
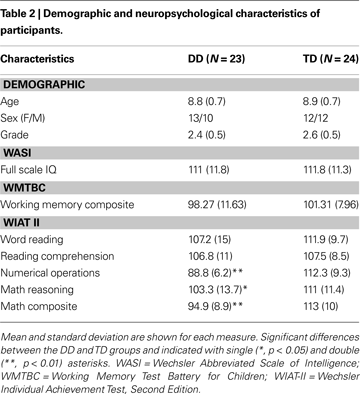
Forty-seven 7–9 year old children (25 females) in the 2nd and 3rd grades were selected from an ongoing longitudinal MRI study of brain structural and functional changes underlying the development of mathematical ability. A group of DD children (N = 23) was selected based on their scores on a standardized measure of mathematics ability, derived from two subscales of the WIAT-II. Children with either a Numerical Operations Score or Math Composite Score at or below 95 were considered DD. A group of gender-, IQ-, reading-ability- and working-memory matched children who did not qualify as DD formed a control group (N = 24). The participants were recruited from the San Francisco Bay Area using advertisements in school and local newspapers, community and electronic bulletin boards, community organizations, and other public locations. Written informed consent was obtained from the children as well as their legal guardians. All protocols were approved by the human participants Institutional Review Board at the Stanford University School of Medicine. All participants were volunteers and were treated in accordance with the APA “Ethical Principles of Psychologists and Code of Conduct.”
Standardized Neuropsychological Assessments
The Child Behavior Check List (CBCL) was administered to all participants to exclude children with behaviors that are highly linked to later psychopathology (Achenbach, 1991
). Participants were administered a demographic questionnaire, the Wechsler Abbreviated Scale of Intelligence (WASI; Weschler, 1999
), Wechsler Individual Achievement Test, Second Edition (WIAT-II; Wechsler, 2001
), and Working Memory Test Battery For Children (WMTBC; Pickering and Gathercole, 2001
). WASI provided a standardized measure of full-scale IQ, while WIAT-II yielded measures of reading ability (Word Reading & Reading Comprehension Scores), and math ability (Numerical Operations, Math Reasoning Scores and derived from them Math Composite Score). A shortened version of WMTBC was also administered to obtain several measures of working memory (Digit Recall, Block Recall, Counting Recall and Backward Digit Recall subscales). For each participant, a composite working memory score was calculated by averaging standardized scores across the obtained WMTBC measures. Neuropsychological tests were administered by trained research assistants, and individual scores were validated using multiple raters.
MRI Data Acquisition
High-resolution structural images were acquired with T1-weighted spoiled grass gradient recalled (SPGR) inversion recovery 3D MRI sequence. The following parameters were used: TI = 300 ms, TR = 8.4 ms; TE = 1.8 ms; flip angle = 15°; 22 cm field of view; 132 slices in coronal plane; 256 × 192 matrix; 2 NEX, acquired resolution = 1.5 × 0.9 × 1.1 mm.
The DTI data was collected using a diffusion-weighted single-shot spin-echo, echo planar imaging sequence (TE = 70.8 ms; TR = 8.6 s; field of view = 220 mm; matrix size = 128 × 128; bandwidth = ± 110 kHz; partial k-space acquisition; 4NEX). We acquired 63 axial, 2-mm thick slices (no skip) for b = 0 and b = ∼850 s/mm2 (the latter by applying gradients along 23 noncollinear diffusion directions). Structural MRI and DTI images were acquired in the same scan session.
Voxel-Based Morphometry Analysis
Voxel-wise differences in brain anatomy were assessed using the optimized voxel-based morphometry (VBM) method described by Good et al. (2001)
. The analysis was performed using the VBM5 toolbox developed by Christian Gaser (University of Jena, Germany)
1
for Statistical Parametric Mapping Software (SPM5, Wellcome Department of Imaging Neuroscience, London, UK).
Prior to analyses, the structural images were resliced with trilinear interpolation to isotropic 1 × 1 × 1 voxels and aligned to conventional AC-PC space, using manually identified landmarks, including the anterior commissure (AC), the posterior commissure (PC) and the mid-sagittal plane.
As a part of the VBM5 pipeline, the images were spatially normalized to the Montreal Neurological Institute (MNI) common stereotactic space. Spatial transformation was nonlinear with warping regularization = 1; warp frequency cutoff = 25.
Spatially normalized images were then segmented into GM, WM, and cerebro-spinal fluid compartments, using a modified mixture model cluster analysis technique (Good et al., 2001
) with the following parameters: bias regularization = 0.0001, bias FWHM cutoff = 70 mm, sampling distance = 3, HMRF weighting = 0.3. As recommended by Gaser for children or elderly populations, we used no tissue priors for segmentation. Voxel values were modulated by the Jacobian determinants derived from the spatial normalization: areas that were expanded during warping were proportionally reduced in intensity. We used modulation for nonlinear effects only (while the warping itself included both an affine and a nonlinear component). When using modulated images for performing subsequent group comparisons, the inference is made on measures of volume rather than tissue concentration (density). The use of modulation for nonlinear but not affine effects ensures that the further statistical comparisons are made on relative (that is, while controlling for overall brain size) rather than absolute measures of volume.
The segmented modulated images for WM and GM were smoothed with an isotropic Gaussian kernel (10 mm full width at half maximum). The size of the kernel for smoothing was chosen as recommended by Gaser for modulated images, since modulation introduces additional smoothing. Between-group comparisons for GM and WM volumes were performed in SPM5 using two-sample t-tests on smoothed images. A voxelwise significance threshold of p < 0.001 (uncorrected) was used in order to facilitate comparisons with previous studies (Isaacs et al., 2001
; Rotzer et al., 2008
). Additionally, in order to integrate VBM and DTI data, we thresholded statistical comparison maps adjusting for search volume with height threshold of p < 0.01, a nonstationary cluster extent (Hayasaka et al., 2004
) threshold of p < 0.05 corrected for multiple comparisons with family-wise error (FWE) correction, and correction for non-isotropic smoothness, as implemented in VBM5 toolbox.
Regions of Interest for the Analyses of White Matter Microstructure
We used the more liberally thresholded maps (p < 0.01, and a cluster extent threshold of p < 0.05 corrected for multiple comparisons) to define GM and WM regions of interest (ROIs), as noted above. Statistical maps corresponding to group differences (TD > DD) images were thresholded, binarized and used in further analyses. They are referred to as “WM ROI” and “GM ROI” for white and grey matter comparisons, correspondingly. Specifically, the voxels where the TD group had significantly greater relative volume measurements were included in the WM ROI mask.
To examine structures that contribute to group differences in WM integrity, the WM ROI was parcellated using the white matter tractography atlas provided by Laboratory of Brain Anatomical MRI, John Hopkins University, hereafter referred to as the JHU atlas (Hua et al., 2008
).
Fractional Anisotropy Analysis
The aim of this analysis was to examine group differences in WM integrity using complementary and independent measures derived from DTI. DTI data were processed using FMRIB Software Library (Beckmann and Smith, 2004
). A diffusion tensor model was fitted on brain data after removing eddy current distortion effects and extracting brain voxels. For every voxel, FA was computed from voxel-wise tensor measures. Each subject’s FA data were then warped into a common space using nonlinear registration with FSL Nonlinear Registration Tool to FMRIB58_FA standard space image available as a part of FSL tools. To examine FA in the regions where reduced WM intensity was observed in the DD children, the mean and standard deviation of the FA values across the voxels within the WM ROI was computed for each participant. The mean FA values were scaled by corresponding standard deviations in each individual, yielding standardized within-WM-ROI FA summary measures. These FA measures were compared between the groups using a two-sample t-test.
Probabilistic Tractography Analysis
The aim of this analysis was to examine regional group differences in projection densities from the WM ROI. The primary question was whether the observed volumetric differences in GM and WM, identified by VBM analyses, can be linked via axonal pathways. Reduced projection densities in pathways linking the GM and the WM ROIs would provide evidence that the observed WM and GM structural differences between the groups reflect impairments of the same network. Probabilistic tractography was performed for each participant with FSL tools, using BEDPOST estimates of diffusion parameters, yielding connectivity distribution seeded from the WM ROI. Probtrackx algorithm draws samples from the probability distributions of fiber directions at each voxel, generating trajectories of fibers and computing the observed frequency of those that originate from the seed voxel (Behrens et al., 2003
). The resulting image describes, for each voxel in the full brain volume, the likelihood of a connection with any voxel within the seed mask, based on 5000 samples. The obtained WM ROI connectivity maps were compared across participants using a two-sample t-test as implemented in SPM, inference limited to the GM ROI in order to test our original hypothesis on relationship between the regions of reduced volume in GM and WM. The resulting maps were thresholded at height threshold of p < 0.05 and non-stationary cluster extent threshold of p < 0.05 with family-wise error (FWE) correction for multiple comparisons and correction for non-isotropic smoothness.
Deterministic Tractography
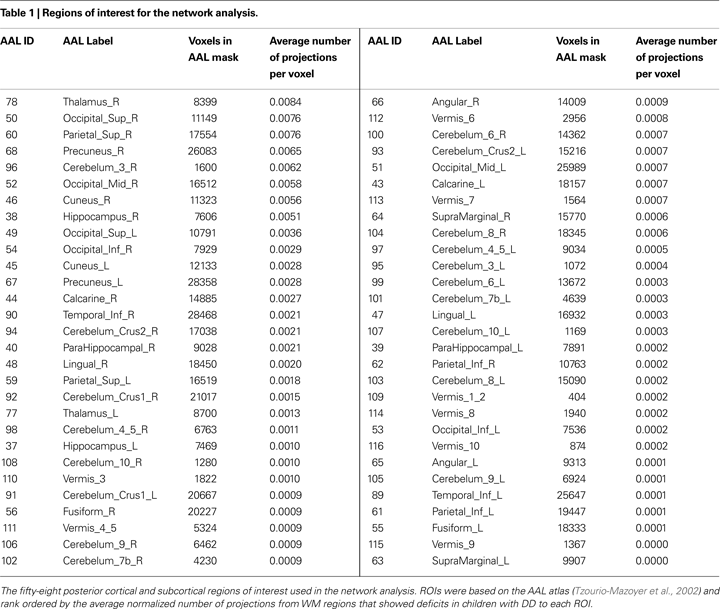
The aim of this analysis was to identify WM tracts traversing the WM ROI that showed deficits in children with DD. Fifty-eight candidate GM targets (Table 1
) were selected from 116 regions defined in Anatomical Automated Labeling (AAL) atlas (Tzourio-Mazoyer et al., 2002
). The ROIs were selected based on AAL regions that overlapped with voxels that showed VBM GM deficits in the DD group; thus, all 58 ROIs chosen were in the posterior part of the brain encompassing dorsal and ventral visual stream areas in the posterior parietal cortex, the inferior temporal cortex, and the occipital cortex, as well as the medial temporal lobe and the cerebellum. Importantly, we excluded regions such as the superior and middle temporal gyri which are typically not activated during mathematical tasks (Rivera et al., 2005
; Wu et al., 2009
). One reason for choosing such large AAL-based ROIs is to recover as many tracts linking distal brain regions as possible. DTI data were preprocessed, and tractography performed, using VISTALAB Software (Stanford University)
2
. Eddy current distortion effects were removed by determining a constrained non-rigid image registration using normalized mutual information (Bammer et al., 2002
). The six elements of the diffusion tensor were determined by multivariate regression (Basser, 1995
; Basser and Pierpaoli, 1996
). The eigenvalue decomposition of the diffusion tensor was computed. For each subject, the T2-weighted (b = 0) images were coregistered to the corresponding T1-weighted 3D anatomical images. A rigid-body transform from the native T1-weighted image space to the conventional AC-PC aligned space was computed using several manually identified landmarks, including the anterior commissure (AC), the posterior commissure (PC) and the mid-sagittal plane. The DTI data were then resampled to this AC-PC aligned space with 2 mm isotropic voxels using a spline-based tensor interpolation algorithm (Pajevic et al., 2002
), taking care to rotate the tensors to preserve their orientation with respect to the anatomy (Alexander et al., 2001
).
Whole-brain fiber tracking was performed on AC-PC aligned tensor maps. The seeds for tractography were selected from a uniform 3D grid with 1 mm step, spanning the whole brain white matter mask (only voxels that had FA > 0.25 were chosen as seeds). Multiple fiber tracts were estimated by using a deterministic streamlines tracking algorithm (Conturo et al., 1999
; Mori et al., 1999
; Basser et al., 2000
) with a fourth-order Runge–Kutta path integration method and 1-mm fixed-step size. A continuous tensor field was estimated by using trilinear interpolation of the tensor elements. Path tracing proceeded until the FA fell < 0.15 or until the angle between the current and previous path segments was >30°. Starting from the initial seed point, fibers were traced in both directions along the principal diffusion axis.
From the resulting whole-brain tracts we extracted the pathways traveling through the WM ROI. Since the tractography was performed in individual AC-PC aligned space, the WM ROI was nonlinearly warped into each individual space using SPM spatial normalization routines. Fiber pathways that did not travel through the WM ROI (minimum distance of 0.89 mm from any point of a fiber to any point within the ROI), as well as fiber tracks whose endpoints were not within the predefined 58 AAL atlas grey matter regions, were omitted from the further analysis. In the areas with high FA, the dense seeding schema often produces a significant number of duplicate pathways that are highly similar in their trajectory. Due to non-uniform spatial FA distribution, fiber pathway count has limited use as a quantitative metric comparable across brain regions and individuals. We removed redundant fibers, frequent in high FA regions, using an algorithm based on three metrics: the length of a pathway (minimum = 10.0 mm), the linear anisotropy along a pathway (minimum = 0.10), and the pairwise distance between pathways (minimum average point-to-curve distance = 2 mm, computed across portions of the pathways where these portions are at least 1 mm apart from each other). For the details on the culling algorithm, please see Zhang et al. (2003
). We argue that this procedure provides a “resampling” of fiber space, approximately representing this space in terms of fascicles with a given unit diameter of 2 mm, subject to finite volume constraint. Pathway count in this regularized space becomes roughly proportional to the cross-sectional area of a fiber group and it can be used as a measure of structural connectivity.
Network Analysis
Based on the deterministic tractography described above, we conducted exploratory classification analysis to examine whether network-level connectivity differs in children with DD and TD children. Culled pathways (2 mm-diameter “fascicles”) in each individual were first classified to 58 AAL labels according to their projection target, each pathway contributing two targets. The two projection targets for each pathway were determined by the AAL labels of pathway origin and termination points. We then performed a classification analysis with a support vector machine (SVM) algorithm using sparse logistic regression with L1 and L2 norm regularization (Ryali et al., 2009
). The number of pathways connecting each pair of ROIs was used as feature vectors and pairs of ROIs which contained no pathways in any participant were excluded. The pathway counts were transformed to z-scores to control for differences in sizes of the ROIs. A grid search was performed to find the optimal L1 and L2 norm regularization parameters to maximize 10-fold cross-validation accuracy across 50 iterations.
Behavioral Profile
Table 2
shows demographic and neuropsychological profiles of the DD and the TD groups. The two groups differed significantly on mathematical abilities as assessed by the WIAT-II, but not on IQ, age, reading ability, or working memory.
Grey Matter Volume
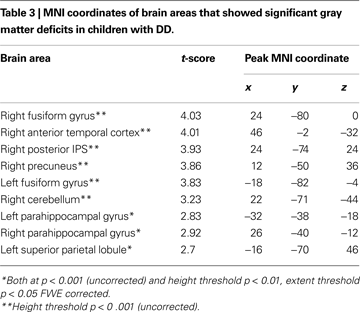
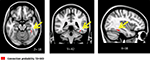
Compared to TD children, children with DD showed decreased GM volume in several posterior brain regions (Figure 1
, Table 3
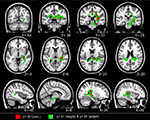
). Within the ventral visual stream, differences were found bilaterally in the cuneus/precuneus, lateral occipital cortex, lingual gyrus, and the fusiform gyrus. Within the dorsal visual stream, children with DD showed GM deficits bilaterally in the superior parietal lobule (SPL) and right posterior IPS. They also showed deficits in the medial temporal lobe, within the right entorhinal cortex and, bilaterally, within the parahippocampal gyrus, and the hippocampus. Peak differences were observed in the right fusiform gyrus (t = 4.03; MNI coordinates: 24, −80, 0), right anterior temporal cortex (t = 4.01; 46, −2, −32), right posterior IPS (t = 3.93; 24, −74, 24), the precuneus (t = 3.86; 12, −50, 36), left fusiform gyrus (t = 3.83; −18, −82, −4), left parahippocampal gyrus (t = 2.83; −32, −38, −18), right parahippocampal gyrus (t = 2.92; 26, −40, −12) and the left superior parietal lobule (t = 2.7; −16, −70, 46). Prominent GM differences were also found bilaterally in the vermis and cerebellar regions 8, 9, 10. Compared to TD children, children with DD did not show increased GM volume in any brain region.
Figure 1. Brain regions where children with DD showed significant gray matter deficits, compared to TD children (two-sample t-test results for TD > DD contrast). Red: p < 0.001; Green: height threshold p < 0.01, extent threshold p < 0.05 with family-wise error correction for multiple comparisons and correction for non-isotropic smoothness. Abbreviations: IPS = intraparietal sulcus; LOC = lateral occipital complex; MOG = medial occipital gyrus; PHG = parahippocampal gyrus; REC = right enthorinal cortex; SPL = superior parietal lobule.
White Matter Volume
Children with DD showed reduced WM in the posterior brain, primarily within WM regions adjacent to the right temporal-parietal cortex (Figure 2
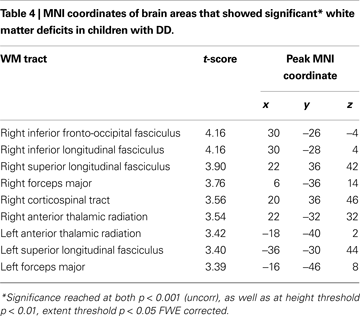
, Table 4
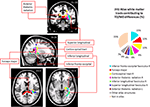
). Roughly two-thirds of the voxels within this WM region overlapped with WM tracts included in the JHU white matter tract atlas (Figure 3
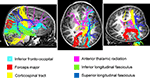
). Prominent right hemisphere WM tracts included the inferior fronto-occipital fasciculus (t = 4.16; 30, −26, −4), the forceps major of the splenium of the corpus collossum (t = 3.76; 6, −36, 14), the inferior longitudinal fasciculus (t = 4.16; 30, −28, 4), the corticospinal tract (t = 3.56; 20, 36, 46), the superior longitudinal fasciculus (t = 3.90; 22, 36, 42), and the anterior thalamic radiation (t = 3.54; 22, −32, 32), as shown in Figure 4
. In the left hemisphere, deficits were observed in the superior longitudinal fasciculus (t = 3.40; −36, −30, 44), forceps major (t = 3.39; −16, −46, 8), and the anterior thalamic radiation (t = 3.42; −18, −40, 2). No clusters showed greater WM volume in DD compared to TD children.
Figure 2. Brain regions where children with DD showed significant white matter deficits, compared to TD children (two-sample t-test results for TD > DD contrast). Red: p < 0.001; Green: height threshold p < 0.01, extent threshold p < 0.05 with family-wise error correction for multiple comparisons and correction for non-isotropic smoothness.
Figure 3. White matter tracts in brain regions where children with DD showed significant gray matter deficits, compared to TD children. Tracts were labeled using the JHU white matter atlas.
Figure 4. Streamlined reconstruction of white matter pathways passing through the right temporal-parietal regions where children with DD showed significant white matter volumetric deficits, compared to TD children. Data is from a representative TD child. Tracts labels are obtained using the probabilistic JHU white matter tractography atlas.
Fractional Anisotropy
Analysis of the region contained within the WM ROI revealed significantly reduced FA in the DD group (p = 0.009, df = 45), as shown in Figure 5
A. FA in this region was significantly correlated with Numerical Operations (r = 0.35, p = 0.007), as shown in Figure 5
B, but not the Mathematical Reasoning (r = 0.002, p = 0.50) or the Word Reading (r = 0.03, p = 0.42) subscores of the WIAT-II. FA did not correlate significantly with IQ (r = −0.18, p = 0.23) or the composite working memory score (r = −0.16, p = 0.28).
Figure 5. (A) Fractional anisotropy (FA) within right temporal-parietal regions that showed white matter deficits in DD children. FA was significantly reduced in children with DD, compared to TD children. (B) Across the two groups, FA was significantly correlated with the Numerical Operations subscore of the WIAT-II.
Probabilisitic Tractography
We used probabilistic tractography to examine structural connections linking specific seed and target regions. Seed regions consisted of voxels that showed lower WM volume in children with DD, and target regions consisted of voxels that showed lower GM in the DD group. This analysis revealed a cluster of voxels in the right inferior temporal gyrus with significantly lower projection density in the DD group, compared to TD children (Figure 6
). The peak difference was in the right fusiform gyrus (38, −42, −18). No voxels showed greater projection density in children with DD.
Figure 6. The fusiform gyrus showed significantly reduced connection probability in children with DD. Results of probabilistic tractography from right temporal-parietal WM regions that showed deficits in children with DD as seeds.
Network Analysis
We used deterministic tractography to examine cortical connectivity of the WM region that showed significant differences between TD and DD children. Whole brain tractography from, on average, 92420 seed voxels (those with FA > 0.25, of 172180 brain voxels) resulted in 43000 to 86000 fiber tracts per participants, of which 9000 to 14000 pathways were found to pass through the VBM-defined WM ROI. Fiber density regularization, performed by removing redundant fibers (see Materials and Methods), resulted in 1500 to 2300 fibers of diameter 2 mm per participant. More than 50% of these fibers originated and terminated within cortical regions in the dorsal and ventral visual stream areas identified using the AAL atlas (Table 1
). SVM-based classification analysis revealed that connectivity patterns in children with DD could be distinguished from those in TD children with a cross-validation accuracy of 70%, which is considerably higher than the 50% chance level. See Supplementary Material for visualization of brain connectivity patterns by group.
The study of developmental dyscalculia is complicated by heterogeneity with respect to severity, specificity, and extent of mathematical difficulties. Mathematical performance can be influenced by nonspecific deficits such as slow speed of processing, poor working memory, inattention, and deficits in long-term storage of arithmetic facts (Temple, 2002
). Additionally, mathematical difficulties can often be accompanied by low IQ and other cognitive deficits (von Aster and Shalev, 2007
). Our study overcomes these issues by using a carefully selected sample of children who scored within the normal range on standardized measures of IQ, reading, and working memory, but had a specific deficit in standardized measures of mathematical ability. Our multimodal structural imaging approach revealed prominent deficits in both GM and WM integrity in this well-characterized sample of young children with DD. In addition to identifying the anatomical location of GM and WM abnormalities underlying DD in young children, our data also points to WM microstructural and connectivity deficits underlying DD.
Grey Matter Deficits in Children with DD
Children with DD showed prominent GM deficits in both dorsal and ventral visual streams as well as the anterior temporal cortex. Unlike Rotzer et al. (2008)
we found no evidence for deficits in the anterior cingulate cortex, the inferior frontal gyrus and the dorsolateral prefrontal cortex, perhaps because of our use of more stringent criteria for matching the groups on IQ, working memory and reading.
The dorsal visual stream regions that showed GM deficits included most prominently the posterior aspects of the IPS and the SPL. Similar to Rotzer et al. (2008)
, we found that children with DD showed deficits in the right IPS, but we also observed differences in the adjoining SPL as well as the left IPS and left SPL. The IPS is a core parietal lobe region implicated in the development of number sense and magnitude judgment (Ansari, 2008
). Functional imaging studies have also shown that the IPS region plays a crucial role in arithmetic calculations, independent of other processing demands such as working memory (Gruber et al., 2001
; Zago and Tzourio-Mazoyer, 2002
; Delazer et al., 2003
; Rivera et al., 2005
; Wu et al., 2009
).
Children with DD also showed significant deficits in the ventral visual stream, within the medial aspects of the inferior temporal gyrus. Deficits were most prominent in the fusiform gyrus and lingual gyrus, extending anteriorly into the parahippocampal gyrus and the hippocampus. These latter regions form part of a hierarchically organized processing stream for encoding complex visual stimuli (Menon et al., 2000
). Reduced GM in the fusiform gyrus (Molko et al., 2003
) and functional deficits (Kesler et al., 2006
) have previously been reported in Turner syndrome, although it should be noted that DD is not the only cognitive deficit that exists in this syndrome. Less prominent deficits were also observed in the lateral occipital complex, a region that subserves processing of complex visual objects (Grill-Spector et al., 2008
). Convergent with our findings, an fMRI study of DD in third graders found deficits in the right parahippocampal gyrus during calculation (Kucian et al., 2006
). Critically, prominent deficits were also observed in the hippocampus and the entorhinal cortex, two regions critical for memory and learning. Previous studies on mathematical cognition in adults have not detected activation in the hippocampus even during tasks that involve learning (Ischebeck et al., 2006
, 2007
), presumably because of greater reliance on long-term neocortical memory representations. Consistent with this view, emerging evidence suggests that the hippocampus plays a greater role in facilitating learning and retrieval in children, compared to adults (Rivera et al., 2005
). Our findings provide the first evidence suggesting that medial temporal lobe deficits may contribute to DD in young children.
While previous studies have emphasized the IPS as the neural substrate most closely associated with DD (Price et al., 2007
), more recent reports have emphasized deficits in a more distributed network (Rubinsten and Henik, 2009
). Functional neuroimaging studies have consistently reported involvement of both dorsal and ventral visual streams in basic number sense (Ansari, 2008
) as well as simple and complex mental arithmetic tasks in children and adults (Zago et al., 2008
). Although initially believed to be distinct and non-overlapping streams, there is growing evidence from both numerical and non-numerical domains that these two streams interact during complex visuo-spatial processing (Konen and Kastner, 2008
). Reduced GM volume in both ventral and dorsal visuo-spatial streams may underlie difficulties in mapping visual numerical symbols to their semantic representations in children with DD (Rosenberg-Lee et al., 2009
). Finally, the novel finding of our study is the identification of right anterior temporal cortex abnormalities in DD. This result is intriguing because the known role of the anterior temporal cortex in semantic processing (Visser et al., 2009
). Functional imaging studies of number processing have generally implicated the IPS in semantic processing of numbers. Beyond this, the role of the IPS in semantic cognition of mathematical information more broadly has been less clear. Our findings suggest that the anterior temporal cortex may be an additional locus within a network of deficits that impair the ability of children with DD to develop semantic memory representations important for rapid fact retrieval.
White Matter Morphometric and Microstructure Deficits in Children with DD
VBM analysis revealed reduced WM volume in the right temporal-parietal region and the splenium of the corpus callosum. The WM region isolated in our study is significantly different from the subgenual aspects of the medial prefrontal cortex and the bilateral parahippocampal gyrus regions reported by Rotzer et al. (2008)
. A close reading of their data, however, suggests that WM differences were primarily localized to the hippocampal region, rather than the paraphippocamapal gyrus. Apart from differences in anatomical location, another key difference is that the WM differences detected in our study overlap with long association fibers in the temporal-parietal cortex, rather than along short-range U-shaped tracts that connect neighboring sulci.
Reduced WM volume can arise from either decreased myelination, which results in slower signal transfer speeds, or smaller number of axons which results in lower signal transfer capacity, causing impaired connectivity among the GM regions connected by the fiber tracts that travel through regions with lower WM volume (Dougherty et al., 2007
). To address this question, we used DTI data to examine microstructural differences within the WM cluster identified by the VBM analysis. Children with DD showed significantly reduced fractional anisotropy (FA) in this right hemisphere WM cluster. Moreover, in the combined DD and TD sample, FA was significantly correlated with the Numerical Operations but not the Mathematical Reasoning subscore of the WIAT-II, suggesting that WM deficits are primarily related to fact retrieval and computation, rather than verbal problem solving skills in young children with DD (Meyer et al., 2009
). This is consistent with the view that the ability to rapidly retrieve and perform exact calculations is a core deficit of children with DD (Jordan et al., 2003
; Fuchs et al., 2006
). Additional analyses confirmed that WM volume and FA in this region were not related to reading scores or working memory, pointing to the specificity of our findings with respect to DD. In spite of differences in FA, mean diffusivity was, however, not significantly different, suggesting that abnormalities in orientation, number and connectivity of axonal pathways rather than overall myelination may be the major source of WM deficits in children with DD (Dougherty et al., 2007
).
The prominent right hemisphere deficits observed in our study may reflect the importance of visuo-spatial processes during the initial stages of mathematical skill acquisition. Behavioral studies have reported that children with mathematical disabilities manifest problems in non-verbal tasks involving visuo-perceptual organization (Rourke, 1993
). Consistent with this view, a recent fMRI study reported weaker activation in the right parahippocampal gyrus in children with DD, compared to TD children, during an approximate calculation task (Kucian et al., 2006
). Deficits in basic number processing skills are thought to be the core abnormality in DD (Landerl et al., 2004
; Butterworth, 2005
; Jordan et al., 2009
). Although the differential contribution of the left and right PPC to basic number processing and calculation is still not well understood, the emerging literature is beginning to point to a critical role for the right IPS in number processing. Using fMRI-guided TMS in healthy adults, Cohen Kadosh et al. (2007)
found that automatic magnitude processing was impaired only during disruption of right-IPS activation clusters. Furthermore, an identical paradigm with dyscalculic participants reproduced a pattern similar to that obtained with nondyscalculic volunteers during right-IPS disruption. Consistent with these results, children with DD appear not to modulate right IPS during non-symbolic (Price et al., 2007
) and symbolic number comparison tasks (Mussolin et al., 2009
). Taken together, these findings suggest that automatic magnitude processing abnormalities within the right hemisphere temporal-parietal WM may adversely impact visuo-spatial operations crucial for numerical and mathematical cognition.
Network Analysis: Linking WM and GM Deficits
We used both deterministic and probabilistic tractography to examine WM pathways that are potentially abnormal in children with DD. Atlas-based tract mapping provided new and detailed information about the major tracts that run through the WM cluster where children with DD showed deficits. Based on the JHU atlas, we identified the inferior fronto-occipital fasciculus, the forceps major of the splenium of the corpus collossum, the inferior longitudinal fasciculus, the corticospinal tract, the superior longitudinal fasciculus, and the anterior thalamic radiation as key fiber tracts that run through this region. Deterministic tractography of DTI data confirmed that children in our age group had prominent tracts in this region. Three major projection fibers are noteworthy here based on the known functional neuronatomy of mathematical cognition (Dehaene et al., 2003
; Wu et al., 2009
) – the superior longitudinal fasciculus emanating from the parietal lobe, the inferior fronto-occipital fasciculus emanating from the occipital-parietal region and the inferior longitudinal fasciculus emanating from the occipital-temporal region (Schmahmann et al., 2007
). Together, these axonal pathways help to link the lingual, fusiform and the parahippocampal gyrus regions in the ventral visual stream with the IPS and superior parietal lobule in the dorsal visual stream. Finally, the caudal most part of the splenium of the corpus collosum which links the left and right inferior temporal gyri (Schmahmann et al., 2007
) also showed significant deficits. This result parallels our finding of both left and right GM deficits in the fusiform gyrus.
In order to relate white and grey matter abnormalities, we next compared WM tract projections from the WM to GM ROIs that showed deficits in children with DD. Differences in tract projections could not be addressed with deterministic tractography, because fiber density regularization essentially eliminates projection density information. Probabilistic tractography with seeds in the temporal-parietal WM ROI and targets in the GM ROI revealed that children with DD had significantly lower density of projections to the right fusiform gyrus in the inferior temporal cortex. This finding, together with concurrent analysis of fiber tracts emanating from the WM ROI, helps to link WM and GM deficits and point to tracts connecting the fusiform gyrus with temporal-parietal WM, most likely via the inferior longitudinal fasciculus, as a major locus of neuroanatomical abnormalities in DD. An intriguing question here is whether there are significant differences in axonal pathways linking the fusiform gyrus with the IPS, given the critical role of the latter in numerical information processing (Cohen Kadosh et al., 2007
). While probabilistic tractography is well suited for tracking medium-range fibers, its main limitation is that it produces accumulating errors when computing long-range fiber pathways, and it is currently difficult to apply distance-corrected measures of connectivity to examine potential abnormalities with connections to the posterior parietal cortex. Further studies with high-resolution diffusion spectrum imaging (Schmahmann et al., 2007
) are necessary to test the hypothesis that fibers linking the inferior temporal cortex with the posterior parietal cortex are a specific source of vulnerability in DD.
Finally, we examined whether connectivity within more extended posterior cortical and related subcortical networks is impaired in children with DD. We used a coarse-grained anatomical parcellation (Tzourio-Mazoyer et al., 2002
) and deterministic tractography to examine network-level abnormalities in WM tracts arising from the WM ROI that showed deficits in children with DD. We found strong overlap between target sites of the WM pathways and regions with reduced GM volume in the DD group. This finding provides additional evidence for links between WM and GM deficits in children with DD. Classification analysis further revealed that connectivity of fibers emanating from the WM ROI is significantly different in children with DD. The precise nature of additional potential deficits in inter-hemispheric connectivity, as well as deficits in connectivity along additional nodes of the dorsal-ventral visual pathways, and the manner in which each contributes to specific behavioral deficits in children with DD remains to be investigated (Rusconi et al., 2009
).
Previous studies of developmental disabilities have in general focused on identification of specific brain regions that may contribute to overall deficits. In most of these studies, brain regions are treated independently, and network connectivity is typically not examined. Our data suggests that analysis of deficits in network connectivity arising from macrostructural WM deficits may prove useful in explaining individual differences in number sense and calculation previously attributed to localized differences in cortical structure and function.
Conclusion
The neurobiological deficits detected in our DD group are particularly noteworthy, given that the children are closely matched to the control group in terms of age, IQ, reading ability, and working memory capacity. Our results provide strong evidence that pure DD is characterized by robust GM and WM deficits in key brain areas that have previously between implicated in mathematical cognition. Integrated analyses of brain structure using a combination of VBM and DTI provide converging evidence for deficits in the ventral and dorsal visual stream. Critically, our findings point to right hemisphere temporal-parietal WM, its microstructure and pathways associated with it, including most notably, the inferior fronto-occipital fasciculus and the inferior longitudinal fasciculus, as key anatomical correlates of DD. Our network analysis further suggests the possibility of multiple dysfunctional circuits arising from a core WM deficit, and lead to testable hypothesis that DD may, at its core, be a disconnection syndrome. We propose that, just as findings from structural neuroimaging studies of dyslexia have paved the way for targeted intervention, the current findings may eventually aid the development of remediation programs designed to enhance mathematical skills in young children with DD.
The authors declare that the research was conducted is the absence of any commercial or financial relationships that should be construed as a potential conflict of interest.
We thank Bob Dougherty, Song Zhang, Stephen Correia, Srikanth Ryali and Kaustubh Supekar for assistance with data analysis and helpful discussions. This research was funded by Stanford Bio-X postdoctoral fellowship to Elena Rykhlevskaia, a fellowship from the Children’s Health Research Program at the Lucille Packard Children’s Hospital to Lucina Q. Uddin, and by the National Institutes of Health (HD047520, HD059205) and the National Science Foundation (BCS/DRL 0449927) to Vinod Menon.
The Supplementary Material for this article can be found online at http://www.frontiersin.org/humanneuroscience/paper/10.3389/neuro.09/051.2009/